随着世界对海洋探索和研究的进一步加快,载人潜水器成为各国研制的热点。观察窗作为潜航员观察外部深海环境的重要手段,其结构安全性、密封性能和光学性能也得到大量研究。Luo等[1]根据有机玻璃材料的结构特性试验建立了有机玻璃在高应力状态下的时间、温度与应力叠加的应用方法。Wang等[2] 对于有机玻璃的粘弹性有机玻璃本构模型进行改进,对有机玻璃在温度影响下的结构特性进行建模分析。HU等[3] 在考虑温度与应变率研究的基础上,建立了有机玻璃观察窗应变率与温度耦合影响的本构模型,理论结果与试验结果吻合度较高。刘道启等[4] 提出观察窗与窗座之间的相对位移由窗体在外压下的挤压变形和观察窗随时间的蠕变变形组成,并建立有机玻璃蠕变变形的本构模型。陈薇等[5] 基于Ansys有限元模拟观察窗结构受压变形状态,根据几何光学原理建立光学偏差和光学畸变计算的理论方法,可以预测深海耐压结构观察窗的光学性能。
制造观察窗的材料主要有玻璃、熔凝石英和有机玻璃(丙烯酸塑料)。有机玻璃相比于其他材料,具有材料再现性好,弹性模量低,允许局部屈服和应力重新分配,以及破坏前有征兆等特点,得到了广泛使用。观察窗的结构形式主要有平圆形、锥台形和球扇形。锥台形相比于其他形式,具有承压能力高,窗座外形小,视野良好的特点,成为载人潜水器观察窗的首选。国内近年研制的“蛟龙”号、“深海勇士”号和“奋斗者”号载人潜水器,全部采用锥台形有机玻璃观察窗结构。然而,随着潜水器深度的不断增加,通过耐压试验发现,锥台形观察窗小端在超高压环境挤压下与窗座端的变形不协调,容易形成银纹甚至裂口,存在安全隐患。
目前,对观察窗局部结构特性分析主要采用有限元方法,由于观察窗与窗体摩擦系数的选取上存在不确定性,导致计算结果失去准确性。观察窗与窗体摩擦系数与窗体粗糙度、润滑油涂抹情况以及安装预紧力有关。本文通过建立有限元计算方法,并依据观察窗有机玻璃的耐压试验数据,修正了摩擦系数,完成了锥台形观察窗有机玻璃结构特性的分析和参数化研究,形成了锥台形观察窗的优化设计。
1 观察窗有机玻璃有限元分析方法观察窗有机玻璃的有限元分析需要考虑有机玻璃的黏弹性特点以及玻璃与窗座的接触分析,因而需要选择合适的黏弹性力学模型和接触力学模型。
1.1 黏弹性力学模型在数值计算中,通过无量纲的松弛模型作Prony级数展开来定义材料的黏弹性力学模型,其切变模量可以表示为:
| $ {g}_{R}\left(t\right)=1-\sum _{i=1}^{n}{g}_{i}^{-P}\left(1-{e}^{-t/{\tau }_{i}^{G}}\right)。$ | (1) |
其中:
对于体积模量作Prony级数展开,可以获得相同的数学形式:
| $ {k}_{R}\left(t\right)=1-\sum _{i=1}^{n}{k}_{i}^{-P}\left(1-{e}^{-t/{\tau }_{i}^{K}}\right)。$ | (2) |
假设:
| $ {\tau }_{i}^{G}={\tau }_{i}^{K}={\tau }_{i},$ | (3) |
无量纲瞬时模量、瞬时模量与初始模量的关系为:
| $ {G}_{R}(\mathrm{t})={G}_{0}{g}_{R}(t),$ | (4) |
| $ {K}_{R}(\mathrm{t})={K}_{0}{k}_{R}(t) ,$ | (5) |
在弹性范围内,泊松比和弹性模量与体积模量和切变模量的关系为:
| $ \left\{\begin{aligned}K=E/3(1-2\mu ),\\ G=E/2(1+\mu )。\end{aligned}\right. $ | (6) |
选择Kinematic接触力学模型,即对于主接触面
| $ \left\|{p}_{c}-{p}_{s}\right\|=\underset{{{P}_{s}ϵ\mathrm{\Gamma }}_{s}}{\mathrm{min}}\left\|{}^{t}{P}_{c}-{}^{t}{P}_{s}\right\|。$ | (7) |
该式为非线性方程,可以通过牛顿-拉菲生方法求解。在
| $ {}^{t+\mathrm{\Delta }\mathrm{t}}G(P)=\left[{}^{t+\mathrm{\Delta }\mathrm{t}}{P}_{c}-{}^{t+\mathrm{\Delta }\mathrm{t}}{P}_{s}\right]\cdot {}^{t+\mathrm{\Delta }\mathrm{t}}N\geqslant 0。$ | (8) |
线性表达式为:
| $ {}^{t+\mathrm{\Delta }\mathrm{t}}G(P)={}^{t}G(P)+\left[\Delta {}^{t}u({P}_{c})-\Delta {}^{t}u({P}_{s})\right]\cdot {}^{t}N\geqslant 0。$ | (9) |
式中:
根据Koulomb 准则,总摩擦力与粘连接触及滑动接触相关,即
| $ f=\left\{\begin{aligned} &\alpha {f}_{s}'\text{,}粘连接触,\\ &{f}_{s}'\text{,}滑动接触。\end{aligned}\right. $ | (10) |
式中:
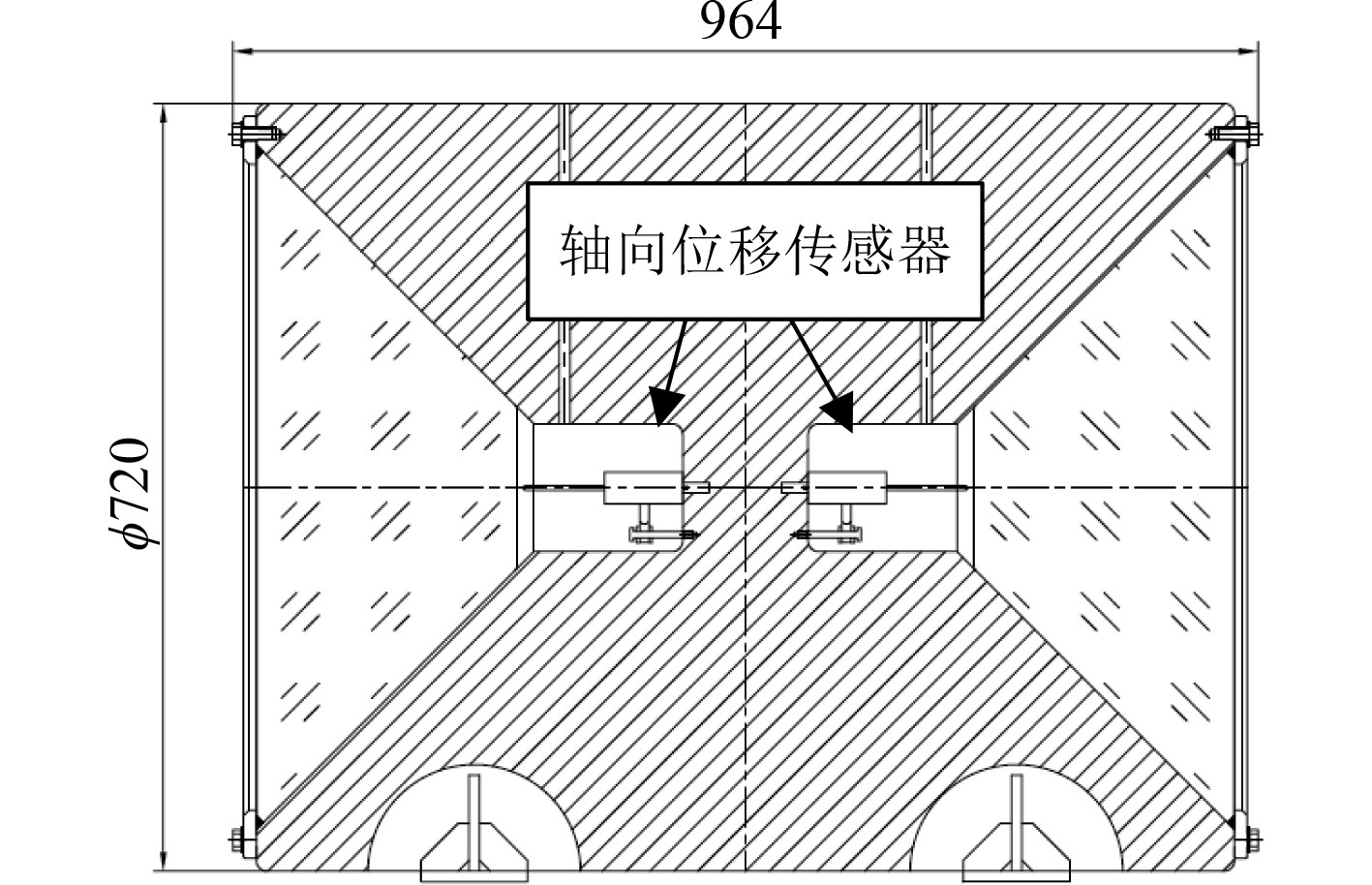
为获取相同窗座粗糙度、润滑油涂抹情况以及安装预紧的观察窗摩擦系数,根据ASME PVHO-1-2016[6] 设计锥台形观察窗的耐压试验模型,如图1所示。试验模型,由2块相同的锥台形观察窗背靠背安装,试验的最大静水压力为90 MPa,玻璃窗主要设计参数由文献[6]计算得到。试验主要采集观察窗小端处轴向滑移量和内外表面应变。有机玻璃为聚甲基丙烯酸甲酯材质,有机玻璃及窗座材料性能如表1所示。
|
图 1 锥台形观察窗耐压试验模型 Fig. 1 Pressure test model of observation window |
|
|
表 1 有机玻璃及窗座材料性能 Tab.1 Properties of Plexiglas and window seat material |
建立锥台形观察窗耐压试验有限元模型如图2所示。在有限元程序Ansys中设置黏弹性力学模型模拟有机玻璃结构的松弛变形特征,并选择接触单元,模拟窗座与有机玻璃之间力和位移的传递。摩擦系数为0.1时位移变形结果如图3所示。

|
图 2 有限元模型 Fig. 2 Finite element model |

|
图 3 位移计算结果 Fig. 3 Displacement calculation results |
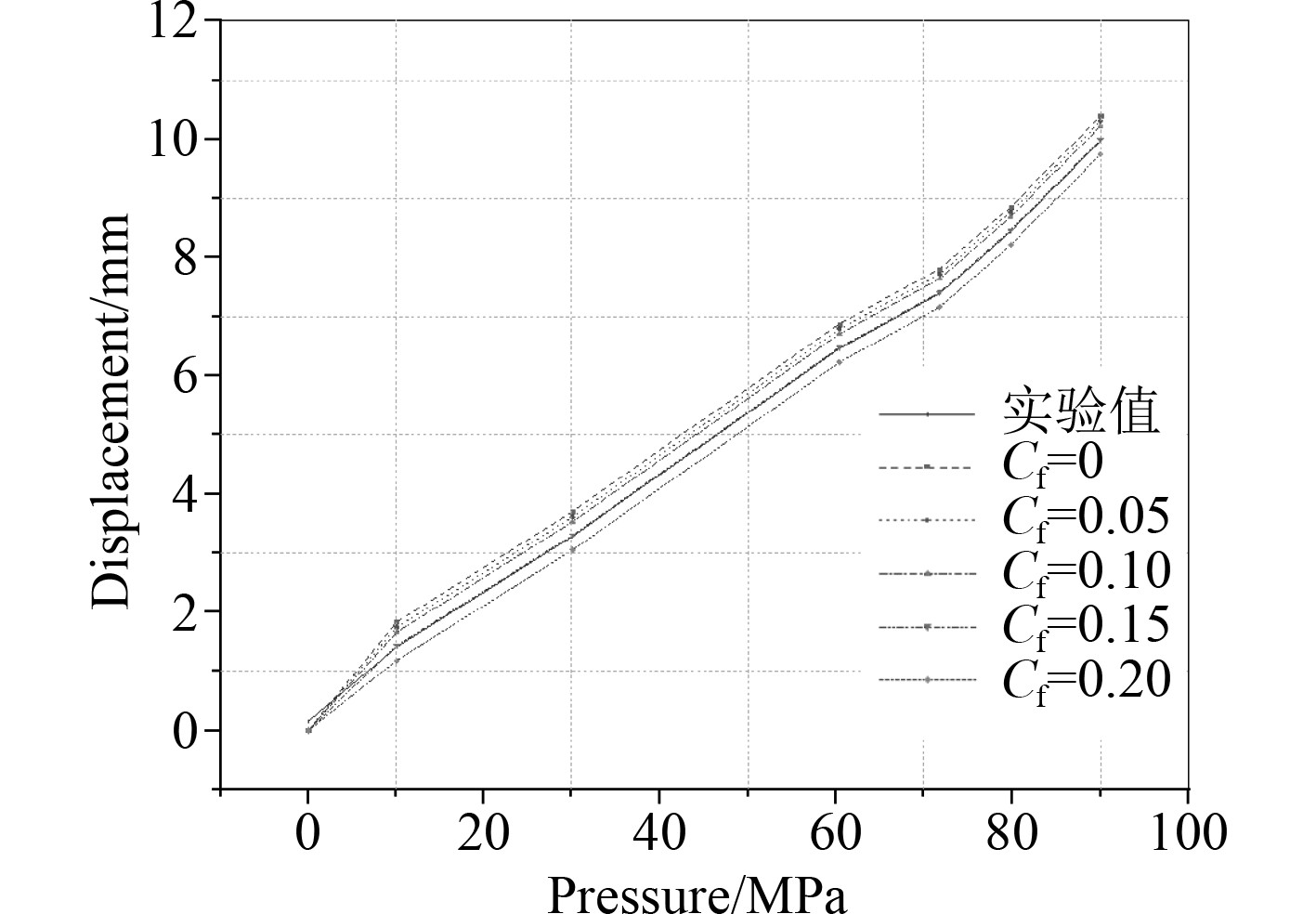
在初步假定摩擦系数为0.00,0.05,0.10,0.15,0.20时,分别进行有限元分析,并提取0~90 MPa压力下玻璃窗小端轴向滑移动量,与试验结果进行比较,如图4所示。
|
图 4 轴向滑移量试验值与有限元计算值比较 Fig. 4 Comparison of axial slippage between experimental value and FEMs |
可知,有限元计算结果与试验结果趋势一致,说明选择黏弹性力学模型和接触力学模型的有限元方法能够用来分析观察窗有机玻璃结构特性。在摩擦系数为0.15时,有限元结果与试验结果最为接近,根据线性差值,窗座与观察窗的摩擦系数为0.153比较合理。
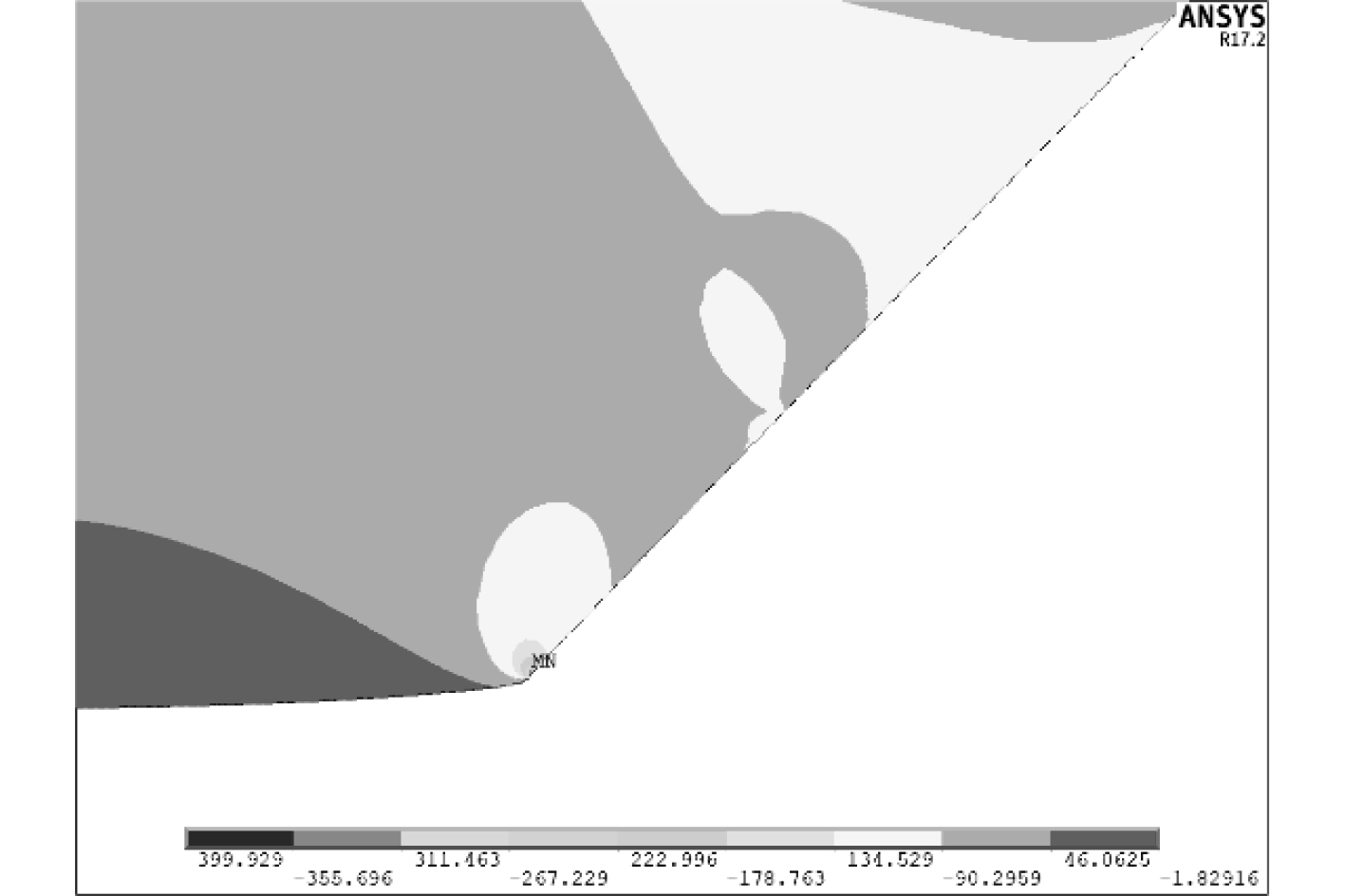
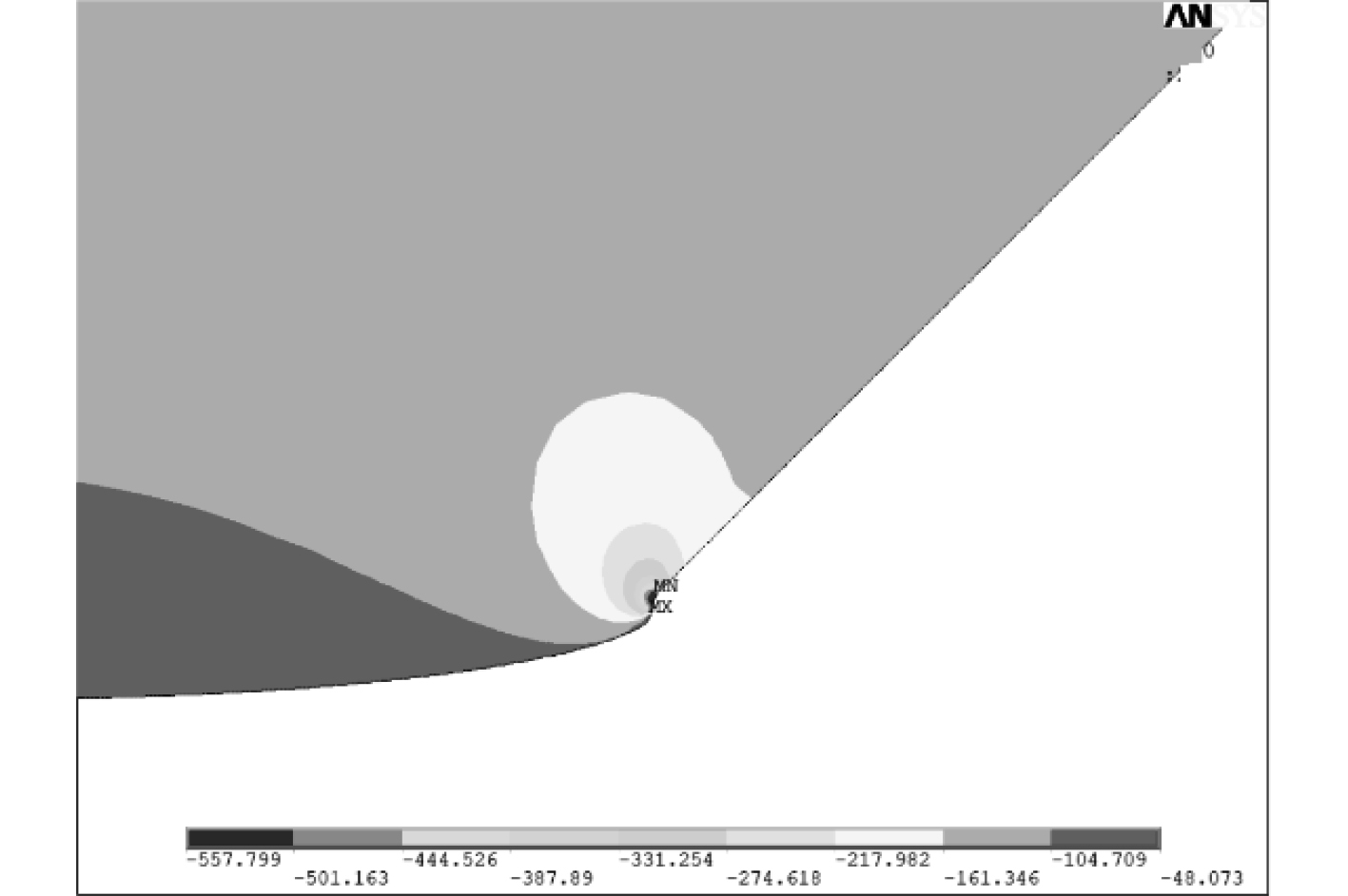
3 参数化研究及优化设计采用本文的有限元方法(摩擦系数设置为0.153),对某型潜水器观察窗和此次耐压试验模型观察窗的结构特性进行对比分析(见图5和图6),根据试验和计算结果可知:某型潜水器观察窗的最大等效应力为399 MPa,位于观察窗小端与窗座接触处,且观察窗能够承受静水外压考核,外观完好;耐压试验模型观察窗最大等效应力为557 MPa,同样位于观察窗小端与窗座接触处,耐压试验后,观察窗小端外缘出现环向损伤。由此可以判断,小端最大等效应力过大是造成耐压试验模型的观察窗损伤的主要原因,需要对窗座夹角和小端倒角半径进行参数化研究(见图7),使得小端最大等效应力低于某型潜水器观察窗最大等效应力的水平。
|
图 5 某型潜水器观察窗最大等效应力 Fig. 5 Maximum equivalent stress of a certain type of observation window |
|
图 6 耐压试验模型观察窗最大等效应力 Fig. 6 Maximum equivalent stress of test bservation window |
|
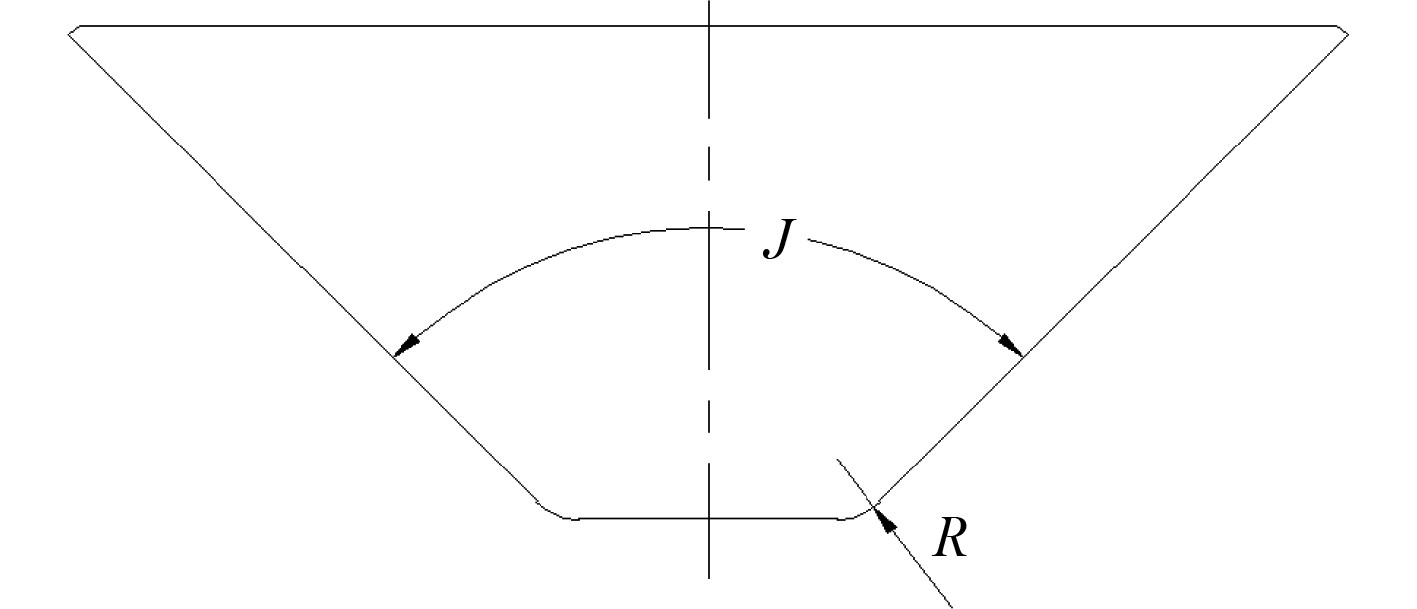
图 7 观察窗优化参数 Fig. 7 Optimization parameters of observation window |
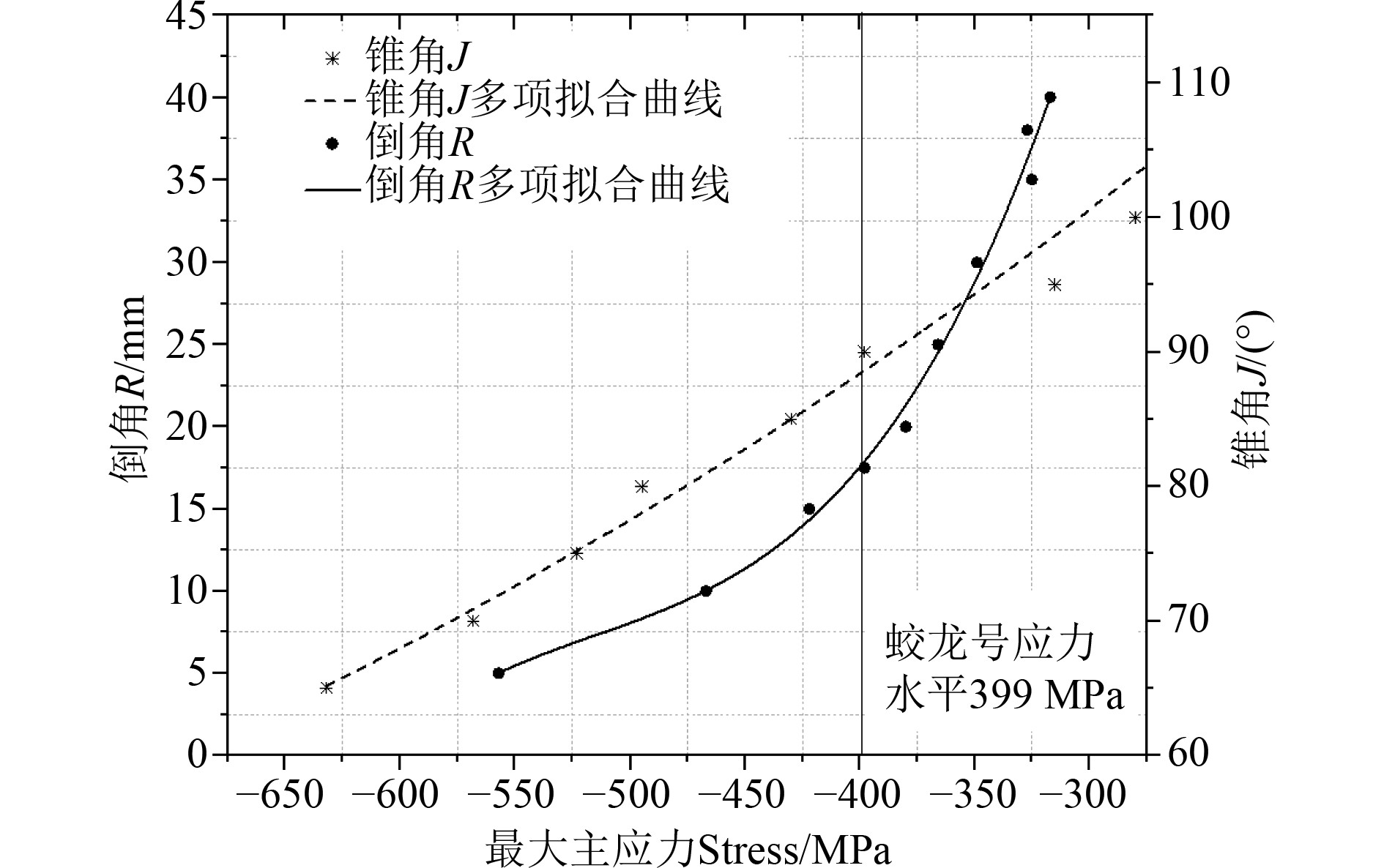
由图8可知,最大等效应力随着倒角R的增加而降低,当R等于17.5 mm时,观察窗的最大等效应力为394 MPa,低于某型观察窗的最大等效应力399 MPa,观察窗的局部应力处于安全状态,不会造成小端挤压裂开。虽然倒角R的增加会缓解小端的应力集中,但也会造成观察窗视野受限,因而将倒角R取17.5 mm比较合理。同样,最大等效应力随着锥角J的增加而降低,当锥角J=90°时,观察窗的最大等效应力为395 MPa,处于安全状态。锥角J的增加会造成观察窗过于庞大,影响外部线型和结构重量的增加,因而锥角J取90°比较合理。
|
图 8 最大等效应力与倒角和锥角的关系 Fig. 8 Relationship between maximum equivalent stress and chamfer and taper angle |
通过上述研究,本文得到以下结论:
1)建立考虑玻璃窗黏弹性力学模型和接触力学模型的有限元方法,并通过试验修正观察窗与窗座的摩擦系数,能够准确进行观察窗有机玻璃的结构应力、变形分析。
2)锥台形观察窗在耐压试验中出现小端外缘损伤的现象,主要是由观察窗向内滑移时,窗体小端与窗座挤压,局部应力过大造成。
3)最大等效应力分别随着倒角R和锥角J的增加而降低,通过优化倒角R和锥角J设计参数,将观察窗计算的等效应力降至399 MPa以内,可避免观察窗小端外缘出现损伤。
| [1] |
LUO Wenbo, WANG Chuhong, ZHAO Rongguo. Application of time-temperature-stress superposition principle to nonlinear creep of poly(methyl methacrylate)[J]. Key Engineering Materials, 2007, 340−341: 1091-1096. DOI:10.4028/www.scientific.net/KEM.340-341.1091 |
| [2] |
WANG Fang, WANG Wuwu, ZHANG Yongkuang, et al. Effect of temperature and nonlinearity of PMMA material in the design of observation windows for a full ocean depth manned submersible[J]. Marine Technology Society Journal, 2019, 53(1): 27-36. DOI:10.4031/MTSJ.53.1.4 |
| [3] |
HU Wenjun, GUO Hui, CHEN Yongmei, et al. Experimental investigation and modeling of the rate dependent deformation behavior of PMMA at different temperatures[J]. European Polymer Journal, 2016, 85: 313-323. DOI:10.1016/j.eurpolymj.2016.10.036 |
| [4] |
刘道启, 胡勇, 王芳, 等. 载人潜水器观察窗的力学性能[J]. 船舶力学, 2010, 14(7): 782-788. LIU Daoqi, HU Yong, WANG Fang, et al. Creep property of observation window on manned deep-sea submersible[J]. Journal of Ship Mechanics, 2010, 14(7): 782-788. DOI:10.3969/j.issn.1007-7294.2010.07.011 |
| [5] |
陈薇, 张爱锋. 基于ANSYS的锥台形观察窗光学性能分析[J]. 船舶力学, 2019, 23(10): 1221−1228. CHEN Wei, ZHANG Ai-feng Analysis on optical performance of conical viewport windows based on ANSYS[J]. Journal of Ship Mechanics, 2019, 23(10): 1221−1228. |
| [6] |
ASME. Safety standard for pressure vessels for human occupancy: ASME PVHO -1-2016[S]. 2016.
|
 2022, Vol. 44
2022, Vol. 44
