0 引　言

操纵性是潜器的重要性能之一，对保证作业的顺利完成具有重要意义，操纵性主要包括运动稳定性、机动性和惯性特性，潜器具有良好的操纵性，既能方便、稳定地保持航向、深度和航速，又能迅速改变航向、深度和航速，准确地执行各种机动^[1]。操纵性运动预报最有效的方法是操纵运动仿真^[2]。目前，对操纵性进行评估是通过时域的数值结算对基于以水动力系数表达力（力矩）的水动力模型进行评估，数学模型和水动力系数尤为重要^[3]。

Debabrata Sen^[4]最先提出水动力系数敏感性指数的概念，为简化潜器六自由度模型。以操纵性指标对潜器的运动模型进行简化。对潜器敏感性指数研究不多，多数着重于研究最大影响变量。刘杨^[5]采用分离型MMG建模思想建立船舶在静水中考虑横倾的四自由度操纵运动模型为基础，应用水动力系数敏感性指数分析方法。王卓等^[6]、李浪涛等^[7]对潜器在运动过程产生的水动力展开分析，得到水平面内潜器的水平面操纵运动模型。在水动力系数的敏感性研究中，在水面舰船的研究中取得了广泛的应用，但在船舶的操纵运动影响参数研究较少^[8-9]。

水动力敏感性指数是一种从操纵性评估指标对潜器水动力模型进行评估的方法。建立潜器的六自由度运动模型，在对回转运动进行仿真的基础上进行水动力系数敏感性分析，除分析其稳态值回转直径的变化，对水动力系数影响横倾角、纵倾角的变化进行分析。为潜器六自由度操纵性方程的简化、舵设计提供指导。

1 六自由度方程

由刚体动力学理论，潜器在水下受到的外力和刚体的运动参数六自由度运动数学模型如下：

轴向力方程

$\begin{split} m(\dot u - vr + wq) =& \frac{1}{2}\rho {L^4}(X'pp{p^2} + X'qq{q^2} + X'rr{r^2} + X'prpr)+\\ & \frac{1}{2}\rho {L^3}(X'\dot u\dot u + X'wqwq + X'vpvp +\\ & X'wqvr + X'q\delta suq\delta s + X'q\delta rur\delta r)+\\ & \frac{1}{2}\rho {L^2}(X'vv{v^2} + X'www{w^2} + X'v\delta ruv\delta r + \\ & X'w\delta suw\delta s)+ \frac{1}{2}\rho {L^2}{u^2}(X'\delta r\delta r{u^2}\delta {r^2} +\\ & X'\delta s\delta s{u^2}\delta {s^2})+ \frac{1}{2}\rho {L^2}({a_T}{u^2} + {b_T}u{u_c} + \\ & {c_T}{u_c}^2)- (P - B){\rm{sin}}\theta，\\[-10pt] \end{split} $

(1)

侧向力方程

$ \begin{split} m(\dot v - wp + ur) =& \frac{1}{2}\rho {L^4}(Y'\dot p\dot p + Y'\dot r\dot r + Y'pqpq + Y'qrqr)+ \\ & \frac{1}{2}\rho {L^3}(Y'\dot v\dot v + Y'pup + Y'rur +\\ & Y'vqvq + Y'wpwp + Y'wrwr) + \\ & \frac{1}{2}\rho {L^2}(Y'vuv + Y'vwvw + Y'\delta r{u^2}\delta r)- \\ & (W - B){\rm{sin}}\phi {\rm{cos}} \theta ，\\[-10pt] \end{split} $

(2)

垂向力方程

$ \begin{split} m(\dot w - uq + vp) =& \frac{1}{2}\rho {L^4}(Z'\dot q\dot q + Z'pp{p^2} + Z'rr{r^2} + Z'prpr)+ \\ & \frac{1}{2}\rho {L^3}(Z'\dot w\dot w + Z'quq + Z'vpvp + Z'vrvr)+ \\ & \frac{1}{2}\rho {L^2}(Z'wuw + Z'vv{v^2} + Z'\delta s{u^2}\delta s) + \\ & (P - B){\rm{cos}}\theta \cos \varphi，\\[-10pt] \end{split} $

(3)

横摇力矩方程

$ \begin{split} {I_{xx}}\dot p + ({I_{zz}} - {I_{yy}})qr =& \frac{1}{2}\rho {L^5}(K'\dot p\dot p + K'\dot rK_{\dot r}'\dot r + K'qrqr +\\ & K'pqpq) + \frac{1}{2}\rho {L^4}(K'\dot v\dot v + K'pup + \\ & K'rur + K'vqvq + K'wpwp + K'wrwr) + \\ & \frac{1}{2}\rho {L^3}(K'vuv + K'vwvw)- \\ & {y_B}B\cos \theta \cos \phi + {z_B}B\cos \theta \sin \phi ，\\ \end{split} $

(4)

纵倾力矩方程

$ \begin{split} {I_{yy}}\dot p + ({I_{xx}} - {I_{zz}})rp = & \frac{1}{2}\rho {L^5}(M'\dot q\dot q + M'pp{p^2} + M'rr{r^2} + \\ & M'rprp) + \frac{1}{2}\rho {L^4}(M'\dot w\dot w + \\ & M'uquq + M'vpvp + M'vrvr)+ \\ & \frac{1}{2}\rho {L^3}(M'uwuw + M'vv{v^2} + M'\delta s{u^2}\delta s) + \\ & {x_B}B\cos \theta \cos \phi + {z_B}B\sin \theta ，\\ \end{split} $

(5)

偏航力矩方程

$ \begin{split} {I_{xx}}\dot r + ({I_{yy}} - {I_{zz}})rp = &\frac{1}{2}\rho {L^5}(N'\dot r\dot r + N'\dot p\dot p + N'pqpq + N'qrqr) + \\ & \frac{1}{2}\rho {L^4}(N'\dot v\dot v + N'pup + N'rur +\\ & N'vqvq + N'wpwp + N'wrwr)+ \\ & \frac{1}{2}\rho {L^3}(N'vuv + N'vwvw + N'\delta r{u^2}\delta r)- \\ &{x_B}B\cos \theta \sin \phi - {y_B}B\sin \theta。\end{split} $

(6)

辅助方程，运动关系式：

$\left\{ \begin{split} &\dot \xi = u\cos \psi \cos \theta + v(\cos\psi \sin\theta \sin\varphi - \sin\psi \cos\varphi ) + \\ &\quad\quad w(\cos\psi \sin\theta \cos\varphi + \sin\psi \sin\varphi ) ，\\ &\dot \eta = u\sin \psi \cos \theta + v(\sin\psi \sin\theta \sin\varphi + \cos \psi \cos\varphi ) + \\ &\quad\quad w(\sin\psi \sin\theta \cos\varphi - \cos \psi \sin\varphi )，\\ &\dot \varsigma = - u\sin \theta + v\cos\theta \sin\varphi + w\cos\theta \cos\varphi，\\ &\dot \varphi = p + q\tan \theta \sin \varphi + r\tan \theta \cos \varphi，\\ &\dot \theta = q\cos \varphi - r\sin\varphi，\\ &\dot \psi = q\sin \varphi /\cos \theta + r\cos \varphi /\cos \theta。\\ \end{split} \right. $

(7)

将其整理为：

$ \left[ {\begin{array}{*{20}{c}} {{a_1}}&0&0&0&{{a_2}}&{{a_3}} \\ 0&{{a_4}}&0&{{a_5}}&0&{{a_6}} \\ 0&0&{{a_7}}&{{a_8}}&{{a_9}}&0 \\ 0&{{a_{10}}}&{{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}} \\ {{a_{15}}}&0&{{a_{16}}}&{{a_{17}}}&{{a_{18}}}&{{a_{19}}} \\ {{a_{20}}}&{{a_{21}}}&0&{{a_{22}}}&{{a_{23}}}&{{a_{24}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot u} \\ {\dot v} \\ {\dot w} \\ {\dot p} \\ {\dot q} \\ {\dot r} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_1}} \\ {{f_2}} \\ {{f_3}} \\ {{f_4}} \\ {{f_5}} \\ {{f_6}} \end{array}} \right] 。$

(8)

从方程中可以看出，水动力系数是描述潜器操纵运动方程特征的重要参数，当潜器的外形设计确认后，可以通过经验公式估算、数值模拟和水池试验获取水动力系数。可以说当模型结构、主尺度确定后，潜器的水动力系数也随之确定，确定了到操纵性参数的映射关系。运动方程中的水动力系数变化会引起操纵性参数变化，对回转运动、横倾纵倾等产生影响。

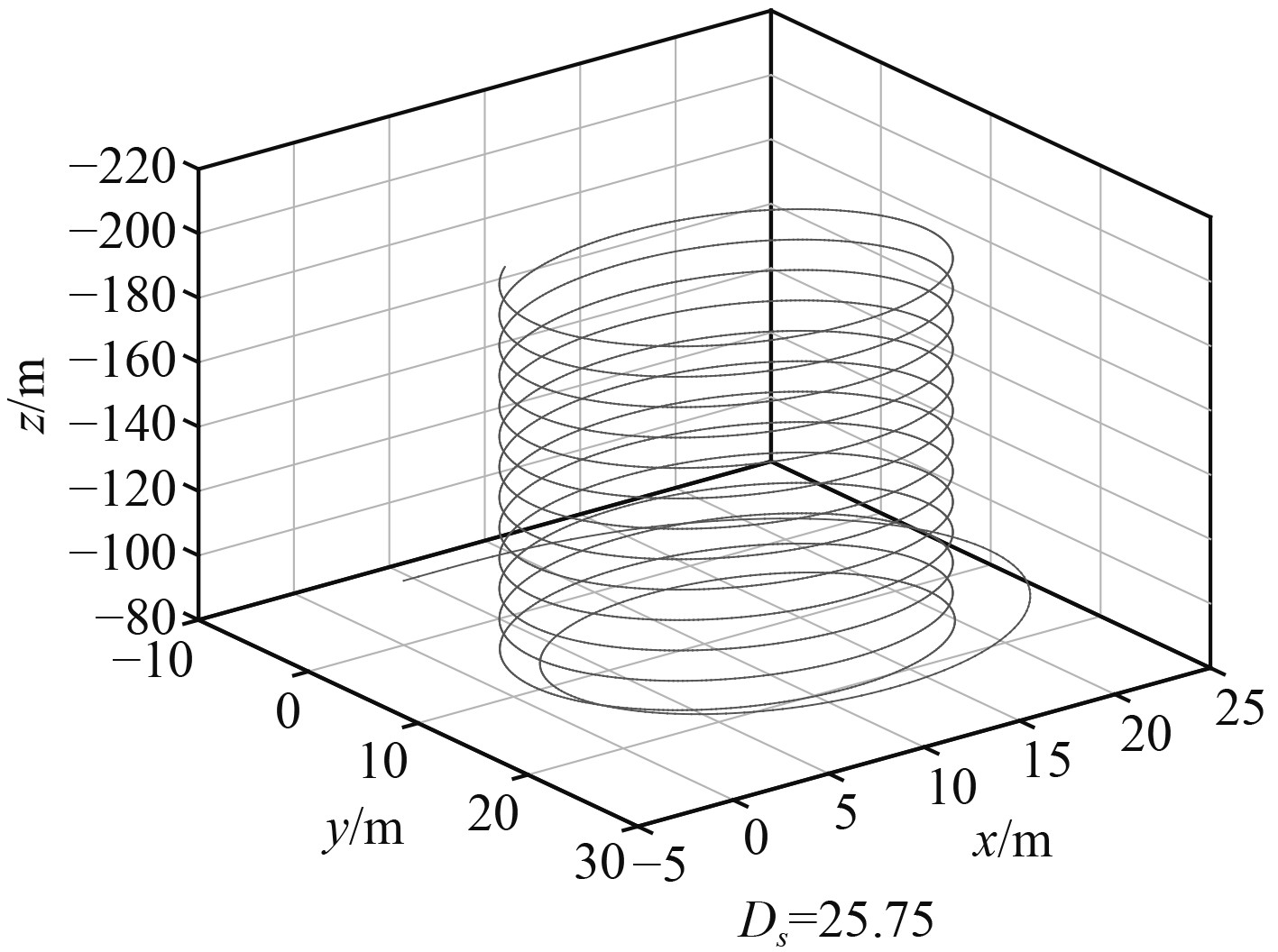
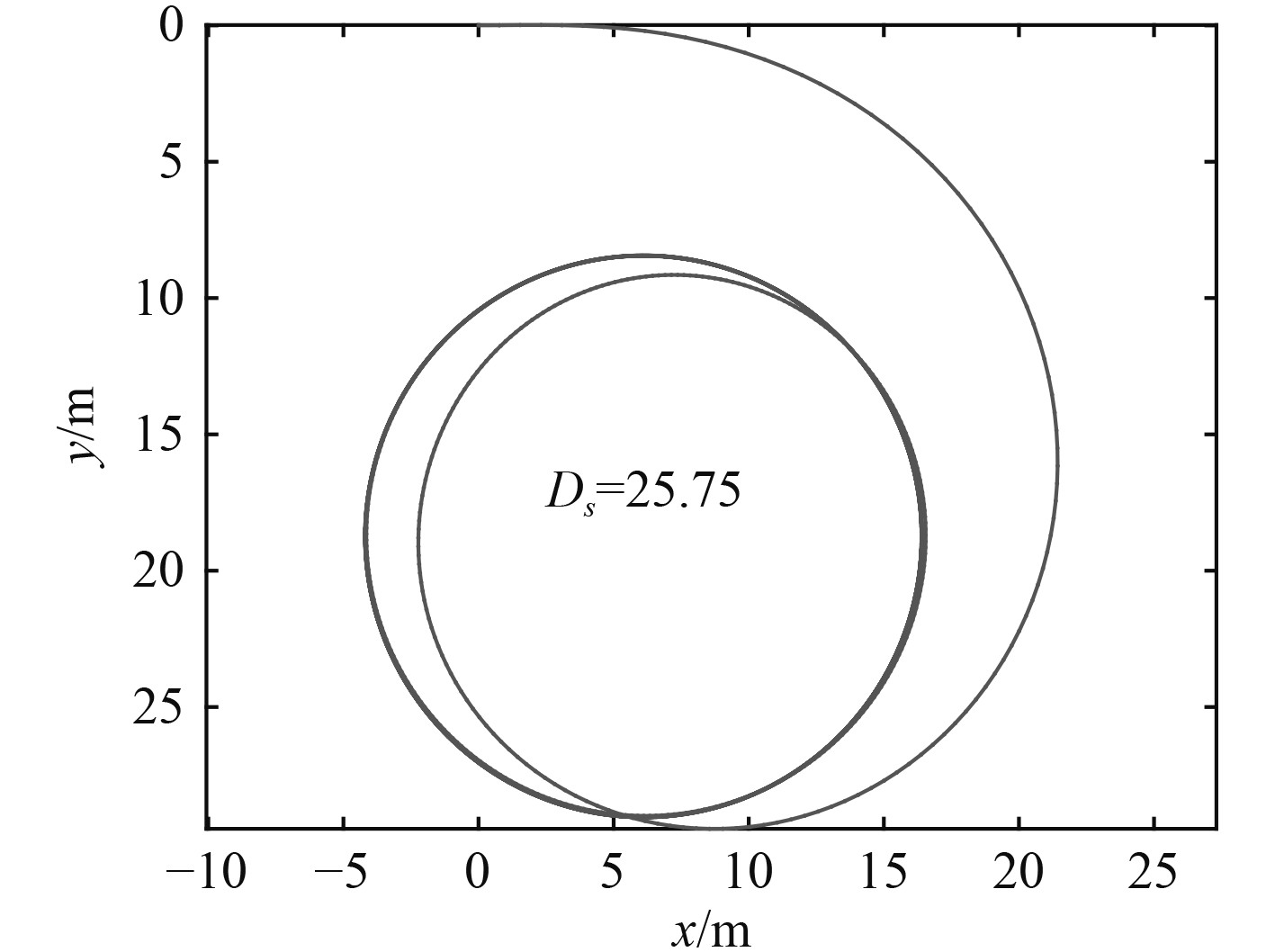
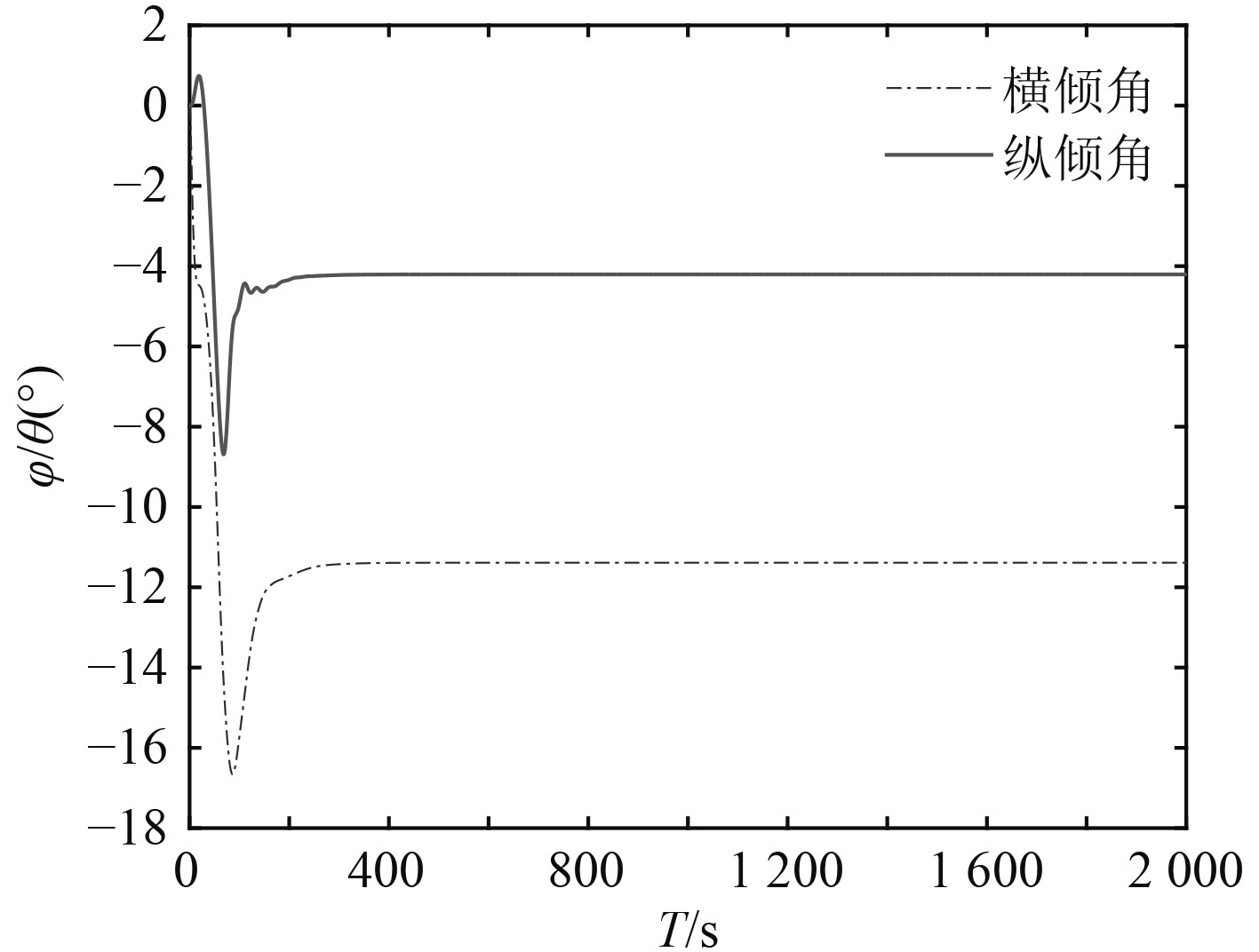
在建立操纵运动方程后，将其进行整理。运用四阶龙格-库塔法进行数值计算，可得到运动参数及运动轨迹。经验证分析大舵角下变化趋势较为明显，选潜器3 kn舵角30°回转轨迹、横倾角和纵倾角示意图。

2 水动力敏感性指数

潜器的操纵运动预报是以水动力系数表达的方程为基础，方程中的水动力系数经过无因次化通常认为是常数。潜器的水动力性能取决于流体动力布局和外形设计，以水动力系数单一变量，分析各水动力系数对操纵参数的影响，确定流体动力布局中的各因素对操纵规律的影响程度，简化操纵运动方程，从而指导潜器的外形设计和流体动力布局，指导外形设计。

为量化水动力系数和操纵运动参数间的关系，引入水动力敏感性指数S，其定义如下：

$ S = \frac{{{\rm{d}}(R/R*)}}{{{\rm{d}}(H/H*)}} = \frac{{\Delta R/R*}}{{\Delta H/H*}} = \frac{{(R - R*)/R*}}{{(H - H*)/H*}}。$

(9)

式中：R为操纵性参数，如定常回转直径，纵倾角，横倾角等；带*表示基准的水动力系数和对应的操纵性系数，无*表示变化后的水动力系数和对应的操纵性系数。

3 敏感性系数计算

根据潜器操纵运动方程和水动力敏感性指数，以单一水动力系数变化为输入量，记录潜器运动过程中的变量，如回转直径、横倾角和纵倾角等潜器稳定航行后的状态量。将水动力系数按照加速度系数，（角）速度系数，舵角系数和其他系数分类，进行数据处理分析。

3.1 加速度系数

潜器做线加速、角加速运动受到的流体动力，由于其粘性力远小于惯性力，可将其简化为流体惯性力。水动力系数中的加速度系数可以简化为运动过程中的附加质量，加速度系数与附加质量间的关系如下式：

$ \begin{split} &X\dot{u}=\lambda_{11}，Y\dot{v}=-\lambda_{22}，Z\dot{w}=-\lambda_{33}，Y\dot{r}=N\dot{v}=-\lambda_{26}\\ &Z\dot{q}=M\dot{w}=-\lambda_{35}，M\dot{q}=-\lambda_{55}，N\dot{r}=-\lambda_{66}。\end{split} $

(10)

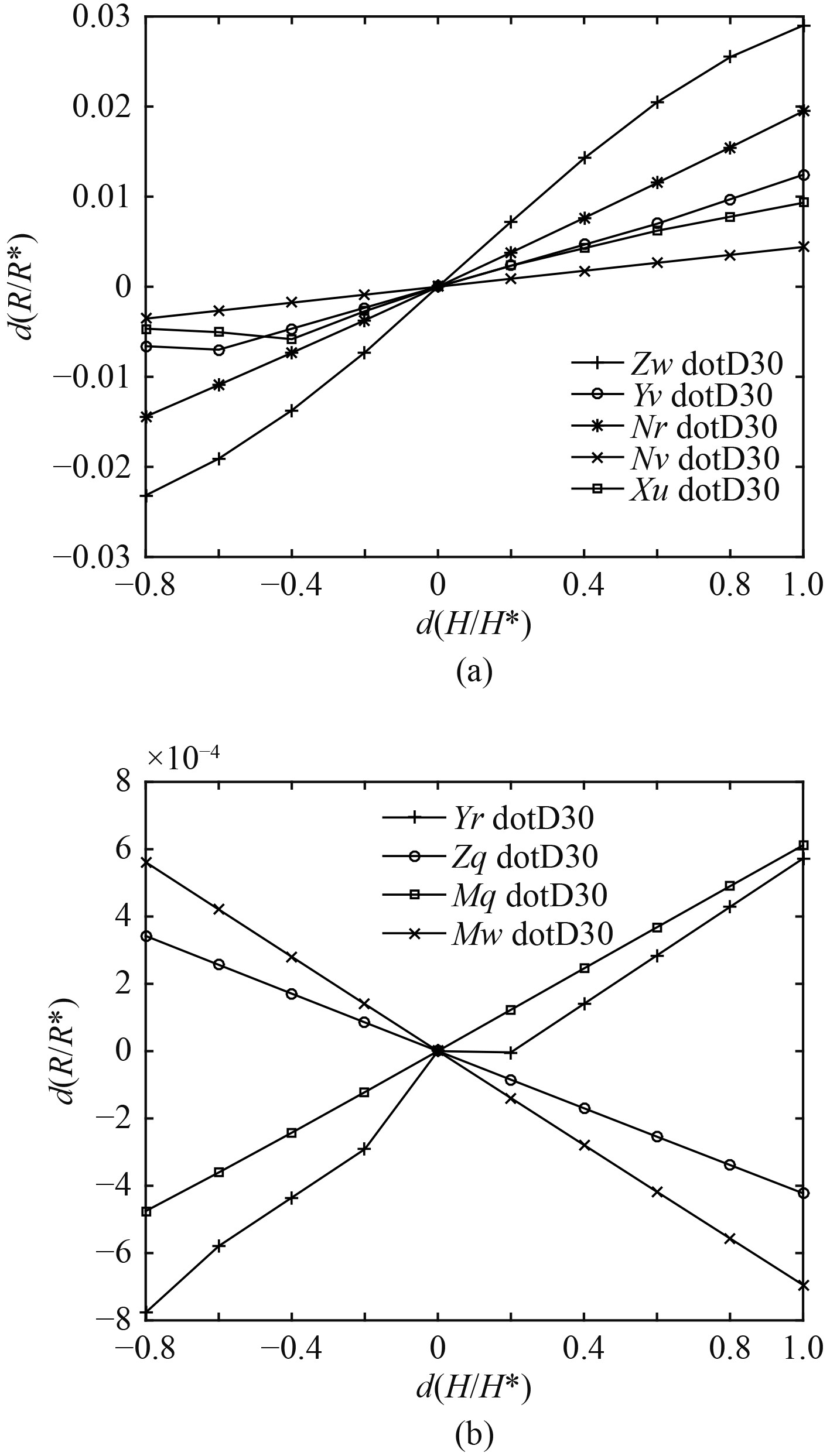
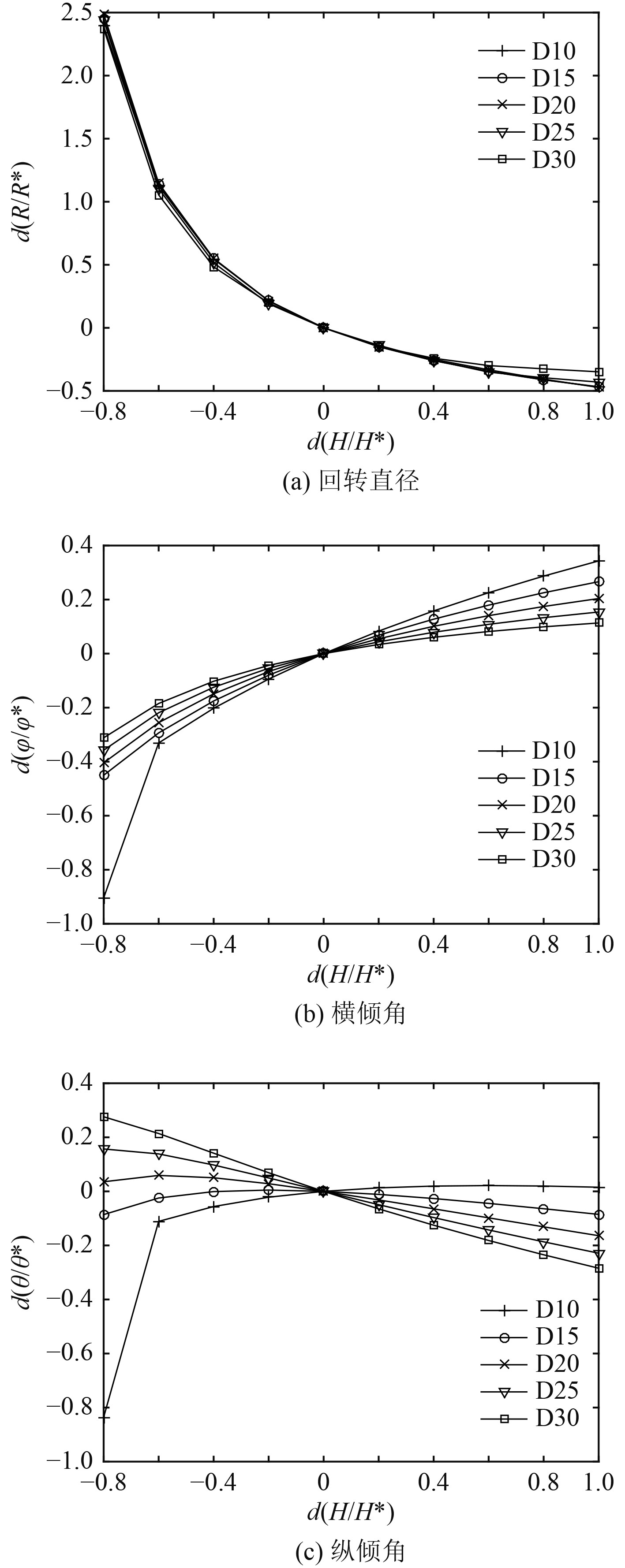
在30°舵角下，操纵性参数（回转半径）随水动力系数变化量如图5所示。

回转半径在大舵角下变化明显，小舵角下无明显变化，且纵倾角和横倾角不会随附加质量系数的变化而变化；加速度系数 $ Z'\dot w $ ， $ Y'\dot v $ ， $ N'\dot r $ ， $ N'\dot v $ ， $ X'\dot u $ 敏感性较大，当加速度系数变为原来2倍时，其回转半径变化最大为3%（见图5（a））；加速度系数 $ Y'\dot r $ ， $ Z'\dot q $ ， $ M'\dot q $ ， $ M'\dot w $ 敏感性较小，当加速度系数为原来2倍时，其回转半径变化最大为0.08%（见图5（b））；加速度系数 $ Y'\dot p $ ， $ K'\dot p $ ， $ K'\dot r $ ， $ K'\dot v $ 在发生改变时，其回转半径大小不发生变化，为操纵性不敏感系数。

3.2 速度、角速度系数

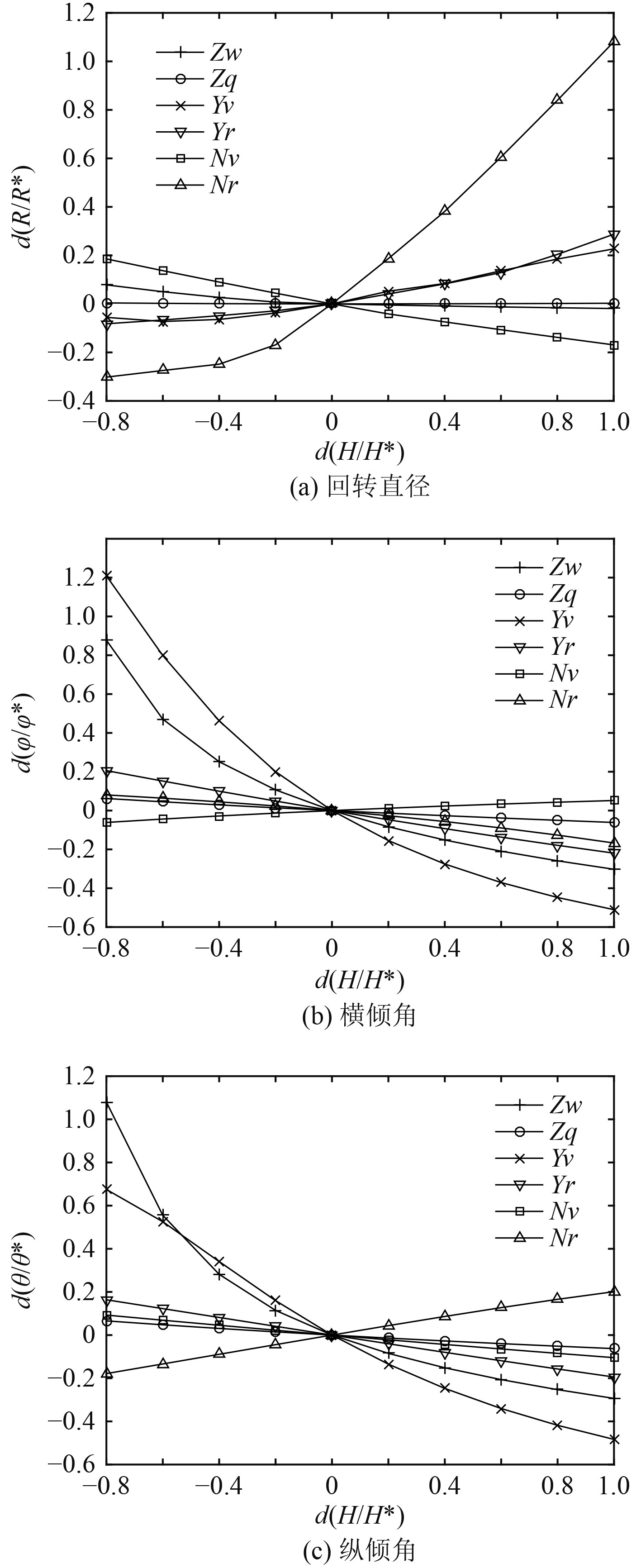
速度系数、角速度系数为潜器受到的粘性类水动力，其数值取决于潜器的运动情况，其表达形式取决于操纵性数学模型和运动特点。速度系数也称为位置导数，角速度系数也成为旋转导数，速度系数、角速度系数与潜器相对来流位置有关。以30°舵角为例，改变其系数大小，其操纵性参数（回转半径、横倾角和纵倾角）变化如图6所示。

可知：速度系数、角速度系数发生改变时其操纵性参数回转直径、横倾角、纵倾角也随之发生变化；水动力系数 $ Y'v $ ， $ N'v $ ， $ Y'r $ ， $ N'r $ ， $ Z'q $ 回转半径敏感性指数数值大小随舵角的增大而减小， $ Z'w $ 相反；水动力系数 $ Y'v $ ， $ N'v $ ， $ Y'r $ ， $ N'r $ 横倾角敏感性指数数值大小随舵角的增大而减小， $ Z'w $ ， $ Z'q $ 相反；水动力系数 $ Y'v $ ， $ Y'r $ ， $ N'r $ 纵倾角敏感性指数数值大小随舵角的增大而减小，系数 $ N'v $ ， $ Z'w $ ， $ Z'q $ 相反；力和力矩对其所在方向的速度、角速度敏感性较高， $ Y'v $ ， $ N'r $ 力和力矩对其他方向上的速度、角速度敏感性较低， $ Y'v $ ， $ N'r $ 值大小取决于潜器主尺度设计。

3.3 舵角系数

舵角系数，也成为控制导数。图7为舵角系为 $ Y'\delta r $ 和 $ N'\delta r $ 操纵性参数与舵角系数间的变化曲线。

可知，舵角系数下的回转直径、横倾角和纵倾角敏感性指数其数值随舵角变化较小，其舵角系数 $ N'\delta r $ 回转直径敏感性导数较大，其数值为−1.197，说明舵大小形状一定的情况下，舵相对其潜器的安装位置较为敏感，其舵的安装位置远离重心、压心，舵的力臂较大。

3.4 其他系数

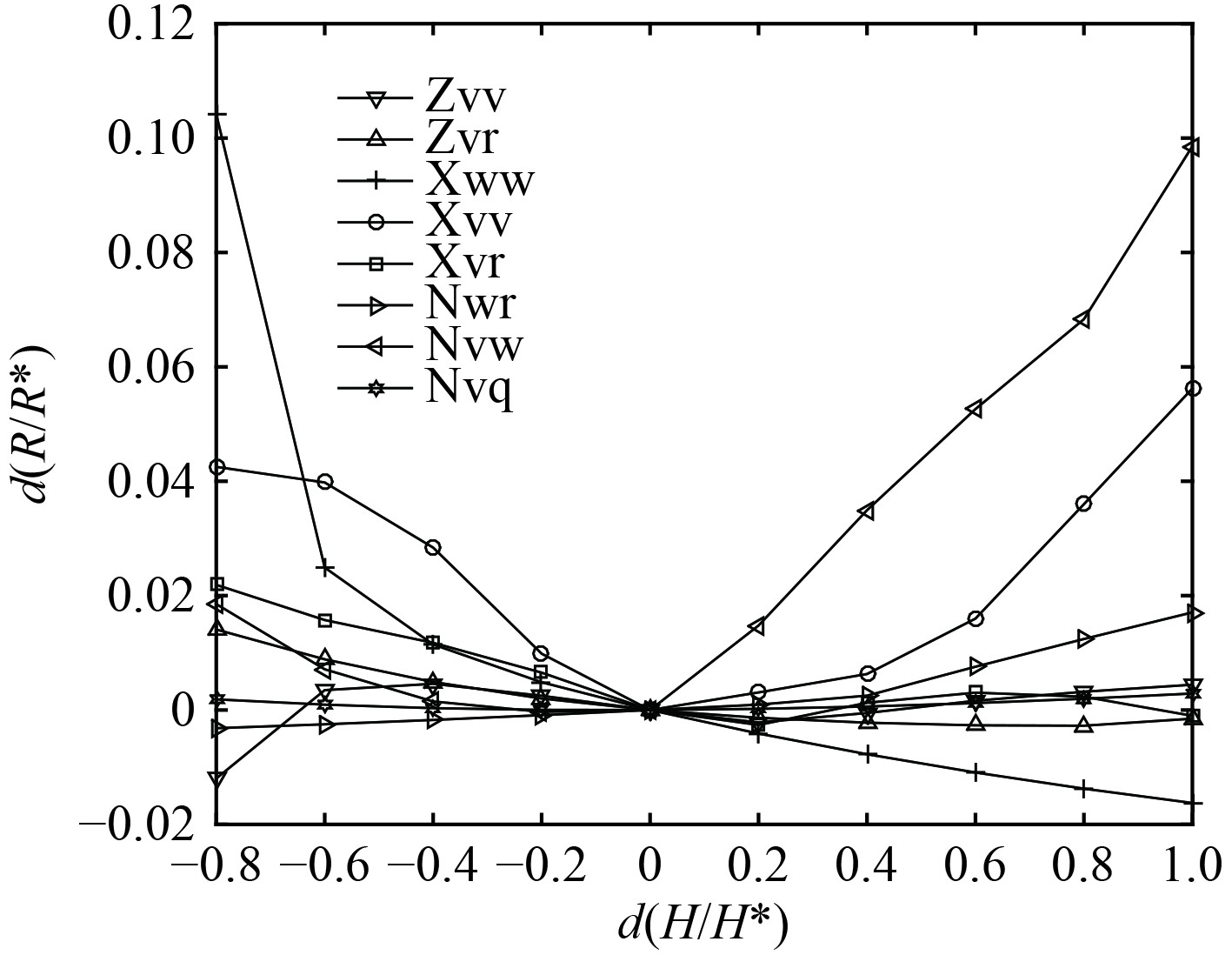
潜器在大舵角下的操纵运动需要考虑非线性项。非线性水动力系数整体为较小值，其在大舵角下的敏感性大于小舵角下的敏感性，以30°舵角为例，仅考虑回转半径。水动力系数 $ Z'vr $ ， $ Z'vv $ ， $ N'vq $ ， $ N'vw $ ， $ N'wr $ ， $ X'vr $ ， $ X'vv $ ， $ X'ww $ 回转半径敏感性指数非线性，如图8所示。水动力系数 $ Y'vw $ ， $ X'wq $ ， $ X'rr $ ， $ K'vw $ 在非线性水动力系数中敏感性较大，其回转半径敏感性导数最大小于2%，系数 $ K'qr $ ， $ K'vq $ ， $ K'wr $ ， $ M'pr $ ， $ M'rr $ ， $ M'uq $ ， $ M'uw $ ， $ M'vp $ ， $ M'vr $ ， $ M'vv $ ， $ N'pq $ ， $ N'qr $ ， $ N'wp $ ， $ X'pr $ ， $ X'qq $ ， $ Y'pq $ ， $ Y'qr $ ， $ Y'wp $ ， $ Y'wr $ ， $ Z'pr $ ， $ Z'rr $ ， $ Z'vp $ 敏感性小于1%。

将水动力系数在30°舵角下的敏感性指数的绝对值进行敏感性划分，如表3所示。

4 结　语

本文研究结果表明，在潜器做六自由度运动时，在众多的水动力系数中，角速度系数、速度系数和舵角系数的敏感性较大，在获取其数值大小时需保证其精度，在设计过程中也是需要重点考虑的因素；在潜器设计过程中为达到理想的航行姿态，重点考虑舵的设计，并对其偏差量的影响有一定的把握，在初始设计的基础上完成设计优化。在保证一定精度下，在误差允许的范围内，可依据水动力系数敏感性大小对操纵运动方程进行简化，将敏感性较小项简化省略；水动力系数对操纵性指数的影响程度并不相同。本文中的运动方程为六自由度方程，与传统简化四自由度模型相比，监测潜器运动过程中产生的横倾角和纵倾角稳态值的变化，更接近潜器在水中运动的真实情况，能够为潜器的设计提供指导。本文在研究潜器水平面内的运动时，考虑耦合水动力系数项，并对其影响因素进行了分析。