2. 上海外高桥造船有限公司,上海 200131
2. Shanghai Waigaoqiao Shipbuilding Co., Ltd., Shanghai 200137, China
在对LNG船的疲劳寿命评估中,由于LNG泄漏对船体的危害极大,因此液舱的裂纹扩展和泄漏分析成为必要。本文对于LNG船的寿命预报采用基于断裂力学的裂纹扩展方法[1],而基于断裂力学的疲劳寿命预报的重点在于准确地计算应力强度因子。ABS规定在裂纹扩展分析中需要考虑的典型节点中,腹板框架和桁材以及加强筋承受较大的相对变形的加强筋过渡处的高应力区域处主要是纵骨端部结构。B型LNG液舱底部支座处纵骨趾端为疲劳热点区域。由于其几何结构和所受载荷复杂,该处表面裂纹的应力强度因子的计算需要有针对性的开展研究。
目前对于求解应力强度因子已经有不少研究,Newman-Raju公式[2]适用于平板上表面裂纹的计算,但计算焊缝焊趾处表面裂纹的应力强度因子时,还需要修正系数Mk进行修正。Bowness和Lee[3]考虑了焊趾形状、焊趾角的大小、初始裂纹的尺寸等因素,并使用有限元软件建立不同尺寸的T型材模型,在控制载荷、约束等条件后计算得到大量结果,在总结规律后拟合得到了T型结构焊接接头焊趾处缺陷的最深点与表面点的应力强度因子修正系数的表达式,这一表达式也被BS7910标准[2]所采纳。Rhee[4]拟合出了T型管节点表面裂纹应力强度因子计算得修正公式,并被IIW [5]规范所采纳。刘帆等[6]分析并拟合了集装箱船纵骨的第2种和第3种节点的应力强度因子,并对公式进行了修正。孔小兵等[7]在Newman-Raju公式的基础上,利用有限元软件模拟了集装箱船纵骨的受力情况,分析并拟合除了纵骨端部应力强度因子计算公式,公式考虑了多种焊接接头形式及水密补板对计算结果的影响。罗盼等[8]使用数值模拟方法分析得出BS7910推荐的T型焊接接头应力强度因子计算公式适用于十字焊接接头应力强度因子的计算。阮宏宝等[9]利用三维裂纹扩展软件模拟了含系列深长比表面裂纹的纵骨端部模型,考虑了焊趾形状和纵骨腹板的影响,拟合了纵骨端部结构的应力强度因子修正系数。
本文考虑裂纹焊趾长度比和纵骨腹板的影响,利用三维裂纹扩展分析软件Zencrack模拟得到了裂纹扩展过程中裂纹深长比的变化,在此基础上拟合得到表面裂纹表面点和最深点的应力强度因子公式。再将此公式应用到基于断裂力学的裂纹扩展计算中,对液舱纵骨端部的寿命进行预报。
1 纵骨趾端处应力强度因子的计算因B型LNG液舱底部支座及附近区域结构几何形状和受力复杂,计算该处纵骨趾端处表面裂纹应力强度因子变得困难。为了准确计算出纵骨端部的应力强度因子,本文利用三维裂纹扩展分析软件Zencrack对该处表面裂纹应力强度因子进行系列计算,裂纹的增量采用该软件分析所得的裂纹扩展增量。首先对Zencrack裂纹扩展分析的准确性进行下列验证分析,然后在系列应力强度因子计算结果的基础上拟合得到该处表面裂纹应力强度因子计算式。
1.1 Zencrack有效性验证三维裂纹扩展分析的关键之一是应力强度因子和裂纹扩展的计算。本文利用Zencrack计算一平板中半椭圆表面裂纹的应力强度因子与扩展寿命,并与根据Newman-Raju计算得到的解进行对比,对Zencrack应力强度因子和裂纹扩展计算能力进行评估。计算对象为200 mm×400 mm×10 mm中心有表面裂纹的平板,受100 MPa垂直于裂纹平面的拉力,考虑到结构的对称性,采用1/4模型进行分析。材料为9%NI钢,屈服强度为400 MPa,抗拉强度为655 MPa,杨氏模量E=2.1×105 MPa,泊松比为0.3。裂纹扩展Paris模型材料常数为C=5.14E-12, m=3。
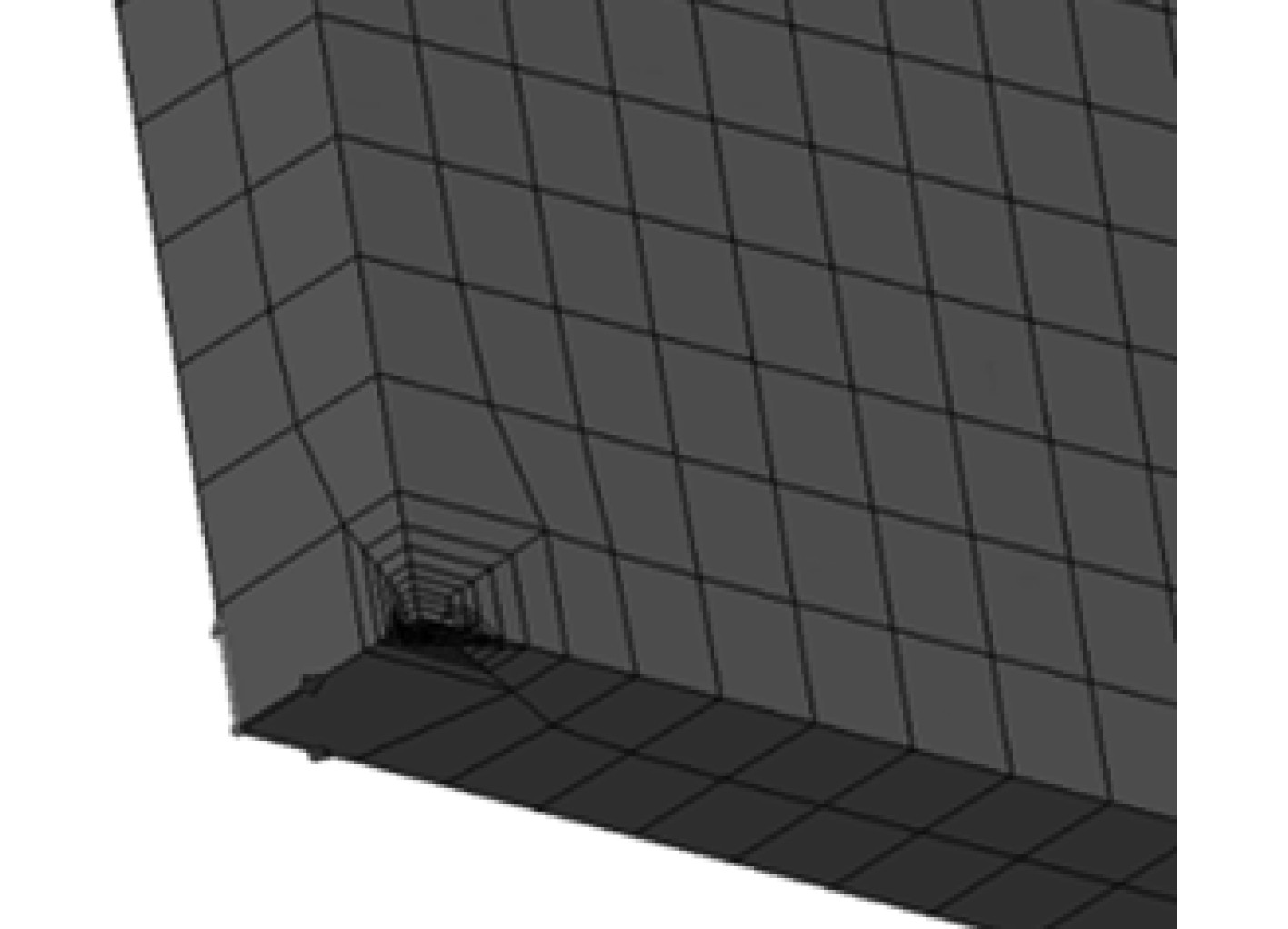
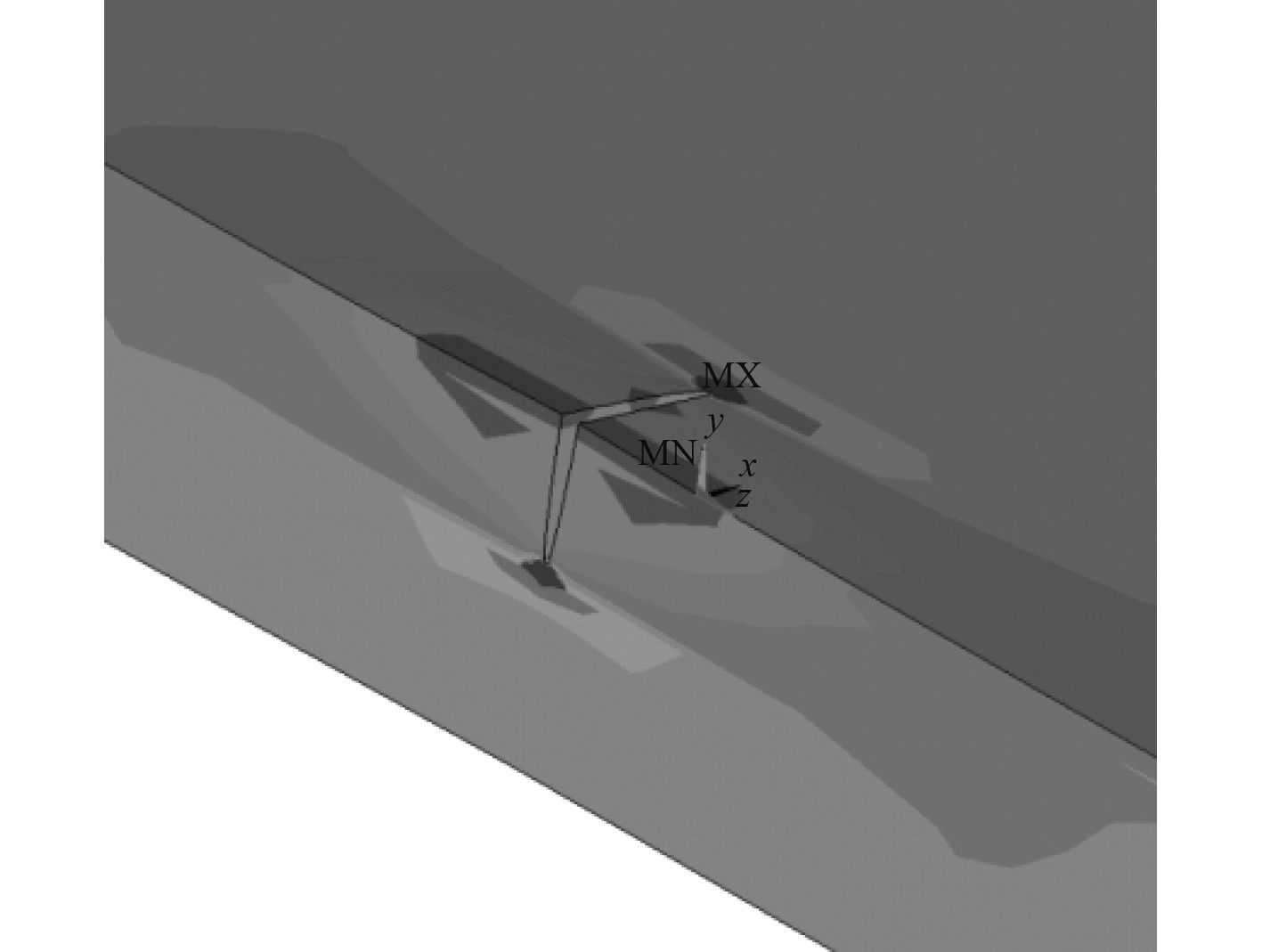
Zencrack裂纹块库中提供不同的裂纹块可供选择,将裂纹块选择组合,可以模拟形式多样的裂纹。将裂纹块插入无裂纹的有限元模型中,生成含初始缺陷的有限元模型[10],如图1和图2所示。将模型提交到Ansys进行计算,即可得到裂纹扩展结果,如图3所示。

|
图 1 无裂纹1/4有限元模型 Fig. 1 1/4 finite element model without crack |
|
图 2 含裂纹的有限元模型 Fig. 2 Finite element model with crack |
|
图 3 裂纹扩展中的应力云图 Fig. 3 Stress contour diagram of crack propagation |
插入不同深度和长度的表面裂纹,Zencrack计算的应力强度因子与Newman-Raju解对比如表1所示。
|
|
表 1 表面裂纹应力强度因子求解对比 Tab.1 Comparison of the stress intensity factors of surface cracks |
从表1和表2可以看出,Zencrack软件计算结果与理论解之间的误差在4%以内,产生误差的原因主要是裂纹扩展过程中网格产生的畸变,误差在可接受范围之内,因此Zencrack软件在进行裂纹的应力强度因子计算的结果可以信赖。
|
|
表 2 表面裂纹扩展求解对比 Tab.2 Comparison of surface crack propagation solution |
T型焊接接头的焊趾处缺陷的应力强度因子一般用以下公式表示:
| $ {K_{weld}} = {M_k} \times {K_{plate}}。$ |
式中:
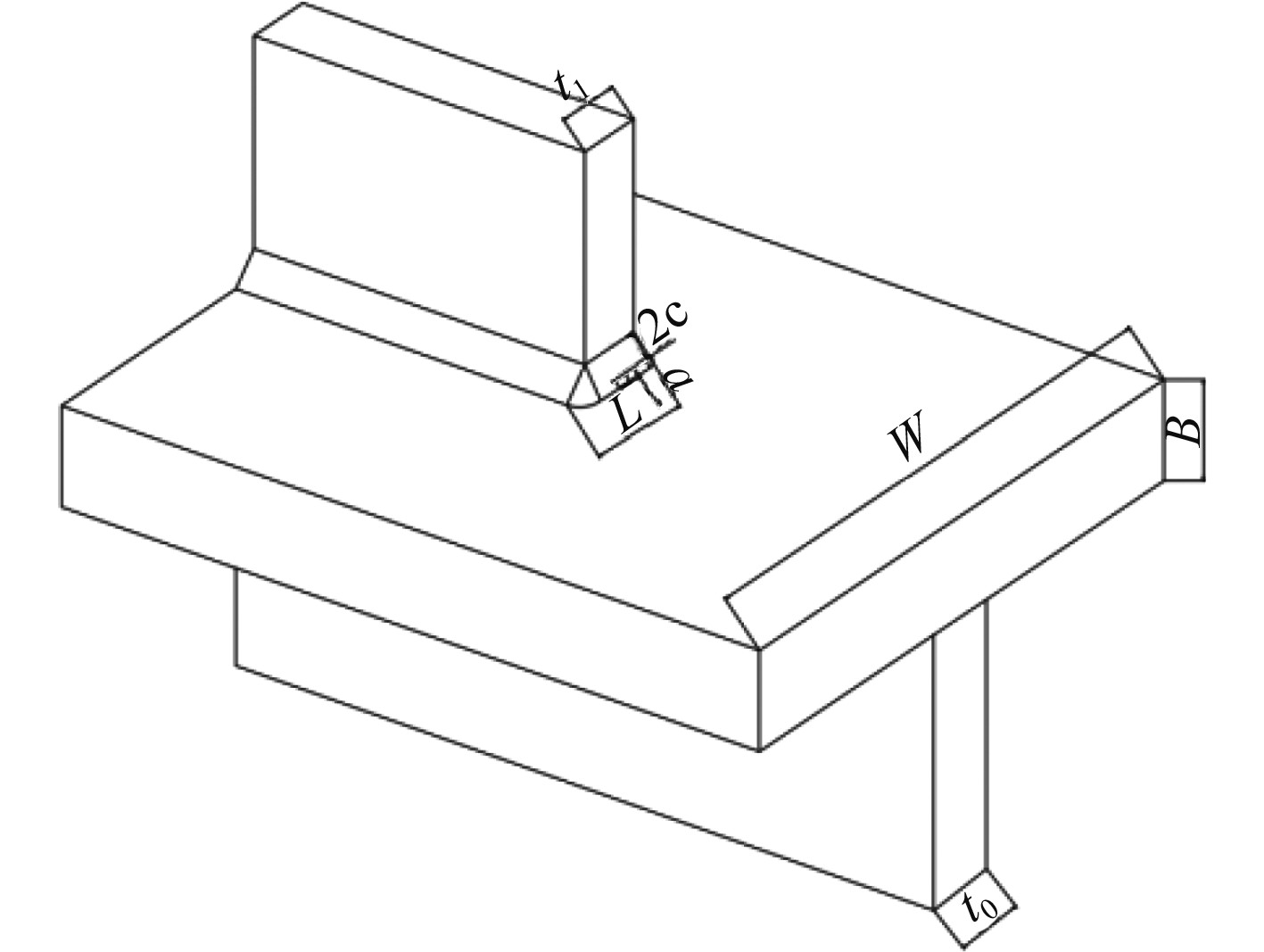
纵骨端部模型可以近似看做为特殊的T型接头的面板下面焊接了一个腹板,如图4所示。在拟合趾端应力强度因子修正系数时,需要考虑各种参数的影响。不少学者对这一问题有着深入的研究。韩芸等对T型结构研究后认为裂纹深长比、裂纹深度比和焊趾角均为重要影响因素;刘帆等对构件形式研究计算后发现缺陷长度与焊缝长度对应力强度因子的影响不可忽略;孔小兵等研究集装箱船纵骨端部认为扶强材的宽度也有一定的影响。阮宏宝等研究LNG液舱纵骨区域的缺陷认为焊趾形状和纵骨腹板厚度对应力强度因子有一定影响。但是阮宏宝的结论是在给定裂纹深长比的情况下计算得到的,这与真实情况有差异。浅长表面裂纹扩展是先在裂纹深度方向上扩展,再在裂纹长度方向上扩展。所以,以固定深长比来考虑裂纹长度对应力强度因子的影响是粗略的。
|
图 4 纵骨端部几何模型 Fig. 4 The geometric model of the end of longitudinal |
基于前者的研究,考虑裂纹扩展过程中应力强度因子的变化拟合裂纹焊趾长度比与纵骨腹板厚度对应力强度因子的影响。在以往的研究中,学者们建立的焊趾模型均为锥形,而实际工程中,焊趾部分应该是近似圆弧形。因此,本文的焊趾模型采用圆弧形的,有限元模型如图5所示。

|
图 5 圆弧形焊趾模型 Fig. 5 Arc welding toe model |
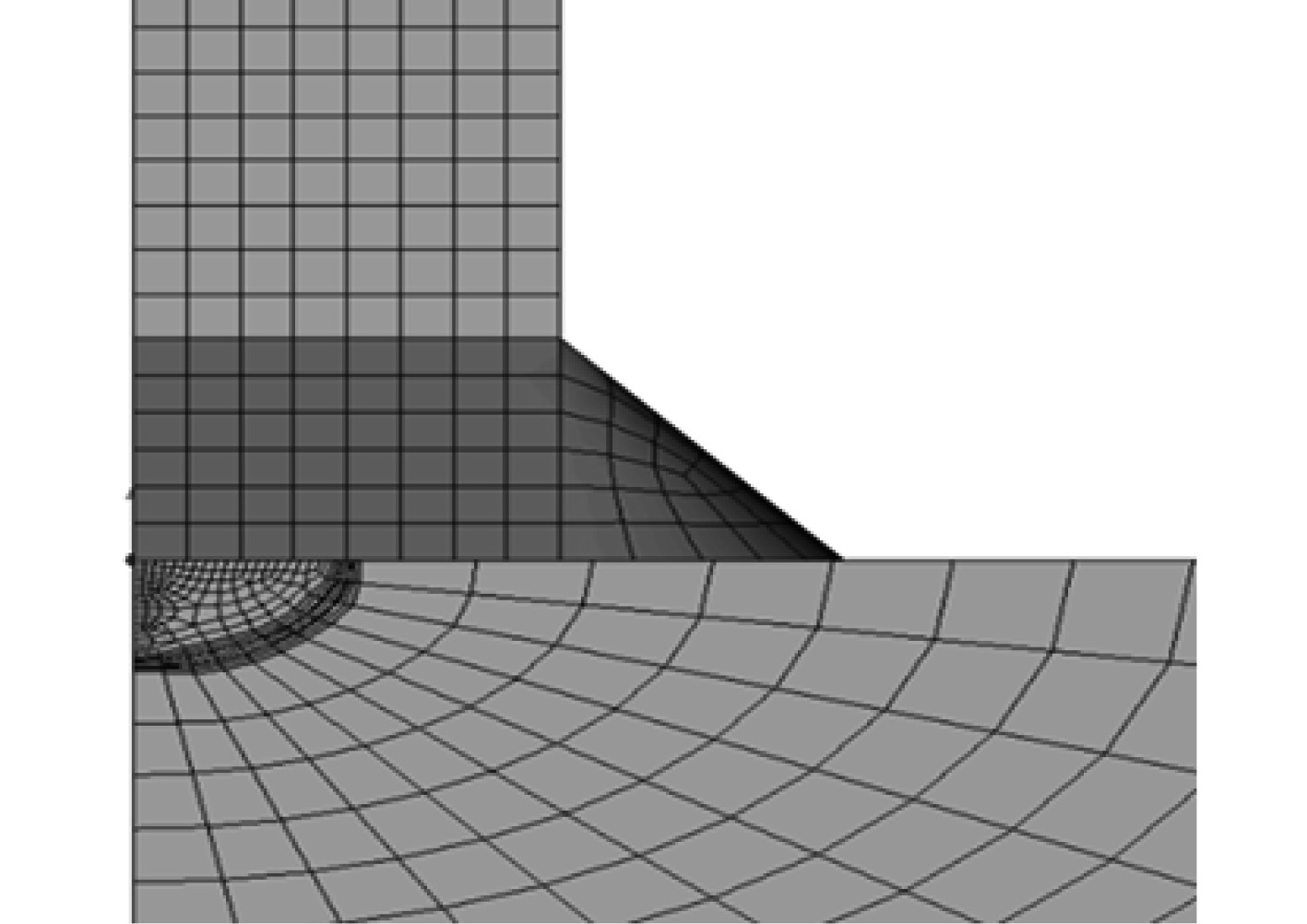
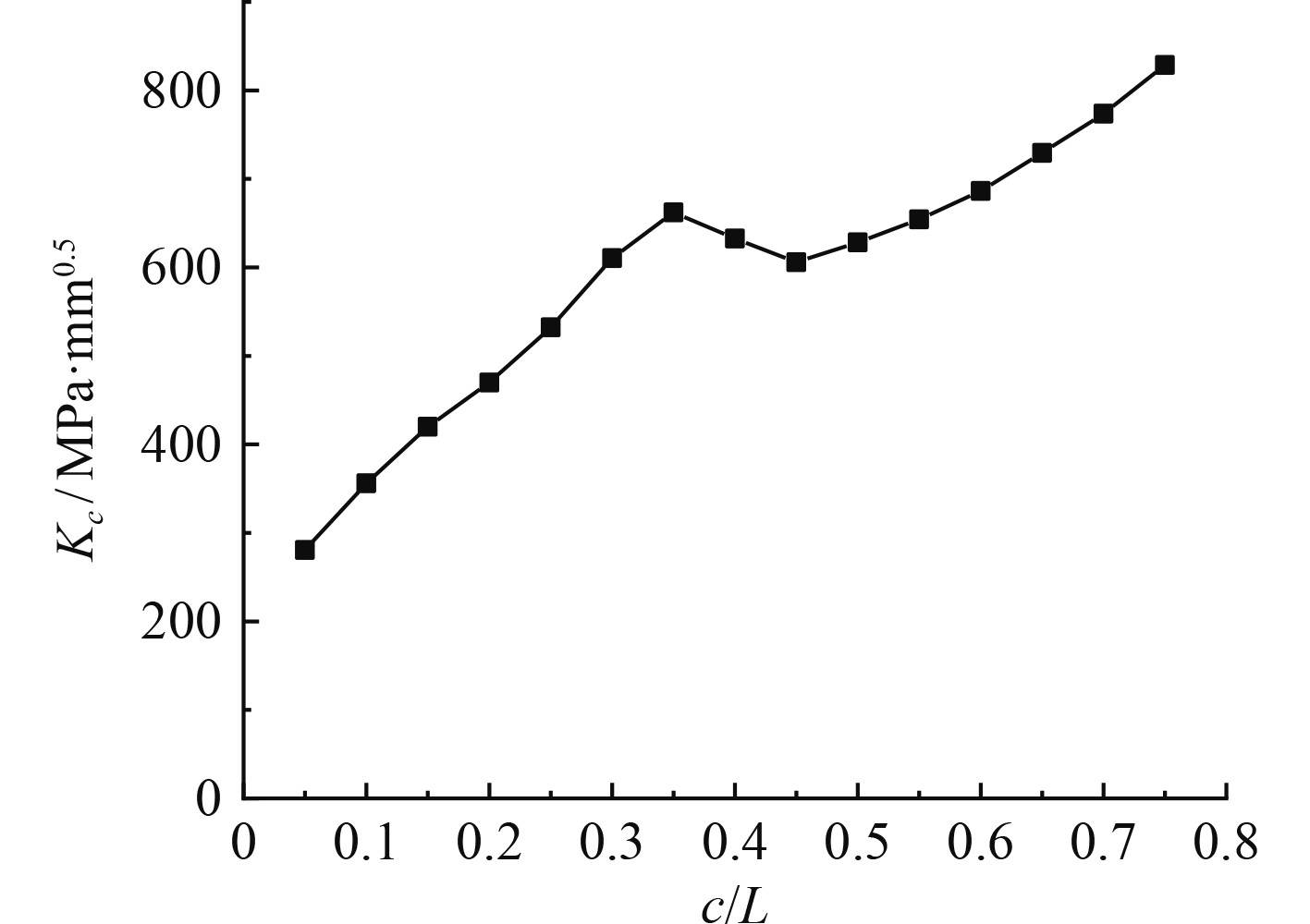
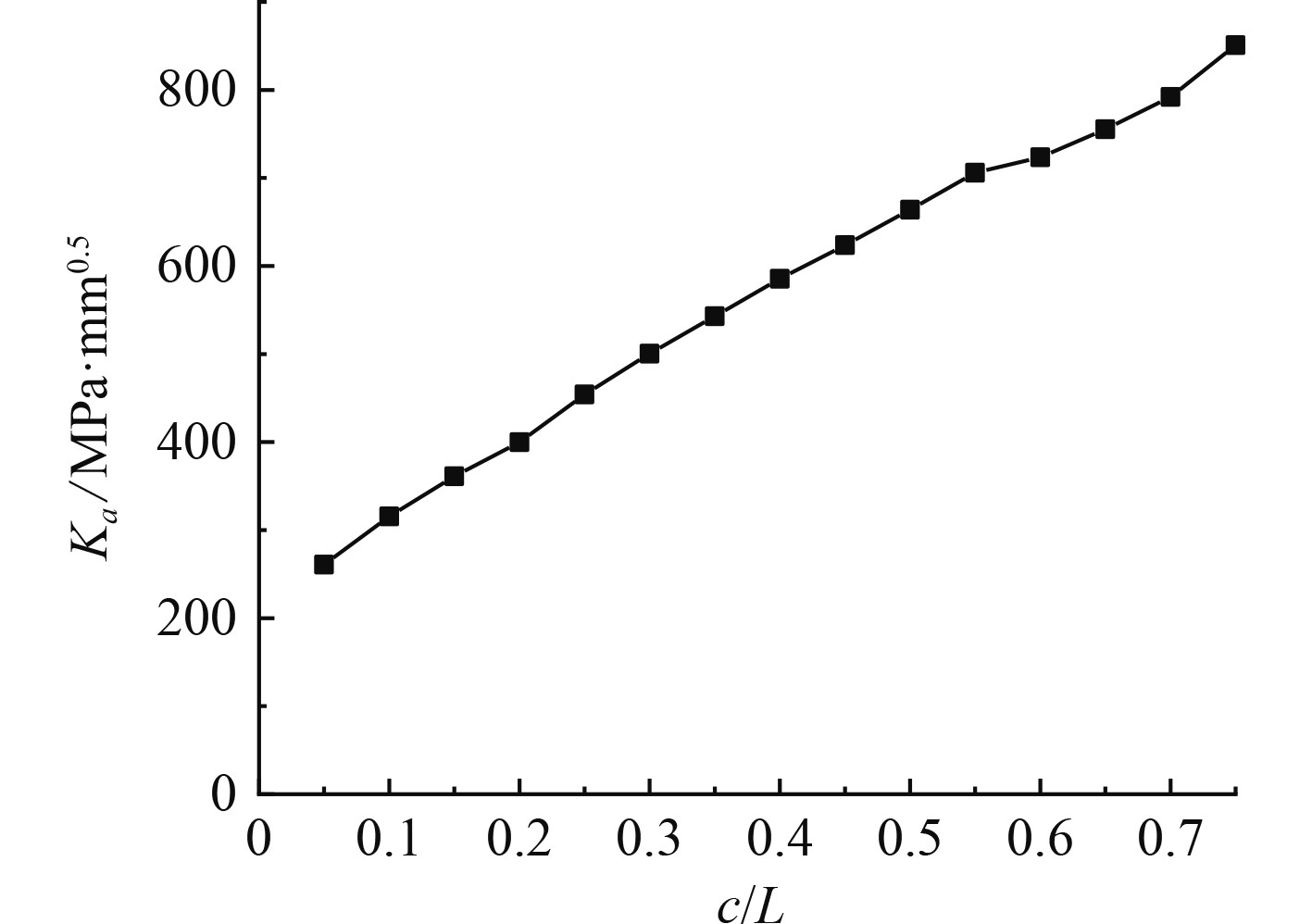
利用Zencrack软件在模型中插入标准裂纹块模拟表面裂纹,如图6所示,其中肘板与纵骨之间采用绑定连接,以确保计算可以正常进行。改变腹板厚度和焊趾厚度,进行一系列不同尺寸裂纹应力强度因子计算,其中裂纹在深度和长度方向的增量由软件确定,裂纹扩展路径如图7所示。裂纹表面点与最深点的应力强度因子随裂纹长度变化的规律如图8和图9所示。应力强度因子与腹板厚度的关系如表3所示。
|
图 6 含裂纹的有限元模型 Fig. 6 Finite element model with cracks |

|
图 7 计算的裂纹扩展路径 Fig. 7 Calculated crack propagation path by Zencrack |
|
图 8 表面点应力强度因子 Fig. 8 Stress intensity factors at the surface point |
|
图 9 最深点应力强度因子 Fig. 9 Stress intensity factors at the deepest point |
|
|
表 3 腹板对应力强度因子的影响 Tab.3 The influence of the web on the stress intensity factor |
首先考虑裂纹焊趾长度比对表面点的应力强度因子的影响,当裂纹长度小于0.4 L时,应力强度因子呈先上升再下降的趋势,当裂纹长度大于0.4 L时,应力强度因子呈上升趋势,焊趾对应力强度因子的影响也越来越小。而最深点的应力强度因子受焊趾长度的影响较小,呈直线趋势。
其次再考虑腹板的存在对应力强度因子的影响,在裂纹长度小于L时,腹板的存在使得表面点的应力强度因子变得更大,当裂纹长度大于L时,表面点的应力强度因子变得更小。对于最深点的应力强度因子,腹板的存在使得其变得更大。
基于BS7910中T型接头应力强度因子修正系数,增加
1)对于表面点的应力强度因子修正
| $\begin{split} {M_{kc}} =& {f_1}\left( {\dfrac{a}{B},\dfrac{c}{a},\dfrac{L}{B}} \right) \times {f_2}\left( {\dfrac{a}{B},\dfrac{a}{c}} \right) \times {f_3}\left( {\dfrac{a}{B},\dfrac{a}{c},\dfrac{L}{B}} \right) \times\\ &{f_4}\left( {\dfrac{{2c}}{L},\dfrac{a}{c}} \right) \times {f_5}\left( {\dfrac{{2c}}{L},\dfrac{{{t_0}}}{{{t_1}}}} \right) 。\end{split}$ |
其中:
| $ {f_4}\left( {\dfrac{{2c}}{L},\dfrac{a}{c}} \right) = \left\{ {\begin{split} &{{g_{14}}{{\left( {\dfrac{c}{L}} \right)}^2} + {g_{15}}\left( {\dfrac{c}{L}} \right) + {g_{16}}},\quad{{c \mathord{\left/ {\vphantom {c {L < 0.4}}} \right. } {L < 0.4}}},\\ & {{g_{17}}{{\left( {\dfrac{c}{L}} \right)}^2} + {g_{18}}\left( {\dfrac{c}{L}} \right) + 1.265},\quad{{c \mathord{\left/ {\vphantom {c {L \geqslant 0.4}}} \right. } {L \geqslant 0.4}}} ,\end{split}} \right. $ |
式中:
| $ {f_5}\left( {\frac{{2c}}{L},\frac{{{t_0}}}{{{t_1}}}} \right) = {g_{19}}{\left( {\frac{{{t_0}}}{{{t_1}}}} \right)^2} + {g_{20}}\left( {\frac{{{t_0}}}{{{t_1}}}} \right) + {g_{21}}。$ |
式中:
2)对裂纹最深处应力强度因子的修正
| $\begin{split} {M_{ka}} =& {f_6}\left( {\frac{{2c}}{L},\frac{a}{c}} \right) \times {f_7}\left( {\frac{{2c}}{L},\frac{{{t_0}}}{{{t_1}}}} \right) \times\\ &\left[ {{f_1}\left( {\frac{a}{B},\frac{a}{c}} \right) + {f_2}\left( {\frac{a}{B}} \right) +{f_3}\left( {\frac{a}{B},\frac{L}{B}} \right)} \right]。\end{split}$ |
其中:
| $ {f_6}\left( {\frac{{2c}}{L},\frac{a}{c}} \right) = {g_9}{\left( {\frac{c}{L}} \right)^2} + {g_{10}}\left( {\frac{c}{L}} \right) + {g_{11}}。$ |
式中:
| $ {f_7}\left( {\frac{{2c}}{L},\frac{{{t_0}}}{{{t_1}}}} \right) = {g_{12}}{\left( {\frac{{{t_0}}}{{{t_1}}}} \right)^2} + {g_{13}}\left( {\frac{{{t_0}}}{{{t_1}}}} \right) + {g_{14}}。$ |
式中:
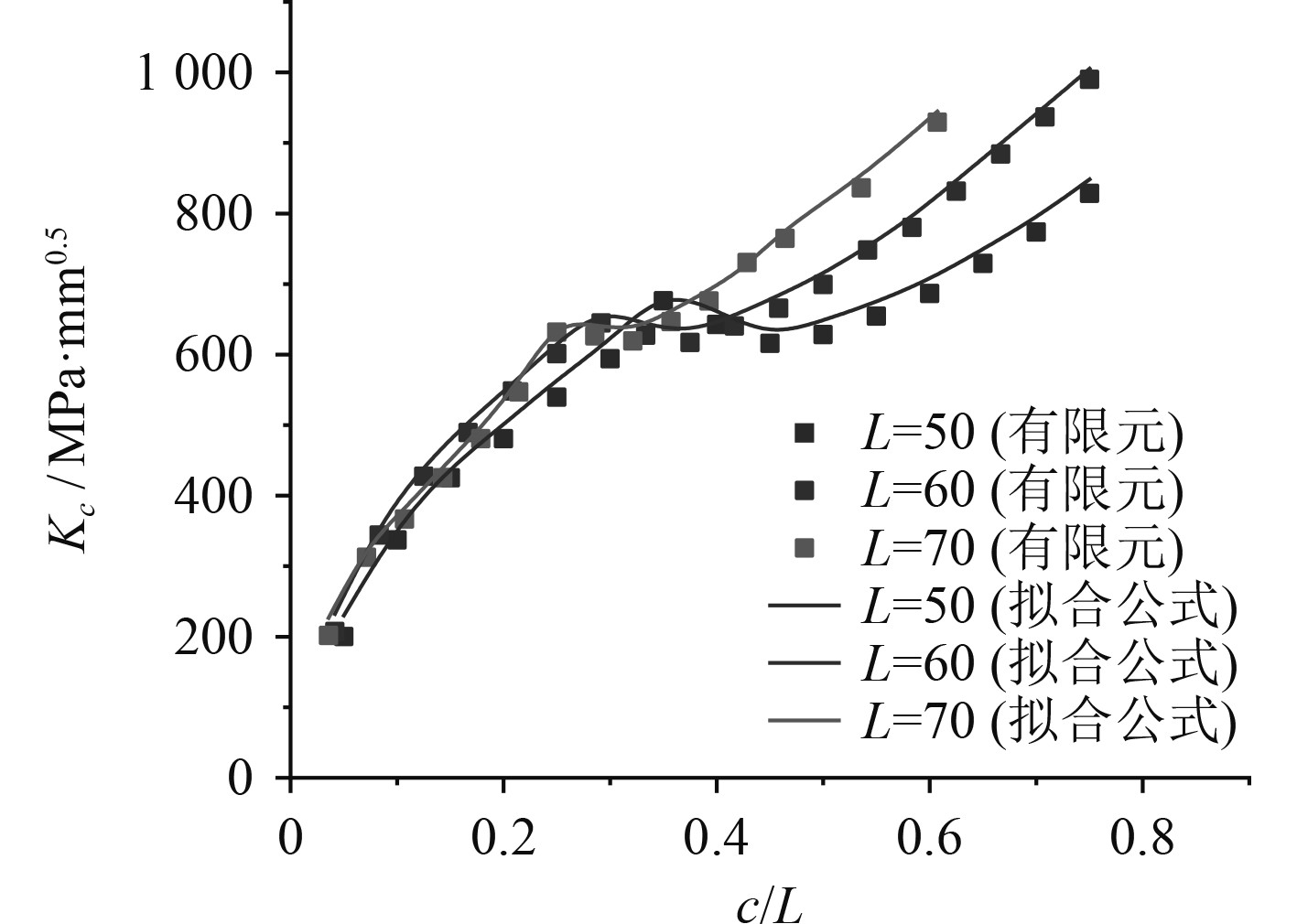
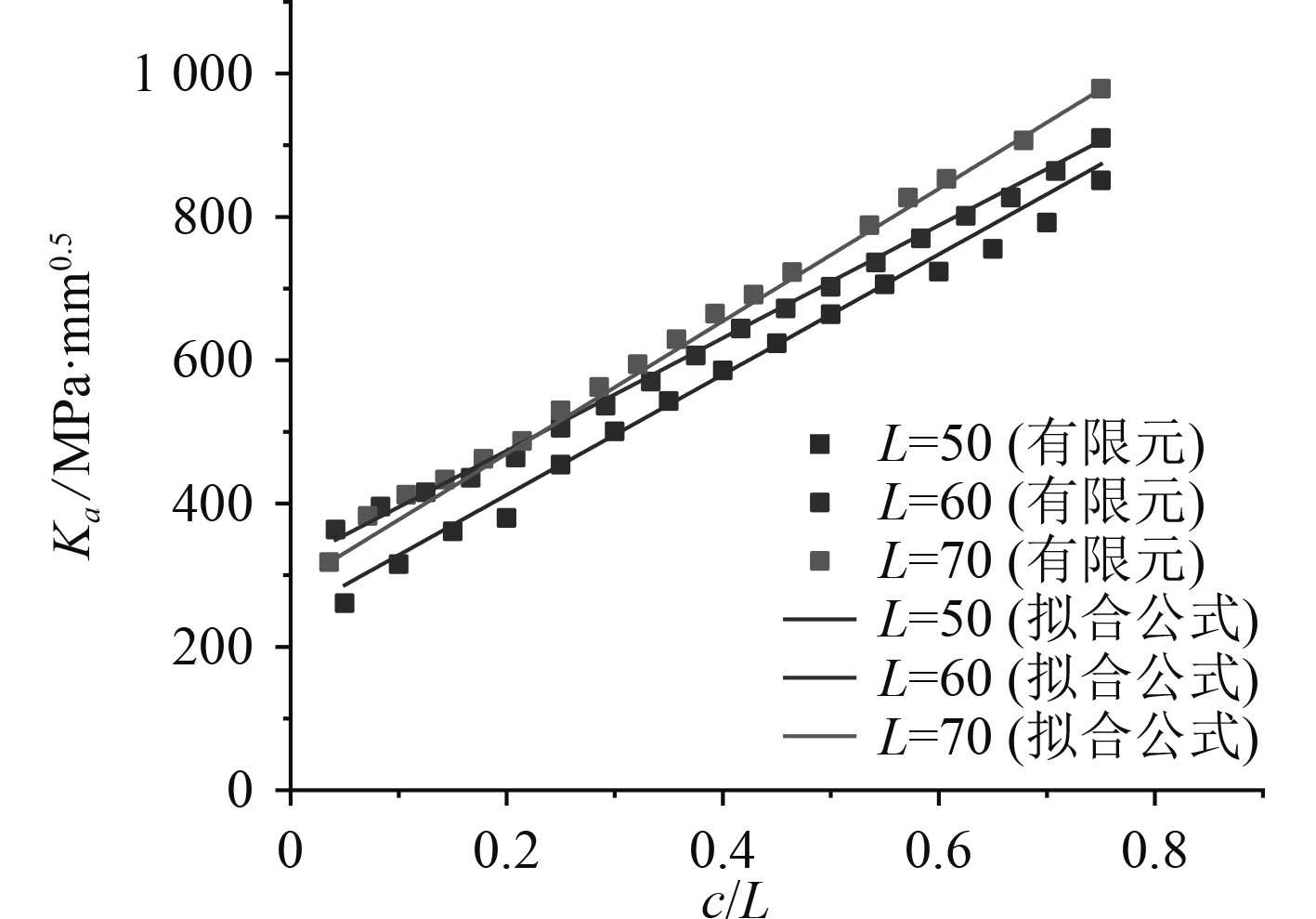
计算不同焊趾长度和腹板厚度时的裂纹扩展过程中的应力强度因子,将其与拟合的公式进行对比,其结果如图10和图11所示,可以看到拟合公式吻合的较好。
|
图 10 表面点应力强度因子对比 Fig. 10 Comparison of surface point stress intensity factors |
|
图 11 最深点应力强度因子对比 Fig. 11 Comparison of stress intensity factors at the deepest point |
采取以上所得的支座处纵骨趾端表面裂纹修正系数公式,参照ABS的相关规范,基于断裂力学的理论,对目标船B型LNG液舱纵骨端部结构焊趾处缺陷进行疲劳寿命预报。
3.1 目标船数据目标LNG 船为某17 万立方米独立B 型LNG 船,目标液舱位于船中位置的3号液舱。有限元模型如图12所示。

|
图 12 B型LNG液舱有限元模型 Fig. 12 Finite element model of type B LNG tank |
|
|
表 4 目标船主尺度 Tab.4 Main dimensions of target ship |
|
|
表 5 目标液舱尺寸 Tab.5 Target tank dimensions |
根据ABS规范《Liquified Gas Carriers With Independent Tanks》[13]的相关规定,裂纹扩展分析所用的载荷主要有液舱内部液体的动载荷、海水的动压力、船舶运动的惯性力以及波浪诱导弯矩。由于B 型LNG 液舱只通过支座和船体相连,液舱本身并不承受外部波浪载荷和波浪诱导弯矩,因此在确定液舱的疲劳热点时,只需要建立液舱和支座的有限元模型。有限元模型应采用三舱段模型(1/2+1+1/2),计算目标为中间液舱。疲劳节点附近网格单元尺寸为t×t,如图13所示。液舱与船体的支座可用壳单元模拟,支座之间的垫木可用体单元或者杆单元模拟,计算时要删去受拉杆单元然后再次计算。在进行疲劳分析时所要考虑的动载荷主要有液舱内部的动载荷和船体弯曲对罐体的支撑的影响。
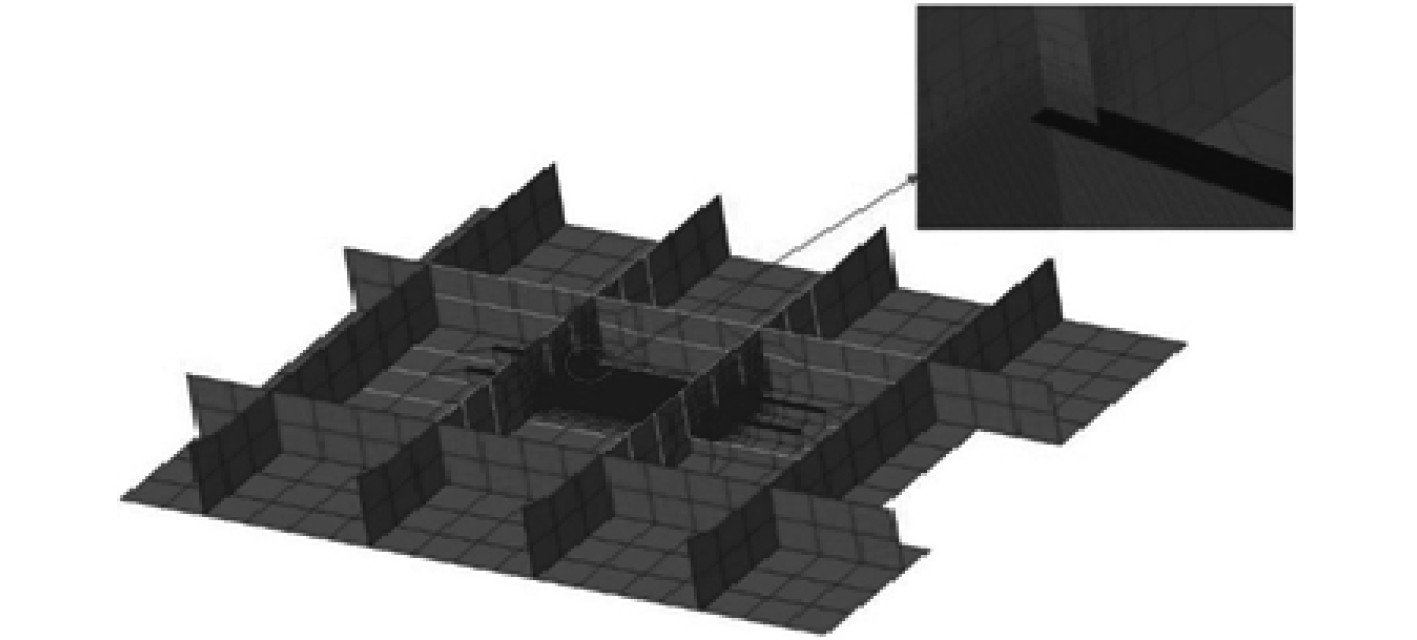
|
图 13 热点细化图 Fig. 13 Hotspot refinement diagram |
评估 LNG 船结点的疲劳强度时,应考虑满载和压载2种装载,并在这2种装载下,分别考虑最大垂向弯矩范围(LC1&LC2)、最大局部应力范围(LC3&LC4)、最大横向加速度幅值(LC5&LC6)以及最大水平弯矩幅值(LC7&LC8),再对这8个工况两两进行组合。
计算得到各个工况的应力分布情况,找出不同工况下应力幅值最大的点作为典型疲劳热点。根据ABS规范的相关规定,应评估以下节点的疲劳强度:
1)液舱外板与框架相连接处,包括:底板,顶板,前板后板以及侧板;
2)横框架肘板连接处;
3)缓冲舱壁肘板连接处;
4)水平桁肘板连接处;
5)支座与底板相连接处;
6)其他的区域及部位:通过结构分析发现船体结构在交变载荷的作用下出现高应力的某些区域。
本文选取目标船LNG罐体底部支座附近纵骨端部处的热点为例,因为给出结构形式和所受载荷复杂,具有难度和代表性。对其进行单元网格细化。加载各工况下的动载荷部分,求取各工况下热点的应力值,得到各个工况的最大主应力值及其寿命占比如表6所示。
|
|
表 6 疲劳计算工况的热点主应力 Tab.6 Hot spot principal stresses under different loading conditions |
在以上计算中,施加给模型的载荷均为10−8超越概率下的载荷,根据ABS规范中规定的简化的应力范围谱的计算方法,可以构造得到载荷谱。对于长期应力范围谱,规范中采用的是船舶在北大西洋海况条件下可能经历的108个应力循环。规范给出了weibull分布中形函数h=1.0时108个应力循环的正则化应力分布,如图14所示。为了消除载荷次序对裂纹扩展的影响,需要将总的载荷谱分成10组以上。图中,
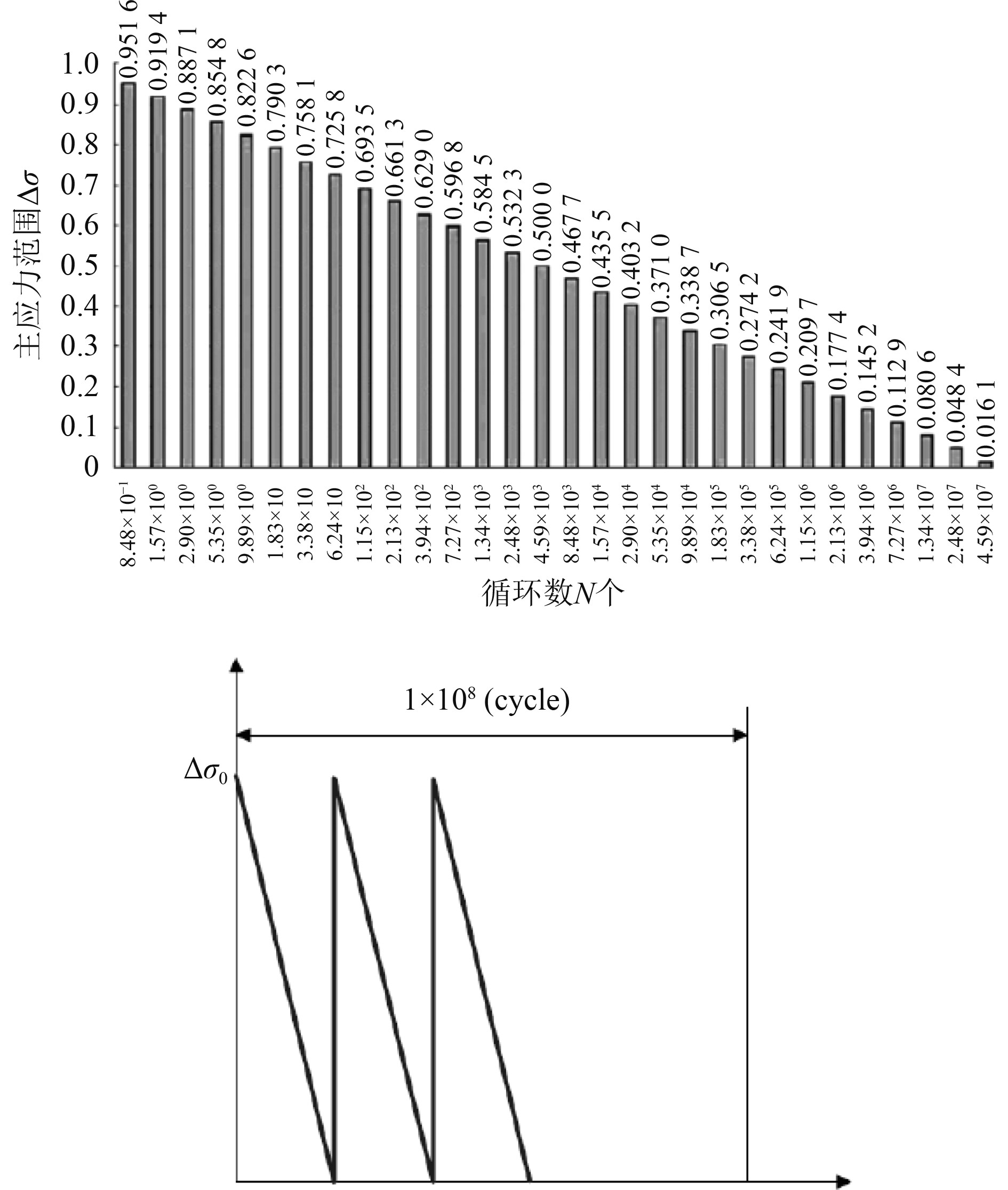
|
图 14 20年长期应力分布 Fig. 14 20-year long-term stress distribution |
采用Paris公式对该纵骨趾端处的裂纹进行扩展分析,在节点插入2c = 5 mm,a = 0.5 mm的表面裂纹,结合本文拟合得到的应力强度因子修正系数,可以得到该热点纵骨趾端处的裂纹扩展如图15所示。利用失效评估图评估裂纹,如图16所示。可以看到裂纹在41.7年之后失效,满足设计要求。
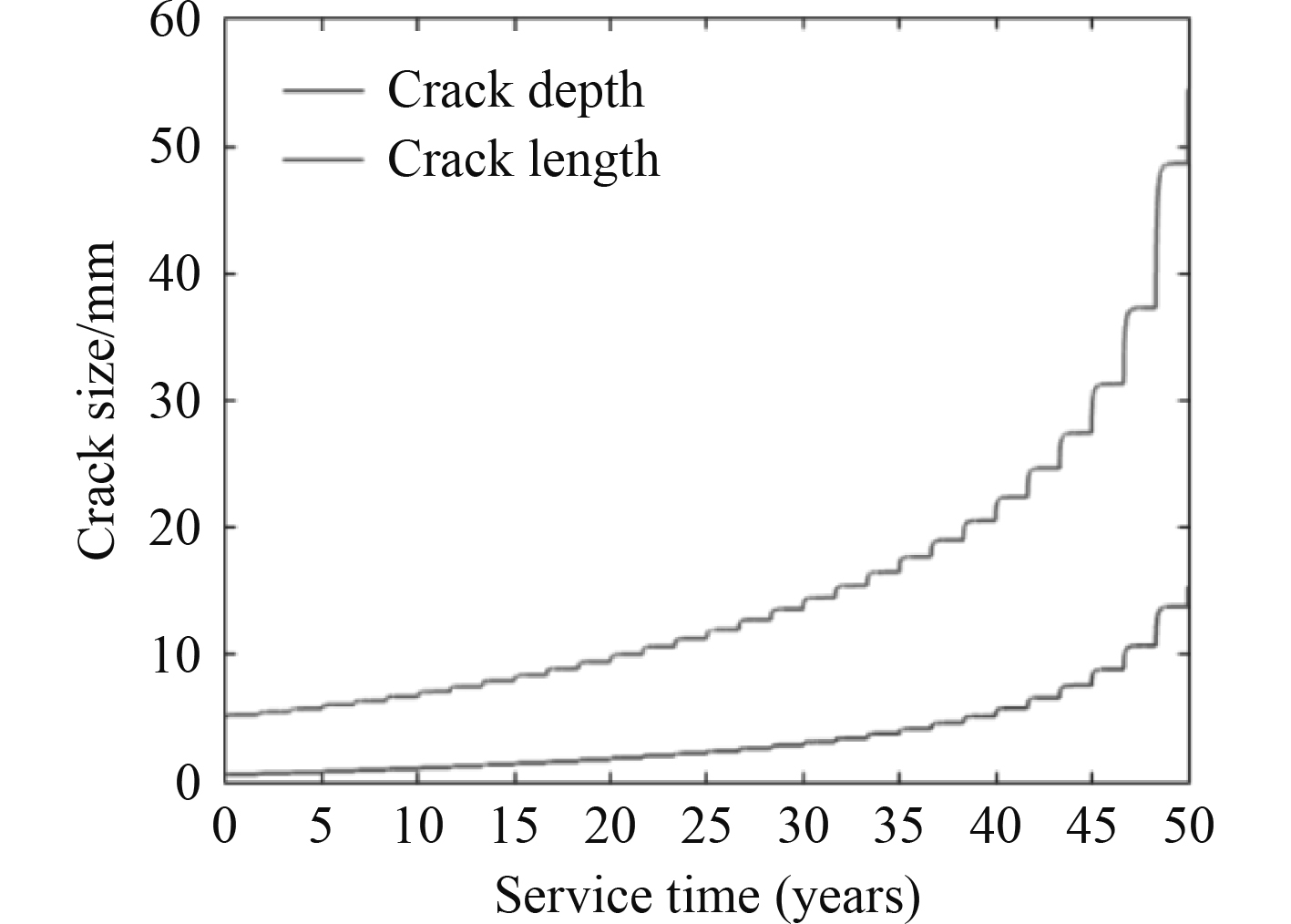
|
图 15 裂纹扩展图 Fig. 15 Crack growth diagram |
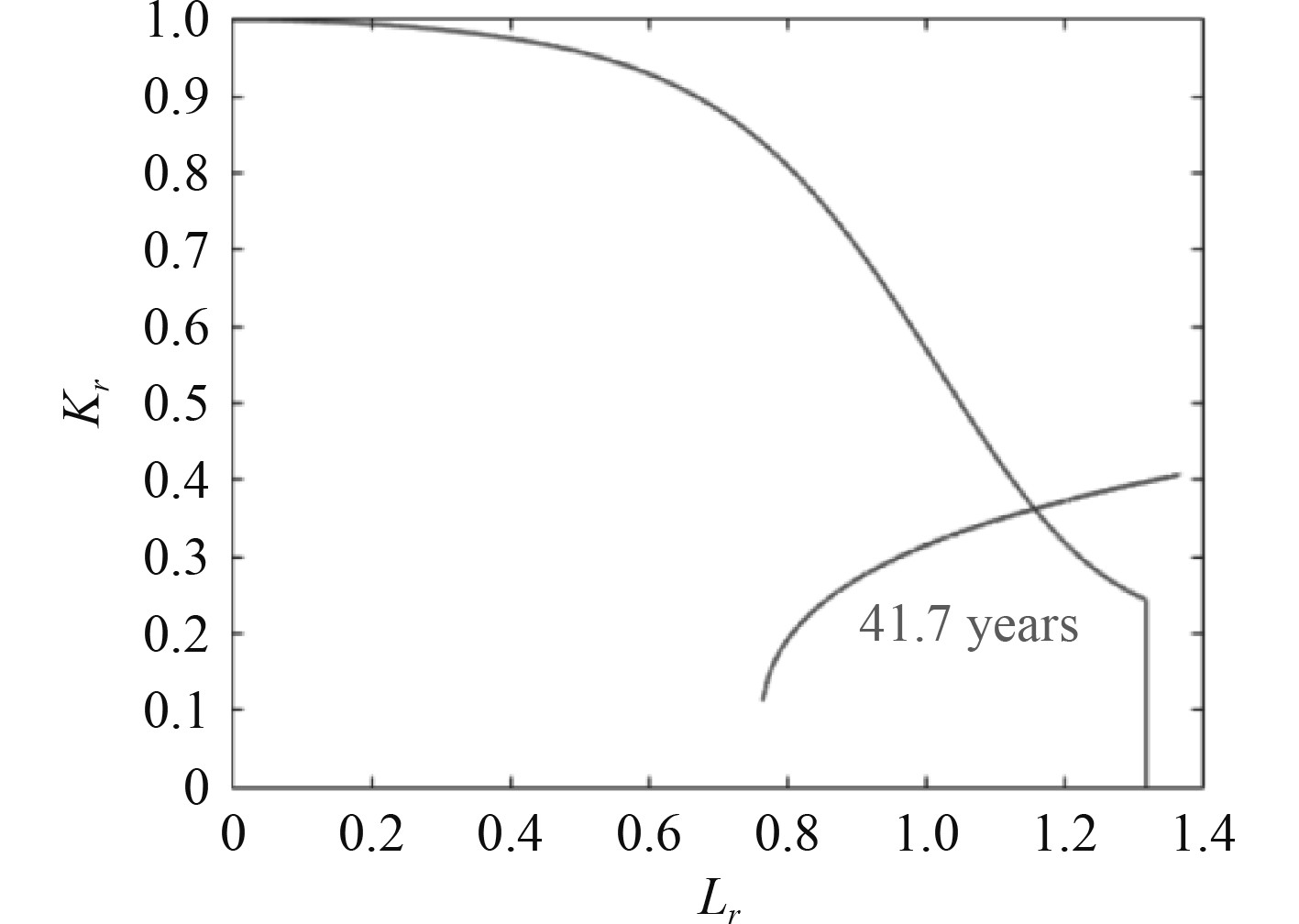
|
图 16 裂纹失效评估图 Fig. 16 Crack failure assessment diagram |
本文采用三维裂纹扩展分析软件对液舱支座附近纵骨趾端处表面裂纹进行裂纹扩展分析,得到液舱支座纵骨趾端表面裂纹应力强度因子修正系数经验公式,并对LNG船液舱底部支座附近的纵骨端部焊趾表面裂纹疲劳扩展寿命进行分析,得到以下结论:
1)影响纵骨趾端表面裂纹应力强度因子的参数较多,主要是裂纹深度与板厚比、裂纹的形状比、裂纹长度与焊缝长度的比值、焊趾形状和腹板的厚度;
2)裂纹表面点受焊趾的影响,其应力强度因子的拟合分为两段,分界点为
3)腹板的存在,使得裂纹表面点的应力强度因子与无腹板时的应力强度因子之比呈先上升后下降的趋势,而最深点的应力强度因子比无腹板时大;
4) 预报了某B型LNG船液舱底部支座纵骨焊趾处裂纹的疲劳扩展寿命,所得结果满足规范对疲劳寿命的要求。
| [1] |
王方, 付一珂, 范晓伟, 等. 液化天然气(LNG)冷能利用研究进展[J]. 化工进展, 2016, 35(3): 748-753. DOI:10.16085/j.issn.1000-6613.2016.03.015 |
| [2] |
檀学燕. 中国进口液化天然气可持续发展战略[D]. 北京: 中国地质大学(北京), 2012.
|
| [3] |
赵南, 顾学康, 李政杰. 超大型浮体结构极限强度研究综述(英文)[J]. 船舶力学, 2021, 25(10): 1412-1426. DOI:10.3969/j.issn.1007-7294.2021.10.013 |
| [4] |
BSI. Guide to methods for assessing the acceptability of flaws in metallic structures: BS7910[S]. 2005.
|
| [5] |
BOWNESS D, LEE M M K. Weld toe magnification factors for semi-elliptical cracks in T-butt joints — comparison with existing solutions[J]. International Journal of Fatigue, 2000, 22(5): 389-396. DOI:10.1016/S0142-1123(00)00013-X |
| [6] |
RHEE H C, HAN S, GIPSON G S. Reliability of solution method and empirical formulas of stress intensity factors for weld toe cracks of tubular joints[J]. Offshore Mech. Arctic Engng. ASME B, 1991, 3: 441-452. |
| [7] |
IIW. Recommendations for fatigue design of welded joints and components[S]. 2014.
|
| [8] |
刘帆, 黄小平. 集装箱船典型疲劳评估节点应力强度因子计算[J]. 中国造船, 2015, 56(1): 27-40. DOI:10.3969/j.issn.1000-4882.2015.01.004 |
| [9] |
孔小兵, 黄小平, 罗盼. 集装箱船纵骨端部焊趾处表面裂纹应力强度因子计算[J]. 中国造船, 2016, 57(2): 67-77. DOI:10.3969/j.issn.1000-4882.2016.02.008 |
| [10] |
罗盼, 黄小平, 孔小兵. 大型集装箱船甲板纵骨节点疲劳寿命预报方法[J]. 船舶与海洋工程, 2016, 32(6): 1-10. DOI:10.14056/j.cnki.naoe.2016.06.001 |
| [11] |
阮宏宝, 黄小平. LNG船纵骨端部表面裂纹疲劳扩展寿命计算[J]. 船舶与海洋工程, 2020, 36(2): 18-25+31. DOI:10.14056/j.cnki.naoe.2020.02.004 |
| [12] |
Zencrack User Manual[M].
|
| [13] |
ABS. Liquified gas carriers with independent tanks[S]. 2019.
|
 2022, Vol. 44
2022, Vol. 44
