0 引　言

入水砰击问题具有砰击区域多、砰击发生过程时间短和砰击压力峰值比较大等特点^[1]，为了深入了解结构物入水砰击现象，通常主要针对局部船体结构或者楔形体的入水砰击过程和载荷特性等问题开展研究。Von Karman^[2]把海上水陆飞机从空中入水时的变化简化为二维楔形体砰击静水面的过程，从而对砰击载荷进行了评估和研究。Wagner^[3]在1932年将该理论进行了推广，通过针对简化结构的分析计算，指出了湿表面在砰击载荷预报中的重要性。随着计算技术和计算能力的发展，许多高精度数值方法被用来解决复杂的水动力砰击问题。Zhao^[4]和Faltinsen^[5]采用非线性边界元研究了恒定位置下楔形体截面的入水问题，将结果与相似解进行比较验证了计算结果。Stenius^[6]采用Ls-dyna中的ALE方法预测了二维结构的砰击载荷。Veen & Gourlay和Seng分别采用光滑粒子流体动力学(SPH)方法和流体体积法（VOF）技术模拟船舶的入水砰击问题。在国内，陈翔等 ^[7]采用自主开发的基于移动粒子半隐式法的求解器对二维楔形体入水问题进行了数值模拟，研究了不同粒子布置方式以及斜升角对计算结果的影响。另外，张智^[8]采用Fluent对三维楔形体从不同高度自由落下进行数值仿真，研究其楔形体上的砰击压力分布。王易君等^[9]学者通过Fluent仿真软件对平底结构的自由落体入水过程进行了数值仿真模拟，得到了此过程的砰击载荷特性。Wang和Soares^[10-12]利用Ls-dyna数值仿真模拟了斜升角不同的楔形体、三维半球与圆锥体，并将仿真结果和试验结果做出比较。本文通过楔形体入水砰击试验来模拟船舶首部入水砰击现象并通过Ansys/Ls-dyna对楔形体入水砰击过程进行仿真分析，通过改变斜升角角度和楔形体下落高度来研究砰击载荷的变化规律，并对楔形体入水时压力的改变和水面抬升情况展开分析。研究成果可为船体首部砰击作用下砰击载荷的变化规律提供参考。

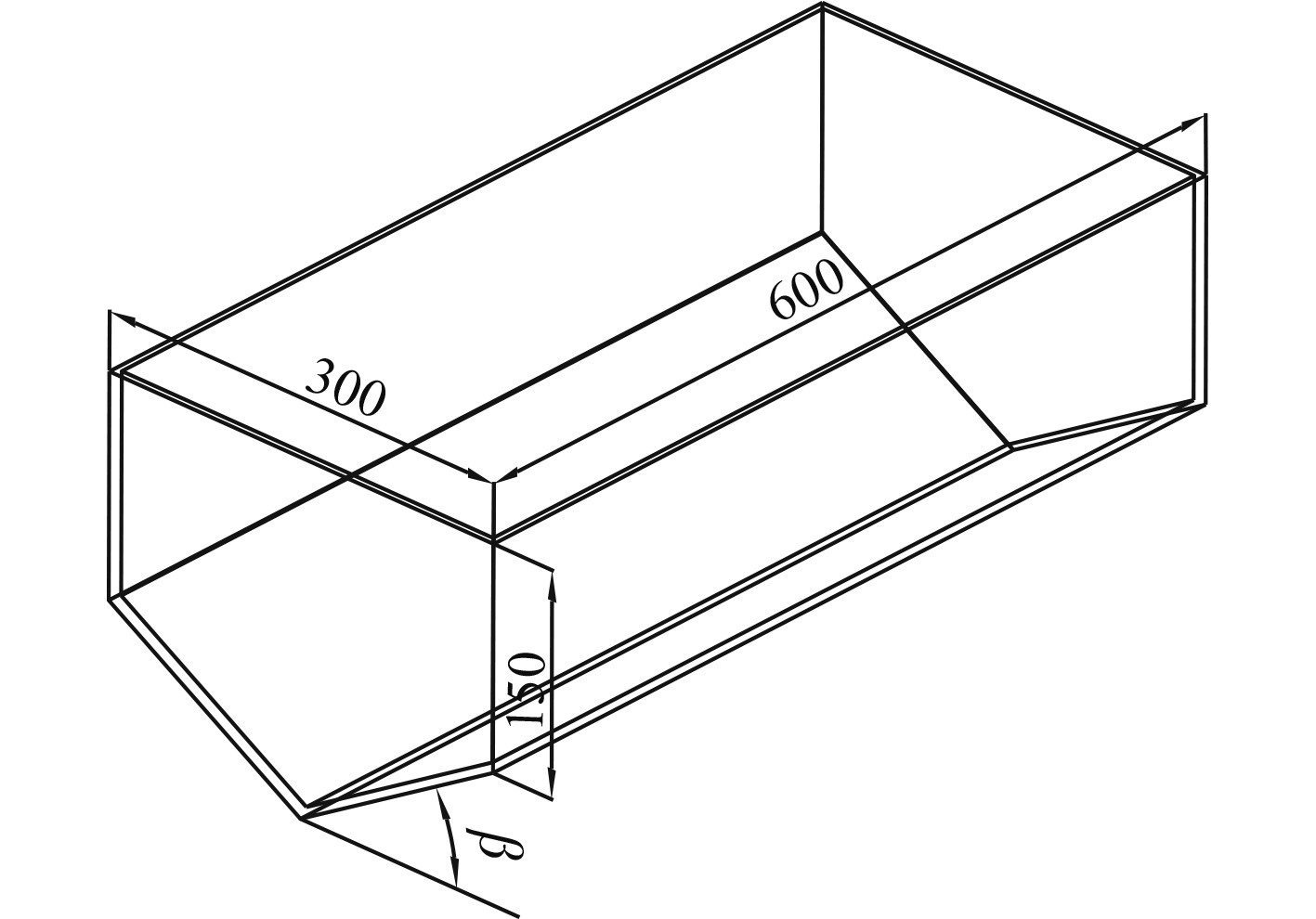
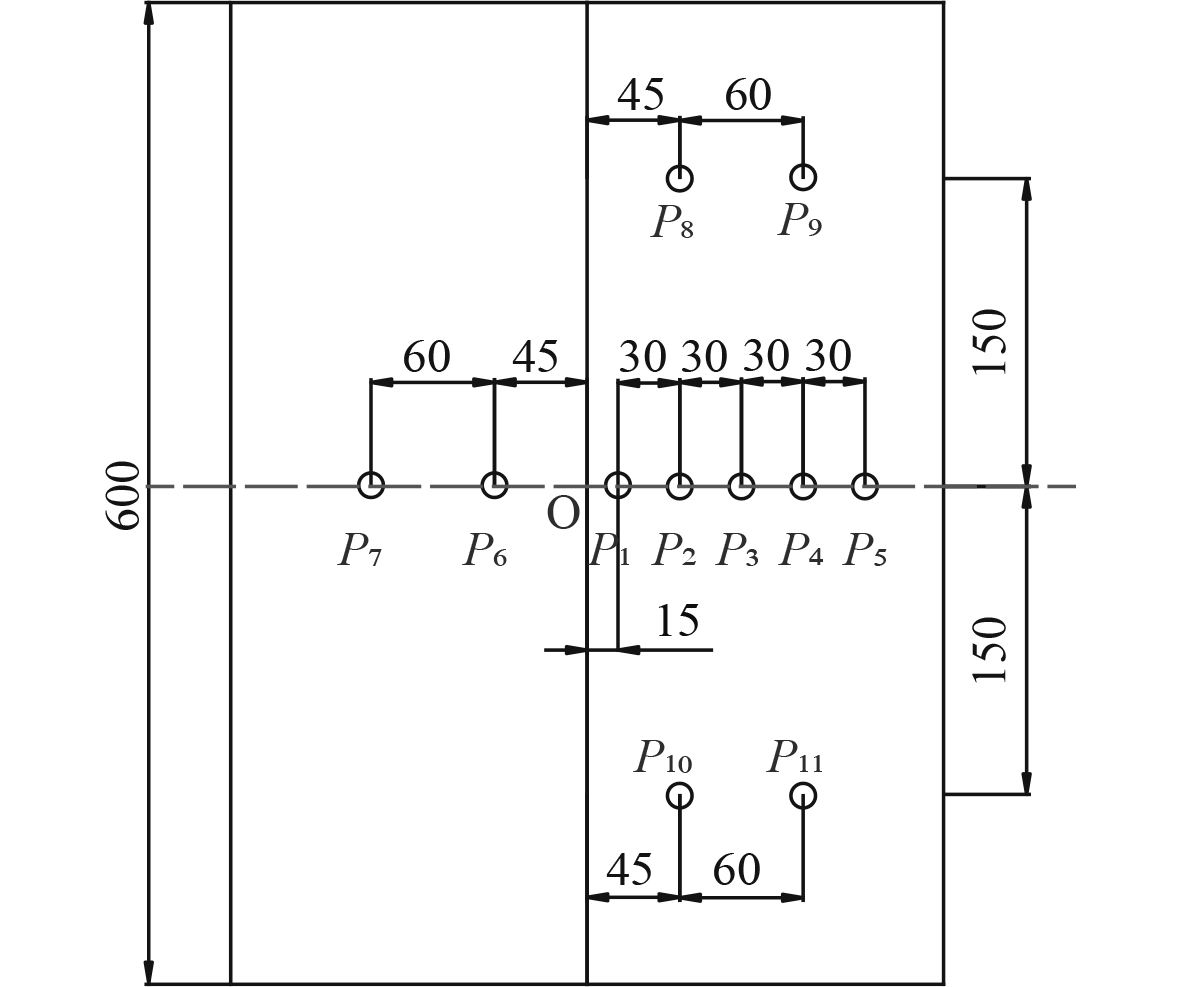
1 有限元模型

此次仿真参考的模型是二维楔形体试验模型，该试验模型进行了一系列试验。此实验模型为V形（楔形）底部剖面，底板分别有10°，20°，30°，40°的倾斜角β，模型尺寸图1所示。在试验过程中，为了测量位于试验模型底板不同位置处的抨击压力，测点以及相应的对比测点布置于试验模型底板的不同垂向位置，具体位置如图2所示。分别将O点视为中心点，把测点P₁放在底板横向中心线离O点15 mm处，测点P₂，P₃，P₄，P₅间隔30 mm，测点P₆与P₇与测点P₂与P₄为对称点，测点P₈，P₉与测点P₁₀，P₁₁为对称点。

每一个楔形体的试验板厚0.05 m，如表1所示。表中给出了不同斜升角楔形体的质量，其中，用于吊装楔形体的吊链为0.6 kg。

通过Ansys/Ls-dyna对不同斜升角的楔形体进行有限元数值仿真分析。结构与流体之间的耦合采用多材料拉格朗日-欧拉（ALE）算法和罚函数耦合算法模拟；楔形体由于其结构尺寸以及入水速度较小，使用刚性材料(*MAT_RIGID)做简化处理。分别采用Gruneisen状态方程和线性多项式Polynomial状态方程表示水和空气，空材料（*MAT_NULL）模型与状态方程联用表示水域和空气域的材料，两者模型都选择的是3D Solid 164单元。

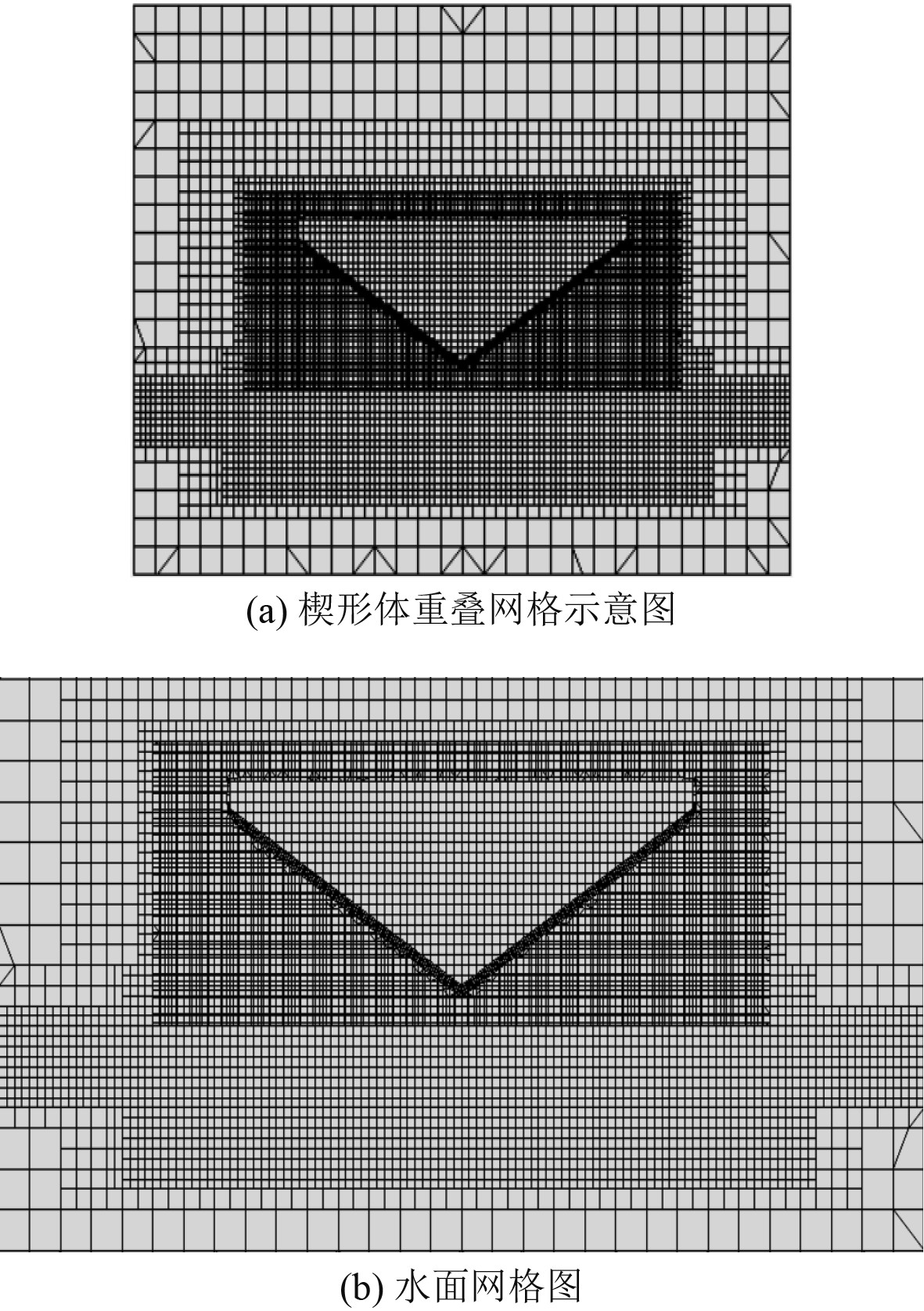
楔形体的网格采用多种不同的方法在计算区域内部设置，由于在2个单元之间放入变量的时候会产生误差，所以在最大的区域和重叠的区域中使用的单元尺寸相同，这样可以有效地减小由于网格尺寸带来的计算问题。楔形体具体的网格设置具体如图3（a）所示，其中背景网格的设置0.02 m，重叠区域的网格设置0.008 m。因为在楔形体入水的过程中，为了能够捕捉到明显的砰击现象，本次模拟是在重叠网格处使用较小的网格，如图3（b）所示。将水面区域的网格进行细化，其中细化区域的网格设置为：计算域在纵向与横向上的网格大小设为8 mm，垂向的网格设置为72 mm。在水面周围设置的网格和水面的网格设置相同，纵向与横向的网格设为8 mm，垂向的网格设置为72 mm。

由于研究的结构为二维结构，因此选择一个单元进行计算（楔形体长度Z方向），同时使用无反射边界条件作为流体的边界，此无反射边界条件可以削弱声波反射的影响。在计算过程中，楔形体位于水面上0.01 m的位置，让楔形体以速度 $ V $ 下落，可依靠试验条件中下落的高度确定速度 $ V $ 。

2 计算结果分析 2.1 不同斜升角对楔形体砰击压力的影响

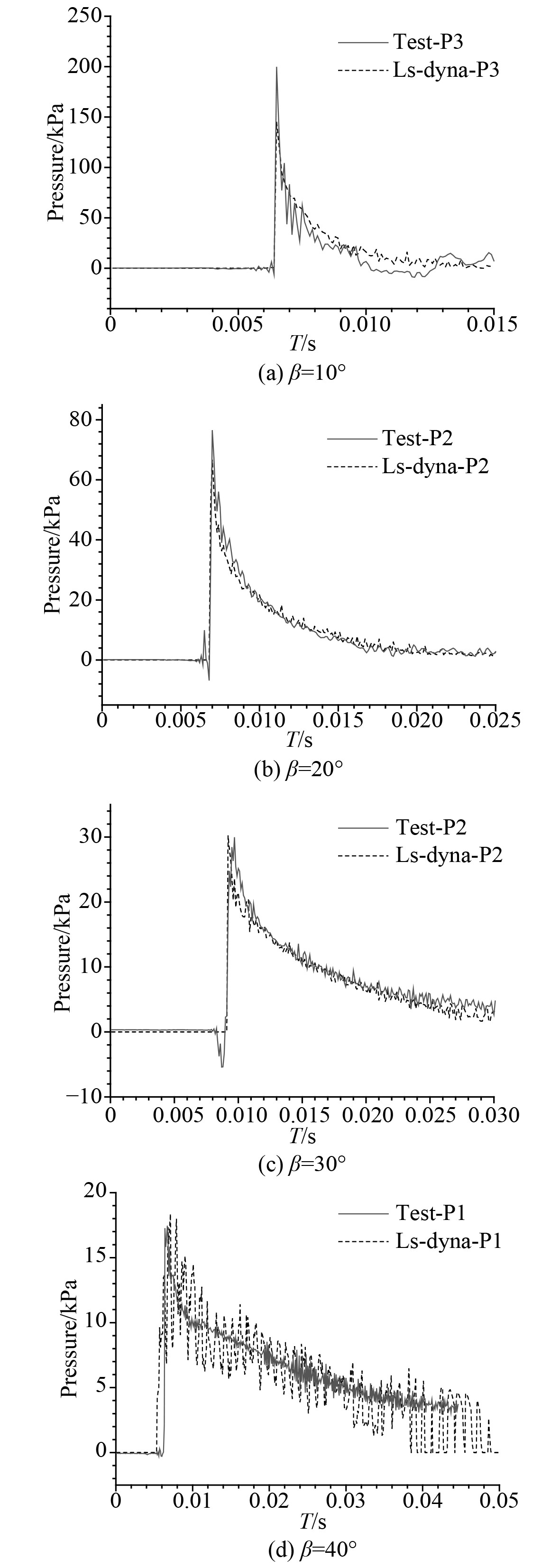
图4为不同斜升角的楔形体的砰击压力试验值和计算值在最大砰击压力峰值的测点的对比，展示了从0.4 m处落下时的砰击压力曲线。由图可知，当楔形体的角度为10°时，楔形体（见图4（a））在刚发生砰击的时刻砰击载荷最大，楔形体上的第一个测点会有较高的砰击载荷，然后再减小并逐渐稳定。图4（b）中楔形体斜升角为20°时在测点P₂的砰击压力峰值的变化曲线和斜升角是10°的相似，变化同样为先变大后变小，且砰击压力在仿真和试验下的变化趋势吻合很好。斜升角分别为30°和40°楔形体和前两种楔形体不同的地方在于砰击压力峰值较小，这是由于当楔形体砰击入水时，斜升角较小的楔形体，即10°和20°楔形体的底板会影响液面抬升，所以当液面在不断抬升时，自由液面会受到底板不断增加的挤压力，因此这时的砰击载荷也会随之不断增大。等自由液面达到特定高度之后，就会发生波浪破碎的现象，这时就会出现砰击载荷的峰值。随后，砰击载荷就会逐渐减小，这时因为楔形体的表面和液面的分开导致的，并且当楔形体的角度较大时，自由液面的上升不会受到底板太大的影响。从总体结果上来看，本文所采用的研究二维楔形体入水砰击问题的数值方法基本能满足研究需要，即证明了该方法的有效性。

楔形体的砰击压力会随着斜升角而变化，即当斜升角的角度越大，砰击压力值就越小。试验值和仿真值的数值对比如表2所示。可以看出，试验值的结果和仿真值的结果较为接近，误差较小，除10°的楔形体的结果误差较大，其余斜升角的误差都在15%以内。

2.2 不同入水高度对楔形体砰击压力的影响

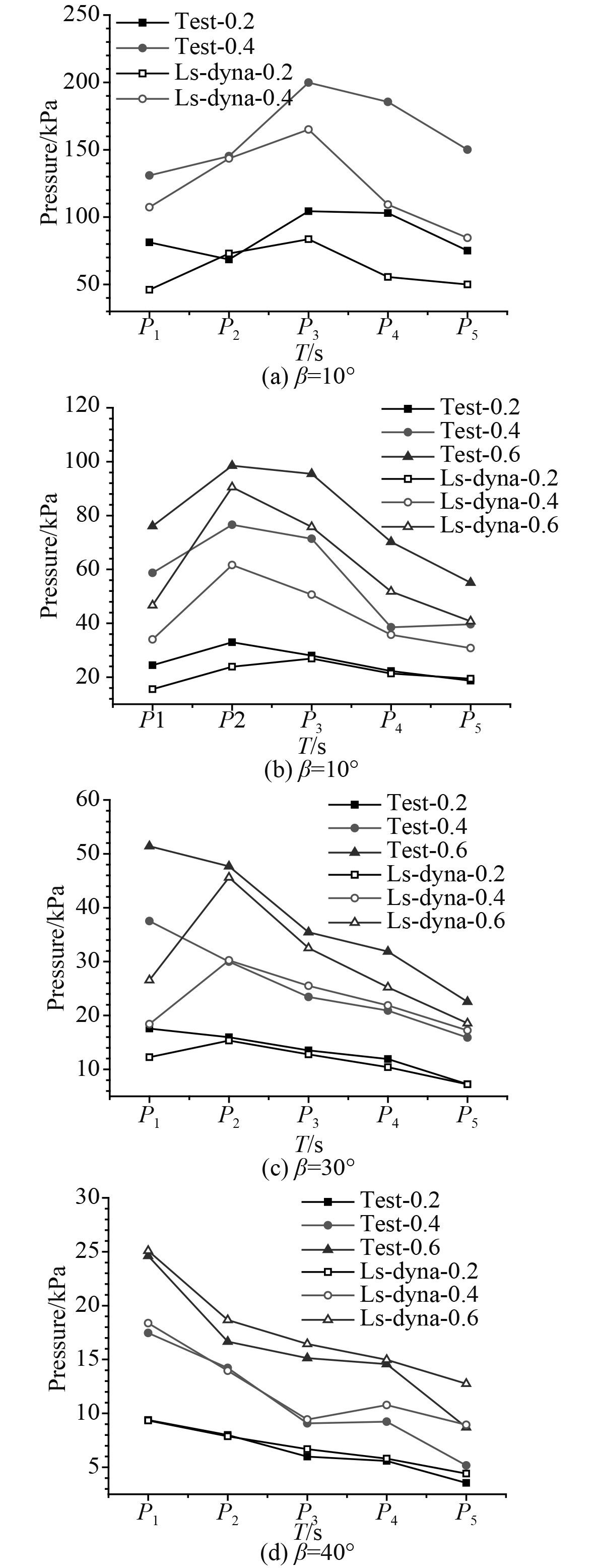
为了研究楔形体在不同入水速度下的砰击压力对比，本文通过改变楔形体的入水高度改变入水速度，在楔形体斜升角为10°时，分别以楔形体在0.2 m，0.4 m高度下落时的入水砰击压力峰值做对比，在楔形体斜升角为20°时，分别以楔形体在0.2 m，0.4 m，0.6 m高度下落时的入水砰击压力峰值做对比，在楔形体斜升角为30°时，分别以楔形体在0.2 m，0.4 m，0.6 m高度下落时的砰击压力峰值做对比，在楔形体斜升角为40°时，分别以楔形体在0.2 m，0.4 m，0.6 m高度下落时的砰击压力峰值做对比。图5为在不同高度处楔形体下落时砰击压力峰值的试验值和计算值在各测点的对比曲线。

从图5可以看出，当入水速度越快时，即入水高度越高时，砰击载荷的峰值也会越来越大，但处于同一速度（即同一高度），不同角度的楔形体入水时，当它们的角度越来越大，最后的砰击载荷峰值就会越来越小，对不同高度下不同斜升角的砰击压力峰值比较，斜升角为10°时，P₃测点处砰击压力值最大，当斜升角为20°和30°时，在P₂测点砰击压力值最大。这是因为当斜升角越来越小时，砰击压力会受到更多的自由液面上升的影响，并且波浪破碎的现象会更加明显，而在楔形体的斜升角越来越大时，自由液面的上升和波浪破碎现象对砰击压力的影响就会越来越小。

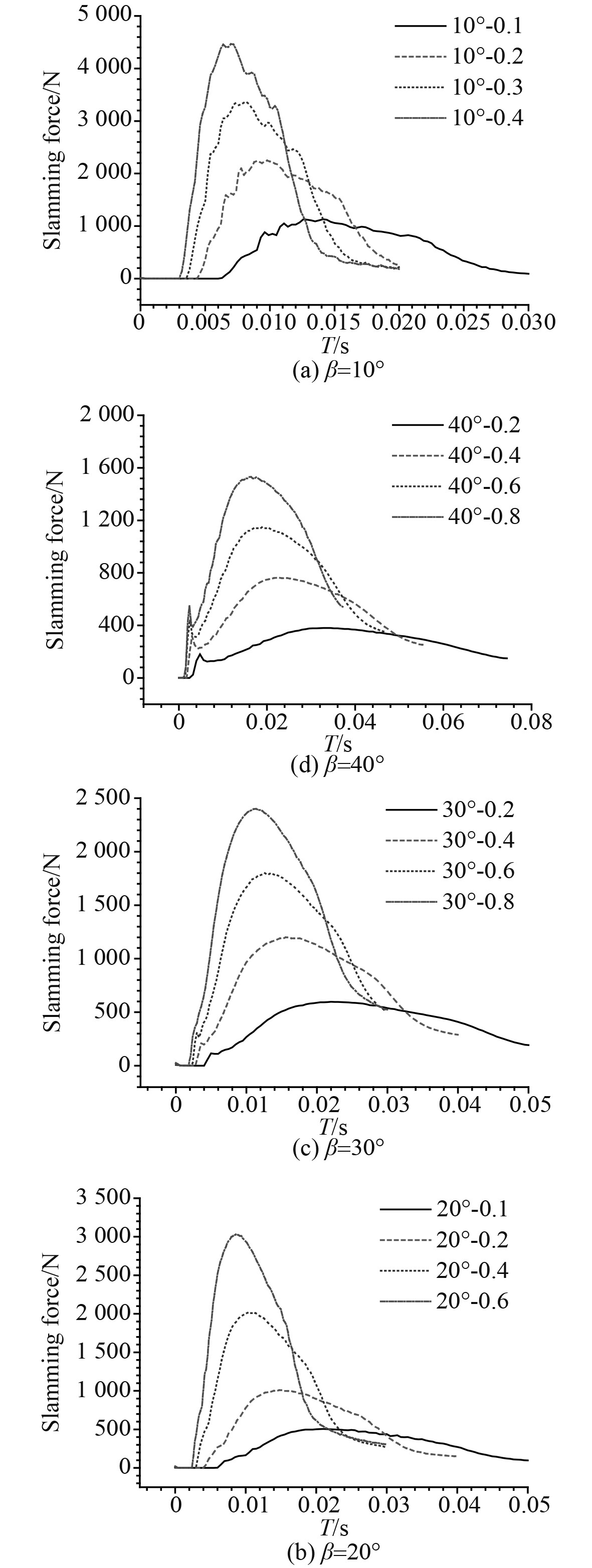
2.3 垂向砰击力

图6给出了不同大小斜升角的稧形体在以不同速度状态下入水冲击静水面时所产生的垂向砰击力。图6中的数字表示楔形体最低点距水面的距离。

根据图6显示，斜升角不同的楔形体在入水与水发生抨击时，垂直方向的砰击力大小具有先变大后变小的趋势，并且垂直方向的砰击力大小变化比较小，这是因为垂向砰击力代表的是整体结构的平均力大小。随着楔形体斜升角的不断增加，垂直方向的砰击力开始明显变小；当楔形体的斜升角一样时，随着物体下降高度的增加，垂直方向的砰击力开始逐渐变大。

2.4 砰击压力系数

砰击压力系数 $ {C_p} $ 是砰击压力 $ P $ 的无因次量，表达式如下：

$ {C_p} = \frac{P}{{\dfrac{1}{2}\rho {V^2}}} 。$

(1)

其中： $ P $ 为结构受到的砰击压力； $\ \rho $ 为水的密度； $ V $ 为结构入水速度。

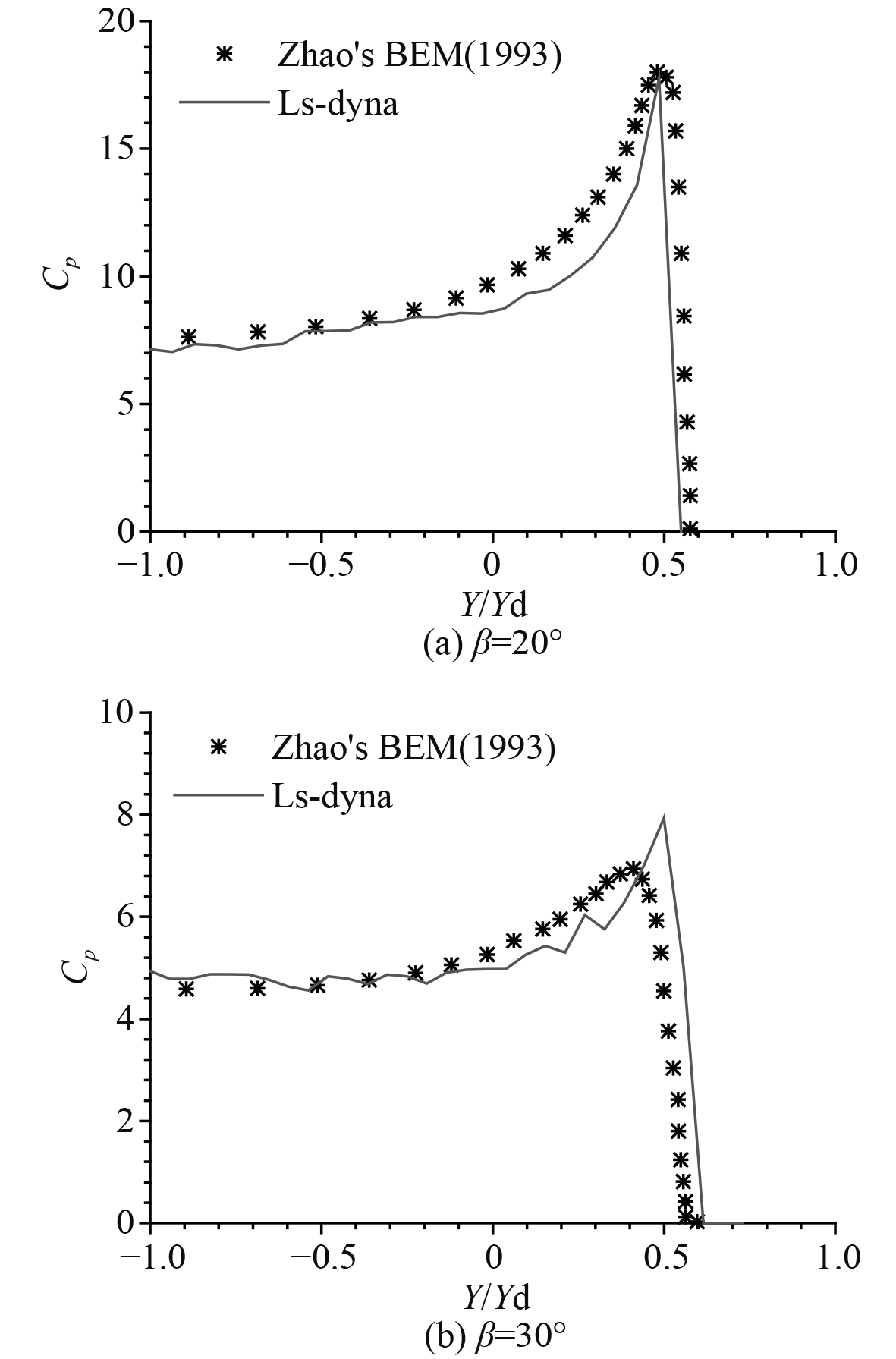
将根据有限元数值仿真结果得到的楔形体湿表面的砰击压力系数与Zhao等^[4]边界元法(BEM)算出的砰击压力系数比较，当斜升角大小为20°和30°，并且楔形体砰击压力达到峰值时，其湿表面的砰击压力系数分布如图7所示。可知，横坐标 $ Y/Y{\text{d}} $ 代表湿表面各点纵坐标与吃水的比值，表面与水面的交点用0表示，1表示楔形体最底端。可以发现，BEM法算出的数据和根据有限元数值仿真得出的结果基本一致，当稧形体的角度是30°时，有限元仿真计算得到的结果高于BEM法计算得到的结果。

图8为根据经典的理论解、试验和有限元仿真结果比较得到的砰击压力系数 $ {C_p} $ 和斜升角 $ \beta $ 的关系曲线。可知，理论、试验和仿真得到的最大砰击压力系数在 $ \beta \geqslant 20^\circ $ 时趋于一致，在 $ \beta < 20^\circ $ 时有明显差别，这种情况是因为对自由液面使用的处理方式有所差别而导致的。当 $ \beta {\text{ = }}10^\circ $ 时，试验和Stavovy和Chuang(1976)得到的最大砰击压力系数趋于一致。而仿真结果得到的最大砰击压力系数则介于Stavovy和Chuang(1976)与Ochi和Motter(1993)所得到的数值之间。

2.5 楔形体入水时自由液面抬升

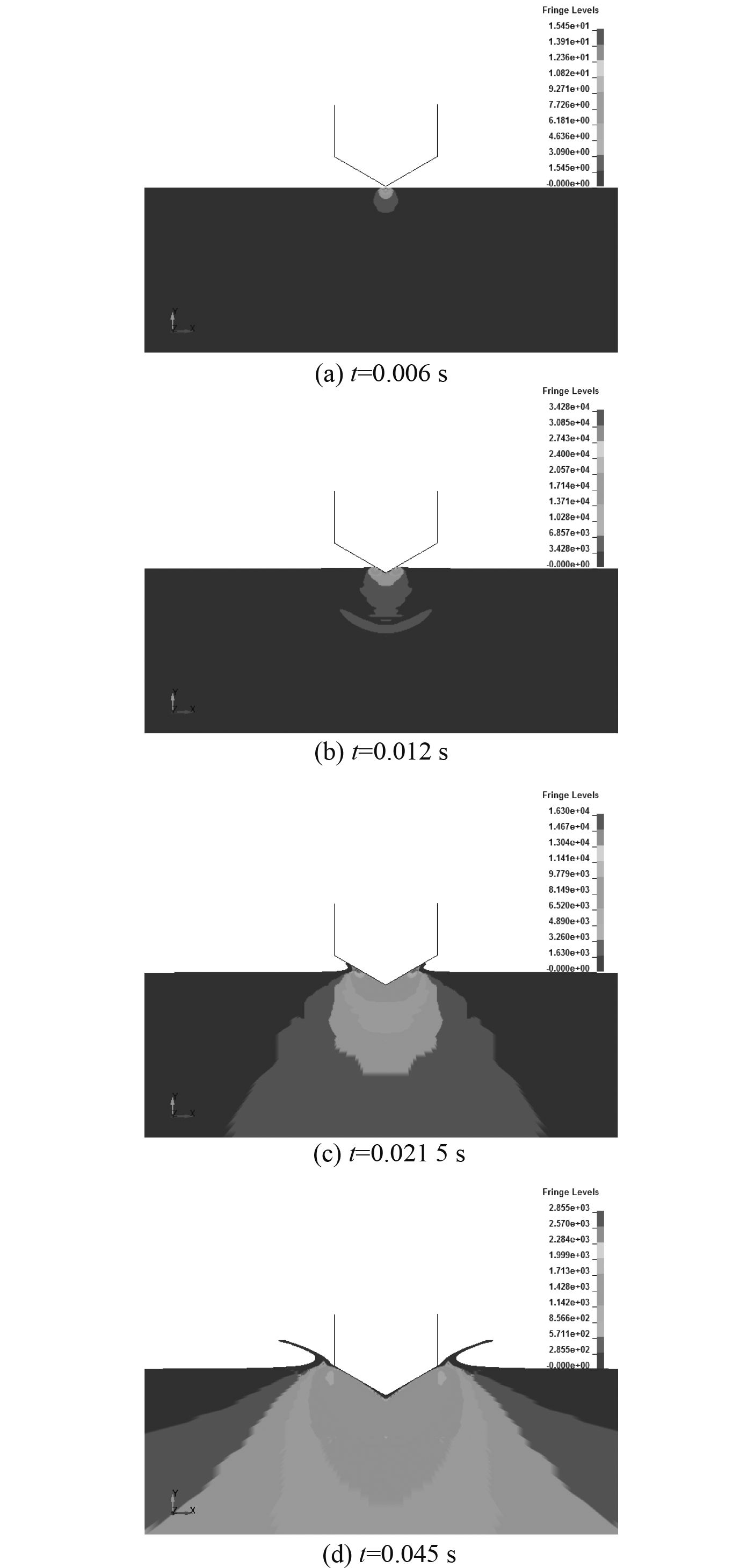
斜升角为30°的楔形体从0.4 m高度处下落时自由液面的变化情况如图9所示。图9（a）为楔形体即将接触水面时的情形，此时楔形体底面受到的砰击压力较小；图9（b）和图9（c）表明，在射流分离之前，最大压力值出现在喷射内域，射流处的压力要比喷射根部的压力小的多，这就是砰击压力在达到峰值后迅速减小的原因；图9（d）给出了射流分离之后，压力沿着楔形体表面的分布情况。可以看出，压力减小的非常快而且压力峰值移动到了楔形体龙骨（即中纵线）附近。

3 结　语

本文以楔形体入水试验为研究对象，通过改变斜升角的大小，入水的高度，采用Ansys/Ls-dyna有限元仿真软件对楔形体的砰击压力和垂向方向的砰击力在入水时的变化规律进行了分析，并和通过试验得到的变化规律进行对比，最后对楔形体入水时自由液面的抬升现象进行了讨论。本文得出的结论主要有以下几点：

1）楔形体的砰击压力在接触水面时瞬间增大，之后逐渐变小趋于稳定。

2）影响砰击压力的主要因素是楔形体的斜升角以及入水时的高度，当斜升角减小，楔形体入水高度越高时，其入水速度增大，砰击压力开始明显增大。

3）在斜升角是30°和40°的，有限元模拟得出的砰击压力与实验结果吻合较好。当斜升角为10°和20°时，有限元模拟得出的峰值与实验的得出的砰击压力峰值相差较大。这个过程需要更细的网格来模拟更薄的射流。