泡沫夹芯结构具有优良的比刚度和比强度、吸收噪声、抑制震动和抗疲劳等特点,自20世纪中期就开始越来越多地被运用于各个领域,如舰船的抗爆抗冲击等[1-3]。船用夹芯板芯层由多孔材料组成,有良好的静力学和动力学特性,能够吸收和衰减爆炸产生的冲击波[4-6]。目前,学者们依旧关注于低速冲击和空爆载荷作用下泡沫夹芯板的结构变形及其破坏机理,而水下爆炸[7-9]过程中炸药爆轰气体挤压周围流体介质,以高压冲击波方式传播,具有瞬态、高频率、强间断性[10-12]等特点,对于这方面的研究十分有限。本文采用Ls-dyna提供的任意拉格朗日-欧拉方法(ALE方法),从结构变形[13]及吸能的角度,探究船用PVC夹芯板在近场水下爆炸载荷作用下的响应,为泡沫夹芯板的应用及舰船结构防护设计提供参考。
1 ALE方法理论ALE方法[14]广泛应用于求解大变形以及流固耦合问题,在求解过程中网格能够根据初始定义的参数进行适当地运动,兼具Lagrange和Euler方法的优点。
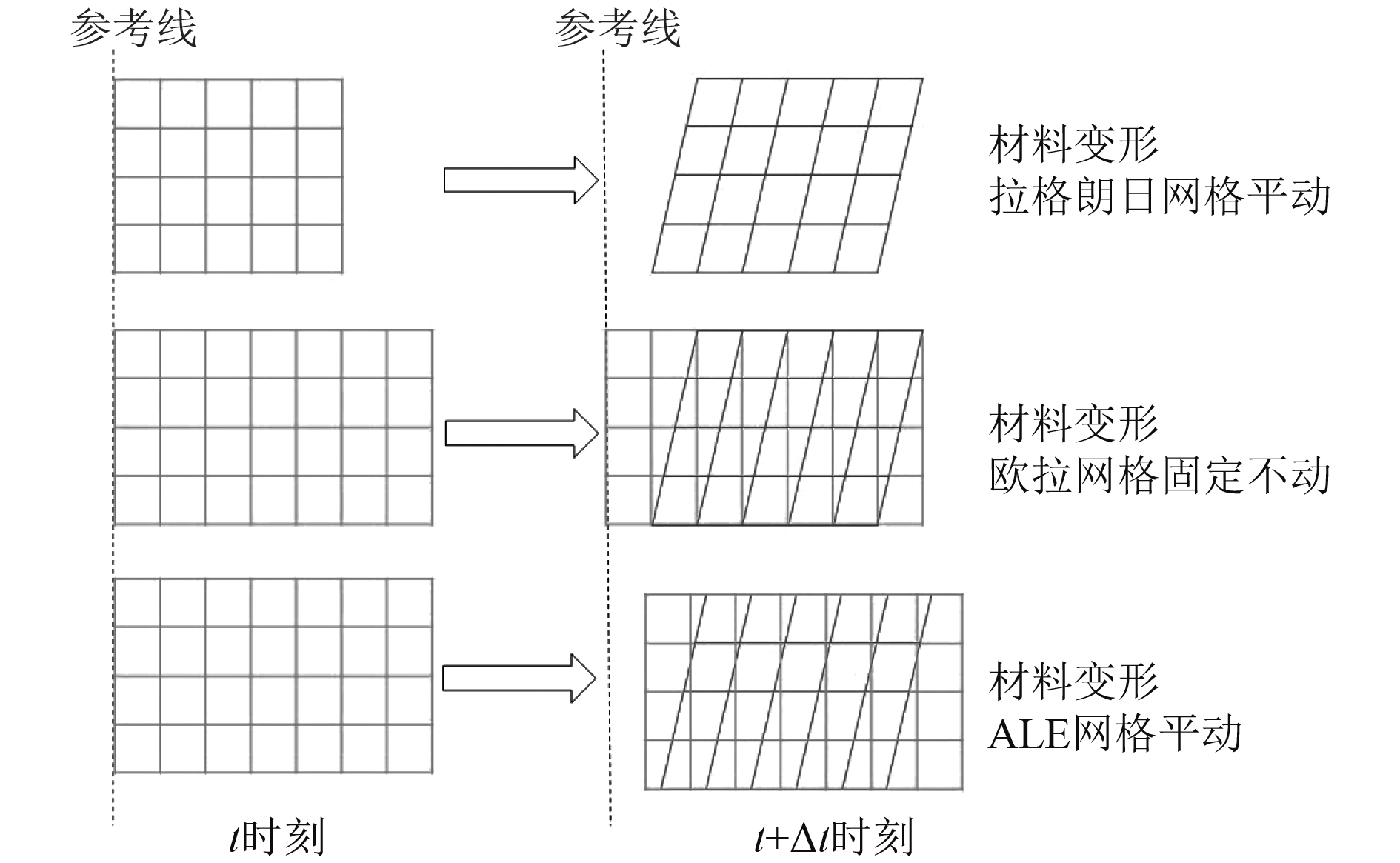
图1介绍了计算中3种不同类型网格变化过程,自上而下分别为拉格朗日网格、欧拉网格和ALE网格。采用欧拉网格进行计算时,结构发生变形但网格是固定的;而在拉格朗日网格描述中,网格跟随结构一起发生变形。ALE网格中包含了2种重叠的网格,一种是背景网格,它能在空间中任意移动,另一种是虚拟的也就是材料网格,它可以在空间中的背景网格中运动。而材料网格的运动被人为地分成了2步。第一步把材料网格定义成了虚假的拉格朗日网格,第2步则是把变形的拉格朗日网格重新映射到背景网格中。对于大变形过程的数值分析,ALE方法的优点表现为其计算网格不依赖于结构与空间运动,可以根据计算需要适当地选择运动状态。因为运动的背景网格,相比于欧拉方法,ALE方法每个时间步内输运的材料距离更短,由此提高了计算效率和精度。与其他有限元方法类似,在求解过程中,需要保持质量守恒、动量守恒和能量守恒。
|
图 1 不同网格描述方法(紫色为材料网格,绿色为背景网格) Fig. 1 Different description of grid methods(purple for material mesh, green for background mesh) |
ALE形式的控制方程为[15]:
| $ \frac{{\partial \rho }}{{\partial t}} = - \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} - \left( {{v_i} - {u_i}} \right)\frac{{\partial \rho }}{{\partial {x_i}}},$ | (1) |
| $ \rho \frac{{\partial {v_i}}}{{\partial t}} = {\sigma _{i,j}} - \rho \left( {{v_i} - {u_i}} \right)\frac{{\partial {v_i}}}{{\partial {x_j}}},$ | (2) |
| $ \rho \frac{{\partial e}}{{\partial t}} = {\sigma _{ij}}{\varepsilon _{ij}} - \rho \left( {{v_i} - {u_i}} \right)\frac{{\partial e}}{{\partial {x_j}}},$ | (3) |
其中:
前处理时,通过定义关键字*CONSTRAINED_LAGRANGE_IN_SOLID来控制流体单元与拉格朗日结构单元之间的耦合,若结构网格与ALE网格发生穿透,假设两者之间有一弹簧结构限制两者发生相对位移,运用阻尼消除高频振荡,接触力[16]表示为:
| $ {F_s} = - {F_c} = k \cdot {\boldsymbol{d}} + {C_i} \cdot {{\dot {\boldsymbol{d}}}}。$ | (4) |
式中:
参照Radford[17]实验,选取表1所示工况进行仿真计算。结构几何尺寸及材料参数参照文献[17]。泡沫夹芯板分为前面板、芯层和后面板,计算工况主要从结构变形及能量吸收角度分析夹芯板的响应特性,并不关注结构损伤。建立模型时,面板采用壳单元,芯层泡沫采用实体单元,并通过关键字*MAT_CRUSHABLE_FOAM各向同性模型来定义其材料属性,该模型能有效地模拟冲击过程中泡沫的屈曲,有利于提高计算效率。面板与芯层进行共节点处理,并且此模型考虑了材料的应变率效应。
图2给出了4组不同速度工况下后面板中心点最终挠度随冲量变化的对比图。可知,工况1中有限元模拟结果要略大于实验结果;后3组工况中,有限元仿真得到的变形均小于文献[17]中的实验所测数据。当冲击速度较低时,实验与仿真误差在15%左右,随着冲击速度的提高,误差随之降低,当速度超过400 m/s时,误差会降至10%左右,从而验证了所选取模型在模拟冲击问题时的有效性。

|
图 2 后面板最终挠度对比(实验数据源自Radford[17]) Fig. 2 The comparison of back plane (experimental data from Radford[17]) |
以圆形泡沫夹芯板为研究对象,其结构组成可分为前面板、后面板及芯层。建模时,前后面板的截面属性定义为单层的各向同性金属板,厚度均为1 mm,材料选用高强度钢,具体参数见表2[7]。夹芯板半径为80 mm,芯层材料为PVC H100泡沫,厚度取20 mm,材料参数见表3。夹芯板结构的边界条件定义为四周刚性固定。
|
|
表 2 高强度钢材料参数 Tab.2 Parameters of high strength steel |
|
|
表 3 PVC H100材料参数 Tab.3 Parameters of PVC H100 |
流场分布及炸药位置用关键字*INITIAL_VOLUME_FRACTION_GEOMETRY定义,炸药为15g TNT,药包中心点距离夹芯板前面板25 mm,距水面150 mm,位置示意如图3(a)所示,有限元计算模型如图3(b)所示。TNT采用JWL状态方程描述,水的状态方程采用*EOS_GRUNEISEN描述,具体参数见文献[18]。空气采用理想气体状态方程进行描述,具体参数见文献[19]。对于边界条件的选择,由于实际水下爆炸过程中,水域相对较大,为了在仿真计算中模拟该条件即减弱甚至消除边界壁面的反射波影响,需要选择无反射边界条件,以提高计算精度。同时为了提高计算效率,在适当区域进行加密处理,在其他区域可选择较为稀疏的网格。在本模型计算时,加密范围为冲击波与结构耦合作用的区域。

|
图 3 有限元模型 Fig. 3 Finite element model |
图4给出了圆形PVC夹芯板在计算工况下的挠度变形云图,其最大变形挠度约为19 mm。不同于空中爆炸与子弹冲击载荷作用下的结构局部剧烈变形,近场水下爆炸载荷作用下的板架结构呈现出整体的变形,挠度的变化特征表现为从药包中心即爆心所对应的结构中部向四周减小,冲击波的指向性不如空中爆炸,这可能与冲击波在水中独特的传播规律以及结构与流场的耦合作用有关。

|
图 4 最终挠度云图 Fig. 4 Final deflection contour |
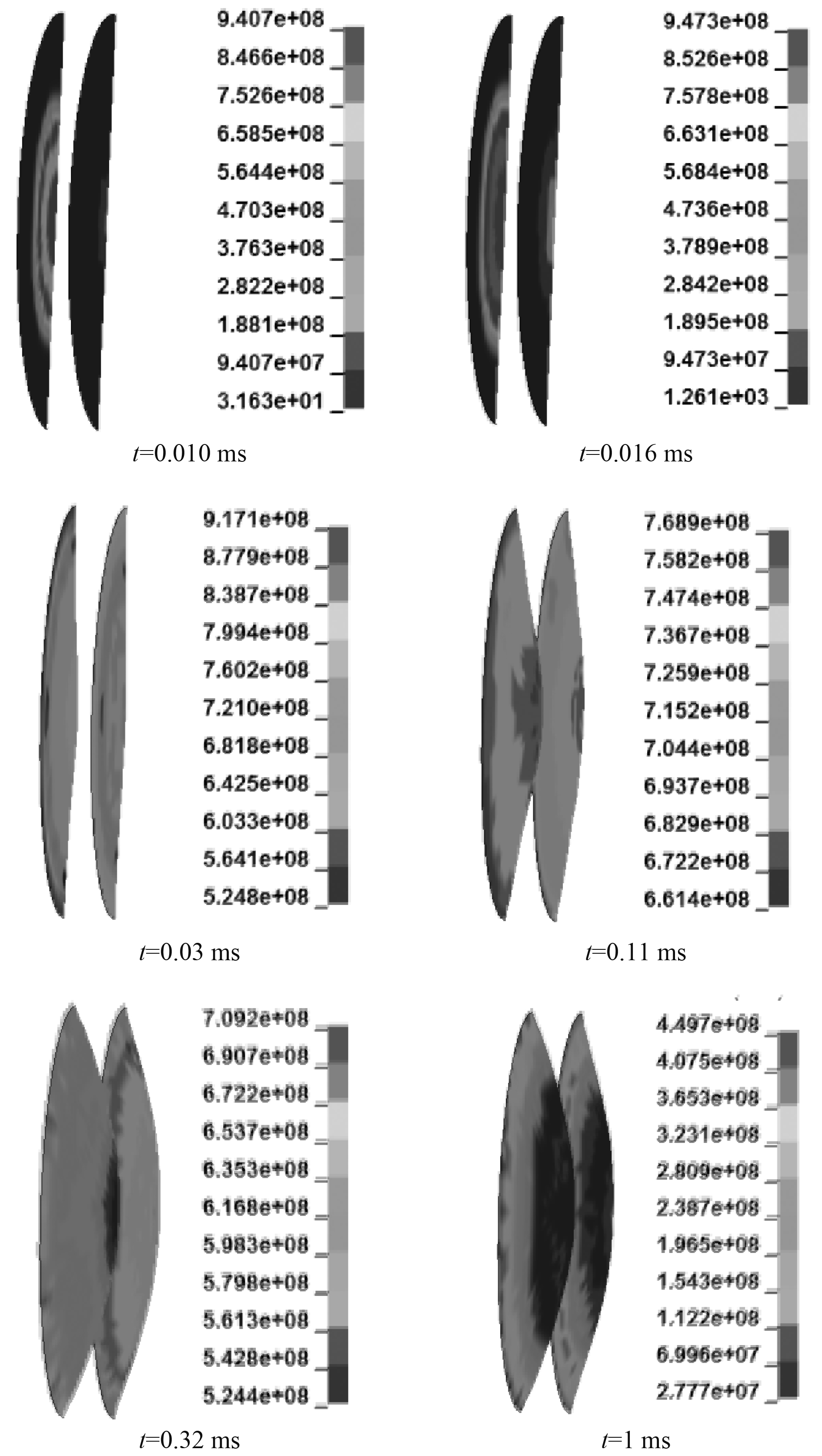
图5给出了夹芯板在计算工况下的动态响应过程,后处理时只显示前后面板的应力云图以便于观察整体变形。可以看出,在t=0.01 ms时,冲击波就已经到达前面板结构并使结构产生了一定的响应,板中出现了显著的应力波。随后t=0.016 ms时,应力波向结构径向传播,同时前面板变形压缩芯层,后面板中心出也出现了应力增强现象。随着应力波继续传播,面板会在惯性作用下继续产生挠度变形,挤压芯层和后面板,直至在t=0.32 ms左右达到最大挠度变形。
|
图 5 计算工况下的响应过程 Fig. 5 The response process of computation condition |
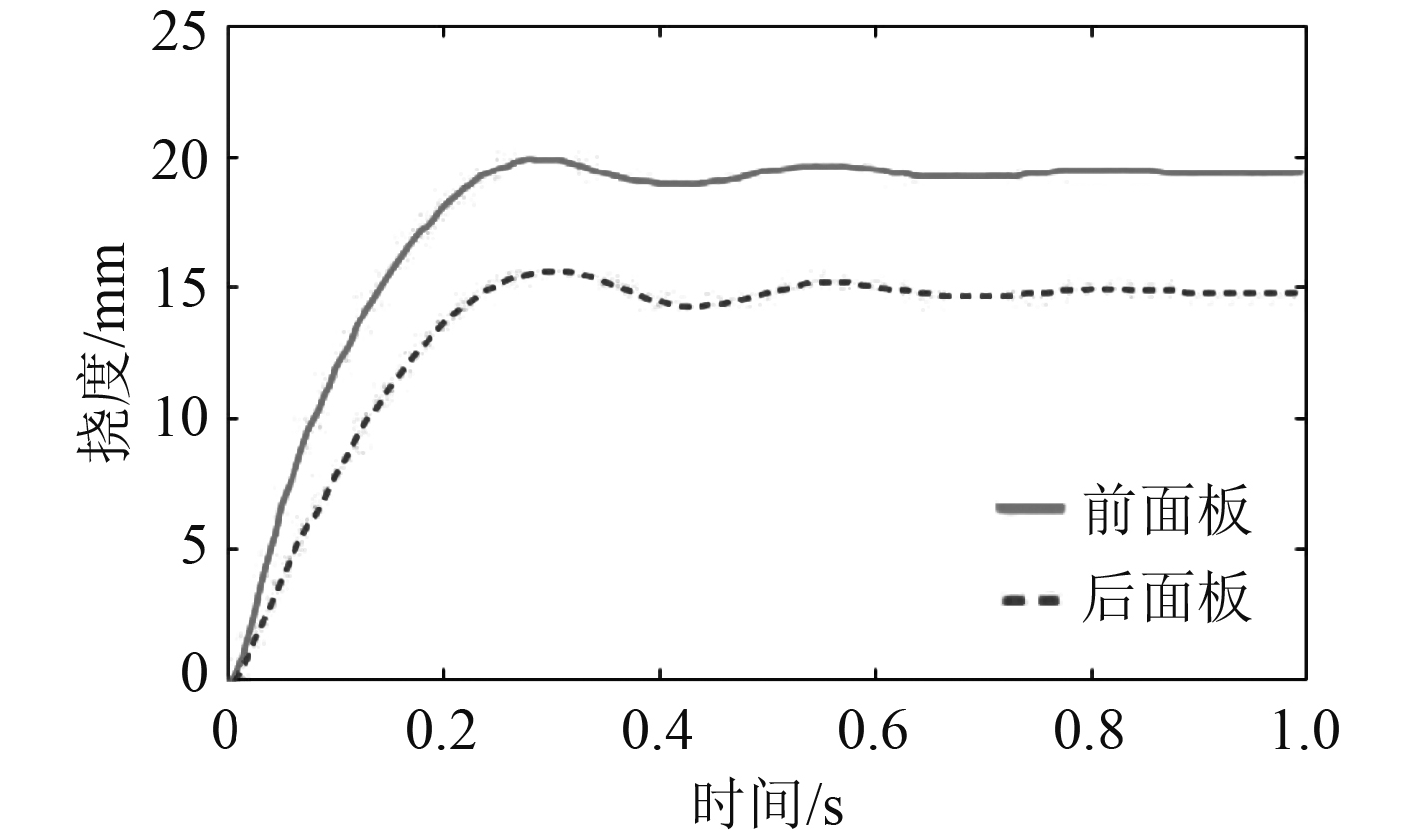
图6给出了前后面板中心处的挠度随时间变化的关系。在达到最大挠度变形即t=0.32 ms之前,前后面板随着爆炸产生的冲击波不断作用,其挠度变形不断增大,但增大的趋势变得逐渐平缓,这可能是因为随着时间增加,爆炸产生的能量耗散得越来越多,使得作用于结构上的能量减少。在t=0.32 ms左右,结构变形达到了最大变形,前面板约为20 mm,后面板约为15.5 mm。在0.32~0.8 ms之间,结构在冲击波和结构自身阻尼作用下于平衡位置震荡,随后趋于稳定,挠度不再发生变化,前面板平衡时挠度约为19.5 mm,而后面板约为15 mm,其变形程度约为前面板的77%。
|
图 6 面板中心点处挠度时历曲线 Fig. 6 Midpoint deflection time historical curve |
图7为前后面板的等效塑性应变云图。可以看出最大塑性应变发生在面板中心处,且塑性应变沿着径向不断减小。从云图中能明显看到前面板的最大等效塑性应变约为0.22,而后面板最大塑性应变相对于前面板降低了约60%,只有0.088。可见在爆炸载荷作用下,前面板和夹芯结构吸收了大量的冲击波能量,有效地保护了后面板,使之不易受损。

|
图 7 等效塑性应变云图 Fig. 7 Effective plastic strain contour |
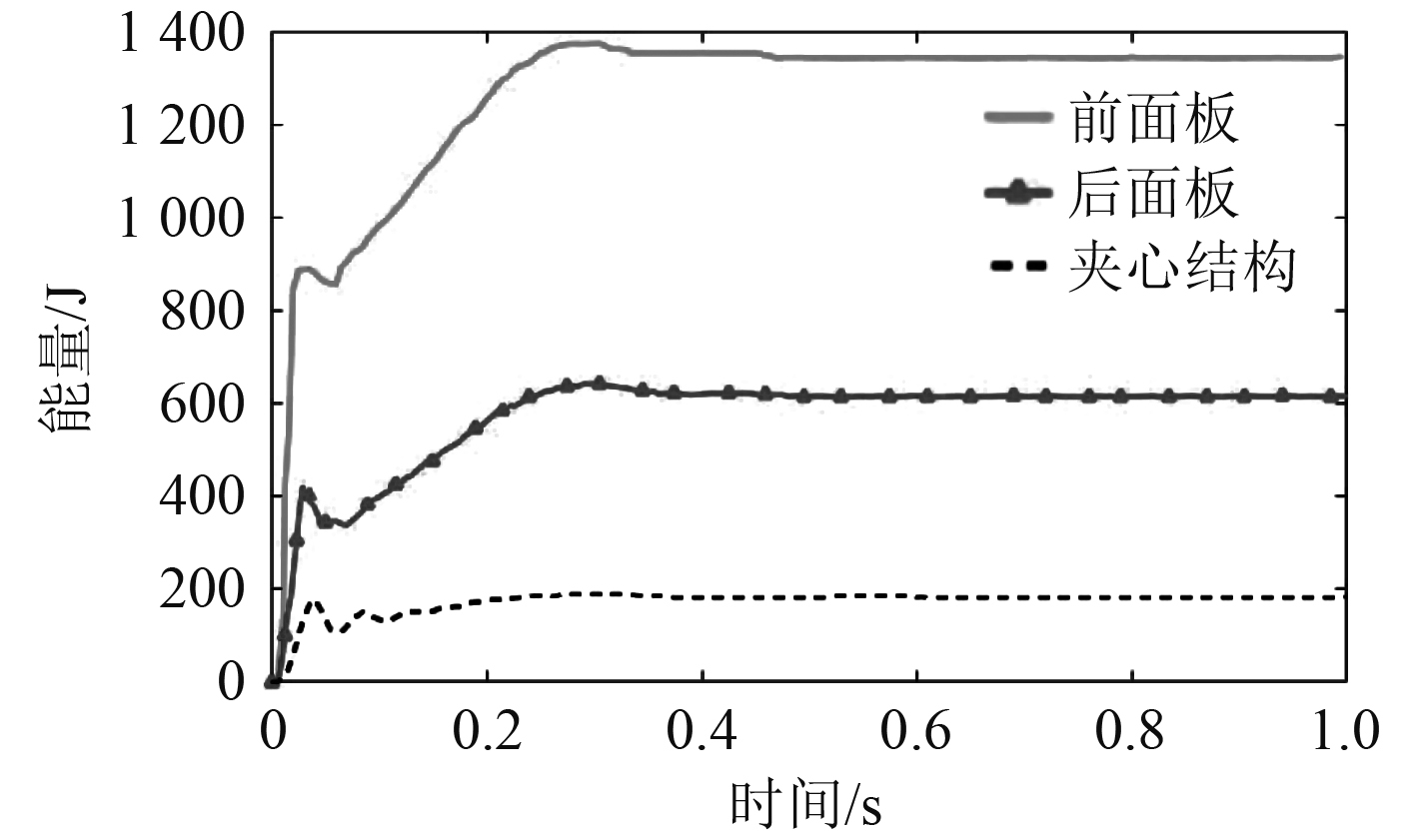
图8给出了前后面板及泡沫夹芯的能量吸收随时间变化的曲线。结合图5所给的响应时历图,在近场水下爆炸冲击波作用下夹芯板的能量吸收过程呈现出多阶段性,大致可以分为4个阶段。第1阶段,0~20 μs冲击波传递到结构中并在其中迅速传播,使得结构的能量吸收急剧爬升;第2阶段,能量吸收会有些许下降并呈现出短时间的震荡;第3阶段,冲击波载荷持续作用下结构强度变弱,能量吸收虽然仍在增加但吸收速率显著降低;第4阶段在30 ms时,能量吸收达到最大值,然后小幅下降至稳定值。
|
图 8 各部分能量吸收时历曲线 Fig. 8 Time histories of energy absorption of each component |
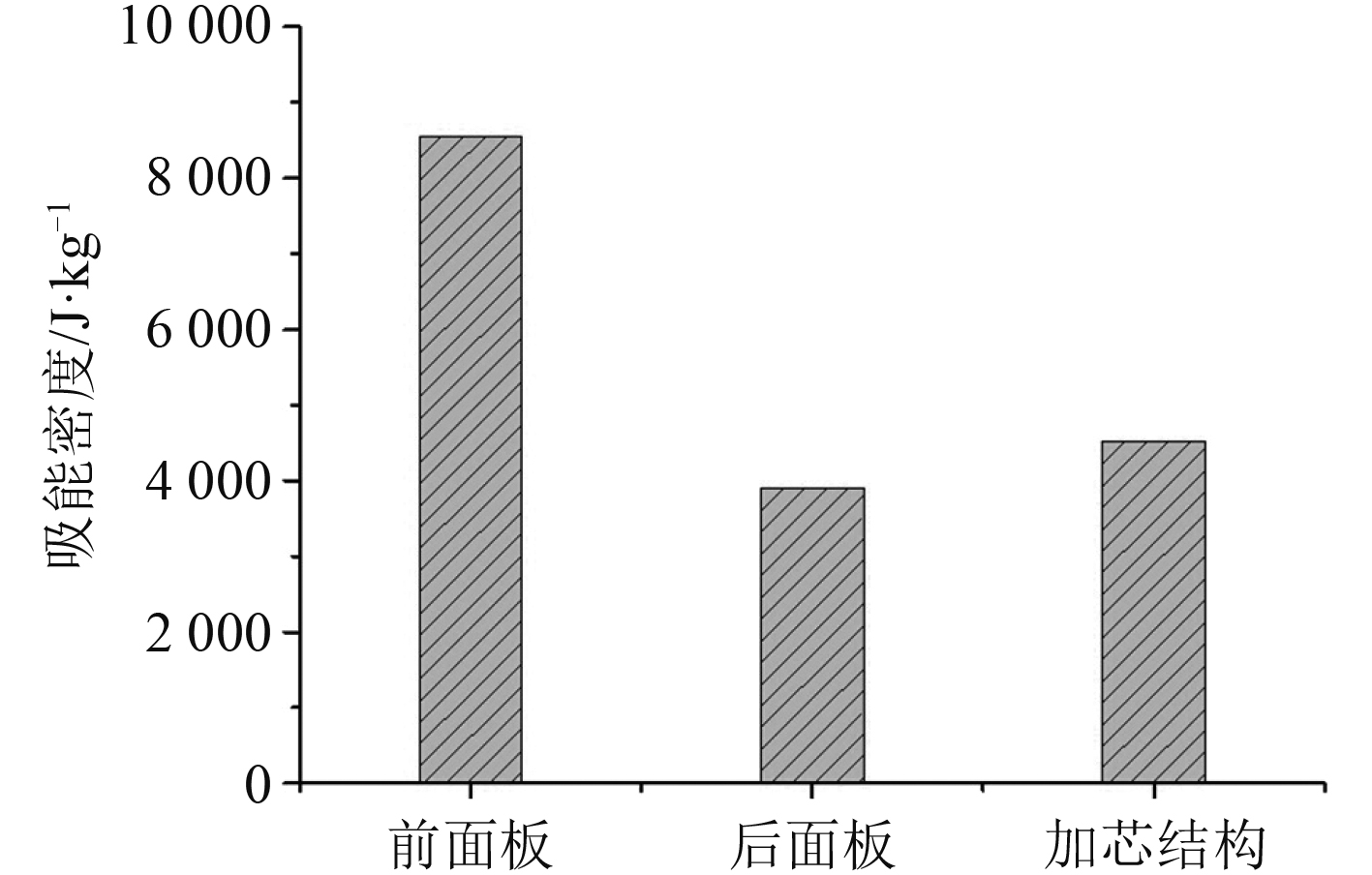
图9给出了船用泡沫夹芯板各组成部分的吸能密度(单位质量吸收的能量)图。从图中可以明显看出,在水下爆炸载荷作用下,背水泡沫夹芯板的前面板吸收能量最多,其次时泡沫夹芯结构,后面板的吸能密度最低,从而推断该结构能很好地保护后面板及后部结构。
|
图 9 各组成部分吸能密度 Fig. 9 Each component of energy absorption density |
在舰船防护中,水下近场爆炸会对泡沫夹芯板结构产生严重破坏,值得注意的是,夹芯板的另一侧可能是液舱,也有可能是空舱。2种不同舱室面对相同药量的爆炸会有不同的响应特性,针对泡沫夹芯板不同的边界条件,对背水板与背空板在近场水下爆炸载荷作用下的响应展开对比研究。
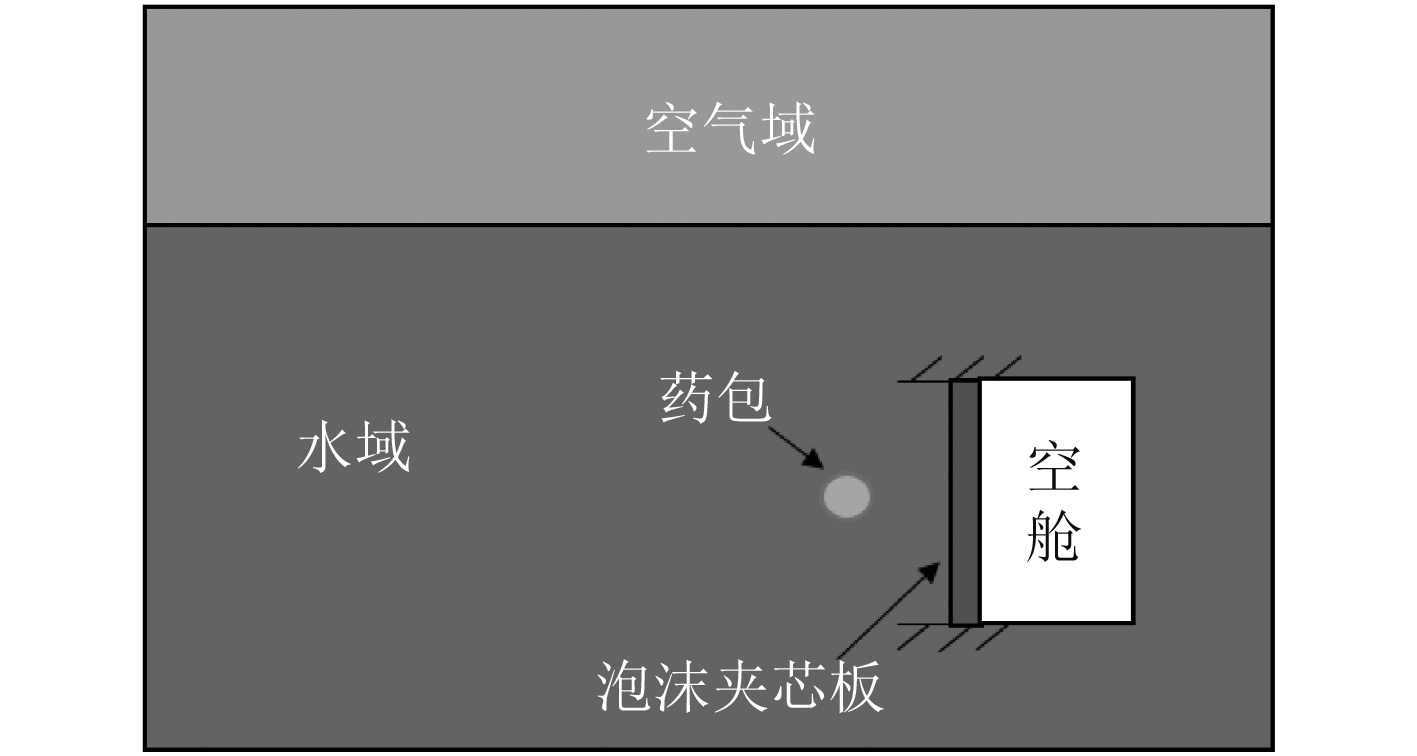
背水夹芯板结构布置如图10左侧所示,分别计算了药量为5 g,10 g,15 g和20 g等4种工况下的变形。背空板的布置如图10右侧所示,在泡沫夹芯板的另一侧建立一个空舱,并填充空气。
|
图 10 工况布置示意图 Fig. 10 Working condition diagram |
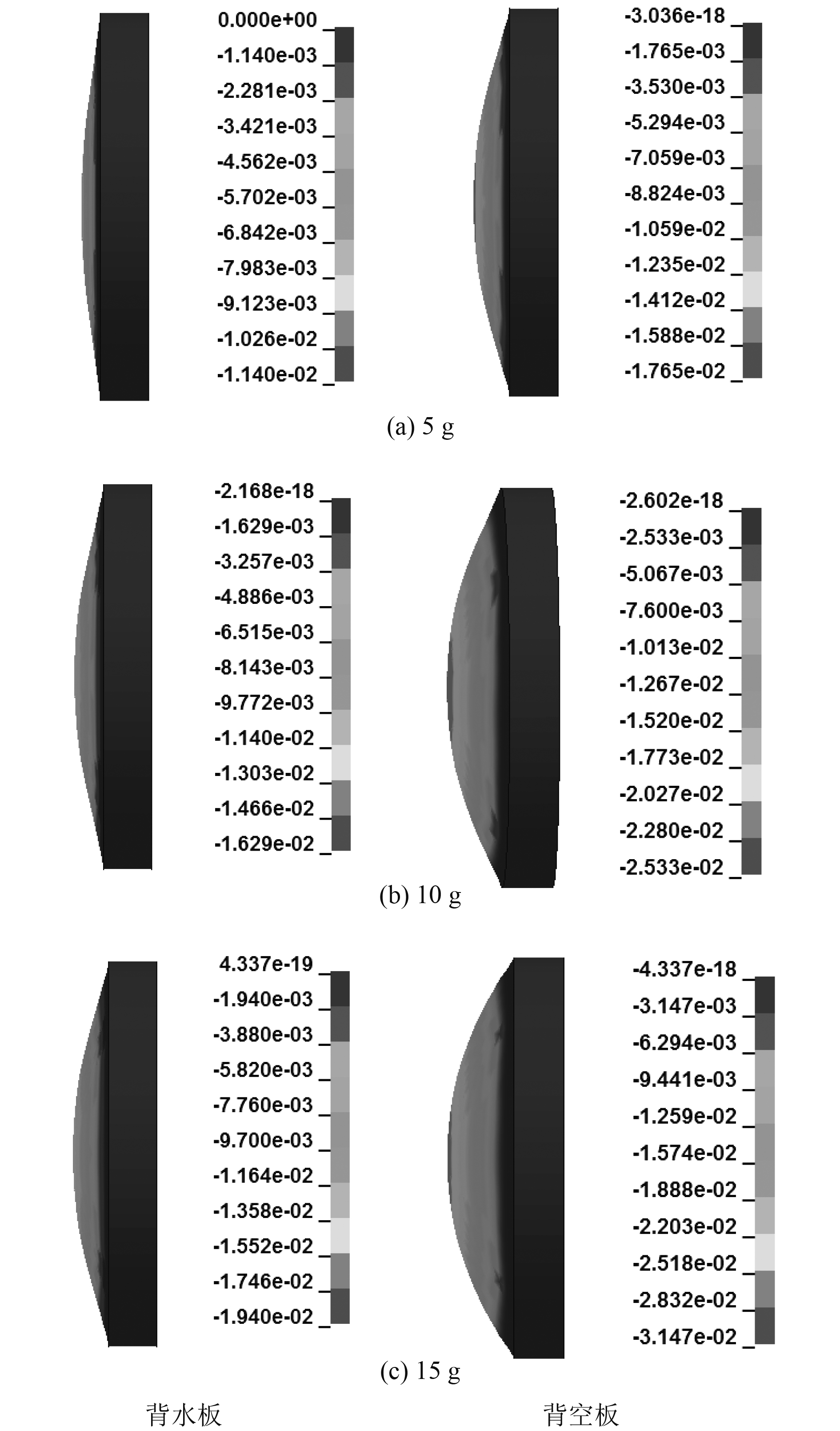
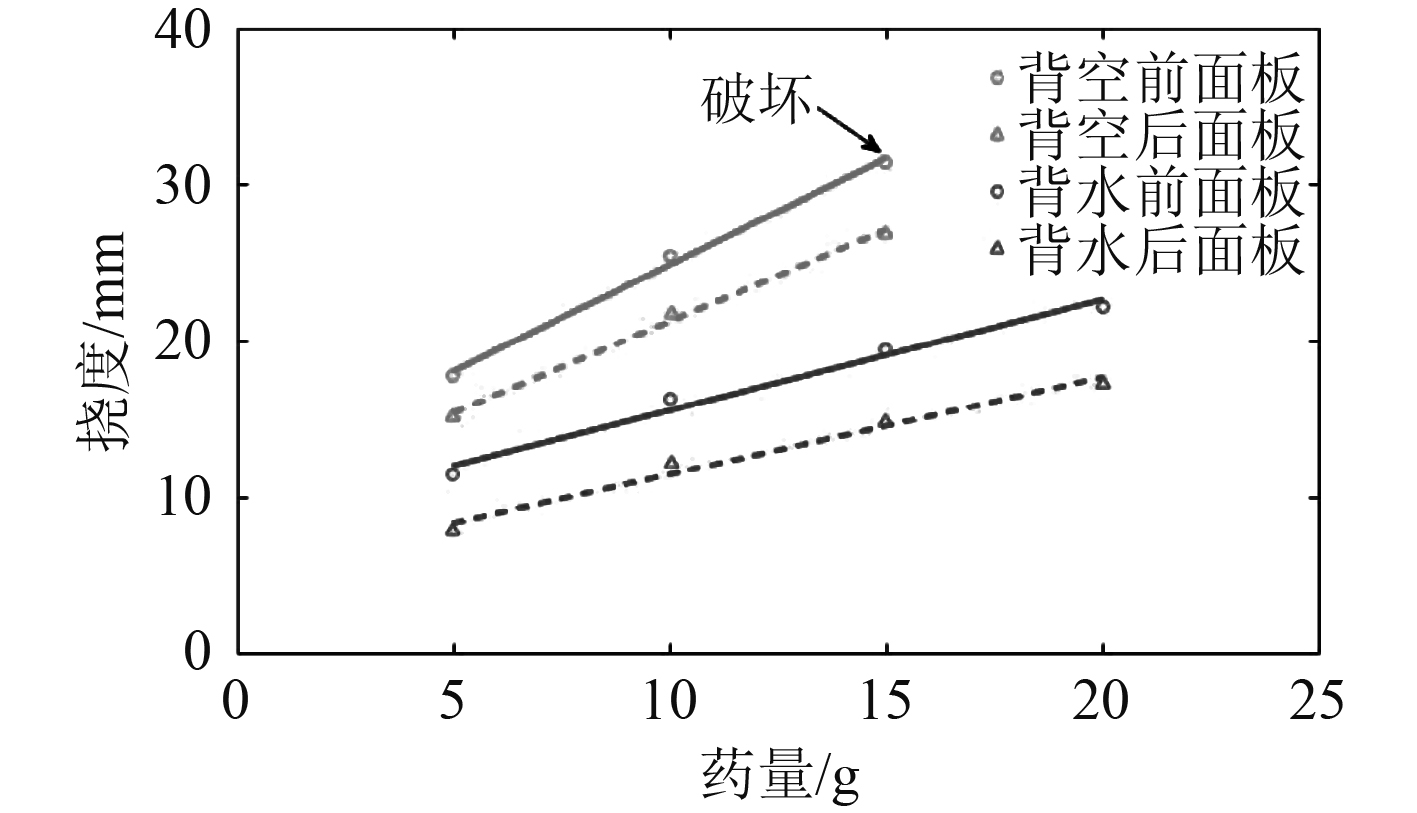
图11描述了3种不同装药工况下背水板和背空板的最终挠度变形。背空板的最终变形始终大于背水板。结合图12分析,前面板的挠度变形一直大于后面板,当药量达到20 g时,背水板的前后面板均未被破坏,但是背空板的前面板在药量为15 g时就发生了破坏、后面板仍呈现正常,这一规律与Huang Wei[19]得到的结论一致。
|
图 11 不同装药工况下最终变形云图 Fig. 11 Final deformation figure under different mass |
|
图 12 不同药量下挠度变化趋势图(直线与虚线为拟合线) Fig. 12 Deformation trend figure under different mass explosive(straight lines and dashed lines are fitted lines) |
为了进一步研究结构响应的特性和差异,图12将挠度与药量进行了线性拟合。可知,随着药量的不断增大,爆炸载荷也不断提高,背空板将会比背水板先发生破坏。从拟合线的斜率可以得知背空板的斜率明显大于背水板,这意味相同药量的爆炸,会使背空板发生更大的挠度变形。这其中的机理是水的声阻抗远大于空气,导致冲击波在背空板的传递过程中,极大部分的能量仍留存于泡沫夹芯板中,只有少数透过夹芯板传入后面的空气中,也就造成了背空板发生了更为明显的变形。通过比较前后面板的挠度变形,能够看出同药量下背空前面板的变形程度约为背水板的1.5倍,后面板的挠度变形约为1.8倍,而且背空板泡沫夹芯层的压缩程度也比背水板大。
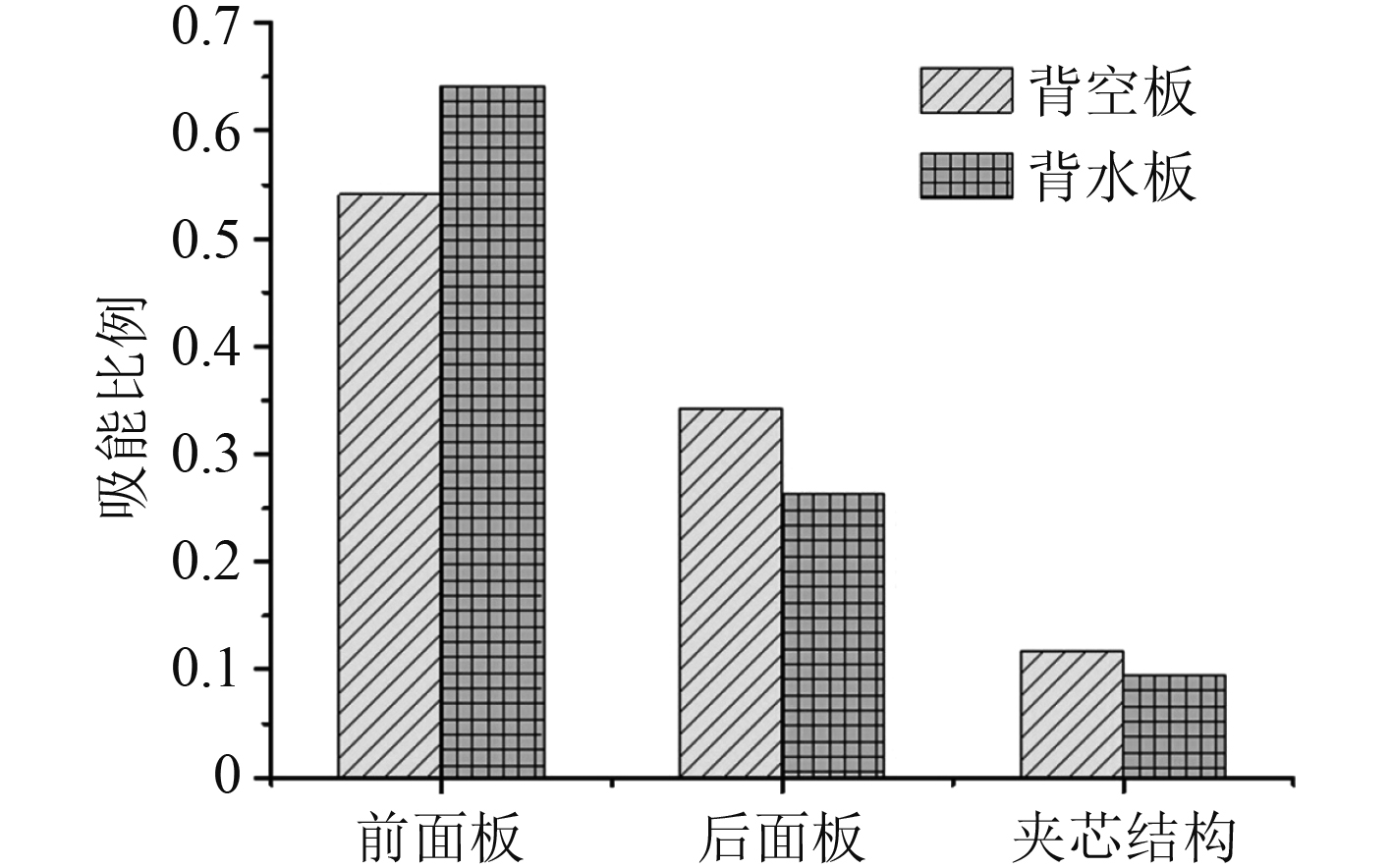
图13给出了在10 g TNT工况下,背空板与背水板不同结构处能量吸收百分比。可以看出背空板结构前后面板吸能比例较为接近,根据能量守恒从而推断出背空板前后面板的载荷相对均衡,而泡沫的吸能占比增加。
|
图 13 10 g TNT工况下结构能量吸收比例 Fig. 13 Structure energy absorption ration under 10 g of explosive |
综上所述,背空板前后面板的变形较背水板分别增加了约50%和80%,在相同载荷作用下,背空板更容易发生破坏。这是因为冲击波在传递过程中,背空板的设置使得能量更少的投射进入空气,更多的保留于结构之中。采用背空板布置,会使泡沫夹芯的吸能占比增加,使得前后面板的吸能更加均衡。
6 结 语夹芯板结构因其优良的抗爆抗冲击、吸能减震特性而在舰船防护上被广泛运用。运用Ls-dyna对船用PVC泡沫夹芯板在近场水下爆炸载荷作用下的吸能特性进行研究,对比背空板与背水板的响应差异,得出如下结论:
1)采用ALE方法对PVC泡沫夹芯板在近场水下爆炸载荷作用下变形进行模拟,并将结果与Radford冲击试验对比,后面板挠度误差在15%以内,表明ALE方法可以有效模拟高速冲击问题。
2)PVC夹芯板在选定计算工况下,后金属面板最终挠度为前面板的77%,塑性应变较前面板降低了约60%。
3)近场水下爆炸载荷作用下,PVC背空夹芯板整体变形明显大于背水板。背空结构使得透射的能量减小,结构本身吸能增加,泡沫芯层的吸能占比增加,前后金属面板吸能变形均衡。
| [1] |
RIMOLI J J, TALAMINI B, WETZEL J J, et al. Wet-sand impulse loading of metallic plates and corrugated core sandwich panels[J]. In International Journal of Impact Engineering, 2011, 38(10): 837-848. DOI:10.1016/j.ijimpeng.2011.05.010 |
| [2] |
TARLOCHAN F, RAMESH S. Composite sandwich structures with nested inserts for energy absorption application[J]. In Composite Structures, 2012, 94(3): 904-916. DOI:10.1016/j.compstruct.2011.10.010 |
| [3] |
敬霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展[J]. 力学与实践, 2015, 37(1): 1-24. DOI:10.6052/1000-0879-14-180 |
| [4] |
赵桂平, 卢天健. 多孔金属夹层板在冲击载荷作用下的动态响应[J]. 力学学报, 2008, 40(2): 194-206. DOI:10.3321/j.issn:0459-1879.2008.02.007 |
| [5] |
宋延泽, 王志华, 赵隆茂, 等. 泡沫金属子弹冲击下多孔金属夹芯板动力响应研究[J]. 兵工学报, 2011, 32(1): 1-7. |
| [6] |
张亭亭. 水下接触爆炸作用下舰船弦侧结构及设备防护特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [7] |
王斌俊. 舰船泡沫夹芯结构在近场水下爆炸载荷下的响应特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [8] |
LIU W T, MING F R, ZHANG A M, et al. Continuous simulation of the whole process of underwater explosion based on Eulerian finite element approach[J]. Applied Ocean Research, 2018, 80: 125-135. DOI:10.1016/j.apor.2018.08.016 |
| [9] |
MING F R, ZHANG A M, WANG S P. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions[J]. Ocean Engineering, 2016, 117: 359-382. DOI:10.1016/j.oceaneng.2016.03.040 |
| [10] |
LIU L T, YAO X L, ZHANG A M, et al. Research on the estimate formulas for underwater explosion bubble jet parameters[J]. Ocean Engineering, 2018, 164: 563-576. DOI:10.1016/j.oceaneng.2018.06.070 |
| [11] |
张阿漫, 王诗平, 彭玉祥, 等. 水下爆炸与舰船毁伤研究进展[J]. 中国舰船研究, 2019(3): 1-13. DOI:10.19693/j.issn.1673-3185.01608 |
| [12] |
MENG Z F, CAO X Y, MING F R, et al. Study on the pressure characteristics of shock wave propagating across multilayer structures during underwater explosion[J]. Shock and Vibration, 2019, 902614. |
| [13] |
ZHANG Z F, WANG C, ZHANG A M, et al. Underwater explosion of cylindrical charge near plates: Analysis of pressure characteristics and cavitation effects. International Journal of Impact Engineering[J]. 2018, 121: 91-105.
|
| [14] |
SOULI, M. (2003). LS-DYNA Advanced course in ALE and fluid/structure coupling notes [R]. Livermore Software Technology Corporation(LSTC), February 2003.
|
| [15] |
AUTODYN A. Theory manual revision 4.3[M]. Century Dynamics, Concord, CA, 2005.
|
| [16] |
HALLQUIST J O. LS-Dyna Theory manual[J]. 2006.
|
| [17] |
RADFORD D D, MCSHANE G J, DESHPANDE V S, et al. The response of clamped sandwich plates with metallic foam cores to simulated blast loading[J]. International Journal of Solids and Structures, 2006, 43(7-8): 2243-2259. DOI:10.1016/j.ijsolstr.2005.07.006 |
| [18] |
张梁. 水下接触爆炸对舰船弦侧多层防护结构毁伤机理研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [19] |
HUANG W, ZHANG W, YE N, et al. Dynamic response and failure of PVC foam core metallic sandwich subjected to underwater impulsive loading[J]. Composites Part B Engineering, 2016, 97: 226-238. DOI:10.1016/j.compositesb.2016.05.015 |
 2022, Vol. 44
2022, Vol. 44
