20世纪以来,随着世界经济的快速发展,化石燃料的大量开发和使用对地球生态环境造成了严重影响,世界各国逐渐开始重视新能源的开发。作为一种环保的可再生能源,风能受到了很多国家的青睐。相对于陆地,海上的风力资源更为丰富,因此海上风电成为世界各国关注的焦点。对于海上风电的安装工程,起重船的作业过程具有高难度、高技术、高投入、高风险的特点[1],因此,利用数值计算方法对起重船进行数值仿真分析,在吊装作业之前进行可行性分析,可以极大地提高海上施工的安全性和作业效率,避免资源浪费。
通常情况下,起重船在进行吊装作业时,与运输船组成多浮体系统,浮体之间的水动力干扰现象对多浮体系统的稳定性有很大程度上的影响,其波浪载荷与运动响应问题也更加复杂。因此,针对多浮体水动力的研究得到世界各国学者的广泛关注。KIM等[2]采用三维Rankine源方法求解多个相邻浮体的时域运动方程,并通过实验数据验证了其合理性。YAN等[3]采用QALE-FEM方法分析2个浮体之间的非线性水动力相互作用。刘培林等[4]采用Newmark-Beta方法求解时域运动方程中的非线性项,得到不同浪向下多浮体系统的运动响应规律。徐华福等[5]采用三维高阶面元法计算了浅水中两船行进时的水动力相互作用,并分析了间距、船速以及水深的影响。Feng[6]基于非线性势流模型,采用耦合辅助函数的方法计算了2艘相互连接驳船的水动力性能。杨云涛等[7]在N-S方程中加入质量源项和阻尼项,建立起数值波浪水池,分析小间隙双浮体系统中的共振问题。周柯[8]采用阻尼盖法分析了双浮体系统船体中间液面的共振,在势流模型中加入实验得到的阻尼因子。晏柳等[9]基于三维源汇分布法,建立起FPSB与浮桥的准静态运动方程,分析了FPSB在满载工况下的波浪载荷和运动响应。何广华等[10]基于CFD理论分析了遮蔽效应对多浮体波浪载荷的影响。李鸿等[11]采用全耦合时域分析方法模拟了多浮体系统在受到撞击后的运动响应,并通过实验数据验证了此方法。黄金等[12]基于Hess&Smith面元法计算了两船平行和会遇时的水动力,并通过实验验证其适用性。黄从亮等[13]基于三维势流理论对钻井支持平台和生产平台近距离靠泊系统进行了研究。匡杨[14]等采用时域脉冲响应函数的方法分析了海洋石油201船靠近Spar平台作业时的动态响应。王文华等[15]建立了FLNG-LNGC双船耦合水动力模型,并分析了系泊系统对卸料臂动态响应的影响。
本文采用SESAM软件,基于三维势流理论,并通过水池静水衰减实验得到无因次阻尼系数计算出浮体的粘性阻尼,在计算中加入粘性阻尼矩阵,采用延迟函数方法,建立起双浮体系统时域运动方程,分析计算了180°浪向下由起重船和运输船组成的双浮体系统在水动力相互作用下的运动响应,得到180°浪向下浮体6个自由度下的运动时程曲线以及缆绳的张力曲线,并与水池模型实验结果进行比较,验证了此数值计算方法的可靠性。
1 数值计算 1.1 频域运动方程根据牛顿第二运动定律,浮体频域运动方程为:
| $ M \times \ddot X(t) = {F_C} + {F_R} + {F_W} 。$ | (1) |
式中:
对于双浮体系统,两浮体的频域运动方程分别为:
| $ \left\{ \begin{gathered} ({{\boldsymbol{M}}^{\boldsymbol{a}}} + {{\boldsymbol{\mu }}^{\boldsymbol{a}}}) \times {\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} + {{\boldsymbol{\mu }}^{{\boldsymbol{ba}}}} \times {\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^{\boldsymbol{b}}} + {{\boldsymbol{\lambda }}^{\boldsymbol{a}}} \times {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} + {{\boldsymbol{\lambda }}^{{\boldsymbol{ba}}}} \times\\ {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^{\boldsymbol{b}}} + {{\boldsymbol{D}}^{\boldsymbol{a}}} \times {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} + {{\boldsymbol{C}}^{\boldsymbol{a}}} \times {\boldsymbol{X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} = {\boldsymbol{F}}_{\boldsymbol{W}}^{\boldsymbol{a}},\\ ({{\boldsymbol{M}}^{\boldsymbol{b}}} + {{\boldsymbol{\mu }}^{\boldsymbol{b}}}) \times {\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^{\boldsymbol{b}}} + {{\boldsymbol{\mu }}^{{\boldsymbol{ab}}}} \times {\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} + {{\boldsymbol{\lambda }}^{\boldsymbol{b}}} \times {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^{\boldsymbol{b}}} + {{\boldsymbol{\lambda }}^{{\boldsymbol{ab}}}} \times\\ {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^{\boldsymbol{a}}} + {{\boldsymbol{D}}^b} \times {\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^b} + {{\boldsymbol{C}}^{\boldsymbol{b}}} \times {\boldsymbol{X(t}}{{\boldsymbol{)}}^{\boldsymbol{b}}} = {\boldsymbol{F}}_{\boldsymbol{W}}^{\boldsymbol{b}}。\\ \end{gathered} \right. $ | (2) |
式中:
求解式(2)即可得到双浮体系统中两浮体的运动响应。
1.2 时域运动方程对于浮体的瞬态问题频域理论难以处理,根据Cummins脉冲响应方法,浮体某时刻的运动可视作多个瞬时脉冲运动的叠加,将频域运动方程进行傅里叶逆变换得到多浮体系统的时域运动方程:
| $ \begin{split} &\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{M}}_{{\boldsymbol{ij}}}^{\boldsymbol{a}} + {\boldsymbol{m}}_{{\boldsymbol{ij}}}^{{\boldsymbol{aa}}}}&{{\boldsymbol{\mu }}_{{\boldsymbol{ij}}}^{{\boldsymbol{ba}}}} \\ {{\boldsymbol{\mu }}_{{\boldsymbol{ij}}}^{{\boldsymbol{ab}}}}&{{\boldsymbol{M}}_{{\boldsymbol{ij}}}^{\boldsymbol{b}} + {\boldsymbol{\mu }}_{{\boldsymbol{ij}}}^{{\boldsymbol{bb}}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^a}} \\ {{\boldsymbol{\ddot X(t}}{{\boldsymbol{)}}^b}} \end{array}} \right] +\\ &\left[ {\begin{array}{*{20}{c}} {\int_{\boldsymbol{0}}^{\boldsymbol{t}} {{{\boldsymbol{H}}^{aa}}} {\boldsymbol{(t}} - {\boldsymbol{\tau ){\rm{d}}\tau }}}&{\int_{\boldsymbol{0}}^{\boldsymbol{t}} {{{\boldsymbol{H}}^{ab}}} {\boldsymbol{(t}} - {\boldsymbol{\tau ){\rm{d}}\tau }}} \\ {\int_{\boldsymbol{0}}^{\boldsymbol{t}} {{{\boldsymbol{H}}^{ba}}} {\boldsymbol{(t}} - {\boldsymbol{\tau ){\rm{d}}\tau }}}&{\int_{\boldsymbol{0}}^{\boldsymbol{t}} {{{\boldsymbol{H}}^{bb}}} {\boldsymbol{(t}} - {\boldsymbol{\tau ){\rm{d}}\tau }}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^a}} \\ {{\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^b}} \end{array}} \right] + \\ & \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{D}}_{{\boldsymbol{ij}}}^{\boldsymbol{a}}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{{\boldsymbol{D}}_{{\boldsymbol{ij}}}^{\boldsymbol{b}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^a}} \\ {{\boldsymbol{\dot X(t}}{{\boldsymbol{)}}^b}} \end{array}} \right] + \\ &\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{C}}_{{\boldsymbol{ij}}}^a}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{{\boldsymbol{C}}_{{\boldsymbol{ij}}}^b} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{X(t}}{{\boldsymbol{)}}^a}} \\ {{\boldsymbol{X(t}}{{\boldsymbol{)}}^b}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}^a}} \\ {{{\boldsymbol{F}}^b}} \end{array}} \right] 。\\ \end{split} $ | (3) |
式中:
在双浮体系统中,频域水动力系数与时域延迟函数之间的关系表达式为:
| $ \left\{ \begin{gathered} \lambda _{ij}^{mn} = \int_0^\infty {H_{ij}^{mn}(t)\cos (\omega t){\rm{d}}t} ,\\ \mu _{ij}^{mn} = \mu + \int_0^\infty {\frac{1}{\omega }H_{ij}^{mn}(t)\sin (\omega t){\rm{d}}t}。\\ \end{gathered} \right. $ | (4) |
傅里叶变换得到延迟函数表达式为:
| $ H_{ij}^{mn}(t) = \frac{2}{\text{π}}\int_0^\infty {\lambda (\omega )\cos (\omega t)} {\rm{d}}\omega 。$ | (5) |
对于延迟函数的求解,常用的方法由2种:数值积分法和半解析法。常规的数值积分方法不仅耗费大量时间与资源,同时准确性也难以保证,相对而言,半解析法具有明显优势。半解析法通过将
根据经验公式,浮体在纵荡、横荡、首摇方向上的粘滞阻尼分别为:
| $ \left\{ \begin{gathered} {D_{11}} = 0.06\sqrt {{K_{xx}}(M + {\mu _{xx}})},\\ {D_{22}} = 0.06\sqrt {{K_{yy}}(M + {\mu _{yy}})} ,\\ {D_{66}} = 0.10\sqrt {{K_{\psi \psi }}\left[ {{I_{\psi \psi }} + {\mu _{\psi \psi }} + \left( {M + {\mu _{yy}}} \right)x_G^2} \right]} 。\\ \end{gathered} \right. $ | (6) |
式中:
浮体在垂荡、横摇、纵摇方向的粘性阻尼为:
| $ D = 2{\mu _0}{\omega _n}I - {\lambda _0}。$ | (7) |
式中:
组成双附体系统的起重船和运输船主要尺度参数如表1和表2所示。
|
|
表 1 运输船的主要尺度参数 Tab.1 Main particulars of the transport ship |
|
|
表 2 起重船的主要尺度参数 Tab.2 Main particulars of the floating crane |
起重船的系泊系统采用12根系泊缆对称布置(编号L1~L12);运输船采用12根旁靠缆(编号C1~C12)旁靠于起重船一侧,两船中间设置10个护舷(编号F1~F10)。
起重船和运输船组成的双浮体系统如图1所示。

|
图 1 多浮体系统示意图 Fig. 1 Schematic diagram of multiple floating body system |
本文通过水池模型实验来验证数值方法的可靠性,定义实验模型的缩尺比为80。
在静水衰减实验中,测得单浮体各自的自由衰减曲线,进而计算得到:起重船横摇、纵摇、垂荡的固有周期为11.2 s,9.9 s,11 s,运输船横摇、纵摇、垂荡的固有周期为12.7 s,8.7 s,8.8 s,起重船横摇、纵摇、垂荡的无因次阻尼系数为0.005848,0.066094,0.10807,运输船横摇、纵摇、垂荡的无因次阻尼系数为0.001997,0.083603,0.120796。
在规则波实验中,选取180°浪向(迎浪),规则波波高取2 m,波浪周期分别取6 s,8 s,10 s,12 s,16 s,20 s,分别测得对应频率下浮吊船和运输船的运动响应幅值,将测得数据除以波幅即可得到运动幅值响应算子(RAOs),通过其可以初步判断浮吊船和运输船的水动力性能。
在不规则波实验中,设定实验环境为:迎浪(180°浪向),有义波高0.03 m(实际值2.5 m),谱峰周期1.1 s(实际值10 s),测得浮吊船以及运输船在此环境条件下30 s的运动响应时程曲线,以及系泊缆L1和L9和靠泊缆C1和C12的张力曲线。
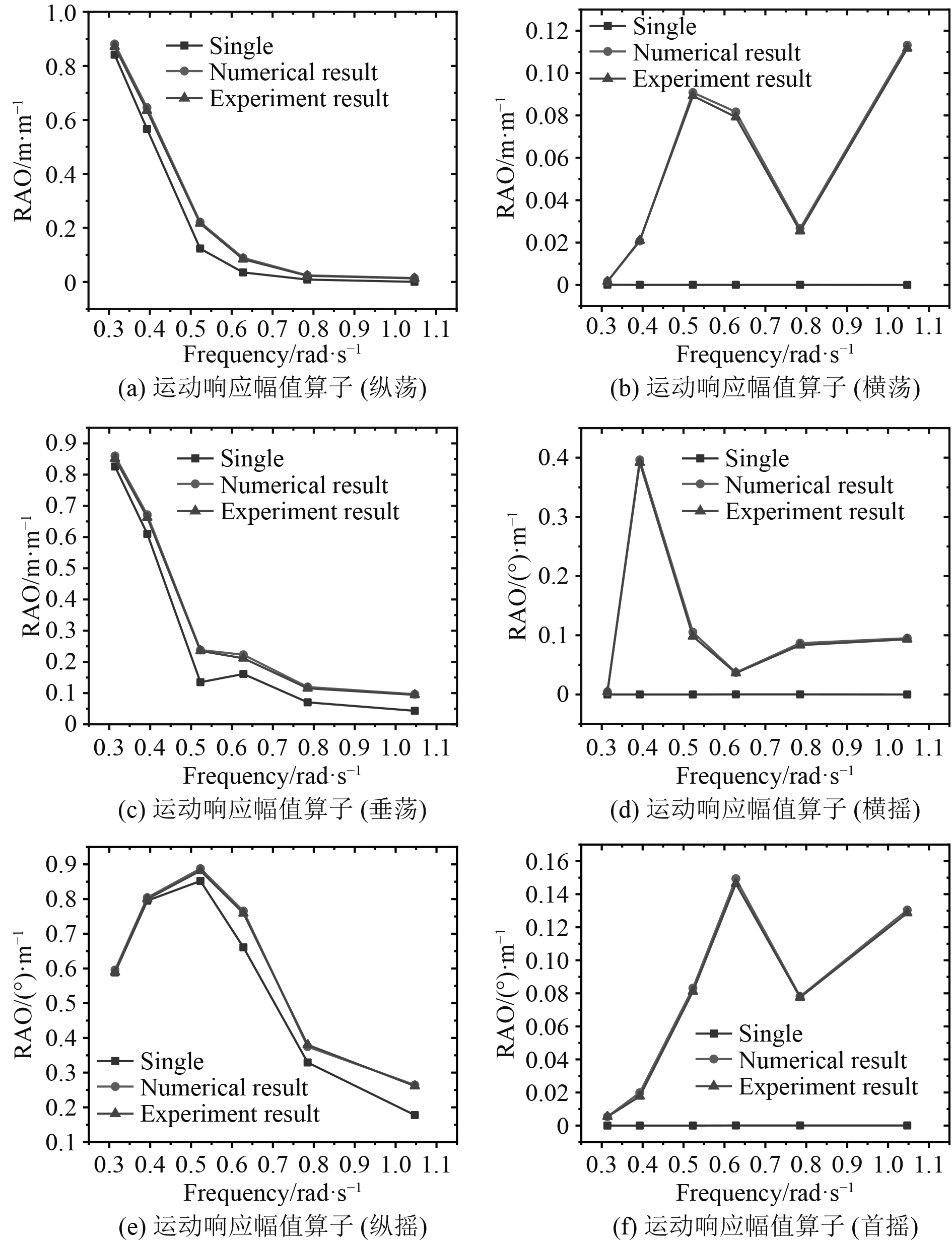
3 数值计算结果与实验结果对比验证 3.1 双浮体RAOs数值计算结果验证图2为运输船在180°浪向时单船状态下和水动力干扰状态下六自由度运动幅值响应算子的数值计算结果以及双浮体系统的实验结果。
|
图 2 运输船运动响应幅值算子 Fig. 2 RAOs of the transport ship |
从图2可以看出,在180°浪向下,浮体之间的水动力干扰作用对运输船RAOs的影响主要体现在横荡、横摇、首摇3个方向上,在波浪频率较低时,水动力干扰作用较小,随着波浪频率的增大,水动力干扰作用对运输船RAOs的影响逐渐增大,最终双浮体系统下运输船的RAOs明显高于单浮体状态。而在纵荡、垂荡、纵摇3个自由度上,水动力干扰作用的影响相对较小。运输船在纵荡和横荡方向的RAOs随着波浪频率的增加总体呈降低趋势,纵摇方向的RAOs呈先增大在减小的趋势,并在
图3为起重船在180°浪向时单船状态下和水动力干扰状态下六自由度运动幅值响应算子的数值计算结果以及双浮体系统的实验结果。

|
图 3 起重船运动响应幅值算子 Fig. 3 RAOs of the floating crane |
从图3可以看出,起重船的RAOs与运输船大致相仿。在180°浪向下,浮体之间的水动力干扰作用对运输船RAOs的影响,主要体现在横荡、横摇、首摇3个方向上,在波浪频率较低时,两者差距较小,随着波浪频率的增大,两者差距逐渐明显。在纵荡和垂荡2个方向上,随着波浪频率的增大,起重船的RAOs逐渐减小。在纵摇方向上,随着波浪频率的增加,起重船的RAOs逐渐增加,并在
对比起重船和运输船RAOs的实验数据和数值计算结果,可以看出两者吻合度较高。
3.2 双浮体六自由度运动响应数值计算结果验证图4和图5分别为运输船与起重船在靠泊状态下的数值仿真计算结果和实验结果。

|
图 4 数值计算结果 Fig. 4 Numerical results |
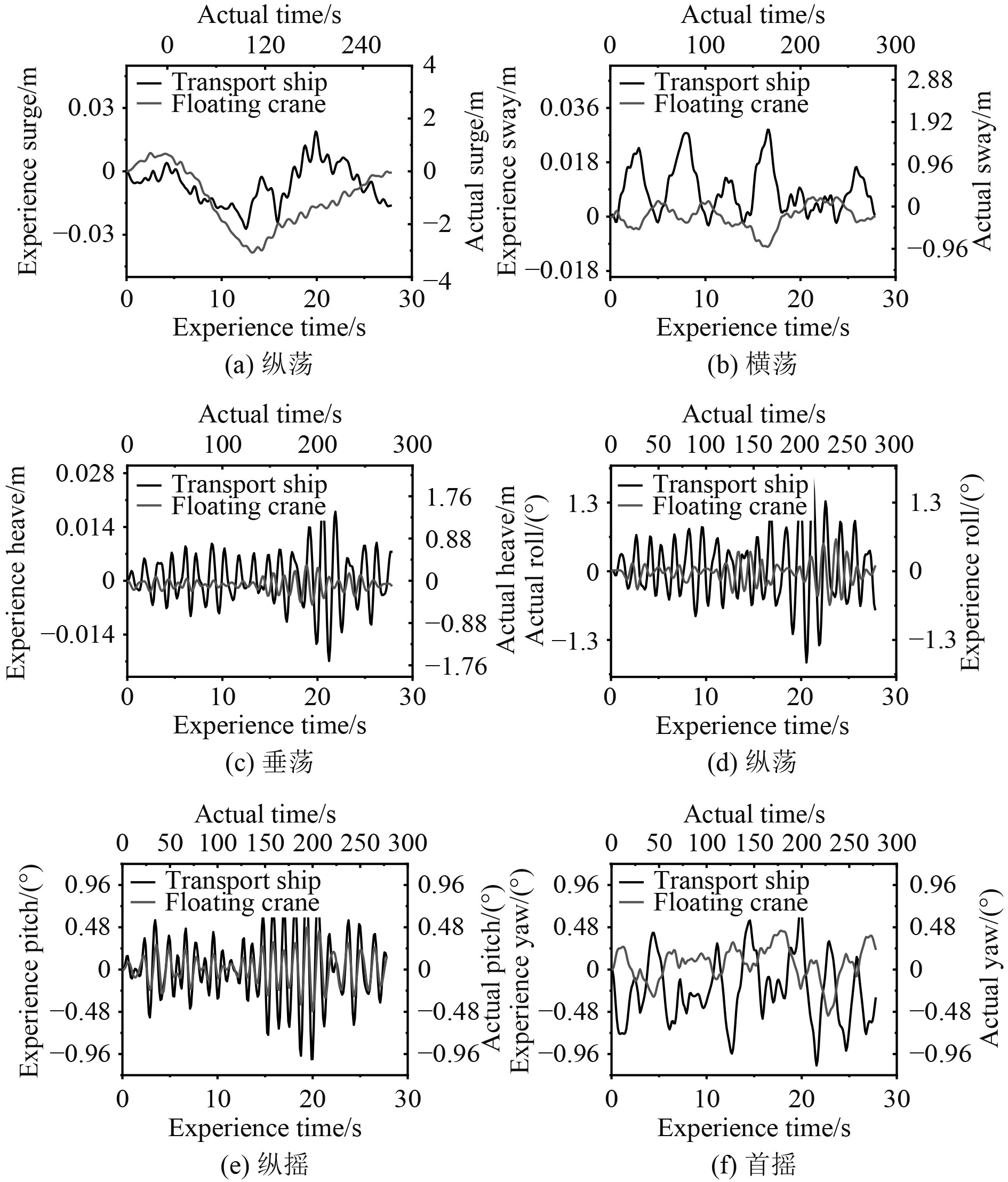
|
图 5 实验结果 Fig. 5 Experience results |
运输船和起重船六自由度响应幅值见表3和表4。通过运动响应幅值数据对比,可以看出实验结果和数值计算具有较高的一致性,而对于实验数据略小于数值计算的现象,可能归因于两船间隙自由表面的共振。
|
|
表 3 运输船六自由度运动响应幅值 Tab.3 Six degrees of freedom motion response amplitude of the transport ship |
|
|
表 4 起重船六自由度运动响应幅值 Tab.4 Six degrees of freedom motion response amplitude of floating crane |
图6和图7分别为系泊缆L4和L9张力曲线图和靠泊缆C1和C12张力曲线图。

|
图 6 系泊缆张力时域曲线 Fig. 6 Mooring line tension |
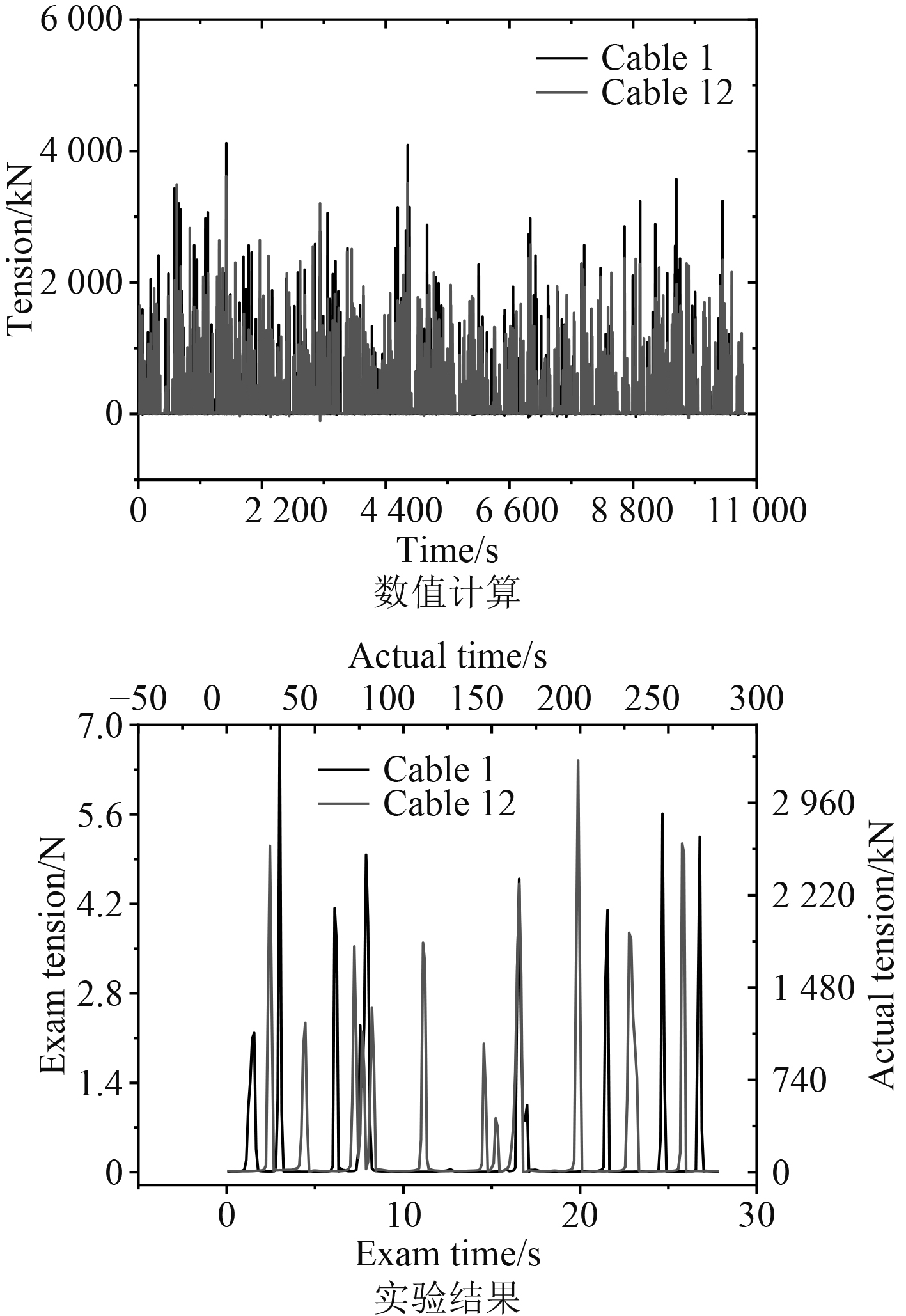
|
图 7 旁靠缆张力时域曲线 Fig. 7 Cable section tension |
表5为系泊缆系泊缆L4和L9及靠泊缆C1和C12张力幅值。
|
|
表 5 缆绳张力幅值 Tab.5 Amplitude of cable tension |
可以看出,通过对比缆绳张力幅值的实验值和数值计算值,可以看出两者之间误差较小,证明了此数值计算结果的合理性。
4 结 语本文通过SESAM软件,建立起重船-运输船组成的双浮体系统,在频域内水动力计算中加入粘性阻尼矩阵,使得计算结果更加符合实际情况,采用延迟函数方法求解双浮体系统的时域运动方程,得到了在水动力干扰下起重船及运输船的RAOs,并与单船状态下的计算结果进行对比分析。
1)对比发现在180°浪向下,两船之间的水动力相互作用对船体在横荡、纵摇、横摇3个自由度上的运动有较为明显的影响。另外在波浪频率较小时,水动力干扰较小,随着波浪频率的增大,双浮体系统中船体的运动响应与单船的运动响应差距逐渐增大。
2)通过水池模型实验,将实验结果与数值计算结果进行对比,结果表明两者具有良好的一致性,证明该数值计算方法具有良好的适用性,可用于多浮体水动力干扰下浮体的动态响应分析,为海上多浮体系统作业的水动力分析提供理论依据。
| [1] |
李树敏. 大型海洋起重平台工作状态下压载水调配的实验研究[D]. 大连: 大连海事大学, 2013.
|
| [2] |
KYONG-HWAN KIM, YONGHWAN KIM, MUN-SUNG KIM. Numerical analysis on motion responses of adjacent multiple floating bodies by using rankine panel method[J]. International Journal of Offshore and Polar Engineering, 2009, 19(2): 151-157. |
| [3] |
YAN S, MA Q W, CHENG X M. Fully nonlinear hydrodynamic interaction between two 3D floating structures in close proximity[J]. International Journal of Offshore and Polar Engineering, 2011, 21(3): 178-185. |
| [4] |
刘培林, 赵君龙, 孙丽萍, 等. 深水平台上层模块海上吊装多浮体响应分析[J]. 中国造船, 2011, 52(1): 157-164. DOI:10.3969/j.issn.1000-4882.2011.01.020 |
| [5] |
徐华福, 邹早建, 刘晓艳. 基于高阶面元法的浅水域中船-船水动力相互作用数值预报[J]. 船舶力学, 2016, 20(12): 1535-1546. DOI:10.3969/j.issn.1007-7294.2016.12.004 |
| [6] |
FENG X, BAI W. Hydrodynamic analysis of marine multibody systems by a nonlinear coupled model[J]. Journal of Fluids and Structures, 2017, 70: 72-101. DOI:10.1016/j.jfluidstructs.2017.01.016 |
| [7] |
杨云涛, 朱仁传, 缪国平, 等. 基于粘性无反射数值波浪水池研究波浪作用下双浮体共振问题[J]. 中国造船, 2018, 59(4): 14-26. DOI:10.3969/j.issn.1000-4882.2018.04.002 |
| [8] |
周珂. 不同浪向下FLNG与LNGC旁靠作业时的水动力干扰分析[D]. 上海: 上海交通大学, 2018.
|
| [9] |
晏柳, 连雪海, 王小春, 等. FPSB与连接浮桥耦合运动响应分析[J]. 舰船科学技术, 2019, 41(3): 112-117. DOI:10.3404/j.issn.1672-7649.2019.03.022 |
| [10] |
何广华, 王正科, 张志刚, 等. 不同入射浪向下群遮效应的CFD分析[J]. 华中科技大学学报(自然科学版), 2019, 47(5): 95-100. DOI:10.13245/j.hust.190518 |
| [11] |
李鸿, 刁景华, 李莉, 等. 船舶撞击作用下系泊多浮体耦合系统的运动响应分析[J]. 舰船科学技术, 2020, 42(11): 9-13. DOI:10.3404/j.issn.1672-7649.2020.11.002 |
| [12] |
黄金, 邓强, 许辰, 等. 限制水域船舶水动力干扰快速计算方法[J]. 哈尔滨工程大学学报, 2021, 42(5): 601-609. DOI:10.11990/jheu.202101042 |
| [13] |
黄从亮, 董晴, 吕海宁, 等. 近距离靠泊条件下钻井支持平台与生产平台相对运动研究[J]. 海洋工程, 2020, 38(3): 42-51. DOI:10.16483/j.issn.1005-9865.2020.03.005 |
| [14] |
匡杨, 李啟宝, 秦立成, 等. 海洋石油201船与Spar平台靠近作业水动力分析[J]. 山西建筑, 2020, 46(9): 190-192. DOI:10.3969/j.issn.1009-6825.2020.09.086 |
| [15] |
王文华, 邸晓宁, 杨光, 等. 连接系统对FLNG和LNGC双体旁靠性能的影响研究(英文)[J]. 船舶力学, 2021, 25(12): 1648-1663. DOI:10.3969/j.issn.1007-7294.2021.12.006 |
 2022, Vol. 44
2022, Vol. 44
