大型集装箱船舶运输货物的能力更强、效率更高，仅需在码头短暂停留，就能实现货物高质量运输。随着经济发展，海洋运输所需要的船舶吨位不断增加，集装箱船的尺寸也不断迭代，逐渐向超大型规模发展，这种发展顺应时代经济进步^[1]。大型集装箱船舶原材料多为金属，长期浸泡于水体环境之中，受到水体中碱性物质和盐性物质的腐蚀，极易出现腐蚀破坏。而且水下环境变幻莫测，一旦航行出现意外，将会导致船体发生损伤，严重时甚至会危机人身财产安全。因此这种大型集装箱船舱需要定时上岸检查、维修，才能延长大型集装箱船舱的使用寿命^[2]。但是这种大型集装箱船舱为降低航行时的阻力，一般会设计成上宽下窄的结构形式，这种结构在水体环境中能够畅通无阻，但是上岸进入船坞后，稳定性较差，需要依靠底座支撑保持稳定，才能开展后续维修工作。应用于大型集装箱船舱的底座一般为金属结构，由一个底座面和支撑构件组成。底座面上没有多余构件，零部件及支撑构件主要集中在底部，底部通常包含多个轴承、涡轮、涡杆等支撑结构，发挥稳定支撑作用。但是目前市面常见底座的支撑性能，无法支撑体量日益增加的大型集装箱船舱，因此需要采取相关措施增强大型集装箱船舱底座的支撑能力^[3]。

刘金梅等^[4]使用模型重构方法计算并评价底座的承载力和结构安全性，同时根据评价结果对底座较为薄弱的部位适当加固，通过数值模拟验证该方法的性能，优化后的底座静力学性能以及动力学性能均较好。但是该方法计算过程过于复杂，需要继续研究并优化。顾俊等^[5]利用Veri STAR Hull软件分析底座结构的强度，并根据分析结果，适当加强结构强度降低结构重量，具有较好轻量化优化效果。但是该方法只考虑降低结构重量，未优化其他影响因素，导致研究结果存在一定的片面性。

本文使用多目标优化方法，确定大型集装箱船舱底座结构加强与改进方向，并适当调整各个构件的尺寸。通过有限元模型，模拟优化前后的变化值，确定大型集装箱船舱底座结构的优化效果。

本文所研究的大型集装箱船舶，型号为20000TEU，使用双燃料动力驱动，船体全长为450 m，宽度约为60 m，船舱内部结构通常会设计一道中纵制荡舱壁，同时还包括纵向、横向强框以及水平强框等数个支撑构件。这种大型集装箱船体量较大，通常重量会超过300 t，常年在水体环境中航行。如果船舱底部出现故障，需要使用机械运输手段将大型集装箱船运输至岸上的船坞之中维修，但是船舱底部结构形状较为特殊，不能保持稳定状态，需要借助底座，支撑大型集装箱船船舱。支撑船舱稳定的底座通常为不锈钢结构，该底座承载竖向载荷的能力较强。本文研究底座为铸钢材质大型集装箱船舱底座，厚度与重量分别为50 cm与100 kg，长度与宽度均为3000 mm，可在−25℃～60℃温度环境中使用。该底座除了一个用于放置船舶舱体的底座面外，下方位置还有几个支撑结构，该结构包含铰链、涡轮外齿环与涡杆，齿环两端与底座面相连，轴承在该结构中发挥连接作用。

大型集装箱船舱底座结构加强改进前后的力学形态变化需要在有限元软件中模拟，因此使用Ansys有限元软件构建大型集装箱船舱底座结构的有限元模型，方便后续模拟分析^[6]。

1）选取单元。根据目前已有的钢结构研究结果来看，模拟大型集装箱船舱底座结构有限元模型时，使用4节点板壳单元就能够模拟底座上的平面结构，底座中负责承载高应力变化的区域则尽量使用3节点板壳单元模拟，底座上的支撑结构使用2节点梁单元实现模拟。底座上的部分零件选取集中质量单元，利用多点约束MPC传输零件质量单元至模型中具体安装位置。

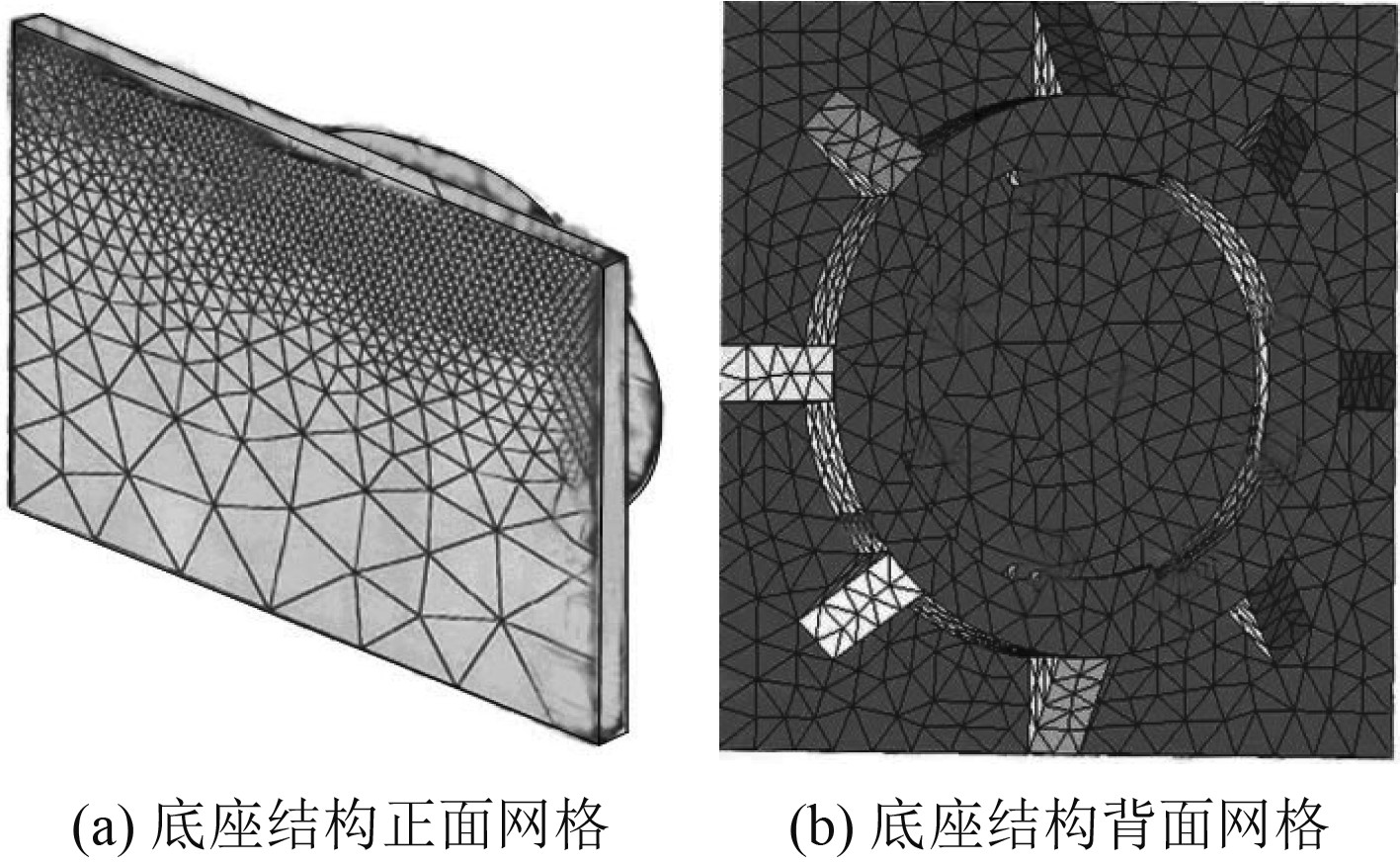
2）划分网格。从纵向和横向2个方向划分网格单元，使用Ansys有限元软件中的Workbench模块实现大型集装箱船舱底座结构有限元网格的智能划分，设置Relevance值为100。经统计，网格划分后共有239255个单元，这些单元包含3679736个节点，大型集装箱船舱底座结构的网格划分结果如图1所示。

图 1 网格划分结果 Fig. 1 Grid generation results

大型集装箱船舱底座内部结构较为复杂，各个构件均是待加强改进的设计变量，实际计算时会导致计算量过大，因此需要探索出最佳构件变量，以此降低计算时间。使用灵敏度分析各个构件原始变量对于底座结构柔度和低阶固有频率的影响程度，选取其中影响最大的构建加强并改进，由此提升计算效率。通过灵敏度分析，确定各个构件变量对于整个大型集装箱船舱底座结构的贡献程度，灵敏度系数 $ {R_i} $ 计算通过结构响应的显示函数实现：

式中： $ {x_i} $ 与 $ {x_j} $ 为第 $ i $ 个和第 $ j $ 个构件随机变量； $ {\delta _{{x_i}}} $ 与 $ {\delta _{{x_j}}} $ 分别为第 $ i $ 个和第 $ j $ 个随机变量的均方差； $ {\mu _{{x_i}}} $ 与 $ {\mu _{{x_j}}} $ 分别为第 $ i $ 个和第 $ j $ 个随机变量均值； $ x $ 为构件变量。各个构件变量的取值上限和取值下限依据《钢规》中的相关要求计算获得。

确保重力作用之下，大型集装箱船舱底座结构不发生显著变形，是加强改进大型集装箱船舱底座的目标之一。一般可以通过刚度变化反映出底座的变形情况，因此将重力作用下，大型集装箱船舱底座结构刚度最大，作为第一个优化目标函数。正常情况下，钢结构的刚度会和柔度呈现出负相关关系，因此可以将底座结构刚度目标函数转换成柔度目标函数，实现求解。一般通过大型集装箱船舱底座结构的应力变化描述柔度情况，所以本文使用折衷规划法获取大型集装箱船舱底座结构柔度 $ B $ 最小目标函数，构建该目标函数时，同时还将底座结构构件变量的灵敏度系数考虑进去，目标函数如下：

式中： $ {B_k} $ ， $ {B_{k\max }} $ ， $ {B_{k\min }} $ 分别为第 $ k $ 种工作情况下底座结构的柔度、最大与最小柔度； $ m $ 为载荷工况的数量； $ q $ 为欧式度量，主要度量理想解和最优解之间的贴近度值； $ {w_k} $ 为第 $ k $ 种工作情况权重值。

大型集装箱船舱底座在工作时，受到船舱的挤压，会出现共振频率。为了帮助大型集装箱船舱底座的低阶固有频率脱离这种共振频率，考虑灵敏度系数的同时，设定最大低阶固有频率作为大型集装箱船舱底座结构增强与改进的另一个目标函数。为避免低阶固有频率优化时出现频率振荡问题，优化大型集装箱船舱底座结构时，不但需要优化某一阶频率，同时还要综合优化整个大型集装箱船舱底座结构的多个低阶阶固有频率。使用大型集装箱船舱底座平均频率定义优化低阶固有频率的目标函数：

其中： $ A $ 用于描述平均频率； $ {\theta _i} $ 与 $ {\omega _i} $ 分别为第 $ i $ 阶频率与频率的权重值，为便于计算，设置频率权重是1/6； $ {\theta _0} $ 和 $ s $ 为用于调整目标函数的任意常数，为便于计算， $ {\theta _0} $ 取值为0； $ f $ 6为用于描述待优化的频率阶数。

重力荷载之下，大型集装箱船舱底座结构加强与改进时，以柔度最小和低阶固有频率最大作为目标，综合式（2）和式（3）获得最终大型集装箱船舱底座结构加强与改进的目标函数为：

其中： $ F $ 为加强改进目标值； $ {A_{\max }} $ 为最大平均频率； $ {A_{\min }} $ 为最小平均频率。

根据以上大型集装箱船舱底座结构多目标优化结果，在底座结构的下方结构安装上支架和下支架，提升底座结构的承载力，确保柔度最低的同时低阶固有频率最下。同时依据变量灵敏度和目标函数优化各个构件变量的数值，得到最优大型集装箱船舱底座结构增强改进结果。

经过灵敏度分析，在众多大型集装箱船舱底座结构构件变量中，确定7个贡献度较高的构件变量，针对这些构件变量，实行加强改造。依据《钢规》相关规定，计算获得各个构件变量的取值上限与取值下限，以这些值作为各个构件变量优化的限定值，依据本文方法中以刚度最大和低阶固有频率最大为目标，加强并改进各个构件值结果见表1。

表 1(Tab. 1)

表 1 待优化构件变量限值与优化值 Tab. 1 Variable limits and optimized values of components to be optimized 待优化变量 下限值 上限值 原始值 优化值 底座厚度/cm 105 225 113 218 支座板厚度/cm 215 354 226 329 圆形支架直径/cm 36 48 37 42 铰链结构厚度/cm 58 79 61 76 涡轮外齿环直径/cm 47 85 52 79 涡杆长度/cm 25 45 35 28 轴承直径/cm 65 85 79 73

表 1 待优化构件变量限值与优化值 Tab.1 Variable limits and optimized values of components to be optimized

表1中数据显示，本文方法加强改进大型集装箱船舱底座结构是将底座厚度、支座板厚度、圆形支架直径、铰链结构厚度以及涡轮外齿环直径增加，同时降低涡杆的长度和轴承的直径，实现大型集装箱船舱底座结构柔度最小和低阶固有频率最大的加强改进目的。

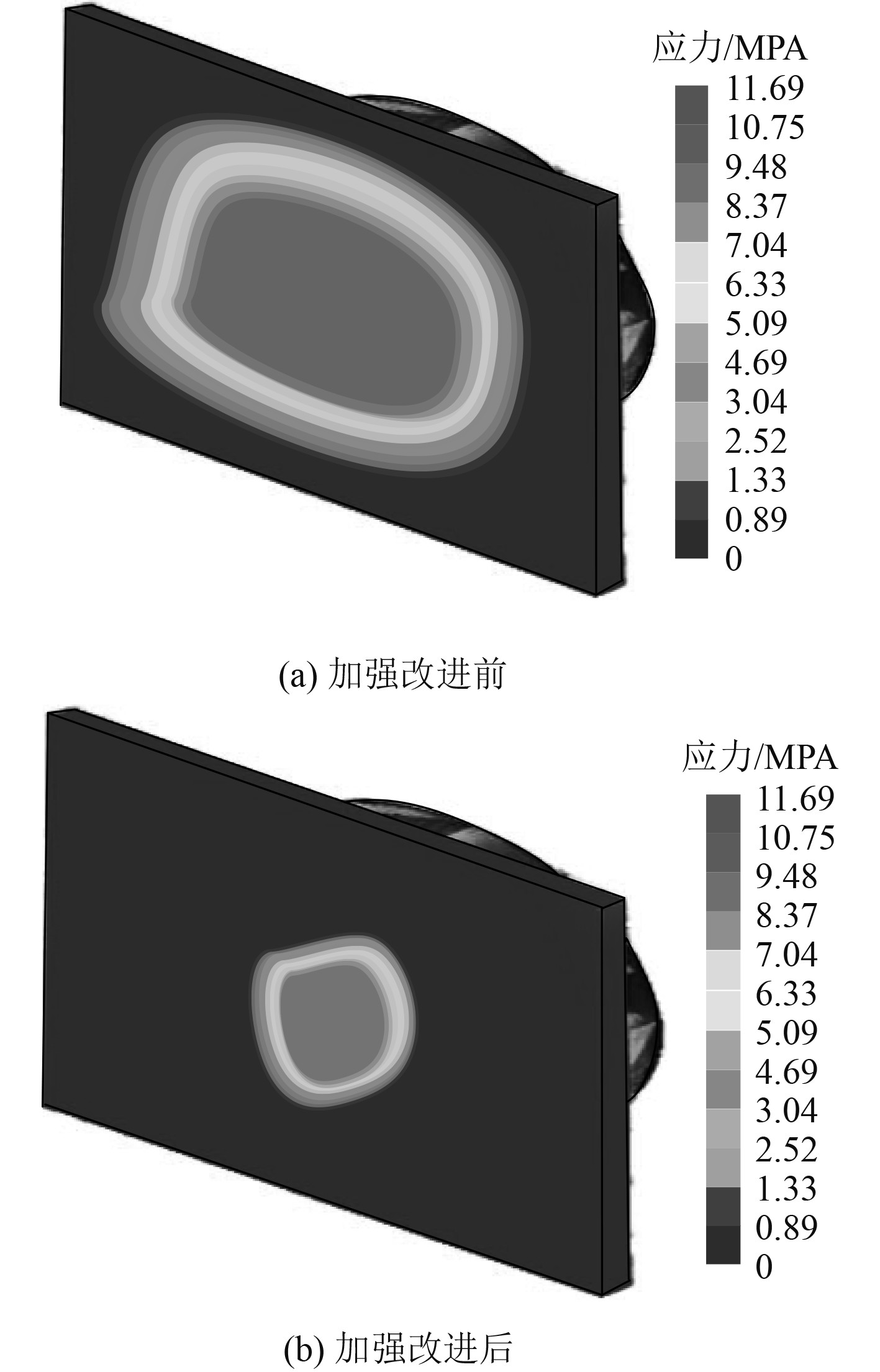
本文加强改进大型集装箱船舱底座结构，将柔度最小和低阶固有频率最大作为优化目标。通过有限元软件对比加强改进前后大型集装箱船舱底座结构的应力变化，由此确定加强改进后大型集装箱船舱底座结构柔度变化。实际工作环境下，船舶的作用力主要集中在底座板上，下部支架提供的支撑力也会反应在底座板上，所以试验以底座板的受力变化为主开展研究。应力变化如图2所示。在有限元软件中，向大型集装箱船舱底座结构有限元模型施加重力荷载，获得加强改进前后该底座结构的应力变化。图2（a）的结果显示，受到重力影响，加强改进前的底座结构模型应力变化面积较大，最高应力为11.69 MPa，刚度较小，大型集装箱船舱底座长时间在这种重力荷载下工作，很容易发生失稳情况，出现严重安全隐患。图2（b）结果显示，使用本文方法添加上下支架加固，同时优化各个构件以后，明显提升大型集装箱船舱底座面板的受力能力，在相同重力荷载下，加强改进后大型集装箱船舱底座结构受力面积更小，最高应力为8.37MPa，相比于未加强改进的大型集装箱船舱底座结构，应力明显降低。说明在大型集装箱船舱底座结构中添加支架并优化构件变量能够降低大型集装箱船舱底座结构的柔度。

图 2 有限元模拟结果 Fig. 2 Finite element simulation results

低阶固有频率加强改进前后性能对比结果见表2。从表2能够看出，前5阶固有频率经过优化均有所提升。通常情况下，低阶固有频率影响关联大型集装箱船舱底座结构的稳定性，低阶固有频率越高，大型集装箱船舱底座结构的稳定性也越强。本文方法中加强改进目标之一是大型集装箱船舱底座结构的低阶固有频率最高。经过本文方法加固后，各低阶固有频率均呈现出明显升高，说明使用本文方法能够使得大型集装箱船舱底座结构更加稳定。

表 2(Tab. 2)

表 2 低阶固有频率加强改进前后对比 Tab. 2 Comparison of low order natural frequency before and after improvement 阶数 1阶 2阶 3阶 4阶 5阶 加强改进前固有频率/Hz 166.8 173.6 185.4 197.3 200.4 加强改进后固有频率/Hz 172.6 185.3 194.2 203.7 215.9

表 2 低阶固有频率加强改进前后对比 Tab.2 Comparison of low order natural frequency before and after improvement

支撑船舱的底座稳定性影响大型集装箱船舱上岸维修的稳定性，所以需要加强并改进该底座的强度和稳定性，保证大型集装箱船舱在一个安全的环境中正常维修。通过灵敏度分析确定待优化的大型集装箱船舱底座结构构件变量，并改变这些构件的厚度或者长度，在底座内部加设上下2个支架，实现集装箱船舱底座结构的加强改进。通过有限元软件模拟加强改进结果，本文方法能够提升底座的刚度和低阶固有频率，获得较为稳定的大型集装箱船舱底座。