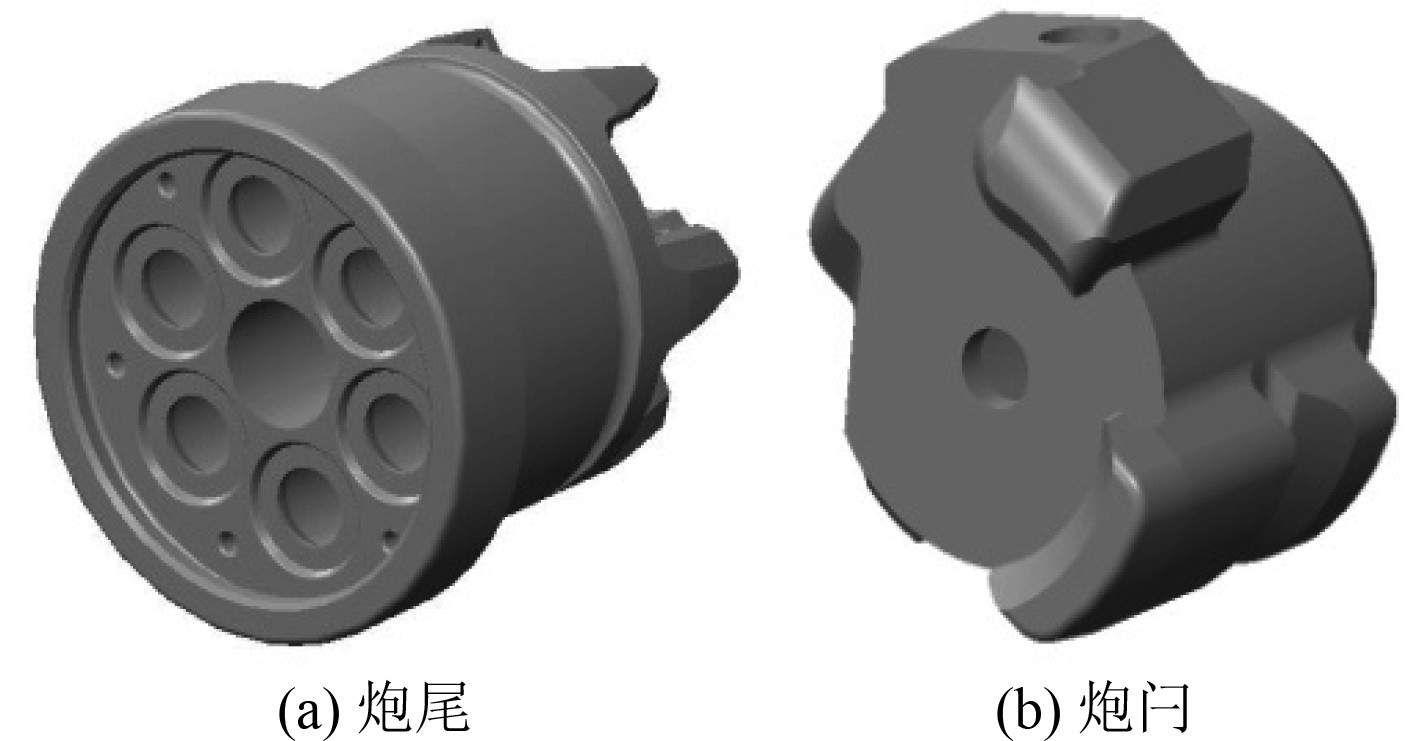
转管航炮射击时,闭锁机构中的炮尾与炮闩(见图1)受到强烈冲击,作为转管航炮的重要承力机构,炮尾与炮闩一起完成药室闭锁,炮尾上的闭锁齿与炮闩上的闭锁齿相互配合,保证炮膛密闭,其刚强度设计好坏直接影响转管航炮连续射击时的工作可靠性[1-2]。
|
图 1 闭锁机构炮尾与炮闩 Fig. 1 Gun breech and breechblock of blocking mechanism |
夏建国等[3]对高膛压炮尾进行了失效分析,发现在炮尾端面和侧壁加工的圆角处发生断裂,裂纹起始于圆角根部,一直延伸到曲臂轴孔和挡板内孔处。安俊斌等[4]基于Abaqus参数化模型对身管部位定位槽强度进行了分析,按照槽底圆角半径为0.3 mm,0.5 mm,1.0 mm和1.5 mm等4种工况进行了分析,结构依次在圆角处出现宏观裂纹。项立银等[5]基于响应面法对炮尾炮闩进行了6σ稳健优化设计,以二维平面结构进行炮尾圆角优化设计,以三维模型进行优化结果验证,结果显示炮尾圆角应力下降42%。
根据以往众多研究得出的结论可知,闭锁机构中的炮尾炮闩闭锁齿设计是转管武器设计的重要一环,必须加以重视,并且炮尾炮闩的圆角根部是火炮关重件设计需要重点考察的危险点[6]。
1 闭锁机构强度理论基于大量的理论研究和实验验证,目前已经提出了上百个强度模型。按照剪应力分类,可以将强度理论划分为单剪强度理论(SSS理论)、双剪强度理论(TSS理论)和八面体剪应力强度理论(OSS理论,octahedral-shear strength theory)三大系列强度理论[7-8]。
最大偏应力屈服条件是TSS理论的单参数准则,其一般表达式为:
| $ \begin{split} &f({J_2},{J_3}) =\\ &\frac{{2\sqrt {{J_2}} }}{{\sqrt 3 }}\frac{1}{{{k_3}}}\max \left\{ {\left| {\sin ({\theta _\sigma } + \frac{{2{\text{π }}}}{{\text{3}}})} \right|,\left| {{\text{sin(}}{\theta _\sigma } - \frac{{2{\text{π }}}}{{\text{3}}}{\text{)}}} \right|} \right\} - 1 = 0,\end{split}$ |
其中,
双剪应力强度理论认为当作用于单元体上的2个较大主剪应力之和达到某一极限值时,材料开始发生屈服,俞茂宏[8]将其表述为:
| $ \left\{\begin{array}{c}f={\tau }_{13}+{\tau }_{12}={\sigma }_{1}-\dfrac{1}{2}({\sigma }_{2}+{\sigma }_{3})=c,({\tau }_{12}\geqslant {\tau }_{23}),\\ {f}^{\text{'}}={\tau }_{13}+{\tau }_{23}=\dfrac{1}{2}({\sigma }_{1}+{\sigma }_{2})-{\sigma }_{3}=c,({\tau }_{12}\leqslant {\tau }_{23})。\end{array} \right.$ |
比Tresca强度理论多考虑了中间主剪应力的影响,在某些应力状态下其理论值与实验结果吻合很好[9]。
Mises屈服条件是OSS理论的单参数准则,其一般应力表达式为:
| $ f({J}_{2},{J}_{3})={J}_{2}-{k}_{2}^{2}=0,$ |
Mises屈服条件认为引起材料屈服的主要因素是畸变能,材料力学将Mises屈服条件处理后称其为第四强度理论,其强度条件在材料力学中被表述为:
| $ {\sigma _{{\text{xd}}4}} = \sqrt {\frac{{{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}}}{2}} \leqslant \left[ \sigma \right]。$ |
式中的等效应力考虑了3个主应力的综合影响,也更符合大量实验验证的结果。
本文闭锁机构炮尾炮闩仿真分析基于八面体剪应力强度理论的单参数准则,即Mises屈服条件,并将分析结果与双剪强度理论分析结果进行对比分析。
2 闭锁机构有限元仿真分析 2.1 有限元模型进行有限元分析时,考虑射击时转管航炮只有一个炮膛进行射击,其他炮膛与对应身管不受载荷,载荷按实际炮膛压力加载于炮尾与炮闩,将炮尾与炮闩作为装配体一起建立有限元模型。炮尾与炮闩材料为某炮钢,其材料属性见表1。
|
|
表 1 闭锁机构材料属性 Tab.1 Blocking mechanism material properties |
转管航炮射击时,炮尾与炮闩在极限受力条件下取一定安全系数进行分析,计算时按照最大膛压pt进行加载。
有限元模型网格及约束和加载情况如图2所示。共划分单元423943个,节点1407145个。约束炮尾前部端面位移,在内膛和炮闩镜面施加均布压力载荷[10]。

|
图 2 炮尾与炮闩有限元模型 Fig. 2 Finite element model of gun breech and breechblock |
对炮尾和炮闩装配体进行接触状态非线性分析,接触部位类型设定为摩擦接触,摩擦系数0.15,接触算法采用增广拉格朗日算法,接触法向接触刚度初始设为0.1,并将法相接触刚度设为动态调整,然后进行有限元分析,得到炮尾炮闩装配体及零件的应力分布如图3~图11所示。
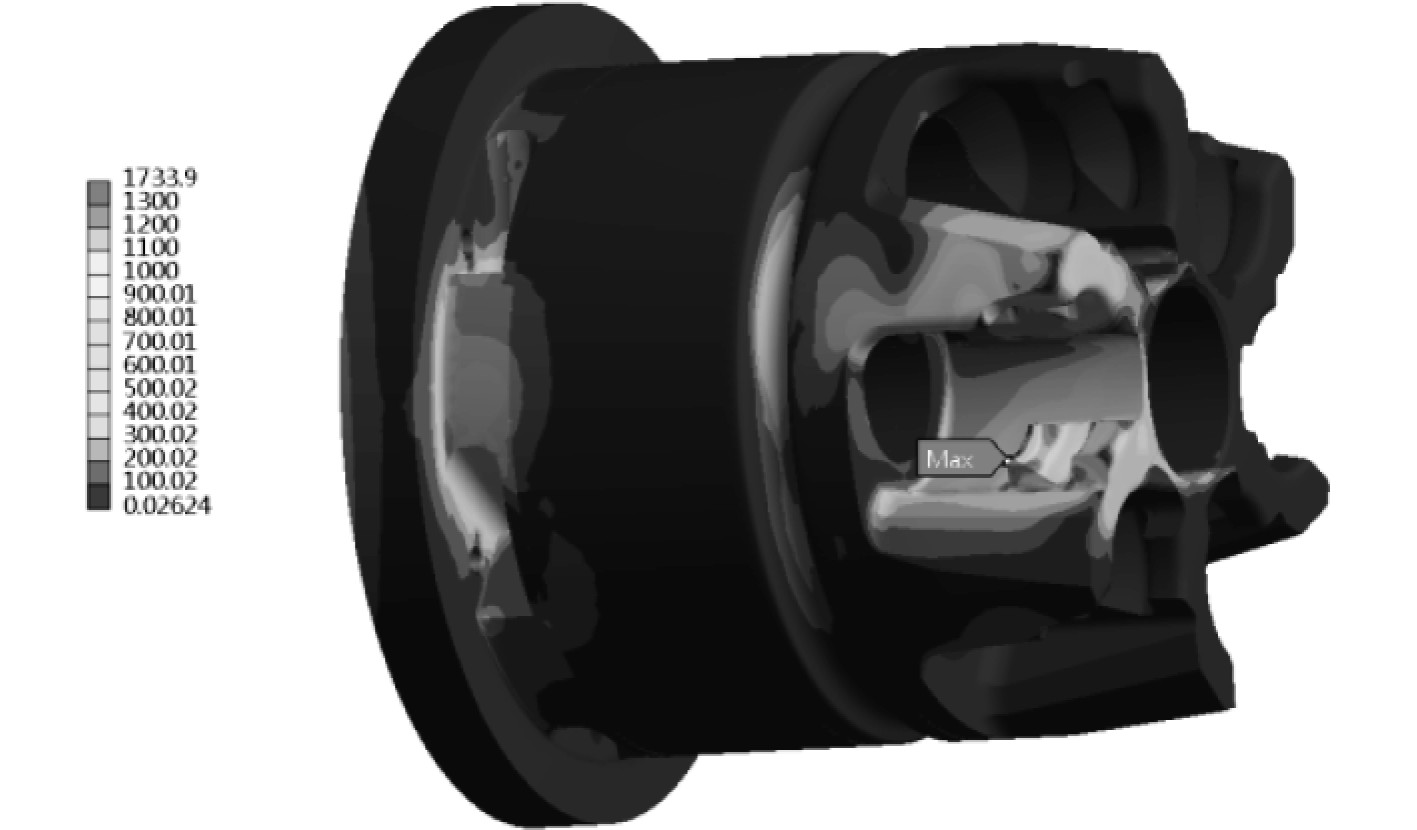
|
图 3 炮尾Mises等效应力分布 Fig. 3 Mises stress distribution of gun breech |
为了便于观察分析,将炮尾处与炮闩配合接触局部截出,其应力分布如图4所示。可以看出,炮尾闭锁齿上Mises等效应力最大为1733.9 MPa,此最大值位于炮尾闭锁齿一个小尖点处,位于一个棱边尖角的小单元上,尺寸大小约为0.1 mm。除此之外,炮尾闭锁齿上的等效应力均远远小于1733.9 MPa,此处为应力奇异点,由于模型应用了理想化有限元模型,忽略了此处的倒角,实际结构此尖角所在棱边有小的倒圆角,不会产生应力奇异性,此棱边尖角处的局部应力奇异点对炮尾总体结构影响可以忽略不计。闭锁齿面上其他部位的Mises等效应力相对较小,且分布较为均匀,等效应力值在600~1100 MPa,且射击过程在10~15 ms内完成,闭锁齿上积聚的能量较小,炮尾处还留有一定的安全余量,炮尾的结构强度符合要求,炮尾是安全的,可以安全地工作。
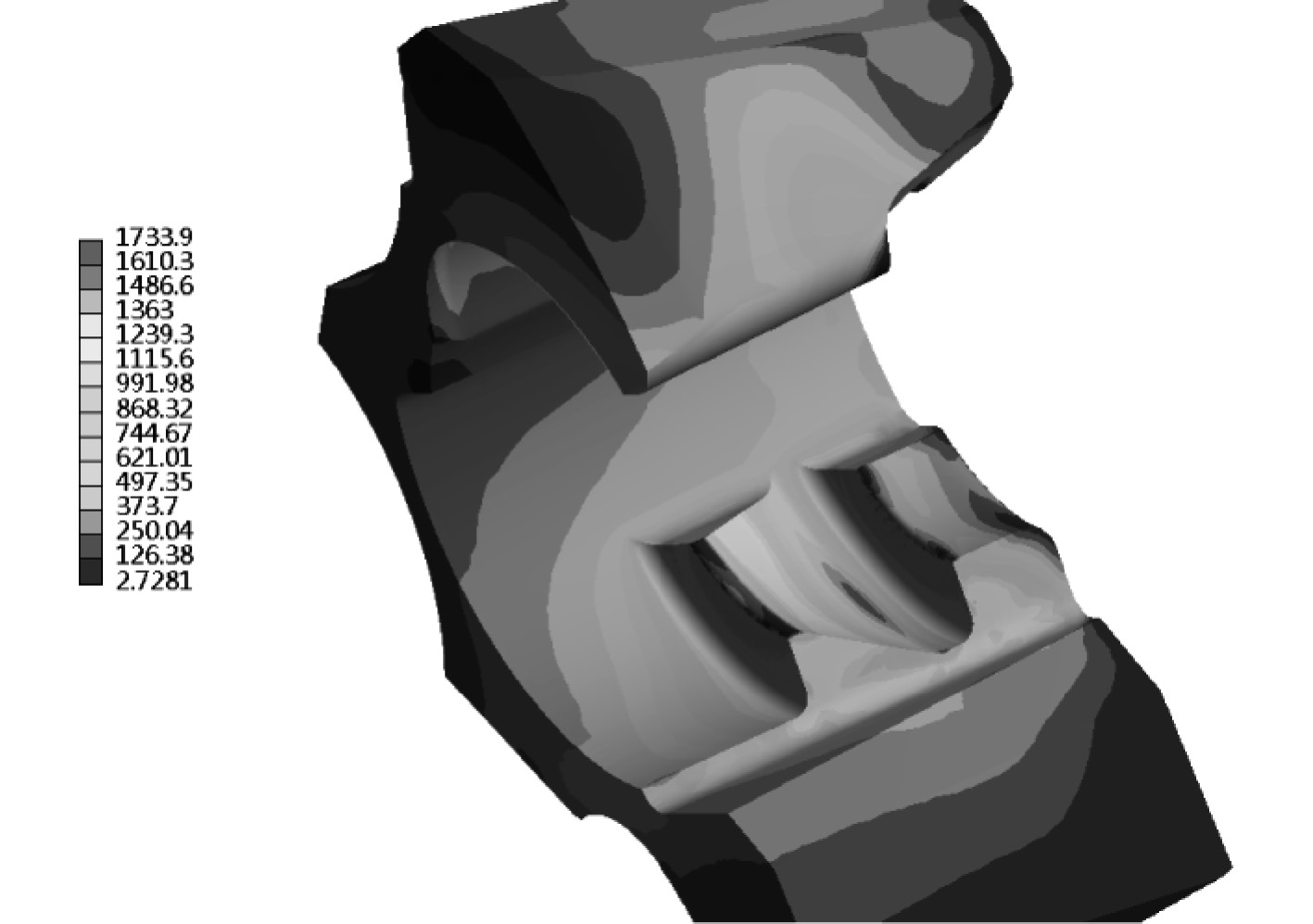
|
图 4 炮尾闭锁齿Mises等效应力分布 Fig. 4 Mises stress distribution of gun breech locking teeth |
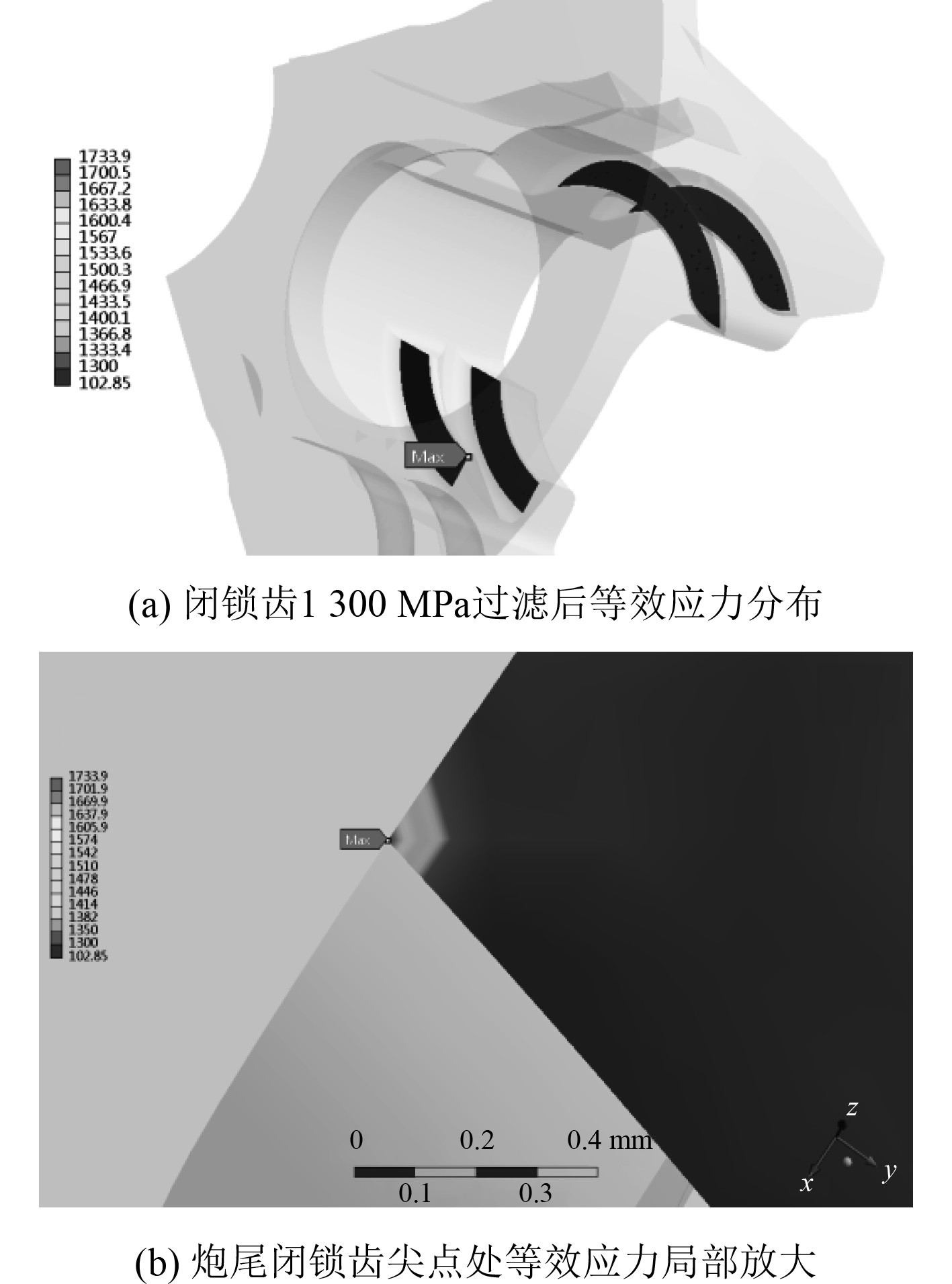
|
图 6 炮尾闭锁齿处Mises等效应力分布及局部放大视图 Fig. 6 Local amplification mises stress distribution of gun breech locking teeth |
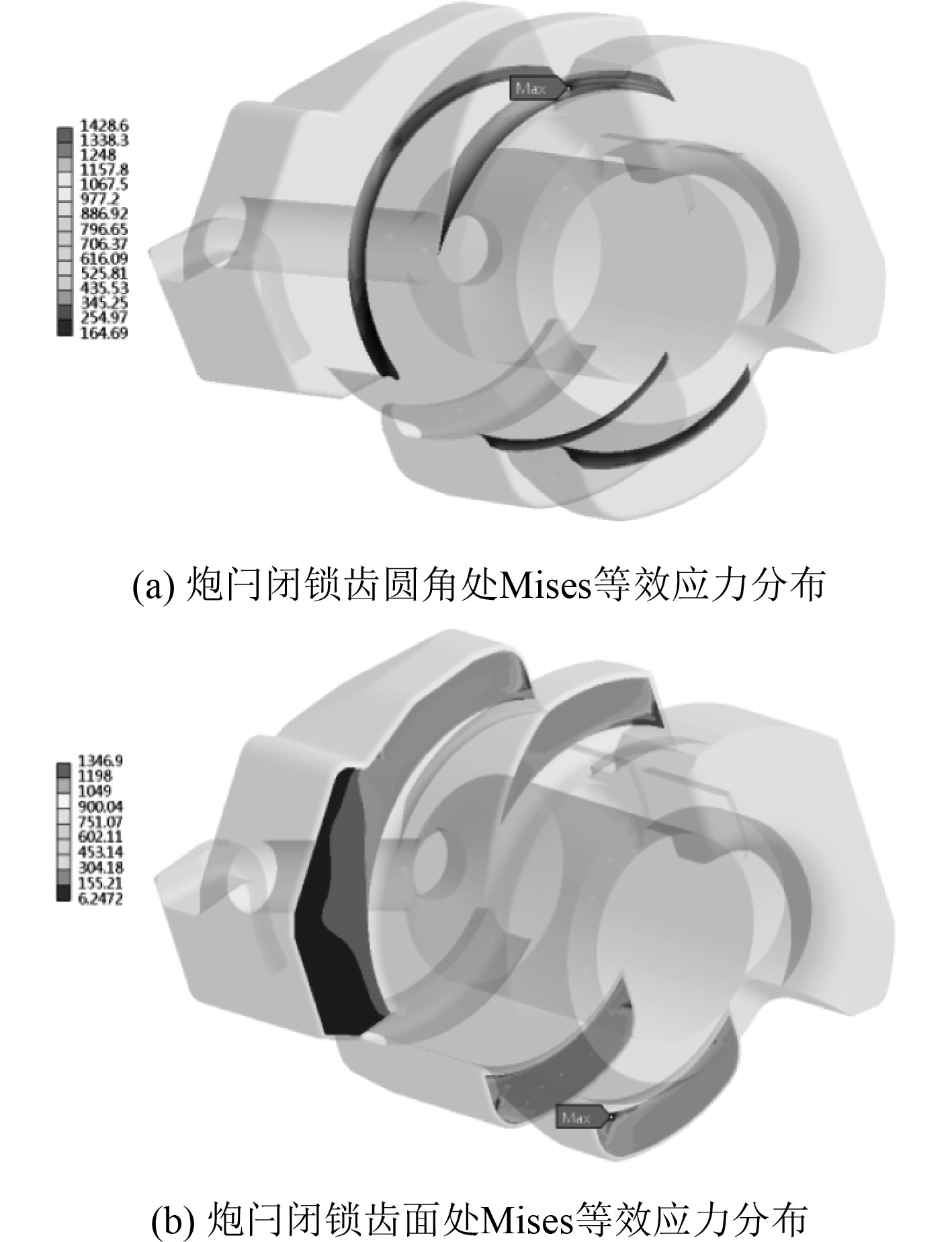
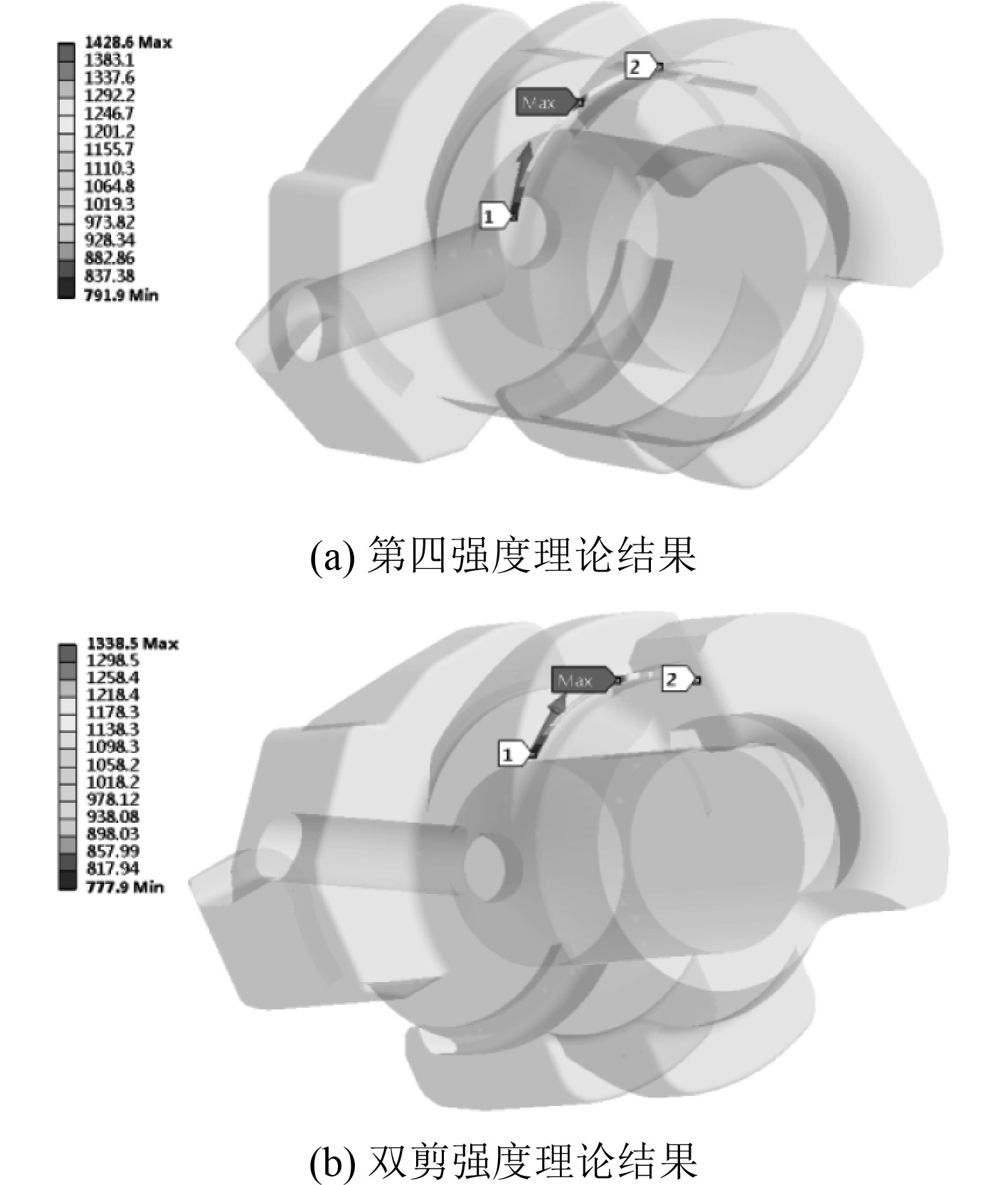
由图7可知,炮闩上的Mises等效应力最大为1428.6 MPa,位于炮闩第一排闭锁齿的倒角根部,靠近倒角的中间位置。
|
图 7 炮闩闭锁齿处Mises等效应力分布 Fig. 7 Local mises stress distribution of breechblock locking teeth |
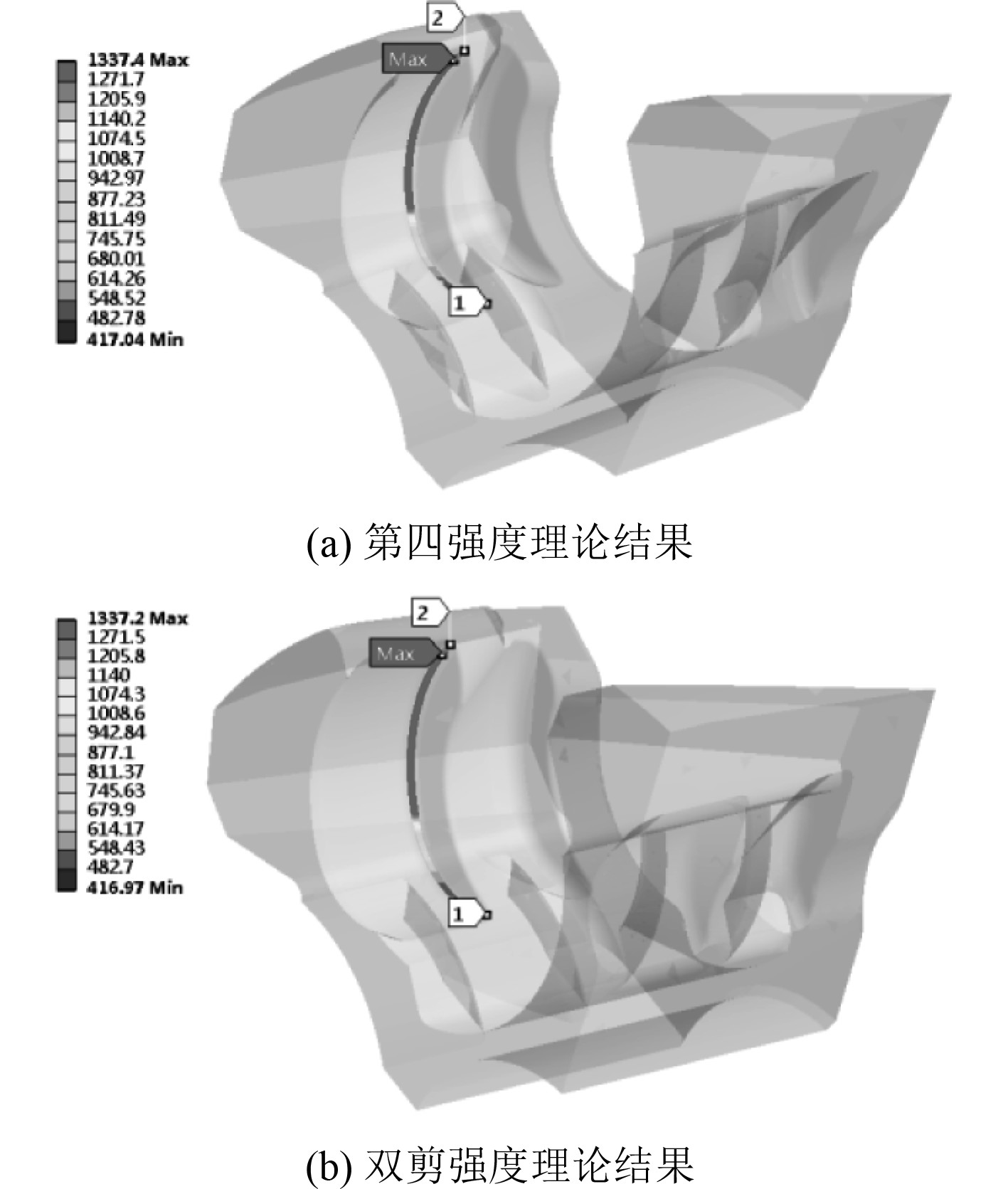
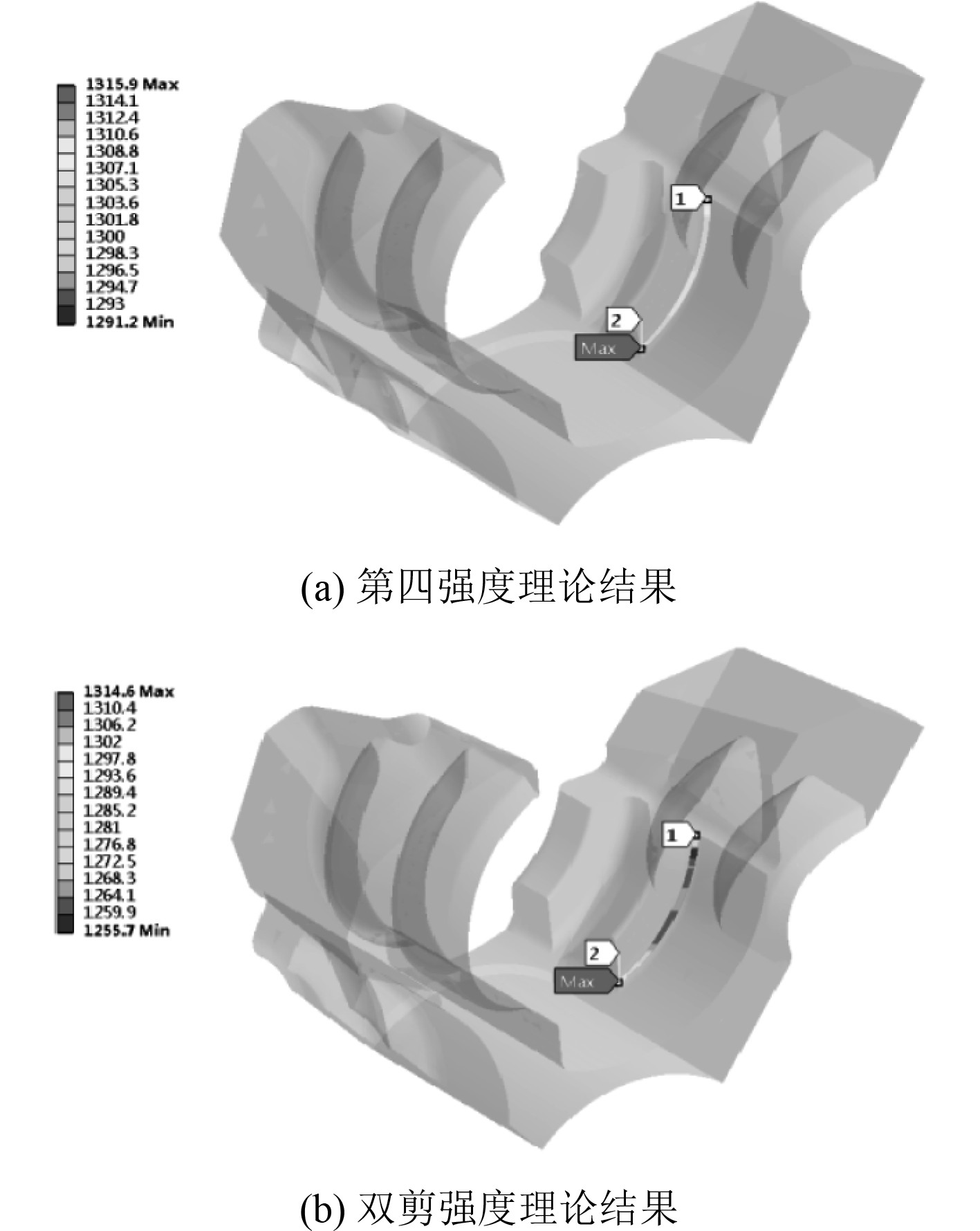
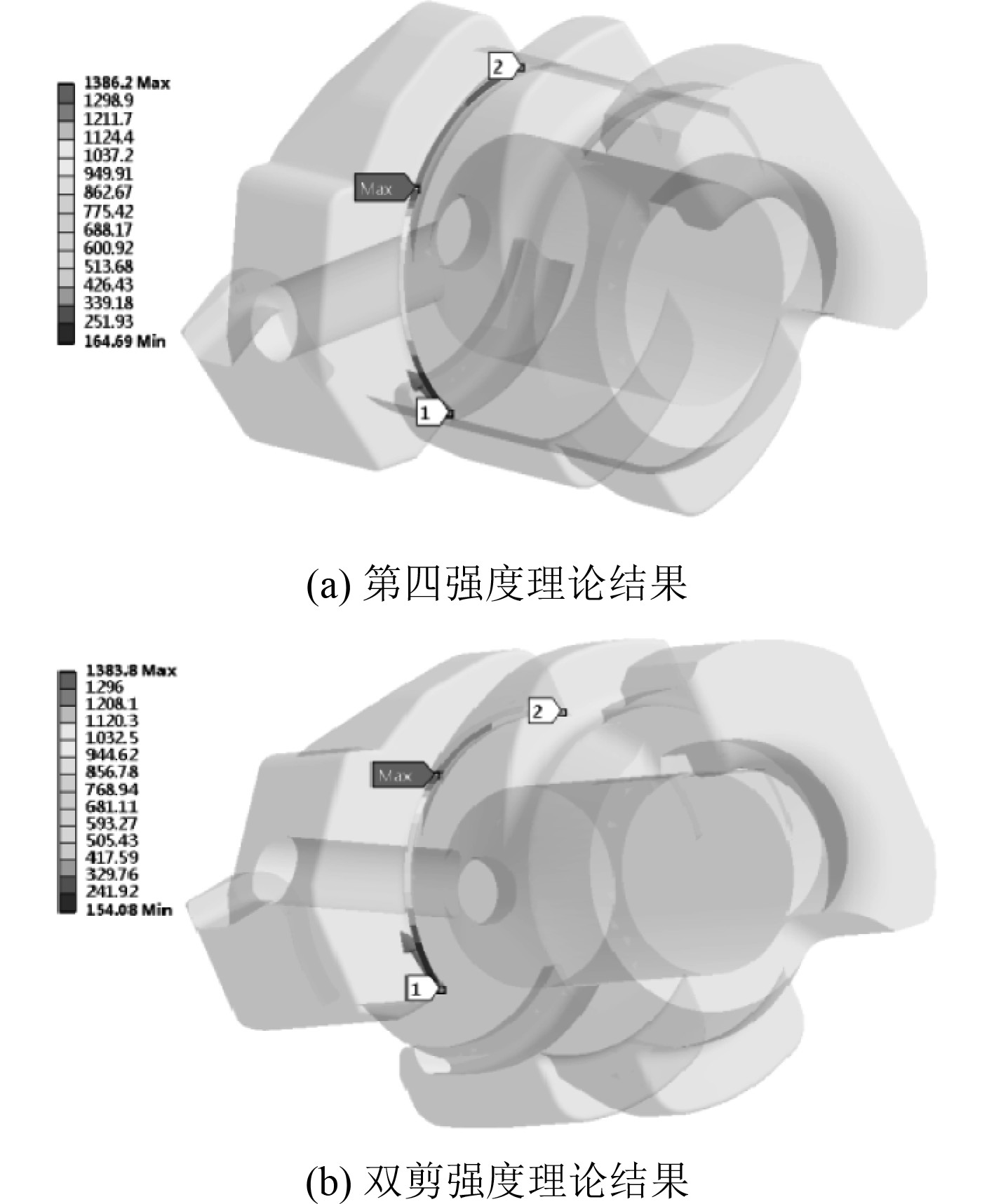
倒角根部是结构重点考察部位,是结构的危险部位。为了详细分析炮闩的强度,选取炮尾和炮闩闭锁齿倒圆角根部的4条路径,提取路径上对应第四强度理论和双剪强度理论的等效应力,其应力分布如图8~图11所示。将路径上等效应力数值处理,得到对比曲线如图12所示。
|
图 8 炮尾path1等效应力分布 Fig. 8 Path1 stress distribution of gun breech |

|
图 12 炮尾和炮闩闭锁齿圆角根部路径上等效应力分布对比曲线 Fig. 12 Stress distribution contrast curves of locking teeth round corners path of gun breech and breechblock |
可以看出,Mises等效应力校核结果与双剪强度理论检核结果相比,部分曲线近似重合,剩下部分曲线前者校核结果大于后者,因为双剪强度理论曲线位于强度理论极限面的上界,这与理论分析结果是一致的,详见参考文献[9]。
|
图 9 炮尾path2等效应力分布 Fig. 9 Path2 stress distribution of gun breech |
|
图 10 炮闩path5等效应力分布 Fig. 10 Path5 stress distribution of breechblock |
由图5和图7应力分布图以及图12的曲线对比可以看出,在最大膛压的静载荷作用下,炮尾和炮闩倒圆角根部的等效应力在炮闩炮尾闭锁齿相互接触的区域较大,在非相互接触的区域较小,在局部某些点处的等效应力达到1300 MPa,甚至超出1300 MPa,但考虑到实际火炮射击是瞬态作用,载荷作用时间较短,且为动态过程,其动态性能、动应力和动应变与静态情况有所不同。

|
图 5 炮尾闭锁齿处Mises等效应力分布 Fig. 5 Local mises stress distribution of gun breech locking teeth |
根据谈乐斌等[11]对受高压厚壁圆筒(所用材料的屈服极限为1260 MPa)动态强度的研究,动态作用比瞬态作用可承受的动态载荷比静载荷高30%以上(计算值为32.3%,实验值为36.7%),一般按照10%~20%的值保守计算,这已经被大量实验结果所证实[12],此时火炮身管在超过极限强度内压10%~20%的载荷下可以安全可靠的射击。据此分析,考虑动态射击的影响,闭锁机构的动态强度极限保守计算可达1430~1560 MPa。由图11~图12可知,闭锁机构倒圆角根部等效应力最大为1428.6 MPa(在path6距离起始点约11 mm处,按照第四强度理论校核),均小于1430 MPa,此时尚未考虑钢材的硬化特性,实际上火炮用钢在高载荷下多次连续射击时,会产生硬化效果,使得结构的动态强度进一步提高。由以上分析可知,此火炮闭锁机构可以安全可靠地承受射击载荷作用,使结构安全可靠的工作。
|
图 11 炮闩path6等效应力分布 Fig. 11 Path6 stress distribution of breechblock |
为进一步摸索合理应力值范围,将此转管航炮炮闩闭锁接触面挤压应力与某转管舰炮的炮闩进行对比分析。
这2型炮闩的结构类似,炮闩上均有2排闭锁齿,每排分别有2个闭锁面,共有4个闭锁面。炮弹击发后,火药燃气作用力通过药筒底部、经炮闩闭锁齿传递至炮尾闭锁齿,再经由滚珠滚道将后坐力传递给炮箱。在计算闭锁支撑面受力时,由于火药燃气作用在膛底的合力比药筒在药室中的摩擦力大得多,为简明起见,通常忽略药筒的影响,这样,发射时垂直作用在闩体镜面上的力可按下式进行计算:
| $ F_j=p_t\frac{\text{π}}{4}d^2_1。$ |
式中:pt为药室底部火药气体的压强;d1为药筒底部内径。
2型转管炮炮闩炮尾材料相同,计算所用参数取值见表2。
|
|
表 2 两型转管炮载荷参数取值 Tab.2 The value of load parameter oftwo type gatling gun |
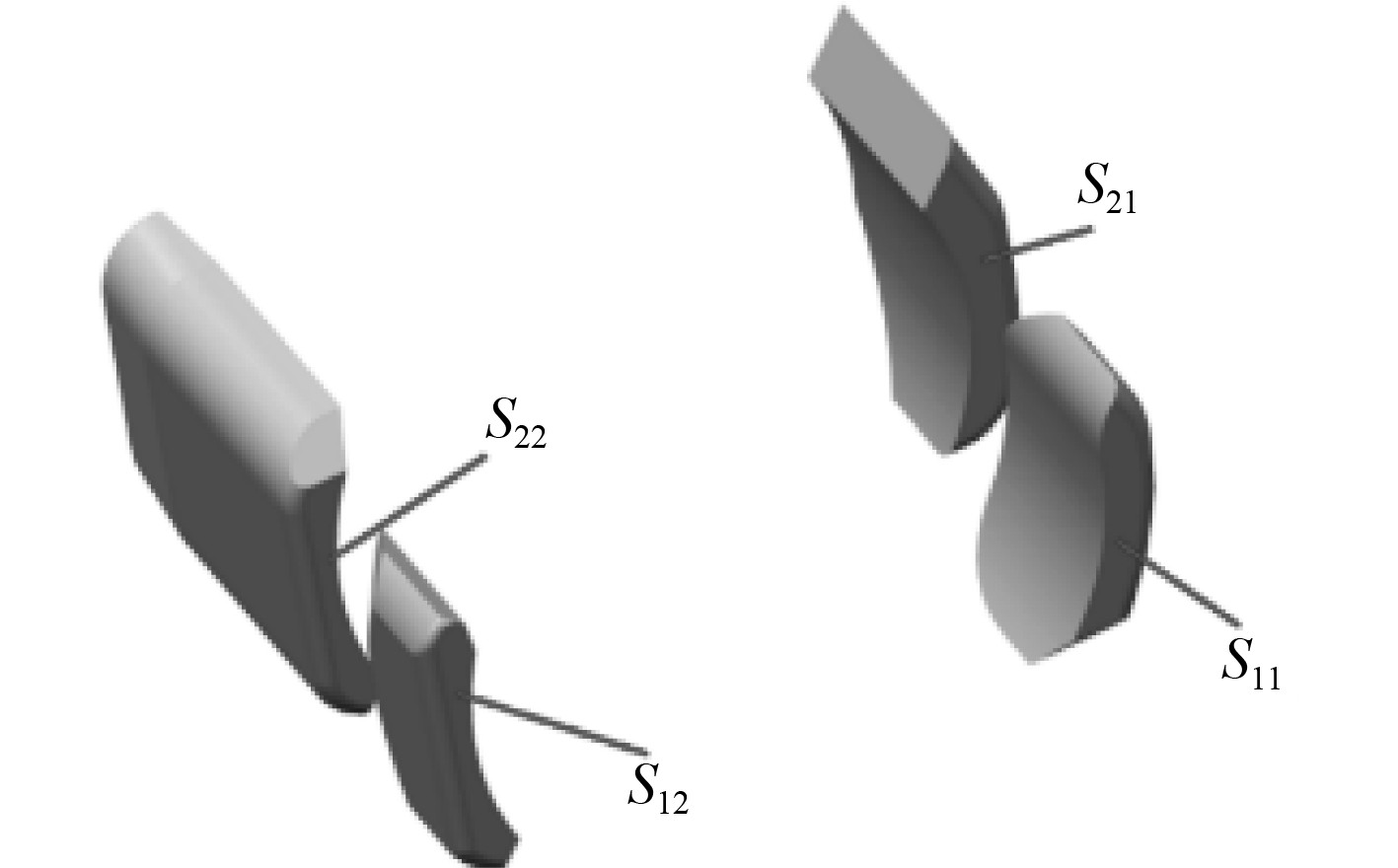
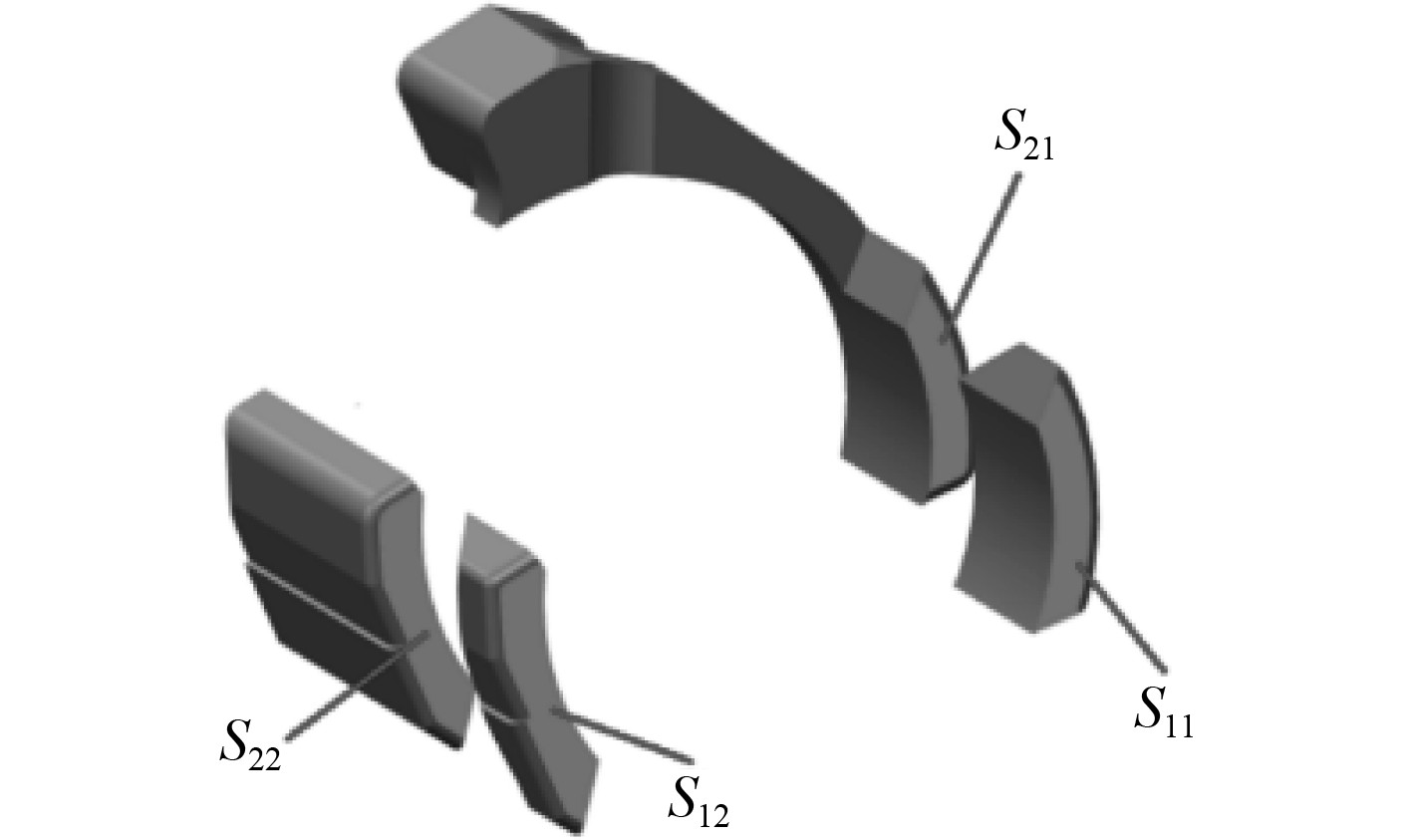
运用三维建模软件对两型转管炮炮闩闭锁面的接触面积分别测量,结果用S11,S12,S21,S22表示,如图13和图14所示。
|
图 13 某转管航炮炮闩闭锁齿接触面图示 Fig. 13 Contact surfaces of locking teeth of breechblock of gatling aircraft gun |
|
图 14 某转管舰炮炮闩闭锁齿接触面图示 Fig. 14 Contact surfaces of locking teeth of breechblock of gatling naval gun |
若不考虑惯性力的影响,则作用在闭锁支撑上的力就等于作用在炮闩镜面上的力Fj。4个闭锁齿,按平均受力进行分析,即每个闭锁齿上受力按Fj/4取值,假定在挤压面上应力也是均匀分布的,则闭锁接触面上的挤压应力可按照下式计算:
|
|
表 3 炮闩闭锁齿接触面对比 Tab.3 Contact surfaces contrast value of locking teeth of breechblock |
通过同类产品对比可以看出,此转管航炮闭锁齿4个接触面上的挤压应力均远小于同类转管舰炮4个接触面上的挤压应力,说明此转管航炮炮尾与炮闩闭锁结构设计较为合理,受力良好,其挤压强度同样满足使用要求。
4 结 语基于前述强度理论,通过对某型转管航炮的炮尾炮闩进行非线性有限元分析,以及与类似某转管舰炮炮闩接触面挤压应力的对比分析,结果表明,此闭锁机构强度均满足使用要求,结构设计较为合理,倒角根部强度足够,闭锁齿接触面上挤压应力大大减小,且通过实物样机试验验证,此闭锁机构是有效的。
从结构设计与强度方面考虑,此转管航炮炮尾与炮闩闭锁齿的设计还有进一步优化的空间,可以继续增大闭锁齿厚度与接触面积,使得倒角根部应力降低,挤压应力减小,进一步提高闭锁机构连续射击时的工作可靠性。
| [1] |
朱延飞, 魏立新. 基于故障树的某闭锁机构故障原因仿真分析[J]. 兵器装备工程学报, 2019, 40(1): 44-46. DOI:10.11809/bqzbgcxb2019.01.009 |
| [2] |
杨明光. 自动机旋转闭锁机构的耐久性提升研究[D]. 太原: 中北大学, 2021.
|
| [3] |
夏建国, 王来生. 高膛压炮尾失效分析[J]. 兵器材料科学与工程, 1991, 117: 15-20. DOI:10.14024/j.cnki.1004-244x.1991.06.005 |
| [4] |
安俊斌, 李强, 谭庆, 等. 基于ABAQUS参数化的身管尾部定位槽强度分析方法[J]. 兵工自动化, 2016, 35(10): 12-16. DOI:10.7690/bgzdh.2016.10.004 |
| [5] |
项立银, 顾克秋. 基于响应面法炮尾炮闩6σ稳健优化设计[J]. 机械制造与研究, 2011, 20-22. |
| [6] |
付帅, 顾克秋, 等. 基于有限元的炮尾结构优化设计[J]. 机械制造与自动化, 2014(3): 137-140. DOI:10.3969/j.issn.1671-5276.2014.03.046 |
| [7] |
俞茂宏. 强度理论百年总结[J]. 力学进展, 2004, 34(4): 529-560. DOI:10.3321/j.issn:1000-0992.2004.04.009 |
| [8] |
俞茂宏. YOSHIMINE M, 强洪夫, 等. 强度理论的发展和展望[J]. 工程力学, 2004, 21(6): 1-20. DOI:10.3969/j.issn.1000-4750.2004.06.001 |
| [9] |
葛书强, 杨彬. 基于应力理论的舰炮炮尾抓钩强度分析[J]. 舰船科学技术, 2021(8): 175-181. DOI:10.3404/j.issn.1672-7649.2021.03.034 |
| [10] |
付立华. 某航炮自动机动力学仿真及其关重件强度分析[D]. 南京: 南京理工大学, 2011.
|
| [11] |
谈乐斌, 蔡樑, 袁人枢. 厚壁圆筒动态强度的有限元分析和实验研究[J]. 弹道学报, 2010, 22(4): 86-88. |
| [12] |
张相炎, 郑建国, 袁人枢. 火炮设计理论[M]. 北京: 北京理工大学出版社, 2014.
|
 2022, Vol. 44
2022, Vol. 44
