0 引　言

随着航海领域的迅速发展，对舰船设备的安全性要求逐渐升高，通常情况下，舰船存在大量关键设备^[1-2]，例如发动机、汽轮主机等，每一设备的运行情况发生变化都会对舰船造成影响，因此，若舰船关键设备无法得到有效控制，则会影响舰船航行安全^[3]。

众多学者对智能控制方法进行了研究。邓华等^[4]。研究船舶航向神经网络优化控制，通过遗传算法改进优化控制效果，但其无法控制船舶速度等。熊中刚等^[5]研究PID自动转向控制系统，通过系统架构完成控制，但控制过程中的安全性不高。PID控制器是目前应用较广的设备控制方法，该控制器可利用控制参数快速对不同设备进行控制。神经网络属于一种网络学习方法，可通过神经网络对PID控制器进行优化，将PID控制器参数输入到神经网络后，经过不断迭代学习获取最佳PID控制参数，以此能够提高PID控制器的控制能力。为此，本文研究神经网络优化PID的舰船关键设备智能控制方法。鉴于灵敏度是一种能够影响舰船设备运行状态的指标，可反映出设备在运行过程中的实时变化能力，为此选取灵敏度作为舰船关键设备智能控制的指标，结合神经网络优化PID控制器进行关键设备智能控制，使控制后舰船关键设备更加稳定。

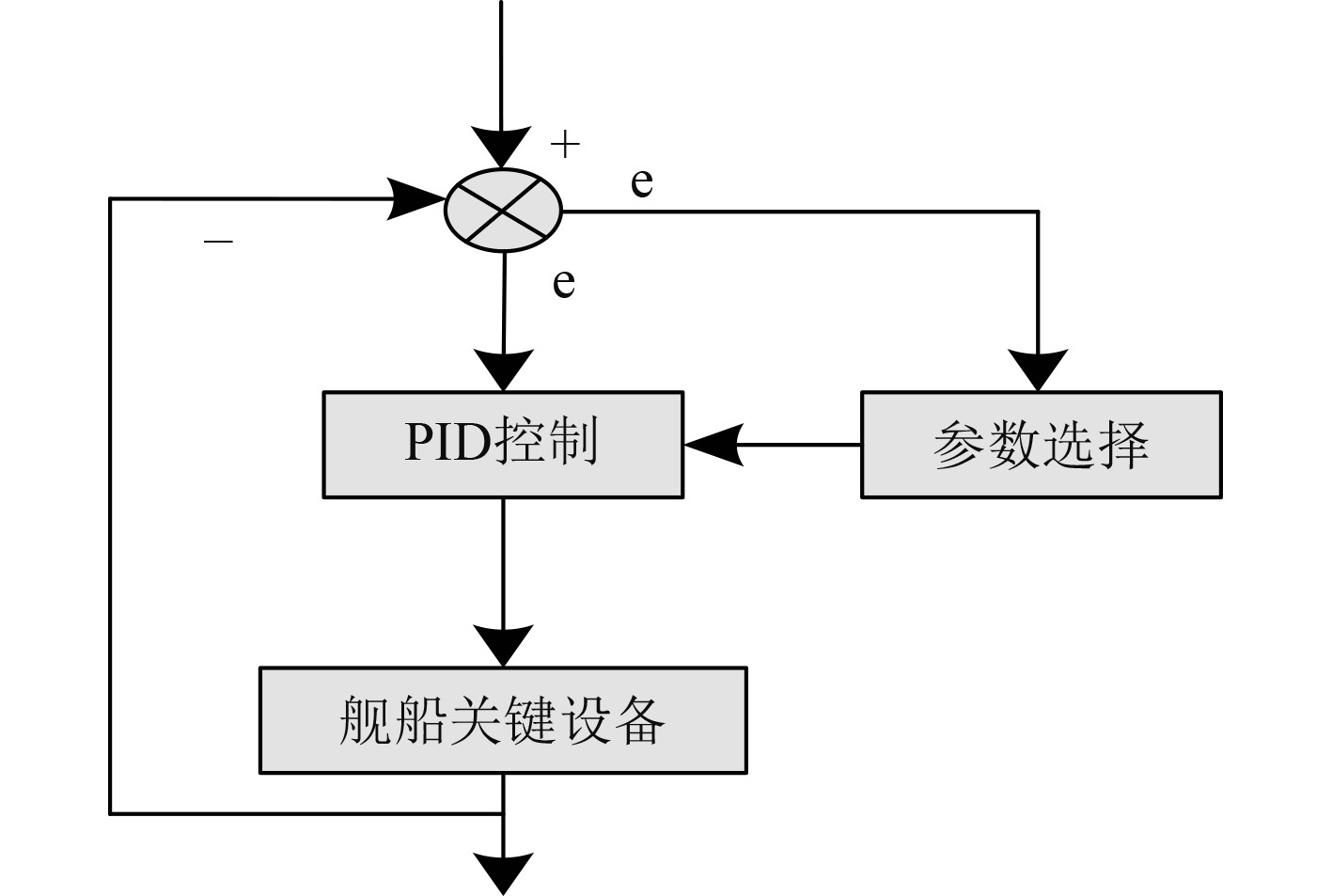
1 舰船关键设备智能控制研究 1.1 基于PID控制器的舰船关键设备控制

PID控制器是一种当前较为流行的控制技术，通过PID控制器可以有效实现多种类型设备的控制问题^[6]。本文通过PID控制器实现舰船关键设备的智能控制。PID控制器属于一种线性控制方法，其中主要包含比例、积分与微分的环节，将舰船关键设备灵敏度作为设备控制指标，设备灵敏度是指设备在运行过程中的实时变化能力。向PID控制器中输入舰船关键设备灵敏度期望值与实际值之间的误差，经控制器控制后，输出使灵敏度误差最小的控制结果，实现船舶关键设备控制。该控制器结构为：

$ U = {k_p}\left[ {e(k) + \frac{1}{{{k_i}}}\int {e(k){\rm{d}}t + {k_d}\dfrac{{{\rm{d}}e(k)}}{{{\rm{d}}t}}} } \right]。$

(1)

式中： $ U $ 为该PID控制器的输出； $ e(k) $ 为舰船关键设备灵敏度的误差，即灵敏度期望值与实际值之间的误差， $ k $ 为采样时间； $ {k_p} $ 为比例系数； $ {k_i} $ 为积分系数； $ {k_d} $ 为微分系数， ${\rm{d}}t$ 表示对时间 $ t $ 的求导； $\dfrac{{{\rm{d}}e(k)}}{{{\rm{d}}t}}$ 表示对 $ e(k) $ 求导。图1为PID控制器控制原理。

1.2 基于RBF神经网络的PID控制器参数优化 1.2.1 RBF神经网络运行模式设计

利用RBF神经网络优化PID控制器控制参数 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ 。RBF神经网络通过3层组成，分别为输入层、隐含层与输出层。在该网络中的隐含层激励函数采用高斯基函数，用于更好调节输入层输入的PID控制器参数，可通过下式表示：

$ {h_j}(k) = \exp \left( { - \frac{{\left\| {x - {c_j}} \right\|}}{{2b_j^2}}} \right),j = 1,2,...,m。$

(2)

式中： $ {h_j}(k) $ 为RBF神经网络中第 $ j $ 个高斯基函数；第 $ j $ 个基函数的中心点为 ${c_j} = {\left[ {{c_{j1}},{c_{j2}},{c_{j3}},...,{c_{jn}}} \right]^{\rm{T}}}$ ； $ x $ 为输入到RBF神经网络的PID控制器参数样本； $ {b_j} $ 为第 $ j $ 个基宽参数，通过 $ {b_j} $ 能够决定高斯基函数围绕中心点的宽度，其值均大于0；隐含层节点数为 $ m $ 。

由于RBF神经网络在PID控制器参数优化控制时不同层之间的变换为非线性的^[7]，因此RBF神经网络第 $ m $ 个隐含层节点的输出 $ {y_m}\left( k \right) $ 可通过下式表示：

$ {y_m}\left( k \right) = \sum\limits_{j = 1}^m {{w_j}{h_j}} \left( k \right)。$

(3)

式中， $ {w_j} $ 为隐含层到输出层的加权系数。

1.2.2 基于RBF神经网络的PID控制器参数优化

通过RBF神经网络对PID参数进行训练，使PID参数得到优化，实现舰船关键设备的精准控制。在利用RBF神经网络进行训练时，隐含层通过监督学习算法，赋予权值 $ w $ 随机数，之后通过该算法训练权值 $ w $ 、基宽参数 $ b $ 以及中心节点 $ c $ ，对全部参数进行误差修正。采用梯度下降算法，作为参数训练时的监督学习算法。依次采用式(4)计算RBF神经网络的代价函数 $ J\left( k \right) $ ：

$ J\left( k \right) = \frac{1}{2}{\left( {y\left( k \right) - {y_m}\left( k \right)} \right)^2}，$

(4)

式中， $ y\left( k \right) $ 为RBF神经网络输出期望值。

采用梯度下降算法，依次求出权值 $ w $ 、基宽参数 $ b $ 以及基函数 $ c $ 的值，具体如下：

$ \begin{split} & \Delta {w_j}\left( k \right) = \eta {\left( {y\left( k \right) - {y_m}\left( k \right)} \right)^2}，\\ & {w_j}\left( k \right) = {w_j}\left( {k - 1} \right) + \Delta {w_j}\left( k \right) + \alpha \left( {{w_j}\left( {k - 1} \right) - {w_j}\left( {k - 2} \right)} \right)，\end{split} $

(5)

$ \begin{split} &\Delta {b_j}\left( k \right) = \eta \left( {y\left( k \right) - {y_m}\left( k \right)} \right){w_j}{h_j}\frac{{{{\left\| {x - {c_j}} \right\|}^2}}}{{b_j^3}}，\\ & {b_j}\left( k \right) = {b_j}\left( {k - 1} \right) + \Delta {b_j}\left( k \right) + \alpha \left( {{b_j}\left( {k - 1} \right) - {b_j}\left( {k - 2} \right)} \right) ，\end{split} $

(6)

$ \begin{split} & \Delta {c_{ji}}\left( k \right) = \eta \left( {y\left( k \right) - {y_m}\left( k \right)} \right){w_j}\frac{{{x_j} - {c_{ji}}}}{{b_j^2}}，\\ & {c_{ij}}\left( k \right) = {c_{ji}}\left( {k - 1} \right) + \Delta {c_{ji}}\left( k \right) + \alpha \left( {{c_{ji}}\left( {k - 1} \right) - {c_{ji}}\left( {k - 2} \right)} \right) 。\end{split} $

(7)

式中： $ \Delta {w_j}\left( k \right) $ 为第 $ j $ 个权值的梯度； $ {w_j}\left( k \right) $ 为更新后的权值； $ \Delta {b_j}\left( k \right) $ 为第 $ j $ 个基宽参数的梯度， $ {b_j}\left( k \right) $ 为更新后的基宽参数； $ \Delta {c_{ji}}\left( k \right) $ 为第 $ j $ 个基函数的梯度， $ {c_{ij}}\left( k \right) $ 为更新后的基函数； $ \alpha $ 为动量因子； $ \eta $ 为学习速率。此时，根据RBF神经网络对权值 $ w $ 、基宽参数 $ b $ 以及基函数 $ c $ 的辨识。取RBF神经网络第 $ j $ 个输入为 $ \Delta u\left( k \right) $ ，即 $ {x_j} = \Delta u\left( k \right) $ ，可通过式(8)表示RBF神经网络的敏捷度信息(Jacobin)矩阵：

$ \frac{{\partial y\left( k \right)}}{{\partial \Delta u\left( k \right)}} \approx \frac{{\partial {y_m}\left( k \right)}}{{\partial \Delta u\left( k \right)}} = \sum\limits_{j = 1}^m {{h_j}} {w_j}\left( k \right)\frac{{{c_{ij}}\left( k \right) - {x_j}}}{{{b_j}{{\left( k \right)}^2}}} 。$

(8)

式中， $ {h_j} $ 为高斯基函数。

采用梯度下降法依次学习PID控制器控制参数初值 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ ，得到各参数的调整量如下：

$ \begin{split} \Delta {k_p} = & - \eta \frac{{\partial J(k)}}{{\partial {k_p}}} = - \eta \frac{{\partial J(k)}}{{\partial y}} \cdot \frac{{\partial y}}{{\partial \Delta u}} \cdot \frac{{\partial \Delta u}}{{\partial {k_p}}} =\\ &\eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}\left( {e\left( k \right) - e\left( {k - 1} \right)} \right)，\end{split} $

(9)

$ \begin{split} \Delta {k_i} =& - \eta \frac{{\partial J(k)}}{{\partial {k_i}}} = - \eta \frac{{\partial J(k)}}{{\partial y}} \cdot \frac{{\partial y}}{{\partial \Delta u}} \cdot \frac{{\partial \Delta u}}{{\partial {k_i}}} = \\ & \eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}e\left( k \right) ，\end{split} $

(10)

$ \begin{split} \Delta {k_d} =& - \eta \frac{{\partial J(k)}}{{\partial {k_d}}} = - \eta \frac{{\partial J(k)}}{{\partial y}} \cdot \frac{{\partial y}}{{\partial \Delta u}} \cdot \frac{{\partial \Delta u}}{{\partial {k_d}}} = \\ & \eta e\left( k \right)\frac{{\partial y}}{{\partial \Delta u}}\left( {e\left( k \right) - 2e\left( {k - 1} \right) + e\left( {k - 2} \right)} \right) 。\end{split} $

(11)

其中， $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ 属于人为经验赋予的PID控制参数初值； $ \partial y/\partial \Delta u $ 表示被优化参数的雅可比信息。

优化后的控制器参数 $ {K_p} = {k_p} + \Delta {k_p} $ ， $ {K_i} = {k_i} + \Delta {k_i} $ ， $ {K_d} = {k_d} + \Delta {k_d} $ 。

通过以下步骤，实现RBF神经网络对PID控制器参数的优化：

1)初始化PID控制器参数 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ ，同时设置RBF神经网络的学习速率与初始权重等参数。

2)利用式(5)、式(6)以及式(7)的计算，优化RBF神经网络参数。

3)对RBF神经网络的Jacobin矩阵信息进行计算。

4)通过式(9)、式(10)以及式(11)得到优化后的PID控制器参数调整量 $ \Delta {k_p} $ ， $ \Delta {k_i} $ ， $ \Delta {k_d} $ 。

5)利用步骤4获取的控制器参数调整量 $ \Delta {k_p} $ ， $ \Delta {k_i} $ 、 $ \Delta {k_d} $ ，优化PID控制器参数 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ ，得到PID控制器参数优化结果 $ {K_p} $ ， $ {K_i} $ ， $ {K_d} $ 。

6)判断迭代次数是否达到最大，若是，则停止采样，完成改进型PID控制器参数优化，否则返回步骤2继续执行。

将优化后的控制参数作为PID控制器的参数，完成以设备灵敏度期望值与实际值之前偏差为PID控制器输入的舰船关键设备智能控制。

2 实验结果与分析

利用Matlab平台对舰船关键设备智能控制方法进行仿真。通过AMESin平台构建舰船液压伺服系统及该系统控制下的关键设备，将构建好的内容导入到Matlab平台中，对舰船液压伺服系统下的关键设备进行仿真控制。实验具体参数如表1所示。

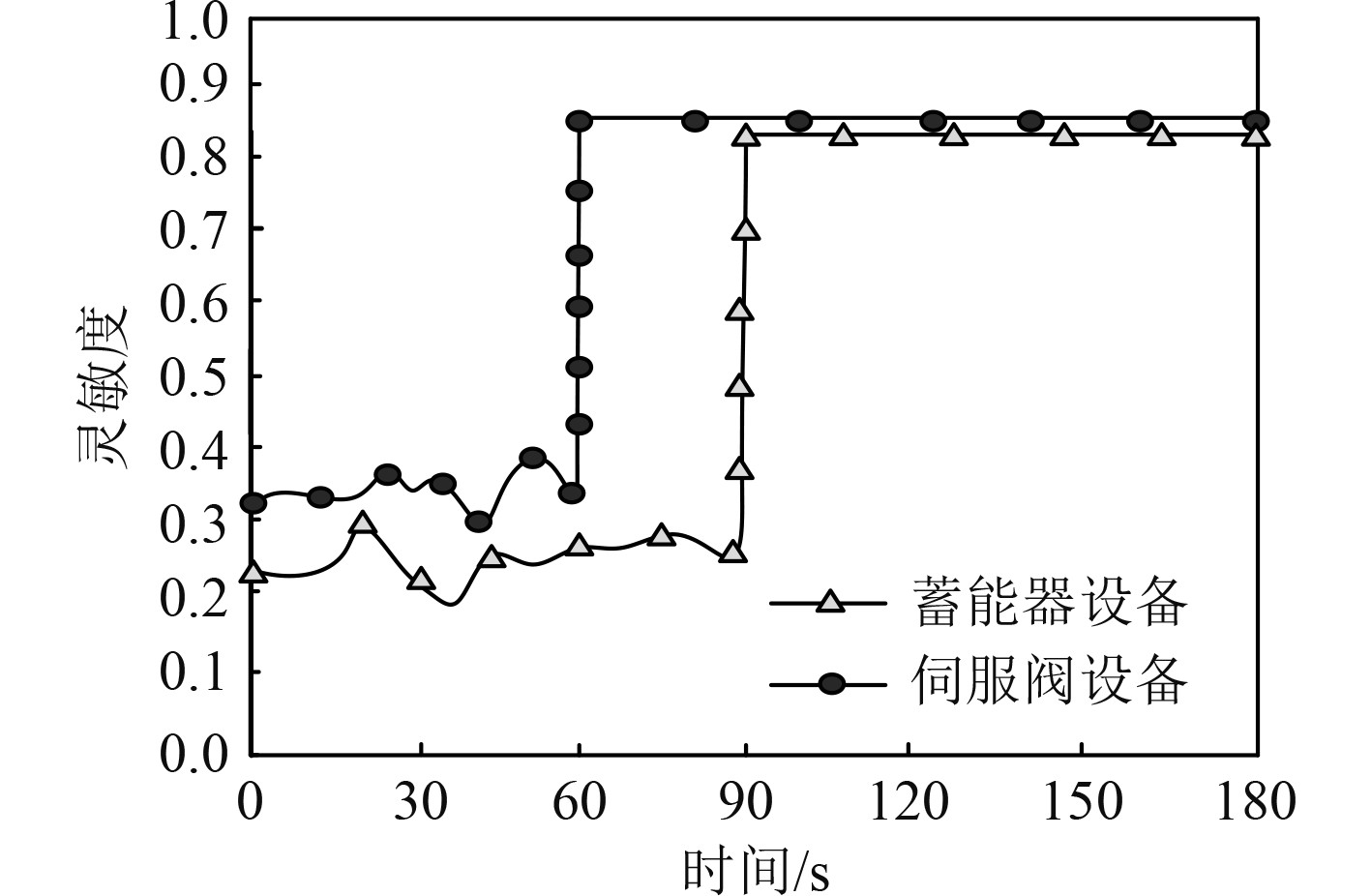
对舰船关键设备中的伺服阀以及蓄能器进行控制，在仿真舰船运行过程中的第60 s时，应用本文方法控制伺服阀设备，在运行第90 s时，控制蓄能器设备，分析应用本文方法后，舰船关键设备的灵敏度变化情况，分析结果如图2所示。根据图2可知，在舰船运行第60 s处对舰船蓄能器设备进行了控制，在控制的瞬间，设备灵敏度迅速上升，达到0.8以上，且在后续运行过程中始终保持这一水平，并未出现灵敏度波动。而在运行第90 s时开始对伺服阀设备进行控制，该设备的灵敏度同样迅速增高，且保持稳定运行，由此可以看出，经本文智能控制方法控制后的设备，可保持较高水平的灵敏度。

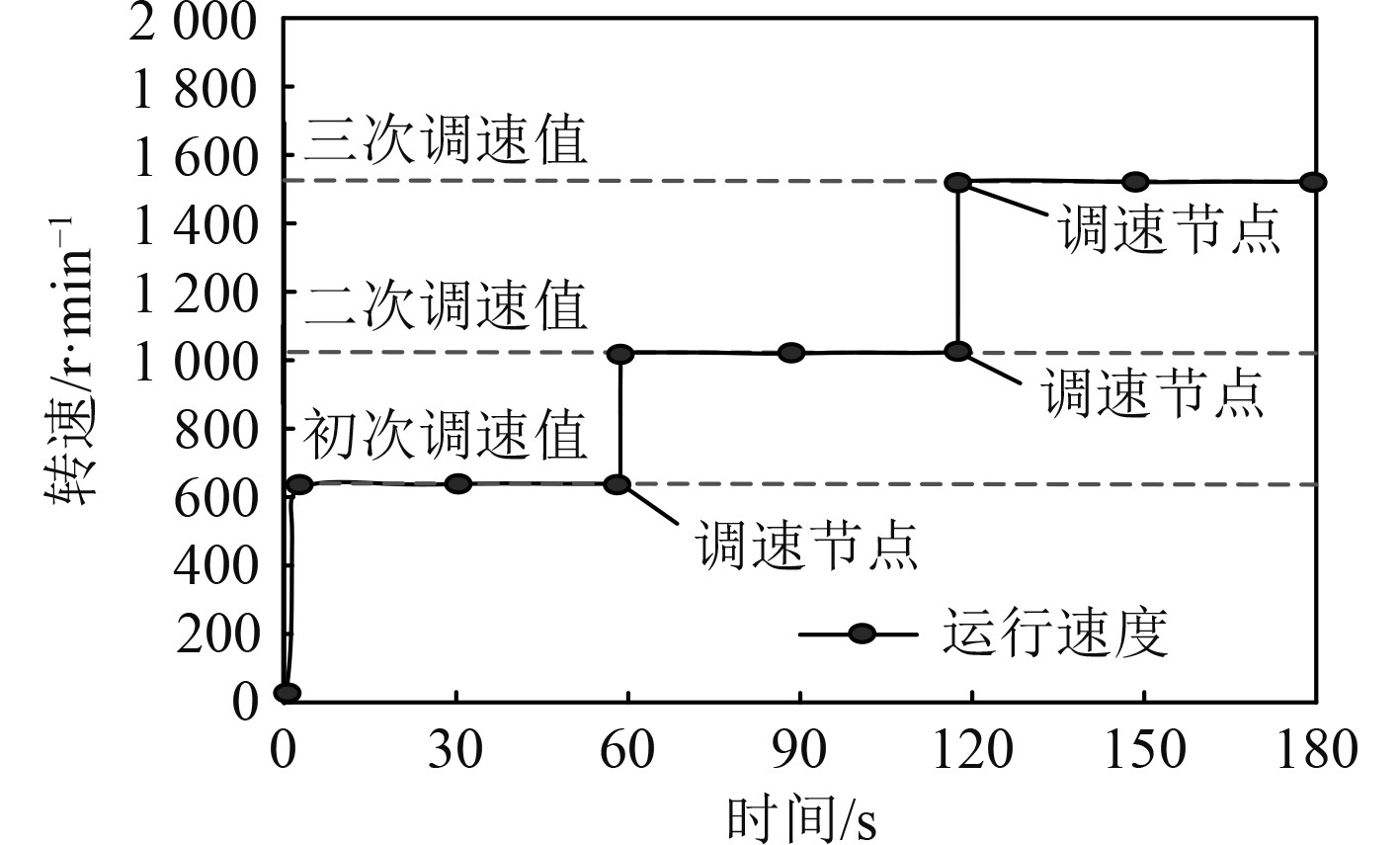
应用本文智能控制方法对发电机转速进行调速，在初始运行阶段控制发电机转速为600 r/min，当运行至60 s时将转速调整至1 000 r/min，当运行至120 s时将转速调整值1 500 r/min。分析应用本文方法控制后对舰船发电机的调速能力，分析结果如图3所示。由图3可知，当舰船在初始运行阶段控制发电机转速为600 r/min时，其转速迅速达到相应值，可以看出该控制方法反应十分迅速。随着舰船的不断运行，在第60 s处调整后，发电机转速迅速变化，且保持在1 000 r/min位置未出现异常变化，进行再次调速后，发电机设备同样可以迅速达到指定转速。由此可以看出，本文方法可有效实现发电机转速控制，在进行调速时并未出现延迟，且调速结果十分精准。

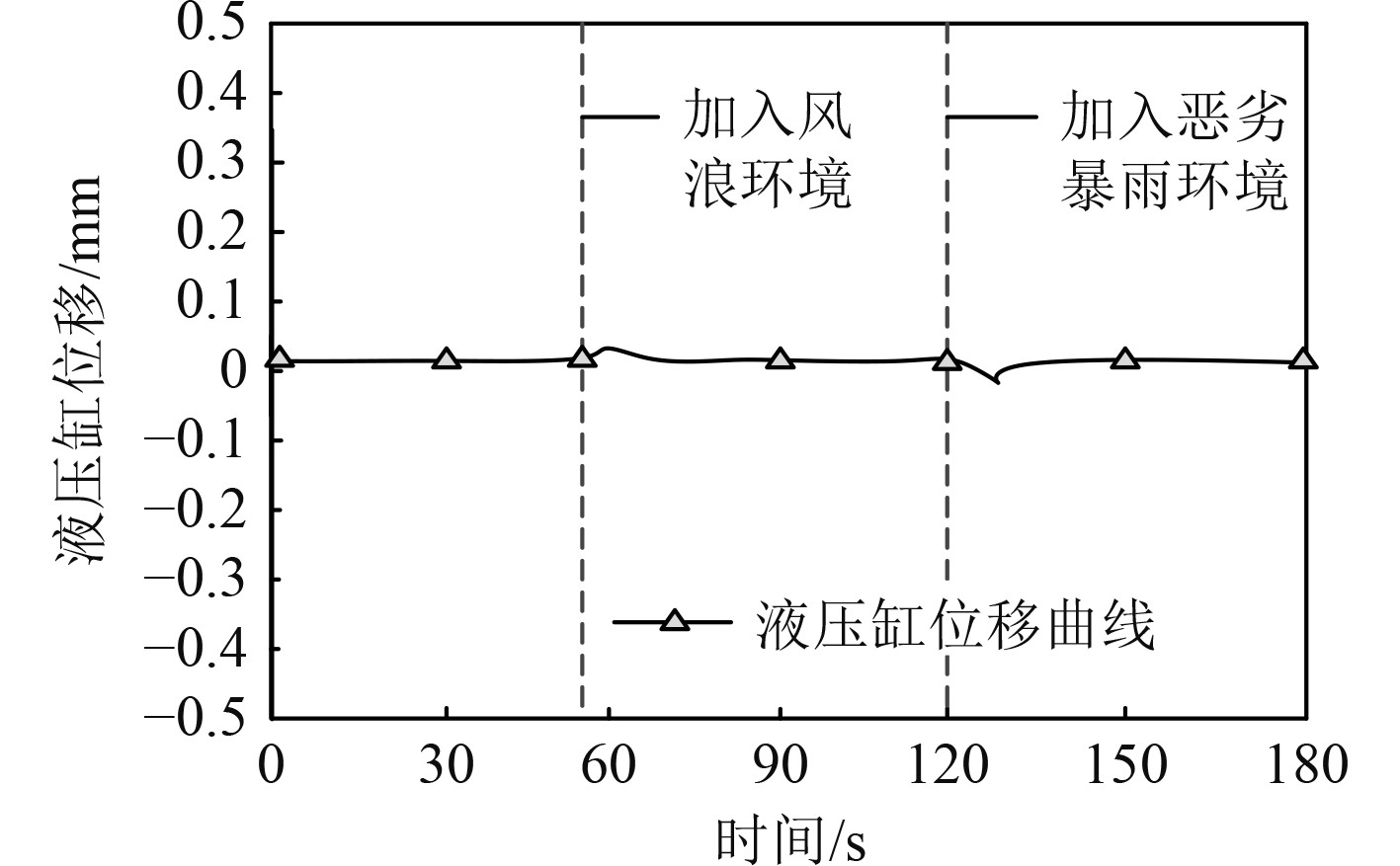
液压缸是影响舰船稳定性的关键设备，本文对液压缸进行控制，在仿真平台中加入恶劣海况现象，分析经过本文智能控制方法对舰船液压缸进行控制后，液压缸的位移情况变化，分析结果如图4所示。根据图4可知，应用本文方法对舰船液压缸设备进行控制后，该液压缸的位移值始终保持在0 mm，当遭遇风浪环境与恶劣暴雨环境时，液压缸位移仅出现小幅度波动，且迅速回归到0位移状态，说明经过本文方法控制后，液压缸可保持良好的运行水平。

3 结　语

本文研究神经网络优化PID的舰船关键设备智能控制方法。传统PID控制无法满足现有舰船关键设备的控制需求，导致设备稳定性不足，通过神经网络优化PID控制器，使PID控制器对设备的控制能力得到提升。在未来研究过程中，可针对当前控制方法继续进行优化设计，使其能够实现更多舰船设备的精准控制。