2. 北华航天工业学院机电工程学院,河北 廊坊 065000
2. School of Mechanical and Electrical Engineering.North China Institute of Aerospace Engineering, Langfang 065000, China
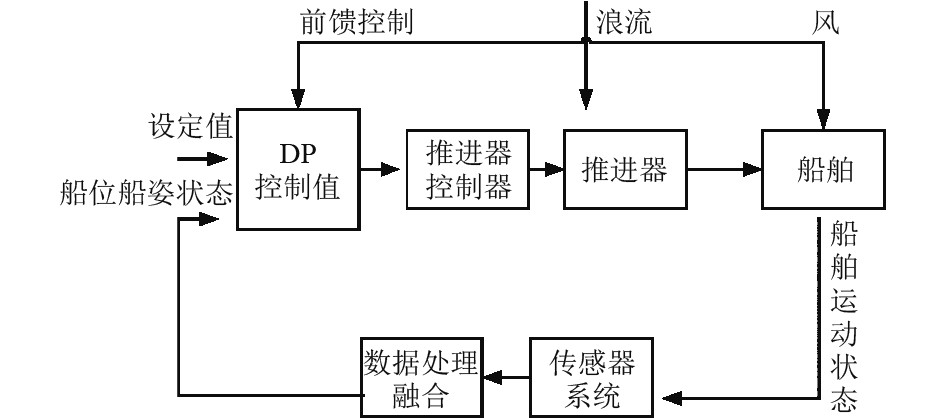
在经济和科技飞速发展的今天,资源已经成为全球经济发展的主要目标。采用导管架将海洋钻井平台固定在海底,而固定的平台不可移动。但是,在钻井平台上,支架的高度受到限制。在海洋深处,为了解决钻探问题,有许多船舶在海洋中漂流,能在某个位置停留很久。这些设备中的大部分都是通过锚固来实现,而这种方法受水深所限。另外,由于其不便于伸缩,所以开发了一种新的技术,即不受限于深度,也不受限于强度。在过去的数十年里,很多国家都在加大对位置测量系统的非线性滤波融合技术的投入。但是,这种船造价昂贵,技术复杂,如果没有精确的定位和速度信息,将会造成定位误差,甚至造成设备的损伤。在海洋环境变化中,各种环境因子如风、浪、流等,使得船舶的运动具有非线性特征。但是,目前对位置传感器进行动态定位的研究还不多,特别是在复杂的非线性环境下,研究一种适合于船舶动态定位的新技术。在某些复杂的海洋环境中,船舶的动力定位技术是一项重要的技术[1-3],它利用电力装置抵御外界的冲击。该技术是现代控制理论、人工智能、能源、通信、船舶结构等多学科交叉技术。传感器检测系统如图1所示。
|
图 1 传感器检测系统 Fig. 1 Sensor detection system |
该系统包括DP控制器、船位测量系统和船位测量设备,用于采集船体和周边环境的倾斜角度等[4-5]。船舶位置测量系统由各种传感器组成,其中包括电压缆线位置测量系统、水声定位系统、GPS定位系统、激光定位系统等。
1 动力定位船舶常用的非线性位置测量系统拉索定位系统是一种机械装置,可实现短程定位。通常情况下,只要船舶在一定的距离内运动,或者在一定的位置上,就能保证测量的准确性。一般情况下,拉索可以安装在船上的任意位置,但是对于钻机来说,为了减小船的移动对风压的影响,一般都会安装在船的中央。张紧绳体系可划分为:轻量张力绳(常用)、表面张力绳、月池张力绳。拉索系统主要由拉索位置跟踪器、拉索、角度传感器、传感器等组成。因此必须采用非线性滤波算法对测量系统的各个参数进行优化,并通过融合计算,得到更为精确的测量参数。测量系统中最长使用的张紧绳定位系统的基本原理是:在一定的电压下,通过对张紧绳的倾斜和间距进行测量,将其转化为电信号,并将其传送到舰船控制系统中,再利用一系列的坐标变换来实现对舰船的定位。张紧索的平面图如图2所示。
|
图 2 张紧绳的平面图 Fig. 2 Floor plan of tight cables |
| $\left\{ {\begin{array}{*{20}{c}} {XT{W^ * } = {{{h}}_{TW}}{\text{tan}}{\theta _{\text{x}}} = \dfrac{{{{{h}}_{TW}}{\text{sin}}{\theta _{{\text{xm}}}}}}{{\sqrt {{\text{1 - si}}{{\text{n}}^{\text{2}}}{\theta _{{\text{xm}}}} - {\text{si}}{{\text{n}}^{\text{2}}}{\theta _{{\text{ym}}}}} }}},\\ {{{YT}}{{{W}}^ * } = {{{h}}_{TW}}{\text{tan}}{\theta _{\text{y}}} = \dfrac{{{{{h}}_{TW}}{\text{sin}}{\theta _{{\text{xm}}}}}}{{\sqrt {{\text{1 - si}}{{\text{n}}^{\text{2}}}{\theta _{{\text{xm}}}} - {\text{si}}{{\text{n}}^{\text{2}}}{\theta _{{\text{ym}}}}} }}},\\ {{\text{ZT}}{{\text{W}}^ * } = {{\text{h}}_{TW}}} 。\end{array}} \right.$ |
式中:θxm为 X轴线上的传感器的测角;θ ym为Y轴上传感器的测角。张紧索的安装误差是通过坐标转换来消除的,公式如下:
| $ \left[ \begin{gathered} PXTW \\ PYTW \\ PZTW \\ \end{gathered} \right] = \left[ \begin{gathered} XTWAB \\ YTWAV \\ ZTWAB \\ \end{gathered} \right] - \left[ \begin{gathered} XTWO \\ YTWO \\ ZTWO \\ \end{gathered} \right] - \left[ \begin{gathered} XTW \\ YTW \\ PZTW \\ \end{gathered} \right] \text{。} $ |
其中:XTW,YTW,ZTW分别为锚杆和张紧索系船点的偏差值。从系船点到锚地的位移,转化为船舶坐标系统:
| $ \begin{array}{l}\left\{\begin{array}{c}{{z}}_{1}={\left[{R}_{1}{}^{2}-{(\text{x}-\text{a})}^{2}-(\text{y}+\text{b}{)}^{2}\right]}^{\raisebox{1ex}{$1$} \left/ \raisebox{-1ex}{$2$}\right.},\\ {{z}}_{2}={\left[{R}_{2}{}^{2}-{(\text{x}-\text{a})}^{2}-(\text{y}-\text{b}{)}^{2}\right]}^{\raisebox{1ex}{$1$} \left/ \raisebox{-1ex}{$2$}\right.},\\ {{z}}_{3}={\left[{R}_{3}{}^{2}-{(\text{x}+\text{a})}^{2}-(\text{y}+\text{b}{)}^{2}\right]}^{\raisebox{1ex}{$1$} \left/ \raisebox{-1ex}{$2$}\right.},\\ {{z}}_{4}={\left[{R}_{4}{}^{2}-{(\text{x}+\text{a})}^{2}-(\text{y}-\text{b}{)}^{2}\right]}^{\raisebox{1ex}{$1$} \left/ \raisebox{-1ex}{$2$}\right.}。\end{array} \right.\\ \end{array} $ |
式中:XTWO,YTWO,ZTWO分别为张紧索在船舶坐标系内与船舶的参考点在3个方向上的位置偏差;在船舶坐标系中,锚地3个方位的定位信息为:
| $ \left[ {\begin{array}{*{20}{c}} {XTWAB} \\ {YTWAB} \\ {ZTWAB} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\phi }&{{\text{sin}}\phi } \\ {{\text{ - sin}}\phi }&{{\text{cos}}\phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {XTWAN} \\ {YTWAN} \end{array}} \right] \text{。} $ |
建立张紧索定位模型的目的是要把船舶北东坐标值变换得到3个量,即绳索长度和2个方向上的偏角。
2 水声定位系统 2.1 水声定位系统简介水下声学定位是目前应用最为广泛的一种动态定位技术,这是一种仅用于特定海域的局部相对位置系统。根据基线长度的差异,将其划分为:1)基线长度在1 m以内的超短基线;2)基线长度为1~50 m的短基线体系;3)基线长度在100~6000 m的长基线体系。水下声学定位系统包括转发器和传感器两部分。该转发器被安置在水下,用于实时监控由传感器发出的询问信号,一旦收到询问信号,就会产生相应的应答。在船身的较低处装有一个转换器,用以发出一个要求的讯号。在收到转发器的应答信号之后,可以利用转发器对其位置信息进行定位,并将其传送给动态定位系统。相对于高压电缆,水下定位系统工作面积大,不受海水深度的影响。但是,它也有其不足之处:当声波传播时,船体发生滚动、倾侧,以及在传输媒体中有环境噪声时,会对测量的准确性产生一定的影响。
2.2 基于非线性滤波算法的水声位置测量系统非线性滤波算法可以将船舶测量系统的测量精度提高到更高的水平,因此短基线水声定位系统必须具备1台发射机、3台水听机,在确定了测距 R后,就可以获得转发器的坐标信息x y z。将基阵中发射和接收的信号设置为0 T,各水听器之间的信号发射时间为 t,由此得到:
| $ {R_i} = c{t_i} - \frac{{c{T_0}}}{2} = c\left( {{t_i} - \frac{{{T_0}}}{2}} \right) \text{,} $ |
应答器的位置坐标为T(x, y, z) ,水听器所围成的矩形边长是2a,2b ,于是得到:
| $ \left\{\begin{array}{l}{R}_{1}{}^{2}=({x\text{-}a}{)}^{2}+({y}+{b}{)}^{2}+{{z}}^{2},\\ {R}_{2}{}^{2}=({x\text{-}a}{)}^{2}+({y-b}{)}^{2}+{{z}}^{2},\\ {R}_{3}{}^{2}=({x}+{a}{)}^{2}+({y}+{b}{)}^{2}+{{z}}^{2},\\ {R}_{4}{}^{2}=({x}+{a}{)}^{2}+({y\text{-}b}{)}^{2}+{{z}}^{2},\end{array}\right. $ |
解得:
| $ \left\{\begin{array}{l}{{z}}_{1}={\left[{R}_{1}{}^{2}\text-({x\text{-}a}{)}^{2}\text-({y}+{b}{)}^{2}\right]}^{1/2},\\ {{z}}_{2}={\left[{R}_{2}{}^{2}\text-({x\text{-}a}{)}^{2}\text-({y\text{-}b}{)}^{2}\right]}^{1/2},\\ {{z}}_{3}={\left[{R}_{3}{}^{2}\text-({x}+{a}{)}^{2}+({y}+{b}{)}^{2}\right]}^{1/2},\\ {{z}}_{4}={\left[{R}_{4}{}^{2}\text-({x}+{a}{)}^{2}\text-({y\text{-}b}{)}^{2}\right]}^{1/2}。\end{array}\right. $ |
GPS 是一种卫星追踪定位系统,利用卫星测量距离。24颗人造卫星分别沿6条轨道倾斜55°,总是绕着地球旋转,大约12个星级的工作。每一颗运行中的 GPS卫星都向用户发出通信信号,以便进行定位和导航。
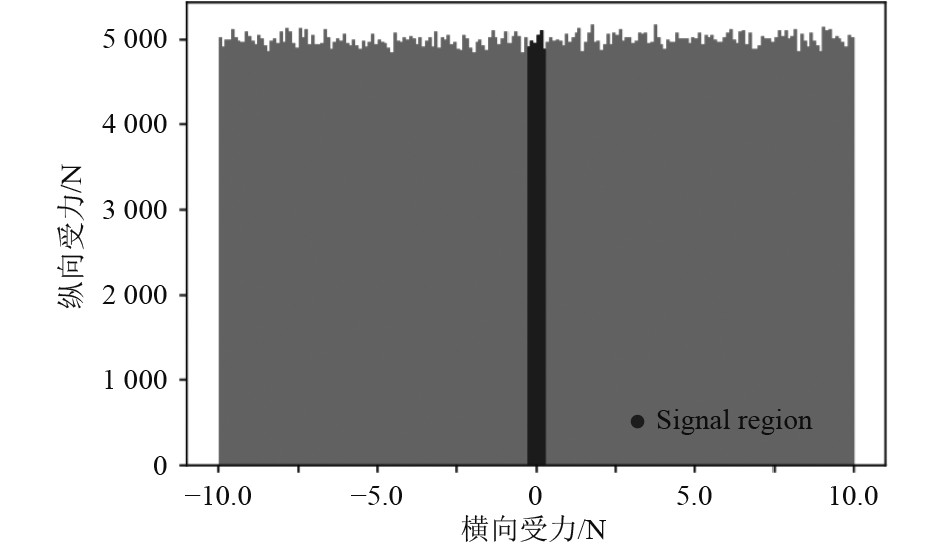
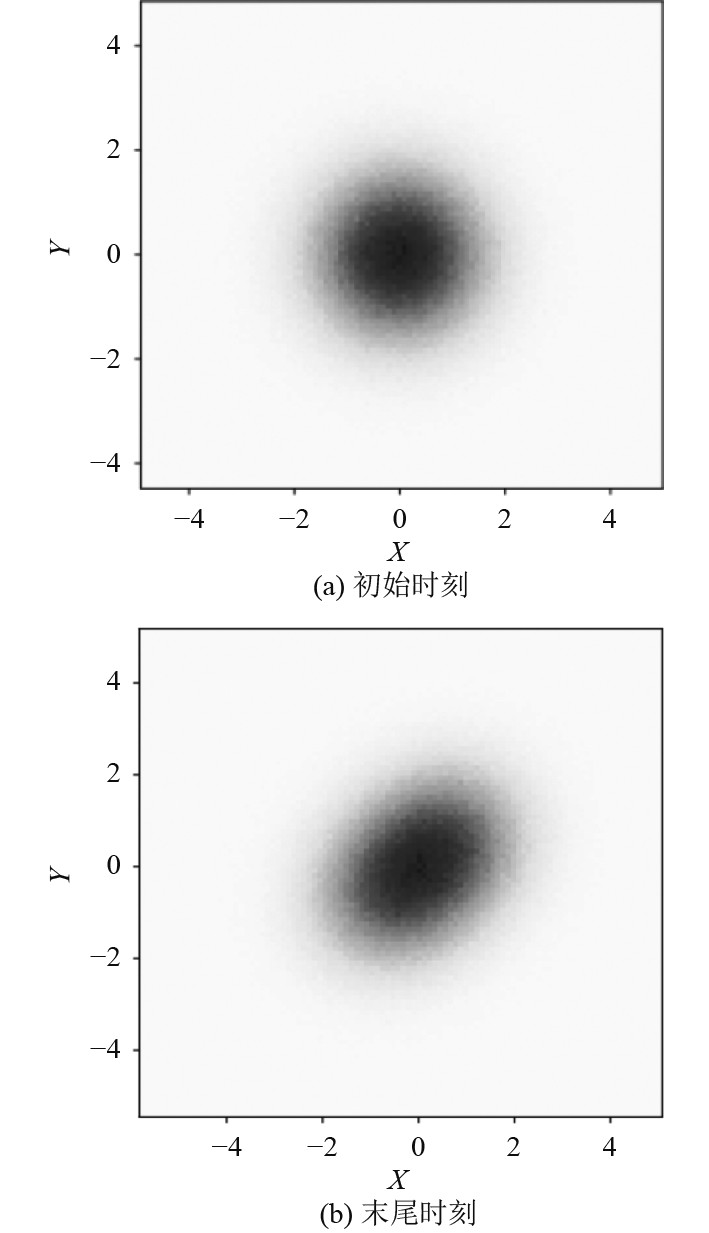
3 船舶位置测量系统的非线性滤波算法 3.1 船舶位置测量系统的非线性滤波非线性滤波的优劣将直接影响到后续多个传感器的精确度和准确度,并对船舶的推力及其他装置的控制有很大的影响。对包括水下声测量系统、GPS测量系统、拉索系统在内的各个位置测量系统进行非线性过滤。其基本思想是对模型产生的资料进行非线性滤波。滤波器的有效性可以从误差和方差中得到反映。运用滤波器对船舶位置进行估计,获得初始时刻和末尾时刻位置如图3所示。从图中可以发现末尾时刻的滤波器船舶位置估计发生了明显的变化。
|
图 3 滤波器船舶位置估计 Fig. 3 Filter ship position estimation |
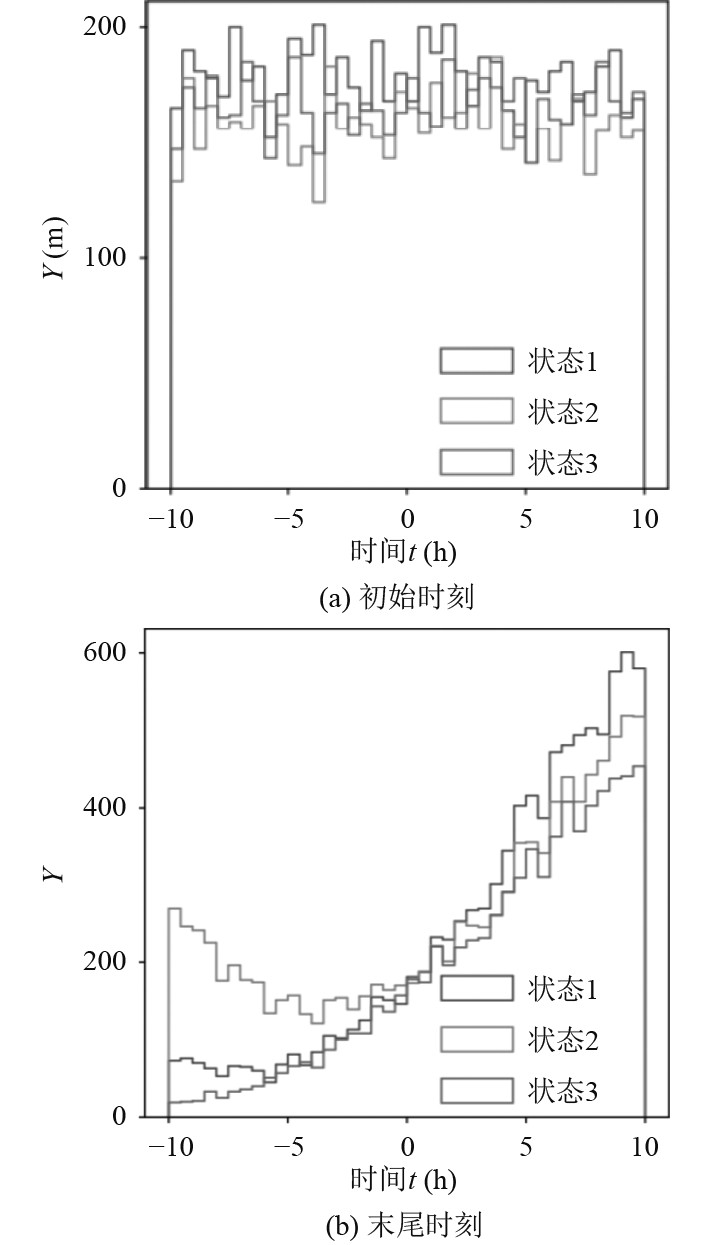
对船舶位置测量系统进行仿真分析。在仿真的过程中,一般使用船舶模型运行船舶的位置信息,并通过逆解得到每个位置测量系统的数据,然后将测量噪声添加到各个位置测量系统中,最后将滤波值与原始真值进行比较,检查滤波算法的滤波性能。3种不同位置状态下的船舶位置和速度估计如图4所示。状态1和状态2的位置最远,状态3的位置最近,从末尾时刻可以看出,不同的位置状态下,测量系统都能够准确定位出相对距离。
|
图 4 船舶位置和速度估计 Fig. 4 Vessel position and speed estimation |
采用多级信息融合技术。实现对船舶的精确定位,多级信息融合又被称作多个传感器的信息融合。由于各种传感器的测量范围和精度都存在限制,因此在技术上存在着对传感器信号的干扰。不同的传感器能够为相同的对象提供不同的测量角度,从而得到更为完整的测量结果。一些算法可以让问题或者物体的描述变得更为可信,多传感器的信息融合技术的关键在于更广泛利用多个传感器所提供的多个信息特性,并通过最优的方法把它们结合在一起,从而得到更准确和全面的观察结果。
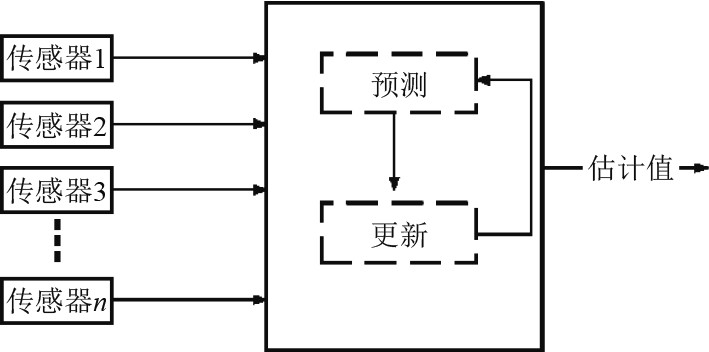
4.1 多级式卡尔曼滤波采用多级式卡尔曼滤波器对位置测量系统的重要非线性参数进行优化。该系统利用卡尔曼滤波器的结构对传感器的全部信息进行集中的处理。多级式卡尔曼滤波结构图如图5所示。该方法的优势在于其包括了最完整的传感资料,但是,伴随着大量的计算工作,电脑的数据处理工作也随之增加。尤其是在传感器需要对测量数据进行高速处理的情况下,会极大地影响滤波的实时、动态特性。
|
图 5 多级式卡尔曼滤波结构图 Fig. 5 Multistage kalman filter structure diagram |
本次模拟的船舶纵向推力为1.8×105 N,横向推力为0 N,综合推力为为1.0×104 N,海风为8 m/s,风向相对于北500,模拟时间为400 s,锚的北坐标和东坐标均为20 m,在东北坐标系中的起始位置为(0.0)。一般的模拟过程是用船舶模型运行船舶数据,通过逆解获得传感器位置测量系统数据,然后将测量噪声加入到位置测量系统中,经过非线性滤波器的算法优化,再通过多级数据融合结构将来自3个位置测量系统的信息进行融合,最后通过将融合后的船舶位置与船舶模型的原始值进行比较,说明该融合算法能够有效提高舰船位置测量系统的准确性。
5 结 语本文针对位置测量系统,设计了3种基于该系统的非线性滤波算法,并结合多级信息融合技术,实现船位信息的估算,从而提高船舶的定位准确率。在融合结构上,采用相对新颖的局部滤波方法,达到理想的融合效果。本文介绍目前常用的几种数据融合技术,并给出一种基于动态定位技术的多层次数据融合结构。在全反馈和不反馈条件下,分别构建了一个环境,并对其进行了实验。结果表明,采用完全反馈的方法比没有反馈的方法更好。在没有考虑到六自由度的情况下,理论上的分析已经达到了预期结果。
| [1] |
刘志强, 刘鑫旺, 万德成. 基于CFD数值模拟和模型试验的三体船片体位置优化[J]. 中国造船, 2022, 63(2): 116-125. LIU Zhi-qiang, LIU Xin-wang, WAN De-cheng. Optimization of trimaran hull position based on CFD numerical simulation and model test[J]. China Shipbuilding, 2022, 63(2): 116-125. DOI:10.3969/j.issn.1000-4882.2022.02.012 |
| [2] |
李恒, 王阳, 王野. 某集装箱船的船体变形对轴承支撑位置的影响分析[J]. 船舶标准化与质量, 2017(5): 16-19. LI Heng, WANG Yang, WANG Ye. Analysis of the influence of the hull deformation of a container ship on the bearing support position[J]. Ship Standardization and Quality, 2017(5): 16-19. DOI:10.3969/j.issn.1007-9750.2017.05.006 |
| [3] |
杨宏, 吴旭光. 卡尔曼滤波算法在多传感器融合技术中的应用[J]. 弹箭与制导学报, 2009, 29(5): 4. YANG Hong, WU Xu-guang. Application of Kalman Filter Algorithm in Multi-sensor Fusion Technology[J]. Journal of Rocket and Guidance, 2009, 29(5): 4. DOI:10.3969/j.issn.1673-9728.2009.05.069 |
| [4] |
岑黎明, 李一兴, 戴娜娜. 基于轴心位置监测的船用汽轮机组对中调整方法研究[J]. 船舶工程, 2016, 38(S2): 117-119+123. CEN Li-ming, LI Yi-xing, DAI Na-na. Research on Alignment and Adjustment Method of Marine Turbine Units Based on Axial Position Monitoring[J]. Ship Engineering, 2016, 38(S2): 117-119+123. DOI:10.13788/j.cnki.cbgc.2016.s2.117 |
| [5] |
田向阳, 林传禄. 一种潜艇水下位置校准方法研究[J]. 舰船电子工程, 2017, 37(10): 50-53+65. TIAN Xiang-yang, LIN Chuan-lu. Research on a calibration method of submarine underwater position[J]. Ship Electronics Engineering, 2017, 37(10): 50-53+65. DOI:10.3969/j.issn.1672-9730.2017.10.012 |
 2022, Vol. 44
2022, Vol. 44
