2. 西北工业大学 航海学院,陕西 西安 710072
2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China
随着陆-海-空-天一体化组网通信技术的迅速发展,跨空海界面通信的研究受到极大的重视。跨空海界面是一种特殊的传输环境,现有的极低频/甚低频(ELF/VLF) 电磁波通信、水声通信、蓝绿激光通信以及光纤通信等方式在进行跨界通信时都存在着各自的问题[1-4]。
近年来,作为一种电磁波通信方式,磁感应(MI)通信技术利用近场区的准静态磁场进行通信传输,在跨界通信中受到关注[5-8]。由于空气和海水的磁导率相似,磁感应通信可以穿透空海分界面,形成相对均匀的传输信道;并且磁感应产生于近场是非辐射的,不易受多径效应影响,传播时延几乎可以忽略。与传统的水声通信、激光通信相比,磁感应通信有着对时变环境敏感度低、不易受多普勒频移影响等特点,在跨空海界面通信中具有独特优势[9]。但是由于磁场分量会随着通信频率和传输距离的增加而急剧衰减,严重限制了磁感应通信的通信范围。
本文研究跨空海界面的磁感应通信,提出基于垂直磁偶极子的电磁场传播模型,基于模型分析通信中的磁场分量,仿真磁感应通信在分层导电媒质中的传输特性,并利用磁感应通信系统进行通信验证性海上试验,并给出部分试验信号的处理结果。
1 传输模型跨空海界面磁感应通信涉及电磁场在空气、海水两种媒质中的传播,空海分界面及海底会对电磁场传播产生影响。跨界通信可以用电磁波在分层导电媒质中的传播来模化,其实质是MaxWell方程在给定边界条件和初始条件下的解。Sommerfeld利用傅立叶-贝塞尔变换来解决存在有耗媒质半空间时偶极子的辐射问题,其解是用无穷积分表示的Hertz矢量位函数,但积分的求解极其复杂。因此,精确而有效的Sommerfeld积分计算决定了分层导电媒质中电磁场传播计算的精度和计算效率[10-15]。
在跨空海界面磁感应通信中,由于电磁波在海水中的衰减随频率的增大而增大,为了增加入水深度,通信信号通常选用极低频(ELF)的信号,信号波长 λ 远大于发射线圈的半径。此时,载有交变电流的环形天线可以模化为由交变电流激励的磁偶极子。众所周知,在磁偶极子的辐射空间中,将 kr << 1( k为波数,r为距离)的区域称为近场区,且磁偶极子中近场区内的电磁场为感应场。海水中的波数 k 约为 1.885f ×10−7,当频率f < 27 kHz时,200 m距离范围内都可近似为近场区;这时的磁场为磁感应场。
对于简谐时间变量
| $ {\nabla ^2}{\mathbf{\Pi }} + k_c^2{\mathbf{\Pi }} = - J/j\omega {\varepsilon _c} 。$ | (1) |
式中:
式(1)中,kc和εc可进一步的表示为:
| $ k_c^2 = {\omega ^2}\mu {\varepsilon _c} ,$ | (2) |
| $ {\varepsilon _c} = {\varepsilon _0} + \sigma /(j\omega ) 。$ | (3) |
式中:
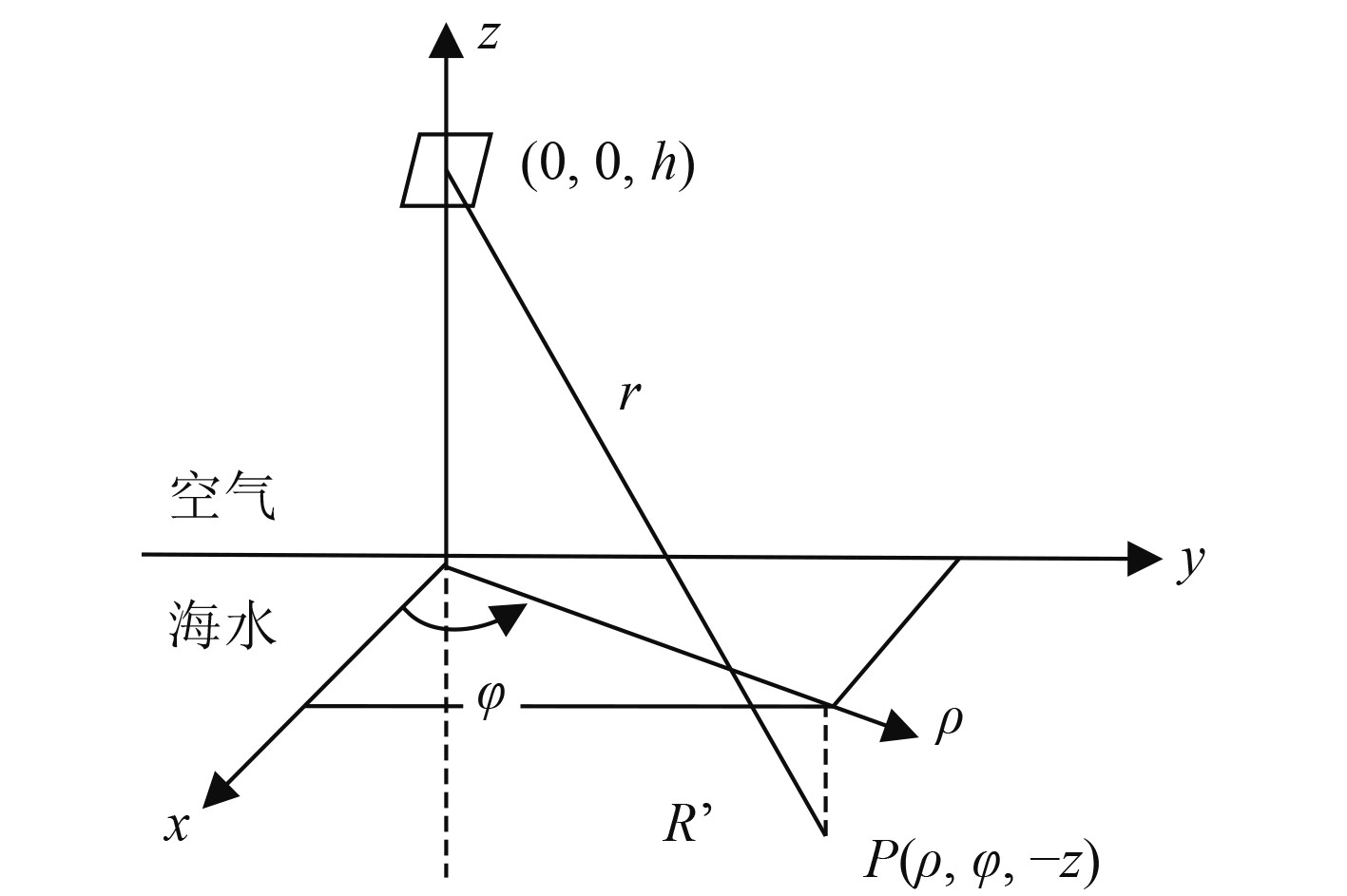
首先建立一个垂直方向的磁偶极子(VMD)模型,设VMD位于空中距海面h的高度处,场点位于水下P点,建立矩形和圆柱形坐标系使空海界面位于z = 0 平面,如图1所示。z >0 半空间为空气( εa, μa, ka),z < 0 半空间为海水( εs, μs, ks),下标a和s分别表示空气和海水。
|
图 1 垂直磁偶极子模型 Fig. 1 Vertical magnetic dipole transmission model |
在图1中,磁偶极子的法向指向z轴方向,空气中的电磁场关于z轴对称分布,磁Hertz位函数仅有垂直分量,即
| $ {\mathbf{\Pi }} = {\vec a_z}{\Pi _z},$ | (4) |
| $ \frac{{{e^{( - jkr)}}}}{r} = \frac{1}{2}\int_0^\infty {\frac{\lambda }{\gamma }{e^{( - \gamma |z|)}}{J_0}(\lambda \rho ){\rm{d}}\lambda }。$ | (5) |
式中:
式(5)中,
| $ r = {[{\rho ^2} + {(z \mp h)^2}]^{1/2}}。$ | (6) |
式中:
由式(5)可得,海水中的磁Hertz位函数为[10]:
| $ {\Pi _{zs}} = 2M\int_0^\infty {\frac{{{J_0}(\lambda \rho )}}{{{n^2}{\gamma _a} + {\gamma _s}}}{e^{({\gamma _s}z - {\gamma _a}h)}}\lambda {\rm{d}}\lambda }。$ | (7) |
式中:
式(7)中,
| $ M = INS/4\pi = m/4\pi,$ | (8) |
| $ {n^2} = k_s^2/k_a^2 = - j{\sigma _s}/(\omega {\varepsilon _0}),$ | (9) |
式中:
利用式(10),将J0(λρ)转换为Hankel函数H02(λρ)。
| $ \left\{ \begin{split} &{J_0}(x) = [H_0^1(x) + H_0^2(x)]/2 ,\\ &H_0^1( - x) = - H_0^2(x) 。\\ \end{split} \right. $ | (10) |
将式(7)中的半无限积分转化为全无限积分,可将磁Hertz位函数表示为:
| $ {\Pi _{zs}} = M\int_{ - \infty }^\infty {\frac{{H_0^2(\lambda \rho )}}{{{\gamma _a} + {\gamma _s}}}{e^{({\gamma _s}z - {\gamma _a}h)}}\lambda {\rm{d}}\lambda } 。$ | (11) |
式中Sommerfeld积分的解析求解极其复杂,但可以利用无穷积分的截断来求其数值解。选择合适的截断积分区域,并沿着组成这些截断和一个无限的半圆的路径进行积分,则可得到一个迭代简化后的结果[10-11, 13]。
引进变量α = jksz,β = -jksh,γ = -jkaρ,在“准近场区”条件下,即
| $ {k_a}\rho < 1 < |{k_s}|\rho ,$ | (12) |
或
| $ \frac{{10}}{{{k_s}}} \leqslant \rho < \frac{{0.1}}{{{k_a}}} 。$ | (13) |
忽略高阶指数项,可得[10]:
| $ \begin{split} {\Pi _{zs}} \approx & - \frac{{2Mj{e^{j{k_s}z}}}}{{{n^2}k_a^3{\rho ^4}}}\Biggr\{ \gamma \Biggr(1 - \frac{1}{2}{\gamma ^2}\Biggr)(1 - \beta ) + \\ &\frac{1}{{2{n^2}}}[3(3\alpha - 3\beta - 3\alpha \beta + 3{\beta ^2} - {\beta ^3}) +\\ & \gamma (2 + 5\alpha - 7\beta - 5\alpha \beta + 6{\beta ^2} - 2{\beta ^3}]\Biggr\} \approx \\ & - \frac{{2M{e^{j{k_s}z}}}}{{k_s^2{\rho ^3}}}(1 + j{k_s}h)。\end{split} $ | (14) |
式中,h < ρ,z < ρ。
电磁场分量可由下式得到:
| $ \left\{ \begin{gathered} \vec E = - j\omega \mu \nabla \times \vec \pi ,\\ \vec H = \nabla \nabla \cdot \vec \pi + {k^2}\vec \pi 。\\ \end{gathered} \right. $ | (15) |
对于垂直方向的磁偶极子,只有Eφ, Hr和Hz分量。将式(4)和式(11)代入式(15),可得海水中的磁场分量为:
| $ \left\{ \begin{gathered} {H_{\rho s}} \approx \frac{{jM{e^{ - j{k_s}z}}6(1 + j{k_s}h)}}{{{k_s}{\rho ^4}}},\\ {H_{zs}} \approx 0 。\\ \end{gathered} \right. $ | (16) |
海水中的磁感应强度表示为:
| $ {B_{\rho s}} = {\mu _s}{H_{\rho s}} = \frac{{j{\mu _s}M{e^{ - j{k_s}z}}6(1 + j{k_s}h)}}{{{k_s}{\rho ^4}}} 。$ | (17) |
由式(16)及式(17)可知,影响海水中磁场强度的因素有很多,如通信信号的频率f、发射天线的磁矩 M、入水深度
针对跨空海界面磁感应通信的传输模型分析及应用场景需求,将利用垂直磁偶极子的分层导电媒质传播模型,对不同信道条件、不同系统参数时的磁感应场在海水中的传播进行仿真分析。
仿真时采用的媒质参数如表1所示。其中,μ0和μr分别为空气、海水中的相对磁导率,ε0和εr分别为空气、海水中的介电常数。线圈天线的电流、面积分别为10 A和4 m2;发射天线距海面的高度h = 5 m;其余信号参数如表2所示。表中,z,ρ,f 和 N 分别为海水中的深度、径向距离、信号频率和线圈匝数。
|
|
表 1 仿真中的介质参数 Tab.1 Medium parameters of air and sea water |
|
|
表 2 仿真参数 Tab.2 Simulation parameters |
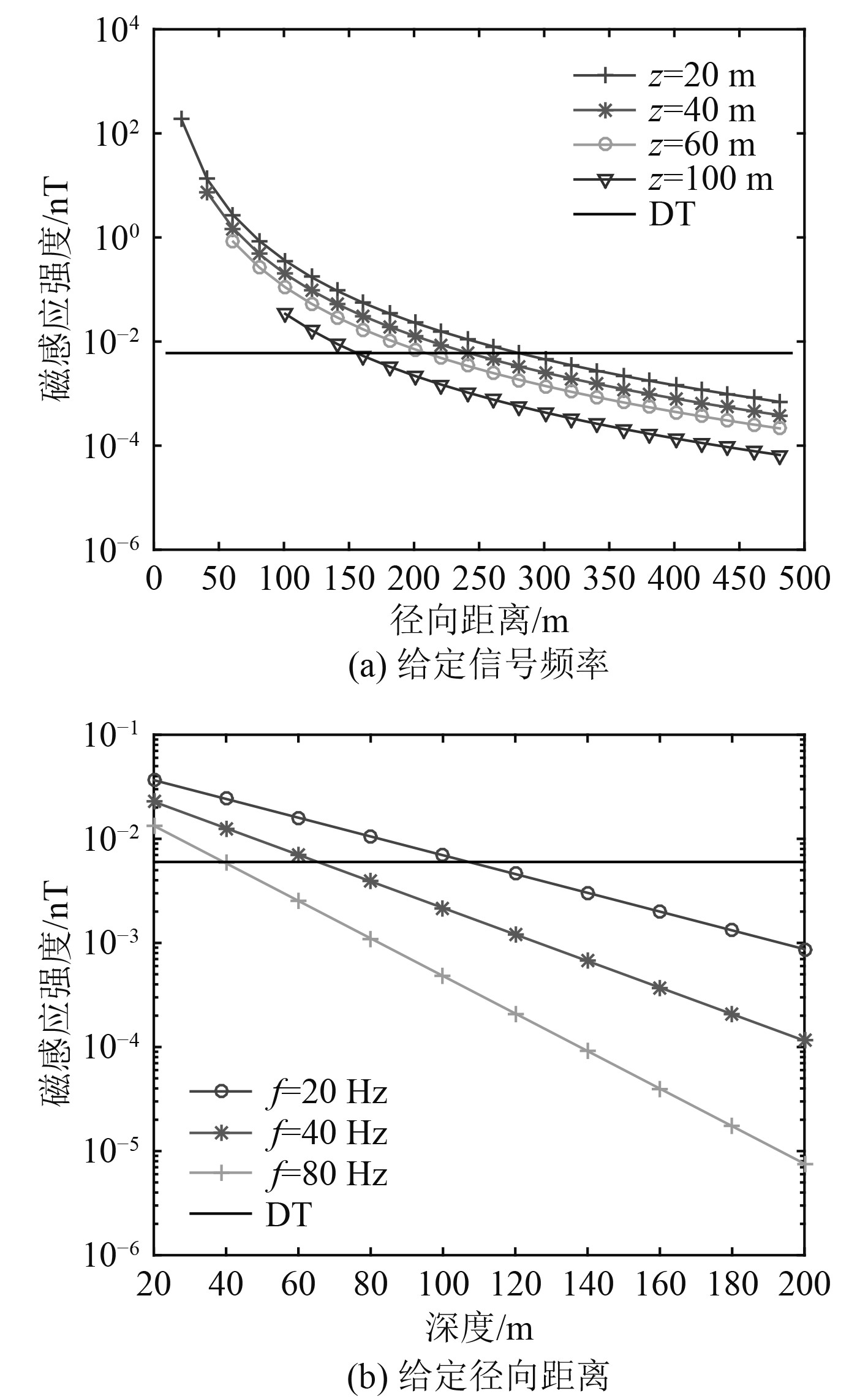
图2(a)为给定信号频率和发射磁矩时磁感应强度的变化曲线;图2(b)为给定径向距离和发射磁矩时磁感应强度的变化曲线。图中同时给出了接收系统的检测阈值。本文仿真是采用的检测阈值为6 pT,是磁感应通信接收系统中三分量磁通门传感器的最小接收灵敏度。
|
图 2 给定信号频率和径向距离时的磁感应强度曲线 Fig. 2 Magnetic induction strength with given frequency and radium range. |
由图2(a)可见,当信号频率为40 Hz,发射磁矩为4000 A·m2时,径向距离的覆盖范围随着垂直入水深度的增加而减小。当垂直入水深度分别为20 m和100 m时,达到检测阈值时的径向距离约为280 m和150 m。由图2(b)可知,当发射磁矩及径向距离一定时,入水深度随信号频率增大而减小。当径向距离为200 m, 频率分别为20Hz和80Hz时,达到检测阈值时的深度分别约为108 m和40 m。
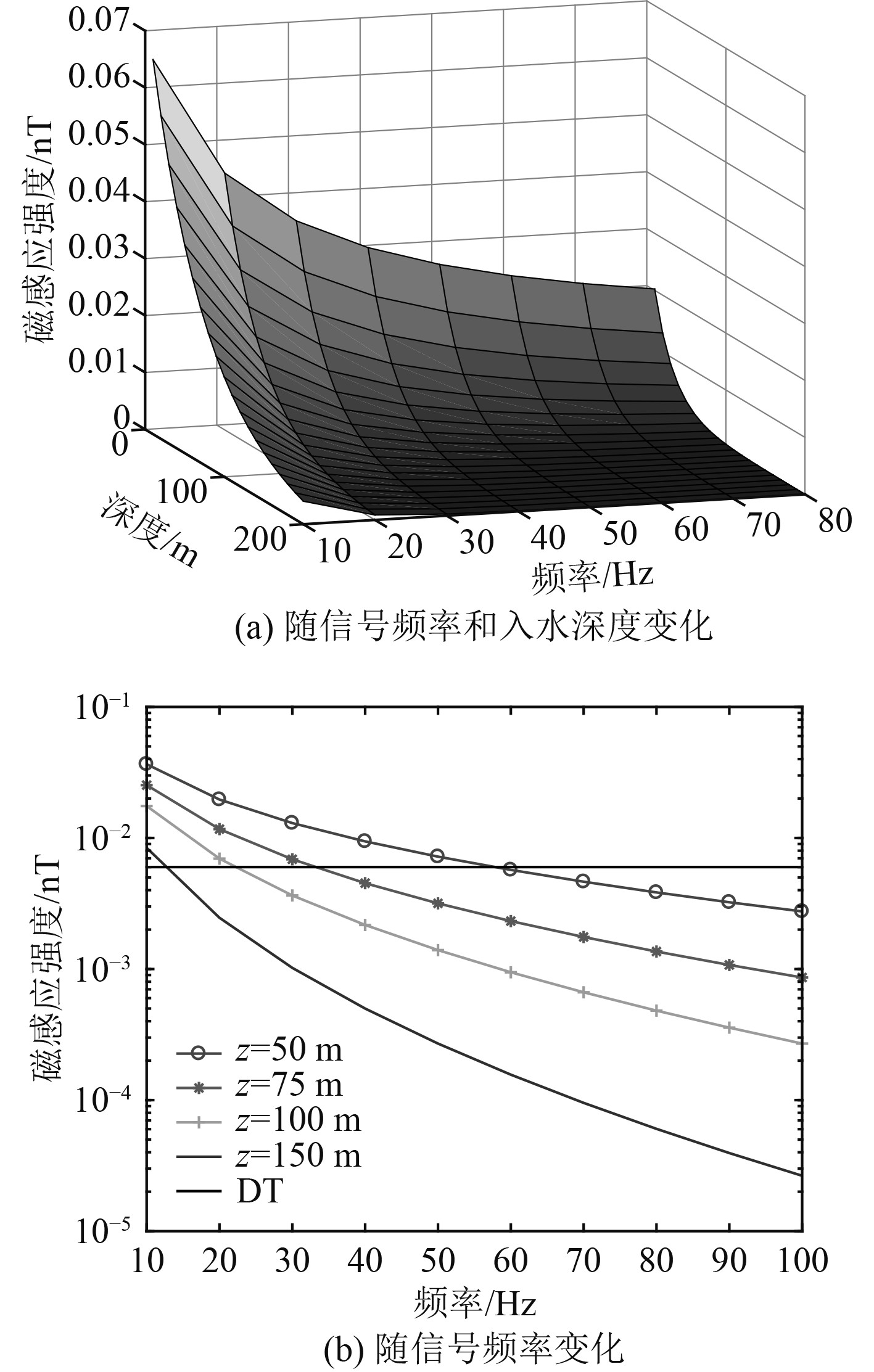
图3(a)为给定径向距离和发射磁矩时,磁感应强度随信号频率和入水深度变化的曲面。对图3(a)取不同入水深度进行分析,可以得到磁感应强度随信号频率变化的曲线,即图3(b)。
|
图 3 不同信号频率和入水深度时磁感应强度变化曲线 Fig. 3 Magnetic induction strength varying with frequencies and depths. |
由图3(a)可知,磁感应强度随信号频率和入水深度的增加而急剧减小,这表明想要达到大的入水深度,就需要采用低信号频率进行通信,且其他条件相同时,频率越低,入水深度越大。由图3(b)可知,当深度为50 m,达到检测阈值时可用的最高频率为58 Hz;而在100 m时,可用的最高频率只有22 Hz。这意味着要保证较大的入水深度,只能采用较低的频率。
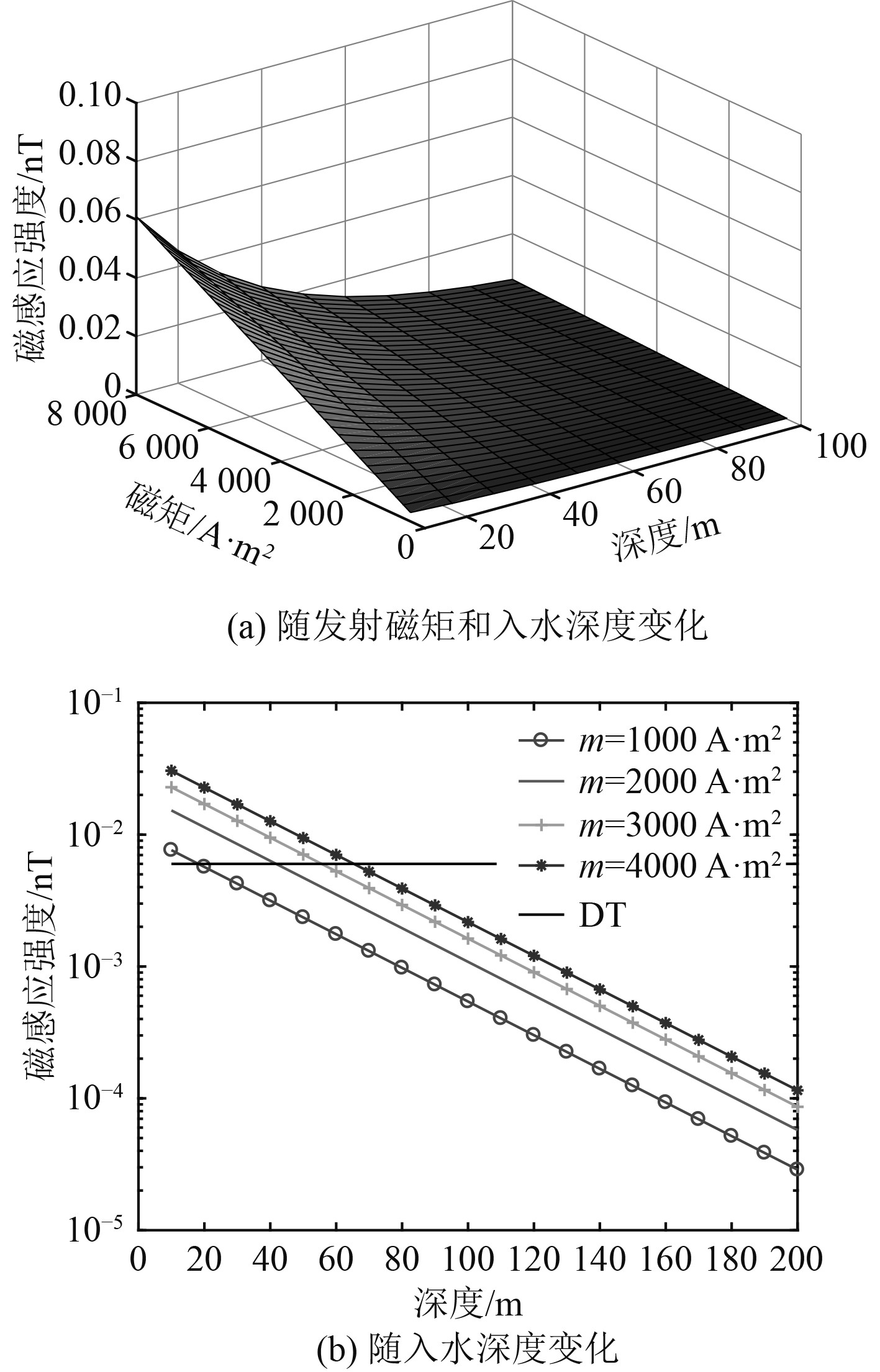
图4(a)为给定径向距离和信号频率时,磁感应强度随发射磁矩和入水深度变化的曲面。由图可知,磁感应强度随入水深度的增加而急剧减小,同时随发射磁矩的减小而急剧减小,这表明在其他条件一定时,可以通过增大发射磁矩以达到增大入水深度的目的。
|
图 4 不同发射磁矩和入水深度时磁感应强度变化 Fig. 4 Magnetic induction strength varying with Emission magnetic moment and depths |
针对图4(a)取不同入水深度进行分析,可以得到磁感应强度随发射磁矩变化的曲线,即图4(b)所示。可知,磁感应强度大小正比于发射磁矩,这与理论公式是相符的,即要想达到较大入水深度,可以增加发射磁矩来实现这一目的。值得注意的是,图4是在不考虑其他因素影响发射磁矩的条件下仿真得到的。由公式(17)可知,发射磁矩与发射线圈匝数、激励电流等参数有关。理论上,可以通过增加线圈匝数、横截面积或者激励电流来增加发射磁矩。
仿真分析表明,信号频率、发射磁矩对水下的覆盖范围有较大的影响,频率越低,磁感应通信入水的深度和径向距离越大;发射磁矩越大,磁感应通信入水的深度和径向距离越大。同时频率越低,磁感应通信的通信速率也越低;发射磁矩越大,通信系统的发射端体积越大,越难以实现。因此,从磁感应通信的覆盖范围与数据率来看,信号频率和发射磁矩应综合通信需求、系统实现等因素折衷考虑。
3 海上通信试验及数据分析 3.1 海上通信试验为了验证跨空海界面磁感应通信,在南海进行通信验证性试验。试验信号采用单频连续波(CW)和频移键控(FSK)调制信号,频率选在4 - 40 Hz 之间。单频CW信号用于验证跨空海界面磁感应通信传输特性以及估算海洋磁场噪声强度;通信信号利用13位巴克码进行扩频编码,扩频后进一步采用2FSK调制,用于完成跨空海界面磁感应通信性能测试。
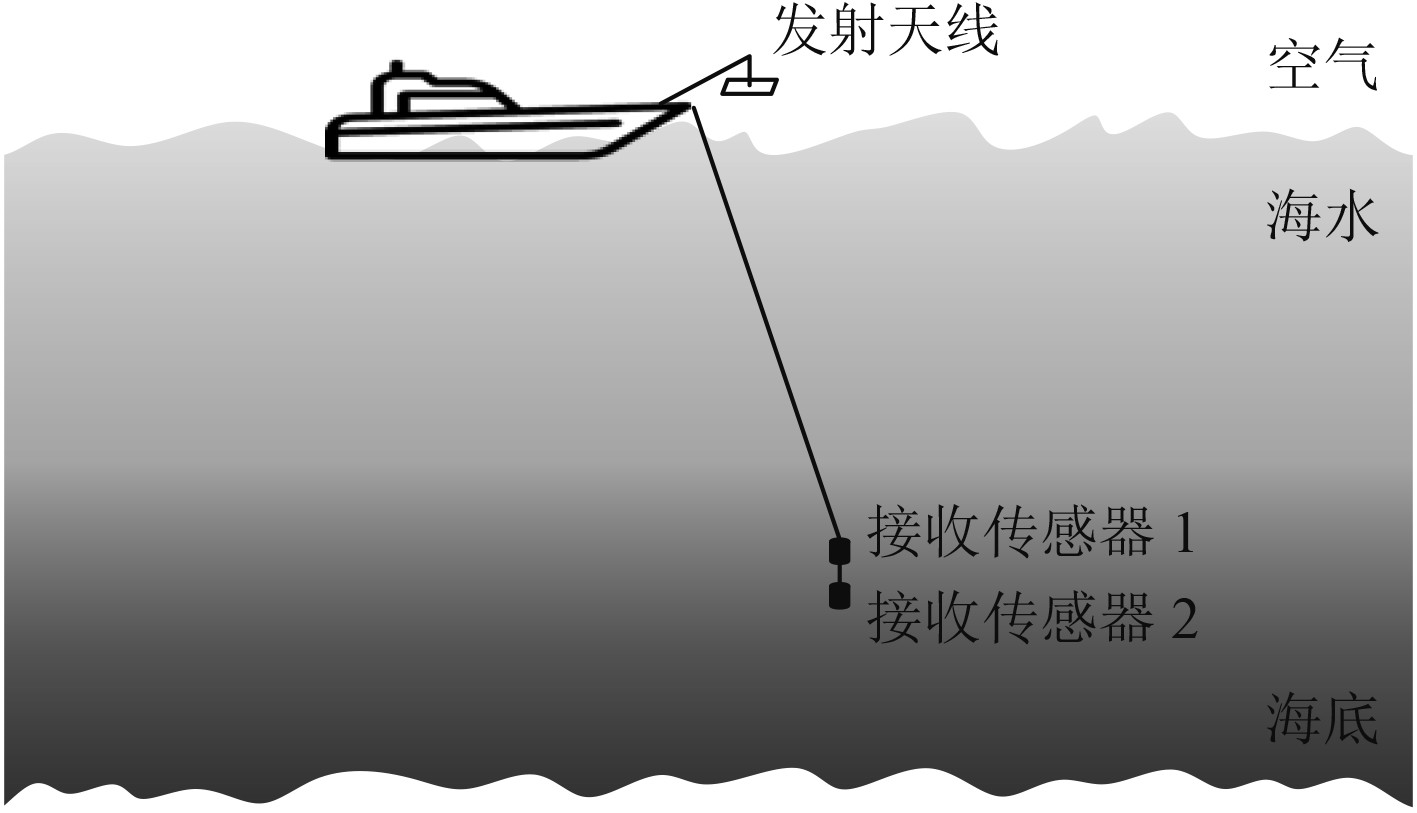
试验中使用的磁感应通信系统,主要包含发射系统和接收系统两部分。其中,发射系统由发射天线、信号产生板和功率放大器组成;接收系统由三分量磁通门传感器、数据采集存储板和密封罐组成。海上通信试验时,选择将发射天线通过船尾的吊车进行悬于水面5 m吊起,且天线轴向垂直于水面。接收端的两个传感器通过绞盘沉入不同深度的海水中,2个接收传感器之间距离10 m,最小接收深度为5 m,最大接收深度为45 m。试验时该海域有5~6级大风,阵风7级,风浪导致传感器与天线轴向方向存在10°~30°的夹角,海上试验示意图如图5所示。试验结束后,打捞并取出接收系统中的数据存储模块,将数据导出后进行信号处理。
|
图 5 海上试验示意图 Fig. 5 Schematic diagram of sea communication test |
根据接收系统采集到的试验数据,利用Matlab软件对信号进行处理分析。由于篇幅有限,本文仅选取接收深度35m处单频CW信号,以及2FSK信号的部分接收数据,并给出信号处理结果。
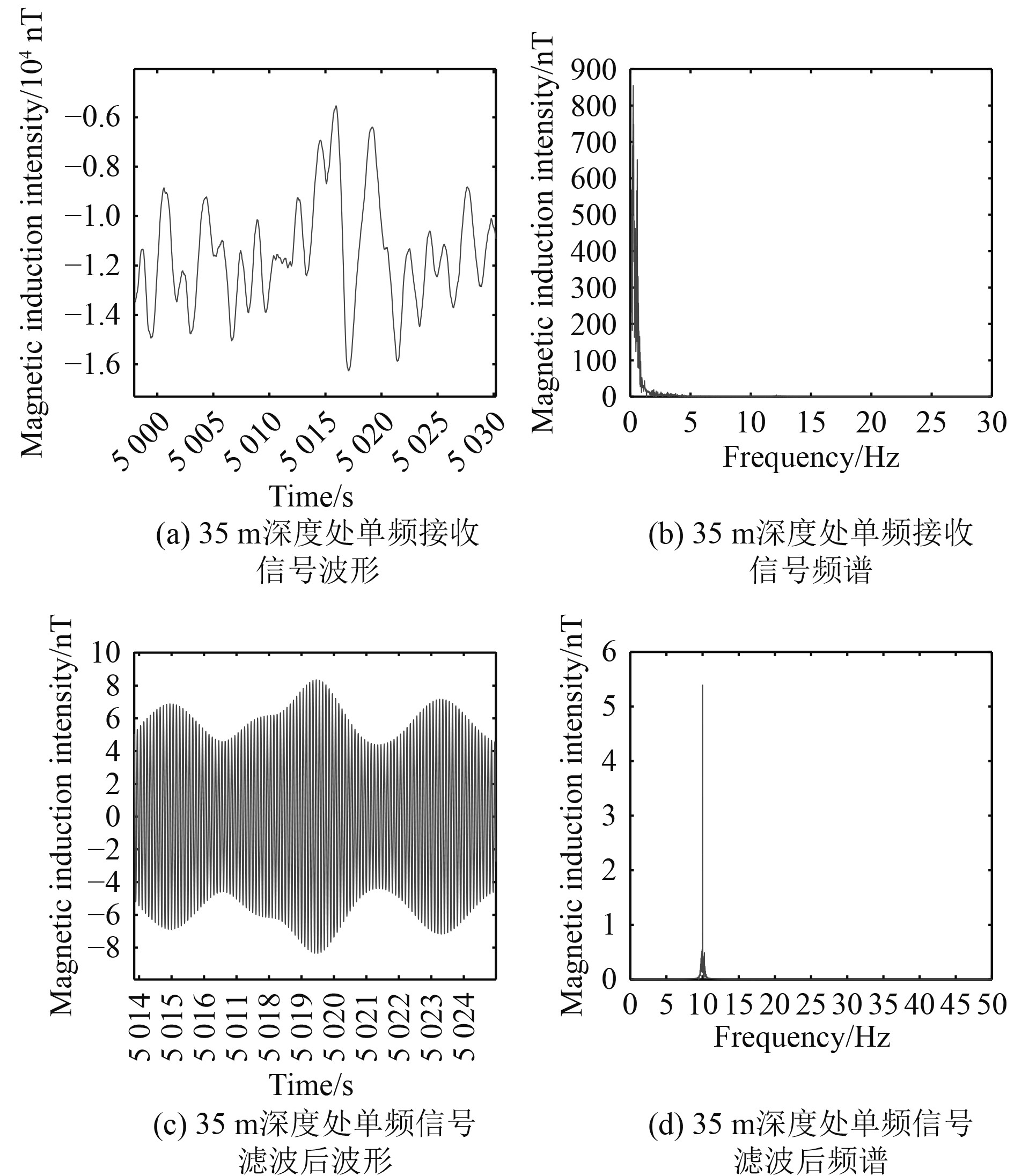
3.2.1 单频连续波(CW)信号由图6(a)和图6(b)可见,在35 m深度处,接收数据中除了有用信号外,在低频区域还存在极强的噪声,噪声能量主要位于0~2 Hz之间,幅度在620~1 200 nT之间;信号波形已完全被低频噪声湮没,频谱上10 Hz频率分量仅为5.54 nT,远低于噪声强度。图6(c)和图6(d)为滤波后的波形和频谱。可见,经滤波处理后35 m深度处的单频CW信号可恢复基本波形,但是信号幅值起伏较大。
|
图 6 35 m深度处单频CW信号滤波前后波形和频谱图 Fig. 6 Waveform and frequency spectra of received CW signals at 35 m depth |
表3给出海水中不同信号频率、不同接收深度处的接收信号强度。可知,海水中的接收信号强度随深度、频率的增大而急剧衰减,且相较于空气和淡水中,衰减的速率更快。试验表明,信号的实际传播特性是与理论仿真结果相符。
|
|
表 3 不同信号频率、不同接收深度处的单频CW信号强度(nT) Tab.3 Received CW signal strength of different frequencies at different receiving depths (nT) |
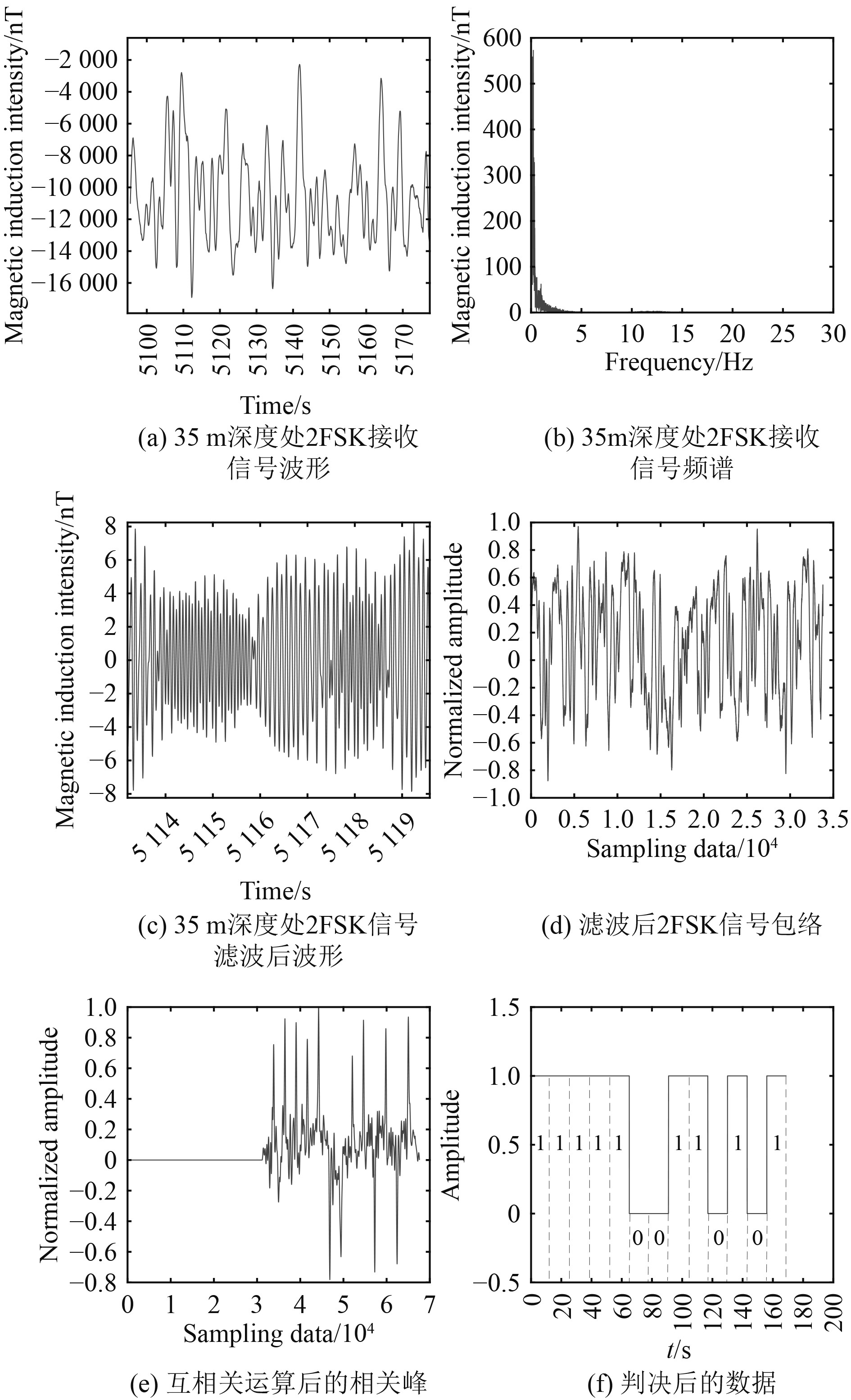
图7(a)和图7(b)为35 m接收深度处的2FSK信号波形和频谱图。可见2FSK接收信号波形已完全被低频噪声湮没,频谱上10 Hz和15 Hz的频率分量仅分别为3.12nT和0.86 nT,远低于噪声强度580.4 nT。图7(c)和图7(d)为35 m深处的一段2FSK接收信号进行滤波、非相关解调处理过程。进一步利用巴克码相关性进行相关接收,判决恢复发射码元信息,则可以将误码率由2.92%提高到无误码,即图7(e)和图7(f)。
|
图 7 35 m深度处的的2FSK信号处理图 Fig. 7 Waveform and frequency spectra of received FSK signals at 35 m depth |
试验数据分析的结果表明,磁感应通信信号在有5~7 级风浪(即存在大多普勒频移)的海洋环境中具有良好的频率稳定性。经滤波、相关接收等简单的信号处理后,此次试验实现了入水深度35 m、数据率15 bps、无误码的跨空海界面磁感应通信。若对接收信号进行微弱信号检测等其他处理方法,进一步提高信噪比,则可实现更大深度的跨界通信。
3.2.3 噪声分析海上通信试验数据表明:由于存在极强的极低频海洋噪声干扰,接收信号的信噪比极低,这势必会影响到通信可靠性和有效性。为了进一步研究跨空海界面磁感应通信特性,分析不同深度处的海洋磁场噪声分布情况。
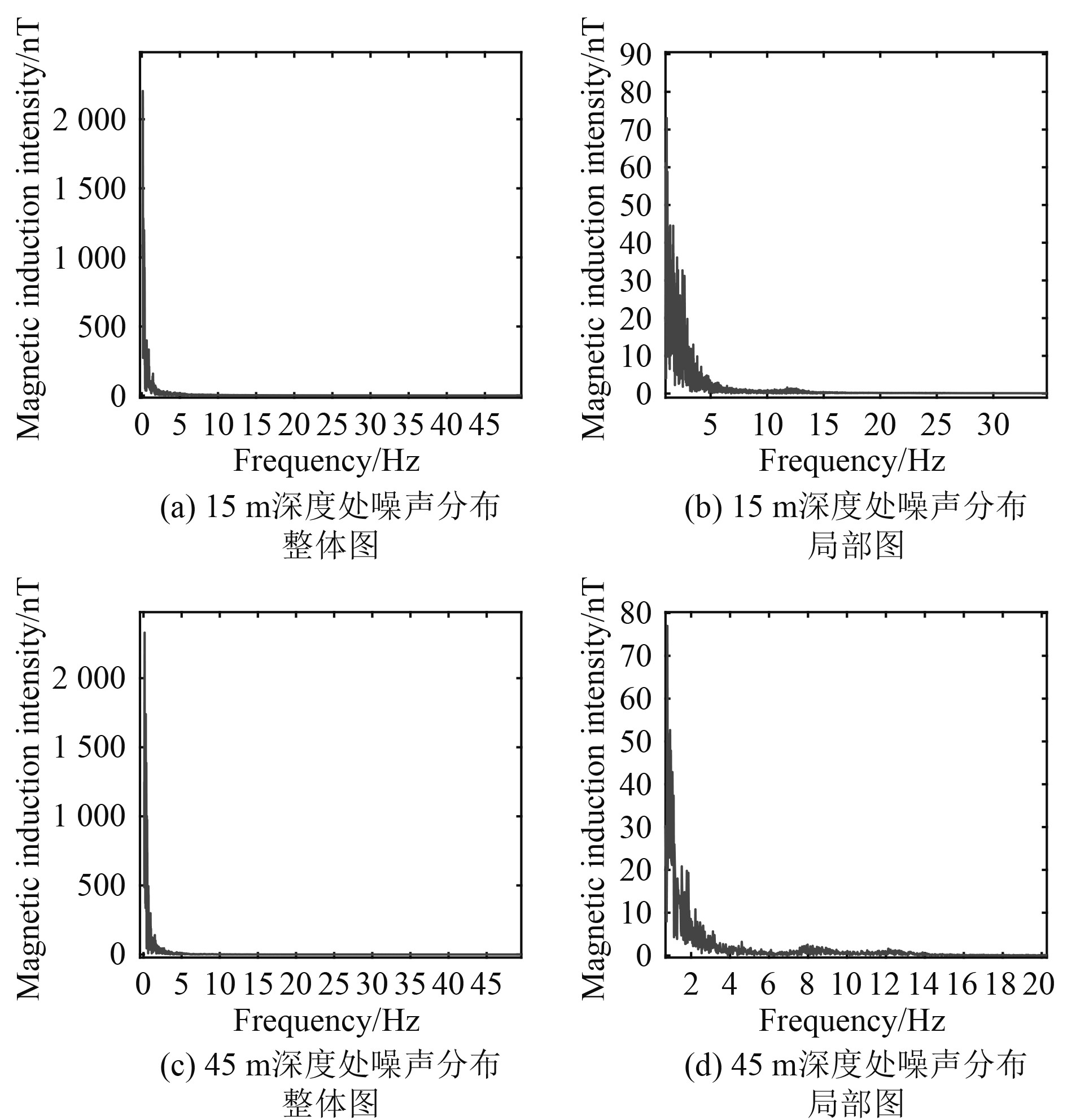
图8为15 m深度和45 m深度处的海洋磁场噪声分布。可见,深度对于海洋磁场噪声分布情况而言基本无影响,海洋磁场噪声主要分为两部分:第一部分为频率分布在0~2 Hz的极低频噪声,此部分噪声能量极强,噪声的磁感应强度可达2 000 nT以上,远大于接收信号强度,即图8(a)和图8(c);第二部分为频率大于2 Hz部分的噪声,即图8(b)和图8(d),此部分噪声的线谱均匀分布在8~9 Hz,12~14 Hz之间,且有小幅度的起伏,能量量级与接收信号大小相差无几,对于接收信号影响极大。由此可见,完成低信噪比接收信号的有效处理,实现稳定、可靠的跨界通信,是下一步研究跨空水界面磁感应通信的关键所在。
|
图 8 不同深度处的海洋磁场噪声 Fig. 8 Distribution of ocean magnetic field noise at different depths |
本文对跨空海界面磁感应通信进行研究,利用分层导电媒质的传播模型,仿真分析跨空海界面磁感应通信的传输特性,并进行跨空海界面磁感应通信海上试验,验证了跨界磁感应通信的可行性和有效性。本文研究表明,信号频率对跨空海界面磁感应通信的水下覆盖有重要影响。频率越低,入水越深,但在极低频段有很强的磁场噪声,且随深度的增加而增加。这导致通信信号的信噪比极低,且过低的频率也使数据率很低。为此,频率的选择需要根据水下覆盖、数据率和信号处理算法的复杂度综合考虑。除此之外,还需要采用有效的技术措施,如选择更合适的天线指向,增加发射磁矩和接收灵敏度,采用微弱信号处理算法,以及采用中继转发技术磁感应通信等,以使空海磁感应通信达到实用的入水深度和数据率。
| [1] |
张歆, 张小蓟. 水声通信理论与应用[M]. 西安: 西北工业大学出版社, 2012.
|
| [2] |
AFANASEV K, GAFUROV S. The overview of underwater connection[C]//International Congress on Sound and Vibration, ICSV22, 12-16 July, 2015, 1–8.
|
| [3] |
李剑汶, 王小阳, 童峰. 浅海信道调频水声语音通信方法比较[J]. 舰船科学技术, 2017, 39(1): 127–131. LI Jian-wen, WANG Xiao-yang, TONG Feng. The comparison of underwater acoustic FM speech communication methods in shallow water channels [J]. Ship Science and Technology, 2017, 39(1): 127–131. |
| [4] |
WIENER T, KARP S. The role of blue/green laser systems in strategic submarine communications[J]. IEEE Transactions on Communication, 1980, 28(9): 1602-1607. DOI:10.1109/TCOM.1980.1094858 |
| [5] |
DOMINGO M C. Magnetic induction for underwater wireless communication networks[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(6): 2929-2939. DOI:10.1109/TAP.2012.2194670 |
| [6] |
GULBAHAR B, AKAN O B. A communication theoretical modeling and analysis of underwater magneto-inductive wireless channels[J]. IEEE Transactions of Wireless Communication, 2012, 11(9): 3326–3334.
|
| [7] |
GUO H, SUN Z, WANG P, Channel modeling of MI underwater communication using tri-directional coil antenna[C]//Proc. IEEE GLOBECOM '15, 2015.
|
| [8] |
王一鸣, 谢旭. 水下磁感应通信阵列天线磁场仿真与特性研究[J]. 舰船科学技术, 2022, 44(6): 106–113. WANG Yi-ming, XIE Xu. Research on magnetic-field simulation and characteristics of underwater magnetic induction communication array antenna[J]. Ship Science and Technology. 2022, 44(6): 106–113. |
| [9] |
柴彬彬. 跨空水界面磁感应通信信号处理[D]. 西安: 西北工业大学, 2019.
|
| [10] |
DURRANI S. Air to undersea communication with magnetic dipoles[J]. IEEE Transactions on Antennas and Propagation, 1964, 12(4): 464-470. DOI:10.1109/TAP.1964.1138240 |
| [11] |
DURRANI S. Air-to-undersea communication with electric dipoles[J]. IEEE Transactions on Antennas and Propagation, 1962, 10(5): 524-528. DOI:10.1109/TAP.1962.1137912 |
| [12] |
ARUTAKI A, CHIBA J. Communication in a three-layered conducting media with a vertical magnetic dipole[J]. IEEE Transactions on Antennas and Propagation, 1980, 28(4): 551-556. DOI:10.1109/TAP.1980.1142378 |
| [13] |
FRASER-SMITH C, BUBENIK D M. ULF/ELF electromagnetic fields generated above a sea of finite depth by a submerged vertically-directed harmonic magnetic dipole[J], Radio Science, 1979, 14(1): 59–74.
|
| [14] |
JIANG B H, LIU Y T. Expansion of spherical wave functions for hertz potential of a vertical magnetic dipole over conducting medium plane[J]. Acta Electronica Sinica, 2005, 34(6): 1152–1155.
|
| [15] |
TANG J F, GONG S G, WANG J G. Computation of energy distribution of the magnetic field induced by ocean waves[J]. Acta Oceanologica Sinica. 2005, 34(6): 1152–1155.
|
 2022, Vol. 44
2022, Vol. 44

