2. 大连测控技术研究所,辽宁大连 116000
2. Dalian Scientific Test and Control Technology Institute, Dalian 116000, China
新时代海洋强国战略与现代化海军建设对水声通信的实时性和稳健性提出了更高的要求,而海洋声场环境的复杂性与水声信道的复杂多变性使得水声信号在传输过程中受到更多的噪声干扰并产生强烈的起伏与波动,所以水声通信系统的自适应与抗干扰能力尤为重要。由于均衡器能够产生与信道相反的特性,帮助通信系统消除不良信道带来的码间串扰,有利于对复杂信道进行特性估计,因此可以将性能优良的均衡器运用于水声通信系统中来提升水声通信系统的通信质量。
传统的水声通信系统通常以单载波做时域均衡,这是由于水声通信系统多径时延长(约为陆地无线通信系统中信道多径时延的103至106倍)的缘故。当对水声通信系统做频域均衡时,由于多径时延比码元宽度大得多,导致在计算其信道特性时,采样点数很大,计算量的飙升对系统的性能提出了更高的要求。本文首先介绍信道均衡技术改进前后的原理,然后从频域的角度分析单载波水声扩频通信系统中以BPSK,QPSK两种方式对信号进行调制和MMSE,ZF两种线性均衡方式进行均衡的星座图分布。最后,通过水池实验验证了算法的可行性。
1 信道迫零均衡技术原理冲激响应分别为
| $ {q_n} = \sum\limits_{j = - \infty }^\infty {{c_j}{f_{n - j}}}。$ | (1) |
式中:
| $ {\widehat I_k} = {q_0}{I_k} + \sum\limits_{n \ne k} {{I_n}{q_{k - n}} + \sum\limits_{j = - \infty }^\infty {{c_j}{\eta _{k - j}}} }。$ | (2) |
式中:第1项表示工程转换形式所带来的信息符号,可以假设
| $ D(c) = \sum\limits_{\mathop {n = - \infty }\limits_{n \ne 0} }^\infty {\left| {{q_n}} \right|} = \sum\limits_{\mathop {n = - \infty }\limits_{n \ne 0} }^\infty {\left| {{c_j}{f_{n - j}}} \right|} 。$ | (3) |
至此,给出了均衡器抽头系数表达式
| $ {q_n} = \sum\limits_{j = - \infty }^\infty {{c_j}{f_{n - j}} = \left\{ \begin{aligned} &1,{n = 0} ,\\ &0,{n \ne 0} 。\end{aligned} \right.} $ | (4) |
对上式进行z变换得到:
| $ Q(z) = C(z)F(z) = 1 ,$ | (5) |
也可以表示为:
| $ C(z) = \frac{1}{{F(z)}}。$ | (6) |
式(6)表示一个传递函数为
| $ C'(z) = \frac{1}{{F(z){F^*}(1/{z^*})}}。$ | (7) |
式中,C(z)为抽头系数
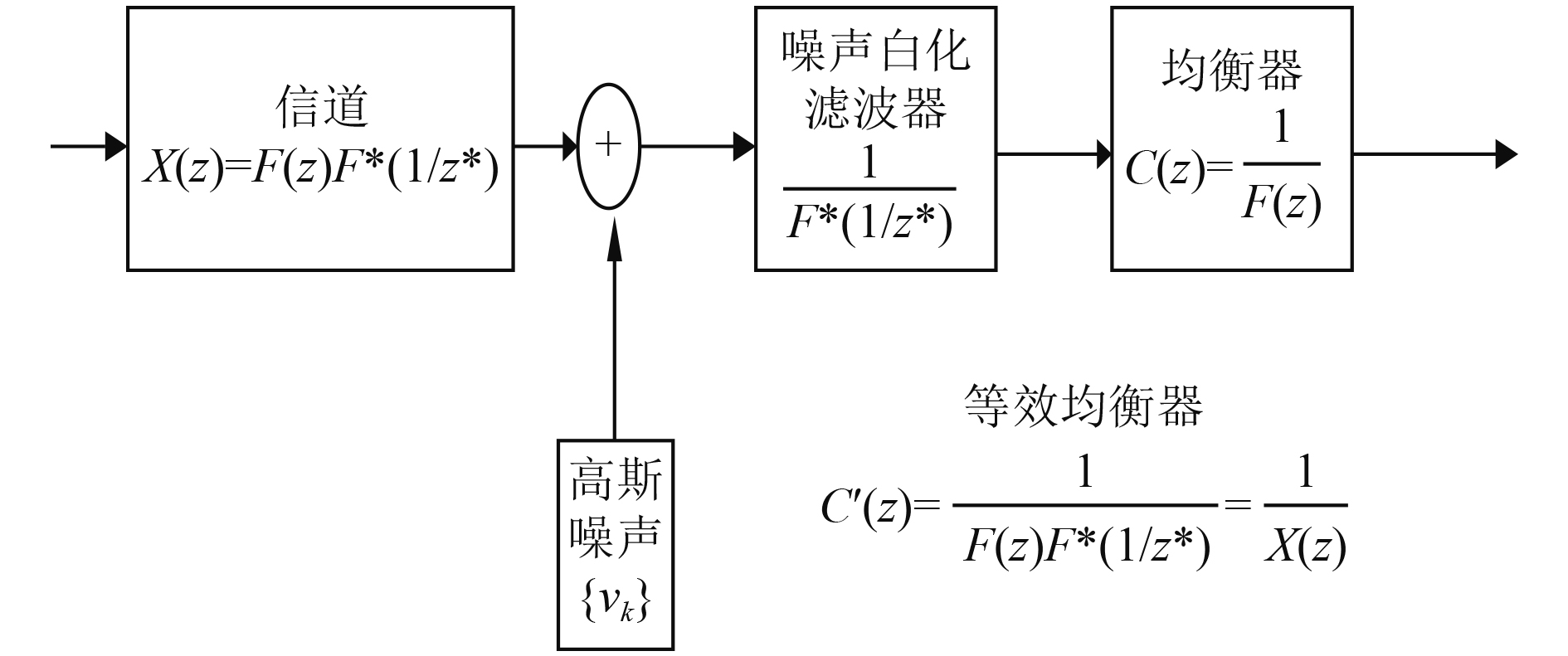
|
图 1 迫零均衡原理框图 Fig. 1 Block diagram of zero-forcing equalization |
根据均方误差准则的均衡模型,改变横向均衡器的抽头向量系数
| $ {\varepsilon _k} = \sum\limits_{j = - \infty }^\infty {{I_k} - {{\widehat I}_k}} 。$ | (8) |
式中:
| $ J = E{\left| {{\varepsilon _k}} \right|^2} = E{\left| {{I_k} - {{\widehat I}_k}} \right|^2}。$ | (9) |
由式(9)可以看出,无论信息码元为实数还是复数,J均可以表示为均衡器模型
首先需要讨论的情况是,对于无限个抽头的均衡器,使得性能函数J最小的抽头权值系数。在这种情况下,估计值
| $ {\widehat I_k} = \sum\limits_{j = - \infty }^\infty {{c_j}{v_{k - j}}}。$ | (10) |
联立式(10)和式(9),便可利用结果展开式中系数
| $ E({\varepsilon _k}{v^*}_{k - l}) = 0 ,- \infty \lt l \lt \infty。$ | (11) |
根据上面的推导,替代式(11)里的误差项
| $ E\left[ {\left( {{I_k} - \sum\limits_{j = - \infty }^\infty {{c_j}{v_{k - j}}} } \right){v^*}_{k - l}} \right] = 0 ,$ | (12) |
上式也等价于:
| $ \sum\limits_{j = - \infty }^\infty {{c_j}E({v_{k - j}}{v^*}_{k - l})} = E({I_k}{v^*}_{k - l}) 。$ | (13) |
频域均衡的目的是选择合适的抽头系数使得对于得到的方程两边做Z变换,有下面的表达式:
| $ C(z)[F(z){F^*}(1/{z^*}) + {N_0}] = {F^*}(1/{z^*}) 。$ | (14) |
由式(14)可知,基于均方误差准则的均衡器传递函数可以表示为:
| $ C(z) = \frac{{{F^*}(1/{z^*})}}{{F(Z){F^*}(1/{z^*}) + {N_0}}}。$ | (15) |
如果将高斯白噪声考虑在内,就需要在信道模型中加入白化滤波器,则式(15)就变化为:
| $ C'(z) = \frac{1}{{F(Z){F^*}(1/{z^*}) + {N_0}}} 。$ | (16) |
将式(16)中的传递函数表达式与峰值失真准则下的均衡器传递函数表达式进行对比,可以看出二者的唯一区别在于基于MSE准则下式(16)中出现了噪声谱密度因子
本文主要对BPSK,QPSK两种调制方式下的单载波水声扩频通信系统信噪比与误码率进行Matlab仿真,通过对比2种不同的线性均衡---MMSE均衡与ZF均衡的星座图和误码率曲线,比较二者的均衡效果差异。仿真环境设置如下:以水声多径信道为传播路径,CHU序列作为UW训练序列,以BPSK,QPSK两种调制方式进行水声信号的调制。信道特性如图2所示。
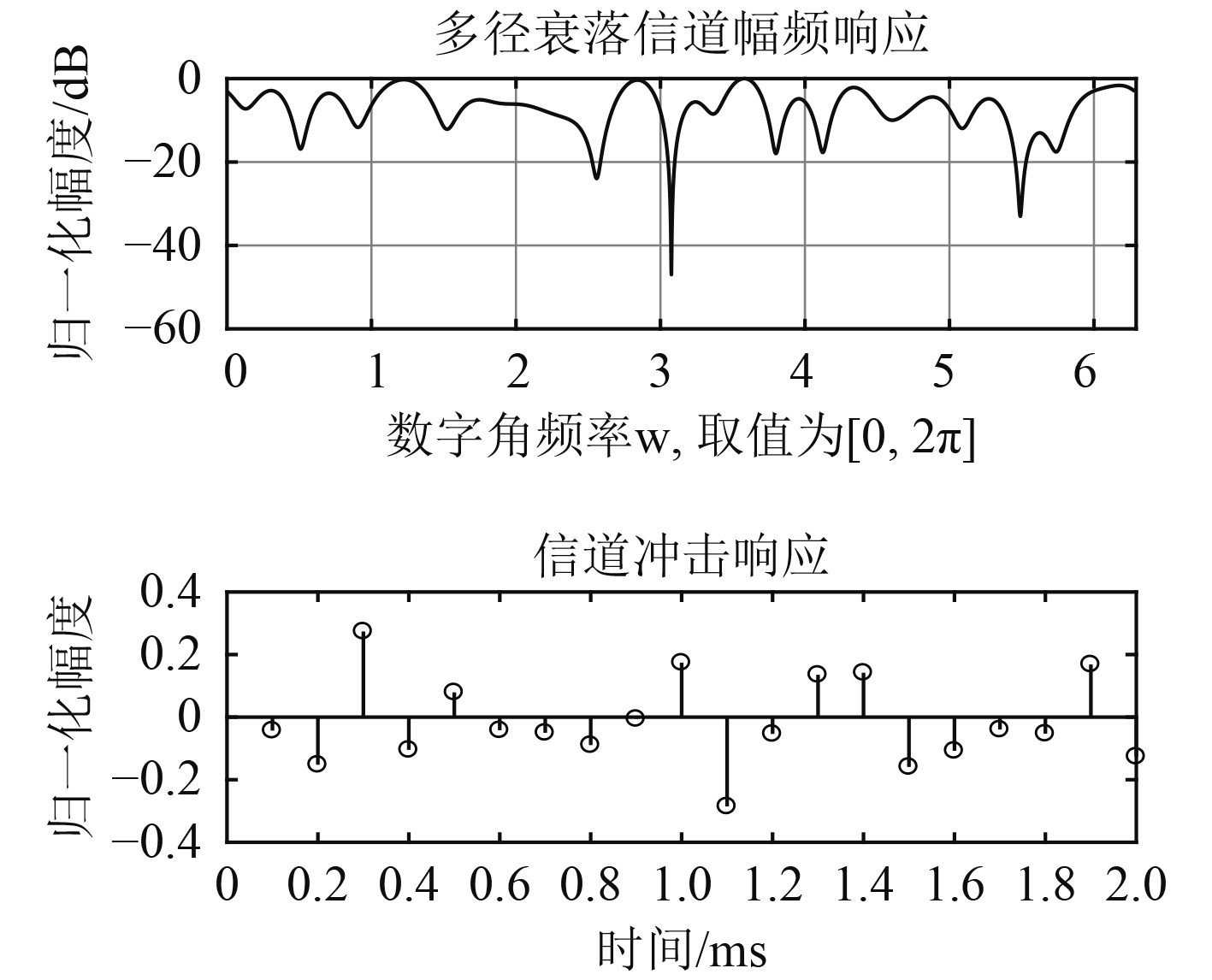
|
图 2 多径信道特性 Fig. 2 Multipath channel characteristics |
表1列出了涉及到的仿真参数。
|
|
表 1 仿真参数表 Tab.1 The table of simulation parameters |
BPSK调制方式下,经过均衡器处理的输出信号信噪比的误码率曲线如图3所示。MMSE均衡与ZF均衡在BPSK调制下处理前后的星座对比如图4所示。
|
图 3 BPSK调制下误码率曲线 Fig. 3 Bit error rate curve under BPSK modulation |

|
图 4 BPSK调制下星座图对比 Fig. 4 Constellation diagram comparison under BPSK modulation |
BER为
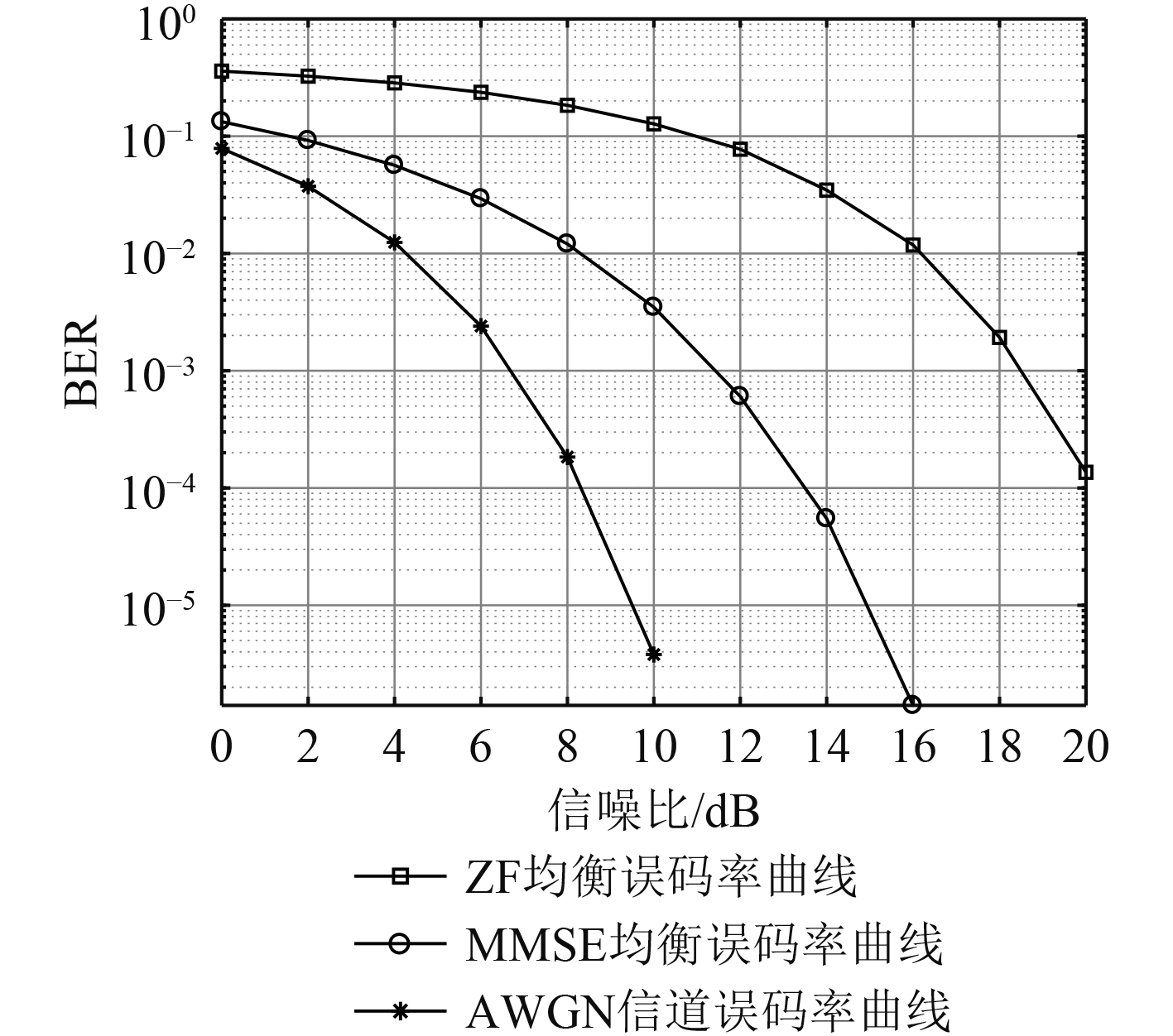
图5和图6分别给出了均衡后QPSK调制下的信噪比误码率曲线及ZF、MMSE两种均衡方式处理前后的星座图对比。

|
图 5 QPSK调制下误码率曲线 Fig. 5 Bit error rate curve under QPSK modulation |
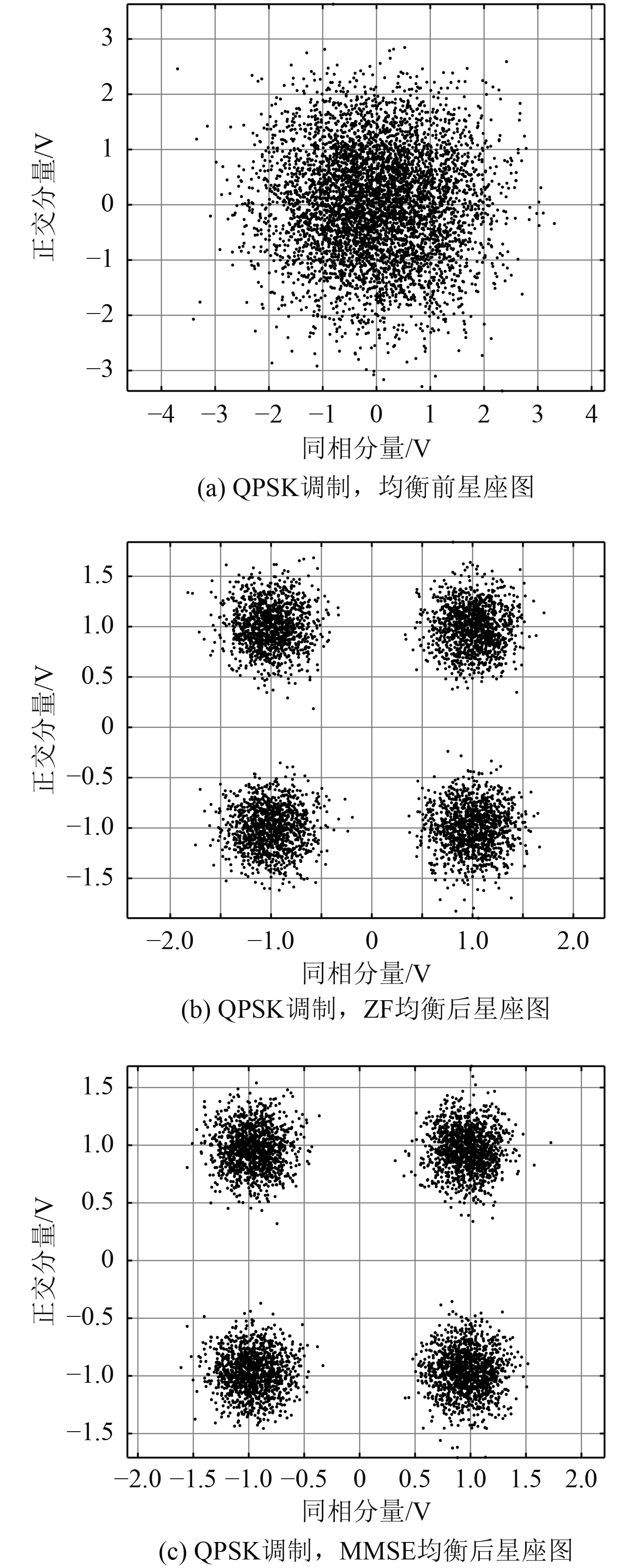
|
图 6 QPSK调制下星座图对比 Fig. 6 Constellation diagram comparison under QPSK modulation |
在20 dB信噪比条件下,由MMSE均衡和ZF均衡的星座图可以看出,前者的分布比后者的分布更集中,所以MMSE均衡的表现比ZF均衡的表现更好。在误码率曲线中,当BER=
本文涉及的实验水池长、宽、深度分别为45 m,6 m,5 m。实验采用的发射换能器与接收水听器布放在2 m深的位置,二者相距8.35 m,均无指向性。借助电脑和Cool Edit Pro软件发送与接收数据。图片等数据经BPSK调制后从发射端发出,接收端通过FFT来估计信号频偏,并利用一阶横向滤波器对解调后的信号进行均衡。数据头部分是长度为1s的线性调频信号,以便确定数据的位置并进行信道参数的估计。本次实验完成了单载波水声扩频通信系统中数据的传输和BPSK通信、线性均衡的验证。BPSK实验中采用的带宽分别是200 Hz,400 Hz,800 Hz,4000 Hz实验结果如图7所示。

|
图 7 单载波BPSK验证实验结果 Fig. 7 Experimental results of single-carrier BPSK verification with different bandwidths |
由单载波BPSK验证实验结果可知,系统的通信速率与通信带宽有关,前者会随着后者的增加而提高,但信道多径干扰会降低通信的正确率。由图7可以看出,在4000 Hz带宽时,图像较为模糊并在底部出现了少许映像,这说明此时的误码率较为严重,原因在于多径信号的延迟远大于码元宽度。
4 结 语本文的主要研究对象是单载波扩频均衡技术,通过仿真与实验分析讨论了如何选取合适的均衡参数。由于水声信道具有频率选择性,并且易受时空变化影响,所以水声信道的估计要借助合适的均衡技术与优良的算法进行,有效抑制水声信道的多径干扰和频率选择性衰落,使单载波水声扩频系统的通信质量得到保障。
本文首先从理论的角度对均衡技术进行分析,以单载波水声扩频通信系统为载体,从频域的角度进行研究。其次,进行了仿真,采用BPSK,QPSK两种调制方式,以Matlab仿真获取了这2种方式下单载波扩频信号经均衡器处理后输出信噪比的误码率曲线以及2种调制方式下MMSE均衡与ZF均衡前后的星座图对比。由此比较了2种线性均衡方式的性能。最后,进行水池实验验证算法可行性并得出结论:在水声单载波扩频通信系统中,通信速率与通信带宽成正比,但信号在水声信道中的多径传播会带来码间串扰,使通信正确率下降。选择合适的均衡器可以很好地避免多径干扰,对比来看,MMSE均衡与ZF均衡相比能更大程度地降低误码率,使判决器得到正确的判决结果。
| [1] |
王峰, 赵俊渭, 李洪升. 一种混合常数模水声信道盲均衡新算法的研究[J]. 声学学报, 2003(2): 137-140. DOI:10.3321/j.issn:0371-0025.2003.02.008 |
| [2] |
郭业才, 郭炎炎, 赵俊渭. 水声信道盲均衡的最小平方峭度恒模算法[J]. 数据采集与处理, 2004(4): 371-375. DOI:10.3969/j.issn.1004-9037.2004.04.003 |
| [3] |
孙丽君, 孙超. 几种适用于水声信道的常模类盲均衡算法研究[J]. 电声技术, 2005(1): 7–8+ 21.
|
| [4] |
张珍, 黄瑞光, 程贯中. 扩频技术在水下声通信系统中的应用[J]. 通信技术, 2002(11): 7–9+ 15.
|
| [5] |
李霞, 方世良, 陆佶人. 水声扩频通信中相关算法的研究[J]. 电路与系统学报, 2005(6): 76-79. |
| [6] |
韩笑. 浅海环境下单载波时域均衡水声通信关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [7] |
RONTOGIANNIS A. A., KEKATOS V., BERBERIDIS K. An adaptive decision feedback equalizer for time-varying frequency selective MIMO channels[C]// 2006 IEEE 7th Workshop on Signal Processing Advances in Wireless Communications, 2006: 1–5.
|
| [8] |
LALOS A. S., VLACHOS E., BERBERIDIS K., et al. Greedy algorithms for sparse adaptive decision feedback equalization[C]// 2011 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), 2011: 240–245.
|
| [9] |
NOUNE M. B., NIX A. Impact of channel estimation errors on the performance of DFE equalizers with space time block codes in wideband fading channels[C]// 2007 IEEE Wireless Communications and Networking Conference, 2007: 2241–2246.
|
 2022, Vol. 44
2022, Vol. 44
