轴是传递动力的重要部件,工程中的机械动力90%以上是依靠轴系传递的。在航空发动机、舰船推进装置、汽轮发电机组等动力系统中,转速的提升与临界转速数目的增加,使得轴系的振动与稳定性成为转子动力学关注的问题,研究的最终目的是控制以轴为核心的机械系统的转动,确保机器设备的平稳运行[1-2]。
经典的轴系振动理论将转子划分为刚性转子和柔性转子,并且对于柔性转子给出了系统可以自动对中的明确结论[1]。由于转动引起的惯性力与转速的平方成正比,因而质量偏心即不平衡惯性力引起的强迫振动就成为轴系振动治理的重要途经,其主要方法是在静平衡的基础上,对于轴系以及其上的转子进行动平衡。
事实上轴系振动的影响因素很多,且带来诸多问题。近20余年里人们一直研究转子的油膜与碰撞等振动问题[3-5],不仅仅呈现复杂的非线性振动特性,而且在振动激励上超出了强迫振动的范畴,尤其是轴系的不对中产生的振动,将呈现包括参数激励和自激振动的多种激励耦合作用结果,并且在某些偏斜(中心线偏移或角度偏斜)情况下,产生轴系的初始运行时期振动幅值小、后续运行阶段振动幅度增高,但是可靠性下降的情形[6-8]。从振动机理上可以看到,轴系的耦合非线性振动不属于动平衡技术可以解决的范畴,因而在施加动平衡技术之前,必须滤掉其他非惯性力因素导致的振动成分,或者通过系统部件的设计、调节措施,尽可能控制非惯性力之外的耦合激励作用下的振动响应,最终为动平衡过程提供干净的振动测试数据,才能达到通过动平衡最终控制振动的目的[2, 9]。偏斜隐藏在转子系统中,有时会被误认作轴系的不平衡,因为在有些情况下,偏斜轴系的振动幅值通过校准反倒降低。但轴系的偏斜不能靠动平衡消除。故控制轴的振动需要研究偏斜情况下轴系的振动规律。
机器的健康监控或其中的故障诊断是研究轴系非线性振动的另一个目的。通过提取振动信号中的故障特征,可以判别机器运行状态,所以需要有针对性地建立轴系的动力学模型,分析掌握动力学特性和振动特征[10-11]。
在转子动力学的研究工作中,相对于其他因素的非线性振动,偏斜轴系的振动研究并不充分,主要有工作模型和有限的振动特征仿真方面。其原因是,偏斜轴系振动比较复杂,最好的振动控制方式是在机器组装环节中实施详细严格的校正措施[2,12-13]。
周奇郑等[14]研究了在加速状态下偏角不对中轴系的横向振动特性,建立并分析油膜、碰摩因素作用下的动力学方程,指出加速度使共振特性更加复杂。韩捷等[15]研究了联轴器在偏斜情况下的倍频特性,发现了不对中的弯曲振动特征依赖于不对中的类型。李明[16]基于谐波平衡法分析了不对中与不平衡转子系统的动力学特性,发现不平衡与不对中振动频率不仅相似,还会相互耦合产生新的频率。安学利等[17]考虑了偏斜与不平衡因素,分析了偏斜转子系统的动力学行为,研究了偏斜量、转速、支撑刚度等对系统的影响。付波等[18]分别研究了偏斜量、不平衡量、阻尼系数等对立式水轮发电机组转子系统的影响。Xu M.等[19]研究了不对中对转子系统倍频特性的影响。
基于上述研究,本文建立偏斜轴系在不平衡、油膜、碰摩耦合影响下的动力学模型,研究其振动机理,分析偏斜因素对动平衡的影响。
1 基本假设图1为由电机、滑动轴承、螺旋桨、联轴器等组成的推进轴系。其中,
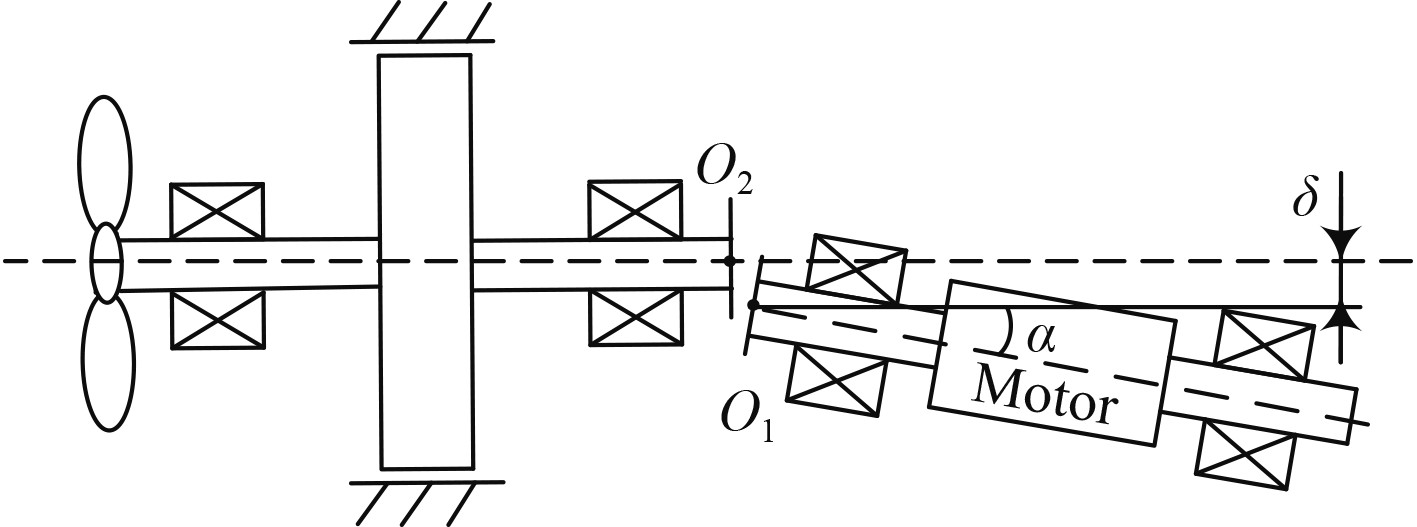
|
图 1 轴系示意图 Fig. 1 Schematic diagram of shafting |
假设电机输出扭矩为

|
图 2 偏角不对中转轴受力分析图 Fig. 2 Stress analysis of transfer shaft with misalignment of deflection angle |
图中,
| $ {T_y} = T\sin \alpha \cos {\theta _M},$ | (1) |
| $ {T_z} = T\sin \alpha \sin {\theta _M} 。$ | (2) |
不考虑从动轴的圆盘转子的安装偏斜,沿
| $ {T_x} = {I_R}{\dot \omega _R}。$ | (3) |
式中:
| $ {\omega _R}/\omega = C/(1 + D\cos 2{\theta _M})。$ | (4) |
其中:
将式(4)对时间
| $ {\dot \omega _R} = 2{\omega ^2}CD\sin (2{\theta _M})/{(1 + D\cos (2{\theta _M}))^2}。$ | (5) |
由图2可得:
| $ T = {T_x}/\cos \alpha 。$ | (6) |
将式(3)、式(5)、式(6)代入式(1)和式(2)可得:
| $ {F_{ny}} = {T_y},$ | (7) |
| $ {F_{nz}} = {T_z} 。$ | (8) |
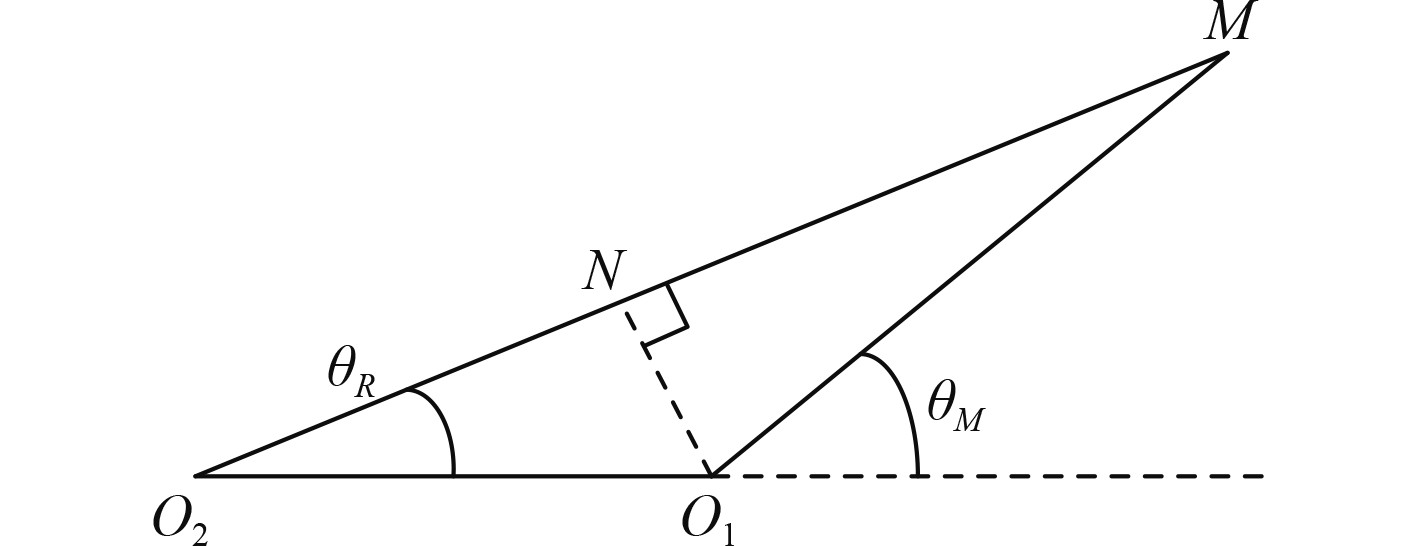
|
图 3 平行不对中联轴器受力分析 Fig. 3 Stress analysis of parallel misalignment coupling |
取
| $ {F_m} = {k_a}\delta \cos {\theta _R}/2。$ | (9) |
由式(5)可知:
| $ {\theta _R} = C\omega t/(1 + D) + {\dot \omega _R}{t^2}/2。$ | (10) |
| $ {F_{my}} = {k_a}\delta /4 + {k_a}\delta \cos (2{\theta _R})/4 ,$ | (11) |
| $ {F_{mz}} = {k_a}\delta \sin (2{\theta _R})/4 。$ | (12) |
假设圆盘存在偏心
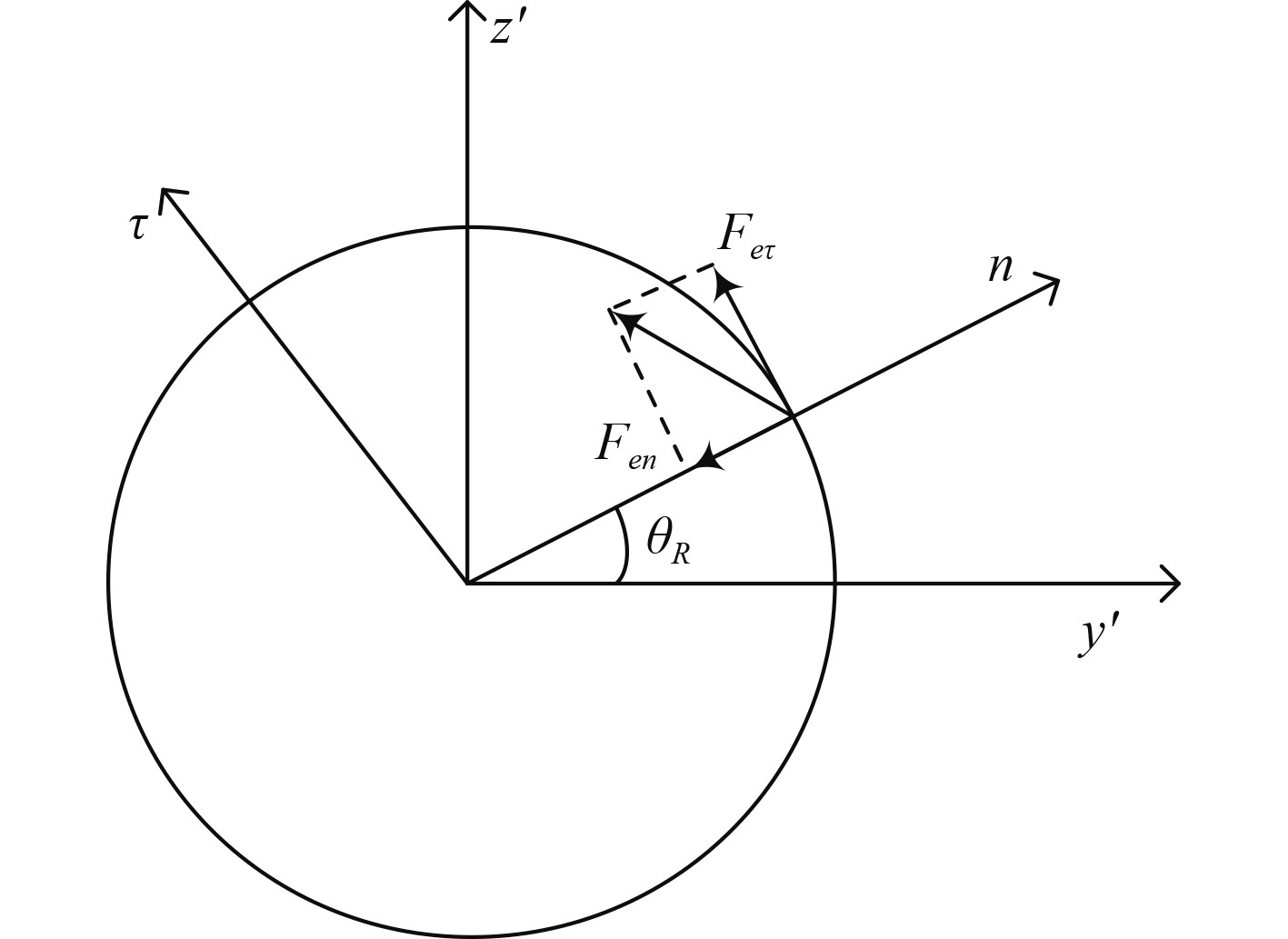
|
图 4 不平衡力的分量 Fig. 4 Components of unbalanced force |
| $ {F_{en}} = {m_2}r\omega _R^2 ,$ | (13) |
| $ {F_{e\tau }} = {m_2}r{\dot \omega _R} ,$ | (14) |
将其投影到
| $ {F_{ey}} = {F_{en}}\cos {\theta _R} + {F_{e\tau }}\sin {\theta _R},$ | (15) |
| $ {F_{ez}} = {F_{en}}\sin {\theta _R} - {F_{e\tau }}\cos {\theta _R}。$ | (16) |
滑动轴承采用修正后的短圆柱瓦轴承油膜力解析模型[13],即Capone油膜力模型。
| $ V(y,z,\alpha ) = \frac{{2 + (z\cos \alpha - y\sin \alpha )G(y,z,\alpha )}}{{1 - {y^2} - {z^2}}} ,$ | (17) |
| $ S(y,z,\alpha ) = \frac{{y\cos \alpha + z\sin \alpha }}{{1 - {{(y\cos \alpha + z\sin \alpha )}^2}}},$ | (18) |
| $ G(y,z,\alpha ) = \frac{2}{{{{(1 - {y^2} - {z^2})}^{\frac{1}{2}}}}} \left[\frac{{\text{π}} }{2} + \arctan \frac{{z\cos \alpha - y\sin \alpha }}{{{{(1 - {y^2} - {z^2})}^{\frac{1}{2}}}}}\right] ,$ | (19) |
| $ \alpha = \arctan \frac{{z + 2\dot y}}{{y - 2\dot z}} - \frac{{\text{π}} }{2}sign\frac{{z + 2\dot y}}{{y - 2\dot z}} - \frac{{\text{π}} }{2}sign(z + 2\dot y) ,$ | (20) |
| $ \sigma = \mu {\omega _R}RL{\left(\frac{R}{{{c_z}}}\right)^2}{\left(\frac{L}{{2R}}\right)^2}。$ | (21) |
其中:
油膜力在
| $ \begin{split} {f_{\mu y}} =& \frac{{{{[{{(y - 2\dot z)}^2} + {{(z + 2\dot y)}^2}]}^{\frac{1}{2}}}}}{{1 - {y^2} - {z^2}}}(3yV(y,z,\alpha ) - \\ & \sin \alpha G(y,z,\alpha ) - 2\cos \alpha S(y,z,\alpha )) ,\end{split} $ | (22) |
| $ \begin{split} {f_{\mu y}} =& \frac{{{{[{{(y - 2\dot z)}^2} + {{(z + 2\dot y)}^2}]}^{\frac{1}{2}}}}}{{1 - {y^2} - {z^2}}}(3zV(y,z,\alpha )+ \\ & \cos \alpha G(y,z,\alpha ) - 2\sin \alpha S(y,z,\alpha )) 。\end{split} $ | (23) |
轴系偏斜产生 的弯矩使轴颈更容易与轴瓦发生碰摩,轴心径向位移
| $ {F_{fn}} = {k_c}\left( {{z_e} - {c_k}} \right),$ | (24) |
| $ {F_{f\tau }} = (f + b{v^n}){F_{fn}} 。$ | (25) |
其中:
| $ {F_{fy}} = - {F_{fn}}\cos {\theta _R} + {F_{f\tau }}\sin {\theta _R} ,$ | (26) |
| $ {F_{fz}} = - {F_{fn}}\sin {\theta _R} - {F_{f\tau }}\cos {\theta _R}。$ | (27) |
将从动轴分离研究,其受力如图5所示。
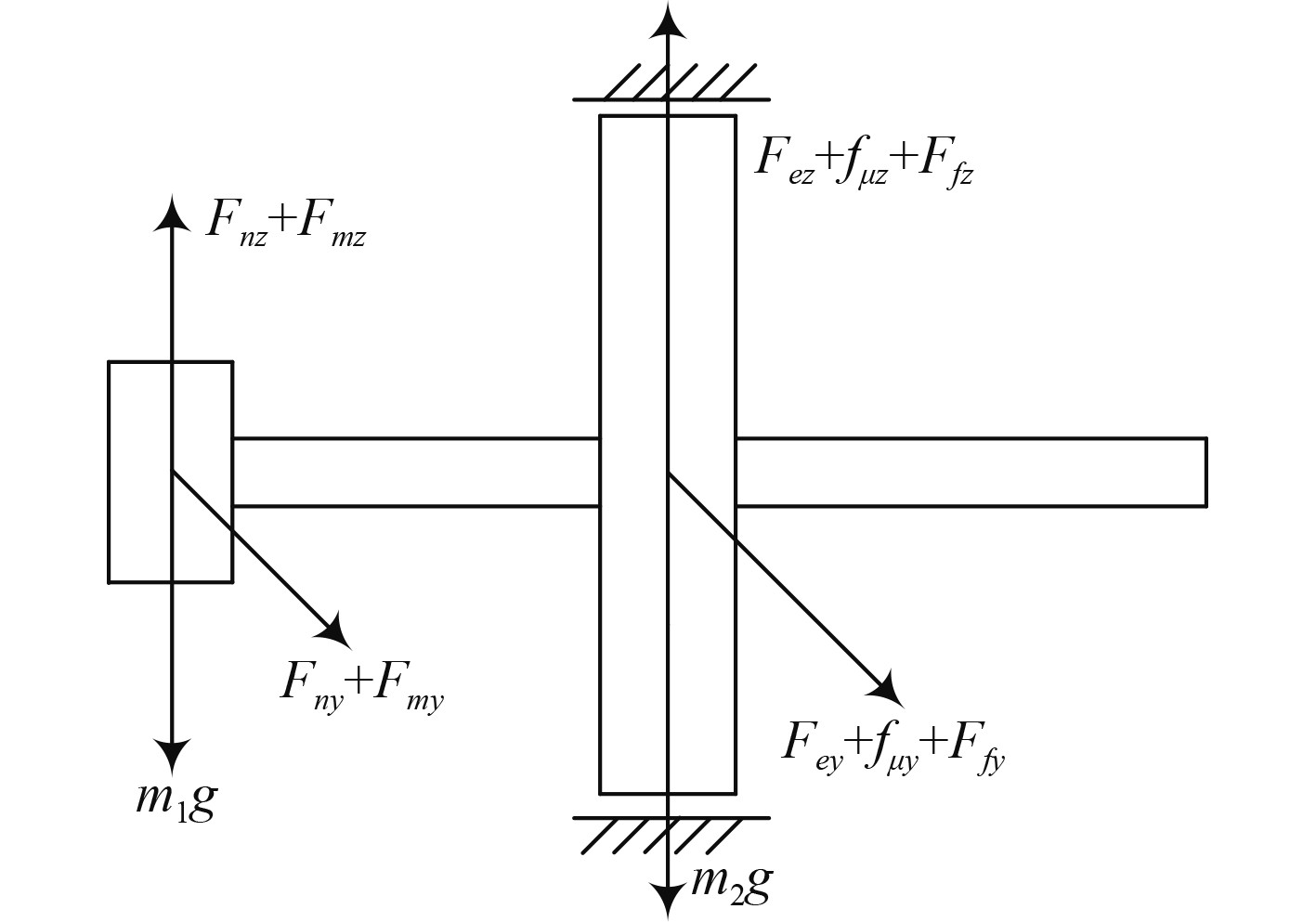
|
图 5 从动轴受力分析 Fig. 5 Stress analysis of driven shaft |
图中:
| $ \left\{ \begin{gathered} {m_1}{{\ddot y}_1} + {D_1}{{\dot y}_1} + {K_1}({y_1} - {y_2}) = {F_{ny}} + {F_{my}},\\ {m_1}{{\ddot z}_1} + {D_1}{{\dot z}_1} + {K_1}({z_1} - {z_2}) = {F_{nz}} + {F_{mz}} - {m_1}g,\\ {m_2}{{\ddot y}_2} + {D_2}{{\dot y}_2} + {K_2}({y_2} - {y_1}) = {F_{ey}} + {f_{\mu y}} + {F_{fy}},\\ {m_2}{{\ddot z}_2} + {D_2}{{\dot z}_2} + {K_2}({z_2} - {z_1}) = {F_{ez}} + {f_{\mu z}} + {F_{fz}} - {m_2}g。\\ \end{gathered} \right. $ | (28) |
由式(28)可以看出油膜力
为发现与识别偏斜轴系的振动特征,采用龙格-库塔法对微分方程组进行求解。取转子参数m1=1 kg,m2=2 kg,D1=D2=100 N·s/m,K1=K2=7×105 N/m,IR=0.02 kg·m2,ck=0.001,cz=2×10−6,b=0.001,n=2,f=0.06,kc=1×107,ka=4×105,µ=0.052,R=0.0205,L=0.003。
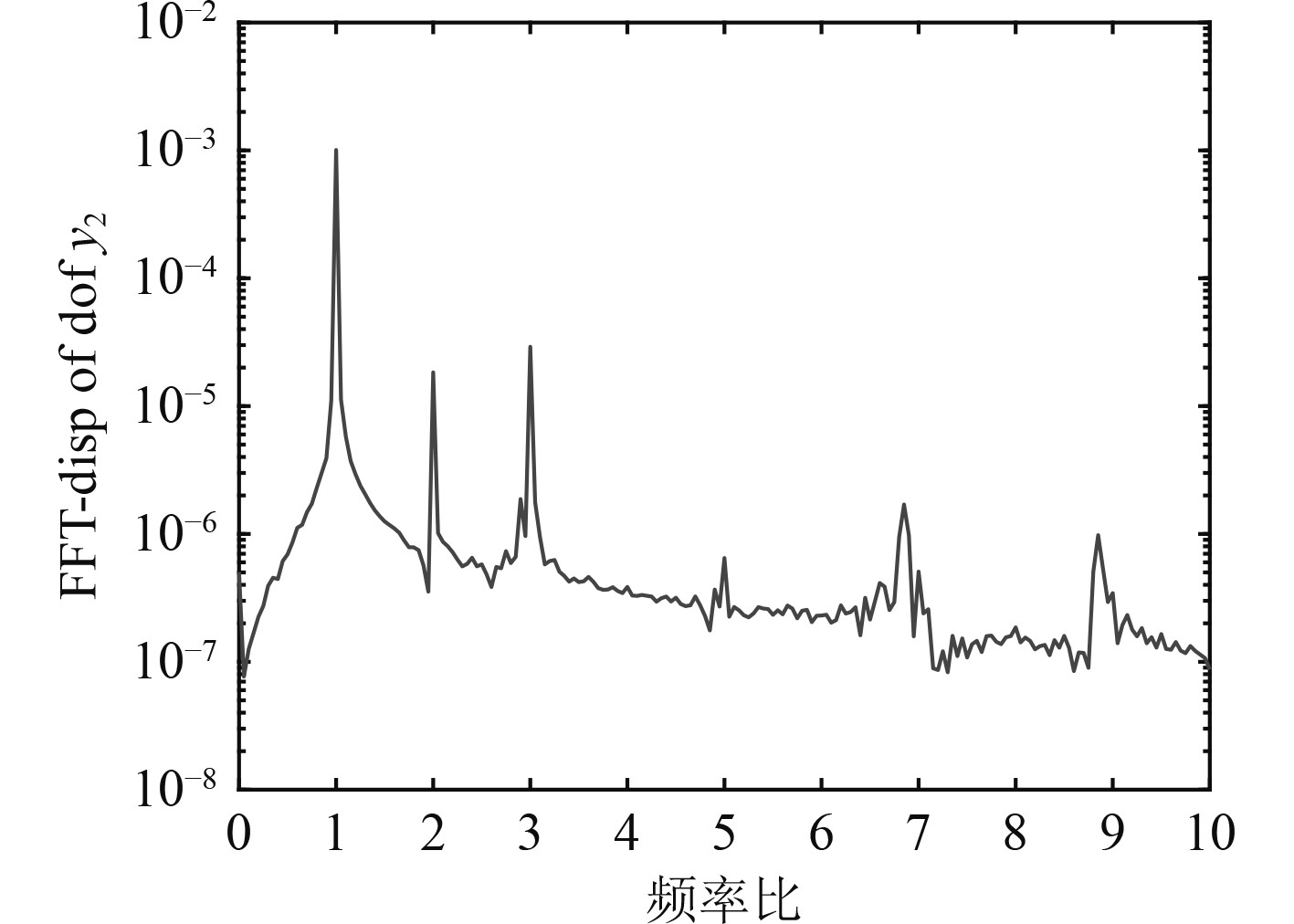
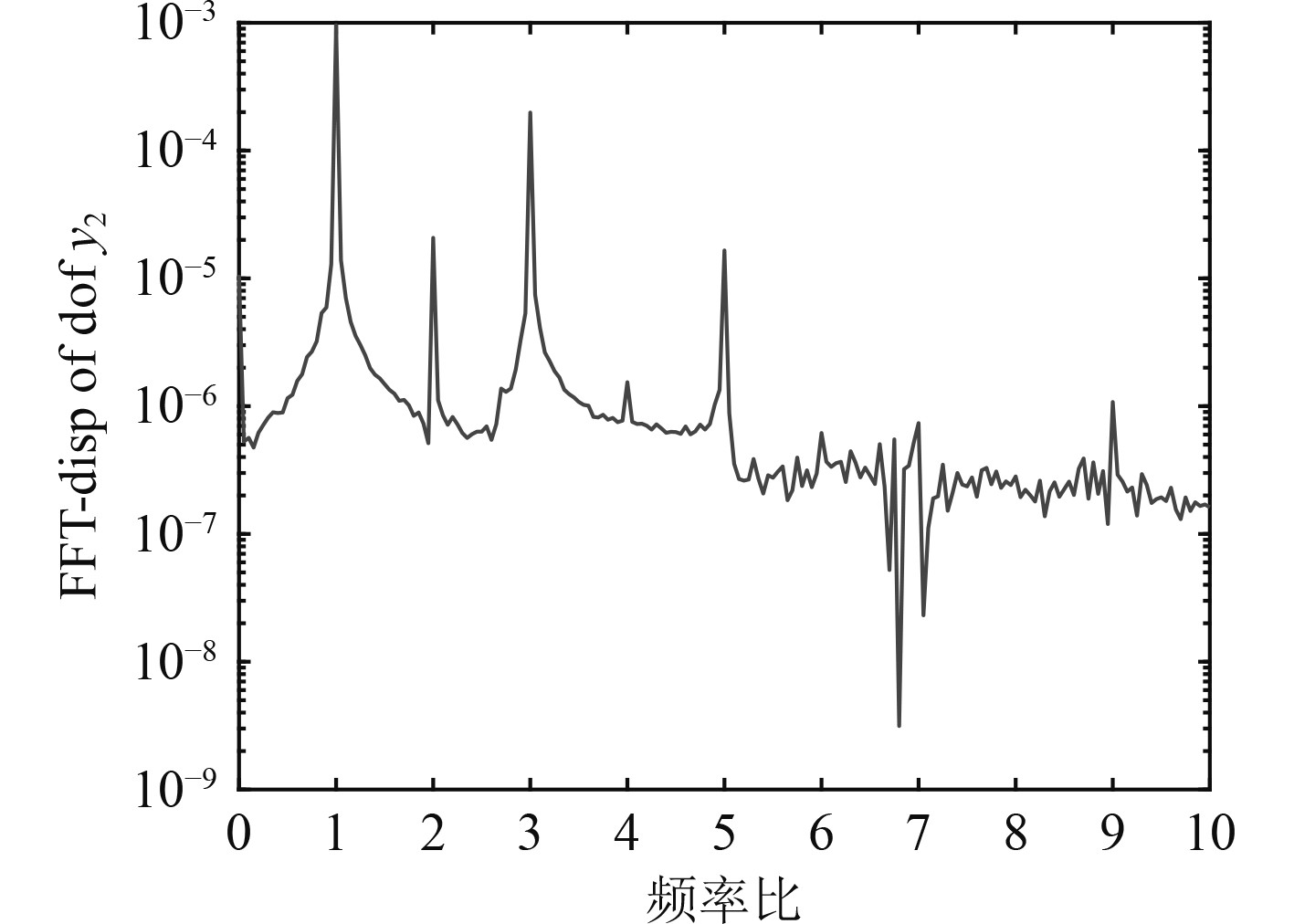
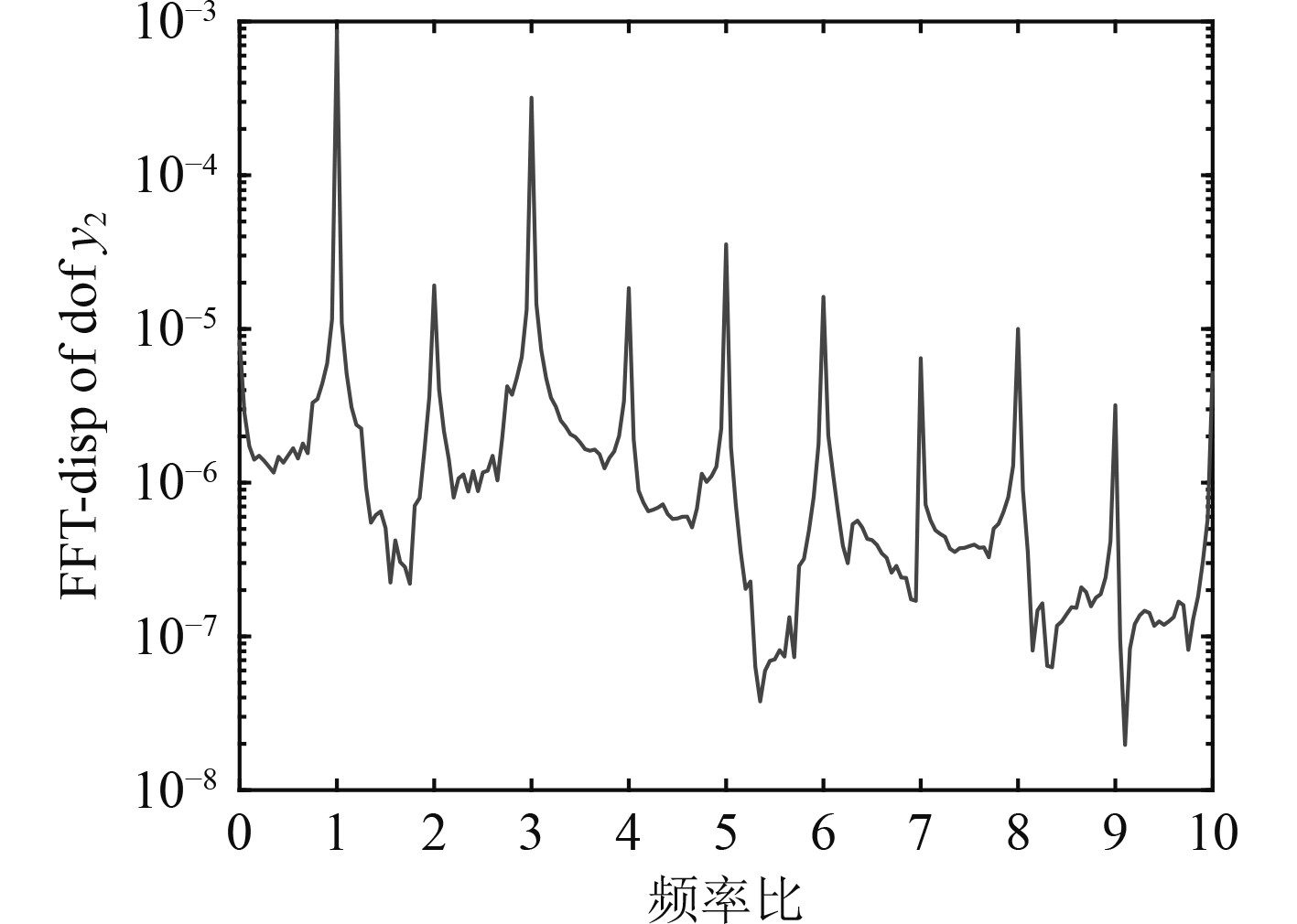
3.1 偏角不对中量对系统响应的影响当只考虑偏斜因素中的偏角不对中时,通过仿真计算得到包含耦合非线性因素的系统响应,图6~图8为偏角不对中量
|
图 6 频谱(α=0.5°) Fig. 6 Spectrum(α=0.5°) |
|
图 7 频谱(α=1.5°) Fig. 7 Spectrum(α=1.5°) |
|
图 8 频谱(α=2.5°) Fig. 8 Spectrum(α=2.5°) |
对比分析图6~图8可知,在转子系统同时存在不平衡、油膜、碰摩非线性因素时,随着偏角不对中量的增大,1倍频、2倍频基本保持不变,3倍频略有升高,但出现了4倍频、6倍频等新的高频成分,且这些高频成分随着偏角不对中的程度增大而升高。
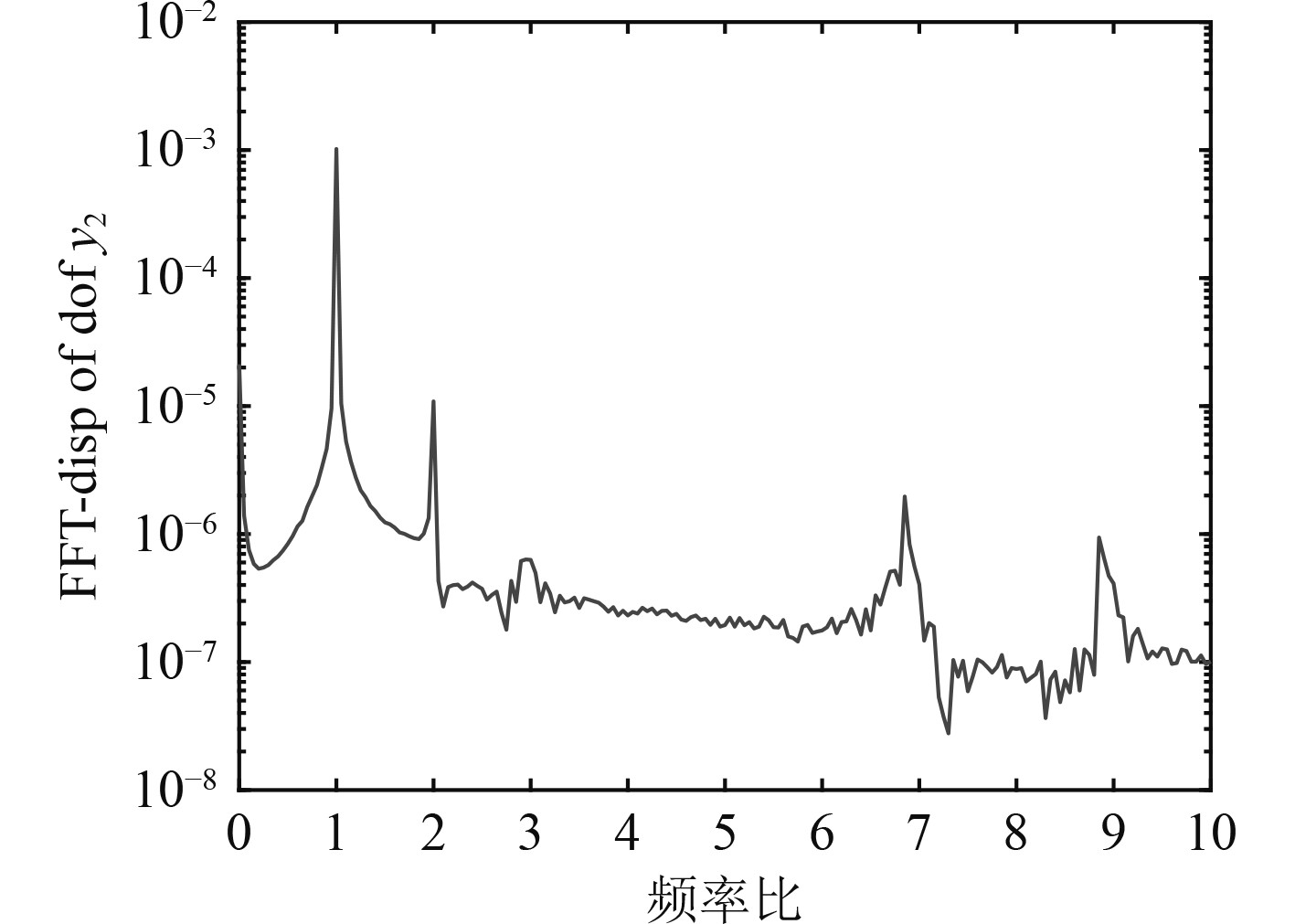
3.2 平行不对中量对系统响应的影响当只考虑偏斜因素中的平行不对中时,图9~图11为平行不对中量
|
图 9 频谱(δ=0.001 m) Fig. 9 Spectrum(δ=0.001 m) |

|
图 10 频谱(δ=0.002 m) Fig. 10 Spectrum(δ=0.002 m) |

|
图 11 频谱(δ=0.003 m) Fig. 11 Spectrum(δ=0.003 m) |
对比分析图9~图11可知,随着平行不对中量的增大,1倍频基本保持不变,3倍频逐渐升高,同时出现了4倍频、5倍频等新的倍频。
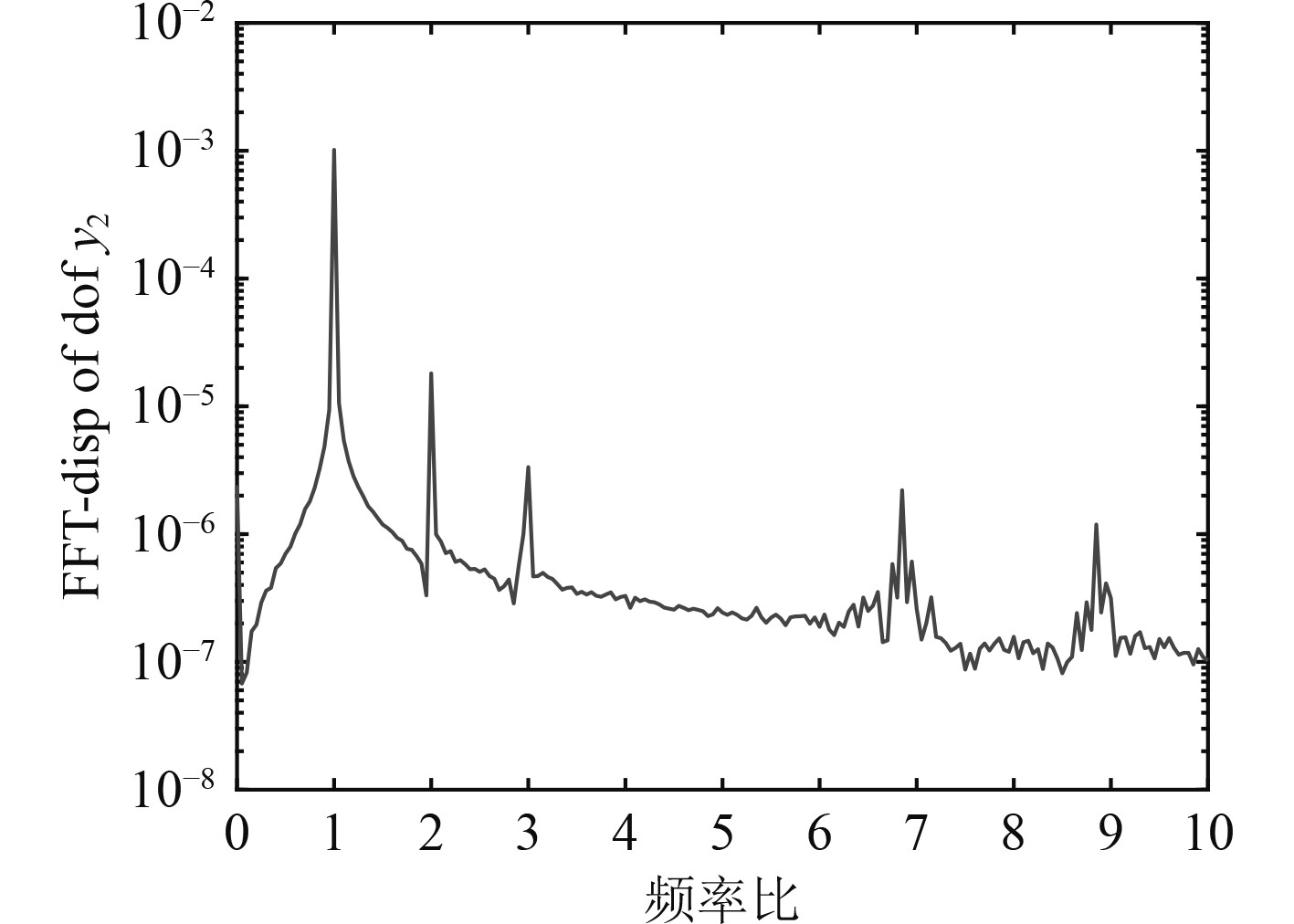
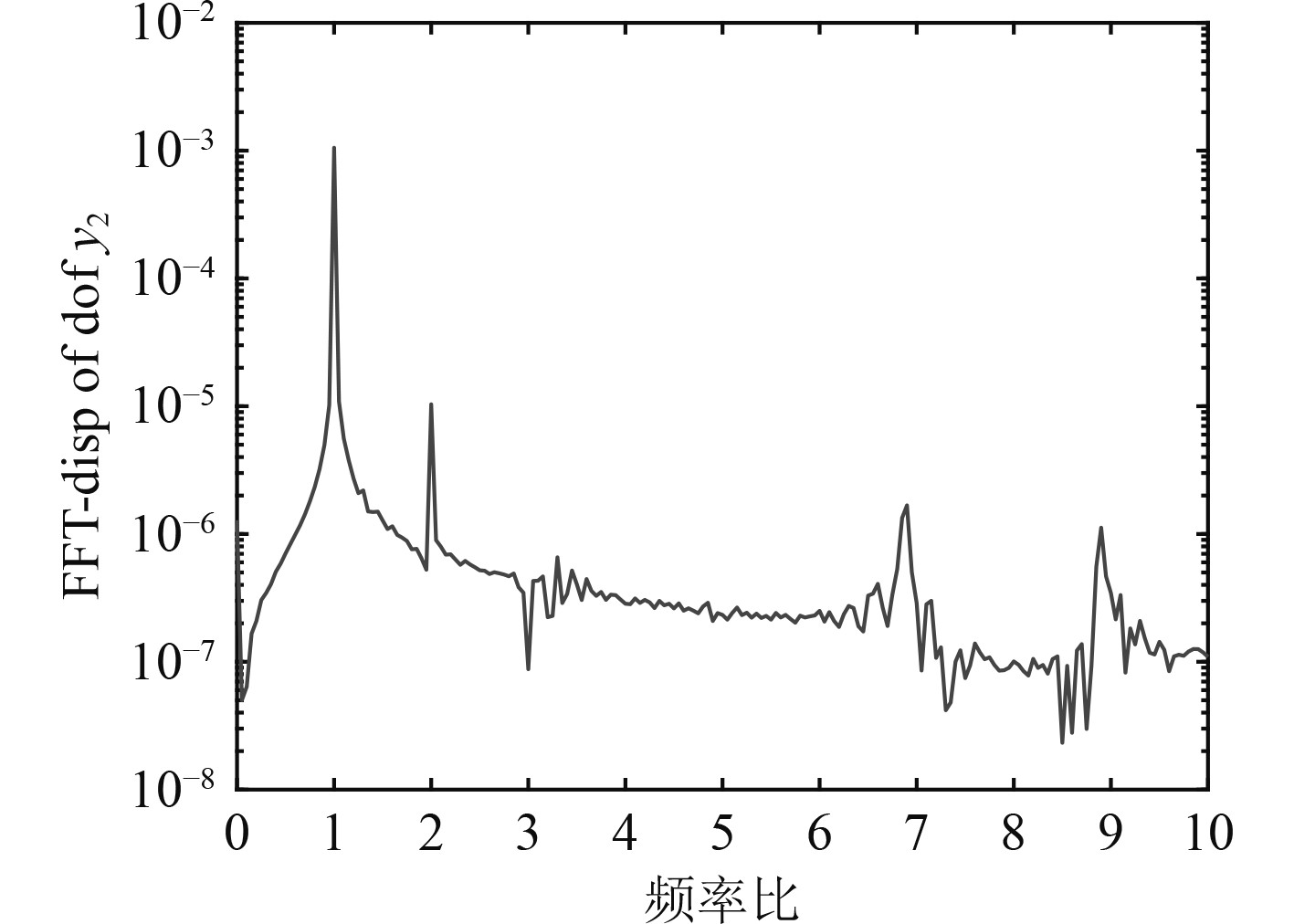
3.3 不平衡量对系统响应的影响为在仿真角度分析处于多种非线性耦合因素下,偏斜因素是否对动平衡有干扰,剔除偏斜因素后,将不平衡量作为变量。分别取
观察图12~图14可知,在非线性因素耦合下,改变不平衡的量主要会影响3倍频与4倍频,同样偏斜也会影响这些倍频,证明偏斜会对动平衡产生影响。
|
图 12 频谱(r=0.004 m) Fig. 12 Spectrum(r=0.004 m) |
|
图 13 频谱(r=0.006 m) Fig. 13 Spectrum(r=0.006 m) |

|
图 14 频谱(r=0.01 m) Fig. 14 Spectrum(r=0.01 m) |
取偏角不对中量
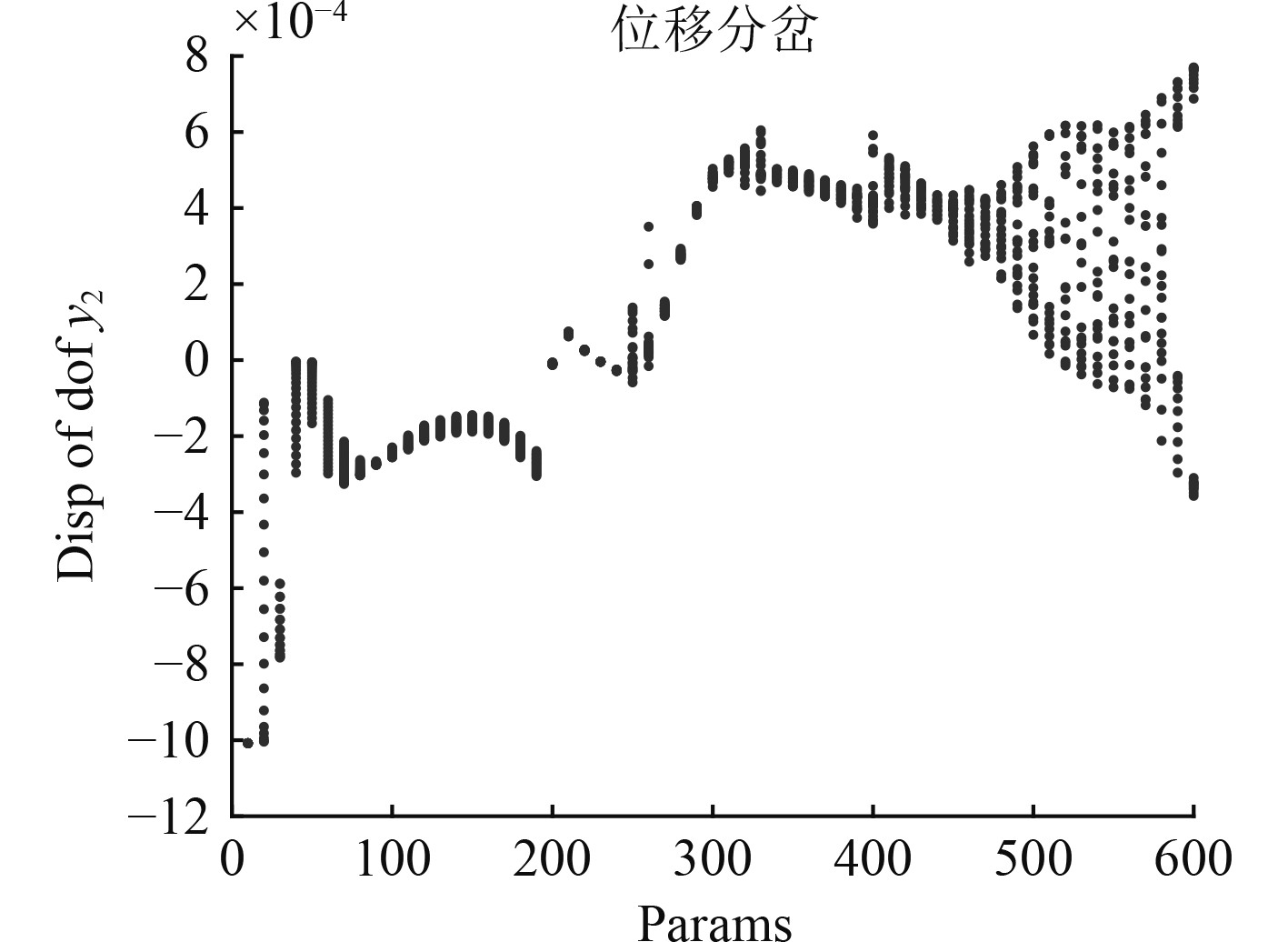
|
图 15 α=2.5°,δ=0.01 m转速分岔图 Fig. 15 α=2.5°, δ=0.01 m Speed bifurcation diagram |
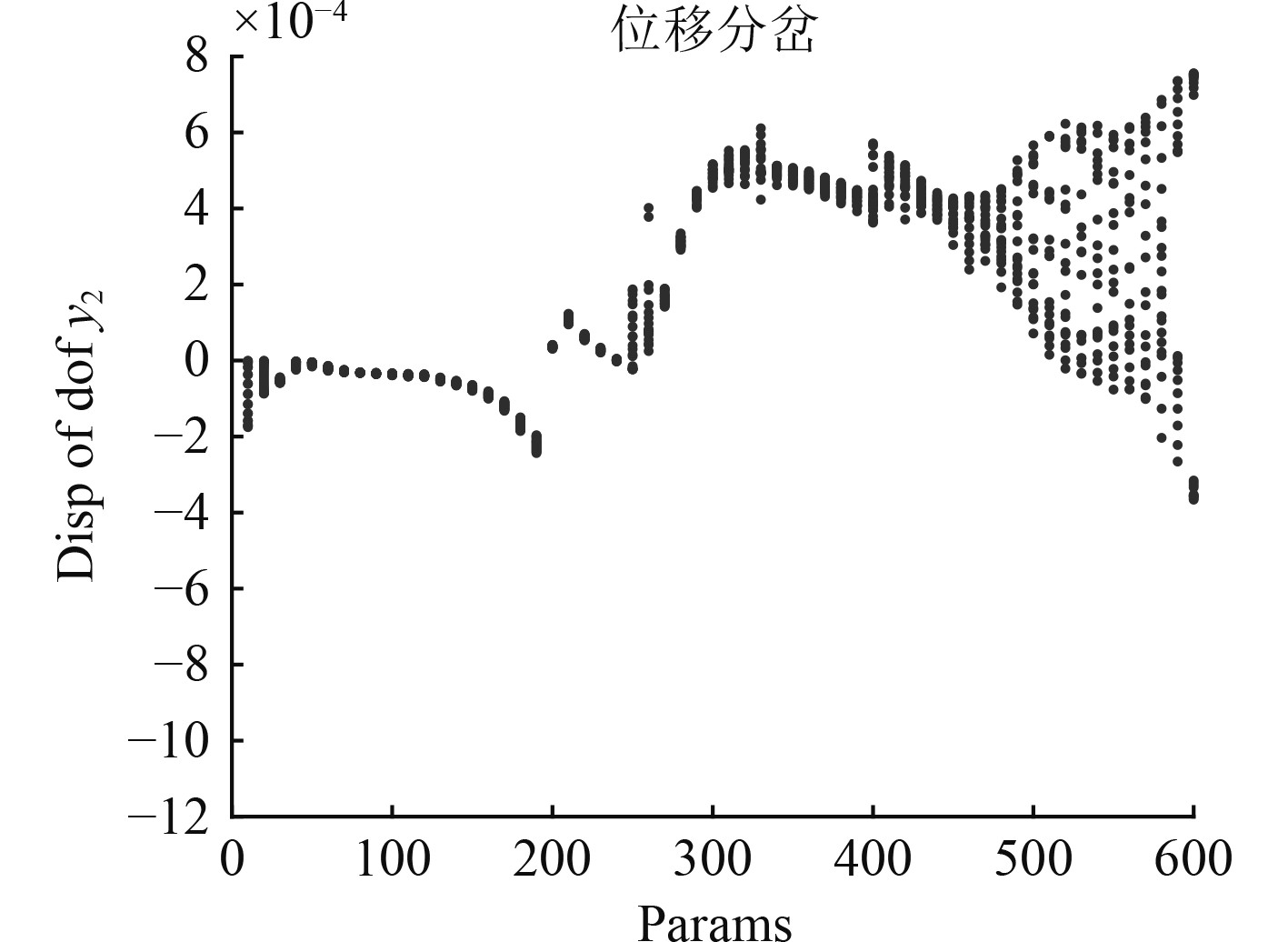
|
图 16 α=2.5°,δ=0.001 m转速分岔图 Fig. 16 α=2.5°, δ=0.001 m Speed bifurcation diagram |
可以看出,在转速区间[50,300 rad/s] ,系统为周期运动。在转速200 rad/s处,振幅发生突变,大小接近于0,此时系统并未发生碰摩,且低速不会发生油膜振荡,可以判断出是偏角不对中使振幅发生突变。以上分析可以得出,在耦合条件下,提高转速或者提升平行不对中量有时会降低振幅,但不能认定其为偏斜的减振效果,更不能在此状态下进行动平衡,因为继续提高转速会使系统进入概周期振动与混沌振动等复杂振动。
为继续探究偏角不对中对系统的影响,在平行不对中量
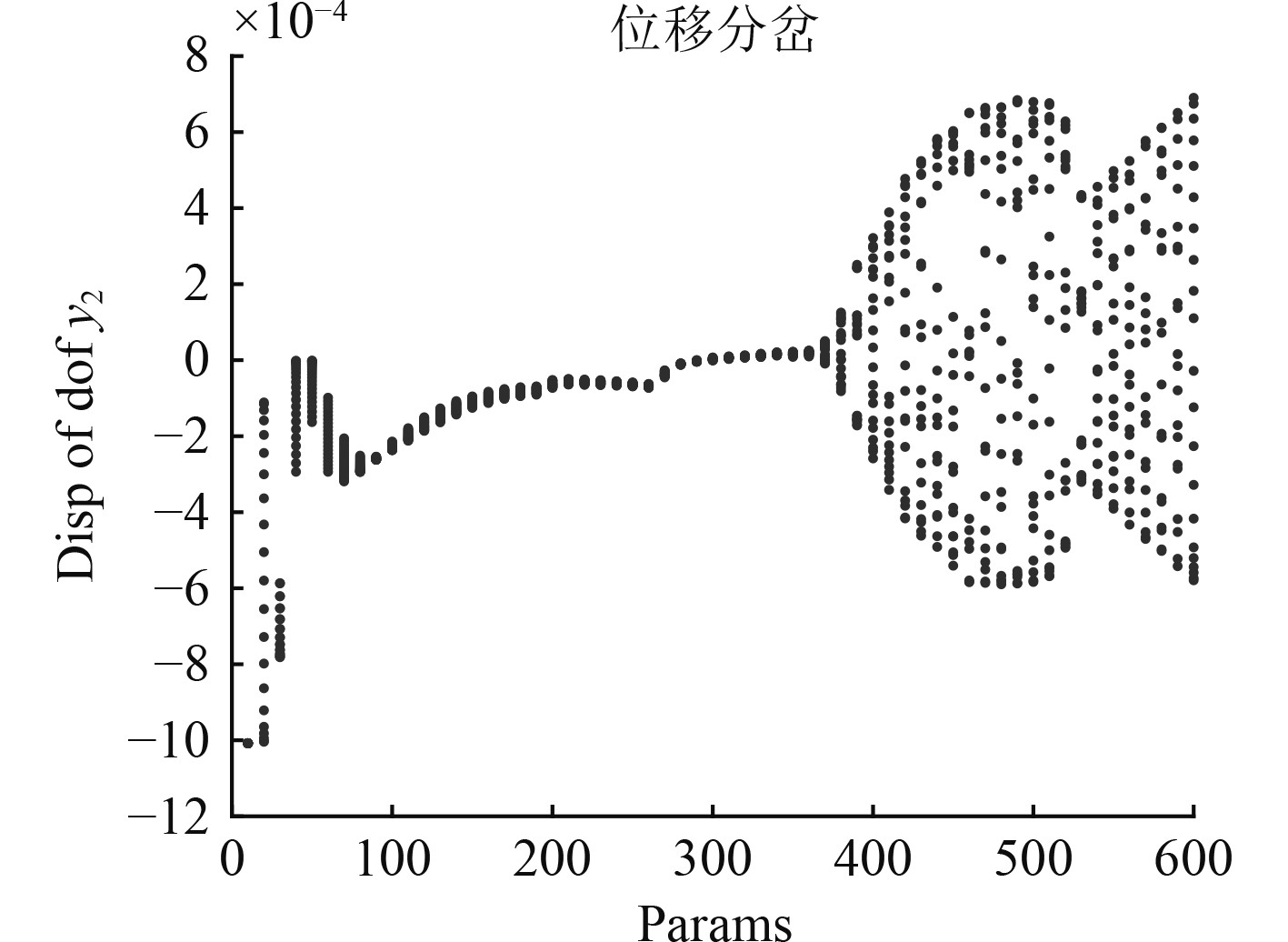
|
图 17 α=0.5°,δ=0.01 m转速分岔图 Fig. 17 α=0.5°, δ=0.01 m Speed bifurcation diagram |
1)在耦合因素下,除了基频外,改变不平衡量也会影响3倍频与4倍频,这与改变偏斜量所影响的倍频相似,所以不对中对动平衡的控制有影响。
2)在低转速范围内,提高转速或者提升偏斜量有时会降低系统振幅,但继续提高转速会使系统进入混沌振动。
| [1] |
钟一谔, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987.
|
| [2] |
王德石, 朱拥勇. 偏斜轴系的振动与稳定性[M]. 武汉: 武汉理工大学出版社, 2020.
|
| [3] |
ADILETTA G, GUIDO A R, ROSSI C. Chaotic motions of a rigid rotor in short journal bearings[J]. Nonlinear Dynamics, 1996, 10(3).
|
| [4] |
陈宏, 张晓伟, 李小彭, 等. 不对称润滑对碰摩转子-轴承系统的动力学影响[J]. 振动、测试与诊断, 2005(1): 13-16+70. DOI:10.3969/j.issn.1004-6801.2005.01.004 |
| [5] |
黄志伟, 周建中, 贺徽, 等. 不平衡磁拉力作用下裂纹转子系统的分岔[J]. 机械工程学报, 2011, 47(13): 59-64. |
| [6] |
JOHN P. Shaft alignment handbook(third edition)[M], New York: CRC Press, 2006.
|
| [7] |
黄典贵. 轴系扭振监测系统及几种典型故障的扭振特征研究[D]. 北京: 清华大学, 1994.
|
| [8] |
李明. 平行不对中转子系统的非线性动力学行为[J]. 机械强度, 2005(5): 580-585. DOI:10.3321/j.issn:1001-9669.2005.05.005 |
| [9] |
AGNIESZKA M. Rotordynamics[M]. CRC Press: 2005-05-20.
|
| [10] |
韩捷. 齿式联接转子系统的对中故障机理与识别[J]. 振动. 测试与诊断, 1997(02): 22-26. |
| [11] |
TEJAS H P, ASHISH K D. Experimental investigations on vibration response of misaligned rotors[J]. Mechanical Systems and Signal Processing, 2009, 23(7).
|
| [12] |
虞烈. 轴承-转子系统的稳定性与振动控制研究[D]. 西安: 西安交通大学, 1987.
|
| [13] |
李明, 姜培林, 虞烈. 转子齿轮联轴器系统振动研究[J]. 机械工程学报, 1998, 34(3): 39-45. DOI:10.3321/j.issn:0577-6686.1998.03.007 |
| [14] |
周奇郑, 王德石, 张恺. 加速过程偏角不对中轴系横向振动特性研究[J]. 动力学与控制学报, 2014, 12(4): 315-320. DOI:10.6052/1672-6553-2013-082 |
| [15] |
韩捷, 石来德. 转子系统齿式联接不对中故障的运动学机理研究[J]. 振动工程学报, 2004(4): 44-48. DOI:10.3969/j.issn.1004-4523.2004.04.009 |
| [16] |
李明. 转角不对中故障的转子系统非线性动力学特征[J]. 振动、测试与诊断, 2011, 31(5): 552-556+660-661. |
| [17] |
安学利, 周建中, 向秀桥, 等. 刚性联接平行不对中转子系统振动特性[J]. 中国电机工程学报, 2008(11): 77-81. DOI:10.3321/j.issn:0258-8013.2008.11.014 |
| [18] |
付波, 周建中, 彭兵, 等. 固定式刚性联轴器不对中弯扭耦合振动特性[J]. 华中科技大学学报(自然科学版), 2007(4): 96-99. DOI:10.13245/j.hust.2007.04.029 |
| [19] |
XU M, MARANGONI R D. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, part i: theoretical model and analysis[J]. Academic Press, 1994, 176(5).
|
 2022, Vol. 44
2022, Vol. 44
