2. 浙江理工大学 机械与自动控制学院,浙江 杭州 310018;
3. 浙江工业大学 信息工程学院,浙江 杭州 310023
2. School of Mechanical Engineering and Automation, Zhejiang SCI-TECH University, Hangzhou 311118, China;
3. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China
在船舶动力装置中,柴油机是最为重要的机械设备,柴油机的转速由车令信号设定,在受到外部干扰时产生波动,柴油机调速系统能根据负载变化自动调节喷油量,使柴油机保持在给定转速上稳定工作,柴油机调速性能的好坏,直接关系到船舶营运的安全性和经济性。目前,在船舶柴油机转速控制系统中,普遍采用的是PID控制器,该控制算法结构简单且易于实现,但随着运行时间累积和工况的变化,控制系统参数将发生改变,由于常规PID控制缺乏对未知干扰的处理能力,控制性能将大大降低,为获取良好的动态和静态性能,只能通过不断调整PID参数,以满足实际系统的需要。
近年来,关于柴油机转速PID控制参数自整定算法的研究,丁连生[1]、顾林林[2] 等提出柴油机转速采用模糊PID控制算法,模糊控制不依赖于控制系统的数学模型,利用专家的先知经验、表述知识转换成“模糊规则”,在线整定PID参数,通过仿真获得了良好的控制效果,但该方法缺乏在线自学习能力,不能自动生成调整模糊控制器的隶属函数和模糊规则。石勇[3]、胡松[4] 等将神经网络PID控制算法应用到柴油机转速控制上,仿真分析表明神经网络 PID 控制响应快、超调小,神经网络对外部环境变化有极强的自学习能力,但该方法难以直观了解,也很难做修改。本文提出船舶柴油机转速模糊神经网络PID控制算法,在常规PID控制器基础上,融合模糊控制系统推理自然语言表达的优点和神经网络自学习、自适应的特点,优势互补,提高整个系统对知识的学习和表达能力,提升柴油机转速控制系统的精度和稳定性。
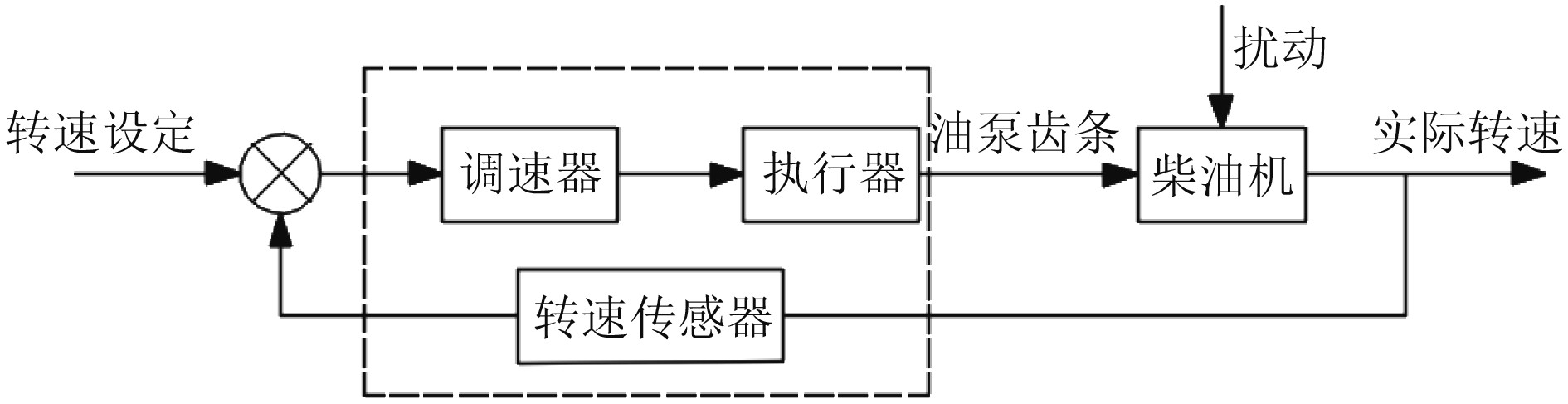
1 柴油机转速控制系统建模柴油机转速控制系统如图1所示,调速器根据转速偏差,计算控制量,通过执行器驱动高压油泵齿条,改变供油量,使其与外部负荷变化相适应,从而使柴油机的转速保持在给定的范围内。
|
图 1 柴油机转速控制系统结构图 Fig. 1 Structure diagram of diesel engine speed control system |
在平衡工况下,柴油机的输出力矩M等于摩擦力矩Mf与曲轴负荷力矩Mt之和,当运行状况或负载发生变化时,力矩平衡被破坏,按小偏差线性化方法得到柴油机轴系的运动方程[2, 5]:
| $ J\dfrac{{{\rm{d}}\left( {\Delta \omega } \right)}}{{{\rm{d}}t}} = \Delta M - \Delta {M_{{f}}} - \Delta {M_{{t}}}{\text{。}} $ | (1) |
式中:J为柴油机机组转化至曲轴处的转动惯量;ω为曲轴角速度。
1.1 柴油机数学模型在平衡工况下,柴油机的负荷不变,只考虑油泵齿条位置的作用,式(1)经进一步计算推理后,得到柴油机的运动方程为:
| $ {T_{{a}}}\dfrac{{{\rm{d}}y(t)}}{{{\rm{d}}t}} + {T_g}y(t) = {K_\eta }\eta (t)。$ | (2) |
式中:y(t)为柴油机输出转速,η(t)为油泵齿条位移,两者都是时间t的函数;Ta为柴油机加速时间常数,表征柴油机在空载状态下,给定额定喷油量时,柴油机转速从零增加到额定转速所需要的时间;Tg为自稳系数,表示柴油机的转速自动平衡能力;Kη为柴油机动态特性参数,表示柴油机油泵齿条位置的变化对柴油机曲轴转矩输出的影响因子。
对式(2)进行拉普拉斯变换,得到柴油机转速对喷油泵齿条位移的传递函数为:
| $ {G_d}(s) = \dfrac{{Y(s)}}{{\eta (s)}} = \dfrac{{{K_\eta }}}{{{T_a}s + {T_g}}},$ | (3) |
在柴油机实际运行过程中,由于燃油喷射系统的容积惯性、燃烧室的热惯性等因素使柴油机动态过程产生迟延,纯迟延环节的传递函数为:
| $ {G_\tau }(s) = {e^{ - \tau s}} 。$ | (4) |
式中,τ为迟延时间。
柴油机转速控制系统状态变量较多,具有时变非线性、不确定等特点,实践表明,考虑柴油机调速系统整体的输入输出关系,用于控制与仿真分析的柴油机数学模型,经过无量纲化并经线性处理后,可采用一阶惯性延迟环节,令Kη=1,Tg=1,得简化后的柴油机数学模型为[2, 5]:
| $ {G_s}{(s)_{}} = {G_d}(s){G_\tau }(s) = \dfrac{1}{{\left( {{T_a}s + 1} \right)}} \cdot {e^{ - \tau s}} 。$ | (5) |
以宁动G6300ZC型船用柴油机为研究对象,其主要技术规格为:四冲程,缸数为6,缸径300 mm,额定功率Pe=750 kW,额定转速ne=400 r/min。
根据以上柴油机的技术参数,可以计算出柴油机额定角速度
柴油机迟延时间τ与柴油机气缸数z、冲程数和转速n有关,四冲程柴油机可以估算为
所以柴油机的数学模型为:
| $ {G_s}\left( s \right) = \dfrac{1}{{2.86s + 1}}{e^{ - 0.06s}}。$ | (6) |
柴油机转速控制系统采用的是电磁式执行器,它的驱动力为电磁力,控制信号是电流信号,通过改变驱动电流的脉宽周期占空比达到控制喷油泵齿条位移的目的,是典型的一阶惯性环节,传递函数[7]为:
| $ {G_z}(s) = \dfrac{{{K_z}}}{{{T_k}s + 1}}。$ | (7) |
式中:Tk电磁执行器的时间常数;Kz为执行器的增益。
通过阶跃响应法计算电磁执行器的无量纲化数学模型:
| $ {G_z}(s) = \dfrac{{0.3}}{{0.1s + 1}} 。$ | (8) |
柴油机模糊神经网络PID控制系统结构如图2所示。控制器包括常规PID控制器[8]和模糊神经网络控制器2个部分,将常规PID控制、模糊控制与神经网络有效结合,神经网络通过训练后可以生成模糊规则和调整隶属函数,具有较强的自学习和自适应能力,控制系统将转速偏差e(t)以及偏差变化率ec(t)传送到模糊神经网络PID控制器中,经过模糊化、模糊推理、反模糊化输出,计算得到对应于柴油机运行工况的3个修正值ΔKp,ΔKi,ΔKd,在线自动调整PID参数Kp,Ki,Kd,使转速控制性能指标最优。

|
图 2 模糊神经网络PID控制系统结构图 Fig. 2 Structure diagram of fuzzy neural network PID control system |
位置式常规PID调节器的输出
| $ u(t) = {K_p}(e(t) + \dfrac{1}{{{T_i}}}\int_0^t {e(t)} {\rm{d}}t + {T_d}\dfrac{{{\rm{d}}e(t)}}{{{\rm{d}}t}}) ,$ | (9) |
离散化后,算式为:
| $\begin{split} u(k) =\;& {K_p}(e(k) + \dfrac{T}{{{T_i}}}\sum\limits_{n = 0}^k {e(n) + \dfrac{{{T_d}}}{T}(e(k) - e(k - 1))} ),\\ u(k) =\;& {K_p}e(k) + \dfrac{{{K_p}T}}{{{T_i}}}\sum\limits_{n = 0}^k {e(n) + \dfrac{{{K_p}{T_d}}}{T}\left( {e(k) - e(k - 1)} \right)},\\ u(k) =\;& {K_p}e(k) + {K_i}\sum\limits_{n = 0}^k {e(n) + {K_d}\left( {e(k) - e(k - 1)} \right)} 。\\[-20pt] \end{split} $ | (10) |
位置式PID控制算法采用全量输出,转速偏差的累积会引起电磁执行器位置的大幅度变化,故一般采用增量式PID调节控制,其算法为:
| $ \begin{split} \Delta u(k) =\;& {K_p}(e(k) - e(k - 1)) + {K_i}e(k) + \\ & {K_d}(e(k) - 2e(k - 1) + e(k - 2)) 。\\ \end{split} $ | (11) |
式中:Kp,Ki,Kd分别为比例系数、积分系数、微分系数;e(k−2),e(k−1),e(k)分别为控制系统第k−2、第k−1、第k步柴油机转速目标值与实际值之间的偏差。
2.2 神经网络模糊控制算法采用RBF径向基网络设计模糊神经网络控制器[9-10],RBF网络用于非线性系统辨识与控制时,具有唯一最佳逼近的特性,能快速计算校正网络隐藏层和输出层的权值,学习收敛速度快,网络结构简单,逼近效果好,模糊RBF神经网络控制器结构如图3所示。控制器采用二输入三输出4层结构形式,输入量为柴油机转速偏差e(t)和偏差变化率ec(t),输出量为PID控制器的3个参数Kp,Ki,Kd,4层依次是输入层、模糊化层、模糊推理层和输出层。

|
图 3 模糊RBF神经网络结构图 Fig. 3 Structure diagram of Fuzzy RBF neural network |
1)神经网络控制算法
输入层计算公式为:
| $ \left\{\begin{split} &{x_1} = e(t),\\ &{x_2} = ec(t),\\ &{o_1}(i) = [{x_1},{x_2}]。\end{split}\right. $ | (12) |
模糊化层采用高斯隶属函数,计算公式为:
| $ \begin{split}& {o_2}(i,j) = \exp \left({{ - {{[{o_1}(i) - {c_{ij}}]}^2}} \mathord{\left/ {\vphantom {{ - {{[{o_1}(i) - {c_{ij}}]}^2}} {{{({b_{ij}})}^2}}}} \right. } {{{({b_{ij}})}^2}}}\right),\\ &i = 1,2;\;j = 1,2, \cdots ,n 。\end{split} $ | (13) |
式中:cij为隶属函数中心值;bij为函数曲线宽度;n为模糊子集个数。
模糊推理层计算公式为:
| $ \left\{\begin{split} &{o_3}(i) = {o_2}(1,k) \times {o_2}(2,k),\\ &{k}_{1}=1,2\cdots ,5;\;{k}_{2}=1,2,\cdots,5,\\ &i=1,2\cdots,25。\end{split} \right.$ | (14) |
输出层计算公式为:
| $ \left.\begin{split} & {o_4}(i) = \displaystyle\sum\limits_{j = 1}^{25} {{o_3}(j)} \times {\omega _{ij}},\\ &i=1,2\cdots,3。\end{split}\right. $ | (15) |
式中,ωij为权值系数。
输出层输出的PID控制参数为:
| $ {o_4}(1) = {k_p},\;{o_4}(2) = {k_i},\;{o_4}(3) = {k_d}。$ | (16) |
2)网络学习算法
模糊神经网络需要学习训练的参数有隶属函数中心值cij、宽度值bij和权值ωij,定义学习的目标函数为:
| $ E(k) = \dfrac{1}{2}{\left[ {r(k) - y(k)} \right]^2}。$ | (17) |
式中:r(k)和y(k)为每一次网络学习的期望输出和实际输出,r(k)−y(k)为控制误差。
隶属函数中心值、宽度值和权值的学习算法为:
| $ \left\{\begin{split} &{c_{ij}}(k + 1) = {c_{ij}}(k) + \lambda \dfrac{{\partial E(k)}}{{\partial {c_{ij}}(k)}} + \eta \Delta {c_{ij}}(k),\\ &{b_{ij}}(k + 1) = {b_{ij}}(k) + \lambda \dfrac{{\partial E(k)}}{{\partial {b_{ij}}(k)}} + \eta \Delta {b_{ij}}(k),\\ &{\omega _{ij}}(k + 1) = {\omega _{ij}}(k) + \lambda \dfrac{{\partial E(k)}}{{\partial {\omega _{ij}}(k)}} + \eta \Delta {\omega _{ij}}(k)。\end{split}\right. $ | (18) |
式中:k为网络的迭代步骤;λ为学习速率;η为惯性系数。
3 系统仿真和结果分析利用Matlab软件中Simulink模块分别建立传统PID、模糊PID控制的仿真模型,根据柴油机转速控制系统进行参数设置,控制器输入变量e(k)和ec(k)的基本论域为:[−5,5],输出变量Kp,Ki,Kd的基本论域为[−4,4],模糊化量化因子为Ke=0.05,Kec=0.04,清晰化比例因子Up=5,Ui=2.5,Ud=1,涵盖输入变量和输出变量论域的模糊子集选用{NB(负大),NS(负小),ZE(零),PS(正小),PB(正大)},二者搭配共生成25条模糊规则。
采用Ziegler-Nichols 法整定柴油机转速控制系统PID参数的初始值Kp=50.26,Ki=18.54,Kd=3.28,利用Matlab软件对模糊神经网络PID控制系统进行编程仿真分析,设置采样周期为0.01 s,仿真时间为50 s,最大训练次数为500次,得到不同工况下3种控制方式的仿真曲线。
1)启动与调速特性
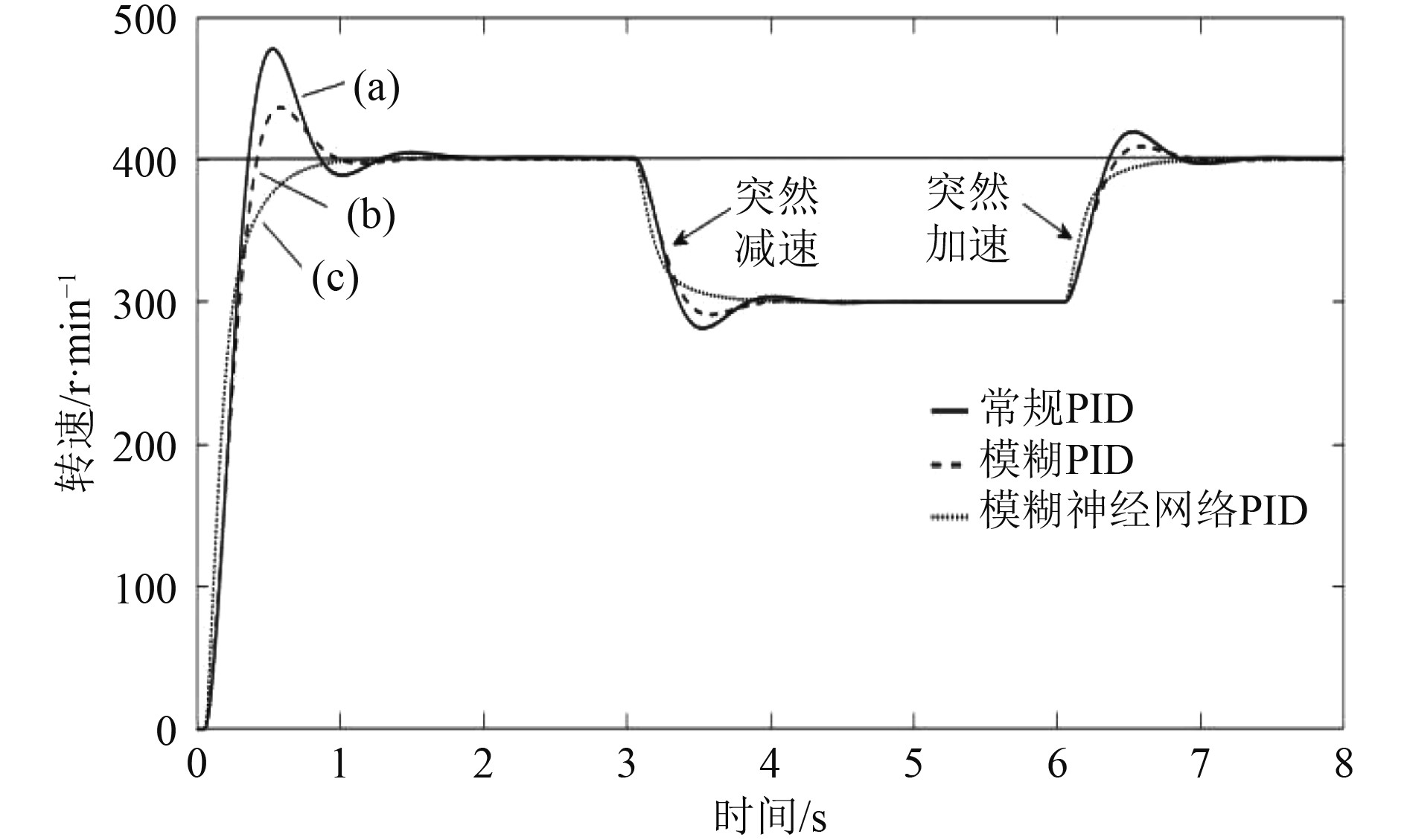
船舶柴油机要求在启动和调速时能够快速并以较小的超调量达到稳定运行状态,输入单位阶跃信号rin(k)=400,稳定后在t=3 s时,突减给定转速为350,t=6 s时,突加给定转速到400,得到如图4所示3种控制方式的响应曲线。
可知:采用传统PID控制方式时,系统超调量达到19.38%,震荡明显,稳定时间2.04 s;采用模糊PID控制方式时,系统超调量下降为9.15%,震荡明显减弱,稳定时间1.46 s。而采用模糊神经网络PID控制方式时,系统超调量接近0,调节过程无震荡,稳定时间仅为1.04 s,启动和调速控制性能都有很大改善。
|
图 4 3种控制方式启动和调速响应曲线 Fig. 4 Response curves of start and speed regulation of three control methods |
2)抗干扰特性
柴油机在实际运行过程中负荷是经常变化的,为验证系统的抗干扰特性,在柴油机稳定运行工况下,在t=10 s时,突加100%负荷,t=13 s时,突减100%负荷,3种控制方式的仿真曲线局部放大图如图5所示。在传统PID控制下,震幅最大,震荡明显,收敛缓慢;在模糊PID控制下,震幅依然较大,震荡有所减缓,收敛加快。而在模糊神经网络PID控制下,仅有小幅震荡,且迅速达到稳定值,系统具有有良好的扰动补偿和抗干扰能力,具有良好的鲁棒性。

|
图 5 负荷突变时3种控制方式的仿真曲线 Fig. 5 Simulation curves on sudden load change of three control methods |
3)自适应特性
船舶柴油机在长时间运行及不同工况运行后,控制系统的参数将发生改变,为了验证控制系统的自适应控制特性,将柴油机转速控制数学模型中的加速时间常数Ta改为3,保持其他参数不变,输入单位阶跃信号rin(k)=400,得到如图6所示3种控制方式的自适应控制仿真曲线。与图4曲线进行比较,传统PID控制方式系统超调量增加了9.8%,稳定时间增加了2.47 s,且有明显震荡;模糊PID控制系统超调量增加了6.33%,稳定时间增加了0.22 s,震荡明显减弱;模糊神经网络PID控制系统超调量为3.8%,调节过程无震荡,稳定时间仅增加0.08 s,具有良好的自适应性能。

|
图 6 3种控制方式的自适应控制仿真曲线 Fig. 6 Simulation curves on adaptive control of three control methods |
本文提出一种模糊神经网络PID控制算法,将该算法应用于船舶柴油机转速控制系统中,基于Matlab/Simulink仿真软件,在不同工况下对柴油机转速控制系统进行仿真分析,通过仿真结果对比表明:
1)在启动和转速突变时,传统PID控制超调量最大,震荡明显,稳定时间最长,模糊PID控制超调量大幅下降,收敛速度加快,稳定时间变短,模糊神经网络PID控制,无超调量无震荡,稳定时间最短,控制效果最佳;
2)在负荷发生突变时,传统PID控制震幅大且震荡明显,模糊PID控制震幅减小,震荡减缓,具有一定的自适应能力,模糊神经网络PID控制震幅几乎为零,能快速达到稳定,受外界扰动的影响小,抗干扰能力强,具有良好的鲁棒性;
3)在系统参数发生改变时,传统PID控制、模糊PID控制无自学习能力,动静态性能均明显变差,模糊神经网络PID控制具有超强自学习能力,能很好适应系统的变化,满足控制系统的要求。
综上,模糊神经网络PID控制算法稳定、快速,对柴油机的时变非线性特性表现出较好的鲁棒性,融合了模糊控制的知识推理优点和神经网络自学习、自适应的特点,可以很好地满足船舶柴油机转速控制系统的各项技术指标要求。
| [1] |
丁连生, 丁洪祥, 等. 柴油机电子调速系统设计及其Matlab仿真[J]. 船海工程, 2005(1): 38-41. DING Lian-sheng, DING rlong-xia, et al. Digital governor for diesel engines based on Matlab[J]. Ship & Ocean Engineering, 2005(1): 38-41. DOI:10.3963/j.issn.1671-7953.2005.01.015 |
| [2] |
顾林林, 张均东. 基于模糊PID控制器的柴油机电子调速器仿真[J]. 大连海事大学报, 2014(1): 57-60. GU Lin-1in, ZHANG Jun-dong. Simulation of diesel engine electronic governor based on fuzzy PID controller[J]. Journal of Dalian Maritime University, 2014(1): 57-60. |
| [3] |
石勇, 齐自达, 等. 船用柴油机齿条位置执行器与转速BP神经网络控制研究[J]. 内燃机工程, 2013, 34(4): 42-47. SHI Yong, QI Zi-da, et al. Research on the control of position actuator and marine diesel engine speed based on BP neural network[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(4): 42-47. DOI:10.13949/j.cnki.nrjgc.2013.04.004 |
| [4] |
胡松, 王贺春, 等. 柴油机BP-PID调速器性能改善研究[J]. 哈尔滨工程大学学报, 2015(12): 1590-1595. HU Song, WANG Hechun1, et al. Performance improvement of a diesel engine speed controller based on BP-PID neural network[J]. Journal of Harbin Engineering University, 2015(12): 1590-1595. DOI:10.11990/jheu.201411056 |
| [5] |
江国和, 刘西全. 柴油机转速智能控制系统仿真[J]. 计算机仿真, 2006(1): 65-67. JIANG Guo-he, LIU Xi-quan. Simulation of intelligent speed control system for diesel engine[J]. Computer Simulation, 2006(1): 65-67. DOI:10.3969/j.issn.1006-9348.2006.01.020 |
| [6] |
腾万庆, 王芝秋. 一种柴油机发电机组的转动惯量估算方法[J]. 内燃机学报, 2010(6): 546-550. TENG Wan-qing, WANG Zhi-qiu. A method for estimating moment of inertia of diesel generator set[J]. Transactions of CSICE, 2010(6): 546-550. DOI:10.16236/j.cnki.nrjxb.2010.06.016 |
| [7] |
花帅, 莫贵情, 等. 基于模糊神经网络PID的发动机调速系统研究[J]. 工业控制计算机, 2016(5): 75-77. HUA Shuai, MO Gui-qing, et al. Research on engine speed control system based on fuzzy neural network PID[J]. Industrial Control Computer, 2016(5): 75-77. DOI:10.3969/j.issn.1001-182X.2016.05.035 |
| [8] |
徐龙, 陈国金, 等. 柴油机共轨压力自适应神经模糊PID控制研究[J]. 机电工程, 2018(2): 213-218. XU long, CHEN Guo-jin, et al. Adaptive neural fuzzy PID control of common-rail pressure for diesel engine[J]. Journal of Mechanical and Elctrical Engineering, 2018(2): 213-218. |
| [9] |
罗泽邦, 辛长范, 夏朋程. 基于模糊神经网络的智能PID控制算法[J]. 海军航空工程学院学报, 2019(5): 430-436. LUO Zebang, XIN Changfan, et al. Intelligent PID control algorithm based on fuzzy neural networ[J]. Journal of Naval Aeronautical and Astronautical University, 2019(5): 430-436. DOI:10.7682/j.issn.1673-1522.2019.05.006 |
| [10] |
赵世海, 韩雪. 基于模糊神经网络PID的焙烘机温度控制[J]. 天津工业大学学报, 2019, 38(4): 83-88. ZHAO Shi-hai, HAN Xue. Temperature control of curing machine based on fuzzy neural network PID[J]. Journal of Tianjin Polytechnic University, 2019, 38(4): 83-88. DOI:10.3969/j.issn.1671-024x.2019.04.014 |
 2022, Vol. 44
2022, Vol. 44

