2. 江苏科技大学 海洋装备研究院,江苏 镇江 212003
2. Marine Equipment and Technology Institute, Jiangsu University of Science and Technology, Zhenjiang 212003, China
推进系统是ROV的重要系统部件,ROV主要进行低速作业机动,其推进器通常选用导管螺旋桨以便获得较好的低速推进性能[1]。为了得到良好的工艺性能和较低的造价,一系列的简易导管螺旋桨方案在消费级领域得到了大量的应用[2],但是其具体性能不明就里,详细的水动力性能鲜有深入的研究。
传统的推进器水动力性能研究主要通过水池实验进行,受到经费和时间等多种因素的影响[3],而数值方法可以克服这些不足。随着计算机性能的提高以及CFD方法的发展,利用计算机求解工程流体问题成本低、周期短、结果数据完整等优点逐渐显现出来,越来越多地应用于工程实践中。势流方法是一种常用的数值模拟方法,计算速度快但在处理一些复杂模型时存在较多困难[4],而粘性CFD方法更加适合复杂几何模型流场的数值模拟。Ehsan Javanmarda等[5]利用CFD方法对一种表面螺旋桨在不同轴角情况下进行了水动力研究;王树齐等[6]进行了自由面条件下水平轴潮流能叶轮水动力研究;Brenden P. Epps等[7]利用CFD方法进行了螺旋桨和叶轮的水动力性能;MAJDFAR S等[8]利用CFD方法进行了导管螺旋桨水动力性能预报;胡健等[9]进行了导管桨水动力特性的数值研究;赵威等[10]进行了前置定子叶片对导管桨水动力特性影响的数值研究;吴家鸣等[11]通过数值模拟方法研究了导管剖面对导管桨水动力特性的影响。以上研究均给出了完整可靠的计算数据,通过对比分析给出了具体的工程应用指导。
本文针对消费级ROV上新出现的平导管螺旋桨推进器,主要在敞水条件下对一系列平导管螺旋桨的流场进行数值模拟,通过对比分析平导管螺旋桨的水动力性能变化,为ROV推进器研制与应用提供参考依据。
1 平导管推进器的数值模拟 1.1 推进器模型的建立所研究的推进器为某型ROV上的平导管螺旋桨,为了达到较好的加工工艺性和布置的便利,采用平的推进器导管,与传统的导管形式有很大不同,图1为其外形图。

|
图 1 平导管推进器外形图 Fig. 1 Outside view of the flat duct propeller |
ROV希望推进器尺度小而推力大,以标准#37导管作为1号模型推进器导管研究的基础,并通过对#37导管进行拉平修改成平导管,建立ROV上使用的2号模型推进器导管,其内外表面均为为直圆柱面,与普通导管相比进行了极大的加工工艺简化,并根据市场上出现的多种平导管推进器形式,对平导管进行了长径比的变化,以便研究导管长度对水动力的影响,从而形成3号、4号模型导管,如图2所示。1号为常用的#37导管,其长径比为0.5,2号模型平导管取同样的长径比为0.5,3号长平导管的长径比参考JD7704导管取为0.65,4号短平导管的长径比缩短同样幅度为0.35。
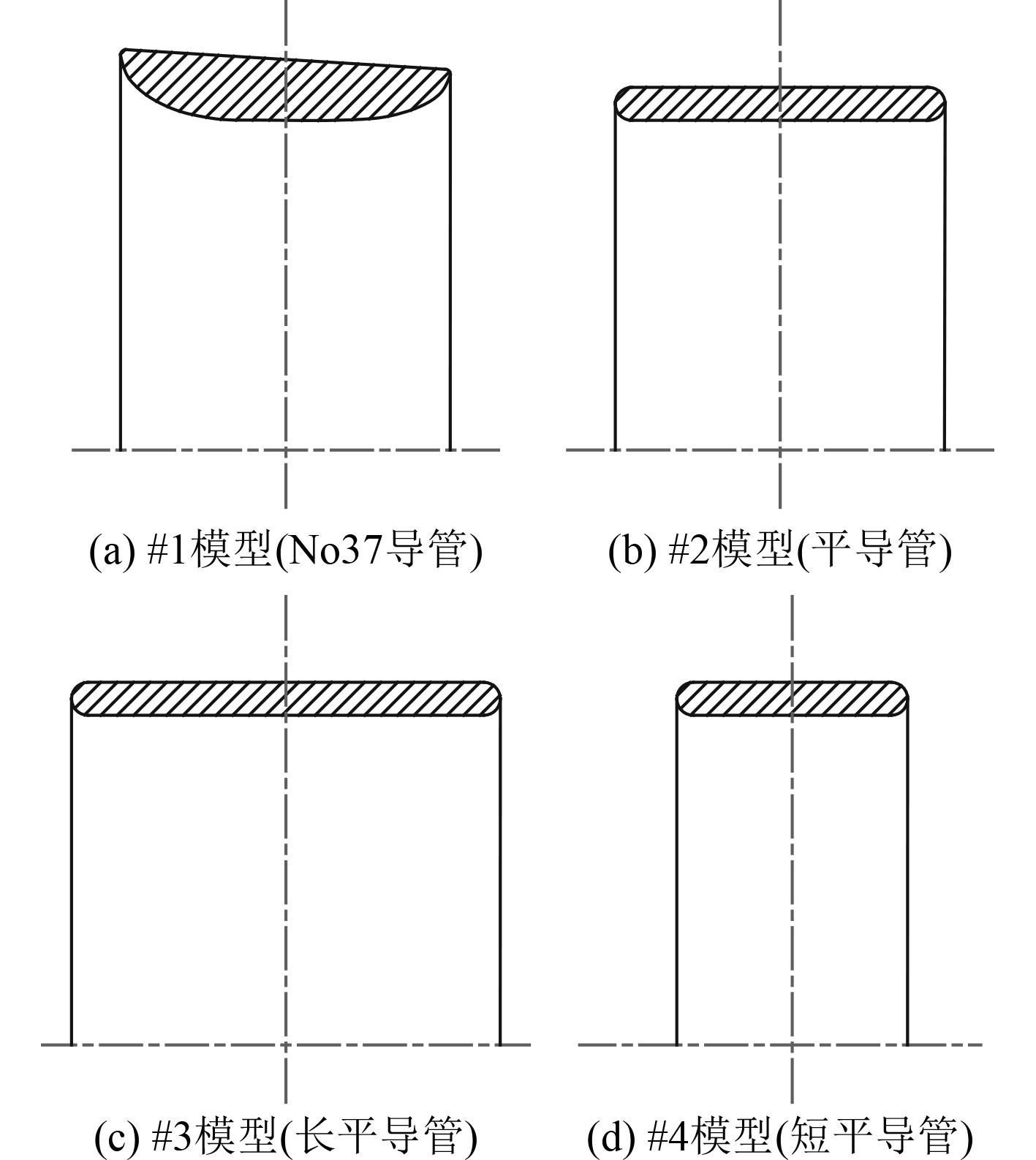
|
图 2 四种计算模型的导管剖面图 Fig. 2 Section plan of the four ducts |
推进器螺旋桨的桨叶参数采用某ROV推进器上配置的Ka4-70导管螺旋桨,直径D为0.235 m,螺距比P/D为1.1。首先将Ka螺旋桨伸张轮廓数据换算成三维空间的数据点[12],然后将各截面上三维数据点导入到三维设计软件SolidWorks中,利用该软件的造型功能得到螺旋桨三维叶片模型,在此基础上分别输入4种导管截面数据点生成各类导管模型,从而得到三维导管螺旋桨实体模型,创建的#1导管螺旋桨实体模型如图3所示。

|
图 3 #1导管螺旋桨三维模型 Fig. 3 3D model of the #1 duct propeller |
将推进器模型置于敞水流场中,考虑到螺旋桨这类旋转机械的特征计算流场取为一个圆柱体,根据目前计算机的运算能力和模型仿真的可靠性,取计算流场外轮廓直径为导管最大外径的8倍,取进流部分长度为5倍导管最大外径,出流部分为10倍导管最大外径。考虑网格划分的需要,把整个域分为中间稍大于推进器的小域和周围的大域,这样可以在划分网格时对该小域进行加密处理,提高计算结果的精确度。
仿真计算精度与网格划分的好坏有密切关系,网格划分过于疏密都会对仿真计算结果产生不利的影响。在网格划分时对中间旋转小域部分进行加密处理,螺旋桨桨叶是空间曲面特别复杂,从螺旋桨表面采用较小的网格尺寸逐步向中间旋转小域和外围大域适当的逐渐增大网格尺寸以形成相对较少的网格总数。这样可以减少仿真计算时的的计算量,同时仿真计算结果也能得到较高的精确度,提高整个仿真效率。建立的网格效果如图4所示。

|
图 4 流场网格划分图 Fig. 4 The flow field mesh division |
进口边界条件设置为速度进口,定速均匀来流,出口边界条件采用自由流动出口,流动出口的速度和压力不定;中部加密的小域选用MRF(moving reference frame)模型,设置为绕轴旋转角速度n为1600 r/min,设定桨叶和桨毂随同小域等速转动,导管则随外大域固定不动,螺旋桨桨叶及桨毂和导管均采用无滑移光滑固壁条件。
2 控制方程与湍流模型选取仿真模拟均匀来流中保持一定转速的导管推进器周围的不可压粘性流场。根据相对运动原理,认为推进器处于静止状态,周围大域水流以恒定速度v相对推进器运动,中间小域的周向上推进器附近的水域还以恒定角速度进行旋转,螺旋桨保持不动,基于雷诺平均的N-S方程包括连续性方程和动量方程为:
| $ \frac{{\partial {u_i}}}{{\partial x{}_i}} = 0,$ | (1) |
| $ \rho \frac{{\partial ({u_i}{u_j})}}{{\partial x{}_i}} = - \frac{{\partial p}}{{\partial x{}_i}} + \rho {g_i} + \rho \frac{\partial }{{\partial x{}_i}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial u{}_j}} + \frac{{\partial {u_j}}}{{\partial x{}_i}} - \overline {{u_i}{u_j}} } \right)} \right]。$ | (2) |
式中:
该方程组还需要湍流特性封闭控制方程组和求解包含湍流动能k和能量扩散
| $ p\frac{{\rm{d}}k}{{\rm{d}}t}=\frac{\partial}{\partial x_i}\left[\left( \mu+\frac{\mu_t}{\sigma_k} \right)\frac{\partial k}{\partial x_i}\right]+G_k+G_b-p\varepsilon+Y_M ,$ | (3) |
| $\begin{split} \rho \frac{{\rm{d}}z}{{\rm{d}}t}=&\frac{\partial}{\partial x_i}\left[\left( \mu+\frac{\mu_t}{\sigma_k} \right)\frac{\partial \epsilon}{\partial x_i}\right]+\rho G_1 s\varepsilon -\\ &\rho c_2\frac{\varepsilon^2}{k+\sqrt{v\varepsilon}}+c_{1\varepsilon}\frac{\varepsilon}{k}C_{3\varepsilon}G_b。\end{split}$ | (4) |
其中:
导管螺旋桨计算仿真通过设定转速1600 r/min不变,改变来流速度的方法来得到各导管桨进速系数J,通常作业型潜水器航行速度较低,最大速度一般在3.5 kn左右,故选取J从0~0.3共4组进速系数进行仿真,其相应航速为0~1.88 m/s。根据电脑运算能力进行试算和调整,桨叶表面网格尺寸取到0.5%导管外径时,仿真数据表明模型1的模拟数据和实验值之间的符合程度较好,表1给出了#1模型和实验值的推力及转矩的相关数据结果,对比整理得到图表计算数据,可以发现推力及转矩的最大误差分别不超过5.97%和7.98%,表明文中CFD计算方法的有效性。
|
|
表 1 #1模型仿真与实验值推力、转矩表 Tab.1 The #1 model thrust and toque table of simulation and experiment |
采用前述的计算方法和参数,对#2,#3,#4模型进行相同的数值计算,得到几种平导管推进器的水动力性能,与#1模型的的数值对比如表2所示。经过对比可以发现,各类平导管的应用都使得推力有不同程度的下降,#2平导管推进器系柱推力比#1No37导管推进器降低6.18%,随着进速的提高推力降低幅度更大,#3推进器采用长平导管推力降幅变化不大,说明加长导管没有作用,#4号推进器采用短平导管,推力降幅有所加大,但是随着进数的提高降幅与#1推进器趋于一致。
|
|
表 2 #1,#2,#3,#4模型推力对比表 Tab.2 The #1, #2, #3, #4 model thrust table |
综合分析可以发现,平导管的采用使得导管推进器的推力下降,进速越大推力下降越大,说明平导管更加不适合应用于高速场合,在低速场合可以综合推力和价格进行权衡。平导管的长度对推力的影响不大,如果布置空间有限也可以采用短平导管推进器。
CFD方法的优势是可以计算得到丰富完整的流场信息,从而可以对导管螺旋桨展开各方面的性能研究,除了可以得到各组模型整体的推进性能,还可以分别得到导管和桨叶对应的推进数据,从而深入对比分析它们对推进性能的影响,表3为#1,#2模型的导管与桨叶数值模拟计算所得的推力T对比表。
|
|
表 3 #1,#2模型导管与桨叶推力对比表 Tab.3 The #1,#2 model thrust table of duct and nuzzle |
数据分析对比发现,#1模型的No37导管在低进速时有较大的推力贡献,并降低螺旋桨的推力负荷,到高进速时推力贡献减小,螺旋桨在各进速时候的推力负荷比较平衡;#2模型的平导管在各进速段推力贡献都不大,主要推力都由螺旋桨部分贡献,螺旋桨的推力负荷在低速时较大。
图5为No.37+Ka4-70导管螺旋桨的轴向速度分布情况。各进速情况下桨前流速都得到了较大的增速,这对于降低螺旋桨桨叶负荷起到了较大的作用,而导管翼型剖面内外表面速度差在低进速时较大,根据机翼理论能得到较大升力,其轴向分量也即推力随之较大。

|
图 5 No.37+Ka4-70导管螺旋桨轴向速度分布图 Fig. 5 The axial velocity distribution of No.37+Ka4-70 duct propeller |
图6为平导管+Ka4-70导管螺旋桨的轴向速度分布情况。对比图5和图6两组模型轴向速度分布图,可以发现导管内外也有较大的速度差,但是因为相当于机翼的攻角较小无法形成较大的升力,继而由轴向分量形成推力,故所有进速下平导管贡献的推力都比较小,且模型2的平导管的前端轴向速度有一定的的下降,容易形成更大的导管阻力,在工程需要的前提下也可以使用较短的平导管,对推力的影响比较小。

|
图 6 平导管+Ka4-70螺旋桨轴向速度分布图 Fig. 6 The axial velocity distribution of flat duct+Ka4-70 propeller |
1)根据数值计算和实验图谱数据的对比分析,推力及转矩的最大误差分别不超过5.97%和7.98%,表明使用CFD方法在导管螺旋桨水动力性能仿真计算时,各项水动力性能数值的误差较小,可以作为一种可靠的计算预报方法。
2)平导管由于加工工艺上的较大优势,在消费级潜器上应用有较大的成本优势。仿真数值分析表明其低进速时最大推力下降约10%,螺旋桨桨叶的负荷也有一定的提高。但这些性能的下降在低速时相对较小,在一些性能要求不高对成本又比较敏感的场合可以考虑采用此类推进器。
3)平导管推进器的劣势主要是在导管上贡献的推力较小,这是因为其相当于没有攻角的机翼,由机翼升力的轴向分量形成的推进力就比较小,故而平导管的长度对推力的影响不大,工程实际中可以采用较短的平导管,从而进一步形成较小的外部轮廓尺寸,减小对布置空间的要求。
| [1] |
柯力, 刘可峰, 李家旺, 等. 变重心潜器操控性能[J]. 造船技术, 2017, 339(5): 33-36. DOI:10.3969/j.issn.1000-3878.2017.05.008 |
| [2] |
夏添, 刘可峰, 郭乔, 等. 基于FDM的船舶模型强度实验[J]. 工程塑料应用, 2019, 47(9): 121-126. DOI:10.3969/j.issn.1001-3539.2019.09.023 |
| [3] |
ABOLFAZL A, URBAN S, RICKARD E. Bensow. Numerical and experimental analysis of cavitation inception behaviour for high-skewed low-noise propellers[J]. Applied Ocean Research, 2018, 79(4): 197-214. |
| [4] |
王超, 韩康, 孙聪, 等. 船用螺旋桨优化设计与参数分析[J]. 华中科技大学学报(自然科学版), 2020, 48(4): 1-8. DOI:10.13245/j.hust.200418 |
| [5] |
EHSAN J, EHSAN Y, JAVAD A M. Numerical investigation on the effect of shaft inclination angle on hydrodynamic characteristics of a surface-piercing propeller[J]. Applied Ocean Research, 2020, 98(1): 2-16. |
| [6] |
王树齐, 张亮, 徐刚, 等. 自由面条件下水平轴潮流能叶轮水动力研究[J]. 哈尔滨工程大学学报, 2016, 37(10): 1330-1334. DOI:10.11990/jheu.201509007 |
| [7] |
BRENDEN P E, BERNARD T R, RICHARD B M, et al.. A viscous vortex lattice method for analysis of cross-flow propellers and turbines[J]. Renewable Energy, 2019, 143: 1035-1052. DOI:10.1016/j.renene.2019.05.053 |
| [8] |
MAJDFAR S, GHASSEMI H, FOROUZAN H, et al. Hydrodynamic prediction of the ducted propeller by CFD solver[J]. Journal of Marine Science and Technology, 2017, 25(3): 268-275. |
| [9] |
胡健, 王楠, 胡洋. 导管桨水动力特性的数值研究[J]. 哈尔滨工程大学学报, 2017, 38(6): 815-821. DOI:10.11990/jheu.201603045 |
| [10] |
赵威, 刘敏, 彭旭, 等. 前置定子叶片周向弯曲对导管桨非定常特性的影响[J]. 中国造船, 2018, 226(2): 24-32. DOI:10.3969/j.issn.1000-4882.2018.02.003 |
| [11] |
吴家鸣, 廖贯宇, 赖宇锋, 等. 导管剖面设计对导管螺旋桨水动力特性的影响[J]. 舰船科学技术, 2017, 39(11): 38-43. DOI:10.3404/j.issn.1672-7649.2017.11.008 |
| [12] |
刘勇杰, 徐青, 胡勇, 等. 基于CATIA的船用螺旋桨三维建模方法[J]. 船海工程, 2018, 47(4): 84-87. DOI:10.3963/j.issn.1671-7953.2018.04.020 |
 2022, Vol. 44
2022, Vol. 44
