在水下机器人的研究中,路径规划技术是一个核心的关键因素。最简单的路径规划问题可做如下描述:给定起始点位置S以及水下机器人的方位角、目标G的位置和方位、障碍物的位置,寻找一条从S到G的无碰并且满足目标方位的路径。
目前可用于水下机器人路径规划的算法有很多,人工势场法是其中出现较早的算法,应用时间长,但人工势场法在障碍物附近时容易出现震荡和陷入局部最优。粒子群算法和遗传算法是近年来出现的群体智能算法,但是粒子群算法容易早熟,遗传算法参数多、计算量大,且这2种算法都容易陷入局部最优。而蚁群算法因具有并行性、强鲁棒性、高可结合性等优点而在路径规划问题中具有广泛运用,蚁群算法最早成功应用于解决著名的TSP(travelling salesman problem)问题。此后,WANG[1]成功将蚁群算法应用于水下机器人的全局路径规划中,在保持较高算法效率的同时得到了平滑度高的最优路径。但是蚁群算法在面对空间较大的环境时,路径搜索效率偏低,还容易陷入局部最优,也很难处理动态实时规划问题[2-3]。
为了解决基本蚁群算法存在的不足,Gambardella等[4]在1995年提出Ant-Q 蚁群算法。此算法在基本蚁群算法的基础上引入当前最优的反馈信息,使算法收敛速度得到很大提升,但还是存在容易陷入局部最优的问题。Porta等[5]提出一种用于AUV路径规划的混合ACO算法SACO,该算法引入模糊推理和记忆系统,将算法效率提升了10倍。Zhang 等[6]为了避免局部最优,引入惩罚因子来保持AUV在运动过程中和障碍物保持安全距离,满足避碰要求。李理等[7]提出一种多启发因素改进蚁群算法,结合路径长度、转弯次数等多项指标对启发函数做出改进,达到了更好的全局优化能力,但算法收敛较慢,路径平滑度也不足。
本文针对基本蚁群算法搜索速度慢、容易陷入局部最优等问题,提出一种改进蚁群算法AW_ACO算法,改进算法引入A*算法作为新的初始路径搜索策略提高初始解的质量,加快搜索速度;针对特殊环境下算法容易陷入局部最优的问题做出优化,同时提出新的启发函数和信息素更新方法,从而在提高算法收敛速度的同时又尽量避免陷入局部最优。
1 环境建模水下机器人在进行路径规划前,需要对环境信息进行抽象化处理,构建相应的数学模型,这就是环境建模,环境建模的方法有维诺图、可视图等多种方法,本文使用的环境建模方法是栅格法。
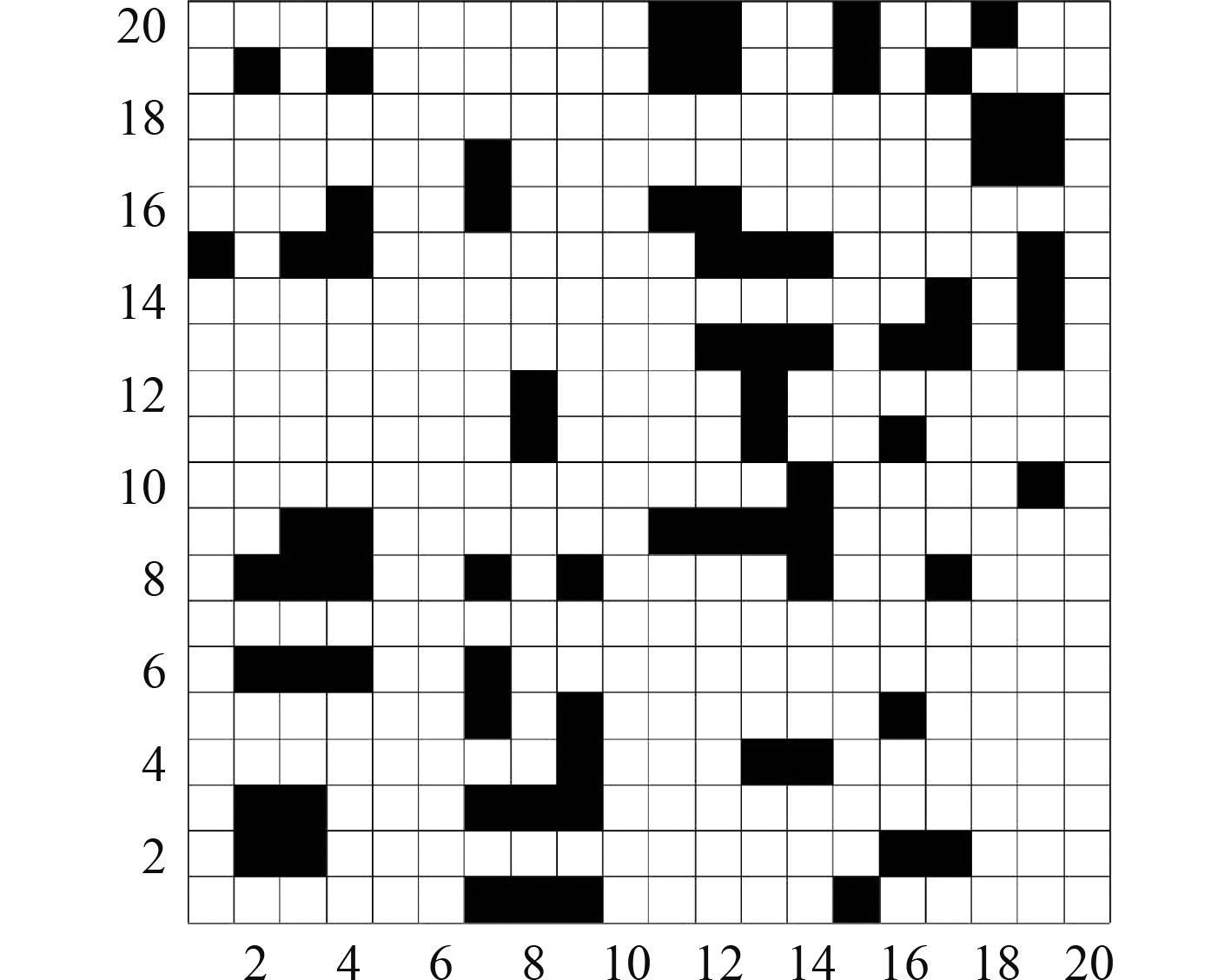
图1是用栅格法表示的一个水下环境模型,它每行有20个网格,黑色网格代表障碍物空间,白色网格代表可行的自由域。
|
图 1 栅格法环境建模示例 Fig. 1 Environment model example using grid method |
栅格法采用0表示障碍物栅格,1表示自由栅格,栅格法描述的是一个静态二维环境,可将其置于正交坐标系XOY中,计算每个栅格的坐标。栅格的几何中心作为机器人移动的节点,不考虑机器人的几何形状对运动的影响。
对于非规则地形,有的非规则形状的障碍物只能占据栅格的一部分,而不能占满,当障碍物占据的面积超过栅格面积的1/4时,对障碍物进行膨胀处理,看作是一个完整的栅格;障碍物占据的面积不超过栅格面积的1/4时,则将其忽略,看作是可行区域。
2 基本蚁群算法传统蚁群算法就是模拟自然界蚂蚁觅食的过程,采用并行计算的方式,利用正反馈迭代的方式找到最优路径。其基本思想是:蚂蚁会在走过的路径上留下信息素,后来的蚂蚁会根据路径上的信息素浓度和节点之间的距离来选择行进路径,直到达到目标点。
假设m为蚂蚁数量,k为蚂蚁编号,有状态转移概率公式为:
| $ {P}_{ij}^{k}=\left\{\begin{array}{ll}\dfrac{{\tau }_{ij}^{\alpha }\left(t\right){\eta }_{ij}^{\beta }\left(t\right)}{\displaystyle\sum _{\mu \in {J}_{k}}{\tau }_{i\mu }^{\alpha }\left(t\right){\eta }_{i\mu }^{\beta }\left(t\right)},&\mu \in {J}_{k}\text{,}\\ 0,&\mu \notin {J}_{k}\text{。}\end{array}\right. $ | (1) |
其中:
每只蚂蚁都会在其经过的路径上留下一定的信息素,当种群中的所有蚂蚁都完成一次迭代后,需要对路径上的信息素进行更新,信息素更新按照下式进行:
| $ {\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\mathrm{\Delta }{\tau }_{ij}\left(t\right)(0 < \rho < 1)\text{,} $ | (2) |
| $ \mathrm{\Delta }{\tau }_{ij}\left(t\right)=\sum _{k=1}^{m}{\mathrm{\Delta }\tau }_{ij}^{k}\left(t\right)\text{,} $ | (3) |
| $ {\mathrm{\Delta }\tau }_{ij}^{k}\left(t\right)=\left\{\begin{array}{c}\dfrac{Q}{{S}_{k}},\\ 0。\end{array}\right.$ | (4) |
式中:
利用基本蚁群算法进行水下机器人的路径规划时,由于算法的启发函数是从局部最优的考虑在进行路径的选择,最终所得的结果并非是全局最优的。此外,基本蚁群算法的信息素挥发因子是静态的,在路径规划过程中不能自适应调整,因此很容易陷入局部最优,导致无法找到全局最优解,同时也会带来时间和能耗的大量浪费。另一个显著问题是,在路径搜索前期,由于信息素浓度较低,蚂蚁的选择是盲目的,这使得最终解的质量严重依赖于初始解的质量,当算法前期产生的劣质解数量较多时,算法的搜索效率十分低下。针对上述问题,提出合理的优化策略和改善方案:包括首先用A*算法的得到一条相对较优的路径作为初始解,提高该路径上的信息素浓度,再使用改进蚁群算法搜索最优路径,从而提高搜索效率;其次提出信息素挥发因子自适应更新策略,减少陷入局部最优的可能,同时针对容易陷入局部最优的特殊地形采取特殊策略来进行规避。最后利用三次B样条法进行路径平滑操作得到最优的机器人移动路径。
3.1 A*算法替代初始算法A*算法是一种启发式搜索算法,它结合单源最短路径算法Dijkstra算法和广度优先算法(BFS)的优点,可以保证得到状态空间的最优效率解。采用的估价函数为:
| $ f\left(n\right)=g\left(n\right)+h\left(n\right)\text{。} $ | (5) |
式中:
| $ h\left(n\right)=l\left(n\right)+v\left(n\right)\text{。} $ | (6) |
式中:
当机器人移动路径上存在一些特殊地形比如U型障碍物时,由于基本蚁群算法缺乏逃离此类特殊环境的方法,机器人可能会陷入局部最优难以脱离,会造成算法搜索效率低下,严重时会导致算法搜索停滞。
为了避免蚂蚁落入U型陷阱造成算法停滞,借鉴狼群分配策略制定蚂蚁回退算法,在基本蚁群算法中,蚂蚁完成一次循环后信息素更新如下:
| $ {\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\mathrm{\Delta }{\tau }_{ij}\left(t\right)(0 < \rho < 1)\text{,} $ | (7) |
引入狼群分配策略后,新的信息素更新方式如下:
| $ {\tau }_{ij}^{n}=\left(1-\rho \right){\tau }_{ij}^{o}+\sum _{k=1}^{m}{\mathrm{\Delta }\tau }_{ij}^{k}+{\mathrm{\Delta }}^{b}{\tau }_{ij}-{\mathrm{\Delta }}^{g}{\tau }_{ij}\text{,} $ | (8) |
| $ {\mathrm{\Delta }}^{b}{\tau }_{ij}=\left\{\begin{array}{c}\xi \cdot \dfrac{Q}{{S}^{b}},如果\left({i},{j}\right)属于本次最优路径\text{,}\\ 0,\left({i},{j}\right)不属于本次最优路径\text{,}\end{array}\right. $ | (9) |
| $ {\mathrm{\Delta }}^{b}{\tau }_{ij}=\left\{\begin{array}{c}\omega \cdot \dfrac{Q}{{S}^{g}},如果\left({i},{j}\right)属于本次最优路径\text{,}\\ 0,\left({i},{j}\right)不属于本次最优路径\text{。}\end{array}\right. $ | (10) |
式中:
在基本蚁群算法中,启发函数
针对这一问题,对算法的距离启发函数进行优化,在基于方向性原则的基础上,利用当前节点和下一节点之间的距离以及下一节点和目标节点之间的距离来改进启发函数,从而在算法运行初期更好地将蚂蚁向目标点引导,从而迅速找到可行路径。优化后的启发函数为:
| $ \left\{\begin{array}{l}{{\eta }_{ij}\left(t\right)}=\dfrac{1}{{{(d}_{i,j}+{d}_{j,T})}^{2}}\text{,}\\ {d}_{j,T}=\sqrt{{({x}_{j}-{x}_{T})}^{2}+{({y}_{j}-{y}_{T})}^{2}}\text{。}\end{array}\right. $ | (11) |
式中:
在基本蚁群算法中,信息素挥发因子通常是静态的,这就导致算法的全局搜索过程中信息素的分配是不合理的,在算法搜索的早期,由于路径中信息素浓度较低,增加了蚂蚁路径搜索的盲目性,导致算法搜寻效率低下。而在算法搜索的后期,由于路径中累积了大量的信息素,导致启发函数权重过低,降低了蚂蚁路径搜索的可选择性。故静态的信息素挥发因子对路径搜索并不是最优的,因此考虑采用动态的方式来设定信息素挥发因子。
本文提出一种基于时空信息交互的信息素挥发因子动态更新策略:
| $ \left\{\begin{array}{l}\rho \left(l\right)=\delta \sqrt{{d}_{avg}/{d}_{best}}\text{,}\\ \rho \left(t\right)=\max\{\mu \rho \left(t-1\right),{\rho }_{\min}\}\text{,}\\ {\tau }_{ij}(t+\Delta t)=[1-\rho (l)-\rho \left(t\right)].{\tau }_{ij}\left(t\right)+\Delta {\tau }_{ij}\left(t\right)\text{。}\end{array}\right. $ | (12) |
式中:
在水下机器人的路径移动中,最优路径的参考指标不仅包括路径长度,也需要考虑能耗和时长等因素。对水下机器人的路径规划来说,所得路径的节点越多,运行时间越长,能耗也会越大。利用基本蚁群算法规划所得路径存在较多的节点,其中存在不少冗余节点,路径平滑度不足。因此考虑使用三次B样条方法去除规划路径中的冗余节点,减少路径长度,保证最终路径的平滑度。
B样条法是一种基于贝塞尔方法的路径平滑方法,和贝塞尔方法相比,具有更好的局部控制性能。由N个控制点
| $ C\left(u\right)=\sum _{i=0}^{N+1}{P}_{i}{N}_{i,3}\left(u\right), 0 < u < 1 \text{,}$ | (13) |
其中
| $ {N}_{i,3} \left(u\right) = \left\{\begin{aligned} &{N}_{\mathrm{0,3}}\left(u\right) = \dfrac{1}{6}(-{u}^{3}+3{u}^{2}-3u+1)\text{,}\\ &{N}_{\mathrm{1,3}}\left(u\right) = \dfrac{1}{6}(3{u}^{3}-6{u}^{2}+4)\text{,}\\ &{N}_{\mathrm{2,3}}\left(u\right) = \dfrac{1}{6}(-3{u}^{3}+3{u}^{2}+3u+1)\text{,}\\ &{N}_{\mathrm{3,3}}\left(u\right) = \dfrac{1}{6}{u}^{3}\text{。}\end{aligned} 0\leqslant u\leqslant 1\text{,}\\[-5pt]\right. $ | (14) |
故有三次B样条方程:
| $ C\left(u\right)=\frac{1}{6}\left[1\;\;u\;\;{u}^{2}\;\;{u}^{3}\right]\left[\begin{array}{cccc}1&4&1&0\\ -3&0&3&0\\ 3&-6&3&0\\ -1&3&-3&1\end{array}\right]\left[\begin{array}{c}{C}_{0}\\ {C}_{1}\\ {C}_{2}\\ {C}_{3}\end{array}\right]\text{。} $ | (15) |
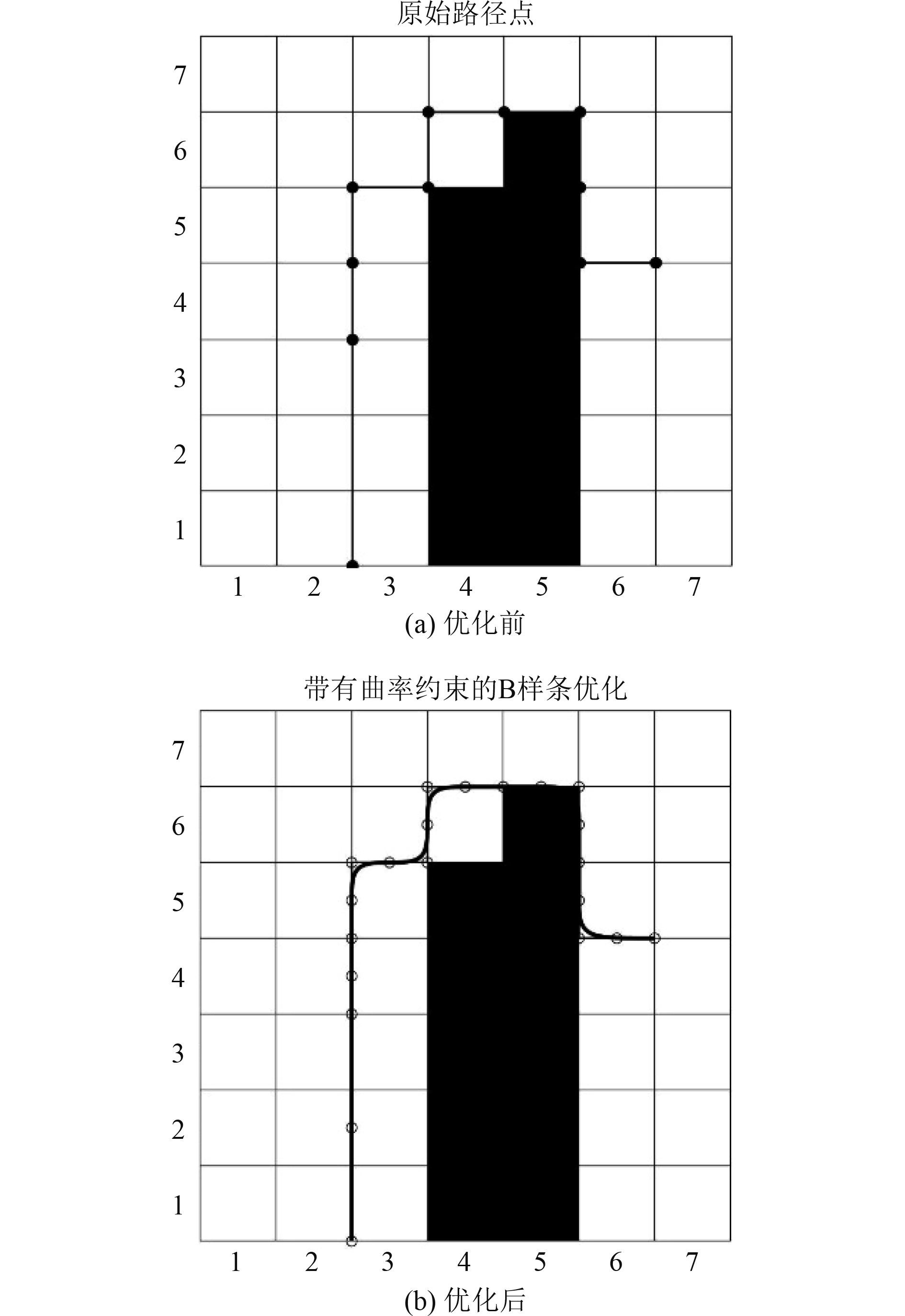
路径平滑的结果如图2所示。
|
图 2 路径平滑处理前后比较 Fig. 2 Comparison of path before and after optimization |
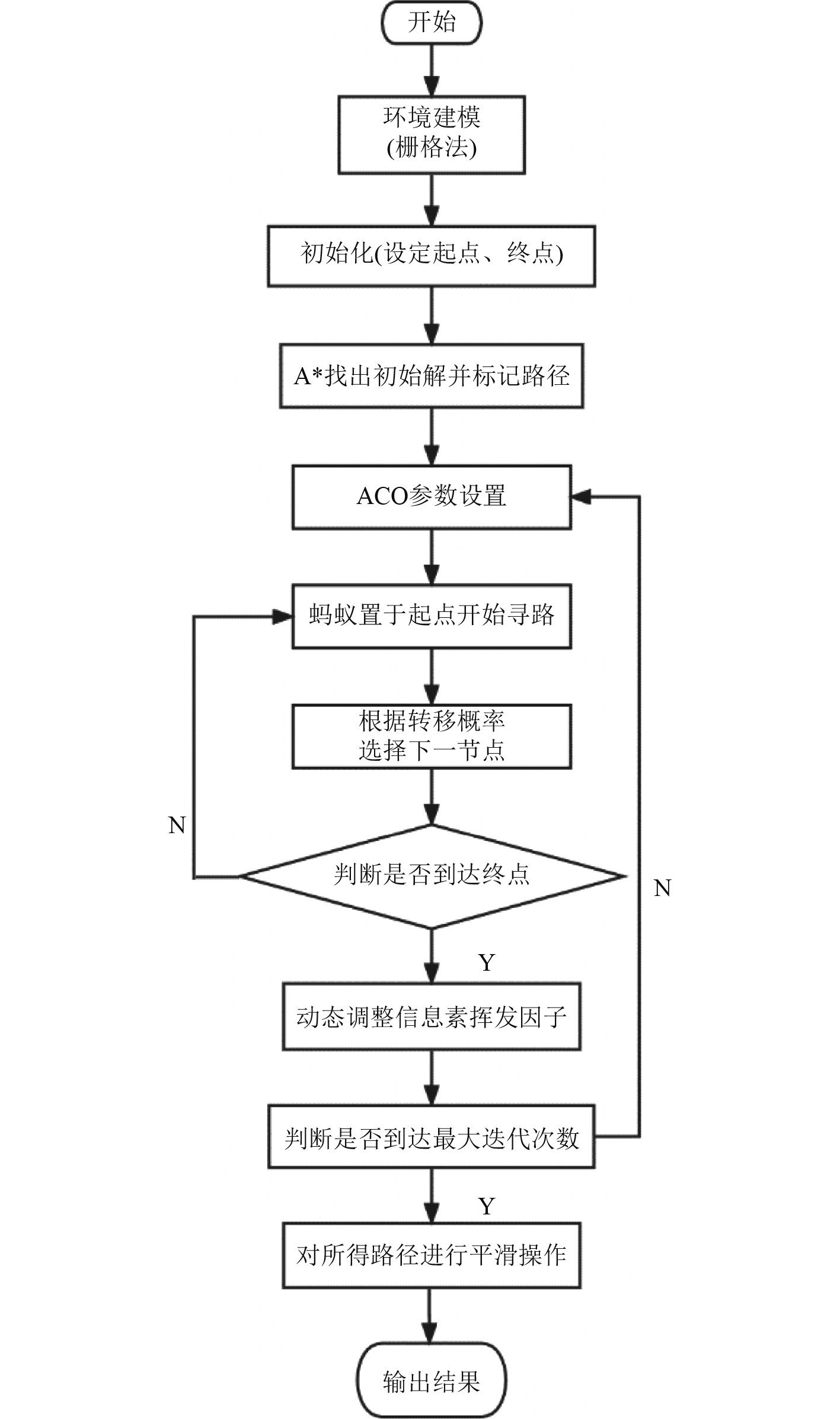
改进蚁群算法的流程如图3所示。
|
图 3 改进蚁群算法流程 Fig. 3 Improved ACO algorithm flow chart |
为了验证本文所提出的改进算法的可行性和稳定性,使用Matlab编写仿真程序,算法的基础仿真参数见表1。
|
|
表 1 Matlab基础仿真参数表 Tab.1 Matlab simulation parameters |
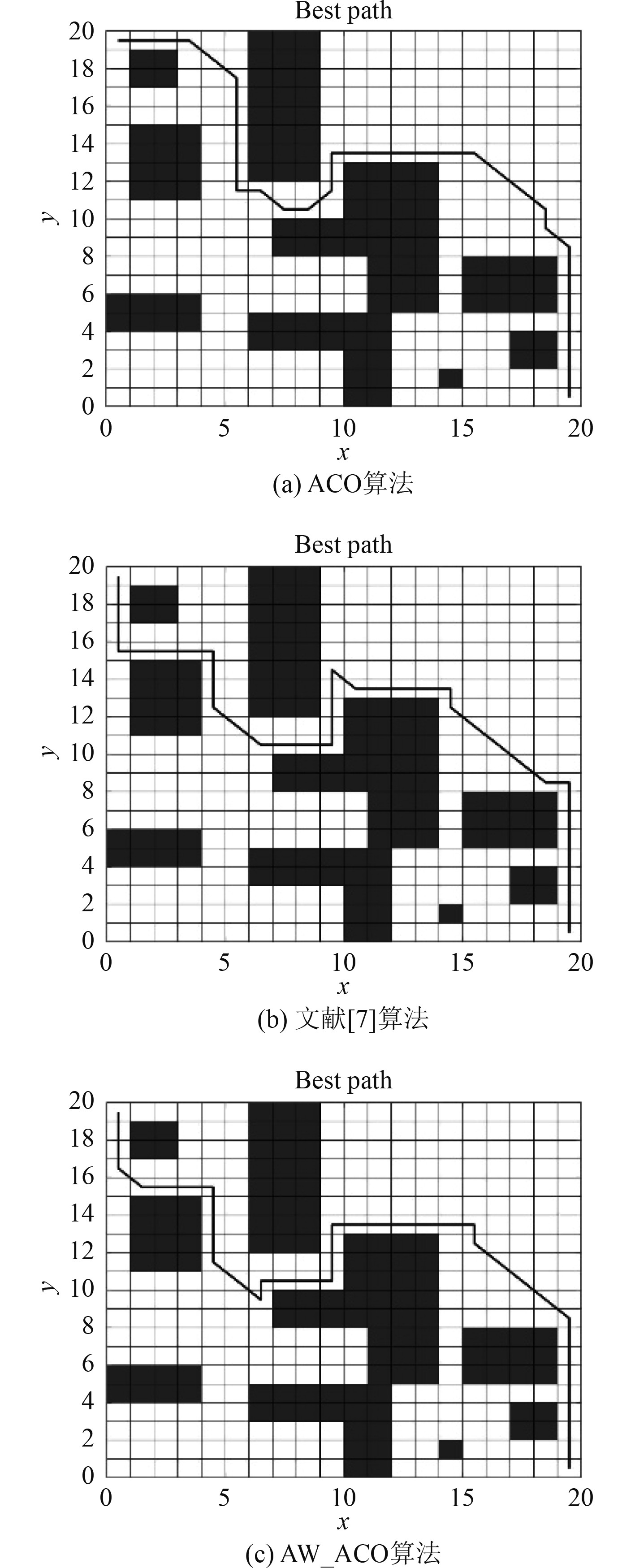
为了验证本文提出的改进蚁群算法AW_ACO的有效性,在2种20×20的栅格环境中进行仿真实验,分别利用基本蚁群算法ACO、文献[7]算法和本文提出的改进蚁群算法AW_ACO对水下机器人移动路径进行规划,其中路径起点设置为
|
图 4 20×20复杂环境1最优规划路径 Fig. 4 Optimal path comparison in 20×20 Environment 1 |
|
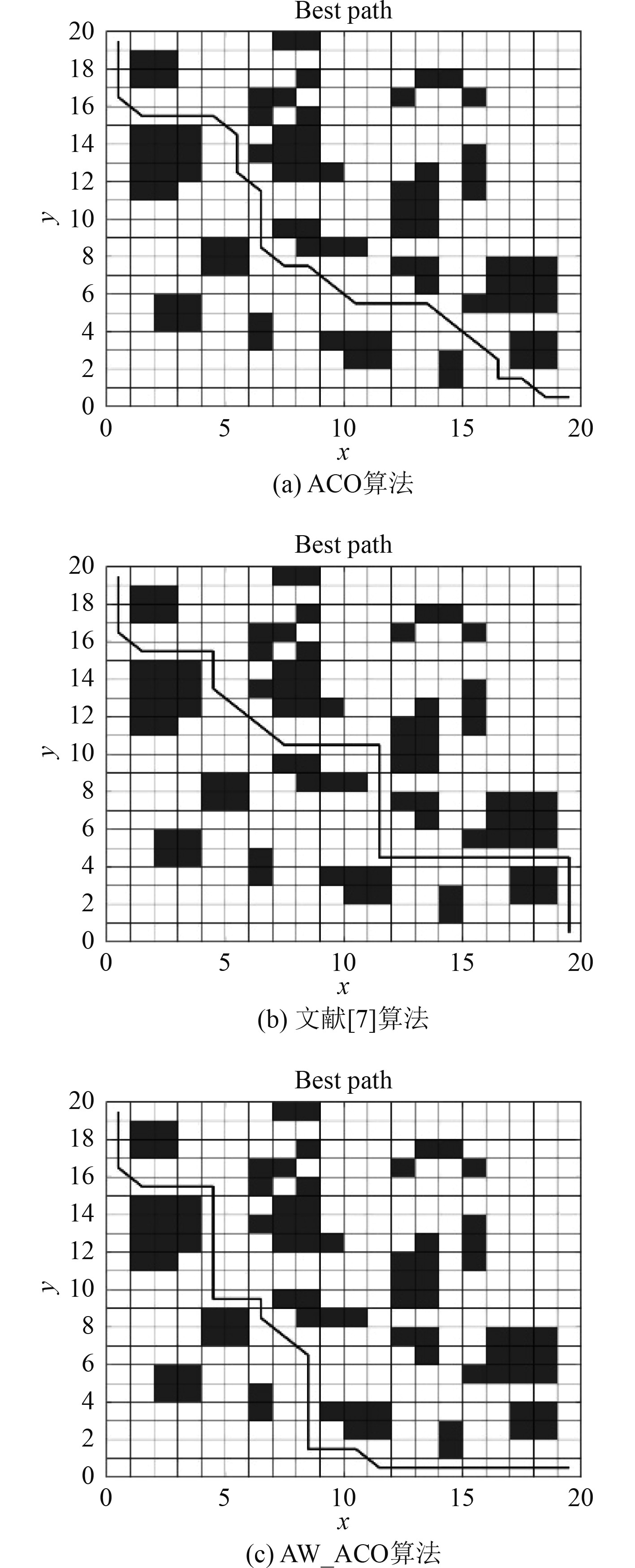
图 5 20×20复杂环境2最优规划路径 Fig. 5 Optimal path comparison in 20×20 Environment 2 |
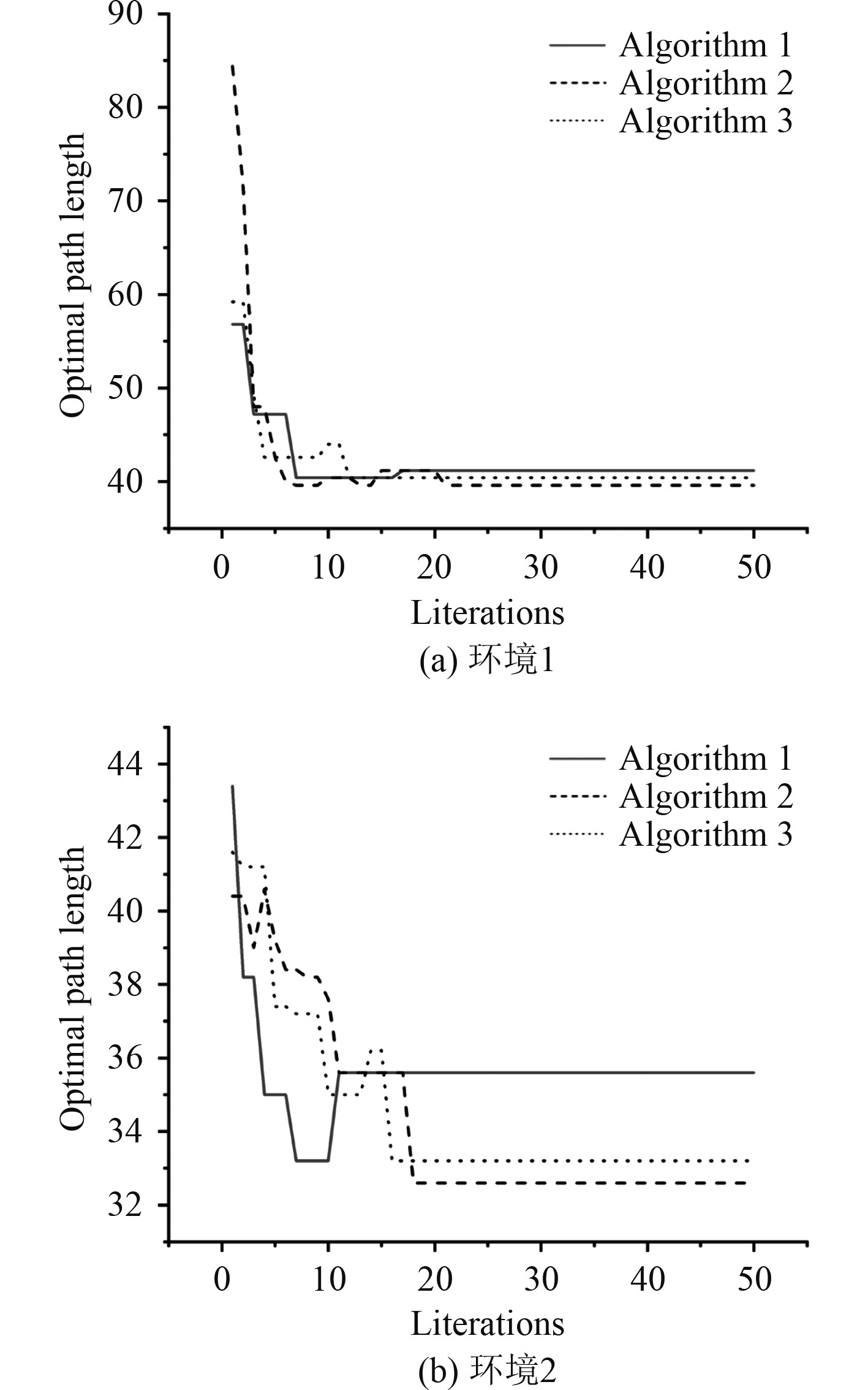
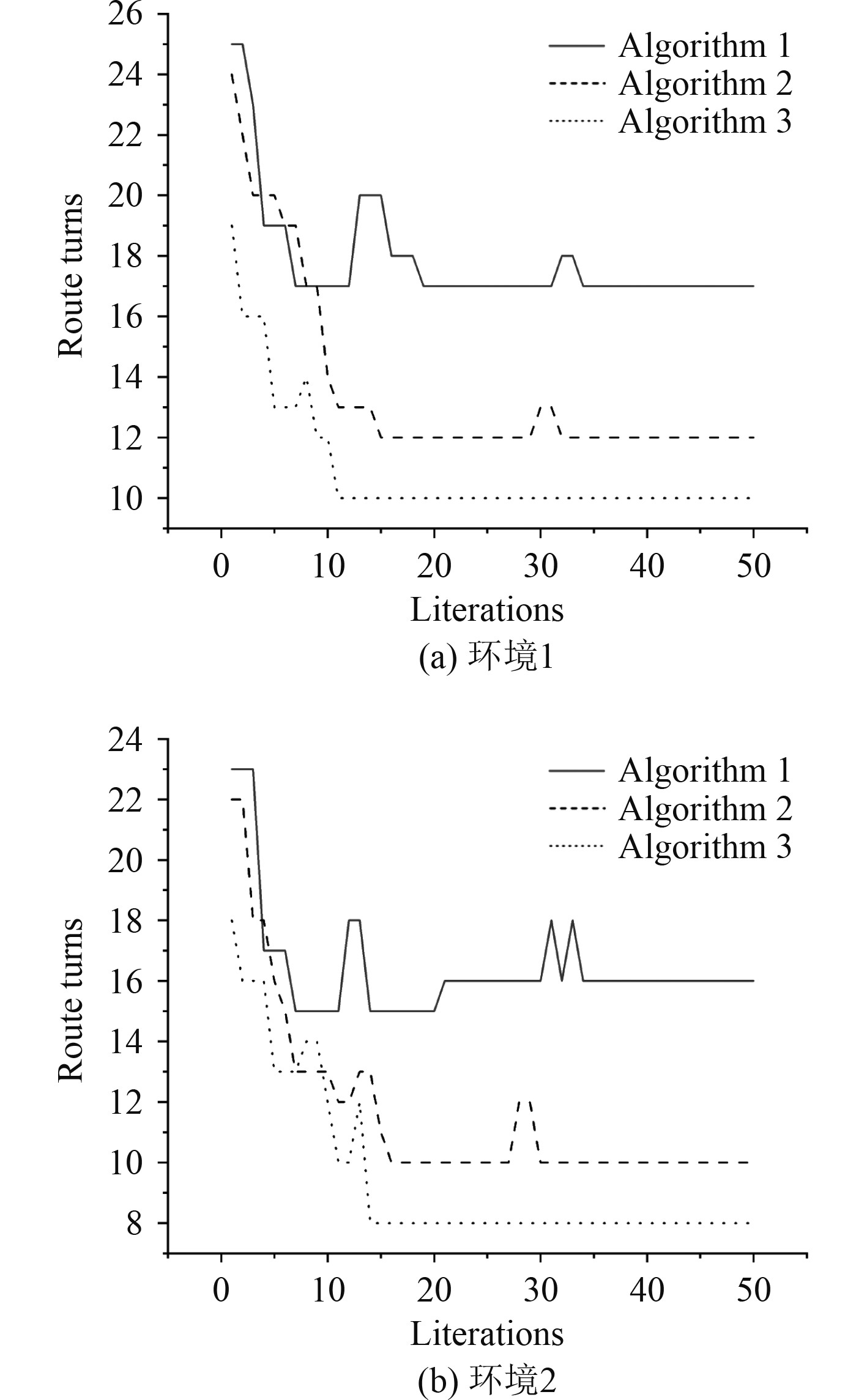
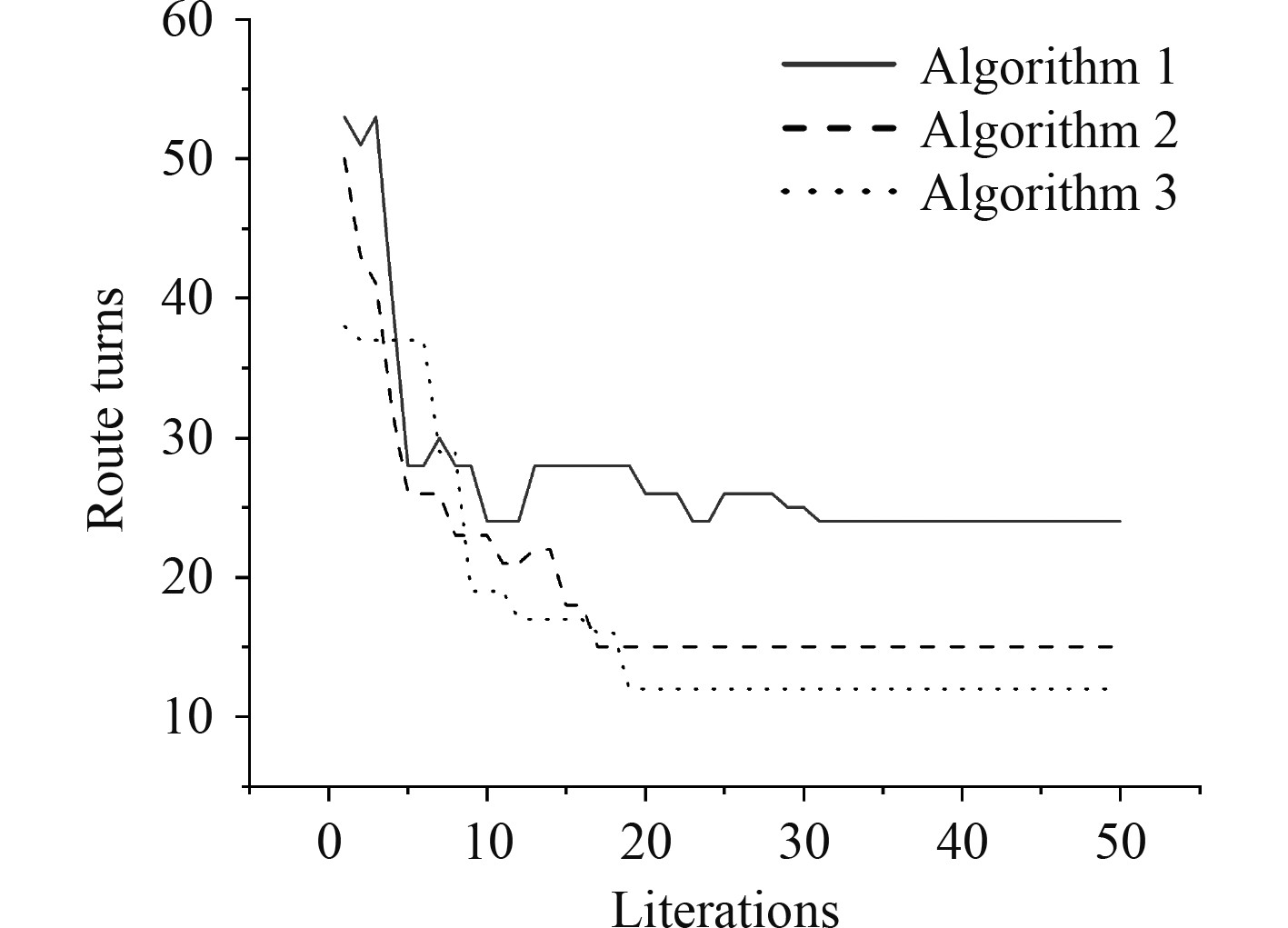
图中,Algorithm 1是基本蚁群算法,Algorithm 2是文献[7]中算法,Algorithm 3是本文提出的改进蚁群算法。从图4~图6可以看出,在障碍物环境1和环境2中,3种算法都能找到最优路径,但基本蚁群算法规划出的路径明显长度较长,拐点较多,文献[7]中算法和本文提出的改进算法得到的最优路径更短。从图6所示的迭代曲线图也可以看出,基本蚁群算法和文献[7]中算法迭代曲线较不稳定,尤其是在算法迭代前期,不稳定性非常明显。而本文提出的改进算法整体迭代过程比较平稳,收敛较快,最终得到的最优路径长度也和文献[7]中结果十分接近。同时,路径拐点少,整体平滑度较高,有利于减小AUV在运动过程中的能耗。从图7可以看出,改进蚁群算法较文献[7]中算法拐点更少,路径更加平滑,且本文改进算法达到路径拐点数收敛所需的迭代次数最少,其次是文献[7]中算法,基本蚁群算法达到路径拐点数收敛所需的迭代次数是最多的,而且基本蚁群算法和文献[7]中算法稳定性都较差,路径拐点数曲线更加震荡,算法性能相对较差。
因此,综合来看,本文提出的改进算法在20×20的障碍物环境下明显优于基本蚁群算法和文献[7]中算法,在保持较高算法效率的同时,得到了稳定性较高的最优路径。仿真实验在20×20的2种障碍物环境下的运行结果对比见表2。
|
|
表 2 20×20环境下三种算法仿真结果对比 Tab.2 Comparison of simulation results in 20×20 environments |
|
图 6 20×20复杂环境最优路径长度迭代曲线 Fig. 6 Optimal path length in 20×20 Environment |
|
图 7 20×20复杂环境拐点个数迭代曲线 Fig. 7 Route turns in 20×20 Environment |
为了进一步说明本文提出的改进蚁群算法的可靠性,在30×30的复杂障碍物环境下进一步仿真实验,其中路径起点设置为

|
图 8 30×30复杂环境最优规划路径 Fig. 8 Optimal path comparison in 30×30 Environment |
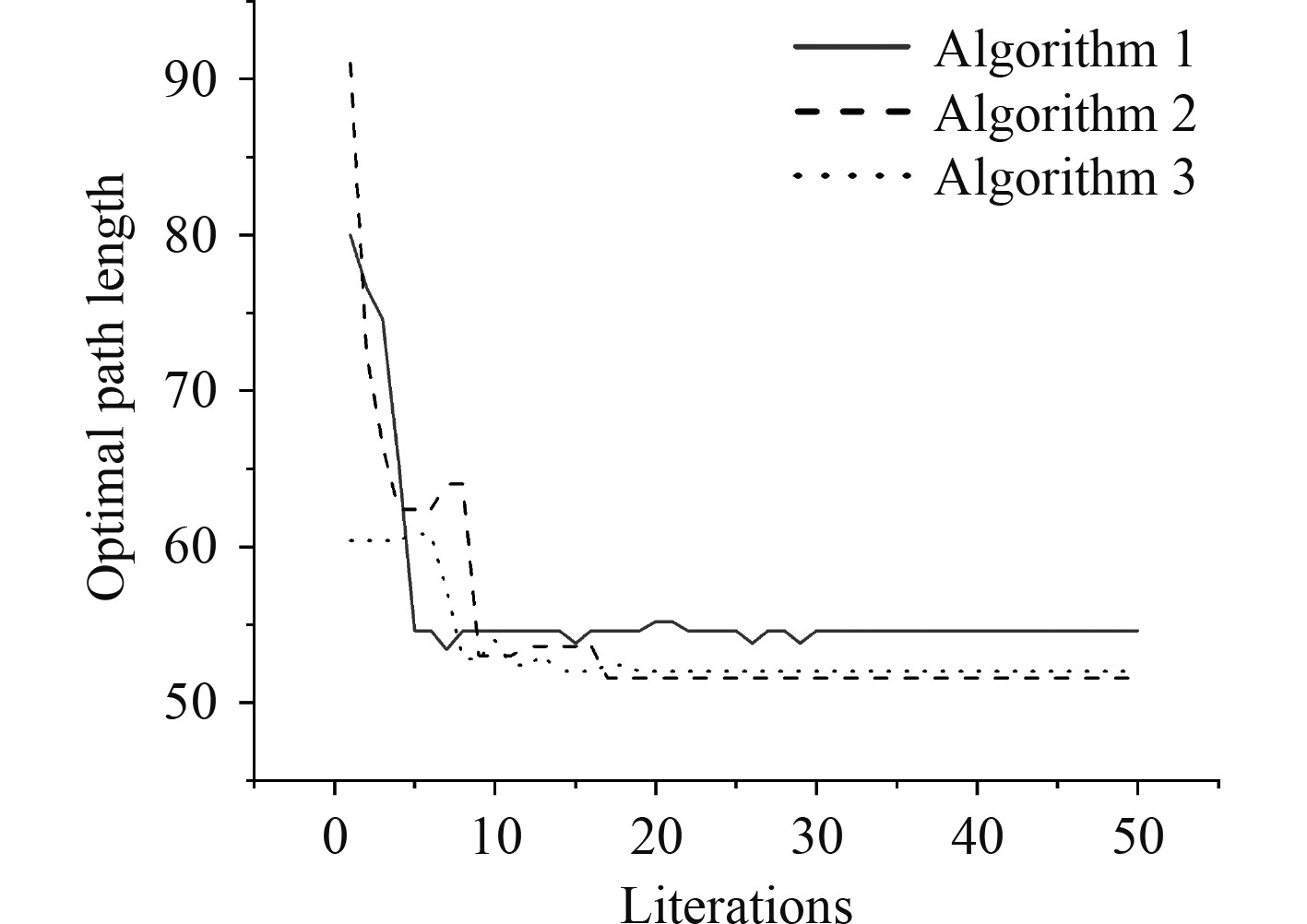
图9和图10中,Algorithm 1是基本蚁群算法,Algorithm 2是文献[51]中算法,Algorithm 3是本文提出的改进蚁群算法。从图8~图10可以看出,在30×30的障碍物环境下,本文提出的改进蚁群算法表现仍然是最优的。仿真实验在30×30的障碍物环境下的运行结果对比见表3。
|
图 9 30×30复杂环境最优路径长度迭代曲线 Fig. 9 Optimal path length in 30×30 Environment |
|
图 10 30×30复杂环境拐点个数迭代曲线 Fig. 10 Route turns in 30×30 Environment |
|
|
表 3 30×30环境下3种算法仿真结果对比 Tab.3 Comparison of simulation results in 30×30 environment |
为了说明本文提出的三次B样条曲线方法的可行性,对所得的路径规划结果进行平滑仿真实验,仿真结果如图11所示。

|
图 11 三次B样条法路径平滑 Fig. 11 Cubic B-spline path smoothing process |
从图11可以看出,3种障碍物环境的路径规划结果利用三次B样条方法进行平滑优化后,都得到了无碰的曲线路径,且优化后的路径能很好地落在障碍物和拐点构成的三角形区域内,这有利于AUV在实际工作时的无碰转向和安全行驶。
6 结 语针对基本蚁群算法在水下机器人路径规划中存在的搜索速度慢,全局最优能力弱的问题。本文提出一种改进蚁群算法,主要体现在以下5个方面:
1)利用A*方法先得到一条相对较优的初始路径,降低了蚁群算法前期搜索的盲目性。
2)引入狼群分配策略进行蚂蚁回退,增强了算法跳出“陷阱”的能力,避免陷入局部最优。
3)对启发函数做出优化,有效提高了算法效率。
4)动态信息素更新策略提高了算法的迭代速率,也增强了算法稳健性。
5)对规划路径进行了平滑处理,去除了冗余节点,减少了水下机器人移动过程中的时间和能量损耗。
仿真实验表明,本文提出的改进算法在两种复杂环境中均有良好的表现不仅收敛速度更快,找到的最优路径也更短更平滑,有利于减少水下机器人移动过程中的能量损耗,改进算法是切实可行的。
| [1] |
WANG H, XIONG W. Research on global path planning based on ant colony optimization for AUV[J]. Journal of Marine Science and Application, 2009, 8(1): 58-64. DOI:10.1007/s11804-009-8002-7 |
| [2] |
DORIGO, MARCO, MAURO B, et al. Ant colony optimization[J]. IEEE computational intelligence magazine, 2006: 28–39.
|
| [3] |
DORIGO, MARCO, CHRISTIAN B. Ant colony optimization theory: A survey[J]. Theoretical computer science, 2005: 243–278.
|
| [4] |
GAMBARDELLA L M, DORIGO M. Solving symmetric and asymmetric TSPs by ant colonies[C]//Proceedings of IEEE International Conference on Evolutionary Computation. IEEE, 1996: 622–627.
|
| [5] |
GARCIA M A P, MONTIEL O, CASTILLO O, et al. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation[J]. Applied Soft Computing, 2009, 9(3): 1102-1110. DOI:10.1016/j.asoc.2009.02.014 |
| [6] |
ZHANG G L, JIA H M. Global path planning of AUV based on improved ant colony optimization algorithm[C]//2012 IEEE International Conference on Auto-mation and Logistics, Zhengzhou, Pis-cataway: IEEE, 2012: 606–610.
|
| [7] |
李理, 李鸿, 单宁波. 多启发因素改进蚁群算法的路径规划[J]. 计算机工程与应用, 2019, 55(924): 219-225+250. |
 2022, Vol. 44
2022, Vol. 44
