0 引　言

现如今人们对海洋资源的开发需求不断变大，从陆地到近海再到深海，面对水下复杂的环境，水下自主航行机器人AUV（autonomous underwater vehicle，AUV）成为人类探索海底世界的重要工具，在民用和军事方面发挥着重要的作用^[1]。深海考察和资源探索面临人员风险大、工作效率低等诸多问题^[2]。当AUV在深海工作，AUV由于受电池发展技术影响，携带能源不能满足自身长期水下工作的要求，需要定期对水下AUV进行能源补充和数据传输。布放和回收要花费相当长的时间，若海况较差，风险增加。为满足AUV在水下作业时间、作业内容和续航能力，为此提出更高的需求^[3]。水下自主回收提高了回收的自动化水平，摆脱了人为干预的繁琐，受时间空间限制小，可节约大量辅助设备费用和人力物力^[4]。

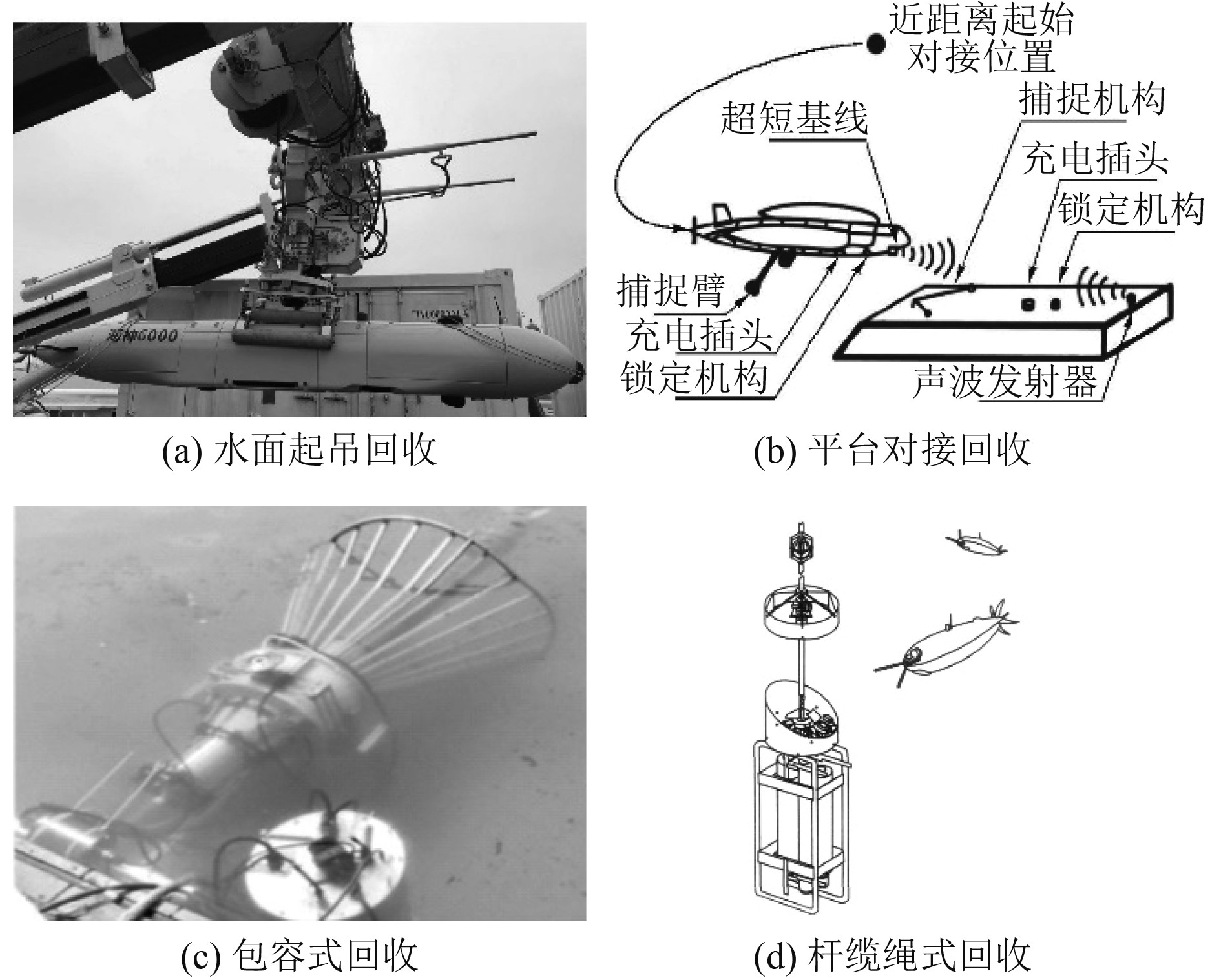
为实现AUV的布放和回收，20世纪90年代初国内外学者设计了各种各样水下机器人回收系统^[5]，其主要的回收方式有4种：水面起吊回收^[6]、平台对接回收^[7]、包容对接式回收^[8]、杆、绳对接回收式^[9]，如图1所示。其中杆绳回收式可以最大限度的减少对AUV外部形状的要求，对AUV航行控制和运动稳定性基本上不产生影响^[10]。

缆绳式回收装置主要包括USV和V型拖曳装置（V型翼）和缆绳3部分。对接技术在回收中起着关键性的作用^[11]，对接完成后，由于受海浪和AUV回收缆绳拉力影响，AUV自身有精密部件，避免回收过程中AUV姿态发生大幅度变化，需要对AUV的姿态进行观测。研究表明，AUV捕获缆绳回收是一种非常有效的回收方法^[12]。

1 回收系统的组成

回收系统由两部分构成，一部分是USV、绞车、夹紧机构、推进器、导向板和控制器；另一部分是挡环、V型翼和AUV。

1.1 回收平台USV

水面无人艇USV是一种能在海洋环境下，可以自主规划、自主避障和自主行航行，能完成目标探测、通信中继和能源补给的小型无人平台，其具有体积小、机动性强等优点，可以承担反潜、扫雷、情报收集、目标打击、水文地质勘测等功能，在军事和民用领域应用较为广泛。

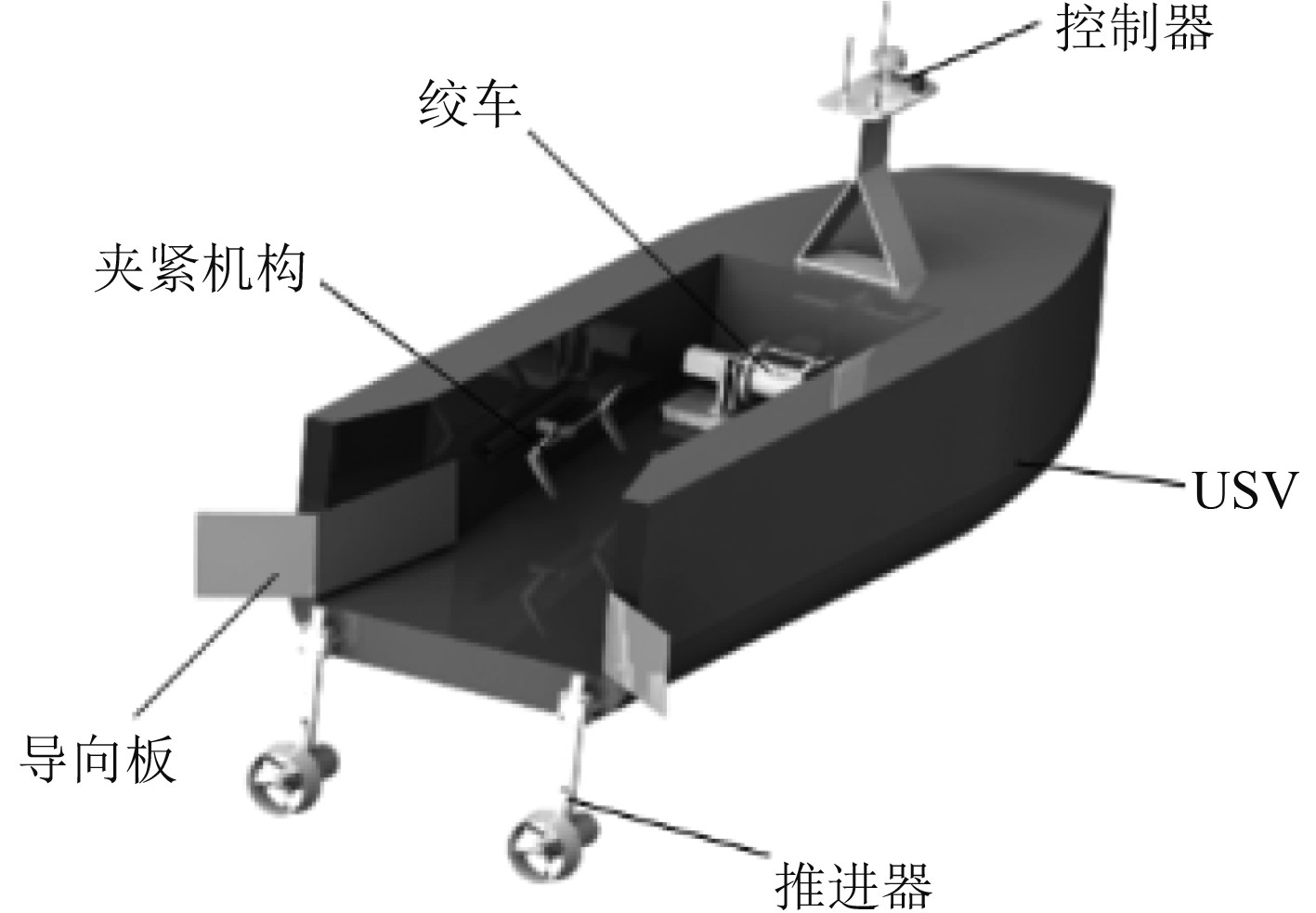
水面无人艇USV自主研制，重量300 kg，长2800 mm，高1600 mm，宽1900 mm，采用双螺旋桨喷水推进，航速最高3.2 m/s，续航时间30 h。该艇搭载控制器、摄像机和声呐等装备，在执行任务时USV具有自主决策功能，USV舱内装有绞车、夹紧机构和导向板，如图2所示。

1.2 自主航行机器人AUV

AUV是深海航行器应用最广泛的无缆水下自主控制的机器人，可用于海底考察、铺设管线、海底施工、布雷、扫雷、侦察和救生等作用。AUV可以依靠自身所带的能源完成所赋予的使命。与传统带缆机器人相比，无缆绳限制、活动范围大、隐蔽性好、灵活性强、回收和布放方便等优点。

使用AUV为60 kg级便携式AUV，长2 200 mm，直径250 mm，尾部安装有4个舵和1个推进器。4个舵可以用来控制AUV的上浮下潜和航向，推进器用来控制AUV的航行速度。AUV前端安装有左、右两卡爪，卡爪内设置有卡簧，卡爪开口直径2 ～20 mm，当AUV捕获缆绳后，左、右卡爪可通过卡簧形成自锁。

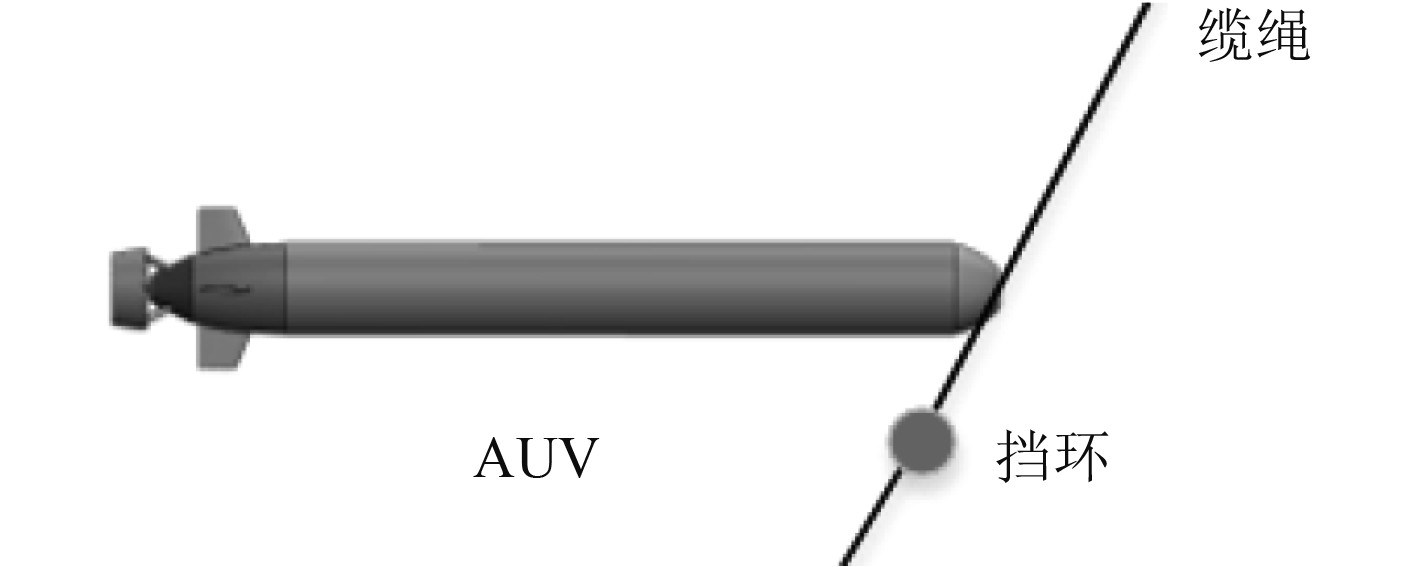
1.3 水下拖曳系统

当AUV捕获缆绳后，缆绳、AUV和V型翼形成一个完整的拖曳系统。AUV在水下捕获缆绳，通过AUV前端卡爪对绳子形成自锁。由于AUV可以沿缆绳上下滑动，AUV首部在其上下运动过程中会击中V型翼，为避免AUV沿缆绳滑动破坏2个系统^[13]，在缆绳上设置有挡环，可以称作对接点，如图3所示。

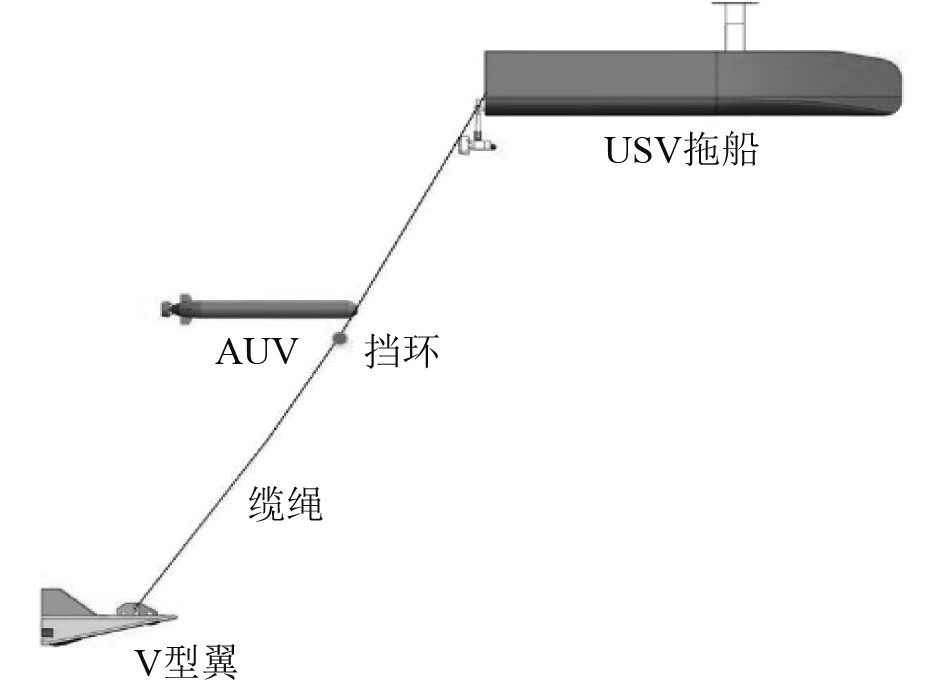
AUV捕获缆绳后控制器控制绞车对缆绳缠绕回收，导向板可防止AUV撞上USV起到引导作用，当传感器监测到AUV回收到位，夹紧机构对AUV体夹紧，进行能源补充、任务下载和情报反馈等工作，即回收完毕，水下回收系统的组成示意图如图4所示。

在拖曳回收过程中AUV和V型翼姿态不断发生变化，针对回收过程中位姿进行仿真模拟，避免回收过程中对AUV载体内部精密设备造成损害。因此为保证回收更安全、高效，对水下AUV回收研究就尤为重要。

2 AUV动力学建模及分析

AUV在水下运动时，海底环境会对AUV产生水阻力等作用力，为了保证AUV回收顺利，有必要对AUV在工作过程中水动力学特性进行分析。

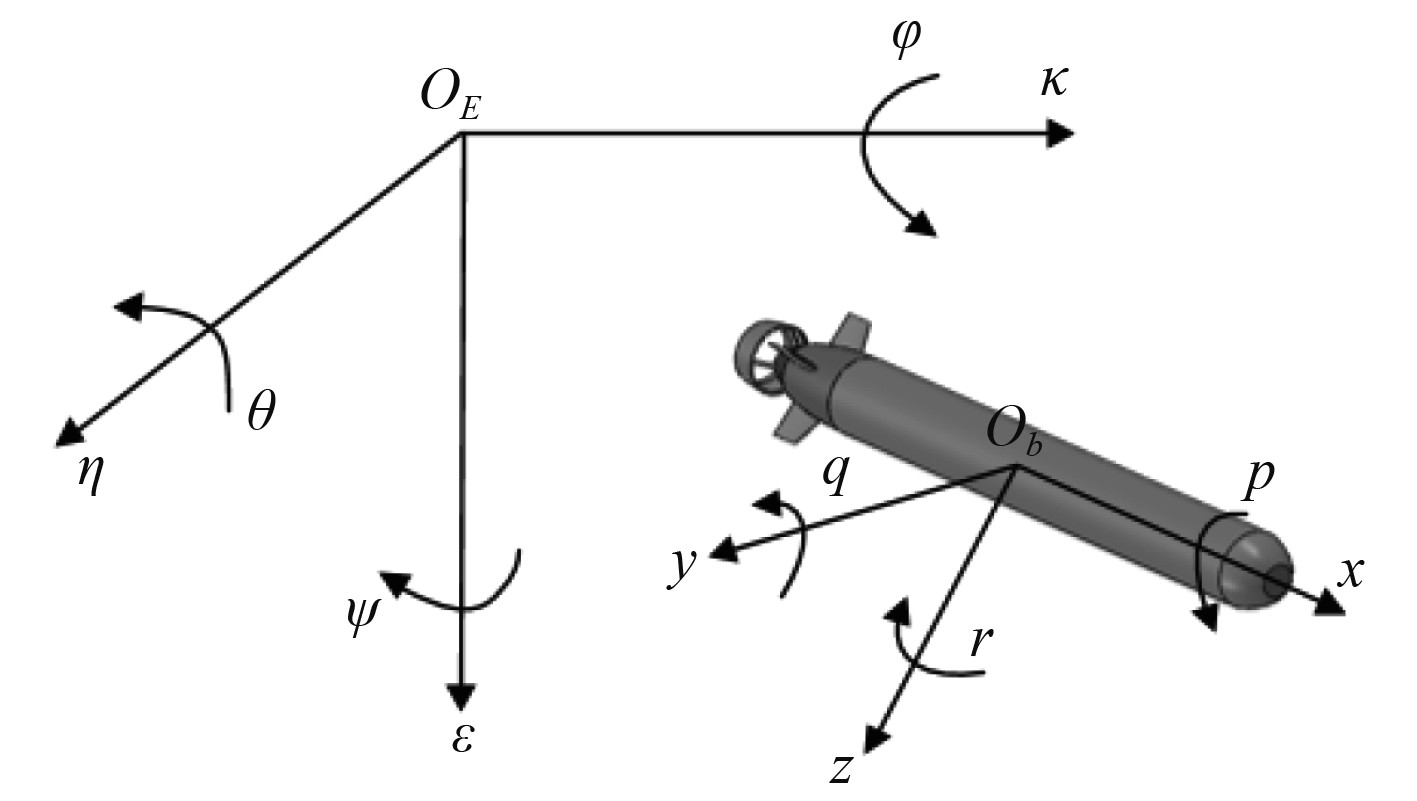
2.1 建立坐标系 2.1.1 固定坐标系和运动坐标系

在研究AUV航行位置姿态的变化中，通常采用不同的坐标系去描述运动问题。在研究AUV的水动力特性和建立运动方程采用2种形式坐标系，一个采用定系固定于大地上某点，用来确定AUV在水中航行的轨迹和姿态，称为固定坐标系；另一个为运动坐标系，固定于AUV的重心位置用来建立运动方程和水动力特性，如图5所示。

固定坐标系 ${O_E} - \kappa \eta \varepsilon $ 满足右手定则， ${O_E}\kappa $ 轴与轴 ${O_E}\eta $ 在水平面互相垂直， ${O_E}\varepsilon $ 轴垂直于水平面 ${O_E}\kappa \eta $ 指向地心为正。运动坐标系 ${O_b} - xyz$ 满足右手定则，坐标原点 ${O_b}$ 取在AUV重心位置， ${O_b}x$ 轴平行于AUV基线指向首为正； ${O_b}y$ 轴平行于纵摇轴指向右舷方向为正； ${O_b}z$ 轴指向水底方向为正。

AUV相对于固定坐标系下的速度V在运动坐标系下的投影分量分别为： $u$ （纵向速度）、 $v$ （横向速度）、 $w$ （垂向速度）；AUV在运动坐标系下绕原点 ${O_b}$ 的角速度 $\Omega $ 投影分量分别为： $p$ （横倾角速度）、 $q$ （纵倾角速度）、 $r$ （偏航角速度）；作用在AUV上的外力 $F$ 在运动坐标系下的分量为： $X$ （纵向力）、 $Y$ （横向力）、 $Z$ （垂向力）；作用在原点坐标系上的力矩M在运动坐标系下的分量为： $K$ （横倾力矩）、 $M$ （纵倾力矩）、 $N$ （偏航力矩）。如表1所示。AUV所运动的位置和姿态，由运动坐标系和固定坐标系的坐标轴夹角 $\sigma \left( {\varphi ,\theta ,\psi } \right)$ 来表示。其中， $\varphi $ 为横倾角； $\theta $ 为纵倾角，抬艏为正； $\psi $ 为艏向角，右偏为正。

2.1.2 坐标变换

AUV运动坐标系相对于水平面有速度、加速度和角速度，因此，它不是一个惯性参考系。所以，在分析AUV运动时，应在固定坐标系中建立运动方程，再转换成运动坐标系下来表示分量，来表达运动坐标系的运动方程，固定坐标系与运动坐标系之间的转换关系如下：

$ \left[ {\begin{array}{*{20}{c}} \kappa \\ \eta \\ \varepsilon \end{array}} \right] = R\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right]。$

(1)

式中：

$ \begin{split}{\boldsymbol{R}} = & \left[ \begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \varphi \sin \psi + \sin \theta \sin \varphi \cos \psi }\\ {\cos \theta \sin \psi }&{\cos \psi \cos \theta + \sin \psi \sin \theta \sin \phi } \\ { - {\text{s}}in\theta }&{\sin \varphi \cos \theta } \end{array} \right.\\ &\left. \begin{array}{*{20}{c}} {\sin \psi \sin \varphi + \cos \psi \sin \theta \cos \varphi } \\ { - \cos \psi \sin \theta + \sin \psi \sin \theta \cos \varphi } \\ {\cos \theta \cos \varphi } \end{array} \right]，\end{split}$

经过反变换后方程为：

$ \left[ {\begin{array}{*{20}{c}} \kappa \\ \eta \\ \varepsilon \end{array}} \right] = {R^{ - 1}}\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right]。$

(2)

其中：

$ \begin{split}{{\boldsymbol{R}}^{ - 1}} = &\left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \theta }\\ {\cos \psi \sin \theta \sin \varphi - \cos \psi \sin \varphi }\\ {\cos \psi \sin \theta \cos \varphi + \sin \psi \sin \varphi } \end{array}} \right.\\ &\left. {\begin{array}{*{20}{c}} {\sin \psi \cos \theta }&{ - \sin \theta } \\ {\sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi }&{\cos \theta \sin \varphi } \\ {\sin \psi \sin \theta \cos \varphi - \cos \psi \sin \varphi }&{\cos \theta \cos \psi } \end{array}} \right]，\end{split}$

运动坐标系和固定坐标系之间转动角速度之间的变换为：

$ \left[ {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&{ - \sin \theta } \\ 0&{\cos \varphi }&{\cos \theta \sin \varphi } \\ 0&{ - \sin \varphi }&{\cos \theta \cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \varphi } \\ {\dot \theta } \\ {\dot \psi } \end{array}} \right]，$

(3)

其反变换为：

$ \left[ {\begin{array}{*{20}{c}} {\dot \varphi } \\ {\dot \theta } \\ {\dot \psi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta } \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{{{\sin \varphi } \mathord{\left/ {\vphantom {{\sin \varphi } {\cos \theta }}} \right. } {\cos \theta }}}&{{{\sin \varphi } \mathord{\left/ {\vphantom {{\sin \varphi } {\cos \theta }}} \right. } {\cos \theta }}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right]。$

(4)

2.2 六自由度方程

在运动坐标系下，定义AUV重心坐标为 ${R_a} = ({x_a},{y_a},{z_a})$ ，根据刚体的动量定理和动量矩的定理，可表示AUV的平移和转动方程式如下：

$ \begin{split} &m\left[ {\dot V + {O_b} \times {R_a} + {O_b} \times V + {O_b} \times ({O_b} \times {R_a})} \right] = F ，\\ &J{O_b} + {O_b} \times (J{O_b}) + m{R_a} \times (\dot V + {O_b} \times V) = M。\end{split} $

(5)

其中： $m$ 为AUV的质量； $J$ 为转动惯量；运动速度 $V = {(u,v,w)^{\rm{T}}}$ ；角速度 $\Omega = {(p,q,r)^{\rm{T}}}$ ；AUV所受外力 $F = {(X,Y,Z)^{\rm{T}}}$ ；AUV所受外力矩 $M = {(K,M,N)^{\rm{T}}}$ 。

AUV完全在水下时远离水面，因此波浪和风负载不是重要的影响因素，在此可以忽略。当AUV在水下时重力和浮力相互抵消，在动力学方程理论上，拖曳系统回收过程中重力、浮力、水动力和AUV推力达到平衡状态。

对AUV进行观测，需要建立AUV的空间六自由度运动一般方程，假设重力和浮力中心重合，可以列出AUV六自由度方程，经过整理结果如下式：

$ \begin{split}X = & {\text{m}}[\dot u - vr + wq - {x_a}({q^2} + {r^2}) + {y_a}(pq - \dot r) + {z_a}(pr + \dot q)]，\\ Y =& m[\dot v - wp + ur - {y_a}({r^2} + {p^2}) + {z_a}(qr - \dot p) + {x_a}(qp + \dot r)]，\\ Z =& m[\dot w - uq + vp - {z_a}({p^2} + {q^2}) + {x_a}(rp - \dot q) + {y_a}(rp + \dot p)] ，\\ K =& {I_x}\dot p + ({I_z} - {I_y})qr - (\dot r + pq){I_{xz}} + ({r^2} - {q^2})yz +\\ &(pr - \dot q){I_{xy}} + m[{y_a}(\dot w - uq + vp) - {z_a}(\dot v - wp + ur)]，\\ M =& {I_y}\dot q + ({I_x} - {I_z})rp - (\dot p + qr){I_{xy}} + ({p^2} - {r^2}){I_{xz}} +\\ & (qp - \dot r){I_{yz}} + m[{z_g}(\dot u - vr + wq) - {x_a}(\dot w - uq + vp)]，\\ N = &{I_z}\dot r + ({I_y} - {I_x})pq - (\dot q + rp){I_{yz}} + ({q^2} - {p^2}){I_{xy}} + \\ &(rp - \dot p){I_{xz}} + m[{x_g}(\dot v - wp + ur) - {y_a}(\dot u - vr + wq)]。\\[-10pt] \end{split}$

(6)

式中： $m$ 为AUV的质量； ${I_x}$ ， ${I_y}$ ， ${I_z}$ 为AUV在 ${O_b}x$ ， ${O_b}y$ ， ${O_b}z$ 轴转动惯量； $u$ ， $v$ ， $w$ ， $p$ ， $q$ ， $r$ 为AUV六自由度的角速度； $\dot u$ ， $\dot v$ ， $\dot w$ ， $\dot p$ ， $\dot q$ ， $\dot v$ 为AUV六自由度的角加速度； $X$ ， $Y$ ， $Z$ ， $K$ ， $M$ ， $N$ 为AUV六自由度的力矩。

3 仿真及分析 3.1 仿真条件设置

将几何模型导入到Adams，在Adams环境中进行修改设置各零部件名称、材质和约束条件基本信息。在Adams/view环境中根据实际状况设置AUV和V型翼的质心、浮心及绳索上对接点位置，设置相应的重力、浮力、水动力和AUV推力，在AUV、缆绳、V型翼之间建立接触添加相关参数。在Adams中通过宏命令建立绳索，仿真模型初始参数设置如表2所示。

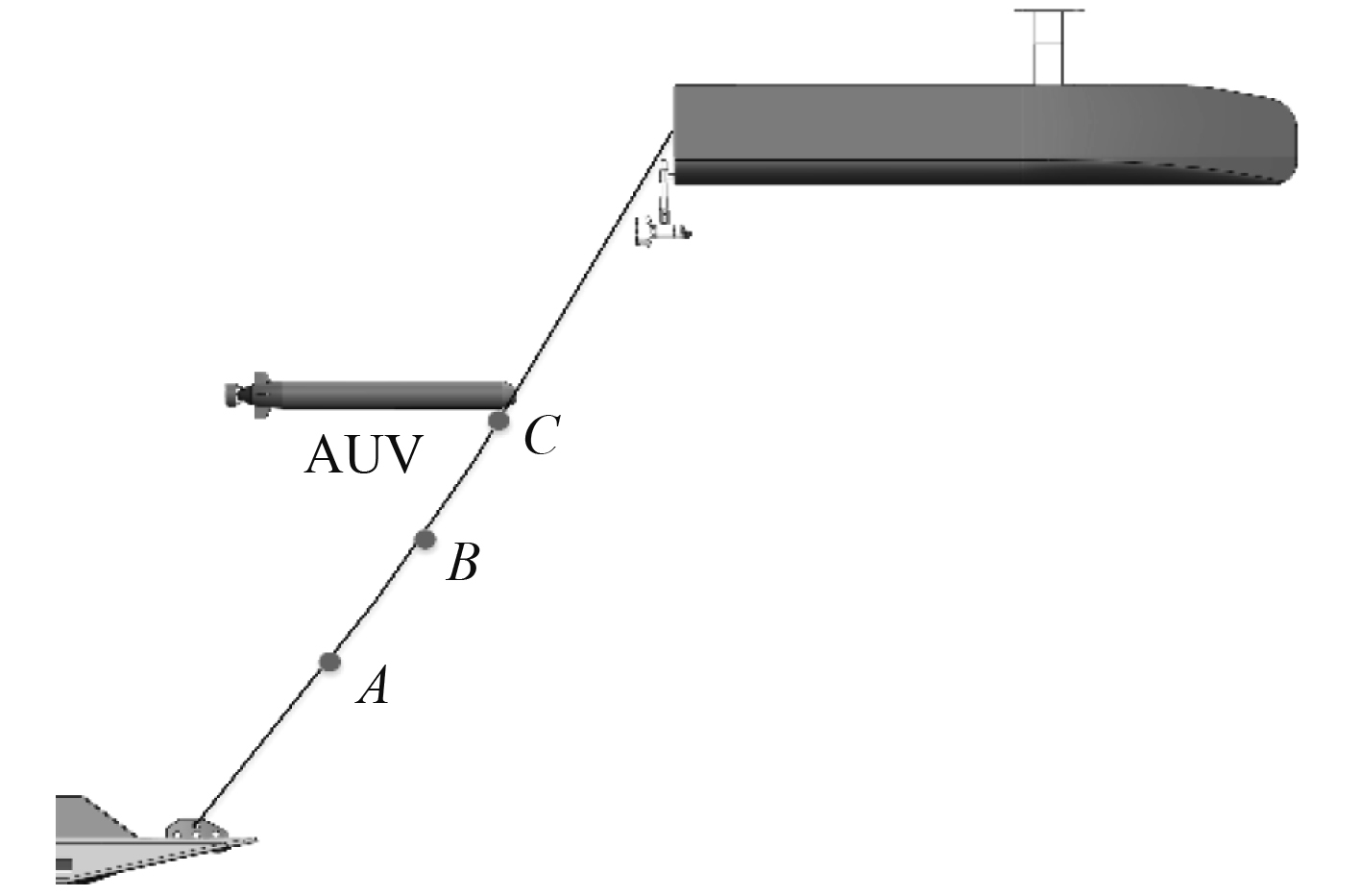
回收缆绳10 m，在缆绳上设置3个对接点，分别距离USV 在8 m，7 m，6 m处，依次标记为A，B，C等3个捕获对接点，如图6所示。

本文研究基于Adams动态回收AUV的仿真主要模拟以下工况：1）动态回收时，其他条件不变，通过改变拖曳速度对AUV回收的影响；2）在最佳拖曳速度下，通过改变收缆速度对AUV的影响；3）在拖曳速度和收缆速度最佳情况下，改变回收对接点位置，分析对AUV的状态和系统的影响。

3.2 仿真过程及分析

在Adams系统仿真时，为模拟回收场景，USV和V型翼均赋予不同的初速度，当USV和V型翼达到稳定状态时，AUV捕获缆绳。仿真过程可分为2个阶段。第一阶段: AUV自由航行到咬住缆绳，USV通过缆绳拖着V型翼，在水面以1.45 m/s稳定航行，时间间隔约为[0，7]；第2阶段：从AUV咬住缆绳，绞车收缆将其回收到USV为第2阶段，回收场景如图7所示。

3.2.1 拖曳速度对载体姿态的影响

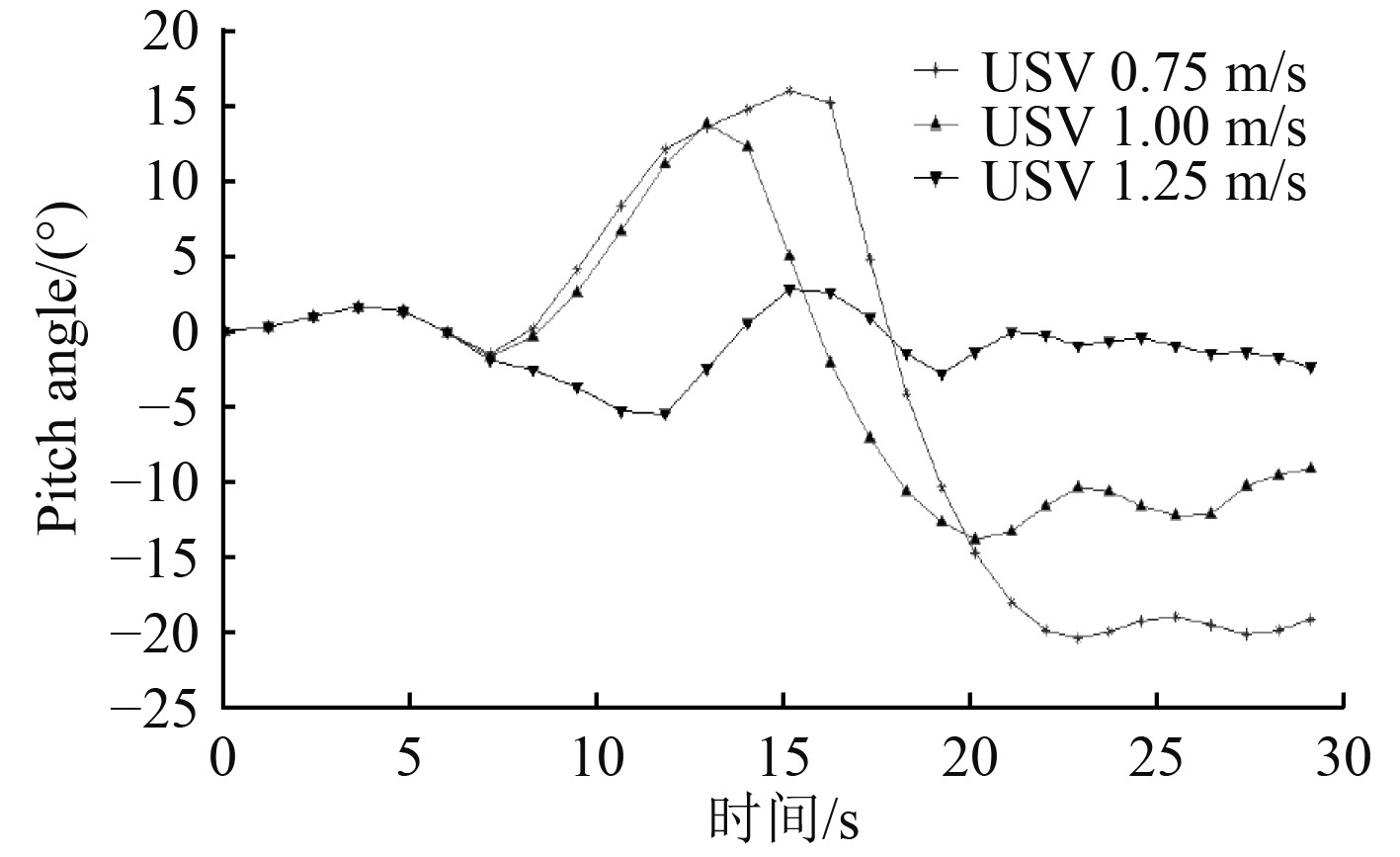
为避免USV拖曳回收过程中，AUV长时间处于大倾角状态，对设备造成损坏，因此对AUV的回收过程进行系统仿真。当改变USV拖曳速度时对应的纵倾角曲线如图8所示。

可知，当拖曳速度在0.75 m/s时，AUV的纵倾角在−20°～+15°之间波动，22 s左右达到平衡状态；当拖曳速度在1 m/s时，AUV的纵倾角在−12°～+15°之间波动，20 s左右达到平衡状态；当拖曳速度在1.25 m/s时，AUV纵倾角在−5°～+5°之间波动，18 s左右达到平衡状态。AUV在[0，7] s回收第1阶段捕获缆绳，捕获缆完成首先是向上抬首正向运动，然后向下埋首负向运动，最后达到平衡位置。这主要因AUV咬绳后无动力，USV拖曳速度快，当AUV速度接近拖曳速度运动呈现抬首负方向运动，速度相同时达到稳定状态。因此在动态回收时拖曳速度越大，对AUV姿态角的影响越小，故在动态拖曳回收AUV时采用拖曳航行速度1.25 m/s时较稳定。

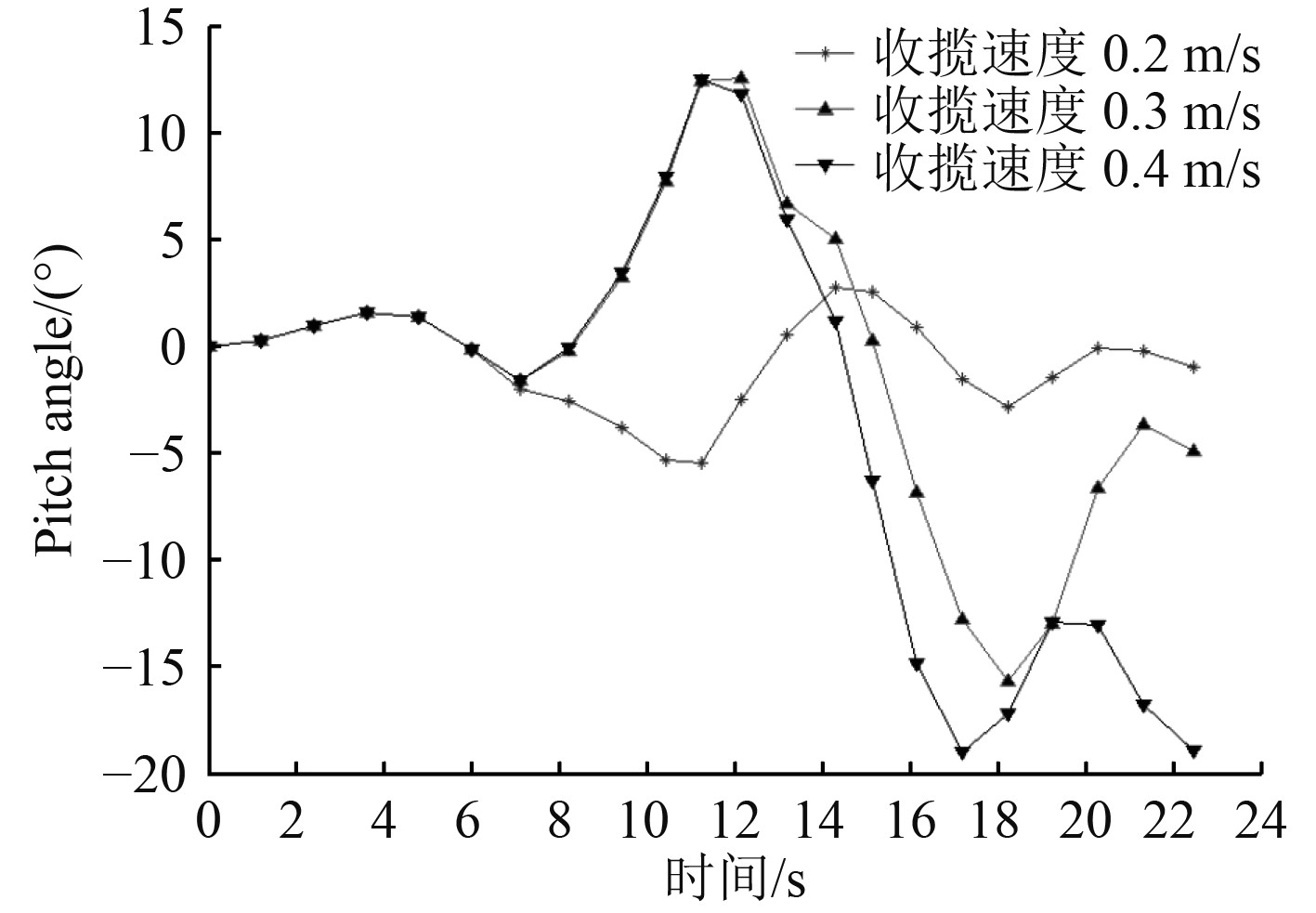
3.2.2 收缆速度对载体姿态的影响

在USV上装有绞车，为避免回收时系统不稳定带来的误差，设计绞车在开始第7 s时开始收缆，当绞车以0.2 m/s速度收缆，在22 s左右可以将AUV回收到水面；当以0.3 m/s速度收缆时20 s左右可以将AUV回收到水面；当以0.4 m/s速度收缆时18 s左右即可完成收缆工作。回收过程中AUV的纵倾角如下图9所示。

可知，当选择1.25 m/s最佳拖曳速度下通过改变收缆速度，对AUV影响不同。当绞车以0.2 m/s速度收缆时，AUV纵倾角在−5°～+5°之间波动，回收状态较为平稳；当绞车以0.3 m/s速度收缆时，在−15°～+15°之间波动，当AUV稳定时纵倾角在5°范围内波动；当绞车收缆速度0.4 m/s时，纵倾角在−20°～+15°之间波动，收缆速度不稳定。由于AUV在捕获缆绳后前进动力停止，缆绳收缆速度远大于AUV速度，AUV纵倾角瞬间变大，短时间内无法达到稳定状态。通过上述分析收缆速度越慢对AUV姿态角影响越小，选择在绞车0.2 m/s收缆时，AUV回收状态比较稳定。

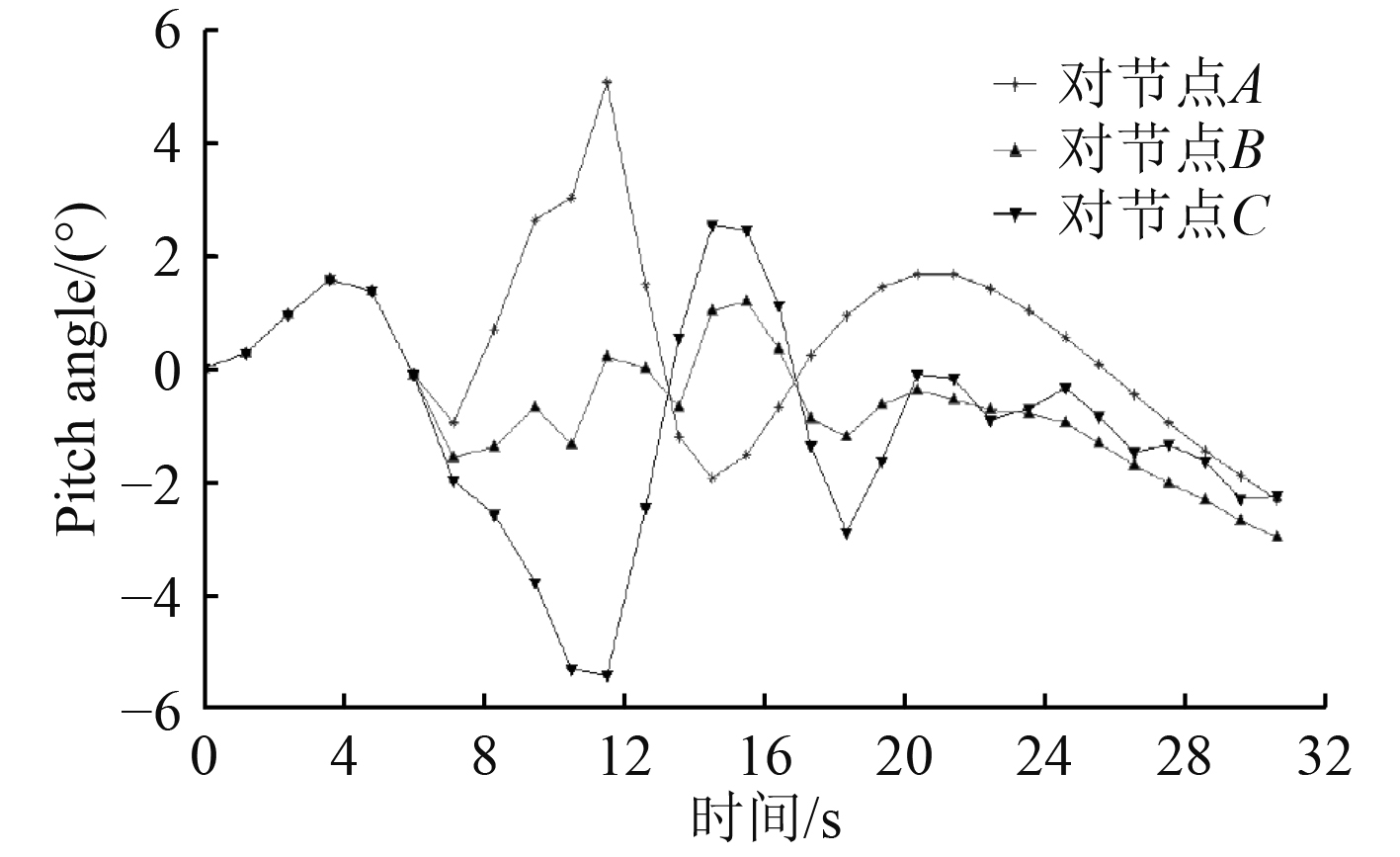
3.2.3 对接点对载体姿态的影响

基于回收缆绳设置的3个对接点分别是A，B，C，为研究在不同对接点对AUV回收过程中姿态的影响，仿真过程如图10所示。

选用最佳拖曳回收速度和收缆速度保持不变的前提下，改变3个不同对接点。可以得出当AUV捕获缆绳在对接点A和C时，AUV纵倾角先增大后减小，波动范围在8°左右，由于缆绳一端连接V型翼呈倾斜状态，缆绳回收开始阶段连接V型翼的一段会迅速靠近USV所以回收开始阶段在A点先抬艏再逐渐变小，C点同理；回收在对接点B时，纵倾角在−3°～+2°之间波动后趋于平缓状态，回收状态较好。回收对接点B处时AUV的姿态较为稳定，故确定B处为最佳对接点。

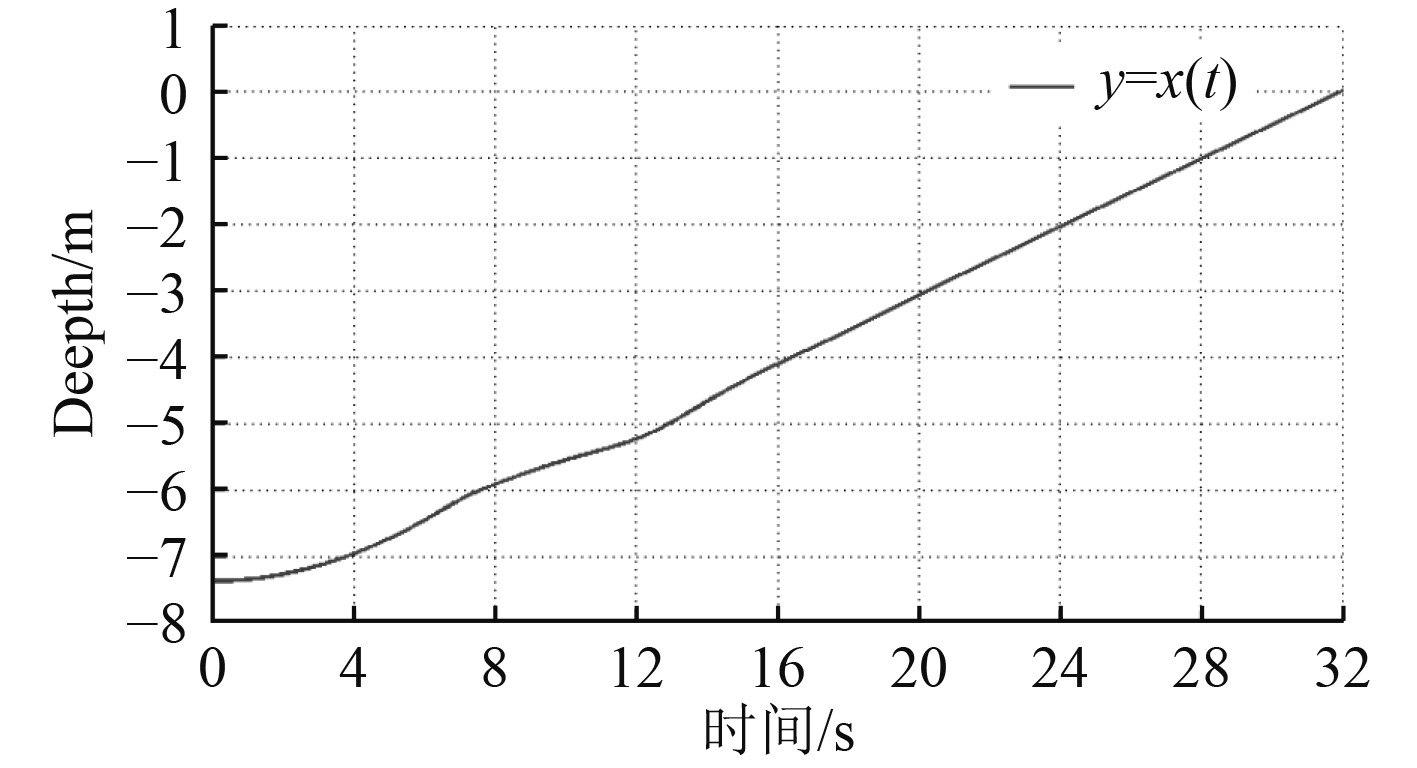
3.2.4 AUV轨迹及姿态角模拟仿真

在USV航行回收AUV过程中，AUV位置是不断变化的，由水下7 m至水平面缓慢上升，由图11仿真曲线可以看出仿真结果符合设计工况。

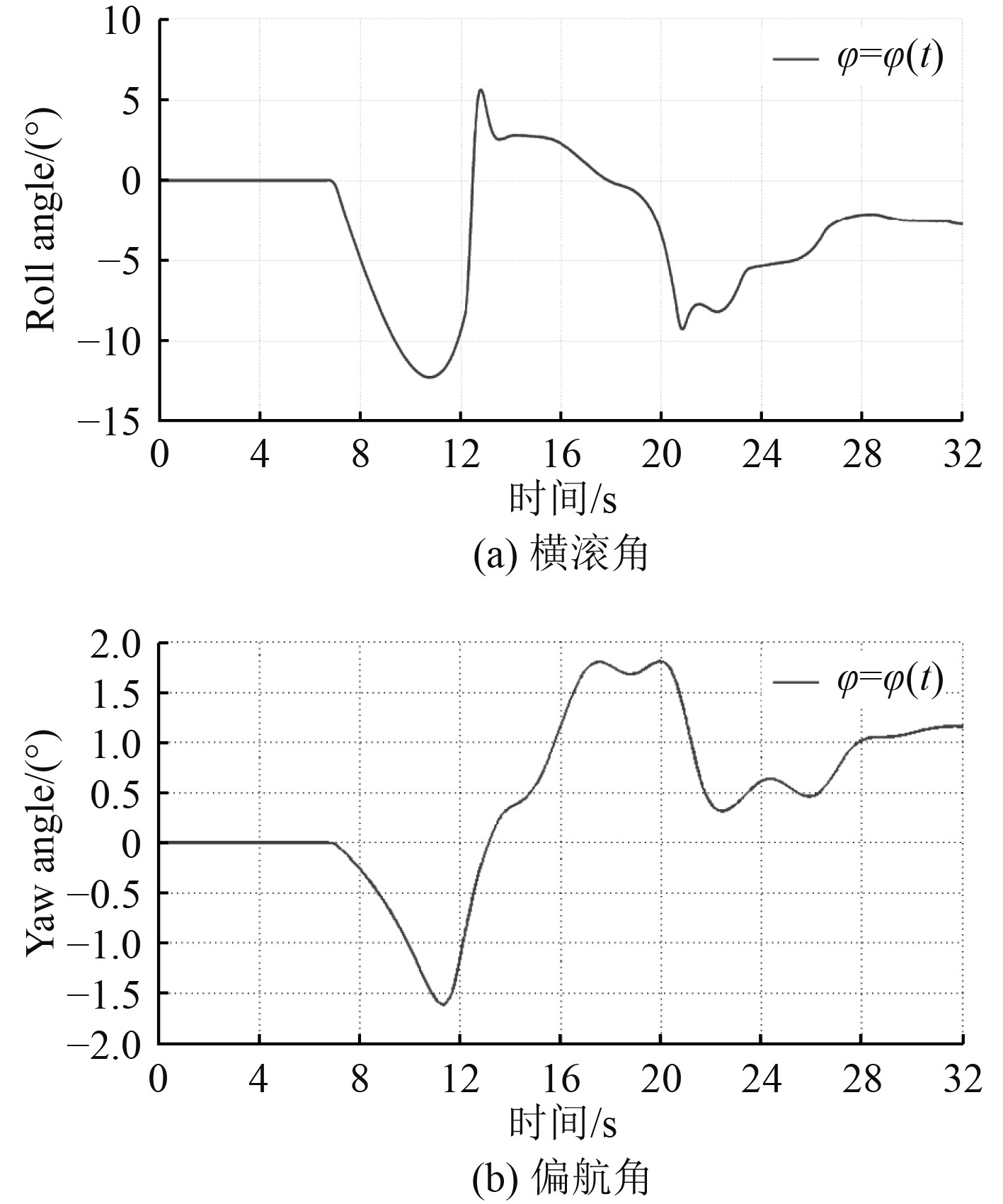
在拖曳速度、收缆速度和对接点选择最佳的同时，对AUV的回收过程进行仿真，在图11路径轨迹仿真图可以看出，模拟仿真和设想结果一致。图12（a）为AUV横滚角，在8～12 s缆绳对AUV速度低拉力增大横滚角变大，当AUV速度接近缆绳回收速度时横滚角逐渐变小。图12（b）为AUV偏航角，在−1.5°～+2°之间正常波动，对回收无影响。

4 结　语

本文模拟水下真实回收场景搭建回收系统，对AUV水下动力学模型建模，建立水动力六自由度方程，通过基于Adams水下模拟仿真，给出了拖曳系统在水下通过缆绳回收AUV的相关仿真参数。对回收工况进行模拟仿真，进行数据对比分析得出如下结论：建立基于Adams的 AUV动态模拟仿真，该AUV动态仿真回收系统可以实时便携地显示AUV模型的运动状态，可以重复调节AUV的回收速度、收缆速度、对接点，水下试验流程复杂，搭建仿真系统可节省人力和物力；在USV动态对接回收AUV过程中，当拖曳速度1.25 m/s，收缆速度0.2 m/s，对接点在B点时，回收对AUV位姿影响最小。本文仿真设计结果与方法对工程应用具有指导作用，为后期试验奠定基础。