最优航行路径规划是船舶应用系统设计的核心[1],其所描述的是航行路线的自动生成与优化,在明确初始点与目的点后,系统根据实际海域信息,通过规划模型实现航行路径规划。科学的航行路径规划结果既可以提升船舶的航行效率,同时还能够降低船舶航行过程中的能量消耗,因此研究船舶航行最优路径规划对于船舶航行产生重要的经济意义[2]。
陈新等[3]在研究船舶路径规划的问题中,以降低航行路程总量为目的,采用改进A~*算法实现路径规划目的。该方法在实际应用过程中未考虑船舶航行海域的复杂海面环境,导致最终的路径规划结果无法达到最优状态。刘雨青等[4]在研究路径规划问题中,构建周边的三维环境模型,以此为基础获取路线图,利用蚁群算法确定最优路径。该方法实际应用过程中路线图构建过程较为复杂。针对这些问题,本文研究复杂海面环境下船舶航行最优路径规划数学模型,确定满足复杂海面环境应用的船舶最优路径。
1 船舶航行最优路径规划数学模型构建 1.1 基于概率路图法的复杂海面路线图构建利用概率路图法将船舶航行的、具有复杂海面环境特征的全局海域环境转换成离散空间,经由连接采样点获取若干条由初始点至目的点的路径,生成路线图。复杂海面环境下的路线图生成需采集一定数量的路径点实现[5]。在复杂海面环境的构型空间内确定初始点与目的点后,在其余区域选取一个点,通过碰撞检测过程对采样点实施分析,如果该采样点处于自由空间内,那么可将该采样点作为路径节点,存储于路线图内;如果该采样点处于威胁空间内,那么需要清除该采样点。将新确定的路径节点同路线图内已存节点连接在一起,通过循环此过程直至复杂海面环境下航行路线图构建完成为止。概率路图法构建复杂海面环境下航行路线图的具体过程描述如下:
1)针对航行海域,构建一个无向图的航行路径网络
2)随机设定路径节点,在
3)针对各新的路径节点
4)将船舶可航行的路径边界
通过最优路径规划数学模型,获取构建的航行路线图最优船舶航行路径。复杂海面环境下船舶航行最优路径规划问题可理解为是在航行海域空间内,符合相应约束条件的条件下,依照某船舶航行性能评价指标
| $ {\min _\gamma }J = Y\rho {v^2}\frac{{SL}}{{2\Re }}。$ | (1) |
式中:
考虑复杂的海面环境,设定数学模型的约束条件如下:
| $ \forall \left( {x,y} \right) \notin {U_f}\mathop {}\nolimits_{} f\left( {x,y} \right) = 0,$ | (2) |
| $ {L_g} + {\delta _g} < {L_{\max }},$ | (3) |
| $ {\phi _i} \leqslant \varphi ,\forall i \leqslant m ,$ | (4) |
| $ {S_k} = \sum\limits_{i = 1}^{m - 2} {\frac{{{e^{\partial \left( {R - {r_i}} \right)}}}}{L}} \leqslant {S_{\max }}。$ | (5) |
式(2)为复杂海面环境下船舶航行最优路径规划过程中,地形与威胁约束。复杂海面环境下,船舶在航行过程中需避开危险区域与地形障碍(即船舶不可航行的区域),由此保障船舶航行的安全性。若当前船舶航行海域内,
式(3)为航程上限约束,其中
式(4)为转弯角度约束。航行过程中受机动性能作用,在转弯时角度需控制在一定角度中,
式(5)为路径平滑度约束,其中
针对式(1)所示的复杂海面环境下船舶航行路线图中航行最优路径规划数学模型,采用基于震荡型入侵野草优化算法进行航行路径寻优。最优路径规划的目的是在所构建的路线图内获取一个符合标准的解向量[7]。震荡型入侵野草优化算法内,不同野草的位置均可理解为路线图内的一条航行路径,不同路径的优化程度可根据航行性能评价指标
| $ J = \left[ {{j_1},{j_2}, \cdots ,{j_n}} \right],$ | (6) |
因此可依照代价函数值确定野草种群内适应度最优与最差的野草
| $ \left\{ \begin{gathered} {j_b} = \min \left( {{j_1},{j_2}, \cdots ,{j_n}} \right),\\ {j_w} = \max \left( {{j_1},{j_2}, \cdots ,{j_n}} \right) 。\\ \end{gathered} \right. $ | (7) |
在船舶航行路径寻优过程中,适应度较好的野草对于最终规划结果影响更显著,所以可将各野草生成后代的数量同
基于震荡型入侵野草优化算法的复杂海面环境下航行路径寻优过程具体描述如下:
1)依照航行实际状态设置科学的种群初始数量、种群数量上限、迭代次数上限、种子数量的上限与下限、非线性指数、标准方法初始值与最终值、寻优过程终止标准;
2)依照复杂海面环境下航行路径规划的要求设定算法维数,初始化野草种群与各株野草位置;
3)依照实际航行性能评价指标
4)分别确定各野草产生的种子数量与
5)在种群数量满足上限标准的条件下,对其中的全部野草,依照
6)更新当前迭代次数条件下寻优过程的标准方差;
7)确定是否满足迭代次数上限标准,若没有满足,则进行步骤4,相反结束寻优;
8)输出全局最优船舶航行性能评价指标值的野草所代表的航行轨迹。
2 实验结果为验证本文所研究的复杂海面环境下船舶航行最优路径规划数学模型在实际航行路径规划中的应用效果,以某运输船为研究对象,该船长度和宽度分别在400 m以上和65 m左右,单次运载能力可达到12500 TEU,其主要功能为向陆上基地与岛屿等传送人员、物资与装备等。设定研究对象在某10000 km×10000 km的海域内航行,采用本文模型对其航行路径进行规划,获取最优路径。表1为本文模型中的参数设定。
|
|
表 1 本文模型中的参数设定 Tab.1 Parameter setting in this model |
采用本文模型构建研究对象的路线图,所得结果如图1所示。
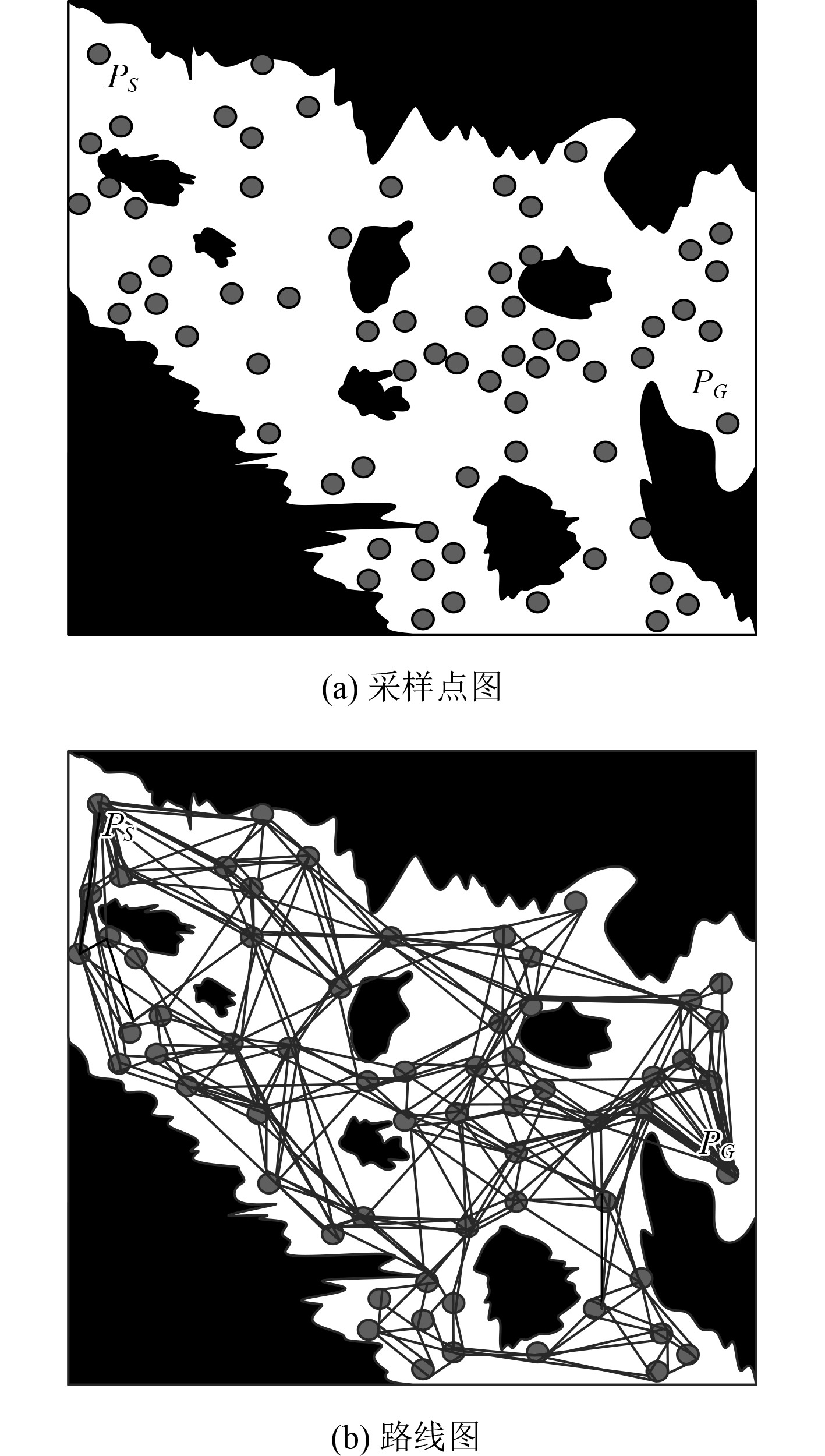
|
图 1 路线图构建结果 Fig. 1 Roadmap construction results |
图1内的黑色区域与白色区域分别为海域内的障碍物与可行区域,点与线分别为海域内的采样点与航行路径。设定船舶航行性能评价指标为能耗最低,所得航行路径规划结果如图2所示。由图2能够得到,在明确航行性能评价指标后,本文模型可有效规划出研究对象的最优航行路径,完全避开全部障碍物,由此验证了本文方法的有效性。
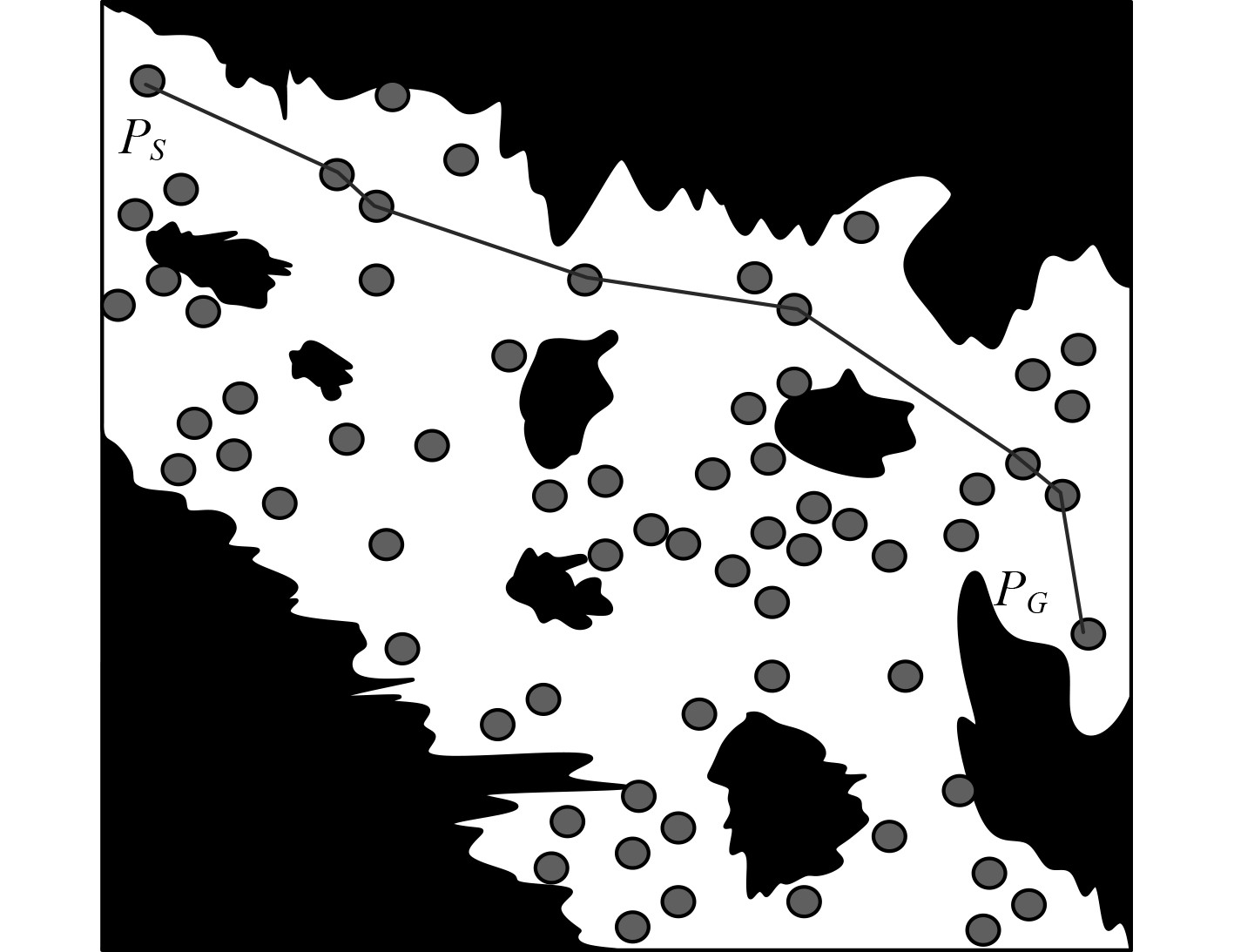
|
图 2 路径规划结果 Fig. 2 Path planning results |
为进一步验证本文模型的应用性能,设定不同海流情况,分析本文模型在航行性能评价指标分别为航行路径最短与能耗最低条件下的路径规划结果,所得结果如表2所示。分析表2能够得到,在研究对象处于顺流的条件下,与以路径最短为航行性能评价指标时相比,以能耗最低为航行性能评价指标时所规划的路径可节省更多能源。在研究对象处于逆流的条件下,以路径最短和以能耗最低为航行性能评价指标时所得的路径长度差异并不显著,以能耗最低为航行性能评价指标时所得路径能耗稍低。由此可知,在本文模型实际应用过程中,以能耗最低为航行性能评价指标可获取更优的规划结果,更利于船舶续航。
|
|
表 2 不同海流条件下本文模型路径规划结果分析 Tab.2 Analysis of route planning results of this model under different current conditions |
本文研究复杂海面环境下船舶航行最优路径规划数学模型。实验结果显示本文模型能够有效规划出研究对象的最优航行路径,并且在以能耗最低为航行性能评价指标时更利于船舶续航。
| [1] |
童帮裕, 胡坚堃. 基于改进蚁群算法的船舶冰区航行路径规划[J]. 中国航海, 2020, 43(1): 24-28. TONG Bangyu, HU Jiankun. Improved ant colony optimization for navigation path planning in ice zone[J]. Navigation of China, 2020, 43(1): 24-28. DOI:10.3969/j.issn.1000-4653.2020.01.005 |
| [2] |
蒋仁炎, 俞万能, 廖卫强, 等. 智能全电船的低能耗路径规划算法研究[J]. 中国造船, 2021, 62(2): 245-254. JIANG Renyan, YU Wanneng, LIAO Weiqiang, et al. Optimal energy consumption based path planning for intelligent all-electric ships[J]. Shipbuilding of China, 2021, 62(2): 245-254. DOI:10.3969/j.issn.1000-4882.2021.02.022 |
| [3] |
姚绪梁, 王峰, 王景芳, 等. 不确定海流环境下水下机器人最优时间路径规划[J]. 控制理论与应用, 2020, 37(6): 1302-1310. YAO Xuliang, WANG Feng, WANG Jingfang, et al. Time-optimal path planning for autonomous underwater vehicles with uncertain ocean[J]. Control Theory & Applications, 2020, 37(6): 1302-1310. |
| [4] |
刘雨青, 向军, 曹守启. 基于改进蚁群算法的水下自主航行机器人路径规划[J]. 计算机工程与科学, 2022, 44(3): 536-544. LIU Yuqing, XIANG Jun, CAO Shouqi. AUV path planning based on improved ant colony algorithm[J]. Computer Engineering and Science, 2022, 44(3): 536-544. DOI:10.3969/j.issn.1007-130X.2022.03.021 |
| [5] |
黄鹤, 李潇磊, 杨澜, 等. 引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划[J]. 西安交通大学学报, 2022, 56(7): 9-18. HUANG He, LI Xiaolei, YANG Lan, et al. Three dimensional path planning of unmanned underwater vehicle based on improved[J]. Journal of Xi'an Jiaotong University, 2022, 56(7): 9-18. |
| [6] |
王鑫, 田艺, 蒋华, 等. 基于锚节点移动路径动态规划的定位算法[J]. 计算机工程与设计, 2020, 41(8): 2135-2140. WANG Xin, TIAN Yi, JIANG Hua, et al. Location algorithm based on dynamic planning of anchor node moving path[J]. Computer Engineering and Design, 2020, 41(8): 2135-2140. DOI:10.16208/j.issn1000-7024.2020.08.007 |
| [7] |
赵苗, 高永琪, 吴笛霄, 等. 复杂海战场环境下AUV全局路径规划方法[J]. 国防科技大学学报, 2021, 43(1): 41-48. ZHAO Miao, GAO Yongqi, WU Dixiao, et al. AUV global path planning method in complex sea battle field environment[J]. Journal of National University of Defense Technology, 2021, 43(1): 41-48. DOI:10.11887/j.cn.202101006 |
 2022, Vol. 44
2022, Vol. 44
