2. 中国船舶集团有限公司第七一四研究所,北京 100101
2. The 714 Research Institute of CSSC, Beijing 100101, China
近些年来,随着国防及经济发展的需要,船舶推进系统的主机功率逐渐增大,所需的航速逐步提高,船体的振动所导致的系列问题也变得越来越显著。船上的管路空间复杂,工作环境多样,例如高温、高压、振动、腐蚀等,其中管路的振动问题是导致管路破坏的重要原因之一。当管系在工作状态下的振动响应过大时,其引起的动载荷会使管道连接位置的密封性降低,进而使管路可能发生泄漏问题,更剧烈的振动会使管路的强度较低的位置产生疲劳损坏,应力较大的位置如弯管和焊点可能由于疲劳而产生局部裂纹,使管路元件的承载强度降低,引起管路元件的疲劳断裂破坏。此外当作用在管系上激振力的频率接近于管路的固有频率时,会发生共振,会导致系统振动响应快速增大,使管路局部发生损坏,可能造成重大的经济损失。
关于船舶管路振动问题开展了很多研究。郭长青[1]研究输流管道与轴向流中板状结构的流固耦合问题,结果表明对于简支输流管道,系统的失稳方式可为发散失稳和单模态颤振;对于悬臂输流管道,系统的失稳方式主要为二、三阶单模态颤振。Ivo Senjanović[2]研究了船舶机舱动力传动系统扭振分析方法和工程验证;Lan Ding[3]研究了轴向荷载和结构阻尼对振动波在管系中传播的影响。张盛等[4]和陈果等[5]考虑到管道振动呈现周向特性,振动的方向可能是沿径向的任一方向,而弹簧和阻尼器都是单向元件,表现出单向性,设计有各向振动特性且便于安装的动力吸振器。穆翔[6]将阻尼橡胶垫与压电陶瓷堆用于管系减振,建立了捷联惯导主被动混合减振系统应用,并应用Ansys进行数值分析。Cha Philip D[7]使用经过适当调整振动吸收装置的参数,在谐波激发过程中抑制梁的过度振动。Gongmin Liu[8]对弹性约束下充液管道的振动分析;张琳等[9]提出了基于动柔度方法的管路动力吸振器,将弹簧和固定圆柱,质量阻尼设计研究;杨凯[10] 提出一种基于反共振原理的管路吸振器调谐方法,该方法利用吸振器带来的反共振物理特性,通过调谐动力吸振器固有频率,改变管路振动传递函数的反共振区域,使需要抑制的线谱频率处于该区域,从而改变管路振动传递特性,实现振动抑制。赵云龙[11]将阻振质量应用于船舶管道,并对其减振效果进行了实验研究。实验结果表明,在入射弯曲波频率较高时,阻振质量可以起到明显的隔振效果。但是在入射弯曲波频率较低时,阻振质量基本无法起到隔振的效果。在各种减振方式中,被动减振是一种经济实用的方式,对于精度等级要求不高的船舶管系减振更具有很大优点。动力吸振是将振动的能量转化为阻尼块的动能,进而达到减振效果。
上述研究主要是某一方向的消振,但是对于船舶管系来说,振动的来源有各种机器振动和外部的波浪冲击等,传递方向大致可以分为径向和轴向,为了保证正常航行,需要针对其特点进行减振研究。
本文对于船舶管路系统减振的问题,基于动力吸振原理,同时结合悬臂梁式吸振装置的特点,设计一种适用于船舶管路的新型动力吸振装置,并且以参数化的方式将装置尺寸与被减振管路外径建立比例关系。利用正交法选定装置参数的配比,并对得到的最优组合进行数值分析,通过隐式动力学对装置进行有限元数值分析,验证装置的减振性能和实用性。
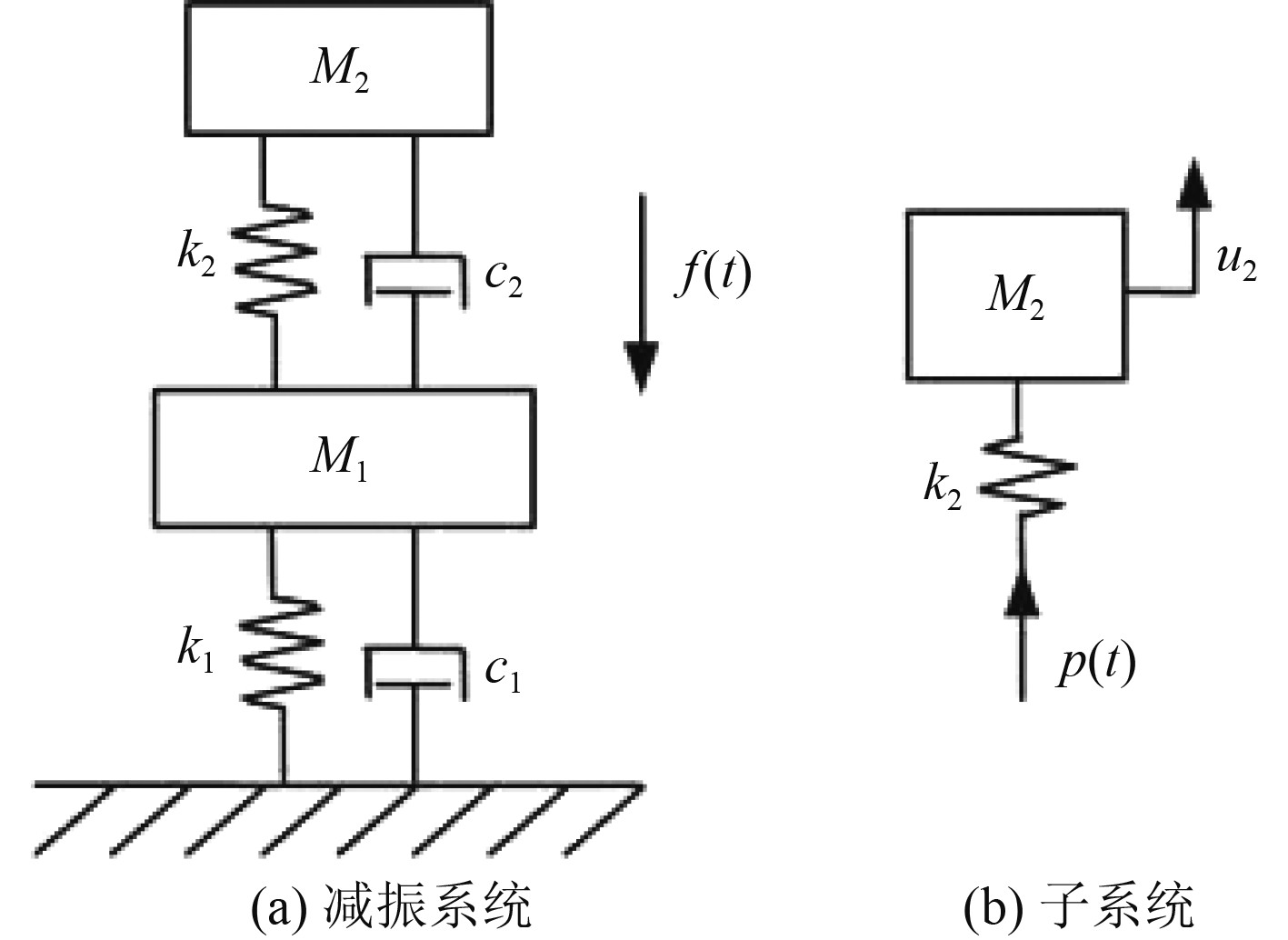
1 吸振装置的设计理论考虑到船舶管路布置及尺寸的特点,在将动力吸振装置应用于管系减振时,需要将船舶管系的特点考虑到减振装置的设计中,在主系统上附加一个子系统,使得通过子系统的运动吸收主系统的振动能量并将其主要转化为机械能释放出来,这样的子系统被称为吸振器。在图1中,由质量M1和弹簧结构k1组成的系统是主系统。为了在相当宽的工作范围内,使主系统振动级减到要求的强度,设计了由质量M2、阻尼c2和弹簧结构k2组成的系统即有阻尼吸振器。被减振的主系统和减振器组成了一个新的二自由度系统。
|
图 1 装置原理 Fig. 1 Device principle |
两系统间作用力
| $ p\left( \omega \right)= - {M_2}{\omega ^2}{U_2}\left( \omega \right) = - {M_2}{\omega ^2}\frac{{{k_2}}}{{{k_2} - {M_2}{\omega ^2}}}{U_1}\left( \omega \right)。$ | (1) |
式中:
| $ B = \frac{{\left( {{k_2} - {\omega ^2}{M_2}} \right) * f\left( t \right)}}{{\left( {{k_1} + {k_2} - {\omega ^2}{M_1}} \right)*\left( {{k_2} - {\omega ^2}{M_2}} \right) - k_2^2}} 。$ | (2) |
可知,当
| $ {k_2}({u_2} - {u_1}) = - {p_0}\sin \omega t \text{。}$ | (3) |
这个力与激振力大小相等,方向相反,从而达到主系统减振的目的(
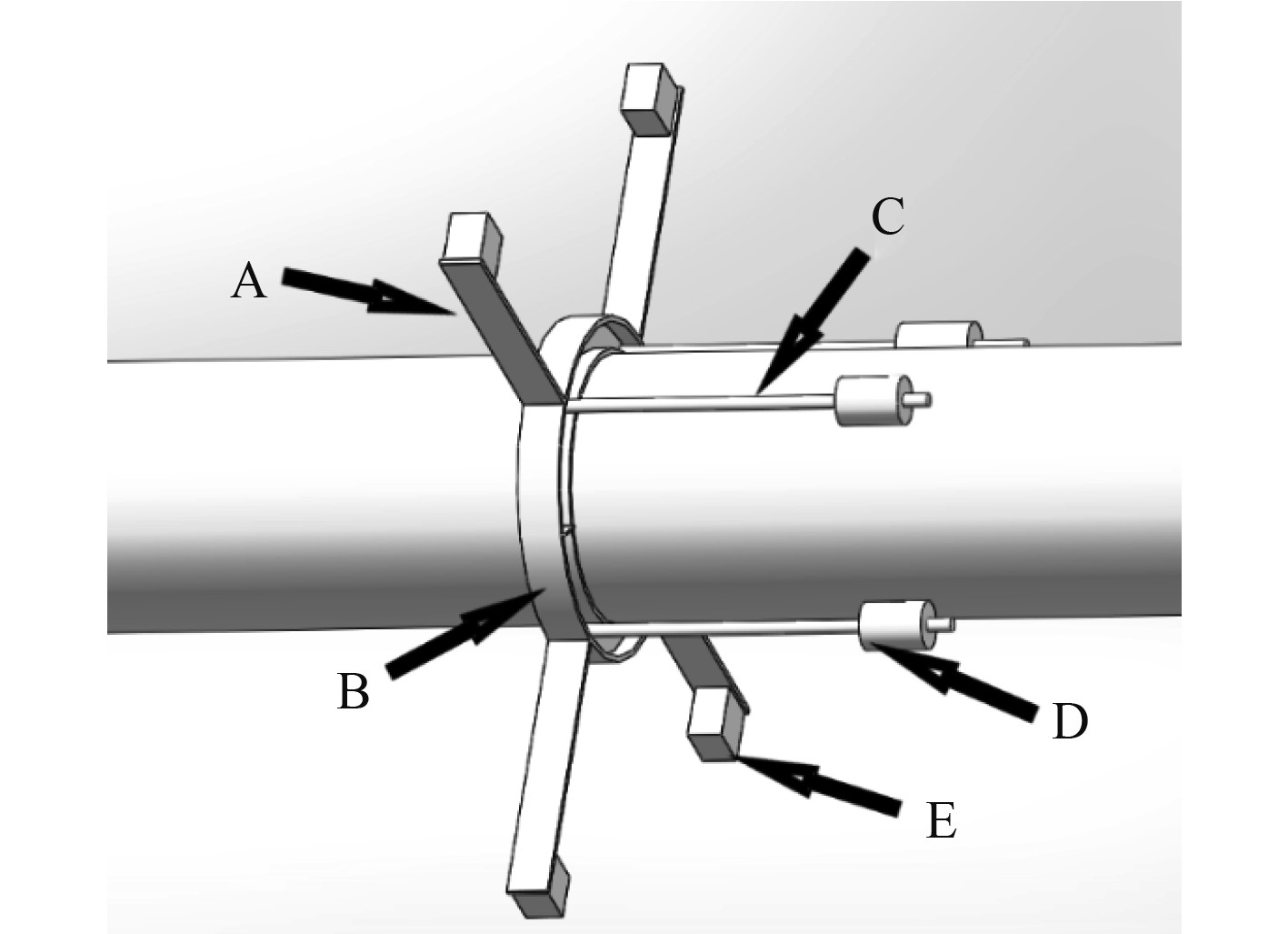
根据吸振原理,结合船舶管系振动特点,提出一种复合式动力吸振装置的设计方案。采用参数化建模的方式,建立整个装置结构参数与管系外径的比例关系。考虑到船舶管系所受的振动激励方向不一,结合传统悬臂梁式减振的特点,该吸振器将一组弹簧类结构-质量块组成系统,将4组弹簧类结构-质量块系统组成的减振装置安装在管路某节点上,以吸收该节点上的激励能量。由于船舶管路系统的结构几何外形大多为不同外径尺寸的圆柱形,将动力吸振器的固定结构(卡箍B)设计为工字形,并将用于吸振的质量阻尼(D和E)附加在弹簧片A和轴向柱状悬臂梁结构C上,上下两部分通过螺栓连接,弹簧片A宽度与卡箍B外宽度一致。图2为装置简化图。
|
图 2 吸振装置简化模型 Fig. 2 Simplified model of vibration absorber |
在图2中,吸振装置的子系统由环状卡箍B提供支撑,因为需要为轴向柱形结构提供运动空间,同时考虑到质量因素,将固定卡箍B的截面设计为工字形,采用密度较小的铝合金,根据陈果[5]的研究结论,装置4个弹簧片-质量阻尼系统固有频率不同,可以使位移频响函数出现4个峰值,增强装置效果,所以本文装置4个弹簧片上阻尼质量的位置不相同,同时在保证装置总质量一定的范围下,阻尼块质量大,可使减振效果更好。质量块的质量通常取被减振系统的1%左右。吸振装置的刚度由弹簧片和轴向悬臂梁提供,其弹性系数可根据管系的目标减振频率确定。
2.2 吸振装置材料设计装置的材料选择综合考虑结构强度、密度、弹性模量,如表1所示。
|
|
表 1 装置材料属性 Tab.1 Material properties of the device |
金属钛合金的密度一般在4.6 g/cm3左右,仅为钢的60%左右,纯钛的强度可以接近普通钢的强度,一些高强度钛合金甚至超过了许多合金结构钢的强度,本文装置的弹性结构为钛合金。质量阻尼块为结构钢,固定卡箍仅起连接和固定作用,固定卡箍的材料选定为铝合金。
3 减振装置效果数值分析 3.1 管路主要参数采用的数值管路来源于某84.6 m散货船,选取其中的机舱滑油输送管系。散货船主机功率735 kW,管路主体材料为结构钢,管系外径86 mm,总质量为146.9 kg,结构阻尼0.005。图3为主机滑油输送管路系统的有限元模型。

|
图 3 机舱滑油输送管路系统 Fig. 3 Lubricating oil conveying pipeline system in engine room |
机舱的滑油输送管系是一个连续的系统,在工程实践中多利用传递函数法或有限元法将其转化为一个多自由度的模型。虽然多自由度系统的振动包含了各阶振型,但若各阶模态频率相隔较远,在共振频率处,通常表现为单一模态的振动。此时,一般可忽略各模态之间的相互影响,将各模态分别进行处理。
3.2 装置对管系固有频率的影响由管系外径可得装置质量为5.58 kg,约束参照实际约束,即两侧固定法兰和中部吊环施加约束,对管系进行模态分析,并在位移危险点布置该减振装置,进而得到装置对管路系统固有频率的影响。表2吸振装置对管系固有频率的影响。
|
|
表 2 管系固有频率的变化 Tab.2 Changes of piping natural frequency |
可以看出对于低阶振型(1阶~3阶),单个减振可以使固有频率最高降低30%左右,对于高阶振型(4阶~6阶)可以使固有频率降低50%~65%左右,而2个装置对于固有频率的影响不明显。
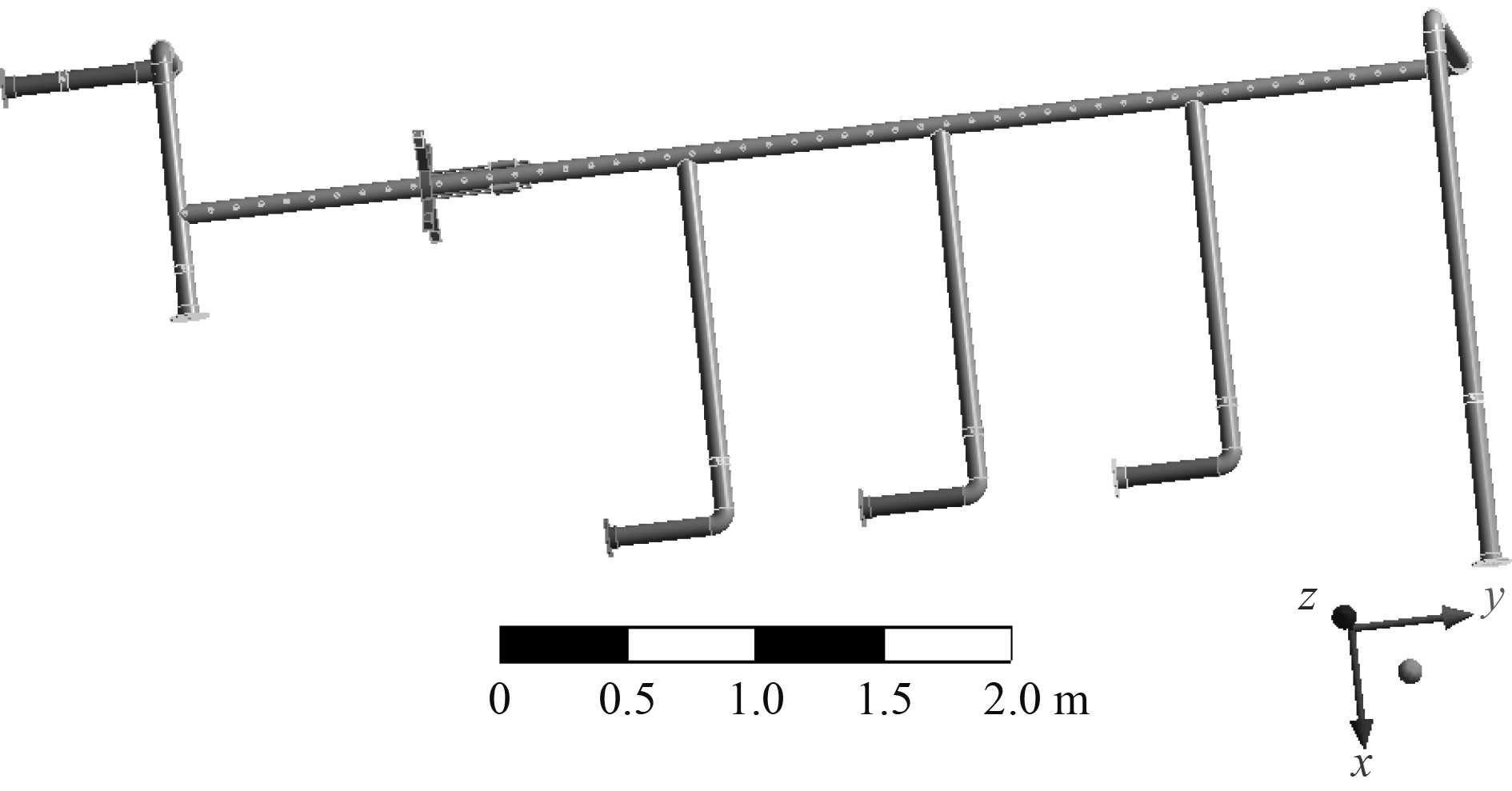
3.3 吸振装置瞬态分析装置性能的分析使用Workbench的隐式动力学模块,在所选用管系的一端施加幅值为500N的正弦激励,并且以装置的位置为中心,在管路外表面设置间隔为100 mm的数值采集点。图4为在管系一侧选定的数值采集点,采集振动的相关数据。
|
图 4 振动测点布置 Fig. 4 Vibration measurement points |
将船舶主机的振动激励施加在管系上,装置总质量取管系总质量1%,本文装置5.86 kg,管系质量148.6 kg,即需要在管系施加2个吸振装置。取激励作用时间为10 s,提取测点振幅Z方向和X方向的数据,加速度Z方向和X方向的数据,并进行前后对照。图5为在激励作用下Z向振幅对比,图6为在激励作用下X向振幅对比。图7 为在激励作用下Z向加速度对比,图8为在激励作用下X向加速度对比。
|
图 5 Z向振幅对比 Fig. 5 Comparison of Z-direction amplitudes |
|
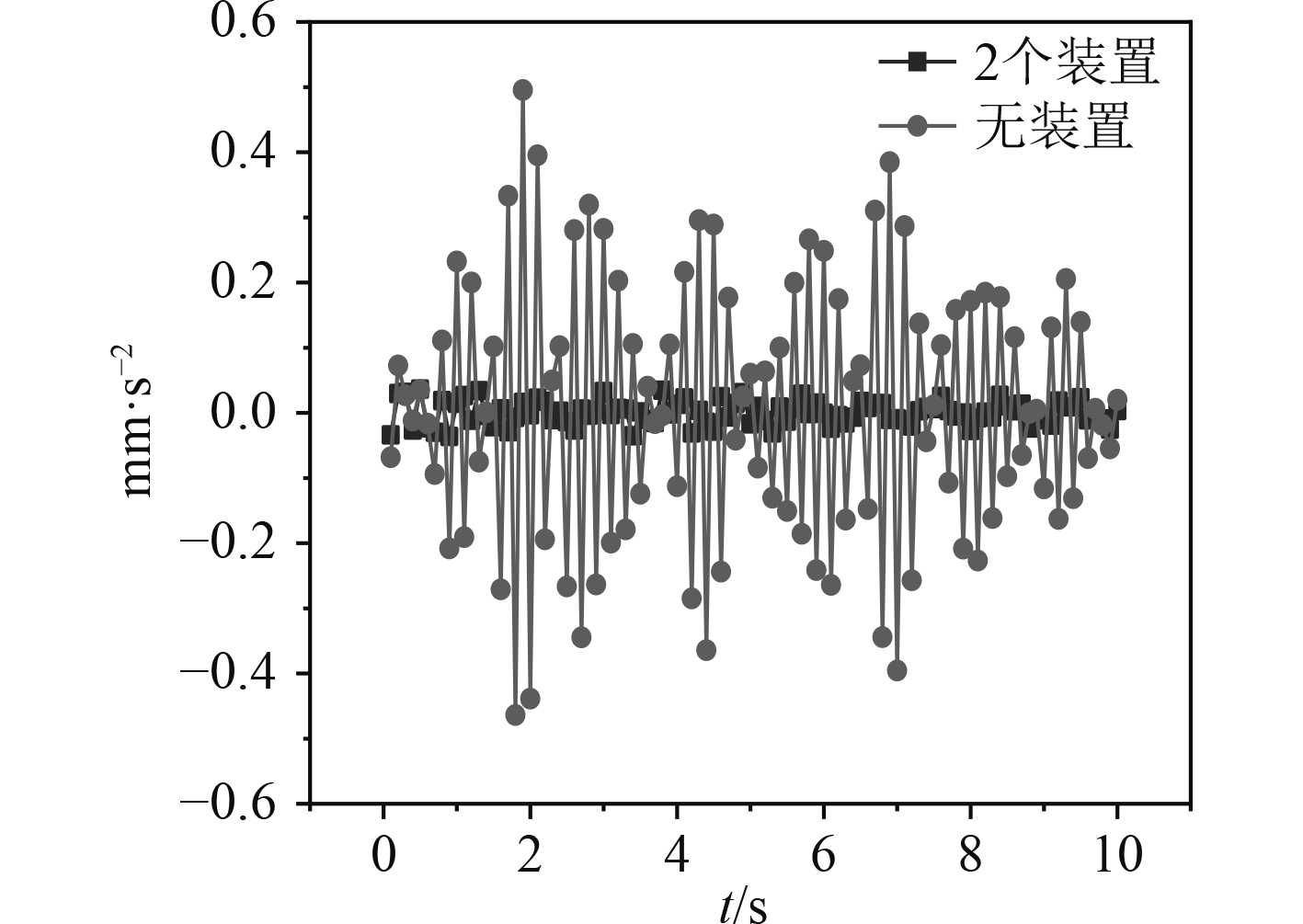
图 6 X向振幅对比 Fig. 6 Comparison of amplitude in X direction |
|
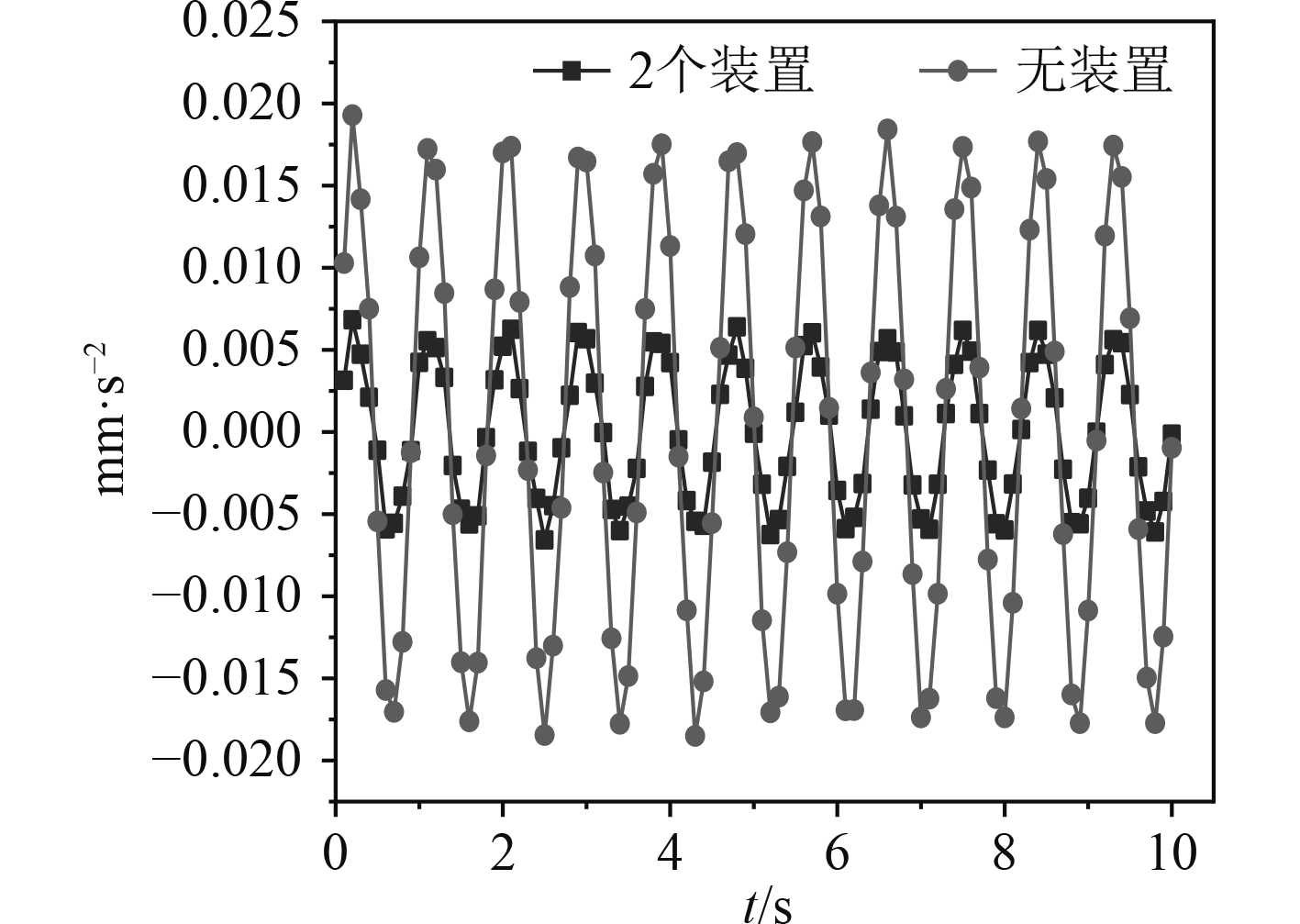
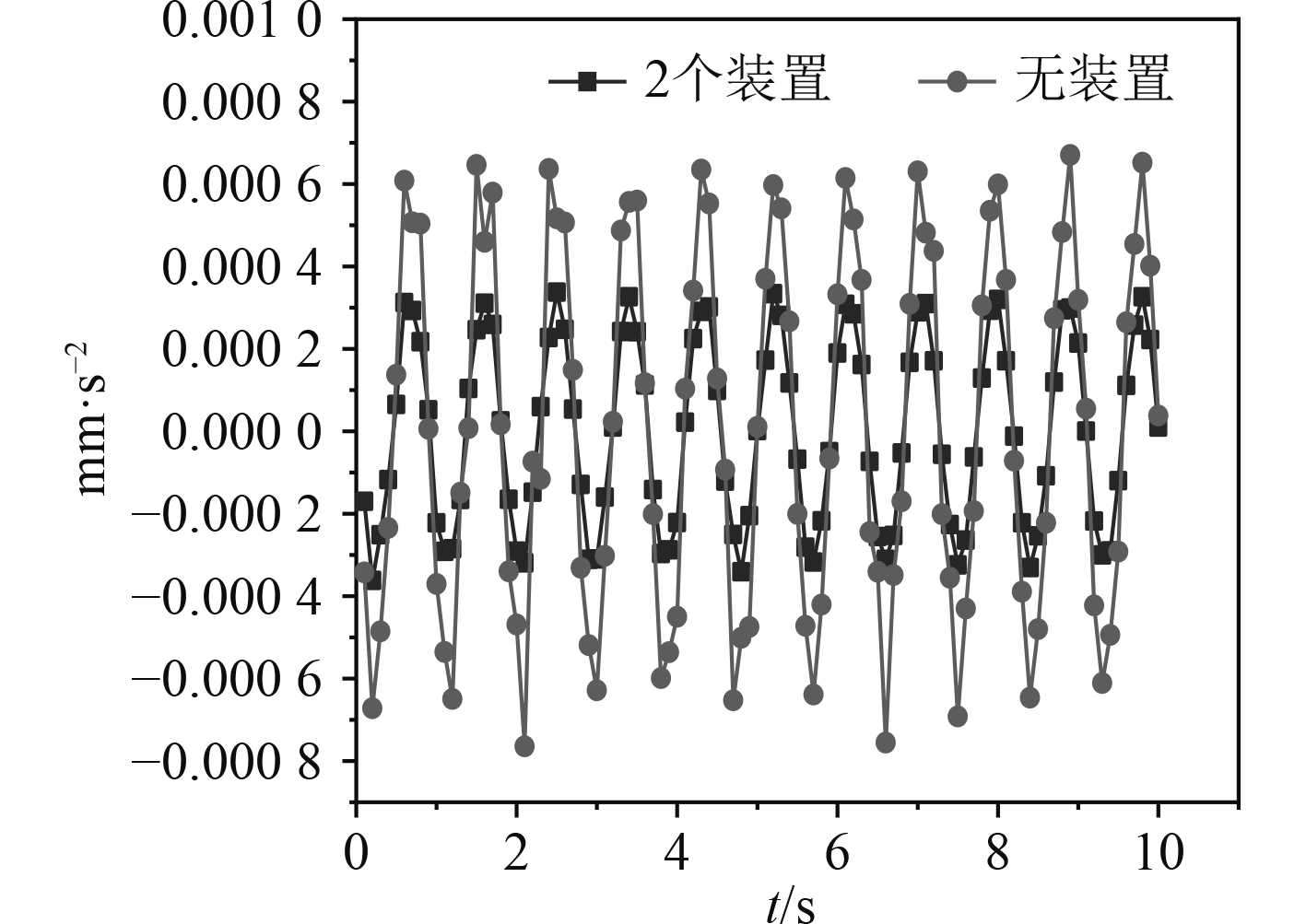
图 7 Z向加速度对比 Fig. 7 Comparison of Z-acceleration |
|
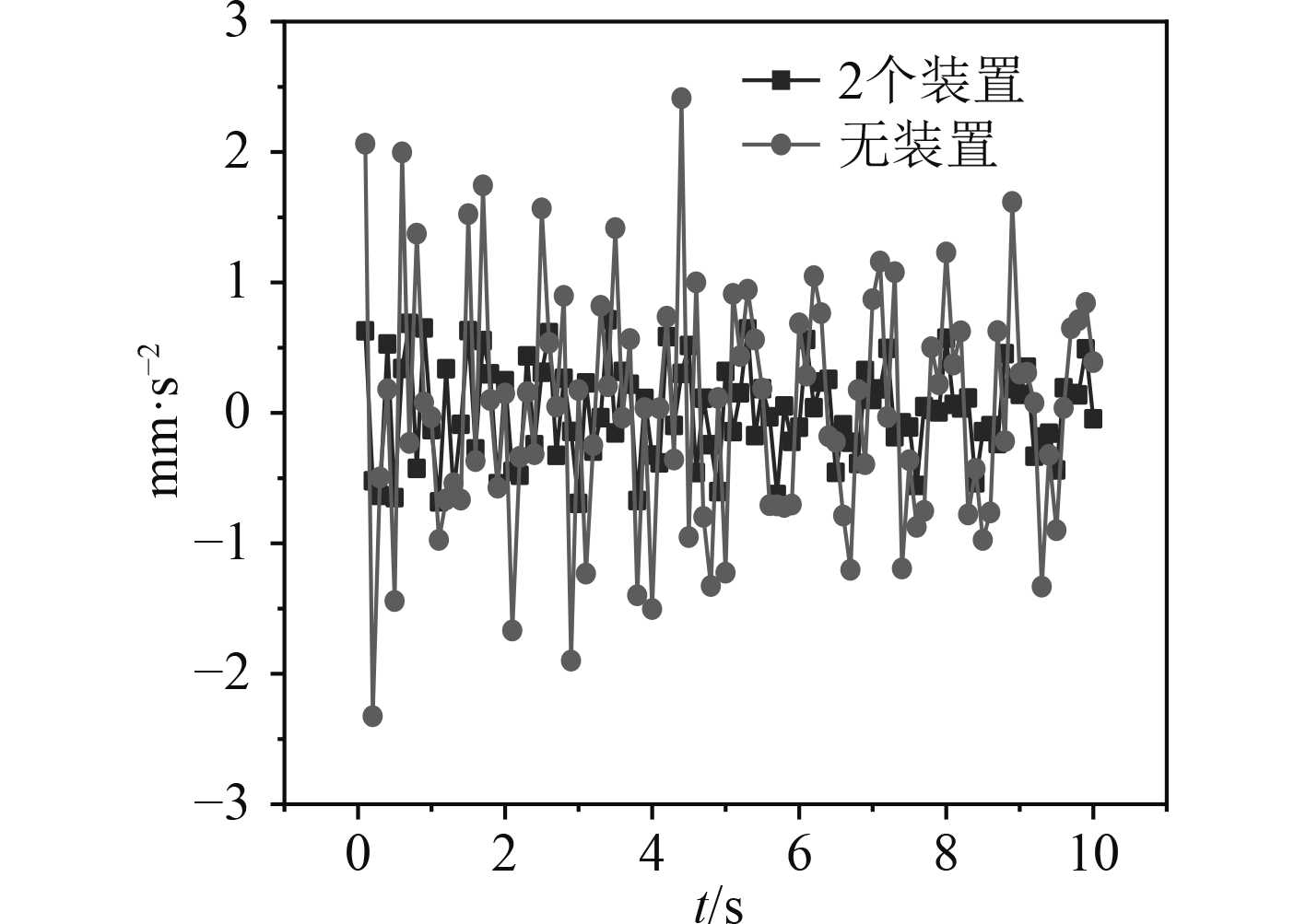
图 8 X向加速度对比 Fig. 8 Comparison of X-direction acceleration |
从图5和图6可以看出,相同主机激励的作用下,在安装吸振装置后,目标测点的位移幅值在Z方向,位移降幅可达65%,在X方向,位移降幅54%,其中Z向为激励作用方向。
从图7和图8可以看出,相同激励的作用下,在安装吸振装置后,目标测点的加速度在Z方向插入损失可达14.5 dB左右,在X方向,加速度插入损失可达23.5 dB左右。
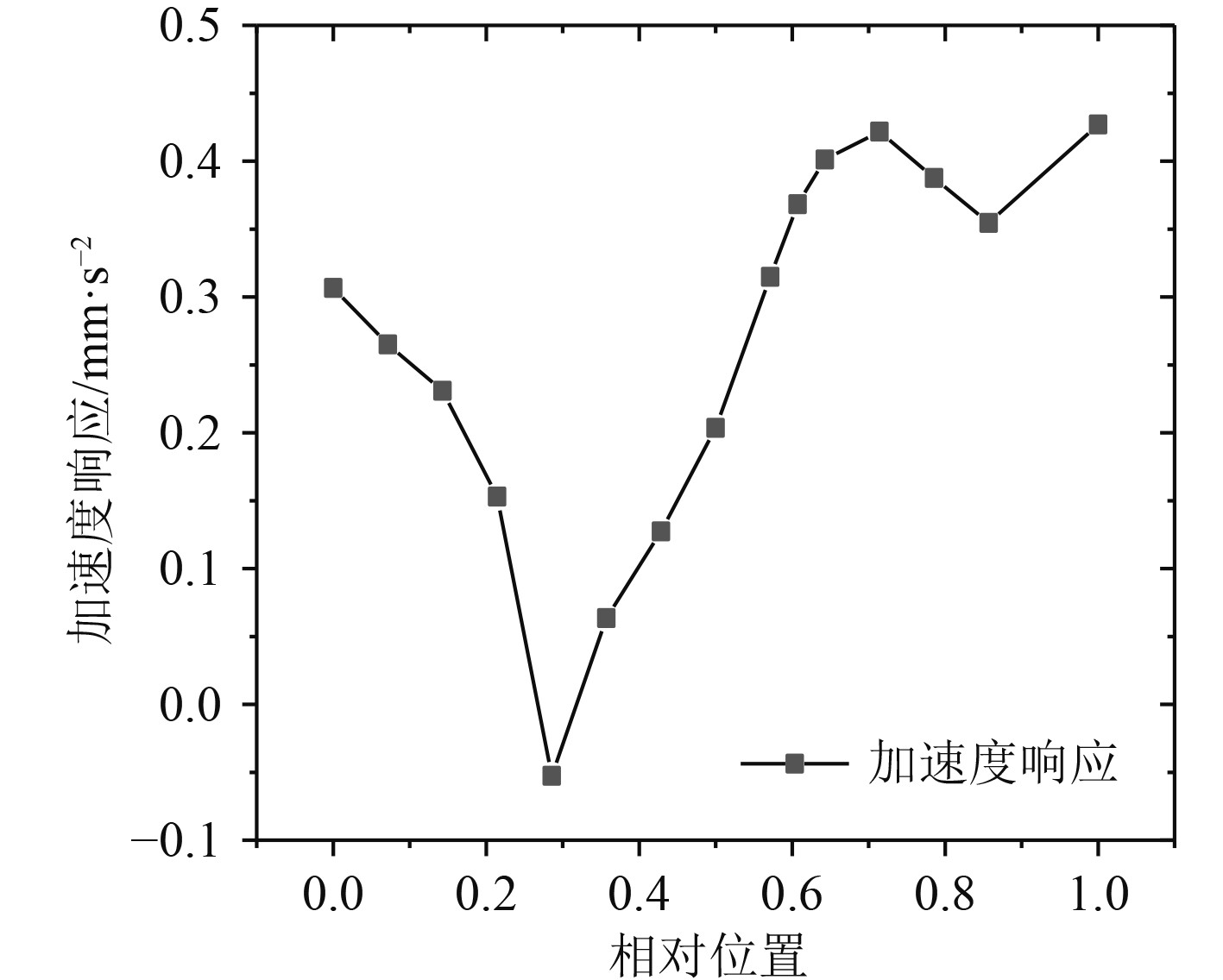
4 动力吸振装置参数分析 4.1 装置布置方式船舶管系在空间上比较复杂,对于装置的布置需要分类研究。本文考虑的因素包括:装置相对于激励的位置,管系空间走向。工况为安装单个吸振装置,正弦激励,根据模态分析,确定最危险点,通过调整吸振装置的位置,采集危险点加速度幅值的变化。图9为主管系不同位置的加速度响应,图10为支管系不同位置的加速度响应。
|
图 9 主管系加速度 Fig. 9 Main acceleration |
|
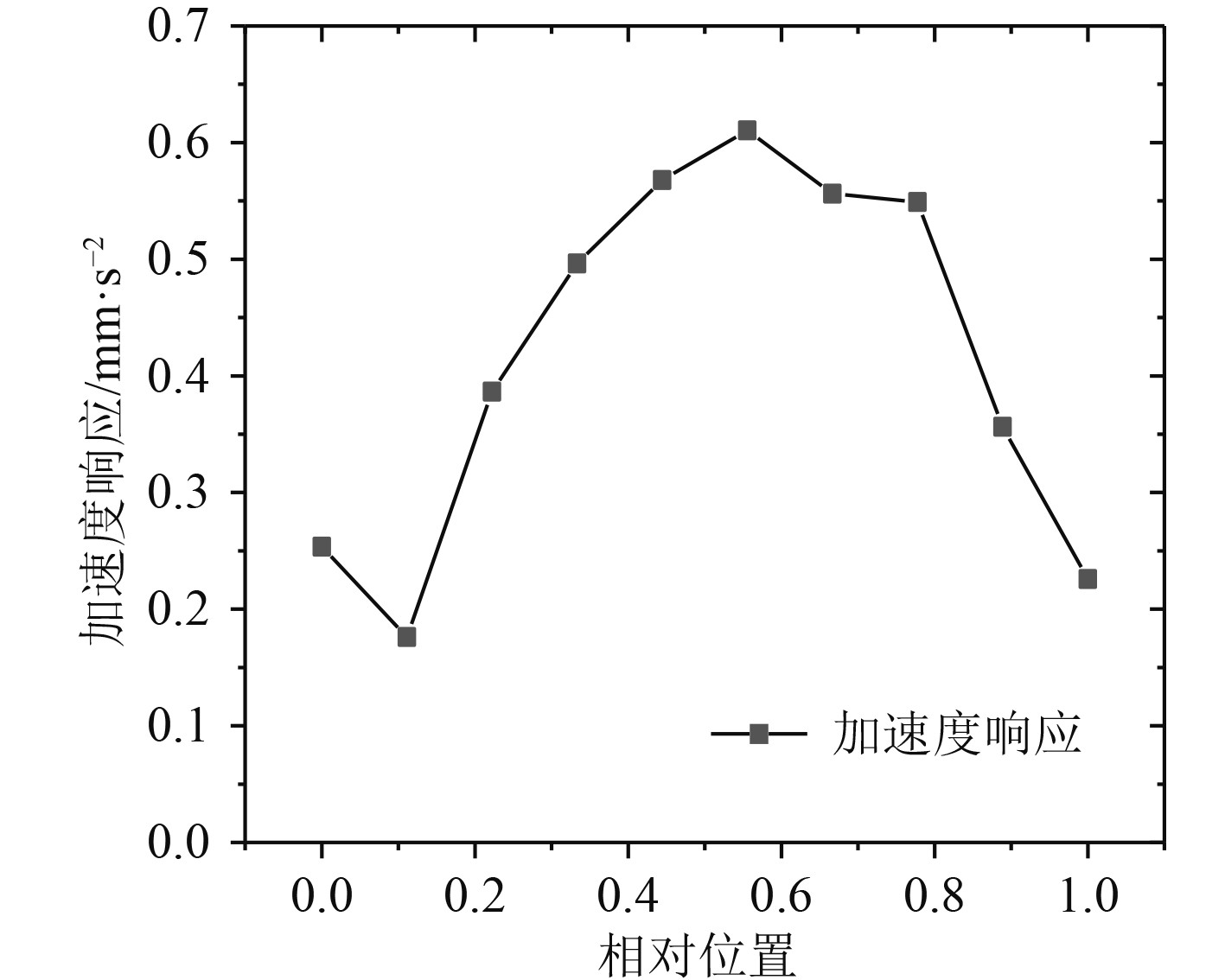
图 10 点支管系加速度 Fig. 10 Acceleration of branch system at point |
图9中零点为靠近激励的一侧,通过归一化得到加速度与相对安装位置的变化关系,可以看出,装置布置在靠近激励的一侧1/3处对于加速度的吸收效果最好;图10中零点为靠近主干管系的一侧,右侧为点约束,当安装在旁支管系时,通过归一化可以发现装置近似布置在1/4处效果最好,相比于其他位置降低程度可以平均增强20%左右。
4.2 装置有效范围分析管系在正弦激励作用下,设置施加吸振装置和无吸振装置作为对比,对振动产生的位移幅值进行分析。图11为在不同频率下,配置一个装置的有效范围,图12为在不同频率下,配置2个吸振装置的有效范围和叠加情况。
|
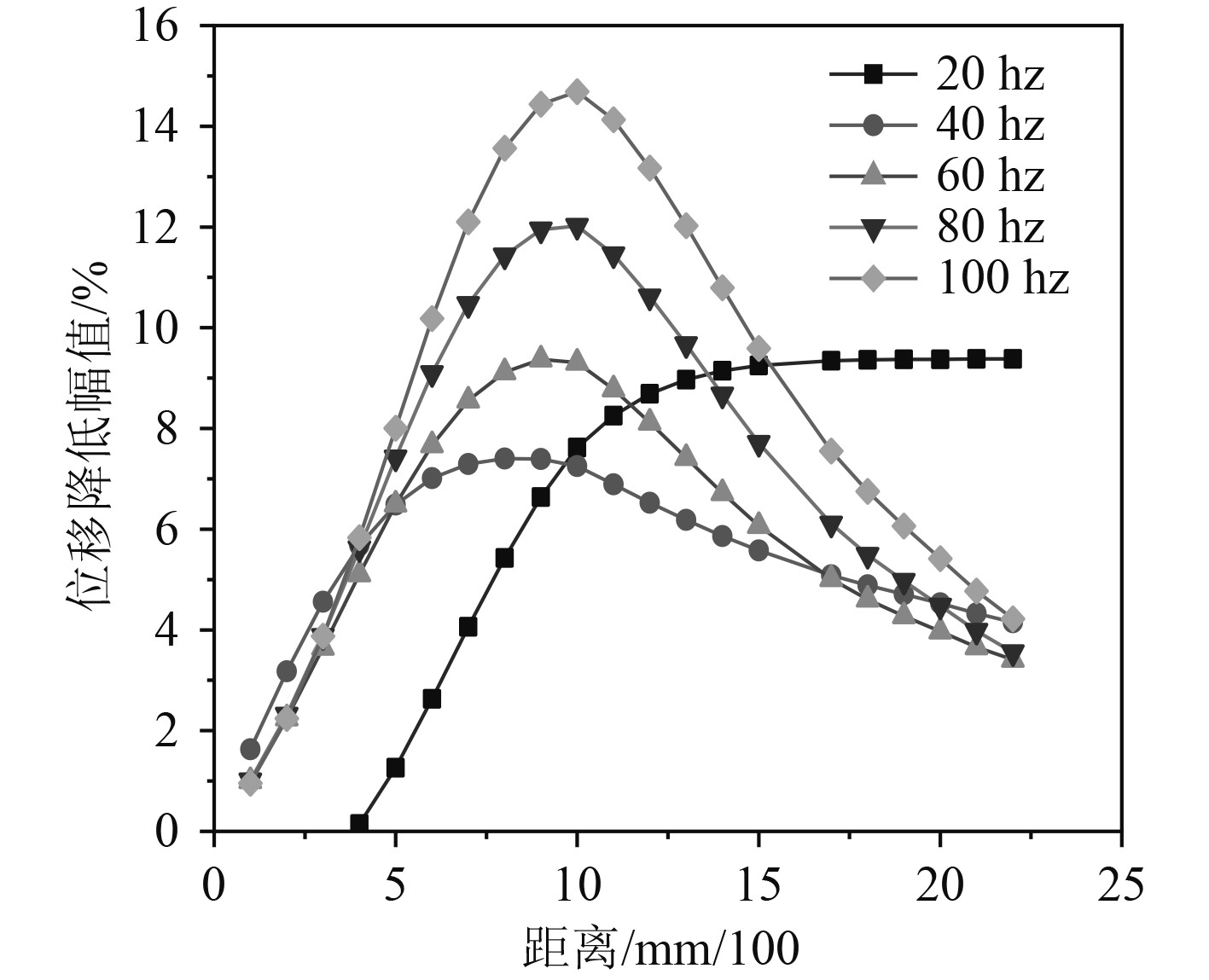
图 11 单个装置有效范围 Fig. 11 Effective range of a single device |
|
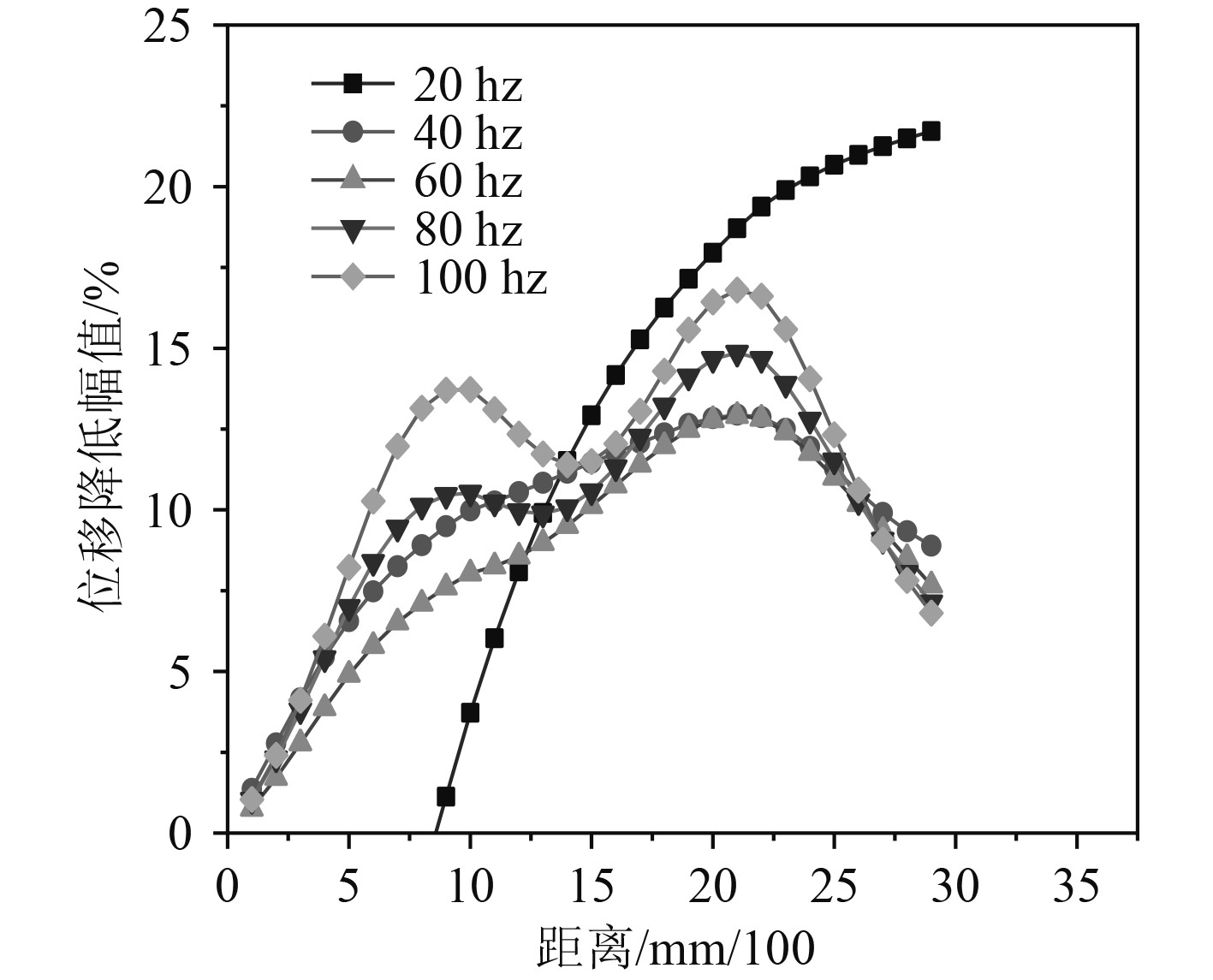
图 12 双减振装置有效范围 Fig. 12 Effective range of double damping device |
由图11可以看出,管系外径为86 mm时,装置有效范围在6R~56R左右,即外径的50倍左右。由图12可以看出,在间距为1250 mm的2个装置作用下,在原幅值曲线基础上,峰值得到了增强,减振效果得到叠加,对于低频的减振增益效果更显著。
4.3 装置设计参数对减振效果影响在总质量一定的情况下,为了达到最优的质量配置,需要研究各结构的尺寸参数对装置减振效果的影响,影响装置减振效果的因素主要有3个,即弹簧片长宽比(A)、弹簧片阻尼质量(B)、悬臂梁阻尼质量(C)。表3所示为装置参数因素调整区间。
|
|
表 3 因素调整区间 Tab.3 Adjustment interval of factors |
根据表3所示的因素调整范围,选定9组工况参数组合,对比同一时刻下的加速度变化,可以选出最优的配置区间。表4为装置参数工况表。
|
|
表 4 装置参数影响 Tab.4 Influence of device parameters |
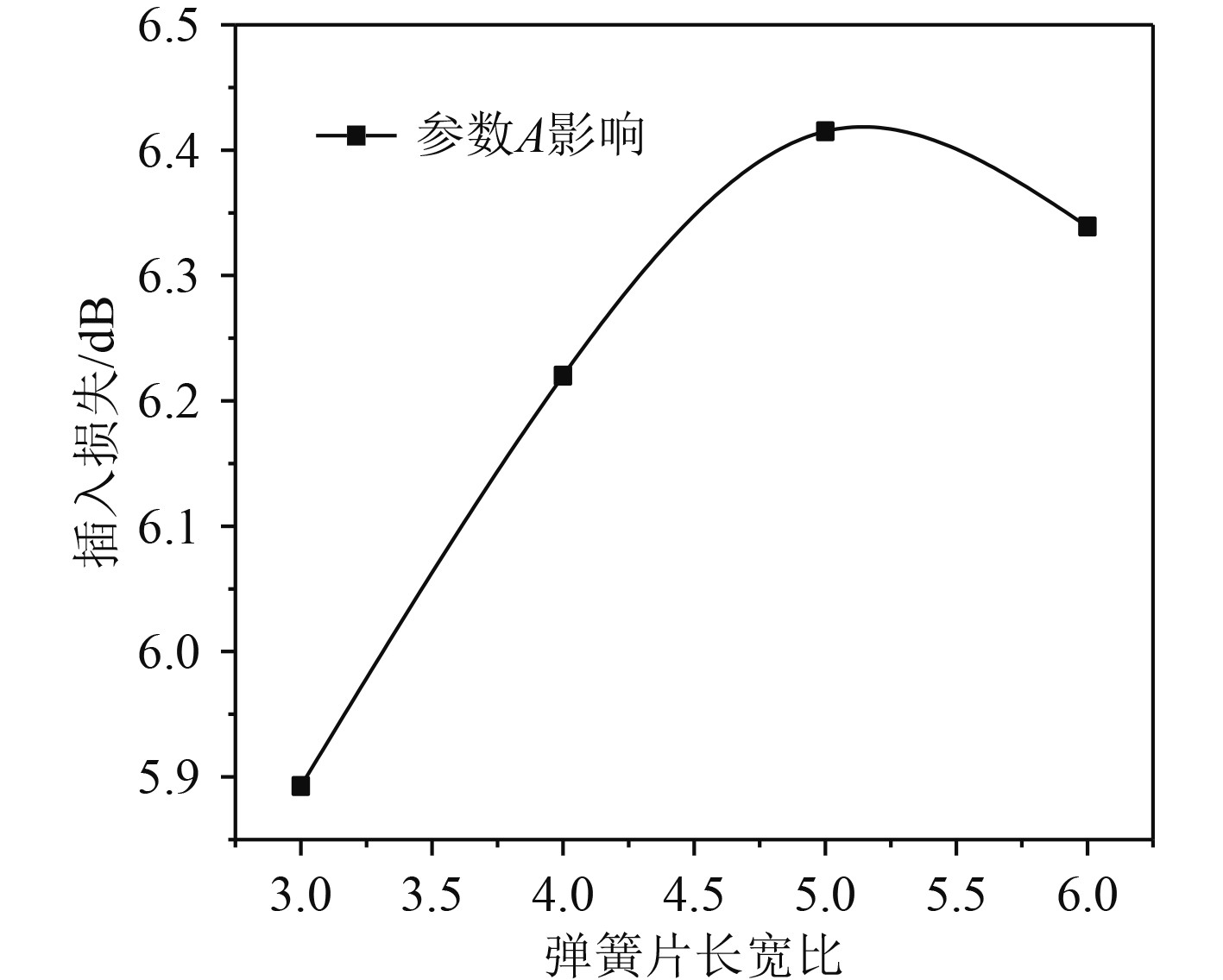
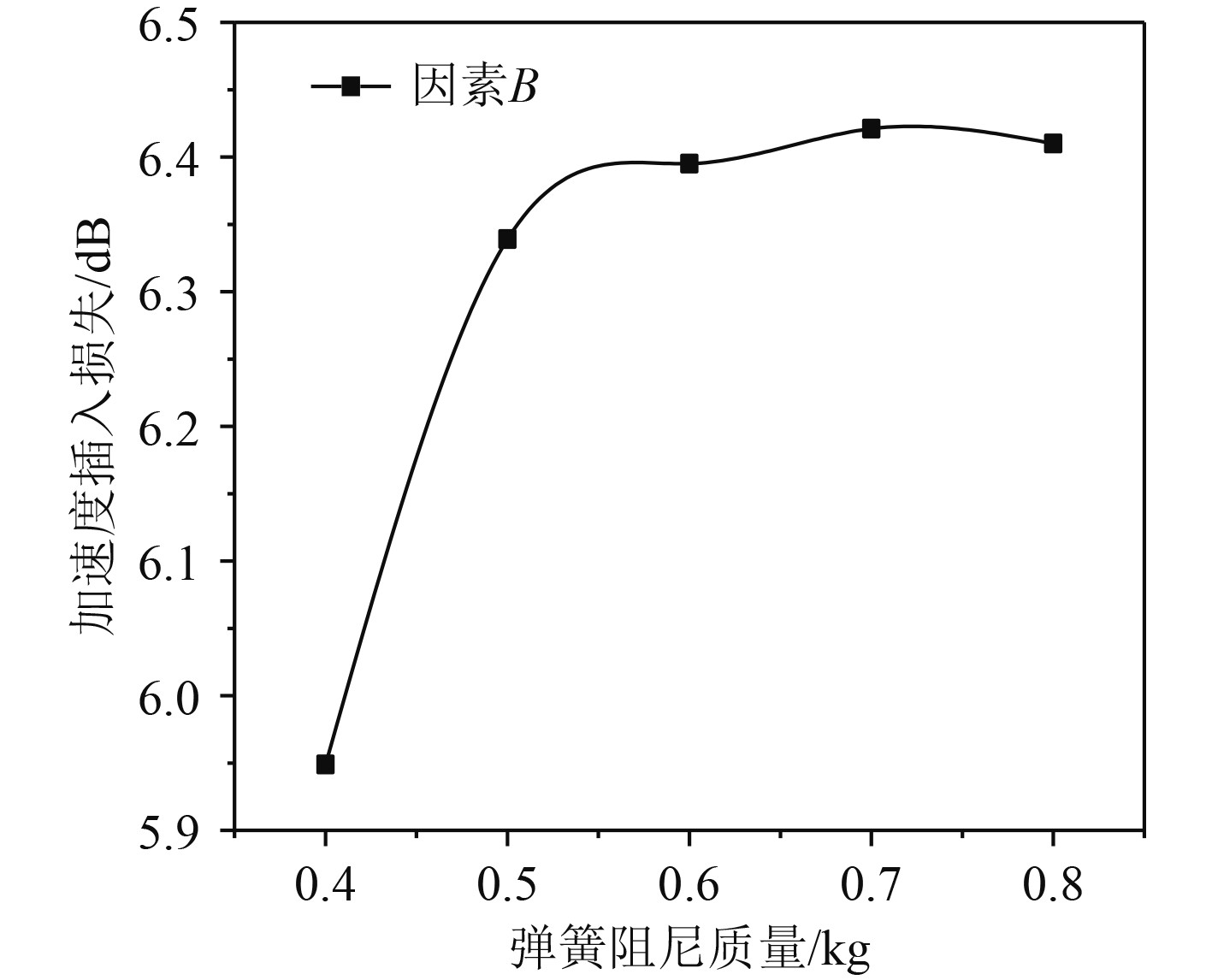
在控制装置总质量一定的情况下,从图13可以看出,卡箍和弹簧片宽度增大,加速度插入损失先增后减;从工况1和工况3可以看出,弹簧片阻尼块对装置效果影响因素大于悬臂梁阻尼块,最高可以增大2.8 dB。在图14中,考虑到装置的减振实际,不能使弹簧片阻尼质量比例过大。
|
图 13 弹簧片长宽比效果影响 Fig. 13 Effect of slenderness ratio of spring |
|
图 14 弹簧片长宽比效果影响 Fig. 14 Effect of slenderness ratio of spring |
本文基于动力吸振理论,设计应用于船舶机舱管系的动力吸振装置。通过正交法配置装置质量,对装置进行隐式动力学分析,得到如下结论:
1)单个装置可以使管系固有频率最高降低30%左右,对于高阶振型(4阶~6阶)可以使固有频率降低50%~65%;装置减振范围可以达到管系外径的50倍左右,并且在管系施加多个装置时,装置对位移降低幅值的叠加效果更加显著。
2)在相同工况和条件下,装置布置在主管系靠近激励的一侧1/3处对于加速度吸收效果最好;当安装在支管系时,装置布置在靠近激励端约1/4处可以充分发挥装置的减振性能,相比于其他位置加速度吸收程度可以平均增强20%左右。
3)在管系的瞬态分析中,吸振装置较好地抑制了管系的多向振动,目标测点的位移幅值在Z方向(激励方向),位移降幅可达65%,在X方向,位移降幅54%;目标测点的加速度在Z方向,加速度插入损失可达14.5 dB左右,在X方向,加速度插入损失可达23.5 dB左右。
| [1] |
郭长青. 输流管道与轴向流中板状结构的流致振动与稳定性[D]. 北京: 清华大学, 2010.
|
| [2] |
SENJANOVIĆ I, ANČIĆ I, MAGAZINOVIĆ G, et al. Validation of analytical methods for the estimation of the torsional vibrations of ship power transmission systems[J]. Ocean Engineering, 2019, 184. |
| [3] |
DING Lan, ZHU Hong-Ping, WU Li. Effects of axial load and structural damping on wave propagation in periodic Timoshenko beams on elastic foundations under moving loads[J]. Physics Letters A, 2016, 380(31−32).
|
| [4] |
张盛, 陈天星, 黄道军. 一款动力吸振器的匹配设计与试验[J]. 现代制造工程, 2016(3): 142-145. DOI:10.16731/j.cnki.1671-3133.2016.03.030 |
| [5] |
陈果, 程小勇, 刘明华, 等. 用于管道减振的新型动力吸振器[J]. 中国机械工程, 2014, 25(23): 3125-3131. DOI:10.3969/j.issn.1004-132X.2014.23.001 |
| [6] |
穆翔. 基于ANSYS的结构减振技术仿真研究[D]. 太原: 中北大学, 2016.
|
| [7] |
CHA P D, RINKER J M. Enforcing nodes to suppress vibration along a harmonically forced damped euler-Bernoulli beam[J]. Journal of Vibration and Acoustics, 2012, 134(5).
|
| [8] |
LIU Gongmin, LI Yanhua. Vibration analysis of liquid-filled pipelines with elastic constraints[J]. Journal of Sound and Vibration, 2011, 330(13).
|
| [9] |
张琳, 李华峰, 陈勇, 等. 基于动柔度方法的管路动力吸振器设计研究[J]. 中国舰船研究, 2019, 14(5): 138-144. DOI:10.19693/j.issn.1673-3185.01394 |
| [10] |
杨恺, 张针粒. 基于反共振原理的管路吸振器调谐方法[J]. 噪声与振动控制, 2017, 37(5): 55-60. DOI:10.3969/j.issn.1006-1355.2017.05.012 |
| [11] |
赵云龙. 船舶管路系统的动力学特性研究及减振降噪[D]. 上海: 上海交通大学, 2016.
|
 2022, Vol. 44
2022, Vol. 44
