2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
由于螺旋桨的悬臂作用,船舶尾轴通常处于弯曲变形状态,对于这种变形,在轴承相关研究中,常用的一种处理方式为忽略尾轴弯曲的影响,即将转轴轴线视为与轴承中心线水平。但实际上轴颈变形时轴线并非处于水平状态,此时轴承的润滑特性也与水平轴线时不同。
Mukherjee等[1]经计算得出了轴线倾斜后的厚膜表达式;朱少禹等[2]提出轴颈倾斜对轴承湍流润滑性能有明显影响;Mallya等[3]研究了轴倾斜时多槽轴承不同槽角下的静态特性;Feng等[4]提出了考虑轴倾斜的湍流模型用于预测动压润滑轴承的性能;张振山等[5]对轴倾斜径向轴承的热弹性流体动压润滑性能进行了深入的研究;王家序等[6]建立了滑动轴承混合热弹流数值计算模型,对热效应下的滑动轴承混合润滑性能进行了研究;王亚兵等[7]指出轴颈可允许倾斜角随偏心率增大而减小;陆金铭等[8]通过对实船轴系进行分析,提出轴颈倾斜角对轴向油膜压力及分布有较明显的影响;Lv等[9]发现轴颈倾斜会导致轴承油膜厚度降低,并讨论了轴承承载力随轴颈倾斜角的变化规律;刘正林等[10]的研究表明,尾轴倾角会使轴承边缘效应更明显;孙丽军等[11]的研究结果表明,重载荷下轴倾斜严重时可能导致轴颈与轴承的碰磨。
在考虑轴颈变形的研究中,多数是将其简化为轴线的倾斜,少有研究依据转轴轴线变形情况建立起轴弯曲条件下的轴承润滑模型。本文针对轴颈变形问题,建立考虑轴弯曲条件下的轴承润滑模型,并将其与忽略轴颈变形及考虑轴倾斜2种模型进行对比,探讨了3种模型下的膜厚分布的差异,同时对忽略轴颈变形和简化轴颈变形2种模型下的液膜压力大小及分布情况进行分析,为水润滑轴承的性能优化提供参考。
1 膜厚方程船舶轴系由于受到载荷的影响,其轴线会偏离水润滑轴承中心线,由此在转轴与轴承之间形成了楔形间隙,同时旋转的转轴带动润滑水从间隙大端向间隙小端运动形成楔形液膜[12],当楔形液膜提供的承载力与转轴载荷平衡时,转轴在轴承中的平衡位置也能随之确定。
不考虑轴颈变形时,可认为转轴轴线与轴承中心线平行,水润滑轴承润滑液膜分布仅在周向发生变化,此时沿周向膜厚分布公式为:
| $ h=c+e{\rm{cos}}\left(\theta -\varphi \right)。$ | (1) |
式中:R为轴承半径;r为转轴半径,半径间隙为
| $ \left\{\begin{array}{c}{h}_{max}=c+e,\\ {h}_{min}=c-e。\end{array}\right. $ | (2) |
本文模型考虑了轴颈变形对于水润滑轴承液膜的影响,此时转轴轴线并非与轴承中心线平行,水润滑轴承液膜膜厚沿轴向方向也随之发生变化,沿轴向方向任意截面的液膜内表面圆心竖直方向的高度都不相同,此时需对膜厚公式进行修正。膜厚公式修正的关键在于沿轴向方向任意截面的偏心距及偏位角的确定。选择轴承端面为初始截面,对考虑轴颈变形后的液膜膜厚公式进行修正,轴颈变形时轴承几何关系示意图如图1所示。

|
图 1 轴颈变形时轴承几何关系示意图 Fig. 1 Geometric relationship of bearing when journal is deformed |
考虑轴颈变形后的任意Z截面的偏心距公式:
| $ {e}_{z}=\sqrt{{e}_{0}^{2}+{\delta }^{2}-{2e}_{0}{\delta cos\varphi }_{0}}。$ | (3) |
式中:ez为Z截面处的偏心距;e0为初始截面的偏心距;
根据正弦定理得到的Z截面处的偏位角为:
| $ {\varphi }_{z}={\rm{arcsin}} \left[\left({e}_{0}/{e}_{z}\right)sin{\varphi }_{0}\right]。$ | (4) |
由Z截面偏心距和偏位角可得Z截面沿周向膜厚分布公式为:
| $ {h}_{z}=c+{e}_{z}{\rm{cos}}\left(\theta -{\varphi }_{z}\right)。$ | (5) |
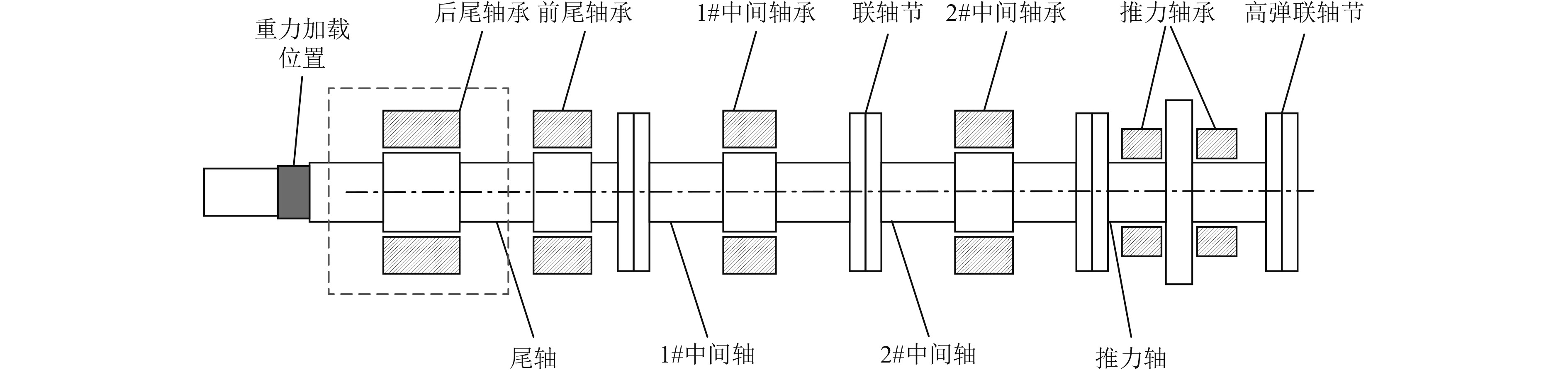
以某试验台轴系水润滑后尾轴承为研究对象,其结构示意图如图2所示。该轴系未安装螺旋桨,尾轴后端有液压加载装置,用来模拟螺旋桨的重力。水润滑后尾轴承基本参数如表1所示。
|
图 2 试验台轴系示意图 Fig. 2 Schematic diagram of test bench shafting |
|
|
表 1 后尾轴承基本参数 Tab.1 Basic parameters of rear tail bearing |
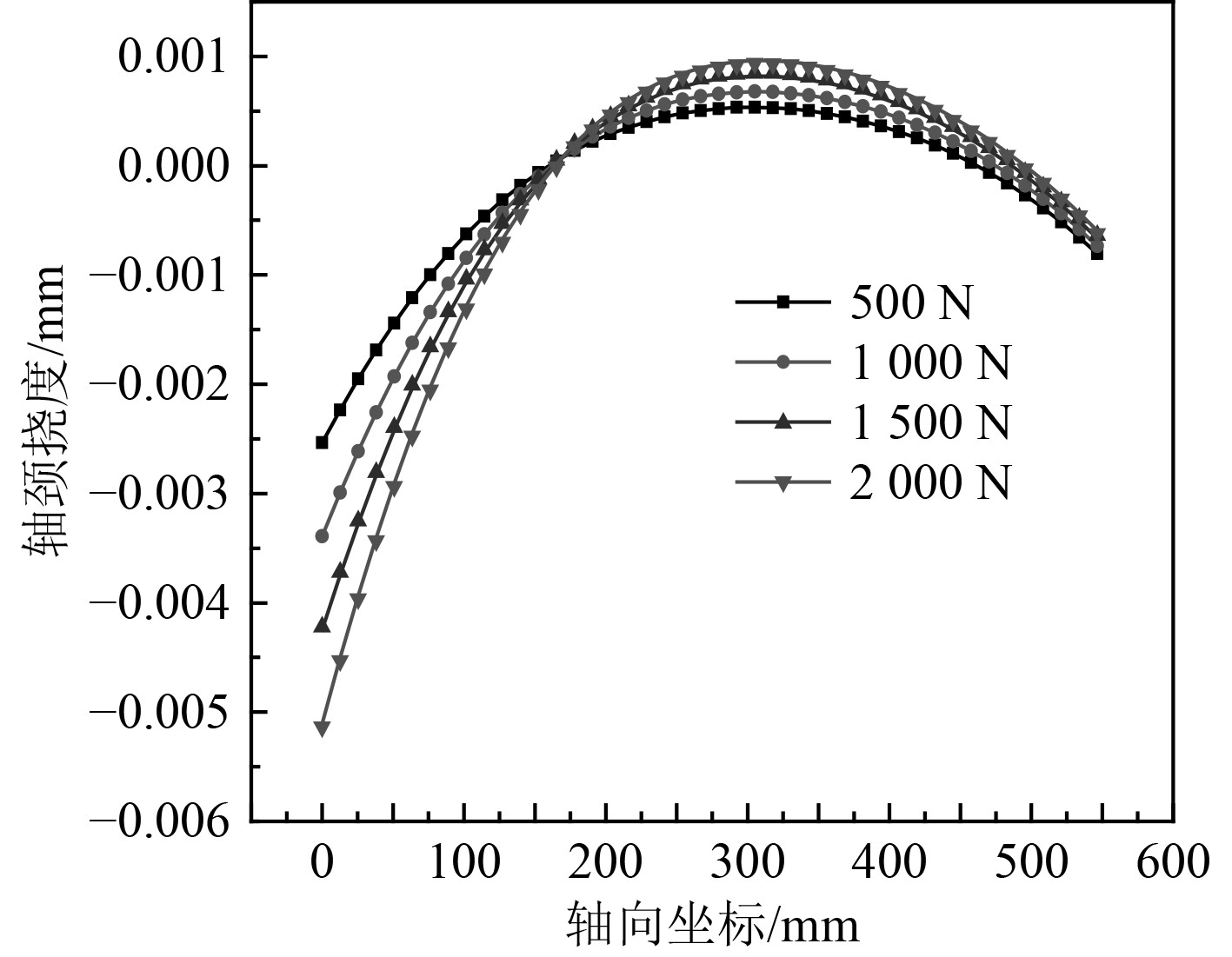
利用有限元软件进行轴系校中计算,图2所示重力加载位置分别对轴系施加竖直向下的500N,1 000 N,1 500 N,2 000 N载荷,并提取后尾轴承处轴颈的挠度参数,不同载荷下后尾轴承处轴颈挠度曲线如图3所示。图中坐标0点为轴承近加载端,负值表示轴颈变形向下。
|
图 3 不同载荷下后尾轴承处轴颈挠度曲线图 Fig. 3 Deflection curve of journal at rear tail bearing under different loads |
在已有的相关研究中,对于轴颈变形的处理方式可分为3种:1)忽略轴颈变形带来的影响,将转轴轴线视为与轴承中心线水平;2)将轴颈变形简化为转轴轴线的倾斜;3)对轴颈变形进行曲线拟合,以拟合得到的曲线方程作为轴颈变形时的轴线开展相关的研究。
本文以有限元校中计算求解得出的后尾轴承处轴颈挠度参数为基础,分别对轴颈变形时3种处理方式下的转轴轴线方程进行拟合,拟合方程如下式:
轴水平拟合方程:
| $ y=b,$ | (6) |
轴倾斜拟合方程:
| $ y=kx+d,$ | (7) |
轴弯曲拟合方程:
| $ y=A+B_{1}x+{B}_{2}{x}^{2}+{B}_{3}{x}^{3} 。$ | (8) |
式(3)中,
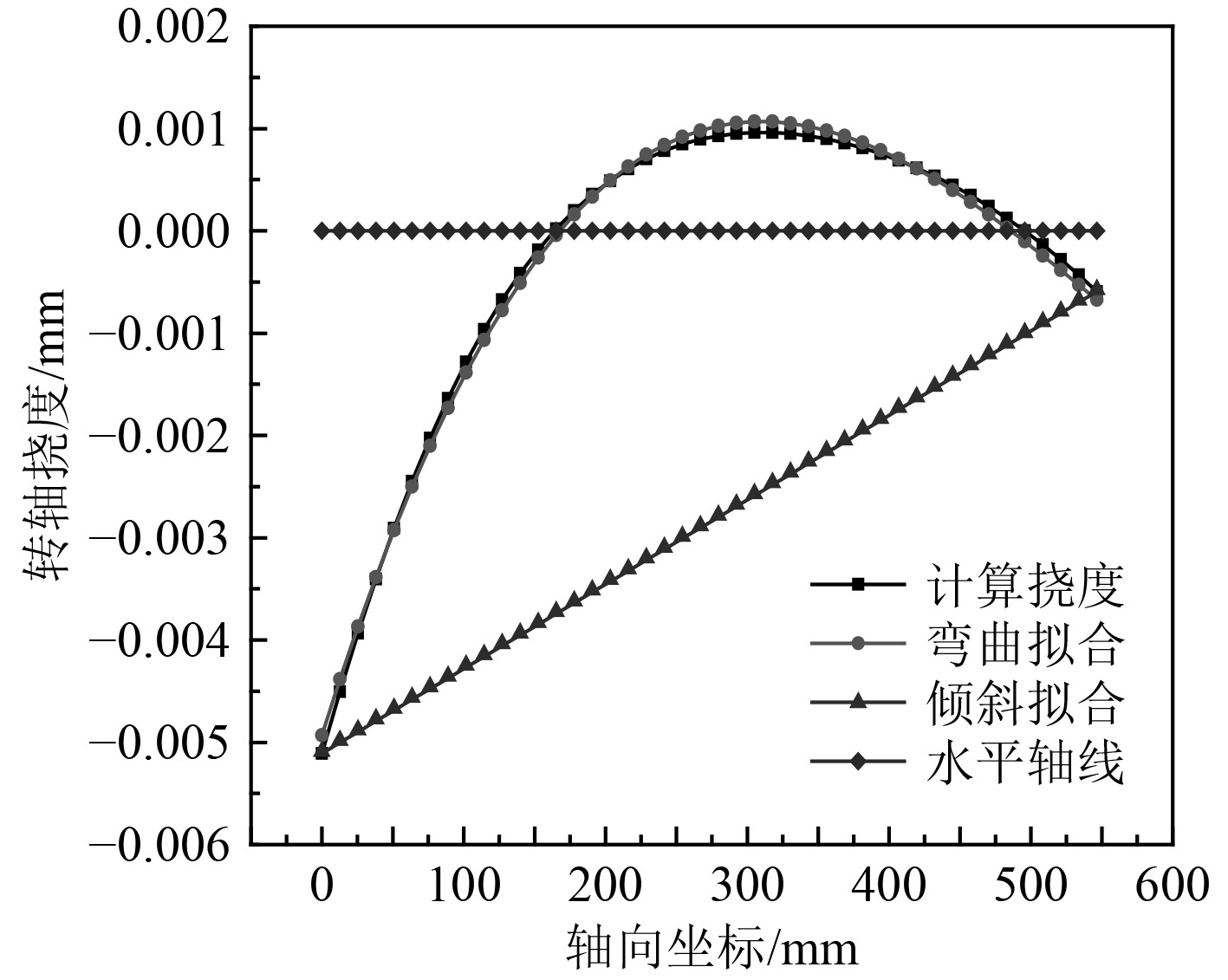
各载荷轴倾斜及轴弯曲拟合方程系数如表2和表3所示。其中施加载荷为2 000 N时后尾轴承处轴颈挠度参数及对应的拟合曲线图如图4所示,图中水平轴线表示转轴挠度沿轴向方向处处为0,即忽略轴颈变形时的转轴挠度曲线。
|
|
表 2 轴倾斜拟合方程系数 Tab.2 Coefficients of shaft tilt fitting equation |
|
|
表 3 轴弯曲拟合方程系数 Tab.3 Coefficients of shaft bending fitting equation |
|
图 4 2 000 N时后尾轴承处轴颈挠度参数及拟合曲线 Fig. 4 Journal deflection parameters and fitting curve at rear tail bearing at 2 000 N |
对轴颈变形进行拟合时,会产生误差,以图3中坐标0点所在截面为初始截面,2 000 N时由各拟合曲线求得的误差如图5所示。

|
图 5
2 000 N时
|
由式(3)~式(5)可知,截面中心高度差
由对轴颈变形3种处理方式产生的误差分析可知,轴弯曲条件下的膜厚分布情况与实际最接近,故以轴弯曲模型为基准,研究忽略轴颈变形以及将轴颈变形简化为轴线倾斜对水膜压力大小及分布带来的误差,分别构建3种水膜模型,进行流固耦合仿真计算。
1)网格划分
进行流固耦合仿真计算时,水膜和轴承内衬需分开建模并完成网格的划分。为便于耦合计算的收敛,二者均选择结构化网格。轴承内衬采用sweep方式在mesh中完成网格划分,水膜利用专业网格划分软件ICEM完成网格划分。为更好反映流体流动及耦合情况,在膜厚方向划分为10层,如图6所示。

|
图 6 水膜网格图 Fig. 6 The chart of water film grid |
2)边界条件
在仿真计算中,需对计算域边界进行约束,即设定相应的边界条件。计算中轴承外表面设定为全约束,内表面定义为流固耦合面;水膜内表面定义为旋转速度边界条件,外表面定义为流固耦合面,润滑水入水口(轴承近加载端)定义为速度入口,流速设置为0.832 m/s,出水口定义为压力出口,工作压力设置为大气压。
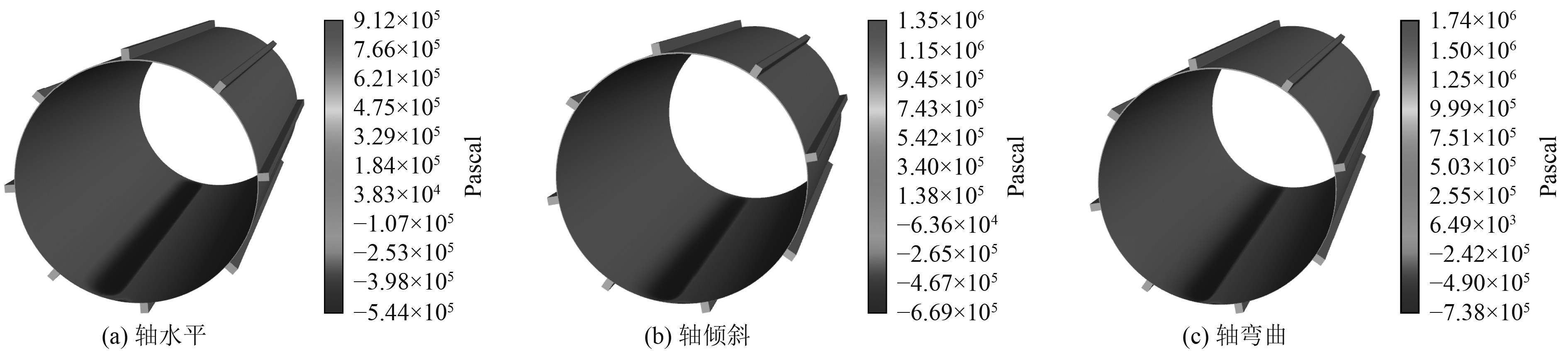
3 计算结果分析当转轴旋转速度为400 r/min,分别进行3种水膜模型下4种不同载荷(500 N,1 000 N,1 500 N,2 000 N)下的水润滑后尾轴承流固耦合仿真。结合水膜压力分布云图及模型参数可知,最大水膜压力出现在水膜最薄处(入水口端),且以此为分界分布着正负压力区域。同时,正压力区域的压力沿着轴向逐渐减小,2 000 N时3种模型下水膜压力云图如图7所示。
|
图 7 2 000 N时各模型下水膜压力分布图 Fig. 7 Water film pressure distribution of each model at 2 000 N |
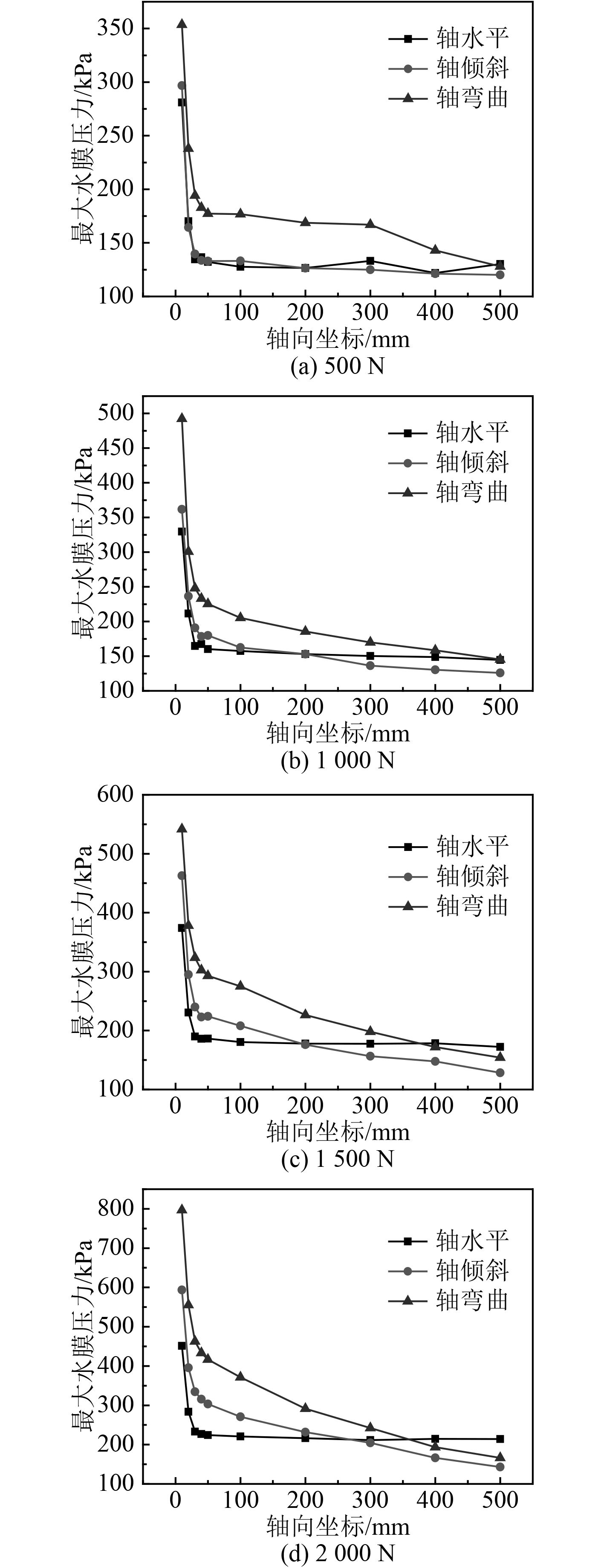
由于对轴颈变形的不同处理方式会直接影响到水膜膜厚沿轴向的分布情况,膜厚的变化会直接影响到压力的分布,现沿轴向选取10个截面提取各个截面最大水膜压力参数,分析各载荷下不同模型沿轴向最大水膜压力的分布情况,如图8所示。
|
图 8 各载荷下不同模型轴向水膜压力分布图 Fig. 8 Axial water film pressure distribution of different models under various loads |
可知,轴弯曲条件下沿轴向水膜压力逐渐减小,这一结果与文献[13]中试验所得趋势相同。同时,各载荷下3种模型时的水膜压力沿轴向均出现了一个快速下降的区域,该区域为水膜最大压力所在区域。忽略轴颈变形的轴水平条件下水膜压力沿轴向先减小后基本不变,与实际情况不符,这是由忽略轴颈变形带来的误差所致。以轴弯曲仿真结果为基准,轴倾斜与轴弯曲条件下水膜压力沿轴向分布趋势较为接近,但压力数值存在误差,误差较大区域为轴向坐标0~200 mm区域,其中水膜最大压力误差为−14.57% ~ −26.54%(随载荷变化),水膜压力均值误差约在−20%左右。
4 结 语1)考虑轴弯曲条件下的水膜膜厚分布情况与实际水膜分布最为接近。
2)以轴弯曲条件下模型为基准,若忽略变形产生的影响,求得的水膜压力分布情况与实际不符。若将轴颈变形简化为轴线的倾斜,求得的水膜压力数值将会产生误差。
| [1] |
MUKHERJEE A, RAO J S. Stiffness and damping coefficients of an inclined journal bearing[J]. Mechanism & Machine Theory, 1977, 12(4): 339-355. |
| [2] |
朱少禹, 孙军, 李彪, 等. 计及轴颈倾斜的径向滑动轴承湍流润滑分析[J]. 摩擦学学报, 2019, 39(2): 235-247. DOI:10.16078/j.tribology.2018133 |
| [3] |
MALLYA, RAVINDRA, SHENOY, et al. Static characteristics of misaligned multiple axial groove water-lubricated bearing in the turbulent regime[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2017, 231(3): 385-398. DOI:10.1177/1350650116657757 |
| [4] |
FENG Huihui, JIANG Shuyun, JI Aimin. Investigations of the static and dynamic characteristics of water-lubricated hydrodynamic journal bearing considering turbulent, thermohydrodynamic and misaligned effects[J]. Tribology International, 2019, 130: 245-260. DOI:10.1016/j.triboint.2018.09.007 |
| [5] |
张振山, 戴旭东, 张执南, 等. 轴颈倾斜的径向轴承热弹性流体动力润滑分析[J]. 上海交通大学学报, 2013, 47(9): 1347-1352. DOI:10.16183/j.cnki.jsjtu.2013.09.003 |
| [6] |
王家序, 倪小康, 韩彦峰, 等. 倾斜轴颈滑动轴承混合热弹流研究[J]. 中南大学学报(自然科学版), 2019, 50(10): 2425-2434. DOI:10.11817/j.issn.1672-7207.2019.10.011 |
| [7] |
王亚兵, 刘洋洋, 王报龙, 等. 轴颈倾斜的水润滑橡胶艉轴承的静态特性[J]. 西安交通大学学报, 2020, 54(5): 61-69. DOI:10.7652/xjtuxb202005009 |
| [8] |
陆金铭, 李儒凡, 倪杰. 船舶推进轴系轴径倾斜对轴承负荷的影响[J]. 江苏科技大学学报(自然科学版), 2015, 29(5): 426-430+442. |
| [9] |
FANGRUI LV, TA Na, ZHUSHI RAO. Analysis of equivalent supporting point location and carrying capacity of misaligned journal bearing[J]. Tribology International, 2017, 116: 26-38. DOI:10.1016/j.triboint.2017.06.034 |
| [10] |
刘正林, 周建辉, 刘宇, 等. 计入艉轴倾角的船舶艉轴承液膜压力分布计算[J]. 武汉理工大学学报, 2009, 31(9): 111-113+131. DOI:10.3963/j.issn.1671-4431.2009.09.028 |
| [11] |
孙丽军, 薛闯, 张立浩, 等. 倾斜轴颈重载轴承润滑性能分析及试验研究[J]. 润滑与密封, 2016, 41(7): 107-111. DOI:10.3969/j.issn.0254-0150.2016.07.019 |
| [12] |
张直明. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社. 1986
|
| [13] |
王楠, 孟庆丰, 王朋朋, 等. 水润滑橡胶轴承特性仿真与试验研究[J]. 机械工程学报, 2014, 50(13): 113-121. |
 2022, Vol. 44
2022, Vol. 44

