2. 哈尔滨工程大学,黑龙江 哈尔滨 150001;
3. 上海船用柴油机研究所,上海 201108;
4. 中国船舶集团有限公司第七一四研究所,北京 100101
2. Harbin Engineering University, Harbin 150001, China;
3. Shanghai Marine Diesel Engine Research Institute, Shanghai 201108, China;
4. The 714 Research Institute of CSSC, Beijing 100101, China
船舶机械设备运行产生的低频噪声在传播过程中具有强穿透、低衰减的特点,是船舶减振降噪的难点问题。传统隔声材料由于质量密度定律[1]的限制,通常需要提高材料面密度增加结构重量来实现低频降噪的目的,在船体狭小空间应用受到很大限制,轻质低频隔声材料技术研究与开发一直以来是船舶减振降噪领域重要内容。由光子晶体概念衍生提出的声子晶体[2],通过采用材料配置优化和结构设计创新,为解决低频隔声问题提供了新的思路和方法,受到研究者广泛关注。刘正猷等[3]提出在亚波长频段利用弹性波的局域共振效应实现低频带隙局域共振型声子晶体为声子晶体材料低频降噪创造了可能。研究人员开展了大量研究[4-6],王添等[7]通过有限元方法研究了一种薄板声子晶体的低频隔声特性,经试验验证,相比同质量单层均质板隔声量提升9 dB。Ho等[8]将橡胶包裹的实心铅球引入格栅结构,实现了200~500 Hz低频段内噪声的有效衰减。徐俭乐等[9]将声子晶体结构与夹层板结合,设计了一种具有优良低频隔声特性的声子晶体夹层板结构。薄膜型声子晶体是局域共振型声子晶体的典型形式,通过附加质量块的共振产生低频带隙,可实现低频隔声效果。Yang等[10]提出薄膜型声子晶体结构,通过多层叠加的方式,实现了声波在共振频率处的良好衰减。Mei等[11]提出一种在低频段内具有宽频吸声性能的薄膜声学超材料,实现了100 Hz~1 kHz频段内噪声的完全吸收,进一步完善声子晶体材料低频噪声控制方案。张玉光[12]提出薄膜型声子晶体隔声特性解析计算方法,揭示了薄膜型声子晶体的隔声机理。
上述研究重点围绕声子晶体结构低频隔声特性机理和特殊控制频段展开设计,关于薄膜声子晶体结构参数对隔声效果的影响少有提及,内在影响规律有待探索。薄膜型声子晶体由附加重物的弹性张紧薄膜固定在框架上组成,通过附加质量块受激共振与弹性波相互作用,可凭借其较小的结构尺寸控制较大波长的弹性波,能够在低频范围内实现有效的隔声,组成部分包括框架、薄膜以及配重块等结构,各部分物理属性是影响薄膜声子晶体材料隔声特性的重要因素。本文基于局域共振隔声理论,利用声学有限元方法,开展框架构型、配重块质量、薄膜厚度等相关参数对薄膜型声子晶体材料低频隔声性能的影响研究,为薄膜型声子晶体材料低频隔声设计提供支撑。
1 局域共振隔声理论薄膜型声子晶体材料在外界激励下散射体产生共振,与弹性波长波行波相互作用,从而抑制弹性波传播,薄膜型声子晶体材料本质上属于局域共振型声子晶体的范畴。一维线性声波方程[13]为:
| $ \frac{{{\partial ^2}p}}{{\partial {x^2}}} = \frac{1}{{c_0^2}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} ,$ | (1) |
其中:
| $ p\left( {x,t} \right) = A{e^{i\left( {\omega t - kx} \right)}} + B{e^{i\left( {\omega t + kx} \right)}} 。$ | (2) |
其中:A和B均为待定系数,
| $ p\left( {x,t} \right) = {p_a}{e^{i\left( {\omega t - kx} \right)}} 。$ | (3) |
声波在入射薄膜型声子晶体材料时,不可避免地会发生反射、透射以及能量损耗等一系列过程,导致声能的降低[14]。如图1所示,声波

|
图 1 声波传播示意图 Fig. 1 Diagram of acoustic propagation |
上述入射、反射、透射波可具体表达为以下形式:
| $ \begin{split}&{p_i} = {p_{ia}}{e^{i\left( {\omega t - {k_1}x} \right)}}\text{,} {p_{r1}} = {p_{r1a}}{e^{i\left( {\omega t + {k_1}x} \right)}} ,\\ & p_t^ * = p_{ta}^ * {e^{i\left( {\omega t - {k_2}x} \right)}}\text{,} p_{r2}^{} = p_{r2a}^{}{e^{i\left( {\omega t + {k_2}x} \right)}}。\end{split} $ | (4) |
其中:
根据声压连续条件,结构边界处的连续方程为:
| $ \left\{ \begin{gathered} {p_{ia}} + {p_{r1a}} = p_t^ * + p_{r2a}^{},\;\;\;\;\;\;\;\;x = 0,\\ p_{ta}^ * {e^{ - i{k_2}d}} + p_{r2a}^{}{e^{i{k_2}d}} = p_{ta}^{},\;\;\;\;x = d。\; \\ \end{gathered} \right. $ | (5) |
由于反射和损耗的存在,透射声波仅是入射声波的一部分,由以上推导可求得透射波
| $ {t_p} = \left| {\frac{{p_{ta}^{}}}{{{p_{ia}}}}} \right| ,$ | (6) |
描述隔声性能通常采用透射系数的倒数
| $ {STL} = 20\lg {\eta _p} = 20\lg \frac{1}{{{t_p}}}。$ | (7) |
薄膜型声子晶体材料结构框架作为起支撑作用的重要结构,直接决定了声子晶体材料的带隙特性,较为常见的声子晶体构型包括三角形、正方形、圆形等。不同构型框架和配重质量块的隔声性能和自身质量有所不同,从而影响薄膜型声子晶体材料的成型工艺、制造成本、有效频段和隔声效果,具有调频特性。
2.1 薄膜型声子晶体简介对比圆形、正六边形和正方形3种构型框架薄膜型声子晶体开展隔声性能和重量分析研究,如图2所示。为保证薄膜面积一致,圆形构型半径R=25 mm,正六边形构型边长L1=25.6 mm,正方形构型边长L2=44.3 mm,结构高度H=20 mm,薄膜和框架采用PVC材料,名义弹性模量E1=3.8 GPa,密度ρ1=1300 kg/m3,框架中间配置的配重块均为圆柱体结构,半径r=10 mm,材料为Q235钢材,弹性模量E2=210 GPa,密度ρ2=7850 kg/m3。
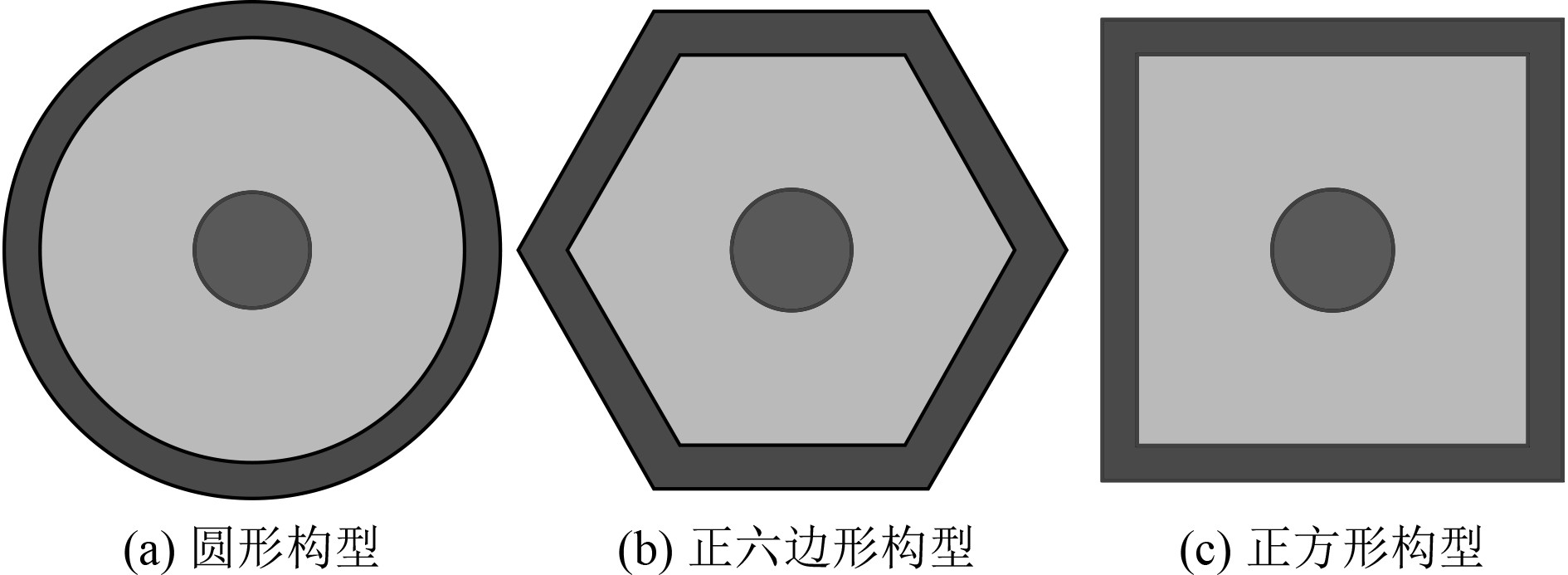
|
图 2 不同构型薄膜型声子晶体单原胞模型 Fig. 2 Cell model of membrane-type phononic crystals with different configurations |
参考阻抗管隔声量测试方法[16],基于声学有限元计算理论,在Virtual.Lab环境中构建薄膜型声子晶体隔声性能计算模型,如图3所示。阻抗管内径d=50 mm,发声管长度l1=400 mm,接收管长度l2=500 mm,在发声管左端模拟平面波声源,声波将垂直入射到声子晶体结构上,在接收管底部设置无反射边界条件模拟声学末端,通过计算声子晶体两侧考核点的声压之比得到声子晶体的声传递损失。针对不同构型声子晶体材料单元开发数值计算模型,采用实体单元离散,对声子晶体单元网格加密,圆形构型声子晶体单元数值模型如图4所示。

|
图 3 计算模型图 Fig. 3 Diagram of calculation model |

|
图 4 数值仿真模型 Fig. 4 Numerical simulation model |
为分析框架构型和配重质量大小对薄膜型声子晶体调频规律的影响,通过改变3种构型声子晶体配重块的高度,实现配重块质量的增减,配重块高度及对应质量如表1所示。
|
|
表 1 配重块高度及质量表 Tab.1 Weighting block height and quality |
通过仿真计算,得到圆形、正六边形、正方形3种构型薄膜型声子晶体各配重质量下的隔声性能,以配重质量m=4 g为例,分析3种构型声子晶体在50 Hz~1 kHz频段内的声传递损失,曲线如图5所示。图6为薄膜型声子晶体配重块质量与峰值频率之间的关系。
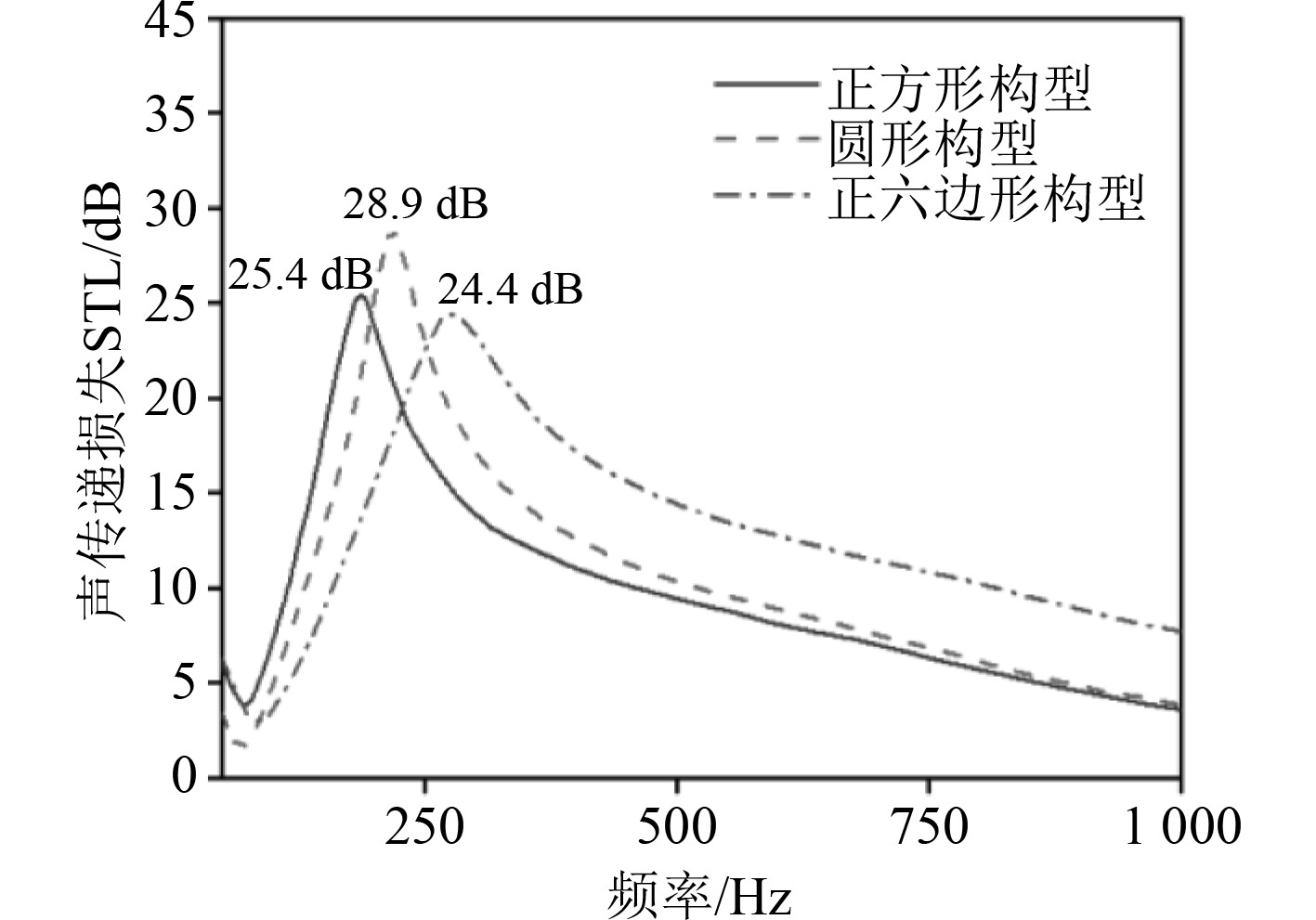
|
图 5 m=4g不同构型声子晶体声传递损失对比图 Fig. 5 Comparison of STL of phononic crystals with different configurations when m = 4 g |
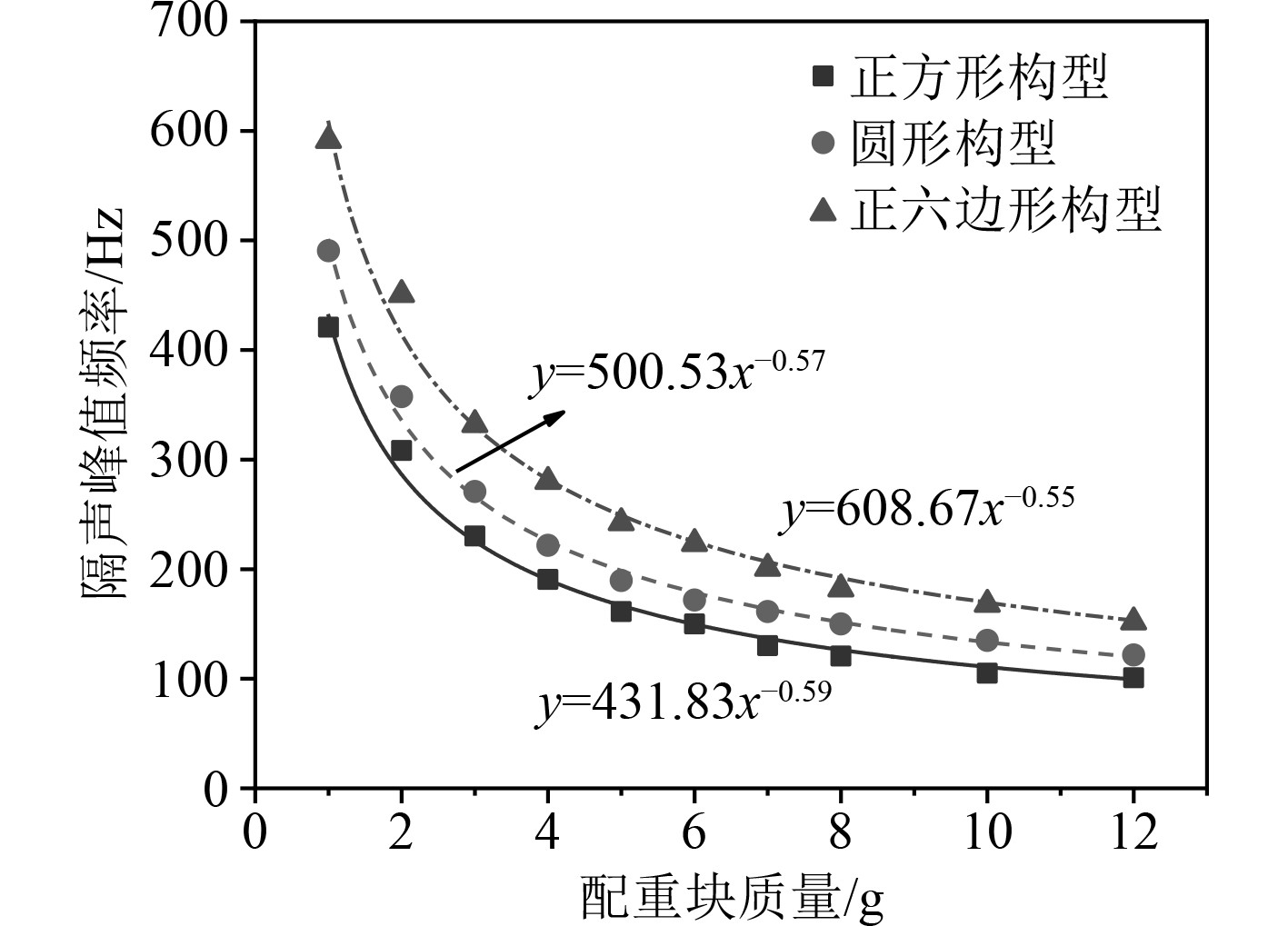
|
图 6 不同构型声子晶体隔声峰值频率与配重关系 Fig. 6 Relationship between peak frequency and counterweight of phononic crystals with different configurations |
由图5可知,当配重块质量m=4 g时,3种构型声子晶体的声传递损失曲线趋势保持一致,均呈现先上升后下降的规律。在隔声性能方面,圆形构型声子晶体隔声性能最佳,其隔声量峰值为28.9 dB,方形构型声子晶体次之;在峰值频率方面,方形构型声子晶体隔声量峰值频率最低,正六边形构型声子晶体隔声峰值频率最高。结合图6可以发现,随着配重质量的增加,3种构型薄膜型声子晶体隔声峰值频率均逐渐降低,配重质量与峰值频率之间成指数关系。由于正六边形薄膜型声子晶体的整体刚度较大,结构固有频率更高,导致在相同配重质量的情况下,隔声峰值频率大于圆形和正方构型的薄膜型声子晶体。因此为实现隔绝低频噪声的目的,正六边形构型声子晶体需配备质量更大的配重块,致使结构质量增加,不利于轻量化设计。从工程实际应用角度出发,正方构型薄膜型声子晶体在保证较好的低频隔声性能的前提下更易于加工,符合结构轻量化设计理念,是3种构型在实际应用中的较优选择。
3 薄膜型声子晶体低频隔声特性分析为进一步分析薄膜型声子晶体低频隔声特性,揭示各组成部分结构参数对其影响的内在规律,针对正方构型薄膜型声子晶体单胞结构开展进一步研究。图7为正方构型薄膜型声子晶体基础模型示意图。其中,模型框架外边长A=50 mm,内边长a=42 mm,高度H=20 mm,薄膜厚度d=0.2 mm;配重块为半径r=10 mm,高h=4 mm的圆柱结构,各组成部分结构材料属性与前文一致。采用前面同样的方法开展隔声特性分析,框架和配重块实体网格、薄膜材料壳单元网格如图8所示。
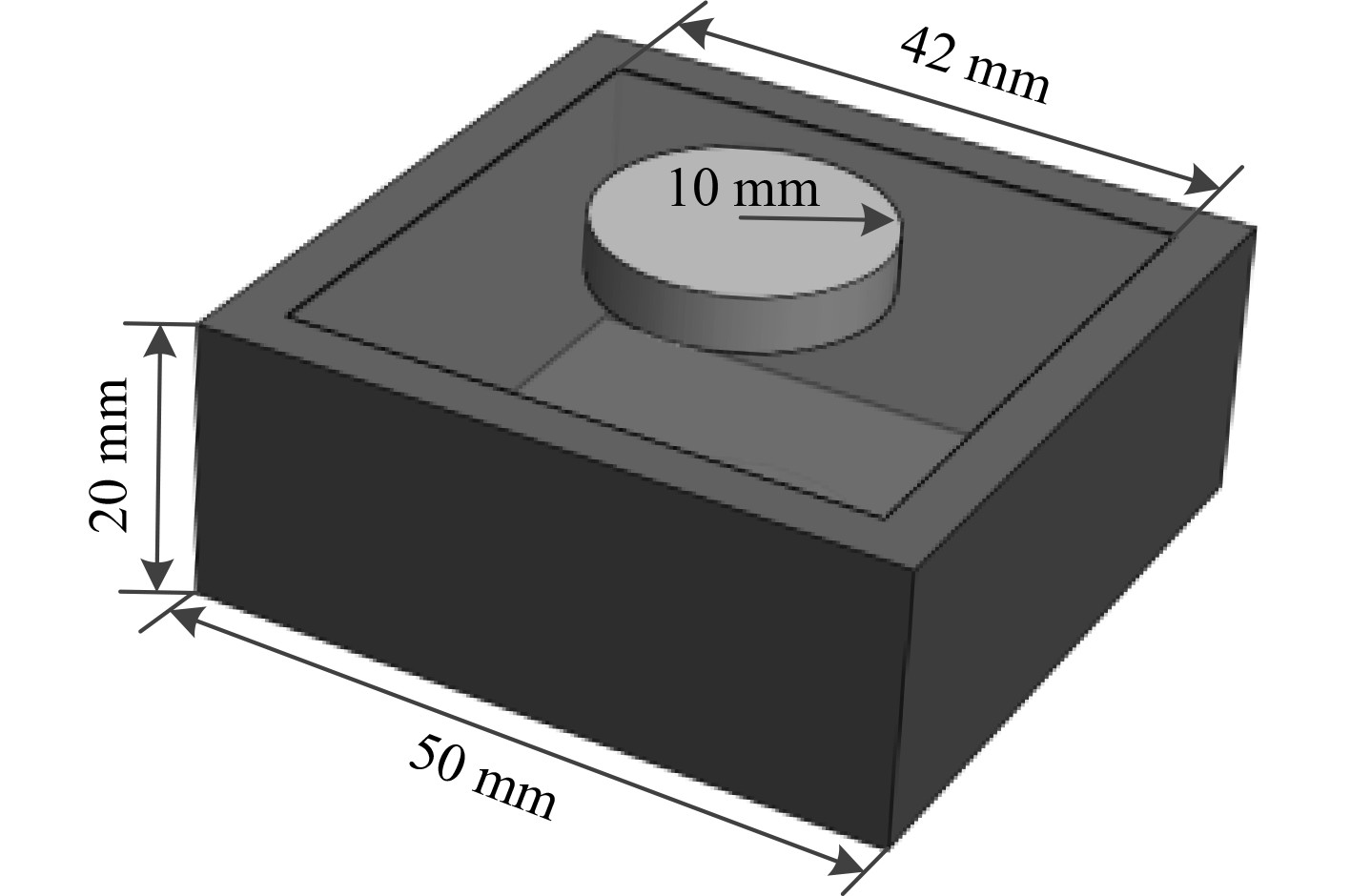
|
图 7 基础模型示意图 Fig. 7 Basic model diagram |

|
图 8 声子晶体原胞数值模型 Fig. 8 Numerical model of the phononic crystal cell |
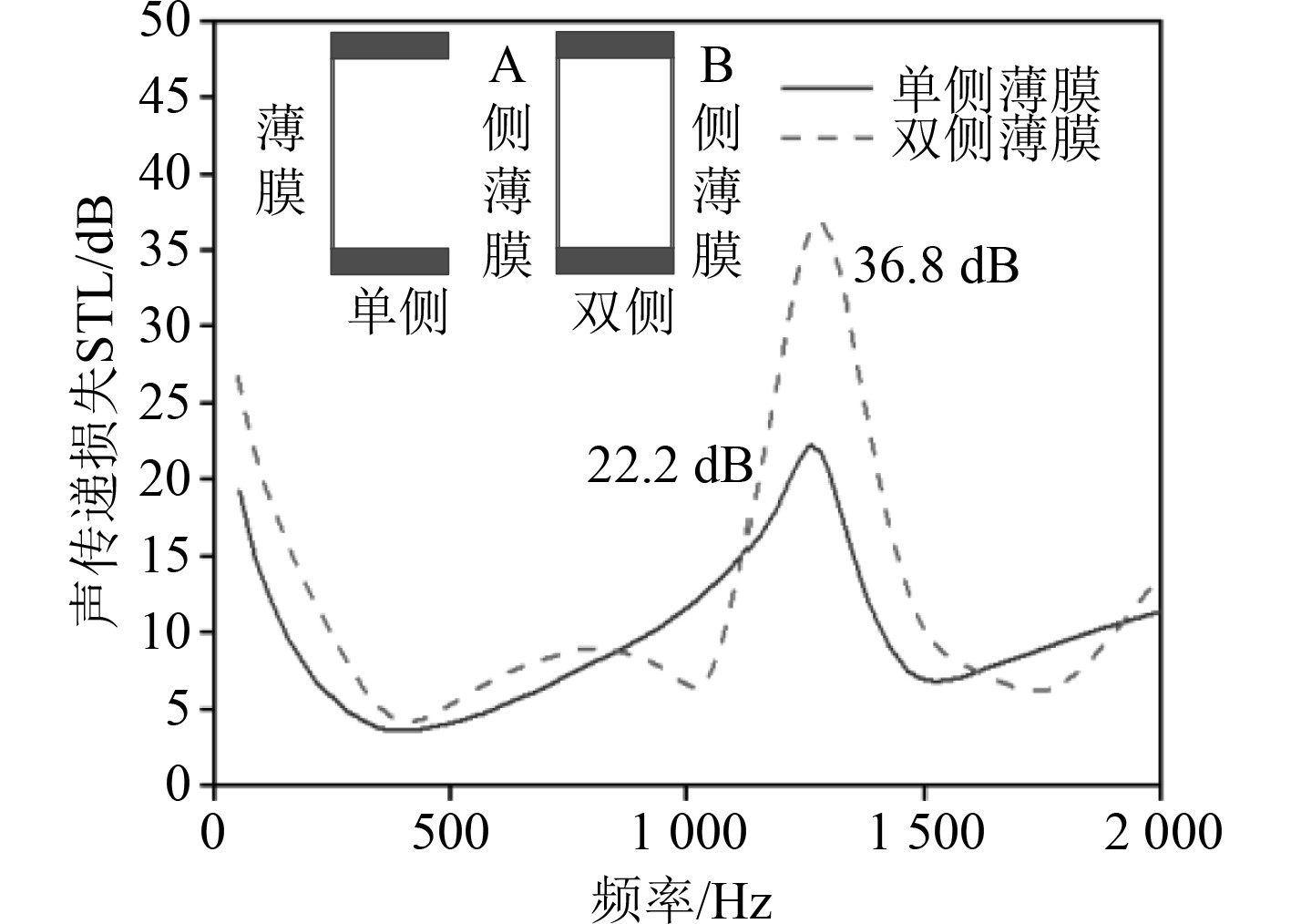
薄膜型声子晶体框架类似于管状结构,可在结构2个端面粘附薄膜。薄膜的存在与否,是影响隔声性能的重要因素。定义单侧薄膜和双侧薄膜型声子晶体结构,分析模型不设置配重块,结构及材料参数与基础模型保持一致,图9为2 kHz以内隔声性能计算分析结果。
|
图 9 单侧/双侧薄膜型声子晶体隔声性能对比 Fig. 9 Comparison of STL of unilateral / bilateral membrane-type phononic crystals |
可知,薄膜配置单侧或是双侧,两者声传递损失曲线总体趋势基本相同,峰值频率也基本相同,相比单侧薄膜型声子晶体,双侧薄膜型声子晶体结构隔声性能在峰值频率处有明显提升,约14.6 dB,其余大部频段也存在2~5 dB的性能提升。
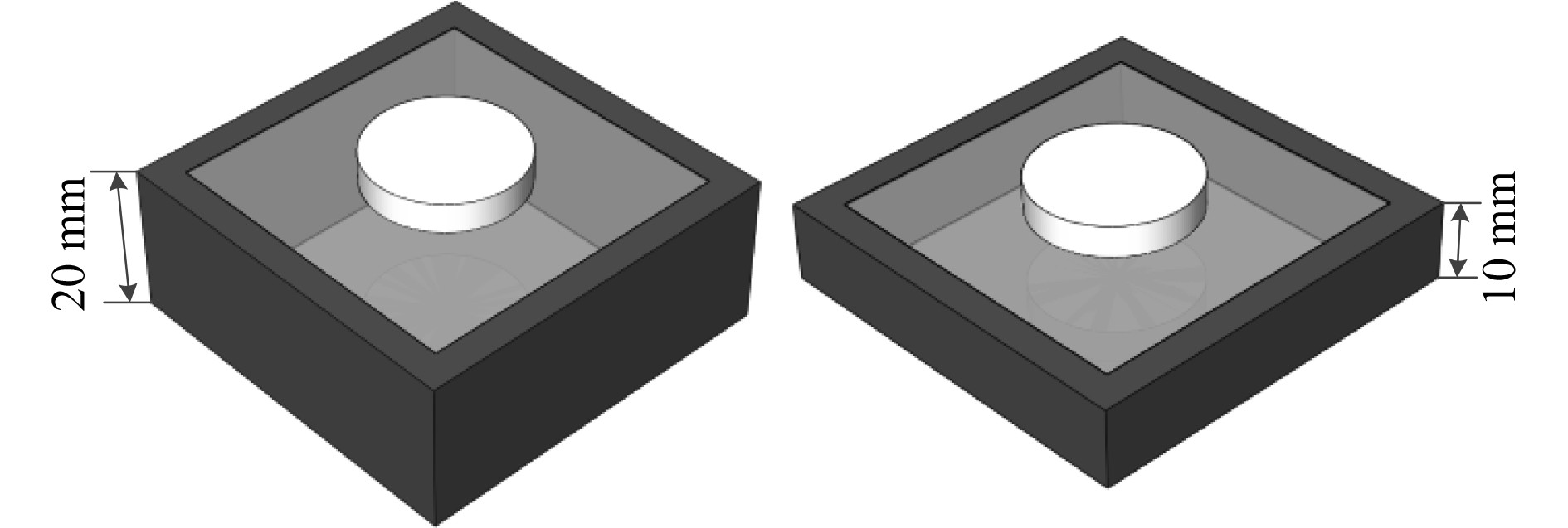
3.2 腔体高度对声子晶体隔声性能的影响薄膜型声子晶体为中空结构,结构高度决定了内部腔体空间大小,空气腔体厚度与两侧薄膜的耦合性强,采用仿真方式开展腔体高度对声子晶体隔声性能影响分析。图10为10 mm和20 mm高度腔体的薄膜型声子晶体示意图,除结构高度外,其余结构、材料参数与基础模型保持一致,声子晶体两侧薄膜处配装质量m=10 g的金属配重块。
|
图 10 薄膜型声子晶体腔体高度示意图 Fig. 10 Cavity height diagram of membrane-type phononic crystals |
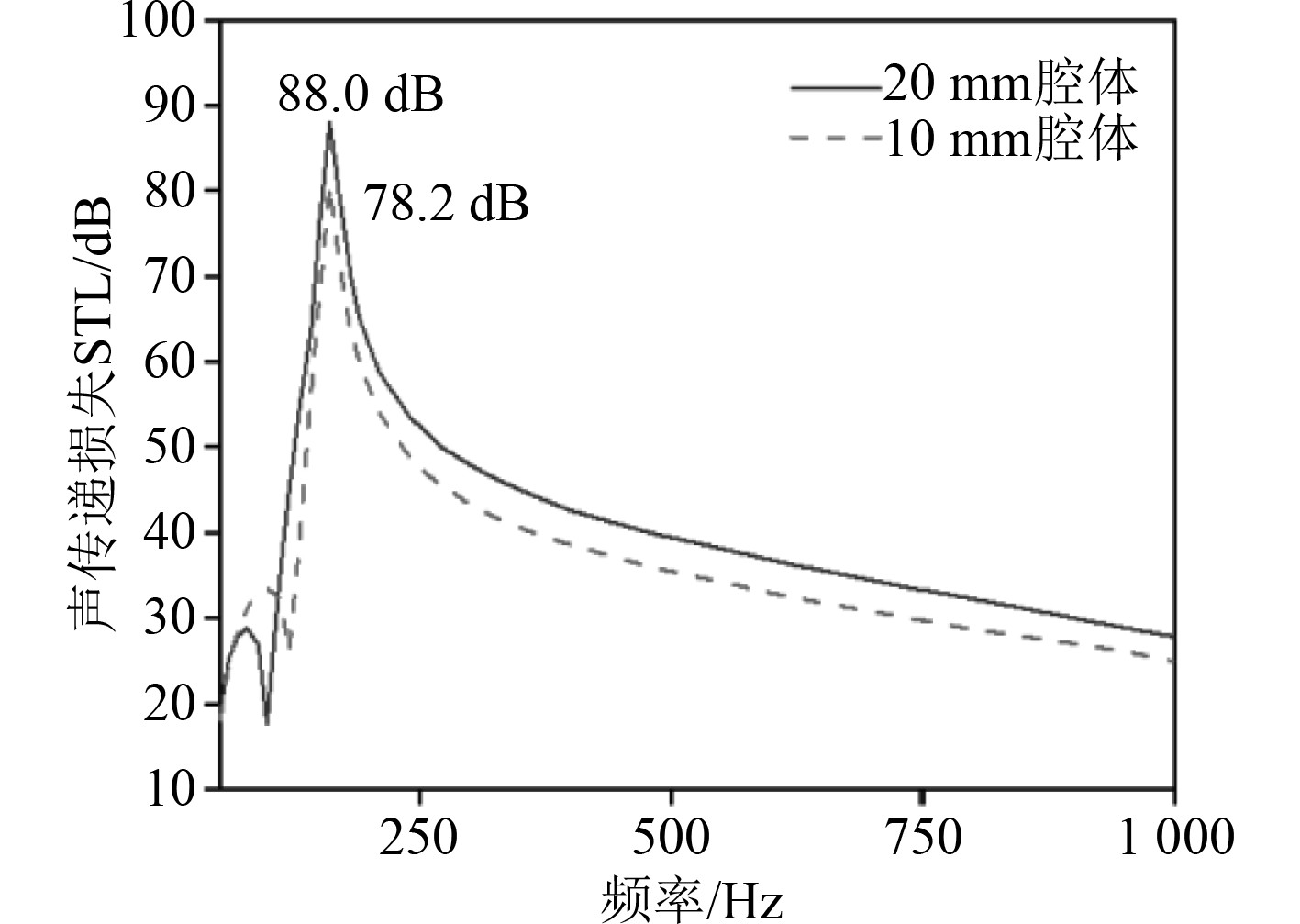
由图11可知,在50 Hz~1 kHz频段,不同腔体高度声子晶体隔声量曲线整体趋势保持一致,2种腔体高度声子晶体隔声量峰值频率均在120 Hz附近,10 mm腔体厚度相对于20 mm腔体厚度的声子晶体隔声量有明显下降,普遍降低2~3 dB,但腔体高度减小确有利于单元重量控制,在腔体高度参数设计上,隔声性能与结构轻量化之间存在取舍,需综合权衡确定。
|
图 11 腔体高度对声子晶体隔声性能的影响 Fig. 11 Effect of cavity height on STL of phononic crystals |
薄膜传递配重块的振动,其厚度是影响声子晶体材料隔声特性的重要因素,在结构两端配置不同厚度的薄膜,分析对声子晶体材料隔声特性的影响,配置方案如表2所示。计算模型中,各参数与基础模型保持一致,在两侧薄膜上配装质量m=10 g的金属配重块。
|
|
表 2 声子晶体薄膜配重方案 Tab.2 Weight Scheme of Phononic Crystal membrane |
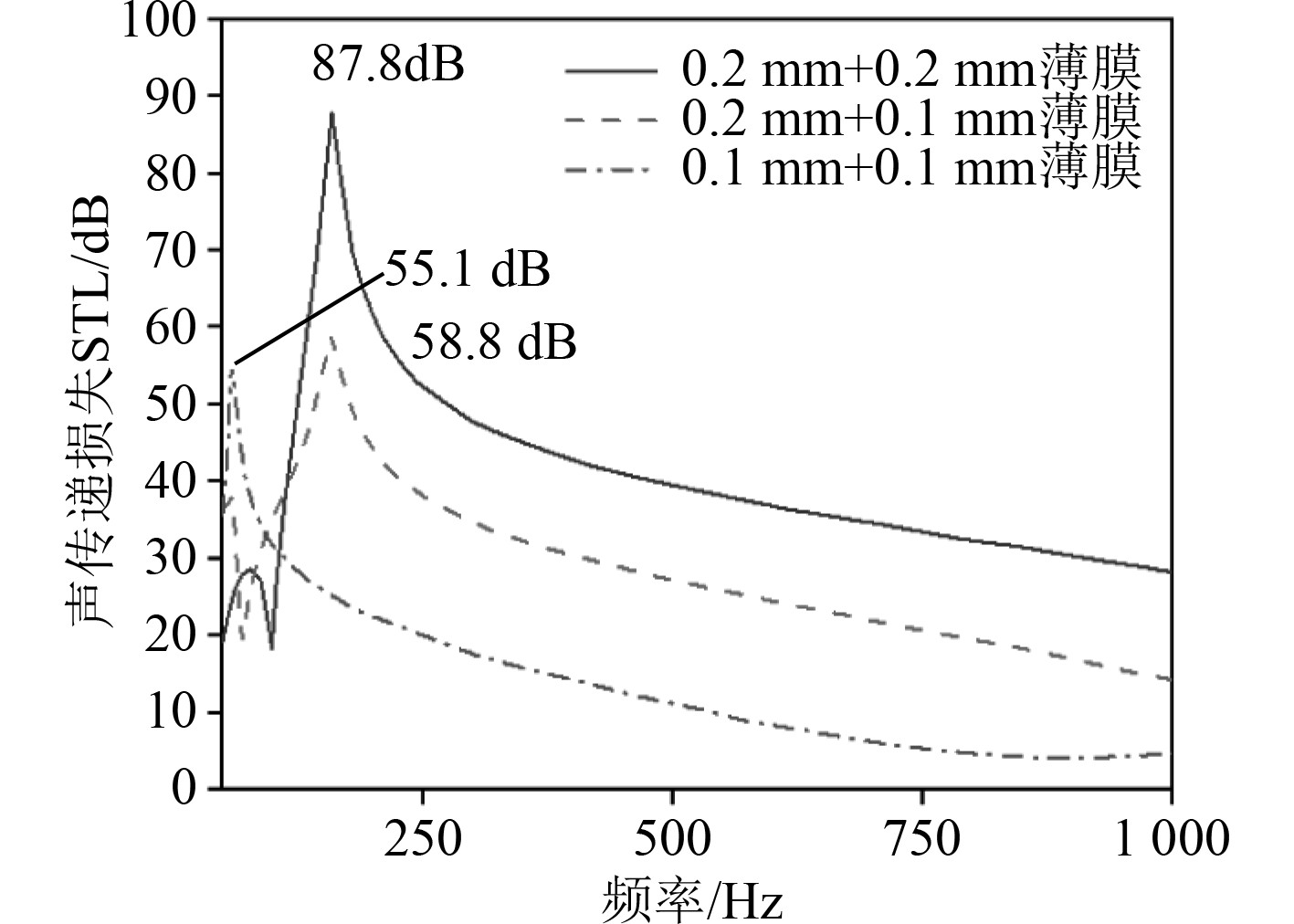
如图12所示,在50 Hz~1 kHz频段内,相比其他结构参数,薄膜厚度变化对隔声量峰值频率影响明显,随着薄膜厚度减小,声子晶体单元结构隔声峰值频率减小,两侧采用不同厚度的薄膜能够在一定程度增大隔声频率宽度。隔声量方面,薄膜厚度越大,隔声量越大,两侧等厚度情况下,薄膜厚度增加0.1 mm,隔声量峰值可提高约32 dB。
|
图 12 薄膜厚度对声子晶体隔声性能的影响 Fig. 12 Effect of membrane thickness on STL of Phononic Crystals |
本文基于局域共振隔声理论结合声学有限元方法,针对薄膜型声子晶体结构,开展了框架构型、配重质量、薄膜数量、空气腔体高度等相关参数对低频隔声特性的影响研究,得到如下主要结论:
1)薄膜型声子晶体配重块质量与隔声峰值频率之间呈指数关系,配重块质量越大,其峰值频率越低,综合考虑隔声性能、单元可延拓性和结构易加工性,正方形构型薄膜型声子晶体相对较优。
2)薄膜型声子晶体薄膜配置数量、腔体高度对其隔声性能均有一定影响。双侧薄膜型声子晶体相较于单侧薄膜方案隔声量在峰值频率处有较大提升,且其隔声性能和自身重量均随腔体厚度的增加而有所提升,隔声性能和轻量化设计的平衡关系需着重考虑。
3)相比其他结构特征参数,薄膜厚度对声子晶体材料隔声性能影响显著,同时减小薄膜厚度可使隔声量峰值频率向低频移动;两侧采用不同厚度薄膜可在一定程度上提升其隔声频带宽度。
| [1] |
康玉莹. 薄膜声学超材料隔声特性研究和优化设计[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [2] |
温熙森. 声子晶体[M]. 北京: 国防工业出版社, 2009.
|
| [3] |
LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736. |
| [4] |
王艺, 郭辉, 吕将, 等. 非均匀局域共振型声子晶体隔声特性研究[J]. 人工晶体学报, 2017, 46(7): 8. DOI:10.3969/j.issn.1000-985X.2017.07.010 |
| [5] |
张若军, 王桂波, 张思维, 等. 四边简支型声子晶体薄板的低频隔声特性验证[J]. 舰船科学技术, 2019(9): 15-18. DOI:10.3404/j.issn.1672-7649.2019.05.012 |
| [6] |
SHEN L, WU J H, LIU Z, et al. Extremely low-frequency Lamb wave band gaps in a sandwich phononic crystal thin plate[J]. International Journal of Modern Physics B, 2015, 29(5): 1550027. DOI:10.1142/S0217979215500277 |
| [7] |
王添, 王桂波, 张若军, 等. 一种薄板声子晶体的低频隔声特性研究[J]. 舰船科学技术, 2019(11): 61-64. DOI:10.3404/j.issn.1672-7649.2019.06.003 |
| [8] |
HO K M, CHENG C K, YANG Z, et al. Broadband locally resonant sonic shields[J]. Applied Physics Letters, 2003, 83(26): 5566-5568. DOI:10.1063/1.1637152 |
| [9] |
徐俭乐, 崔洪宇, 洪明. 声子晶体夹层板结构的隔声性能研究[J]. 振动与冲击, 2021, 40(9): 7. DOI:10.13465/j.cnki.jvs.2021.09.037 |
| [10] |
YANG Z, MEI J, YANG M, et al. Membrane-type acoustic metamaterial with negative dynamic mass[J]. Physical Review Letters, 2008, 101(20): 204301. DOI:10.1103/PhysRevLett.101.204301 |
| [11] |
MEI J, MA G, YANG M, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound[J]. Nature communications, 2012, 3(1): 1-7. |
| [12] |
张玉光. 薄膜型声学超材料隔声特性研究[D]. 长沙: 国防科学技术大学, 2014.
|
| [13] |
杜功焕, 朱哲民, 龚秀芬. 声学基础. 第3版[M]. 南京: 南京大学出版社, 2012.
|
| [14] |
刘如. 声子晶体隔声罩研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [15] |
WANG X, CHEN Y, ZHOU G, et al. Synergetic coupling large-scale plate-type acoustic metamaterial panel for broadband sound insulation[J]. Journal of Sound and Vibration, 2019, 459: 114867. DOI:10.1016/j.jsv.2019.114867 |
| [16] |
张苗, 漆琼芳, 李英伟. 隔声量的阻抗管法和混响室法仿真计算对比[J]. 噪声与振动控制, 2021, 41(4): 6. DOI:10.3969/j.issn.1006-1355.2021.04.033 |
 2022, Vol. 44
2022, Vol. 44
