水下平台在规避或跟踪敌方威胁目标时,通常只考虑目标的当前位置及其作用域,而航海计算过程中,为保持隐蔽性由纯方位法计算的目标运动要素往往不准确,不确定的要素信息极大地降低了平台的生存概率,且平台航行的实际航迹与理想航迹总是有偏差,因此需要同时评定平台及目标在多个方向上的向量误差合成的精度。
水下平台在执行任务过程中,会遭遇突发敌方威胁目标,虽然平台可以依靠被动声呐[1]隐蔽获取目标方位要素信息,进行目标运动状态的实时估计[2-3],但在某些情况下,由于方位信息的系统误差和随机误差导致的要素解算结果与实际相差甚大,且平台并不能持续获得目标的方位信息,目标要素(距离,航向,航速等)随着时间推移误差累积效应逐渐明显,此时目标的概略要素散布估计显得尤为重要。目标要素计算误差受传感器精度、滤波算法的有效性等多种因素影响,以存在测方位误差时的纯方位法[4-6]得到的目标要素作为研究目标实时散布误差椭圆的依据。
1 相对误差散布椭圆域模型由于探测器材精度以及目标要素解算方法的限制,目标的航向、航速以及水下平台与目标的距离等都带有初始误差,而且这类误差会随着时间累积导致目标散布域不断扩大。由于这类误差作用中心相同,方向不同,因此误差可相加合成为误差椭圆域。研究水下平台与目标的相对位置散布关系,对于平台规避、跟踪和攻击等具有辅助决策的作用。
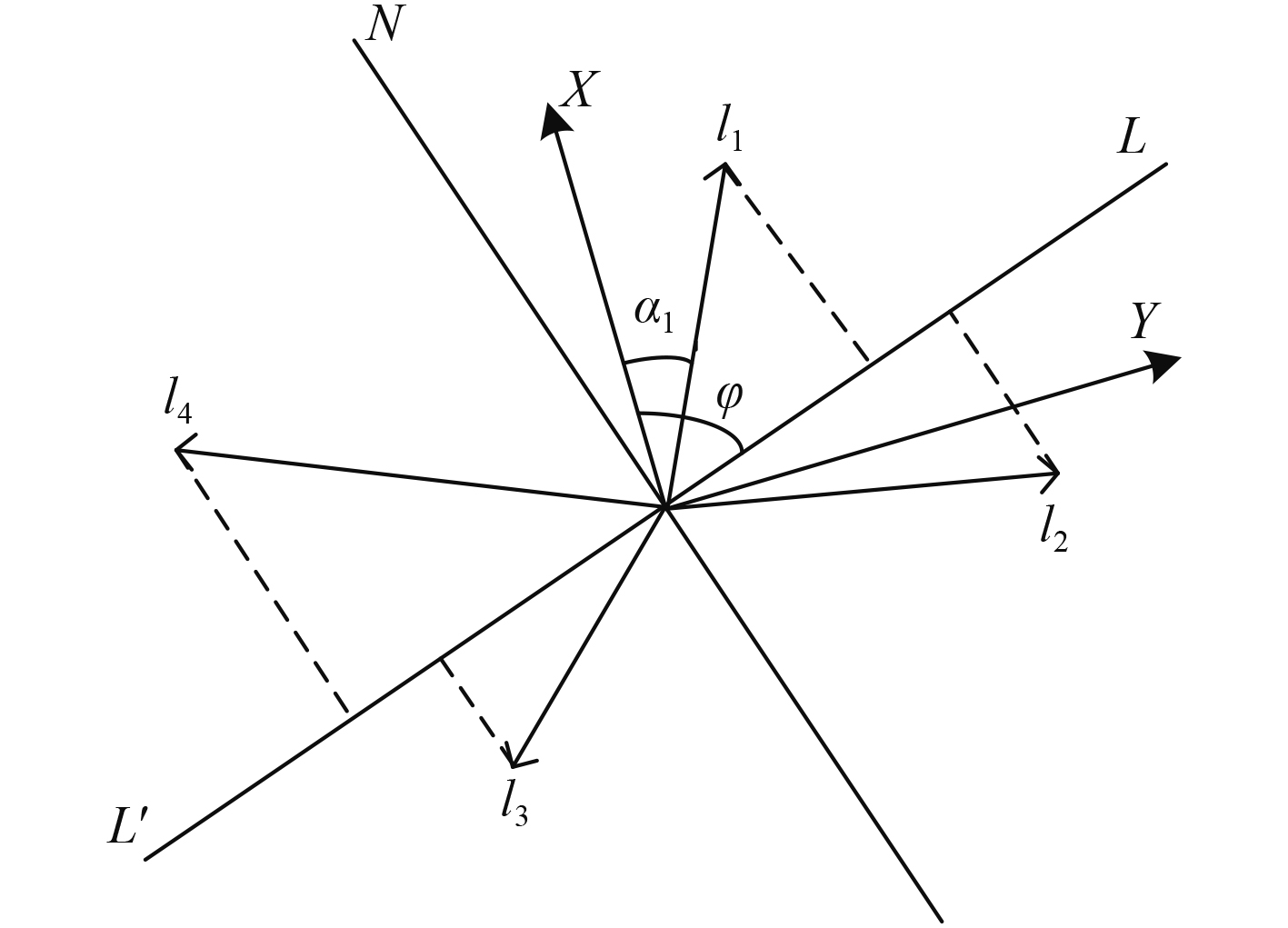
如图1所示,设运动要素向量误差作用于同一中心O点,各向量误差对已知轴N-N′的偏差等于该向量误差在N-N′的垂直轴上的投影。
|
图 1 向量误差投影图 Fig. 1 Vector error projection |
为求得误差椭圆要素(椭圆大小和方向),需确定合成偏差的极大值和极小值,即确定使得合成偏差取得极大值的投影轴
向量误差在
| $ \begin{split} {L^2} =& \sum\limits_{j = 1}^5 {{l_j}^2{{\cos }^2}({l_j},LL')} = {\left| {\Delta {{\boldsymbol{V}}_{wi}} } \right|^2} \cdot {\cos ^2}(\Delta {{\boldsymbol{V}}_{wi}},LL') + \\ & {\left| {\Delta {{\boldsymbol{D}}_i} } \right|^2} \cdot {\cos ^2}(\Delta {{\boldsymbol{D}}_i},LL') + {\left| {\Delta {{\boldsymbol{H}}_{wi}} } \right|^2} \cdot {\cos ^2}(\Delta {{\boldsymbol{H}}_{wi}},LL') + \\ & {\left| {\Delta {{\boldsymbol{H}}_{mi}} } \right|^2} \cdot {\cos ^2}(\Delta {{\boldsymbol{H}}_{mi}},LL')+ {\left| {\Delta {{\boldsymbol{V}}_{mi}} } \right|^2} \cdot {\cos ^2}(\Delta {{\boldsymbol{V}}_{mi}},LL') 。\end{split} $ | (1) |
式中:
由
| $ {\left[ {{l_j}\cos ({l_j},LL'){\kern 1pt} } \right]^2} = {({X_j}\cos {\varphi _1} + {Y_j}\sin {\varphi _1})^2}。$ | (2) |
其中:
结合式(1)可得:
| $ \begin{split} {L^2} = &\sum\limits_{j = 1}^5 {X_j^2{{\cos }^2}{\varphi _1}} + 2\sum\limits_{j = 1}^5 {{X_j}{Y_j}\sin {\varphi _1} \cos {\varphi _1}} + \sum\limits_{j = 1}^5 {Y_j^2{{\sin }^2}{\varphi _1}} = \\ & \sum\limits_{j = 1}^5 {X_j^2{{\cos }^2}{\varphi _1}} + \sum\limits_{j = 1}^5 {{X_j}{Y_j}\sin 2{\varphi _1}} + \sum\limits_{j = 1}^4 {Y_j^2{{\sin }^2}{\varphi _1}} ,\\[-20pt] \end{split} $ | (3) |
令各常数为:
| $ \begin{split} {K_1} =& \sum\limits_{j = 1}^5 {{X_j}^2} = \sum\limits_{j = 1}^5 {{L_j}^2\cos {\alpha _j}^2} =\\ &{\left| {\Delta {{\boldsymbol{V}}_{wi}}} \right|^2} + {\left| {\Delta {{\boldsymbol{D}}_i}} \right|^2} \cdot {\cos ^2}{\alpha _{D1}} + {\left| {\Delta {{\boldsymbol{H}}_{wi}}} \right|^2} \cdot {\cos ^2}{\alpha _{Hwi}} +\\ &{\left| {\Delta {{\boldsymbol{H}}_{mi}}} \right|^2} \cdot {\cos ^2}{\alpha _{Hmi}} + {\left| {\Delta {{\boldsymbol{V}}_{mi}}} \right|^2} \cdot {\cos ^2}{\alpha _{Vmi}},\end{split} $ |
| $ \begin{split} {K_2} =& \sum\limits_{j = 1}^5 {{X_j}{Y_j}} = \sum\limits_{j = 1}^5 {{L_j}^2\cos {\alpha _j}\sin {\alpha _j}} =\\ &{\left| {\Delta {{\boldsymbol{D}}_i}} \right|^2} \cdot \cos {\alpha _{D1}} \cdot \sin {\alpha _{D1}} + {\left| {\Delta {{\boldsymbol{H}}_{wi}}} \right|^2} \cdot \cos {\alpha _{Hwi}} \cdot \\ &\sin {\alpha _{Hwi}} + {\left| {\Delta {{\boldsymbol{H}}_{mi}}} \right|^2} \cdot \cos {\alpha _{Hmi}} \cdot \sin {\alpha _{Hmi}}+\\ &{\left| {\Delta {{\boldsymbol{V}}_{mi}}} \right|^2} \cdot \cos {\alpha _{Vmi}} \cdot \sin {\alpha _{Vmi}},\end{split} $ |
| $ \begin{split} {K_3} = &\sum\limits_{j = 1}^5 {{Y_j}^2} = \sum\limits_{j = 1}^5 {{L_j}^2\sin {\alpha _j}^2} =\\ &{\left| {\Delta {{\boldsymbol{D}}_i}} \right|^2} \cdot {\sin ^2}{\alpha _{D1}} + {\left| {\Delta {{\boldsymbol{H}}_{wi}}} \right|^2} \cdot {\sin ^2}{\alpha _{Hwi}} +\\ &{\left| {\Delta {{\boldsymbol{H}}_{mi}}} \right|^2} \cdot {\sin ^2}{\alpha _{Hmi}} + {\left| {\Delta {{\boldsymbol{V}}_{mi}}} \right|^2} \cdot {\sin ^2}{\alpha _{Vmi}} ,\end{split} $ |
故式(1)可改写为
| $ {L^2} = {K_1}{\cos ^2}{\varphi _1} + {K_2}\sin 2{\varphi _1} + {K_3}{\sin ^2}{\varphi _1}。$ | (4) |
为求向量误差投影的平方和
| $ - 2{K_1}\cos {\varphi _1}\sin {\varphi _1} + 2{K_2}\cos 2{\varphi _1} + 2{K_3}\sin {\varphi _1}{\kern 1pt} \cos {\varphi _1} = 0 ,$ | (5) |
故有
| $ \tan 2{\varphi _1} = \frac{{2{K_2}}}{{{K_1} - {K_3}}} 。$ | (6) |
通过上式可求得极大和极小的2个
| $ \begin{split} ({L^2})'' =& - 2{K_1}\cos 2{\varphi _1} - 4{K_2}\sin 2{\varphi _1} + 2{K_3}\cos 2{\varphi _1} =\\ & - 2\cos 2{\varphi _1}({K_1} + 2{K_2}\tan 2{\varphi _1} - {K_3}) ,\end{split} $ | (7) |
结合式(6)可得:
| $ ({L^2})'' = \frac{{ - 2\cos 2{\varphi _1}}}{{{K_1} - {K_3}}}\left[ {{{({K_1} - {K_3})}^2} + 4{K_2}^2} \right]。$ | (8) |
由式(8)可见,当
| $ \left\{ {\begin{array}{*{20}{l}} {\varphi _1} = {\varphi _1} ,&{\rm{sign}}(\cos (2{\varphi _1})) = {\rm{sign}}(A - C)\\ {\varphi _1} = {\varphi _1} + \dfrac{\text{π} }{2} ,& {\rm{sign}}(\cos (2{\varphi _1})) \ne {\rm{sign}}(A - C)。\end{array}} \right. $ | (9) |
研究水下平台与目标的运动问题必须将其统一到一个坐标系中,以真地平面上东向、北向作为直角坐标系的两坐标轴,则椭圆长轴与坐标轴X轴夹角进一步改写为:
| $ \varphi = - \left(\frac{\text{π} }{2} - {H_w}\right) + {\varphi _1}。$ | (10) |
根据式(6)可得偏差最大最小平方和对应的两个角度值分别为
| $ \left\{ {\begin{array}{*{20}{c}} {{a^2} = {K_1}{{\cos }^2}\varphi + {K_2}\sin 2\varphi + {K_3}{{\sin }^2}\varphi },\\ {{b^2} = {K_1}{{\sin }^2}\varphi - {K_2}\sin 2\varphi + {K_3}{{\cos }^2}\varphi }。\end{array}} \right. $ | (11) |
由式(11)可进一步得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{a^2} + {b^2} = {K_1} + {K_3}{\kern 1pt} },\\ {{a^2} - {b^2} = \dfrac{{\cos 2\varphi }}{{{K_1} - {K_3}{\kern 1pt} }}({{({K_1} - {K_3})}^2} + 2{K_2}{\kern 1pt} ({K_1} - {K_3}{\kern 1pt} )\tan 2\varphi ),} \end{array}} \right. $ | (12) |
另有关系
| $ {a^2} - {b^2} = \sqrt {{{({K_1}{\kern 1pt} - {K_3}{\kern 1pt} )}^2} + 4{K_2}{{\kern 1pt} ^2}},$ | (13) |
顾及式(12)最终可得相对误差椭圆的长短半轴分别为:
| $ \left\{ {\begin{array}{*{20}{c}} {a = \sqrt {\dfrac{{{K_1} + {K_3}}}{2} + \sqrt {{{\left(\dfrac{{{K_1} - {K_3}}}{2}\right)}^2} + {K_2}^2} } } ,\\ {b = \sqrt {\dfrac{{{K_1} + {K_3}}}{2} - \sqrt {{{\left(\dfrac{{{K_1} - {K_3}}}{2}\right)}^2} + {K_2}^2} } } ,\end{array}} \right. $ | (14) |
由平台与目标的位置关系可得相对误差椭圆方程为:
| $ \begin{split} & \frac{{{{((x - {w_{mi}}) \cdot \cos ( - \varphi ) + (y - {u_{mi}}) \cdot \sin ( - \varphi ))}^2}}}{{{a^2}}} + \\ & \frac{{{{((x - {w_{mi}}) \cdot \sin ( - \varphi ) - (y - {u_{mi}}) \cdot \cos ( - \varphi ))}^2}}}{{{b^2}}} = 1 。\end{split} $ | (15) |
式(15)即代表作用中心相同,方向不同的向量误差合成的误差椭圆域。
2 平台及目标运动向量误差分析目标散布[7]包括两方面内容:目标运动要素解算误差引起的初始目标散布和目标航行误差引起的连续目标散布。目标散布主要由目标航向误差、航速误差、平台与目标的距离误差引起,并随时间累积。平台在航行过程同样存在散布问题,研究规避过程中目标实时散布误差椭圆[8]对于保证平台的生命力十分必要。由于平台与目标的深度差相比于距离差非常小,因此可将平台与目标看作位于同一水平面上。
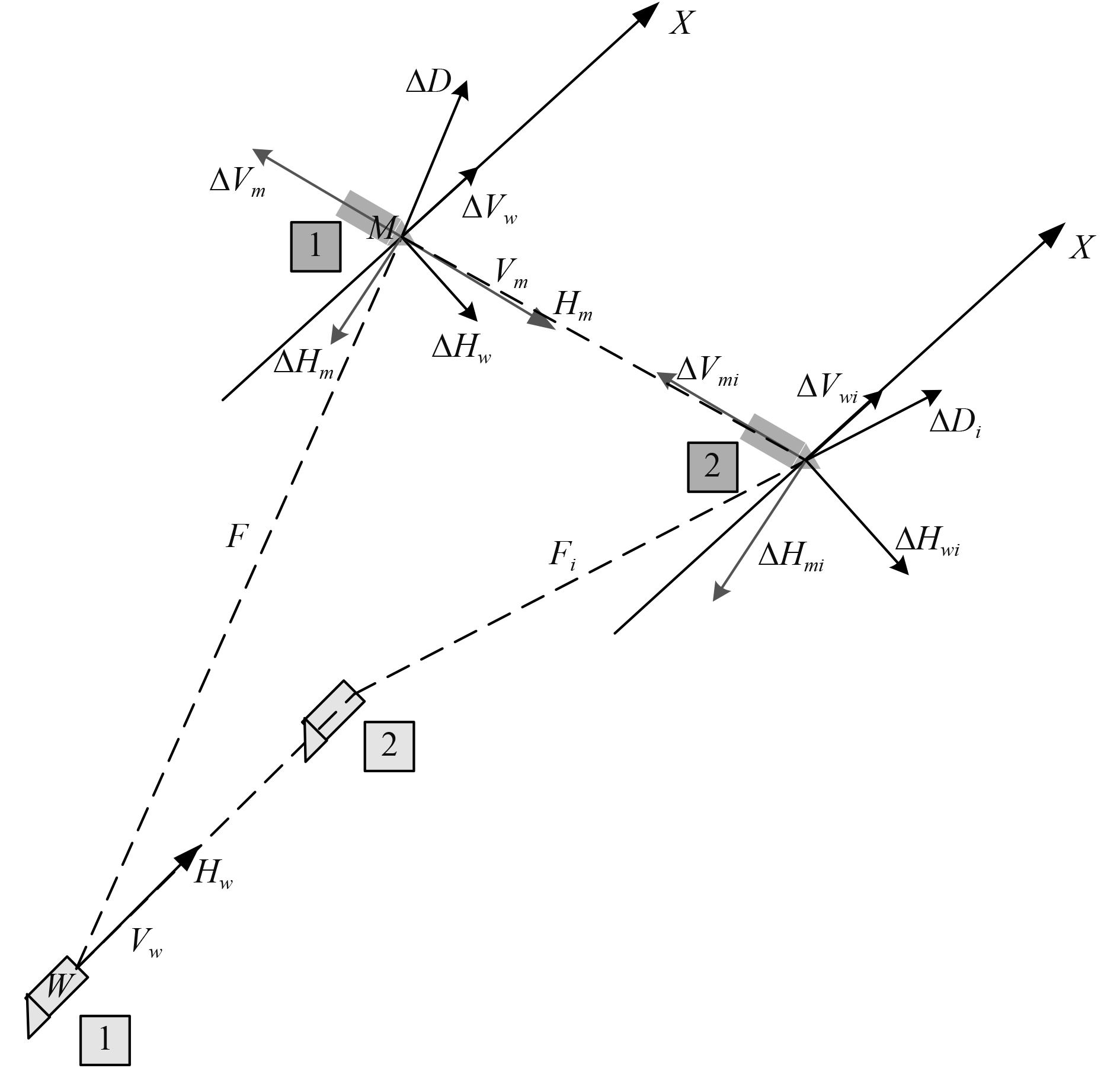
图2描述了水下平台及目标的向量误差分布图,
|
图 2 水下平台与目标的误差分布图 Fig. 2 Error distribution diagram of submersible and target |
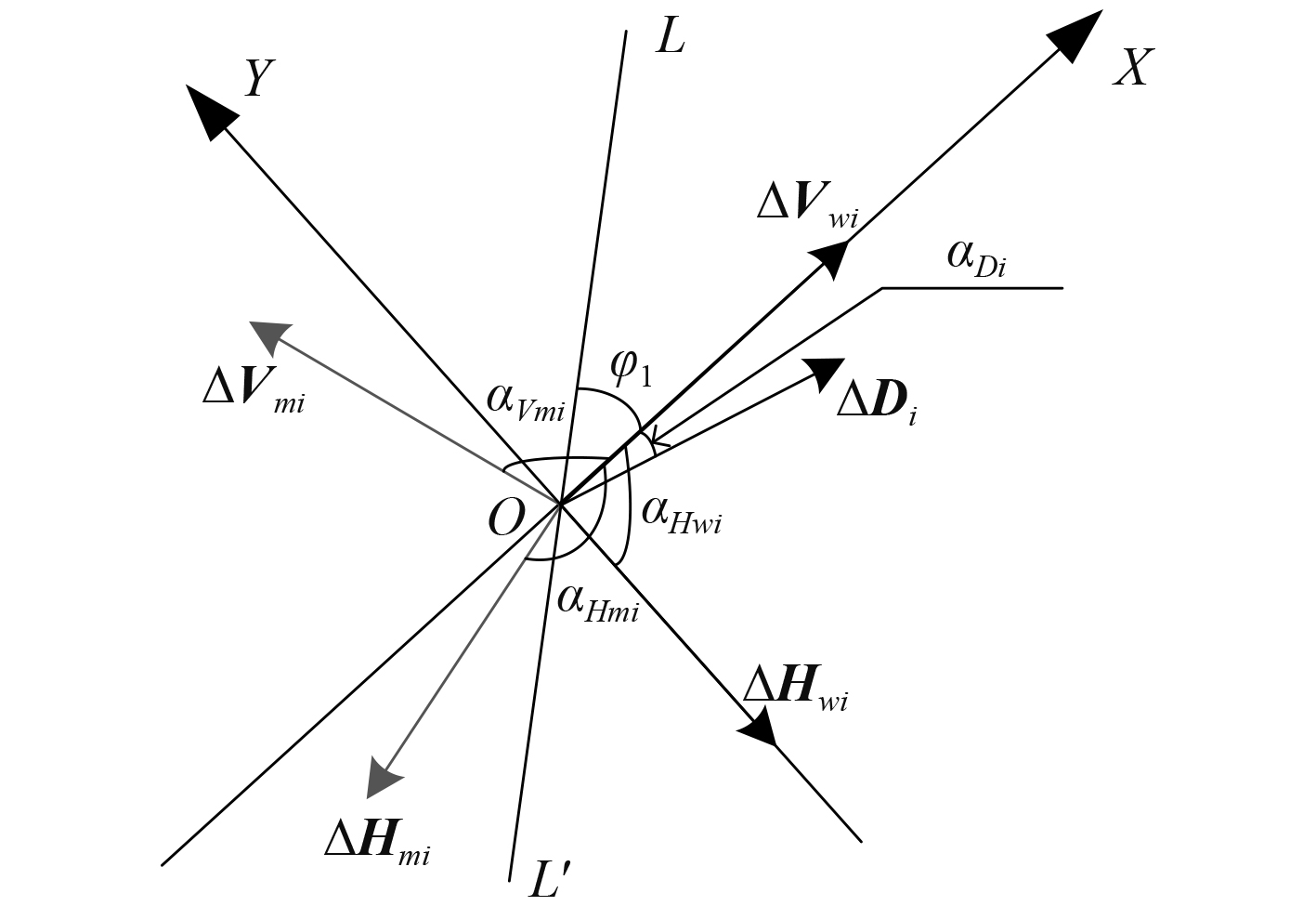
计算
|
图 3 向量误差投影图 Fig. 3 Navigation vector error projection |
| $ {\alpha _{Di}} = {\tan ^{ - 1}}\left(\frac{{\Delta w}}{{\Delta u}}\right) - {F_i} = {\tan ^{ - 1}}\left(\frac{{{w_{mi}} - {w_{wi}}}}{{{u_{mi}} - {u_{wi}}}}\right) - {F_i}。$ | (16) |
式中:
向量误差
| $ \left| {\Delta {{\boldsymbol{H}}_{wi}}} \right| = {V_w} \cdot {t_i} \cdot \tan (\sigma {H_w}) ,$ | (17) |
其中,
向量误差
| $ \left| {\Delta {{\boldsymbol{H}}_{mi}}} \right| = {V_m} \cdot {t_i} \cdot \tan (\sigma {H_m}),$ | (18) |
其中,
| $ {\alpha _{Hmi}} = {H_m} - {H_w} + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2} ,$ | (19) |
| $ {\alpha _{Vmi}} = {\alpha _{Hmi}} + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2} = {H_m} - {H_w} + \pi 。$ | (20) |
目标航速引起的目标散布主要体现在航程误差上,因此有
将各向量误差代入椭圆散布域模型中,可以求得误差椭圆的长短轴长度及椭圆长轴方向与平台航向X轴的夹角。
3 时间累积的误差椭圆域仿真模拟平台与目标的实际运动态势分析双方均存在运动要素误差情况下的相对误差散布域,仿真初始条件为:
平台初始位置
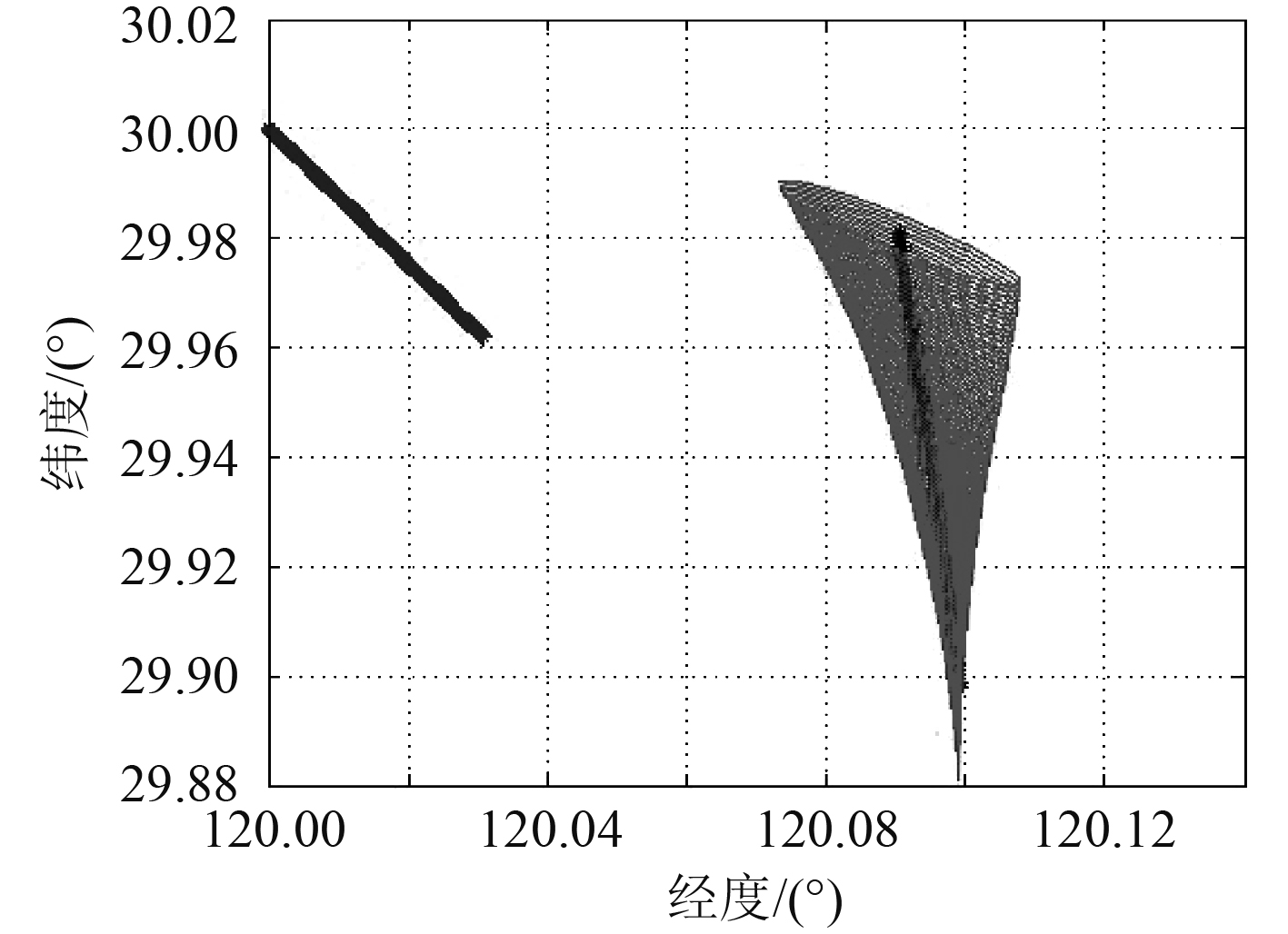
以水下平台航向不变为例,研究平台与目标的态势图及相对误差散布情况,仿真时长为600 s,时间间隔为
|
图 4 平台与目标的态势及相对散布域 Fig. 4 Submersible and target situation and relative error ellipse distribution diagram |
|
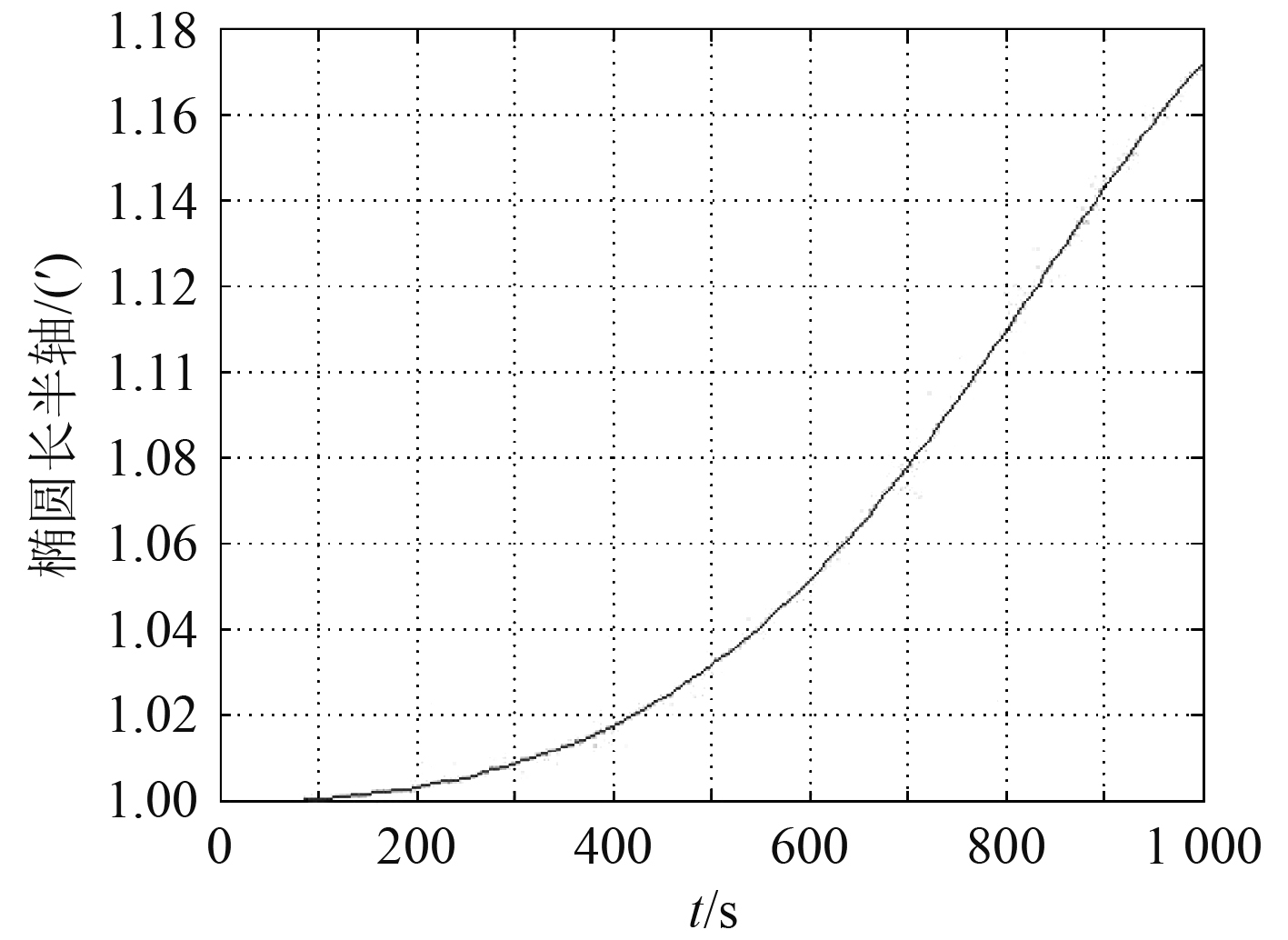
图 5 椭圆长半轴变化曲线 Fig. 5 Ellipse long semi-axis curve |
|
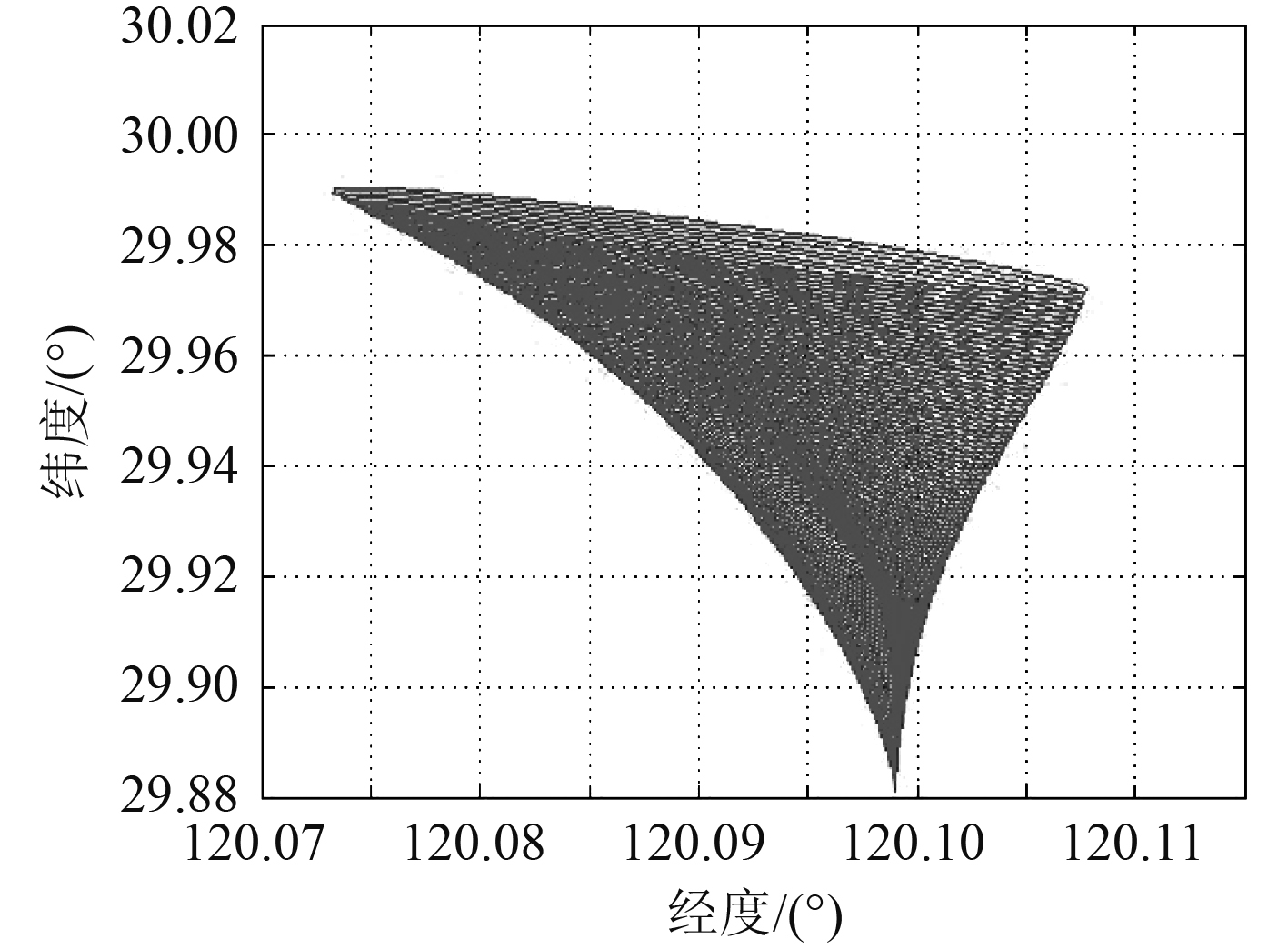
图 6 相对误差散布椭圆变化图 Fig. 6 Relative error spread elliptic variation |
图4中直线1表示600 s过程中平台的运动轨迹,直线2刻画出目标的运动轨迹,椭圆为以t时刻目标位置为中心的相对误差椭圆散布域,可以看出随时间推移椭圆长短半轴不断增大,说明在初始时刻解算目标要素存在误差的情况下,目标推算位置的散布域会逐渐增大。
4 结 语为提高平台水下活动时的生存概率,以平台及目标运动的向量误差构建相对误差散布域。基于目标散布要素和平台散布要素,研究时变相对误差椭圆系统。通过相对误差散布域的构建,为水下平台更有效地规避威胁目标提供依据。
| [1] |
李关防, 崔杰, 袁富宇. 基于线谱瞬时频率估计的被动声纳目标运动分析[J]. 兵工学报, 2017, 38(7): 1395-1401. DOI:10.3969/j.issn.1000-1093.2017.07.018 |
| [2] |
赵建昕, 笪良龙. 基于异方差伪线性模型的纯方位目标要素估计[J]. 探测与控制学报, 2017, 39(2): 7-12. |
| [3] |
王燕, 邹男, 付进, 等. 基于同态滤波技术的水下目标运动参数估计[J]. 兵工学报, 2014, 35(7): 1045-1051. DOI:10.3969/j.issn.1000-1093.2014.07.017 |
| [4] |
WANG Bao-bao, WU Pan-long. Underwater bearing—only tracking based on square-root unscentedKalman filter smoothing algorithm[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 180-184. |
| [5] |
郁涛. 固定单站纯方位目标运动参数的解析方法[J]. 电波科学学报, 2014, 29(4): 634-638. DOI:10.13443/j.cjors.2013080503 |
| [6] |
鹿传国, 冯新喜, 张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J]. 系统工程与电子技术, 2012, 34(1): 28-33. DOI:10.3969/j.issn.1001-506X.2012.01.06 |
| [7] |
宗方勇, 王树宗, 刘辉. 潜射声自导鱼雷两雷平行航向齐射遮盖目标散布[J]. 弹道学报, 2007, 19(2): 16-20. DOI:10.3969/j.issn.1004-499X.2007.02.005 |
| [8] |
王立安, 徐卫昌, 李永峰, 等. 基于弹着点椭圆散布的射击方位角选取[J]. 弹箭与制导学报, 2015, 35(2): 17-20. DOI:10.15892/j.cnki.djzdxb.2015.02.005 |
 2022, Vol. 44
2022, Vol. 44
