0 引　言

复合材料作为新型结构/功能材料，凭借其优良的性能特征在航空、航天、船舶等领域得到越来越多的应用，然而相对于金属结构而言，复合材料结构的设计形式、力学特征都有很大不同，尤其是连接结构。复合材料连接接头作为复合材料结构中的重要部件，不仅构造复杂且需承受交变载荷等作用，是结构承载中较为薄弱的环节，其疲劳特性是复合材料工程应用的关键。

复合材料接头通常为胶结层合结构，分层是最常见的损伤模式，因为胶结面强度相比基体结构要小很多，在经历交变载荷过程中胶结面易出现层间损伤，导致层间可承受的应力水平降低，长时间长周期处于循环交变载荷下，层间损伤会累积并最终发展成影响结构承载的宏观分层裂纹。

目前复合材料分层损伤的主要研究方法是内聚力单元法，这个方法是将分层扩展的上下2个面通过一个内聚力单元连接起来，内聚力单元的失效通过损伤量的累积来控制，用单元的失效有效地模拟界面的分层。该方法最先由Dugdale^[1]和Barenblatt^[2]发展起来，之后Needleman^[3]基于此方法，使用不同的内聚力本构模型模拟了一系列的基本问题，提出为了模拟疲劳裂纹的扩展，必须在内聚力模型中加入不可逆转的刚度折减来对内聚力单元进行控制。Foulk^[4]在本构模型中加入加载与卸载行为，并获得了单元不可逆转的拉伸分离关系。de Andrés^[5]也用类似的方法，并且定义了单元的损伤量。Nguyen^[6]使用一个指数衰减的损伤变量控制单元刚度随着循环次数的缩减；Yang^[7]提出损伤在循环过程中的卸载端也会得到累积。Robinson^[8]将损伤变量分成两部分来考虑：一部分为静态裂纹扩展，一部分为疲劳裂纹扩展，通过施加一个恒定的最大载荷值来模拟疲劳的加载过程，以每次增量步增加的时间来代替增加的循环数。Kawashita^[9]利用内聚力单元分析了高循环载荷作用下复合材料的分层问题；Laurent Gornet^[10]研究发展了一个可以实现复合材料疲劳分层模拟的数值模型，在模型中对传统用于预测静态脱胶的界面单元法则进行修改和发展，使它可以用于模拟高循环的疲劳分层，并通过相关试验进行了验证。Atsushi Hosoi^[11]研究了准各项同性CFRP层合板在高循环次数下的疲劳特性，研究中考虑了横向裂纹对边远分层起始和扩展的影响。Jianyu Zhang^[12]研究了复合材料疲劳裂纹门槛值对疲劳裂纹扩展速率的影响，研究中疲劳分层抗性作为一个控制性参数用来预估疲劳裂纹扩展速率和门槛值。

本文主要通过内聚力单元方法，开发层间材料模型，研究分析内聚力单元在疲劳载荷作用下的损伤演化过程，建立其疲劳损伤计算方法，同时基于有限元对复合材料T型接头结构在疲劳载荷下的损伤演化行为进行数值仿真研究。

1 损伤演化及判据

采用有限元方法模拟复合材料分层损伤主要通过2个判据实现：分层起始判据和分层演化判据，本文采用二次名义应力准则作为单元损伤的起始判据：

$ {\left\{ {\left. {\dfrac{{\left\langle {{t_n}} \right\rangle }}{{t_n^0}}} \right\}} \right.^2} + {\left\{ {\left. {\dfrac{{{t_s}}}{{t_s^0}}} \right\}} \right.^2} + {\left\{ {\left. {\dfrac{{{t_t}}}{{t_t^0}}} \right\}} \right.^2} = 1，$

(1)

损伤扩展判据采用由Benzeggagh和Kenane提出的B-K准则：

$ {f_{propagation}} = \frac{{{G_T}}}{{{G_C}}} - 1 = 0，$

(2)

其中 ${G}_{T}\;=\;{G}_{shear}\;+\;{G}_{\mathrm{Ⅰ}}$ ， ${G}_{shear}\;=\;{G}_{\mathrm{Ⅱ}}\;+\;{G}_{\mathrm{Ⅲ}}$ ， ${G_C}\; =\; {G_{1C}} \;+ ({G_{shearC}} - {G_{1C}}){\left( {\dfrac{{{G_{shear}}}}{{{G_T}}}} \right)^\eta }$ 。

G_shear/G_T可以用B表示能量混合率比率：

$ B = \frac{{{G_{shear}}}}{{{G_T}}} = \frac{{{\beta ^2}}}{{1 + 2{\beta ^2} - 2\beta }} ，$

(3)

其中 $\beta = \dfrac{{{\delta _{shear}}}}{{{\delta _m}}}$ ， ${\delta _m} = \sqrt {{{\left\langle {{\delta _1}} \right\rangle }^2} + {\delta _2}^2 + {\delta _3}^2} $ 。

2 内聚力单元本构关系

内聚力模型定义了界面应力与相对位移间的关系，常见的本构模型有梯型、多项式型、指数型及双线性型，这些模型中双线性本构关系因其模型简单、容易定义且准确性和收敛性好应用较多，因此本文采用双线性本构模型对复合材料接头的层间分层进行研究。

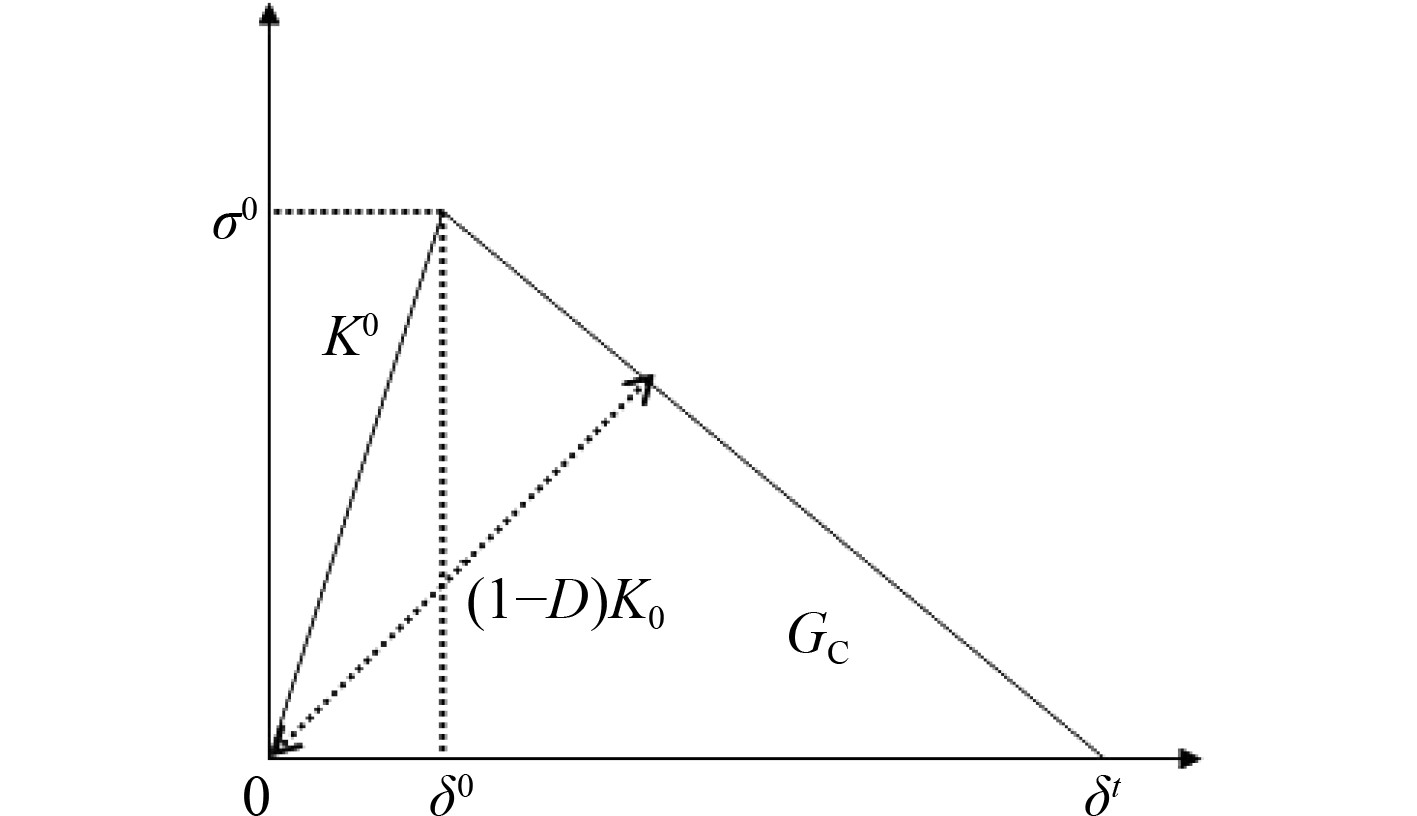
图1为K₀为初始单元刚度， $ {\sigma ^0} $ 为材料的强度极限，当内聚力单元的相对位移超过 ${\delta ^0}$ 时，随着相对位移的继续增加，损伤量D开始积累，单元的刚度即变为(1-D)K₀。内聚单元在损伤前是线弹性的，应力随着内聚单元位移的增加而线性地增加(即图1上升段)，当单元的应力达到极限时，刚度开始降阶，单元开始损伤演化，最终材料的承载能力降低，整个双线性本构模型的围城面积为内聚力单元完全破坏的应变能释放率。根据这一原理可以求出单元极限强度对应的相对位移 ${\delta ^0}$ ，表达式如下：

$ \delta _n^0 = \frac{N}{{{k_n}}}，\delta _s^0 = \frac{S}{{{k_s}}}，\delta _t^0 = \frac{T}{{{k_t}}}。$

(4)

式中：N为内聚力单元法向强度；S和T为内聚力单元剪切强度。

单元完全失效位移可以通过应变能释放率求得：

$ \delta _n^f = \frac{{2G_I^C}}{N}，\delta _s^f = \frac{{2G_{II}^C}}{S}，\delta _t^f = \frac{{2G_{III}^C}}{T} ，$

(5)

在混合模式的作用下，用 $ \delta {}_m $ 表示当前的相对位移，则其可表示为：

$ \delta {}_m = \sqrt {{{\left\langle {{\delta _1}} \right\rangle }^2} + \delta _2^2 + \delta _3^2} = \sqrt {{{\left\langle {{\delta _1}} \right\rangle }^2} + \delta _{shear}^2} 。$

(6)

其中： $\left\langle {{\delta _1}} \right\rangle = \left\{ {\begin{aligned} &{0 \Leftarrow {\delta _1} \leqslant 0} \\ &{{\delta _1} \Leftarrow {\delta _1} > 0} \end{aligned}} \right.$ ， ${\delta _{shear}}$ 为内聚力单元切向相对位移 $ \delta _{shear}^2 = \delta _s^2 + \delta _t^2 $ 。

将式（3）、式（4）、式（6）代入式（1）得到混合模式下的初始相对位移：

$ \delta _m^0 = \left\{ {\begin{aligned} &{\delta _1^0\delta _2^0\sqrt {\dfrac{{1 + {\beta ^2}}}{{{{\left( {\delta _2^0} \right)}^2} + {{\left( {\beta \delta _1^0} \right)}^2}}}} }，\\ &{\delta _{shear}^0 \Leftarrow {\delta _1} \leqslant 0} 。\end{aligned}} \right. \Leftarrow {\delta _1} > 0，$

(7)

将式（5）、式（6）代入式（2）即B-K失效准则，得到混合模式下最终失效相对位移：

$ \delta _m^f = \left\{ {\begin{aligned} &{\frac{2}{{K\delta _m^0}}\left[ {{G_{IC}} + \left( {{G_{IIC}} - {G_{IC}}} \right)} \right]\left( {\frac{{{\beta ^2}}}{{1 + {\beta ^2}}}} \right)}，\\ &{\sqrt {{{\left( {\delta _2^f} \right)}^2} + {{\left( {\delta _3^f} \right)}^2}} \Leftarrow {\delta _1} \leqslant 0} ，\end{aligned}} \right. \Leftarrow {\delta _1} > 0。$

(8)

当没有损伤发生时，内聚力单元本构关系如下：

$\begin{split} \sigma = & \left\{ {\begin{array}{*{20}{c}} {{\sigma _n}} \\ {{\sigma _t}} \\ {{\sigma _s}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{k_n}}&{}&{} \\ {}&{{k_t}}&{} \\ {}&{}&{{k_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _n}} \\ {{\varepsilon _t}} \\ {{\varepsilon _s}} \end{array}} \right] =\\ & \left[ {\begin{array}{*{20}{c}} {{k_n}}&{}&{} \\ {}&{{k_t}}&{} \\ {}&{}&{{k_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\Delta _n}} \\ {{\Delta _t}} \\ {{\Delta _s}} \end{array}} \right] = \left[ K \right]\left[ \Delta \right]。\end{split}$

(9)

式中： ${k_n},{k_s},{k_t}$ 分别为内聚力单元法向刚度和切向刚度。

定义损伤变量d为刚度的损失比例：

$ d = \frac{{\delta _m^{} - \delta _m^0}}{{\delta _m^f - \delta _m^0}}，$

(10)

含损本构关系可以表示为：

$\begin{split} \sigma = & \left\{ {\begin{array}{*{20}{c}} {{\sigma _n}} \\ {{\sigma _t}} \\ {{\sigma _s}} \end{array}} \right\} = (1 - d)\left[ {\begin{array}{*{20}{c}} {{k_n}}&{}&{} \\ {}&{{k_t}}&{} \\ {}&{}&{{k_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\Delta _n}} \\ {{\Delta _t}} \\ {{\Delta _s}} \end{array}} \right] -\\ &d\left[ {\begin{array}{*{20}{c}} {{k_n}}&{}&{} \\ {}&0&{} \\ {}&{}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\left\langle {\left. { - {\Delta _n}} \right\rangle } \right.} \\ 0 \\ 0 \end{array}} \right]。\end{split}$

(11)

其中：符号<>的含义为 $\left\langle x \right\rangle = \left\{ {\begin{aligned} &{0 \Leftarrow x \leqslant 0 ，} \\ &{x \Leftarrow x > 0 。} \end{aligned}} \right.$

3 疲劳损伤计算

通过引入B-K准则的假定，可以得到混合模式分层能量释放率门槛值为：

$ {G_{th}} = {G_{Ith}} + ({G_{IIth}} - {G_{Ith}}){\left(\frac{{{G_{shear}}}}{{{G_T}}}\right)^{{\eta _2}}}，$

(12)

在疲劳载荷作用下的损伤量D可以看成两部分的组合，即准静态加载造成的损伤和疲劳载荷造成的损伤：

$ {D_{tot}} = {d_s} + {d_f}。$

(13)

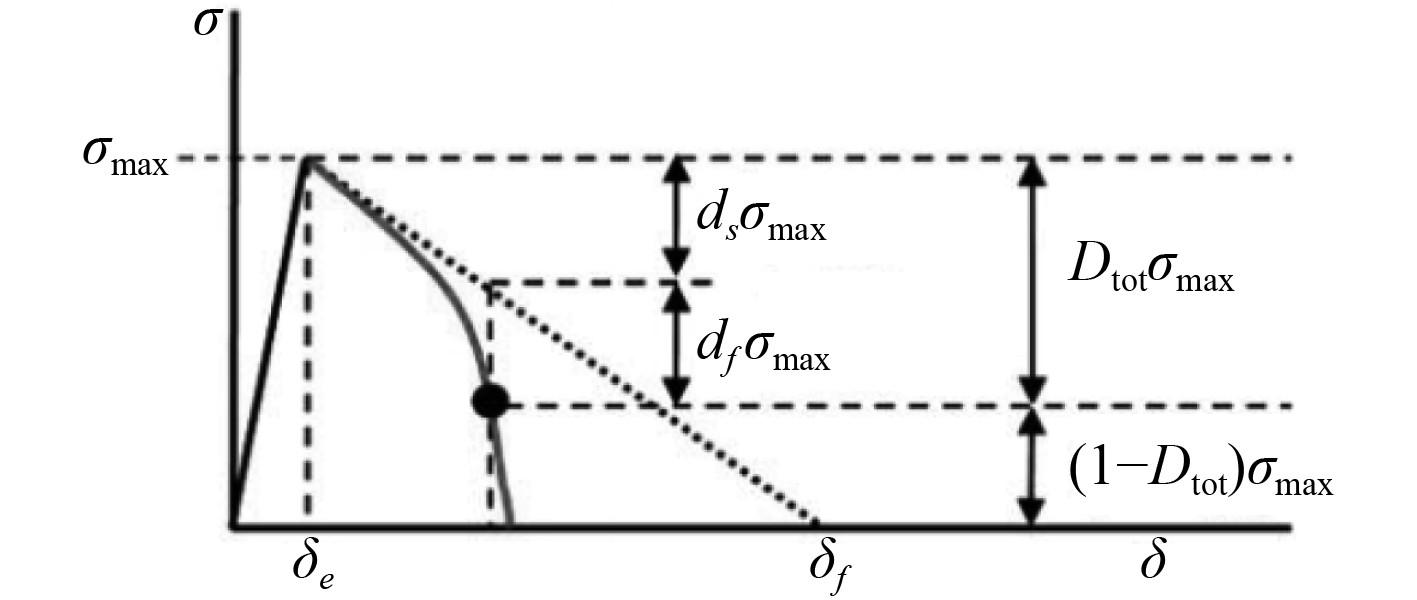
图2为疲劳载荷参加计算时内聚力单元的本构关系，图中的虚线为准静态加载时内聚力单元的本构关系，实线为施加疲劳载荷后的本构关系。当单元应变能释放率超过门槛值之后，由于疲劳载荷作用，单元的损伤量开始积累，内聚力单元离裂纹尖端越近，其应变能力释放率越大，导致其强度下降的也就越快，而这些远离裂纹尖端的刚度下降相对较慢。

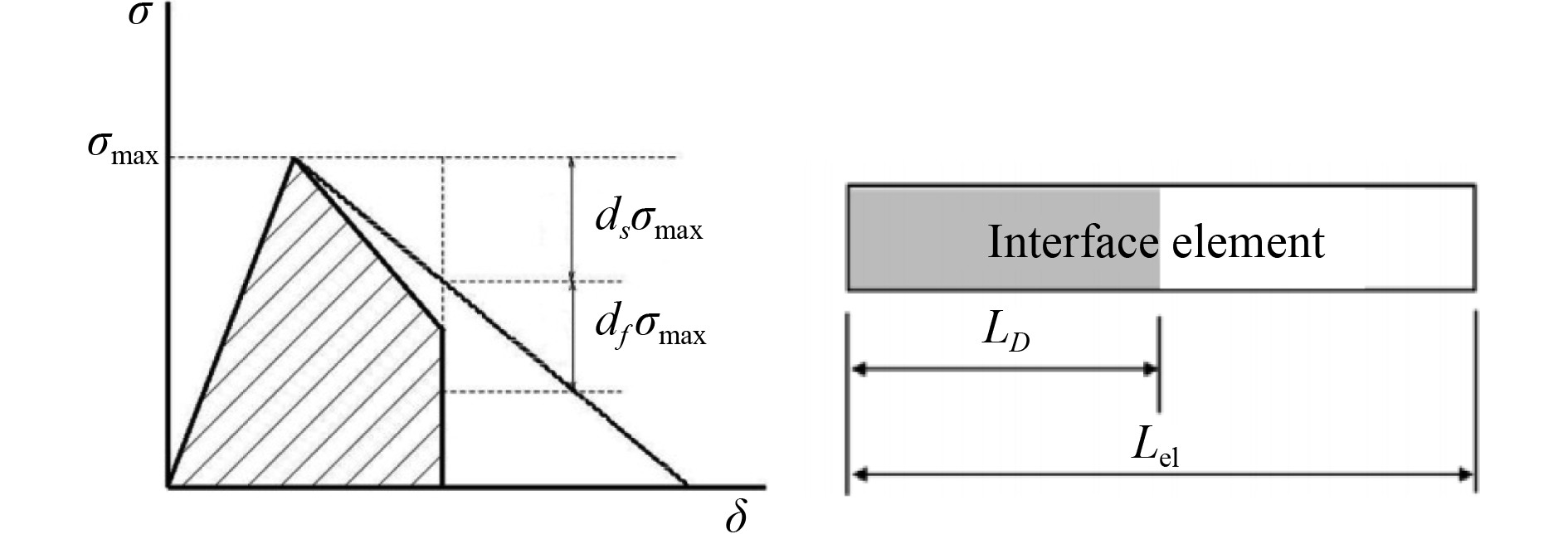
将疲劳载荷参与下的内聚力单元本构模型简化如图3所示。

单元没有完全失效时疲劳载荷造成其裂纹扩展长度为L_D，其占整个单元的长度表达式为：

$ \frac{{{L_D}}}{{{L_{el}}}} = \frac{{{d_f}}}{{1 - {d_s}}}，$

(14)

新增裂纹长度假设等于所有处于疲劳损伤区域单元损伤的总和：

$ a = \sum\limits_{e \in {L_{fat}}} {{L_D}} ，$

(15)

从而裂纹增长率可以表示成：

$ \frac{{\partial a}}{{\partial N}} = \sum\limits_{e \in {L_{fat}}} {\frac{{\partial {L_D}}}{{\partial N}}} 。$

(16)

假设所有处于疲劳损伤区域的单元的裂纹增长率相同，则公式可以简化为：

$ \sum\limits_{e \in {L_{fat}}} {\frac{{\partial {L_D}}}{{\partial N}}} = \frac{{{L_{fat}}}}{{{L_{el}}}}\frac{{\partial {L_D}}}{{\partial N}}，$

(17)

式（16）可以表示为：

$ \frac{{\partial a}}{{\partial N}} = \frac{{{L_{fat}}}}{{{L_{el}}}}\frac{{\partial {L_D}}}{{\partial N}}。$

(18)

建立损伤量与循环数之间关系如下：

$ \frac{{\partial {d_f}}}{{\partial N}} = \frac{{\partial {d_f}}}{{\partial {L_D}}}\frac{{\partial {L_D}}}{{\partial N}} ，$

(19)

对式（14）求偏导数：

$ \frac{{\partial {d_f}}}{{\partial {L_D}}} = \frac{{1 - {d_s}}}{{{L_{el}}}}。$

(20)

将式（18）、式（20）代入式（19）中得到：

$ \frac{{\partial {d_f}}}{{\partial N}} = \frac{{1 - {d_s}}}{{{L_{fat}}}}\frac{{\partial a}}{{\partial N}}，$

(21)

内聚力区域的计算公式：

$ {L_{CZ}},i = b\frac{{9\text{π} }}{{32}}\frac{{{E_3}{G_{i,c}}}}{{{{(\tau _i^0)}^2}}},i = {\text{I,II,III}}，$

(22)

$ {L_{CZ.mix}} = m(min({A_{{\text{CZ,I}}}},{A_{{\text{CZ,II}}}},{A_{{\text{CZ,III}}}})) 。$

(23)

式中： $ m $ 为修正参数，一般取值在0.5～1之间； $ b $ 表示分层前缘宽度； $ {G_{i,C}} $ 为各单一模式的最大能量释放率；E₃为垂直于裂纹扩展面方向的层合板杨氏模量； $ {\tau ^0} $ 表示层间强度。

假设疲劳损伤区域占的比例为0.5：

$ {L_{fat}} = 0.5\left( {\frac{{{G_T}}}{{{G_C}}}} \right){L_{CZ,f}}，$

(24)

随着每次计算增量步疲劳损伤参数也随之更新：

$ {d_{f,new}} = {d_{f,old}} + \vartriangle N\frac{{\partial {d_f}}}{{\partial N}} 。$

(25)

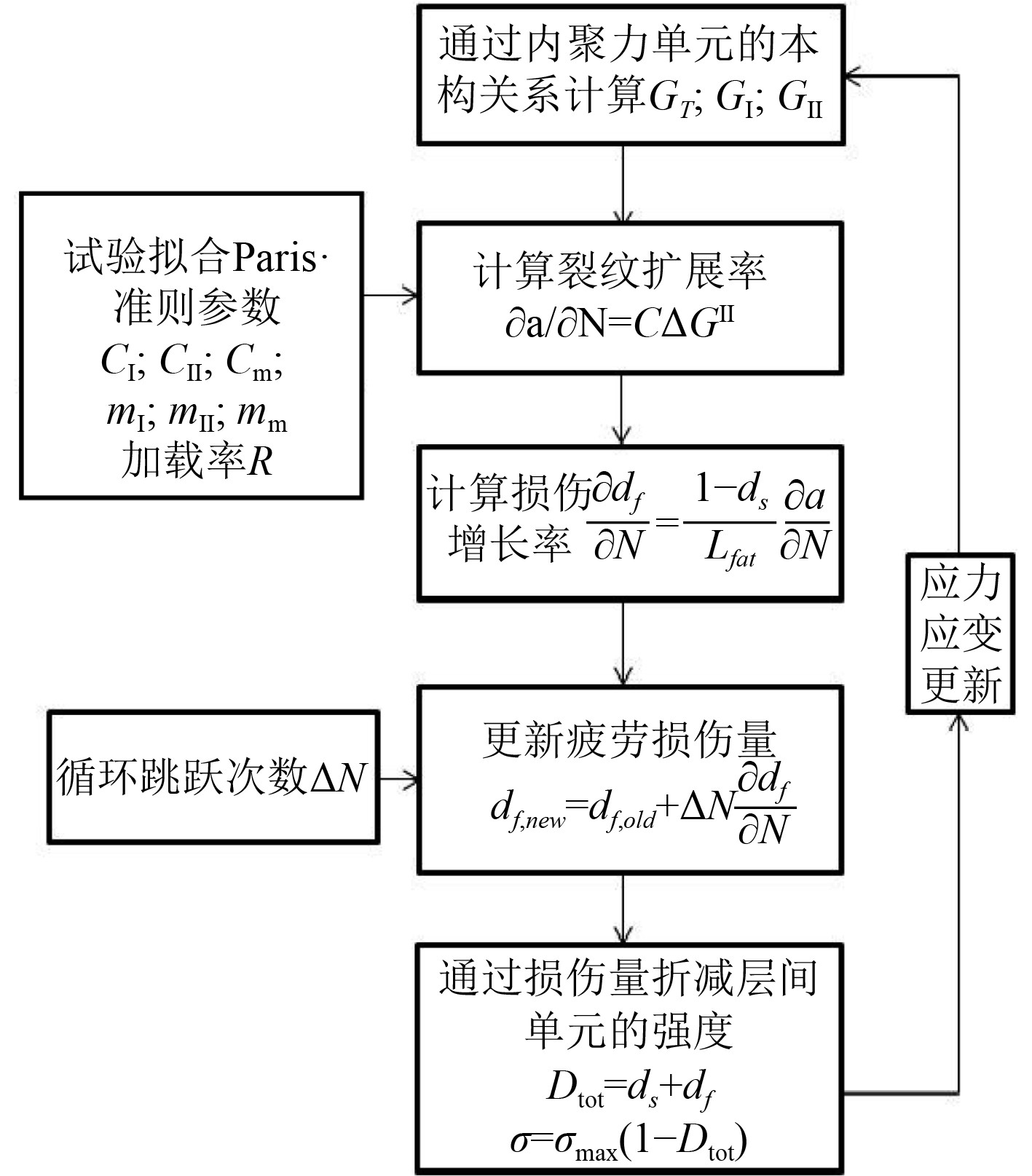
内聚力模型损伤演化与疲劳计算具体流程如图4所示。

4 T型接头疲劳分层算例

采用简化二维有限元模型，T型接头长200 mm，高150 mm，圆弧过渡区尺寸R为5 mm，T型接头底板部位两边固支，接头上端施加载荷，具体示意如图5所示。

腹板和底板使用4结点平面应变单元，单层厚度为0.125 mm，腹板厚度为1.75 mm，铺层顺序为[45/−45/0/90/−45/45/0]_s，底板厚度为10 mm，铺层顺序为[0/45/−45/90]_{10 s}。材料为T700/QY8911，具体参数见表1。腹板、底板、三角填充区3个部件连接面及三角填充区采用4结点内聚力单元，材料选用HTA/6376C^[13]，具体参数见表2。

4.1 位移加载控制结果分析

对二维T型接头进行静力分析，得到50%对位的位移值为0.64 mm，据此对试件上端施加0.64 mm的位移载荷。

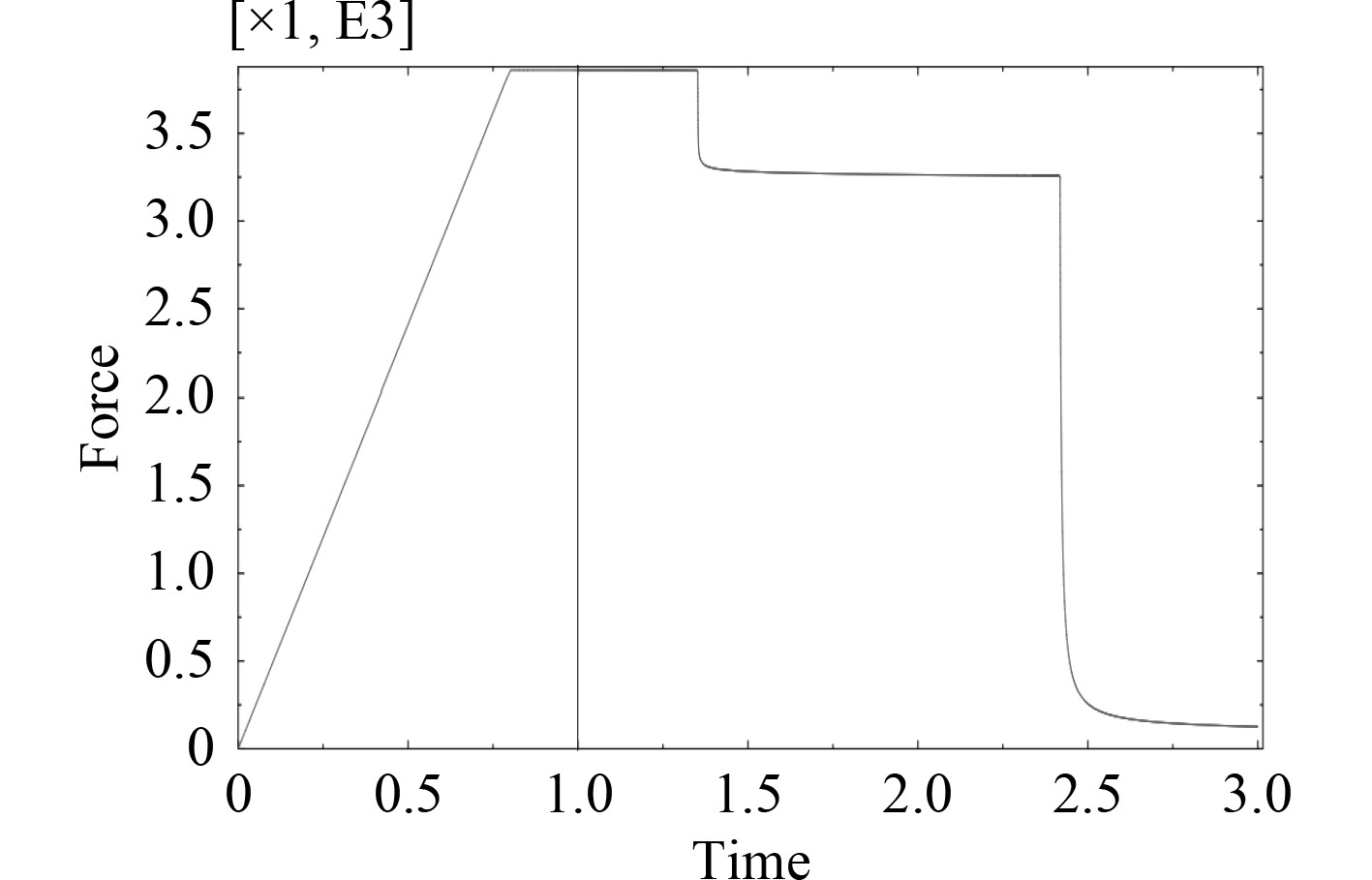
图6为接头载荷历程曲线，时间1之前为准静态加载段，时间1之后为疲劳加载段。疲劳加载过程中载荷有两次突降，第1次突降载荷幅度约15%，接头还有一定承载能力，随着循环次数的继续累积，接头发生第2次载荷的突降，载荷承载能力下降约96%，接头完全失去承载能力。

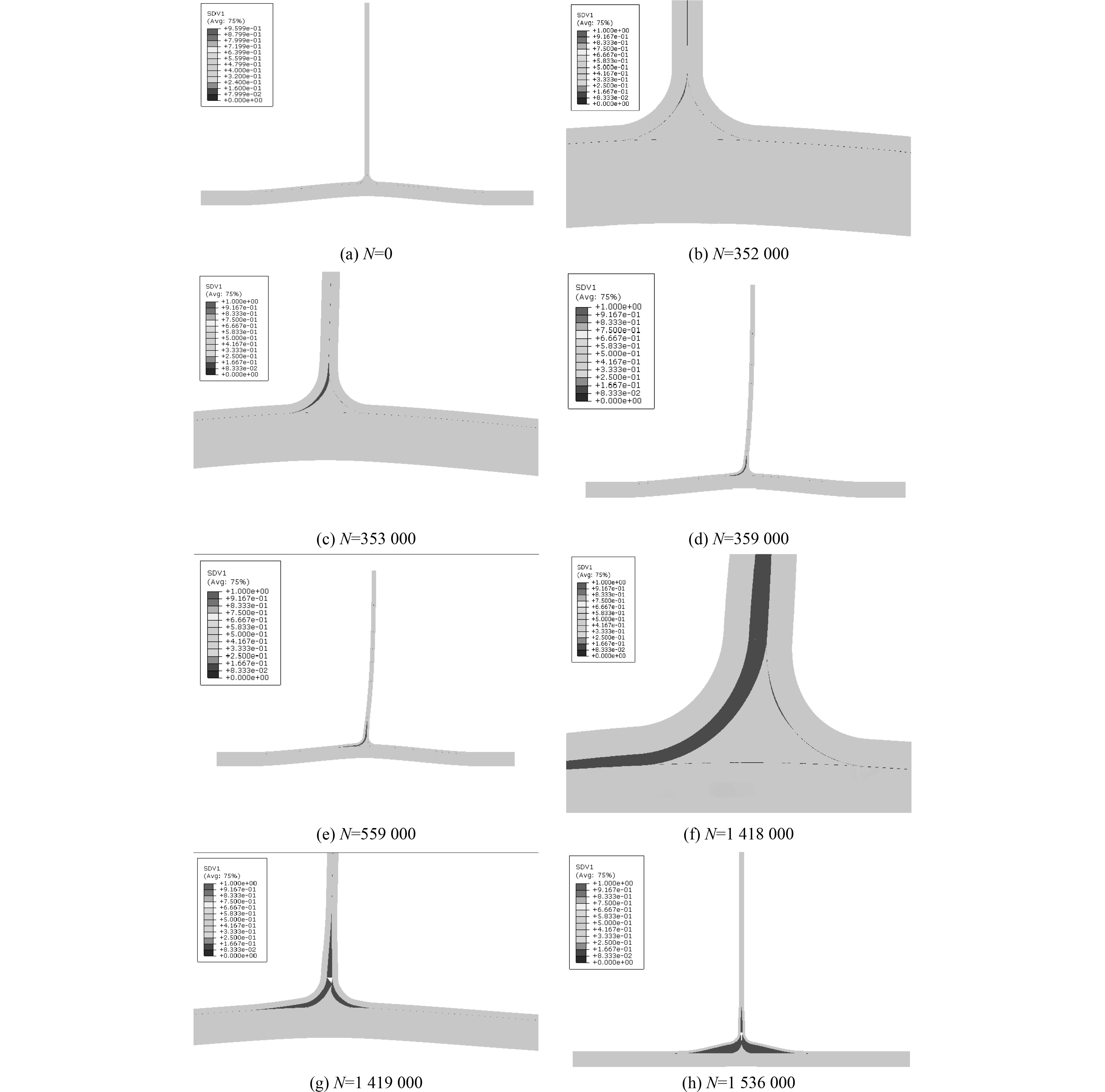
从图7可以看出，在循环次数到352000次时，T型接头的圆弧过渡区左侧最先产生裂纹，对应在载荷历程上就是载荷的第1次突降，随着循环次数继续增加，载荷变化不大，但裂纹沿着左侧的圆弧过渡区向上和向左继续缓慢扩展，在裂纹扩展到一定范围内，接头剩余承载能力基本保持不变，当循环次数达到1418000时圆弧过渡区右侧也产生了裂纹，对应在载荷历程上就是载荷的第2次突降，循环继续累积1000次左右接头就完全失效。

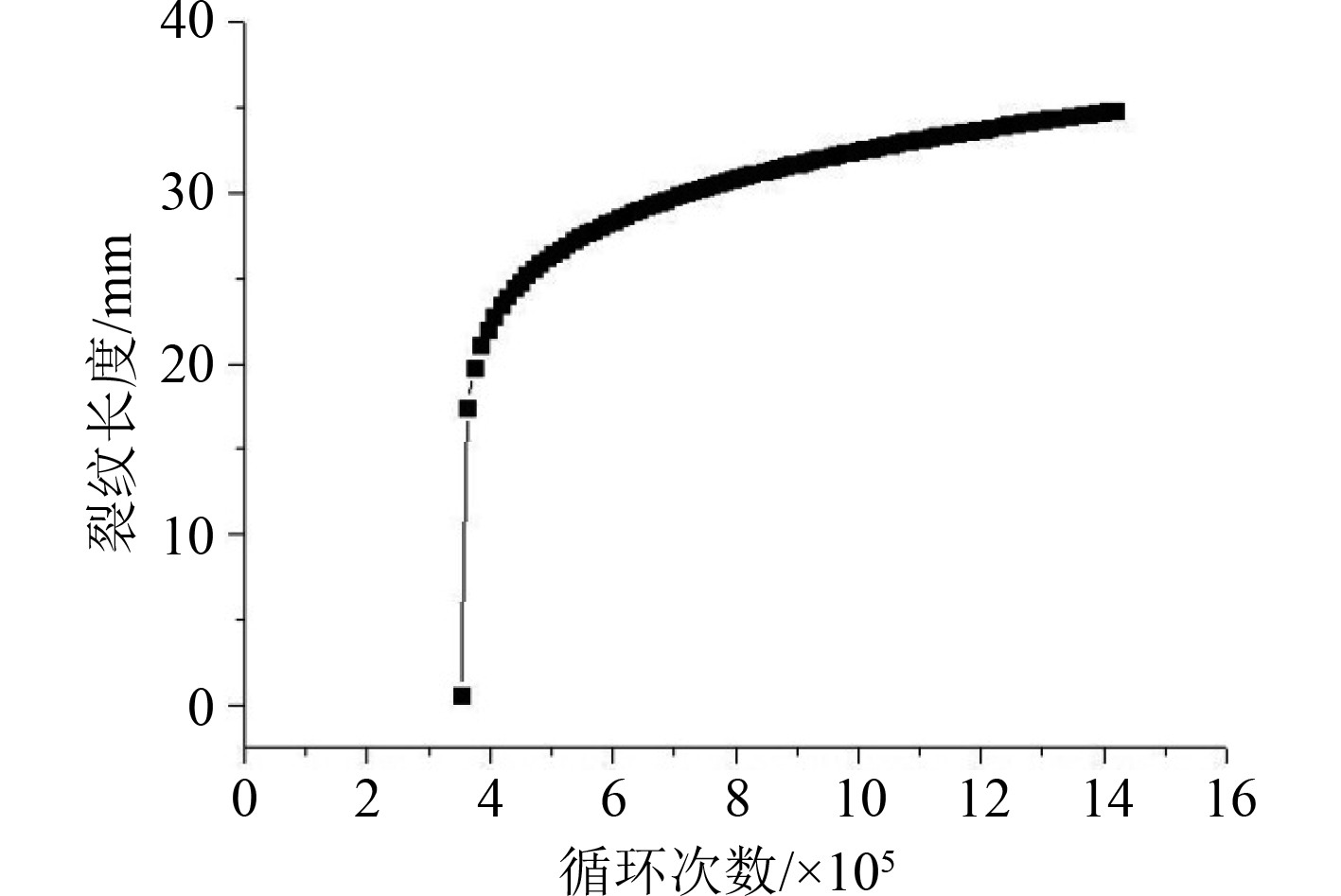
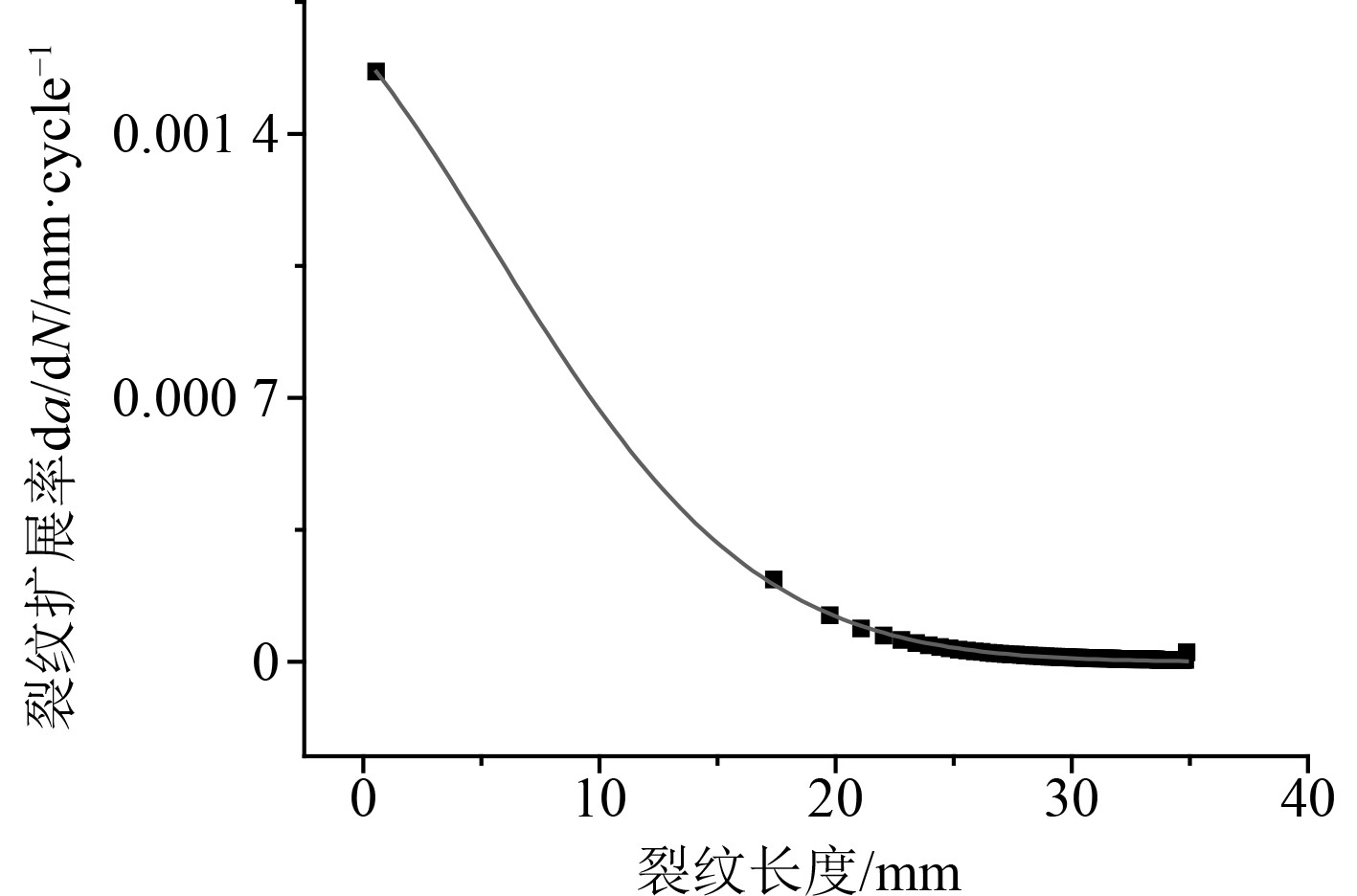
从图8可以看出，在裂纹产生的初期载荷降低约15%，后面循环过程中裂纹迅速扩展，随后载荷第2次突降，在较小载荷作用下裂纹缓慢扩展直至临界长度之后T型接头发生完全失效。从图9可以看出，裂纹长度越短，裂纹扩展速率越快，主要是因为初始载荷较大，随着裂纹扩展长度变长，载荷有所降低。

4.2 载荷加载控制结果分析

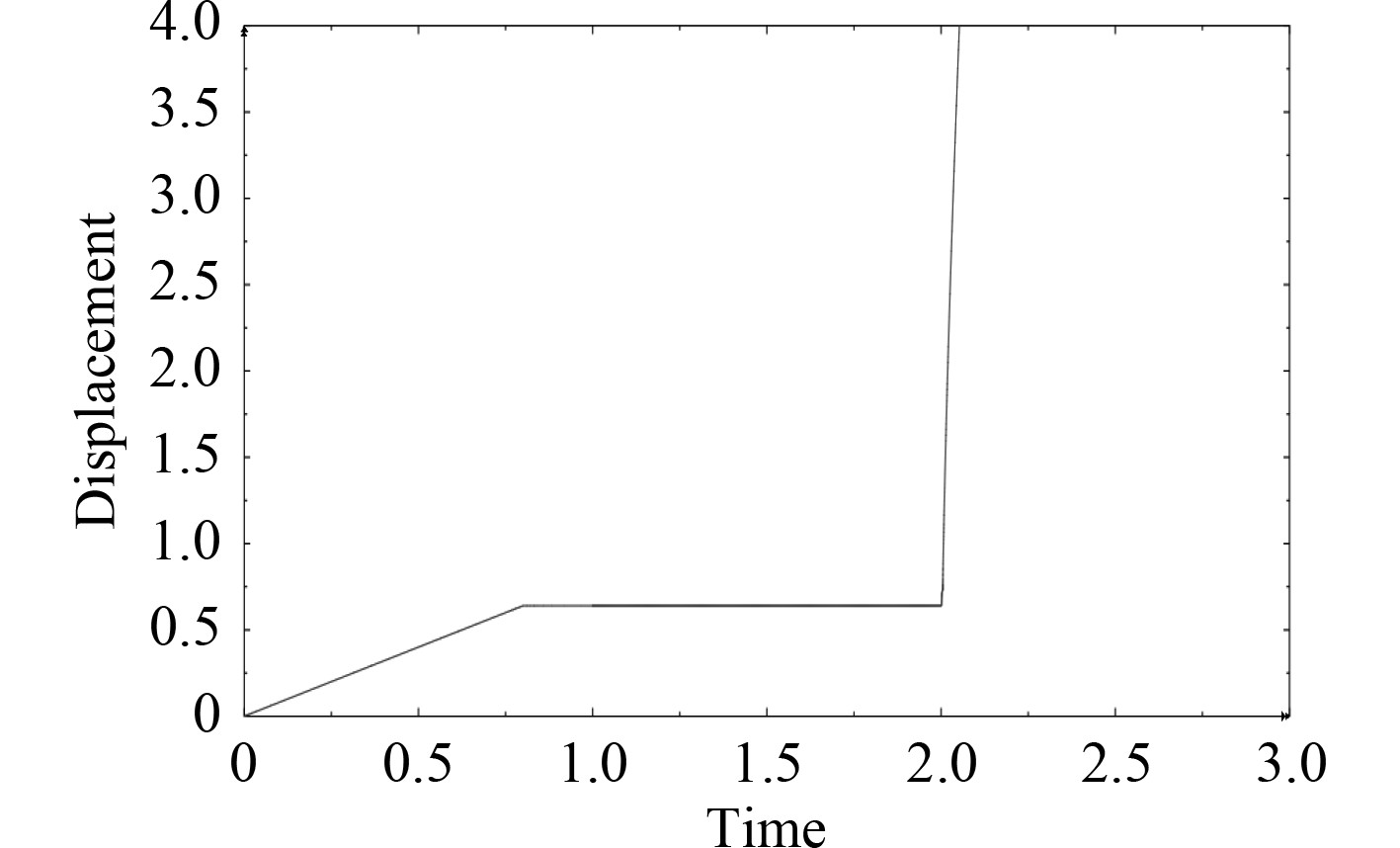
使用载荷加载控制时位移时间历程如图10所示，载荷大小为3859.79N。从位移时间历程可以看出，保持控制力循环一段时间后，T型接头因疲劳失效而失去承载能力，从而使得位移急剧增加。在循环1001000次后圆弧过渡区右侧产生裂纹，之后较短的循环次数内，裂纹迅速扩展，并且圆弧过渡区左侧相继产生裂纹，接头在循环1005000次之后完全失效。

由于采用的是载荷加载控制，力的大小始终保持不变，随着裂纹不断扩展，力相对于裂纹尖端的力臂在不断变长，对裂纹尖端施加弯矩也相应增长，所以在裂纹产生之后，还没有相对扩展到一定长度接头就完全失效了。

5 结　语

通过建立的内聚力单元疲劳损伤计算方法，针对复合材料T型接头的疲劳失效进行了数值仿真研究，得出以下结论：

1）位移控制下，T型接头承载能力发生2次突降，第1次是在裂纹产生初期，载荷折减幅度较低，结构保持承载能力，第2次则对应结构失效，失去承载能力，2次间隔时间较长；

2）载荷控制下，接头在产生裂纹后很快就失效，失去承载能力；

3）位移加载控制下，裂纹在形成初期扩展是较快的，之后因为裂纹长度的增长和载荷的降低，裂纹扩展速率逐渐缓慢，而载荷控制正相反，其裂纹扩展速率因裂纹的增长而呈现加速扩展的趋势。