2. 深海技术科学太湖实验室,江苏 无锡 214082
2. Taihu Laboratory of Deep-sea Technology Science, Wuxi 214082, China
巡逻艇为了满足日常巡逻警戒的需求,航行速度通常较高,一般而言其最高航速对应的长度傅氏数Fr达到1,体积傅氏数Fr▽也接近3左右,按照高速船不同航速下其水动力性能差异可知,当1≤Fr▽≤3时,巡逻艇处于过渡半滑行状态,此时船底的流场较常规低速船更敏感,细微的扰动都会影响整个流场的品质。以往针对中高速船的研究主要集中在其船型本身对其水动力性能的影响,比如长宽比、舭部斜升角度、重心位置等对航行过程中阻力性能的影响范围和程度。杨良军[1]采用CFD数值模拟的手段对隧道尾双体船的阻力性能开展相关研究,验证了该隧道尾双体船型具备优良的阻力性能,较适合用于甲板面积要求较高的无人船型研发。陈顺怀等[2]针对双隧道船型的设计方法进行研究,开发了隧道船型参数化设计程序,实现了隧道曲面的参数化设计,为隧道船型开发设计提供了指导。通过对现状的分析可知,对过渡艇的研究主要还是集中在常规的阻力性能方面,隧道船型的研究也大都集中在隧道船体本身参数尺寸的设计、隧道船型的总体布局以及隧道形式对阻力性能影响等方面,而针对隧道船型在尾部隧道附近的流场,比如重心纵向位置变化对隧道内螺旋桨盘面处的流场分布情况基本未见相关报道。
本文聚焦某沿海巡逻艇,采用基于RANS方程结合重叠网格的技术,对巡逻艇的水动力性能进行数值模拟,数值预报软件采用自研的OSHIP粘流计算软件[3],对不同重心纵向位置下该巡逻艇阻力性能以及尾部螺旋桨盘面处流场的分布情况进行预报,同时采用自研的桨盘面流场提取程序对盘面处的标称伴流进行定量计算,获得桨盘面处的流场不均匀度和伴流分数量化值。通过对比分析获得了本船重心纵向位置的最佳布置区间,为同类型隧道船型重心纵向位置的确定提供技术支撑。
1 计算对象及其主要尺度参数表1为巡逻艇主要尺度参数,图1为该艇的外形示意图,本艇为单体、V型、双折角隧道艇型。
|
|
表 1 巡逻艇主参数(缩尺比1∶7) Tab.1 Main parameter of patrol boat (scale ratio 1∶7) |

|
图 1 巡逻艇外形示意图 Fig. 1 The outline diagram of patrol boat |
采用高精度RANS方法进行水面船自由面绕流问题的数值模拟,湍流模型采用SST
不可压缩流体连续方程与RANS方程为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\nu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \overline {{u_i}^\prime {u_j}^\prime } } \right) 。$ | (2) |
式中:
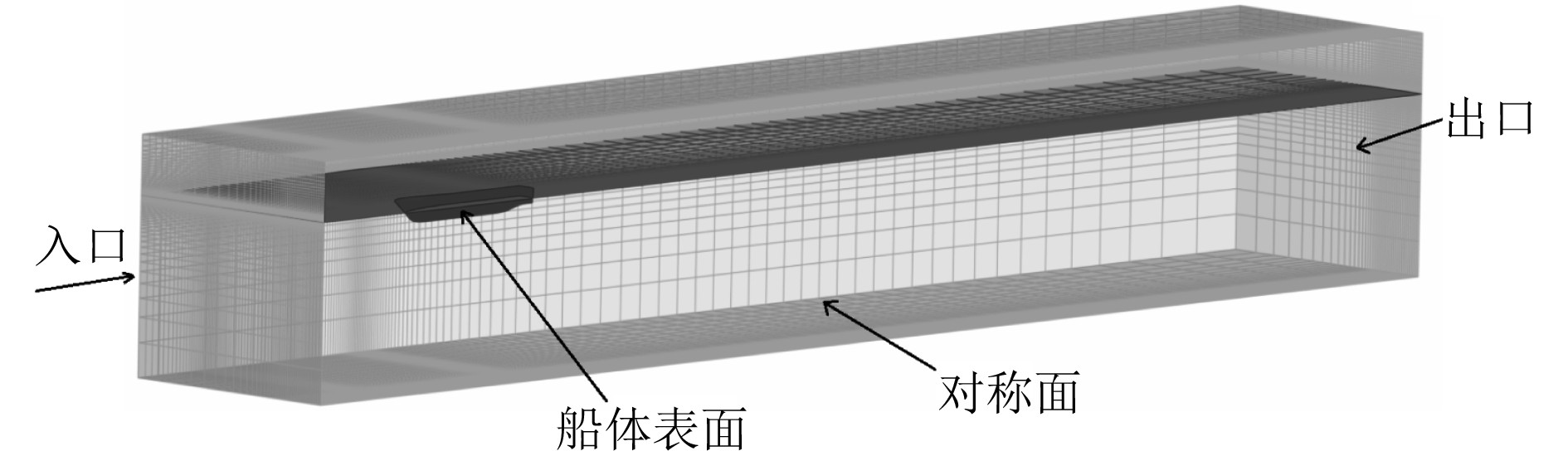
网格划分采用重叠网格技术,单块网格均为结构化网格,多快网格之间通过信息的交换实现流场的计算。为了保证数值模拟的精度,满足工程实际应用要求,分别对计算域大小、网格数量以及差分格式等主要因素进行数值预报方法研究,通过与水池模型试验结果进行比对,明确具体的计算区域、网格数量及计算参数配置,预报精度满足工程误差要求。图2为巡逻艇表面网格划分,图3为巡逻艇数值模拟域。

|
图 2 船体表面网格划分 Fig. 2 The mesh generation of surface of the hull |
|
图 3 数值模拟域 Fig. 3 The numerical computation field |
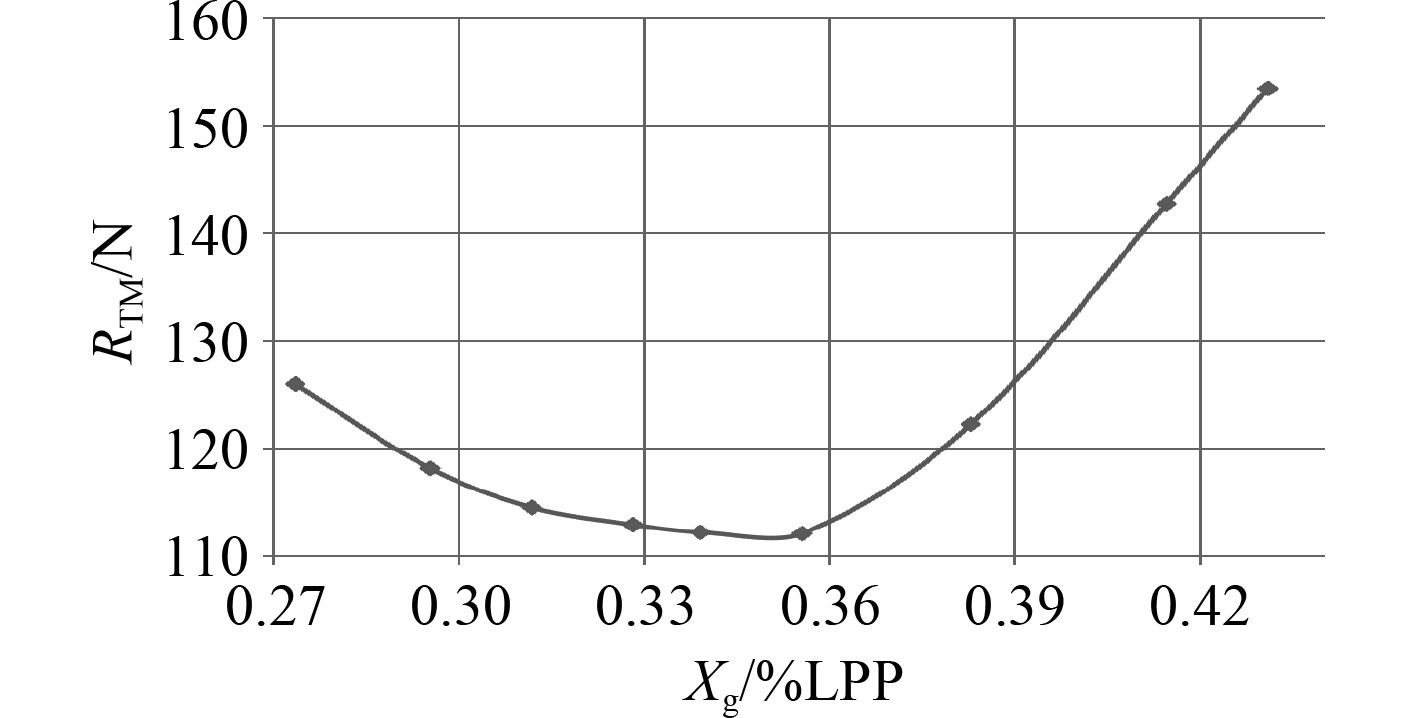
对巡逻艇在设计航速Vs=28 kn下的模型阻力性能进行计算,给出9个不同重心纵向位置下巡逻艇模型阻力大小及运动姿态,分析阻力、运动姿态随着重心位置变化的趋势。表2为巡逻艇在设计航速下的阻力性能数值模拟结果,图4为模型总阻力随着重心位置变化曲线图。表中重心纵向位置是以巡逻艇尾垂线为基准,向船首方向长度与垂线间长Lpp的比值即为表中数值,其中0.43Lpp为正浮状态下的重心纵向位置。
|
|
表 2 巡逻艇阻力性能计算结果(Vs=28 kn,Fr▽=2.64) Tab.2 Calculation results of resistance performance of patrol boat (Vs=28 kn,Fr▽=2.64) |
|
图 4 模型总阻力随着重心位置变化的趋势 Fig. 4 The trend of the total resistance of the model with the position of the center of gravity |
由表2及图4可知,重心纵向位置对本巡逻艇模型阻力性能的影响随着其纵向位置的不断前移呈现出先减小后增大的趋势,重心在Xg=0.27 Lpp变化到Xg=0.36 Lpp过程中阻力为递减趋势(递减段),重心在Xg=0.36 Lpp变化到Xg=0.43 Lpp过程中阻力为递增趋势(递增段),当重心在Xg=0.36 Lpp时阻力值出现拐点,并在此位置阻力值最小。分析阻力随重心位置的增减幅值大小,以Xg=0.36 Lpp对应的阻力最佳位置为基准,重心位置在递增段中变化时模型阻力的变化快慢程度要大于重心位置在递减段中的变化值,即在递增段中,重心的变化对阻力性能的影响更加敏感,曲线的斜率更大。通过阻力随着重心位置变化的增减幅值可知,当Xg在0.31 Lpp到0.36 Lpp区间变化时,阻力性能的变化量不大。因此从影响阻力性能方面来讲,本巡逻艇的重心纵向位置设置在0.31 Lpp~0.36 Lpp之间为最佳,对应纵倾角θ在2.1°~3.5°之间,航行视眼也能够得到保证。
对上述不同重心位置开展了水池模型试验,表3为模型阻力试验结果。
|
|
表 3 巡逻艇阻力性能水池试验结果(Xg=0.36Lpp,Vs=28 kn) Tab.3 Pool test results of resistance performance of patrol boat(Xg=0.36Lpp,Vs=28 kn) |
|
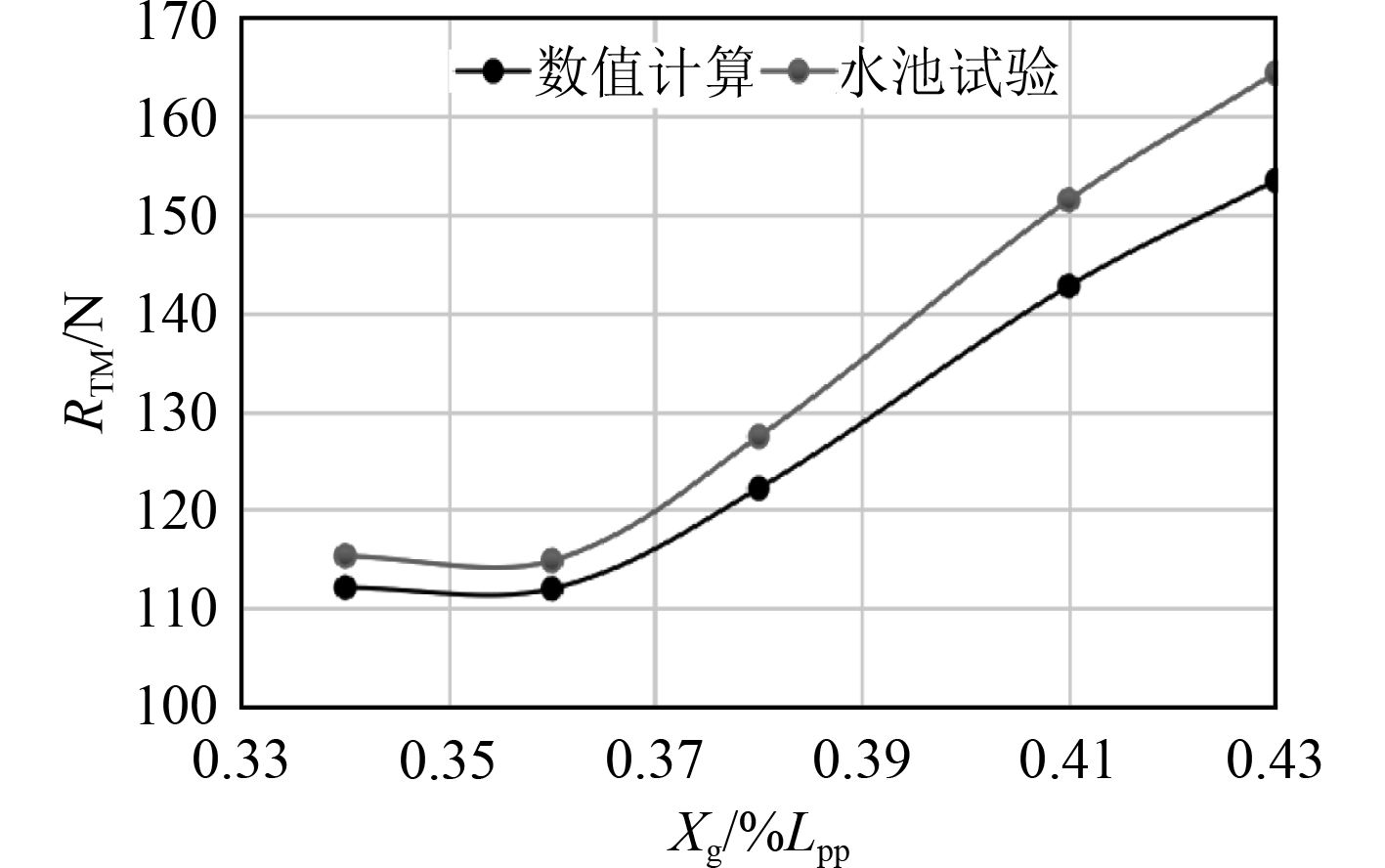
图 5 数值模拟结果与水池试验结果曲线对比(Vs=28 kn,Fr▽=2.64) Fig. 5 The contrast curve of numerical calculation results and pool test results (Vs=28 kn,Fr▽=2.64) |
通过对水池模型试验结果与数值模拟结果的对比分析可知,该巡逻艇的阻力性能随着重心位置变化的趋势与数值模拟结果一致,数值模拟误差也在可以接受的范围内,一方面验证了上文所采用的数值模拟方法的可行性,另一方面也为通过数值模拟获取巡逻艇尾部隧道内桨盘面流场提供了可靠的分析手段。
3.2 巡逻艇尾隧道桨盘面流场隧道型艇虽然能够布置更大的螺旋桨,降低螺旋桨转速,提高推进效率,但是隧道的存在实际上对船尾部的流场是不利的,特别是螺旋桨盘面处伴流及流场均匀度,严重的情况下水流还会产生流动分离现象,从而对螺旋桨的推进效率产生不利影响。通过对桨盘面轴向无因次速度的处理,采用自研的桨盘面流场提取程序对盘面处的标称伴流进行了定量计算,获得桨盘面流场的不均匀度量化值,桨盘面轴向无因次速度的不均匀度定义如下:
| $ {W_f} = \sum\limits_i^N {\sqrt {\frac{1}{M}\sum\limits_j^M {{{({V_{xij}} - {{\bar V}_{xi}})}^2}} } }。$ | (3) |
式中:
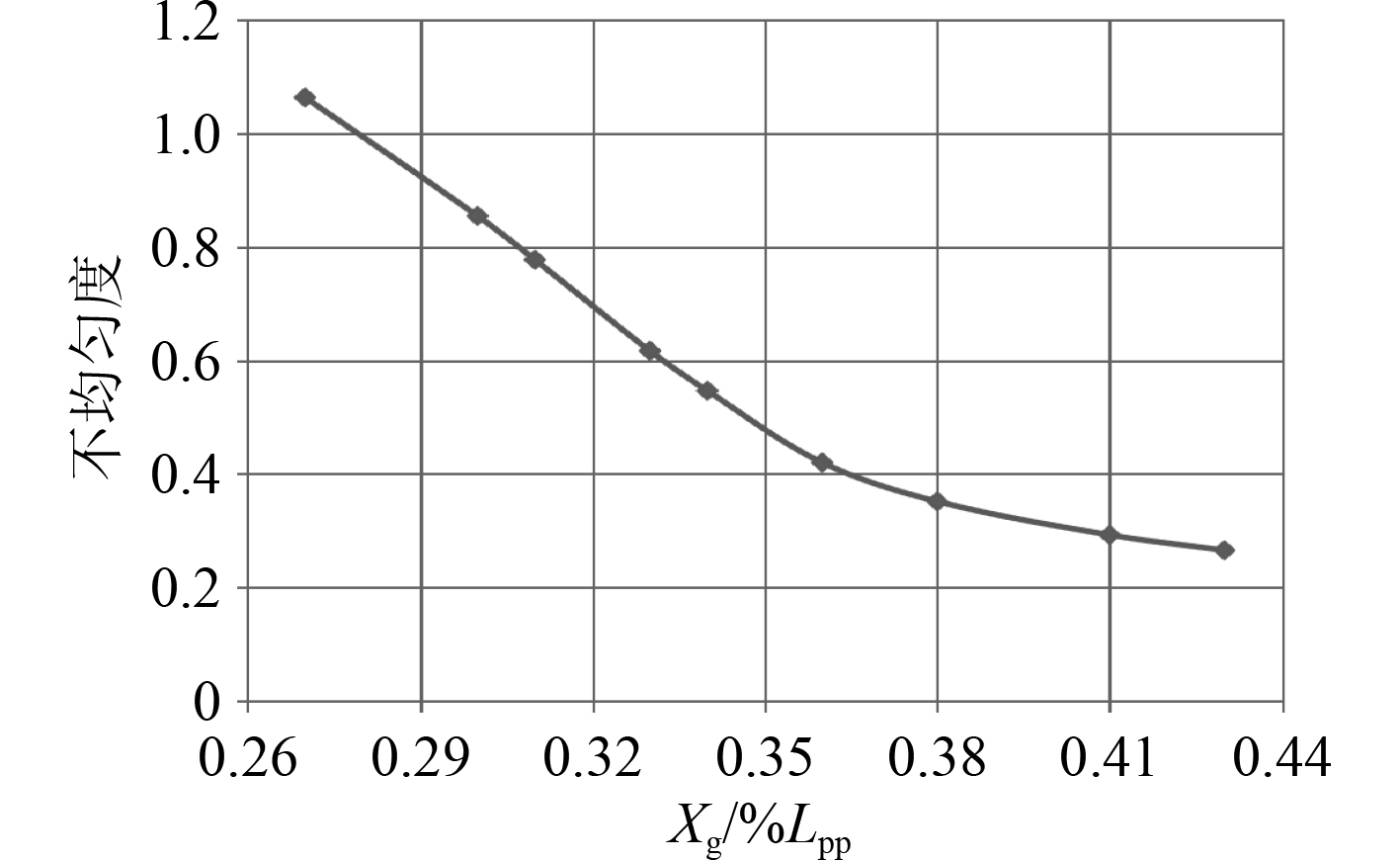
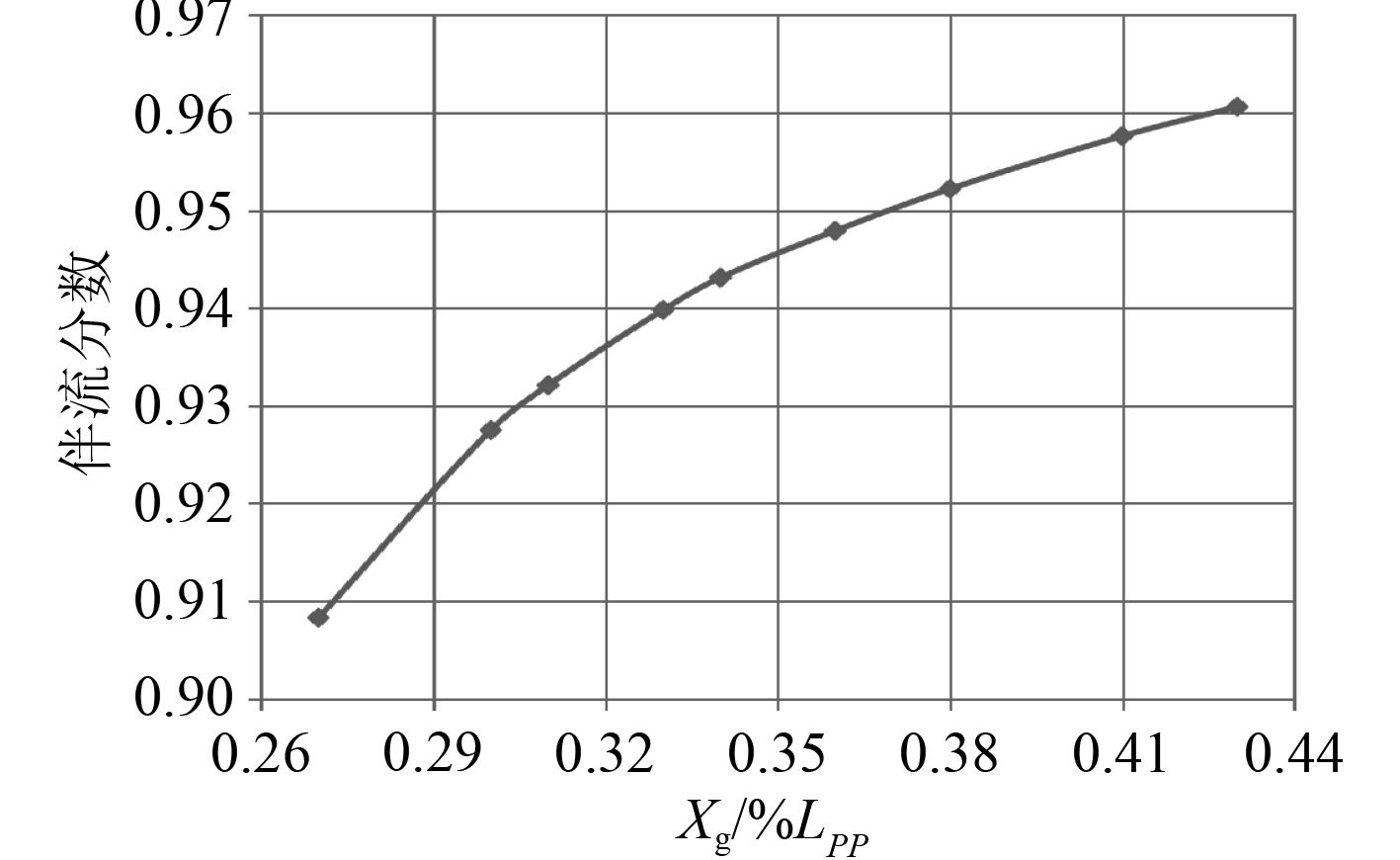
表4给出了不同重心位置下桨盘面处伴流场不均匀度值及伴流分数,图6和图7为不均匀度和伴流分数随着重心位置变化曲线图。
|
|
表 4 巡逻艇桨盘面伴流场不均匀度及伴流分数(Vs=28 kn,Fr▽=2.64) Tab.4 Unevenness of wake field and wake fraction of paddle surface of patrol boat (Vs=28 kn,Fr▽=2.64) |
|
图 6 尾部隧道螺旋桨伴流场不均匀度值曲线 Fig. 6 The unevenness curve of wake field of propeller in tail tunnel |
|
图 7 尾部隧道螺旋桨伴流分数曲线 Fig. 7 The wake fraction curve of propeller in tail tunnel |
分析可知,尾部隧道处螺旋桨盘面的流场不均匀度值随着重心的前移出现单调递减趋势,伴流分数则随着重心的前移出现单调递增趋势。从盘面处的流场不均匀度值可知,重心位置的前移降低了桨盘面处流场的不均匀度值,提升了盘面处的流场品质,对推进效率的提升有利;从盘面处的伴流分数可知,重心位置的前移增大了桨盘面处的伴流分数,增加了螺旋桨的滑失比,提高了螺旋桨的推力,进而提高螺旋桨的推进效率。综上所述,在本文所述重心变化范围内重心前移能够有效降低伴流场不均匀度,提高伴流场品质,增大伴流分数,提高推进效率。
图8为不同重心位置下桨盘面无因次轴向速度云图。可知,桨盘面处的轴向速度分布随着重心位置的前移也不断改善,不均匀度得到降低,伴流速度得到提高。

|
图 8 不同重心位置下桨盘面无因次轴向速度云图 Fig. 8 The dimensionless axial velocity cloud of paddle surface under different center of gravity positions |
本文采用基于RANS方程的数值模拟技术,完成了不同重心纵向位置下巡逻艇阻力性能CFD数值模拟,获得了在设计航速下不同重心纵向位置巡逻艇阻力性能以及尾部隧道内螺旋桨盘面处的流场分布情况,得出以下结论:
1)从影响阻力性能方面,重心纵向位置Xg布置在0.31 Lpp~0.36 Lpp之间最佳,此时阻力性能较优;
2)从影响尾部伴流场分布方面,重心位置越靠近正浮状态下的浮心位置(Xg=0.43 Lpp)为最佳,此时桨盘面流场不均匀度最小,同时伴流分数最大;
3)综合考虑阻力性能和桨盘面流场分布情况,建议本巡逻艇重心纵向位置Xg布置在0.36 Lpp较为合适。
本文只对重心纵向位置的变化对阻力性能和桨盘面流场不均匀度做了单独的分析,未对尾部流场不均匀度对推进效率的影响做深入研究,后期可以开展带螺旋桨下伴流场不均匀度对推进效率及其对整船航速的影响研究。
| [1] |
杨良军. 隧道尾双体船性能分析研究[J]. 中国水运, 2021, 2: 121-122. DOI:10.13646/j.cnki.42-1395/u.2021.02.049 |
| [2] |
王海涛. 内河浅吃水肥大船双隧道尾型设计方法研究[D]. 武汉: 武汉理工大学, 2011.
|
| [3] |
周秀红, 赵发明, 王丽艳. 船舶粘流计算软件“OShip”开发[J]. 中国造船, 2014, 55(1): 90-103. |
| [4] |
王明辰. 基于CFD的浅水双尾船尾型优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [5] |
周广礼, 欧勇鹏. 中高速船航行姿态及阻力数值预报方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(4): 637-640. |
| [6] |
朱锋, 陈公羽, 李胜忠. SBD技术在高速排水型艇艇型优化上的应用[C]//. 第二十一届船艇发展与水系旅游学术交流会, 2020, 舟山
|
| [7] |
赵发明, 高成君, 夏琼. 重叠网格在船舶CFD中的应用研究[J]. 船舶力学, 2011, 15(4): 332-341. DOI:10.3969/j.issn.1007-7294.2011.04.002 |
 2022, Vol. 44
2022, Vol. 44

