0 引　言

机舱数据采集系统的功能是实时采集机舱动力系统、电力系统等关键模块的运行参数，通过数据分析和处理获取系统的运行工作状态，以达到对舰船关键系统的监控目的。同时，机舱数据采集和处理也决定了舰船的自动化程度，将计算机控制技术、数据挖掘技术、现代通信技术集成到船舶机舱数据采集系统已经成为一种发展趋势。

本文的研究方向侧重于机舱数据采集系统的数据分析，从粗糙集理论和包络分析理论出发提高机舱运行数据的处理能力。粗糙集理论能够降低数据的维度，过滤系统采集的重复数据，形成具有更大使用价值的数据集，这种数据预处理方式对于提高机舱数采系统的信息处理效率有明显提升；包络分析理论也是一种数据整体分析理论，该理论将多个数据集进行输入量与输出量的合并，合并之后的每个数据集都包含相对比的子单元。数据包络分析有助于从整体上得到数据的规律，对于识别舰船机舱运行参数中的故障信号等问题有良好效果。

1 粗糙集理论

数据挖掘技术是近年来的研究热点，特别是针对工业系统中海量数据的整理、规律分析等应用场景，利用数据挖掘技术可以从海量数据中发现有用的信息，以船舶机舱为例，船舶运行过程中机舱数据采样频率高，每天都会产生大量的数据，想要快速识别故障导致的数据异常，必须要借助数据挖掘技术。粗糙集理论在数据处理方面有明显优势，基于粗糙集理论的数据挖掘也发展迅速。

粗糙集理论的关键概念包括：

1）知识表达系统

主要是指在粗糙集理论中数据以何种形式表现，粗糙集理论的知识表达以表的形式为最多，通常表的列坐标描述对象的属性，表的行坐标描述对象的分类，粗糙集理论的数据简化建立在数据表的基础上，实际上也是对表的约简。

2）决策表

决策表在粗糙集理论中指代决策问题，其定义式为：

$S{\text{ = }}\left( {U,V,f} \right),U = C \cap D \text{，}$

式中： $C$ 为决策表的决策属性集合， $D$ 为决策表的条件属性集合， $V$ 为属性的值域， $f$ 为对象到值域的函数映射关系。

定义 $S{\text{ = }}\left( {U,R} \right)$ 为粗糙集的知识表达系统，则 $U \cup D = R$ ， $U \cap D = \emptyset$ ，决策表记为 $T = \left( {U,R,C,D} \right)$ 。

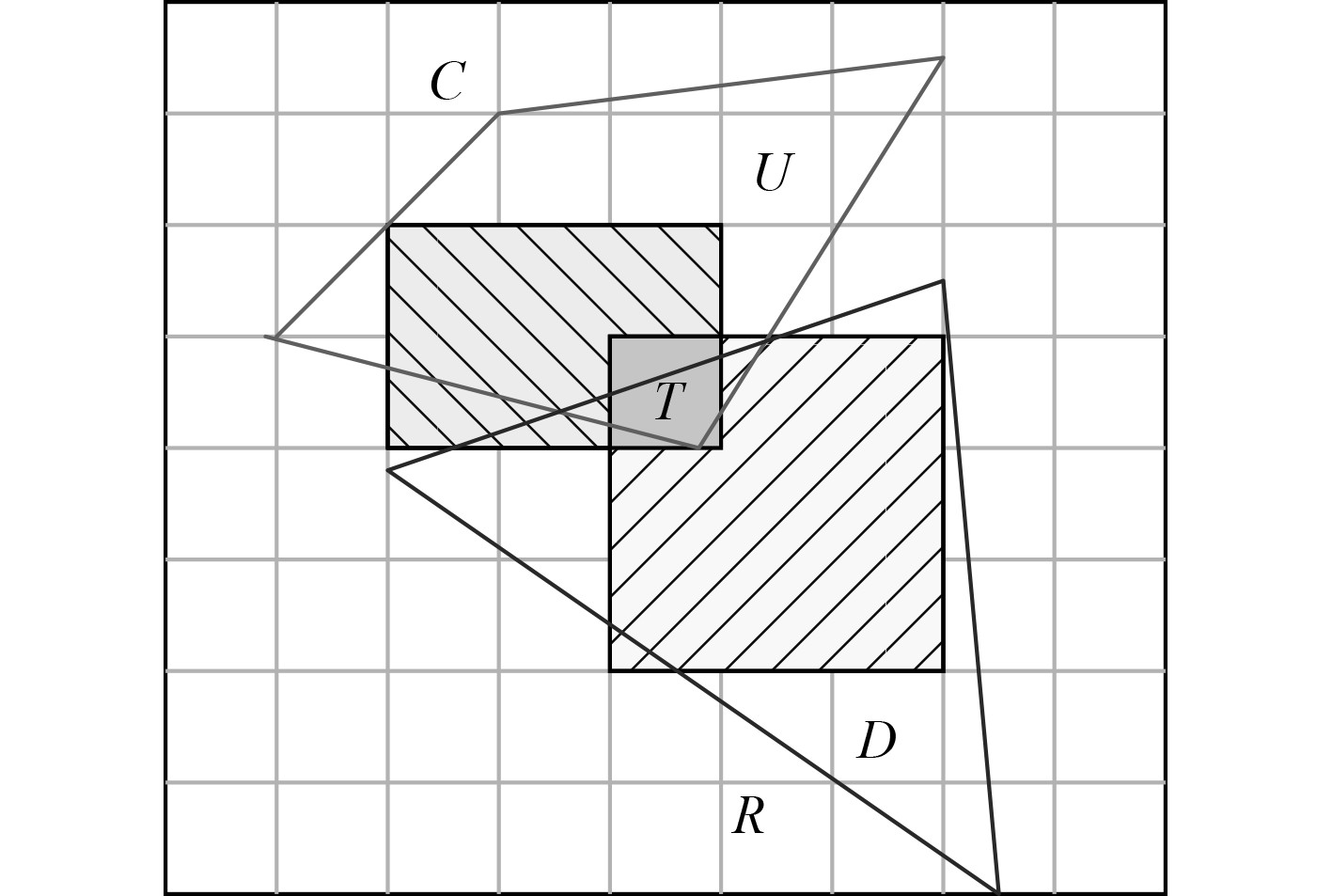
粗糙集理论的决策表原理图如图1所示。

3）分辨矩阵和分辨函数

由前文定义 $S{\text{ = }}\left( {U,V,f} \right),A = C \cap D$ 的信息系统，令子集 $C = \left( {{a_i}\left| {i = 1,2,...,m} \right.} \right)$ ， $U = \left( {{x_i}\left| {i = 1,2,...,n} \right.} \right)$ ，定义系统的分辨矩阵为 $M\left( s \right){\text{ = }}\left( {{m_{ij}}\left| {i,j = 1,2,...,n} \right.} \right)$ ，则

${m_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{a_i} \in C,\quad {a_i}\left( {{x_i}} \right) \ne {a_k}\left( {{x_j}} \right)}，\\ {\phi ,\quad U\left( {{x_i}} \right) = U\left( {{x_j}} \right)\quad i,j = 1,2, \ldots ,n} 。\end{array}} \right.$

4）粗糙集的约简

利用分辨矩阵可以方便地进行数据决策属性 $C$ 的约简，条件属性集合 $D$ 对应于决策属性 $C$ 的核，即是所有数据集的约简结果，为：

$core\left( C \right) = \left( {{a_i} \in D:mij = \left( {{a_k}} \right),1 \leqslant j \leqslant i \leqslant n} \right) 。$

5）粗糙集理论的流程

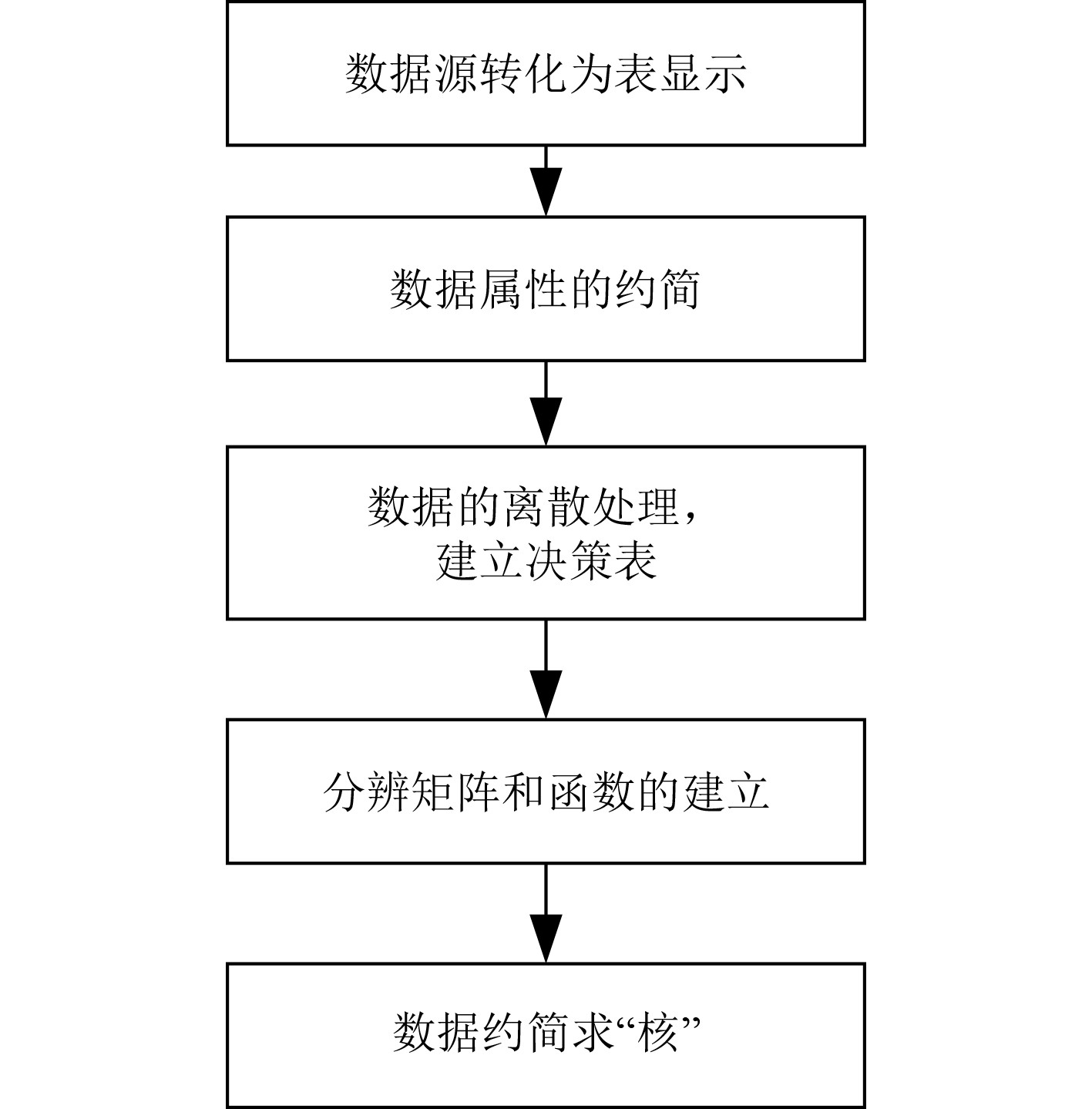
粗糙集理论进行数据预处理的流程如图2所示。

2 数据包络分析理论

数据包络分析理论在计算系统的投入、产出比等场景下有重要应用，在数据处理场景下能够对不同类的数据提取基本特征，与数据整体规律形成差异性对比，实现数据聚类。原理如下：

假定包络分析输入量为 $X = {\left( {{x_1},{x_2},...,{x_n}} \right)^{\rm{T}}}$ ，输出量为 $Y = {\left( {{y_1},{y_2},...,{y_n}} \right)^{\rm{T}}}$ ， $T\left( {X,Y} \right)$ 为包络分析过程，定义数据集合为：

$\left\{ {\begin{array}{*{20}{l}} {{X_j} = \left( {{x_1},{x_{2j}}, \cdots ,{x_{mj}}} \right)} ，\\ {{Y_j} = \left( {{y_{1j}},{y_{2j,}}, \cdots ,{y_{kj}}} \right)}，\\ {j = 1,2, \cdots ,n} 。\end{array}} \right. \text{}$

$\left( {{X_i},{Y_i}} \right)$ 集合的包络分析表示为：

$T = \left\{ {(X,Y)\mid \sum\limits_{j = 1}^n {{x_j}} ,\sum\limits_{j = 1}^n {{y_j}} ,j = 1, \cdots ,n} \right\} \text{。}$

${C^2}R$ 模型是数据包络分析的基础模型，构建 ${C^2}R$ 模型：

$\left( {{C^2}R} \right) = \left\{ {\begin{array}{*{20}{l}} {\min \theta } \\ {\displaystyle\sum\limits_{j = 1}^m {{X_j}} {\lambda _j} \leqslant \theta {X_{jn}},} \\ {\displaystyle\sum\limits_{j = 1}^j {{Y_j}} {\lambda _j} \geqslant {Y_{jn}},} \\ {{\lambda _j} \geqslant 0,j = 1, \cdots ,n} \end{array}} \right. \text{，}$

式中： $\theta$ 为有效值， $\theta \in \left( {0,1} \right)$ ， ${\lambda _j}$ 为指标的权重系数，在多目标函数的包络分析中， ${C^2}R$ 计算值越小，数据的包络性越高。

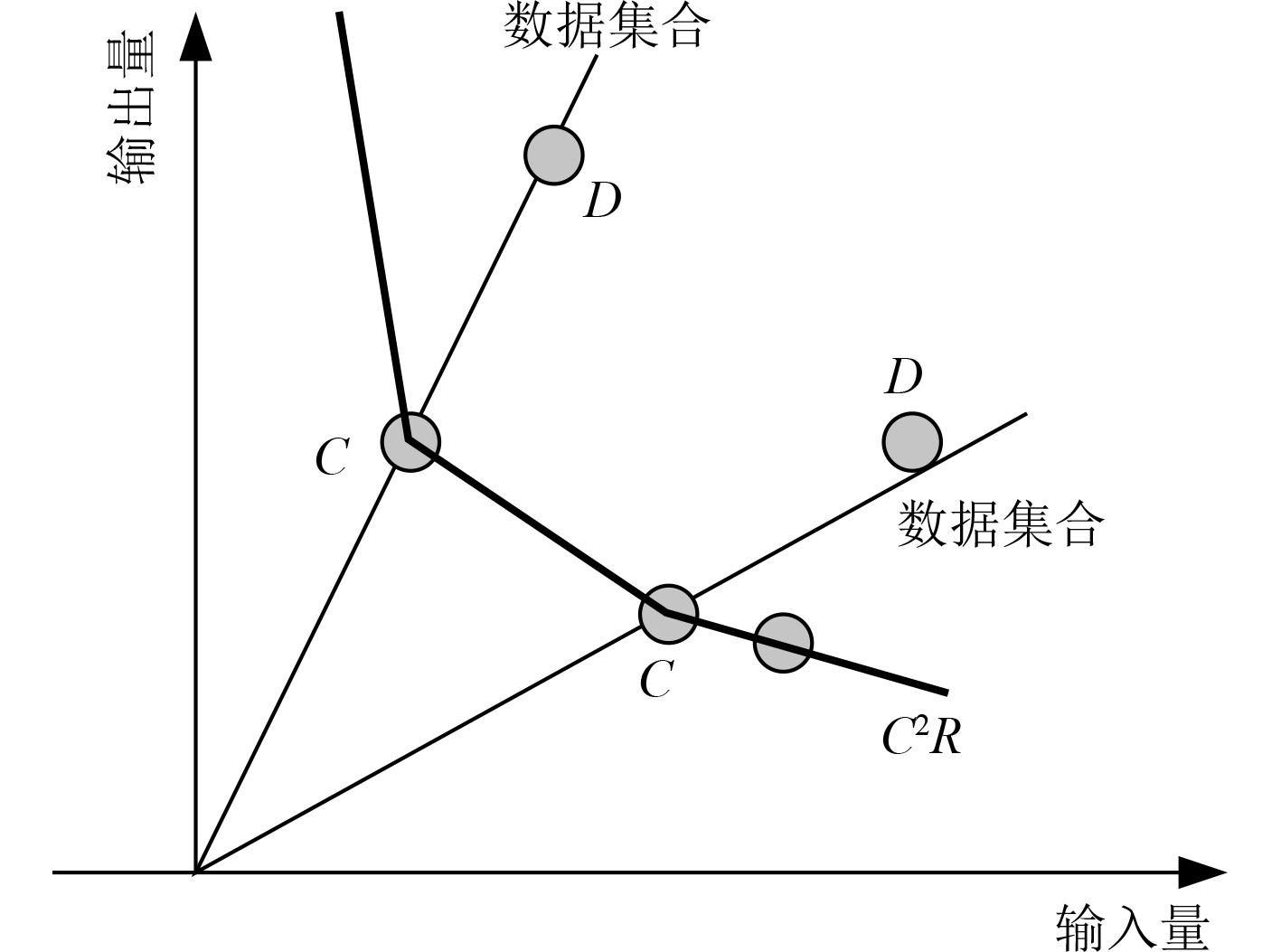
数据包络性 ${C^2}R$ 模型如图3所示。

3 基于粗糙集与包络分析的舰船机舱运行数据聚类分析 3.1 舰船机舱运行数据采集系统

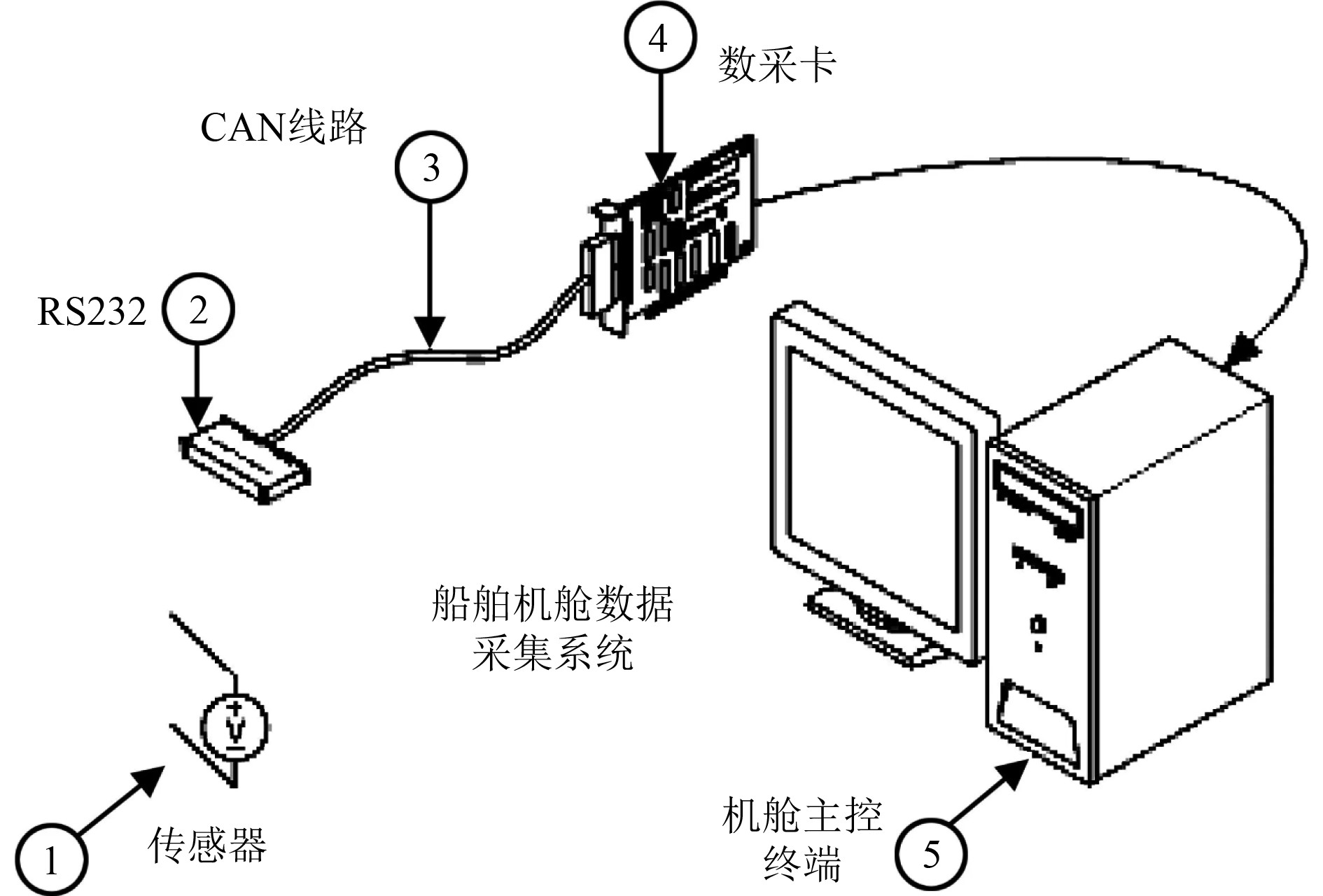
船舶机舱数据采集系统主要由传感器、RS232通信接口、数采卡、CAN总线电路、机舱主控终端等组成，原理图如图4所示。

1）传感器

船舶机舱数据采集系统的传感器类型多样，其中，以监测动力系统振动特性的振动传感器、温度传感器、压力传感器为主，振动传感器采用MEMS加速度计，可以监测三自由度的振动速度和振动加速度；温度传感器采用PT100电阻测温，重点监测发动机等系统旋转部件轴承的温度数据；压力传感器以压力表和测压探头为主，重点监测润滑系统、冷却系统的液体压力，防止出现管路堵塞等问题。

2）CAN总线

机舱运行数据采集系统的传感器信号通道大量使用CAN总线，这种通信方式在有限的空间下具有灵活度高、通信效率高的优点，且介质采用同轴电缆或光纤，便于维护。

3）RS232接口

RS-232C标准协议是一种数据终端设备和通讯设备之间的二进制接口标准，最早由美国电子工业协会联合开发，RS-232C标准协议规定了0~20 kb/s传输速率的通信信号。在RS232接口中，电平介于−3~3 V时信号无效，当传输电平的绝对值大于3 V时可以视为有效电平。

4）机舱主控终端：机舱主控终端使用C#编写程序，接收传感器采集的数据并将数据进行分析，在分析后对数据进行显示，并绘制相关曲线。

3.2 基于粗糙集与包络分析的舰船机舱运行数据聚类分析

对船舶机舱数采系统的振动测试数据进行聚类分析，结合粗糙集理论和包络分析算法，对部分无效数据进行了剔除，提取机舱设备的关键振动数据。

1）获取数采系统的振动信号为：

${X_0} = \left( {{x_0}\left( 1 \right),{x_0}\left( 2 \right),...,{x_0}\left( n \right)} \right) \text{，}$

结合粗糙集理论，将振动信号转化为决策数据表：

${X_i} = \left( {{x_i}\left( 1 \right),{x_i}\left( 2 \right),...,{x_i}\left( n \right)} \right)\;\;i = 1,2,...,n 。$

2）进行数据的无量纲处理分别得到：

${X_0}* = \left( {{x_0}\left( 1 \right)*,{x_0}\left( 2 \right)*,...,{x_0}\left( n \right)*} \right) \text{，}$

${X_i}* = \left( {{x_i}\left( 1 \right)*,{x_i}\left( 2 \right)*,...,{x_i}\left( n \right)*} \right)\;\;i = 1,2,...,n \text{。}$

3）建立振动信号数据的粗糙集分辨函数如下：

$\gamma \left( {X_0^*(k),X_i^*(k)} \right) = \frac{{m + \rho M}}{{{\Delta _i}(k) + \rho M}} \text{。}$

其中： $X_0^*(k)$ ， $X_i^*(k)$ 分别为时间k的振动信号数值， ${\Delta _i}(k)$ 为绝对差值，用下式计算：

${\Delta _i}(k) = X_0^*(k) - X_i^*(k) 。$

4）结合分辨函数建立振动信号的包络性 ${C^2}R$ 模型： $\gamma \left( {{C^2}R} \right) = \left\{ \begin{array}{l} \min \theta ，\\ \displaystyle \frac{1}{n}\sum\limits_{i = 1}^n {} \gamma \left( {X_0^*(k),X_i^*(k)} \right) \\\end{array} \right.$ 。

5）结合包络模型，得到舰船振动信号的数据聚类分析结果。

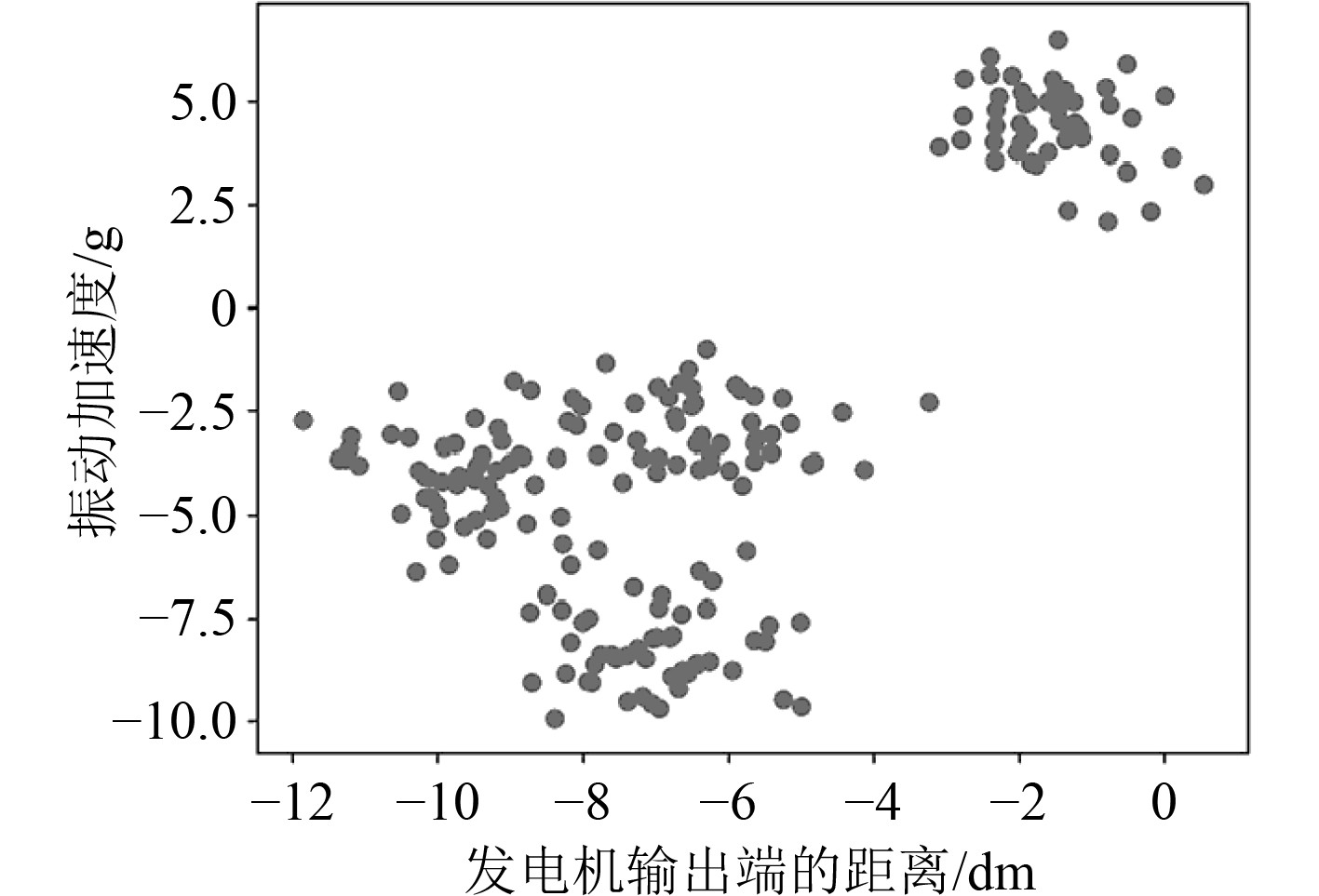
图5为距离舰船发电机输出端不同位置振动信号的聚类分析结果。可以发现通过聚类分析有效提升了数据分析的效率。

4 结　语

本文结合粗糙集理论和包络分析算法，对船舶机舱数据采集系统的振动信号进行了分析，有助于提高船舶机舱数采系统的信号分析效率与准确性。