2. 江苏杰瑞科技集团有限责任公司,江苏 连云港 222006;
3. 哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001
2. Jiangsu JARI Technology Group Co.Ltd., Lianyungang 222006, China;
3. College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China
在船舶制造过程中,各种设计、生产数据呈现多源异构、形式多样、实时变更、快速增长、数据分散又相互关联的特点。现有的数据处理技术中,针对船舶制造海量数据的多元性、关联性,通常都是对不同的数据源进行单独解析,这种方式仅适用于单一数据格式,很难考虑不同数据源之间的关联性[1]。因此,关联规则挖掘对船舶制造数据分析具有重要意义。
关联规则挖掘是由Agrawal等[2]于1993年提出的概念,是一种简单但是很实用的查找数据之间关联关系的算法,常用于挖掘大量数据中可能存在的内在联系。Zaki等[3]于2000年提出了Eclat算法,Eclat是一种基于垂直数据库结构的数据关联规则挖掘算法,在垂直结构中,每个项目集关联一个发生这个项的事务序号集合(transaction id set,Tidset),所有频繁项集都可以通过简单的事务集比较进行生成,整个挖掘过程对数据库的读取只需要一次,因此挖掘过程中I/O成本较其他算法相对更低,挖掘的速度也相对较快,然而Eclat存在着存储空间消耗过多和挖掘过程中逻辑运算耗时长等问题[4]。
针对Eclat存在的问题,Kaur等[5]对Eclat进行了改进,采用了自顶向下的挖掘方式。Baka等[6]提出使用第三方结构化数据库软件MySQL等对数据集进行存储。Man等[7]提出了R-Eclat算法,通过深度优先搜索的方式对非频繁项集进行挖掘。Abbasi等[8]提出一种基于布隆过滤器的挖掘算法Bloom Eclat,提高挖掘过程中逻辑运算速度。Muralidharan等[9]提出一种增强型挖掘算法E-Eclat,实现对挖掘信息根据优先级进行排序。高强等[10]提出了一种对数据类型进行连接限制的i-Eclat算法,通过建立非频繁项集来对项集进行过滤。Yu等[11]提出了Bi-Eclat算法,通过对事务集支持度的排序,实现挖掘过程中不必要的操作的提前剪枝。Ma等[12]提出将FP-Growth与Eclat结合的算法Eclat-growth,在构建模式树时将内存中的项集逐渐加入到模式树中。田攀博[13]提出使用局部敏感哈希的思想对Eclat进行剪枝并根据MinHash的近似计算提出Sim-Eclat算法。吕世鑫等[14]采用Apriori中对项集进行先验剪枝和后验剪枝的思想对Eclat进行改进。李成严等[15]提出一种大数据并行关联规则挖掘算法Sp-IEclat(Improved eclat algorithm on spark framework),该算法基于Spark框架,使用位图运算降低交集的时间代价并减少CPU占用。
基于上述研究,本文提出一种基于LBM的关联规则挖掘算法LBM-Eclat,该方法可以提高事务集存储效率,减少内存消耗,提升关联规则挖掘效率。
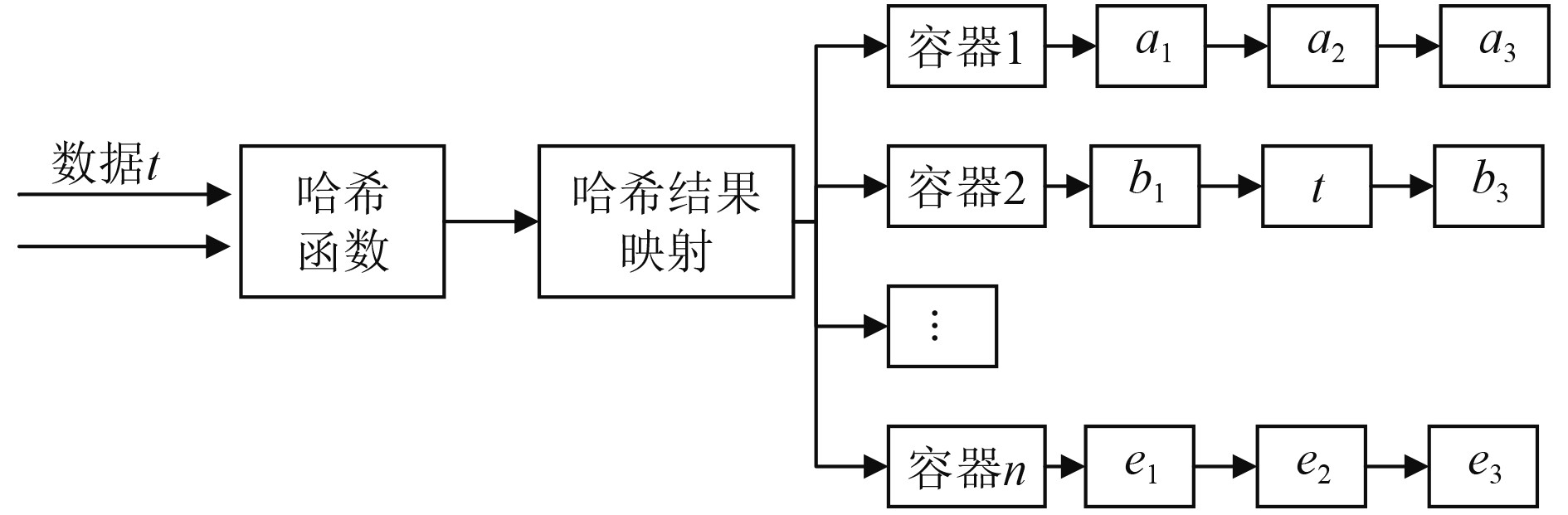
1 数据压缩存储 1.1 局部敏感哈希局部敏感哈希(locally sensitive Hash, LSH)是一种利用哈希冲突对原数据信息进行划分的数据结构。LSH通过哈希映射将数据划分为容器组成的数据集,在数据查找的过程中,通过对容器的查找,可以过滤其他容器中存储的数据,因此提高了数据的查询效率。通过LSH对数据进行映射的过程如图1所示。
|
图 1 LSH数据映射过程 Fig. 1 LSH data mapping process |
根据上述思想,可以得到以下2个公式:
| $ \left| {A \cap B} \right| = \sum\limits_{i = 1}^k {{A_i} \cap {B_i}} ,$ | (1) |
| $ \left| {A \cap B} \right| \leqslant \sum\limits_{i = 1}^k {\min (\left| {{A_i}} \right|,\left| {{B_i}} \right|)} 。$ | (2) |
上述公式可用于在进行事务数据集的交集操作之前,若当前项集支持度上界仍然小于最小支持度,即说明当前新生成的项集为非频繁项集,可以对其进行过滤,减少后续不必要的逻辑操作。
局部敏感哈希利用MinHash对集合间的相似度进行估算,MinHash是一种处理Jaccard相似度计算的哈希计算方法[16]。Jaccard相似度也称为Jaccard系数,主要用来度量集合与集合之间的相似度,如下式:
| $ Jaccard(A,B) = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}} ,$ | (3) |
但是随着集合内元素个数的增加,计算Jaccard相似度的计算成本也越来越大,因此需要利用MinHash来对元素进行降维以减少计算量。MinHash的定义如下:
假设
| $ has{h_{\min }}(A) = \mathop {\min }\limits_{o \in A} hash(o) ,$ | (4) |
其中
| $ P[has{h_{\min }}(A) = has{h_{\min }}(B)] = Jaccard(A,B) 。$ | (5) |
其中:A和B都为任意的集合,当
Jaccard相似度计算如下式:
| $ Jaccard(A,B) = \frac{{\displaystyle\sum\limits_{j = 1}^k {{I_{X_A^j = X_B^j}}} }}{K} 。$ | (6) |
其中
位图是一种使用紧凑格式存储给定范围内数据的数据结构,通常以二进制格式来存储数据的布尔状态信息。当每一个项集所持有的事务数量足够大时,使用压缩位图[17]可以很好对数据进行压缩。
WAH(word-aligned hybrid algorithm)是一种位图压缩算法,WAH压缩算法采用Word-Aligned和Hybrid这2种计算机数据处理思想。WAH算法采用Word-Aligned的方式将Word进行对齐,然后根据对齐的Word将位图进行分组压缩;Hybrid则是针对位图中存在的大量连续的“1”或“0”数据段与混合存在的“1”和“0”数据段分别进行压缩编码操作。通过这种方式对数据进行区分,在面对存在大量的连续的数据段时,可以有效地对数据进行压缩,减少不必要的比较。
2 LBM-Eclat算法实现LBM-Eclat算法的主要思想是将事务集中32位int型数据Tid通过哈希索引进行拆分,尽可能地均匀分散到各个容器中进行存储。LBM-Eclat算法中的LBM在创建时,主要根据不同数据集中最大数据量确定其哈希映射函数的基数,映射基数的计算公式如下:
| $ {\text{base = Math}}{\text{.floor(lo}}{{\text{g}}_2}(DB.length)/2) 。$ | (7) |
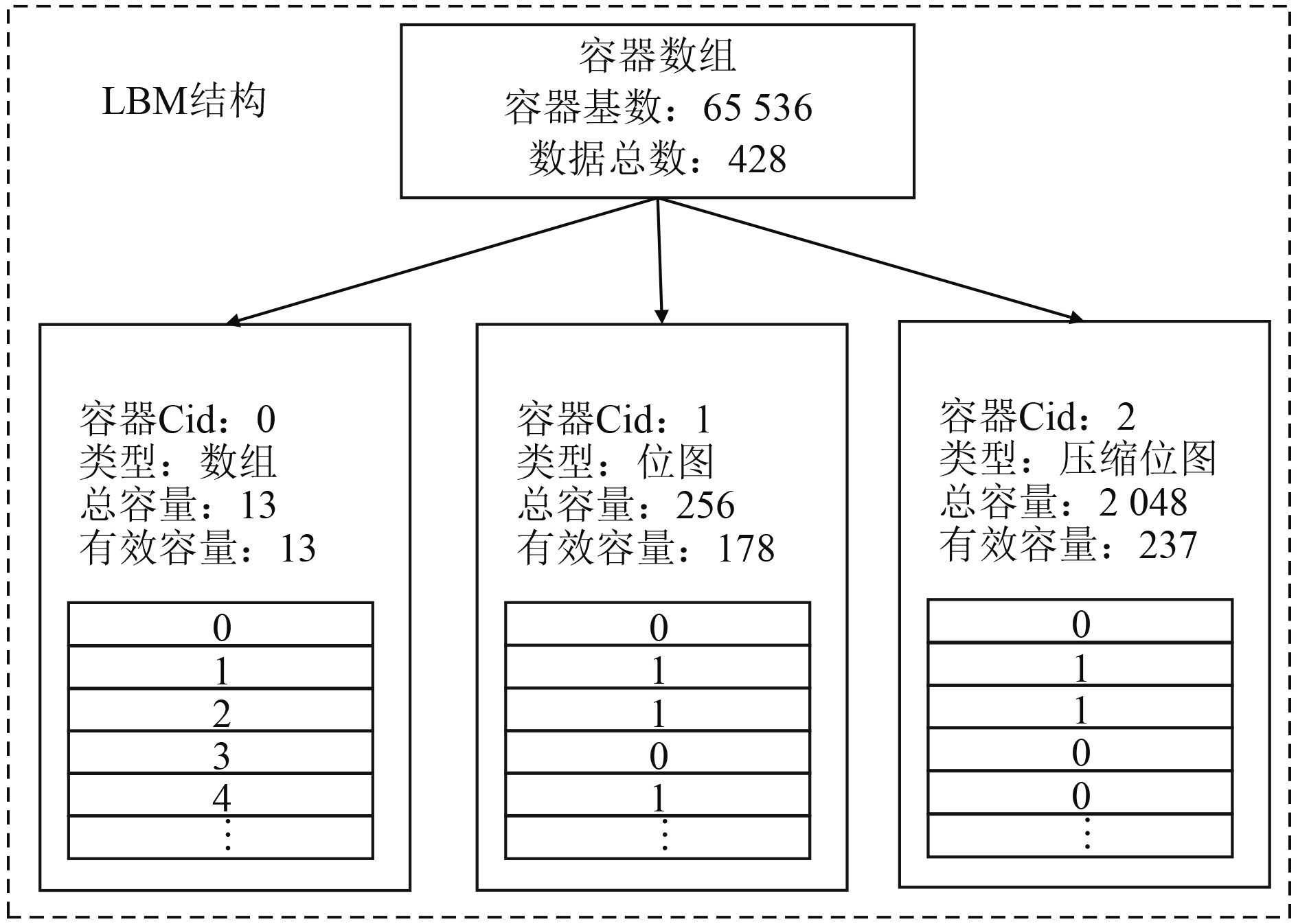
每个数据通过哈希映射得到对应容器的索引(container index,Cid)。LBM-Eclat算法中LBM具体结构如图2所示。
|
图 2 LBM数据结构 Fig. 2 LBM data structure |
可知,各个容器数据量的累加和表示为LBM的数据总数,即当前项集对应的事务集的支持度。每个LBM对应一个基数,数据通过哈希计算获得容器的位置Cid,然后找到对应的容器并将数据存储于其中。
在存储事务集进行交集操作时,可以通过局部敏感哈希的性质对交集结束后的支持度进行估算。对任意2个事务集A和事务集B,若已知2个集合的Jaccard相似度,可以通过以下公式快速计算事务集A和B交集的支持度。
| $ |A \cap B| = \frac{{Jaccard(A,B)}}{{Jaccard(A,B) + 1}}(|A| + |B|) 。$ | (8) |
哈希函数选择会影响到对Jaccard的估算结果,通过MinHash能较准确地估算出Jaccard,但是与实际的支持度会存在部分误差,因此通过设置一个范围阈值用于判断是否可以进行真实事务集逻辑运算。对阈值范围的概念公式如下:
| $ \frac{{\left| {\min Sup - S} \right|}}{{\min Sup}} \lt B 。$ | (9) |
其中:minSup为预设的最小支持度,S为Jaccard估算得到的值,B为阈值范围。此时,阈值范围外的事务集可以判断为频繁项集或非频繁项集,若认为是频繁项集,可以进行直接逻辑运算。但是对阈值范围内部的支持度,可能存在非频繁项集的情况,因此此时也需要进行准确的支持度上界计算。
LBM-Eclat算法的具体实现流程为,在对项集数据进行交集操作时,每次会生成一个新的容器存储2个交集生成的结果,根据交集的2个 LBM内容器类型以及预计生成的数据量大小,能够确定新生成容器的类型。同时根据得到的容器内数据量与最小支持度进行比较,对项集进行过滤,最终得到新的频繁项集,用于后续的挖掘,并通过前缀树Trie进行存储。
3 实验分析 3.1 实验目的为验证LBM-Eclat算法在挖掘性能方面的提升,设置Eclat算法与基于位图的Eclat算法作为参照实验。一共设置2个实验,第1个实验分析LBM-Eclat算法的支持度评估方法中参数设置对挖掘耗时以及精确度的影响。第2个实验验证LBM-Eclat算法在挖掘密集型数据集时有较高的效率。
3.2 实验数据集本次实验数据集包括bom,sectional,pumsb和connect。实验数据集bom和sectional分别由船舶物料数据和分段车间制造数据整理而成,属于典型的密集型数据,因此同时引用pumsb和connect典型数据集进行对比实验分析如表1所示。
|
|
表 1 数据集特征信息 Tab.1 Dataset characteristic information |
实验1 分析LBM支持度估算公式参数设置对挖掘的耗时以及精确度的影响。
由于MinHash中对Jaccard进行估算运用到了参数K,其中K表示对数据进行MinHash映射后,各数据集选择最小的K个容器进行比较,同时支持度阈值范围B的选取对实验结果的准确性也存在一定影响,因此需要设计实验验证参数K和B的变化对实验结果的影响。对实验的评价指标有2个,分别是挖掘所消耗的时间和挖掘的精确度。其中精确度由F1值表示。F1的计算方式如下:
| $ P = \frac{{TP}}{{TP + FN}} ,$ | (10) |
| $ R = \frac{{TP}}{{TP + FN}} ,$ | (11) |
| $ F_{1} = \frac{{2P \times R}}{{P + R}} 。$ | (12) |
其中:TP表示挖掘得到的频繁项集数目,FP表示挖掘得到的非频繁项集数目,FN为挖掘过程中被遗漏的频繁项集的数目,P表示挖掘结果的准确率,即挖掘得到的频繁项集在所有项集间的比例,R表示执行结果的召回率,即挖掘得到的频繁项集数目和真实的频繁项集的数目之比。F1综合考虑准确率和召回率2个指标,因此使用F1表示挖掘的精确度。实验使用的数据集为bom,设置最小支持度为1%,根据数据集的事务集长度得到容器大小为512,因此容器数量最多为195。
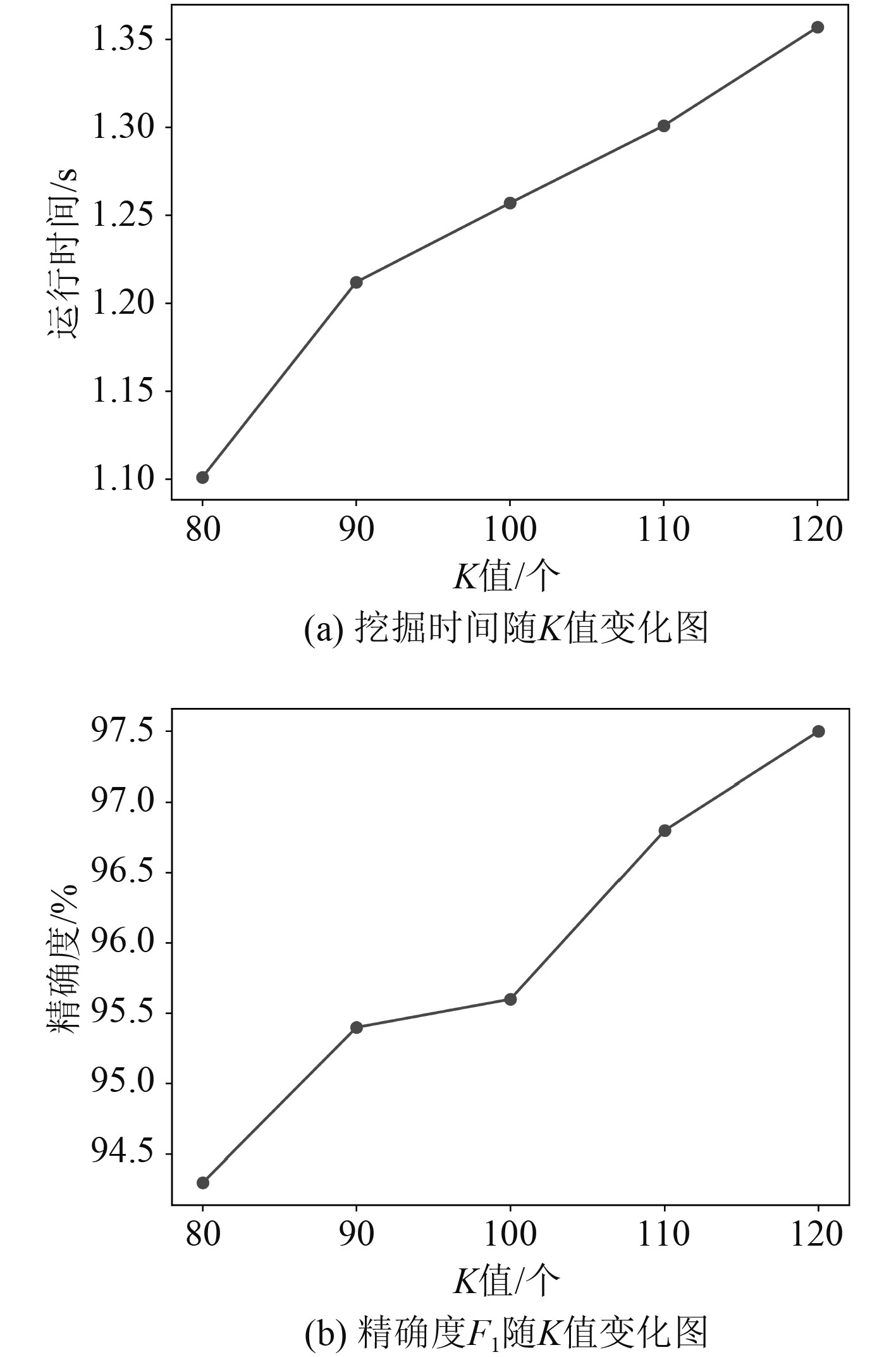
首先验证容器比较数量参数K对实验的影响。设置支持度阈值范围参数B为20%,并设置参数K由80逐渐增加到120,随参数K的变化,得到的LBM-Eclat算法运行结果如图3所示。
|
图 3 K值变化引起的挖掘时间和精确度变化图 Fig. 3 Variation diagram of excavation time and accuracy caused by change of K value |
可知,随着K值的增加,运行时间不断增加,同时挖掘的精确度也随着K的增加而增加。当K值增加到90左右时,精确度的提升不是很明显,但是当K值增加到100以上时,精确度仍然会在95.5%的基础上有所提升。
其次验证参数B对实验的影响。设置参数K值为固定100,并设置支持度阈值范围由20%逐渐增加到40%,观察支持度阈值范围的变化对算法挖掘的影响,算法的运行结果如图4所示。

|
图 4 B值变化引起的挖掘时间和精确度变化图 Fig. 4 Variation diagram of excavation time and accuracy caused by change of B value |
可知,随着支持度阈值范围B增大,LBM-Eclat算法所消耗的时间逐渐增加。当B值范围在20%~30%之间时,精确度的提升随B值的变化的幅度较大,而当B值超过30%时,LBM-Eclat算法的精确度逐渐趋近于96%。支持度阈值范围提高了Jaccard估值的容错度,只要Jaccard估计值不低于最小支持度范围,即可以对其进行挖掘,避免当估算值小于支持度阈值范围时项集被判断为非频繁项集而被放弃挖掘的情况。因此支持度阈值B的范围越大,就会对更多的估值在支持度附近事务集进行挖掘,精确度更高,同时消耗的时间也会随之增加。
实验2 验证LBM-Eclat算法对密集型数据集挖掘的影响。
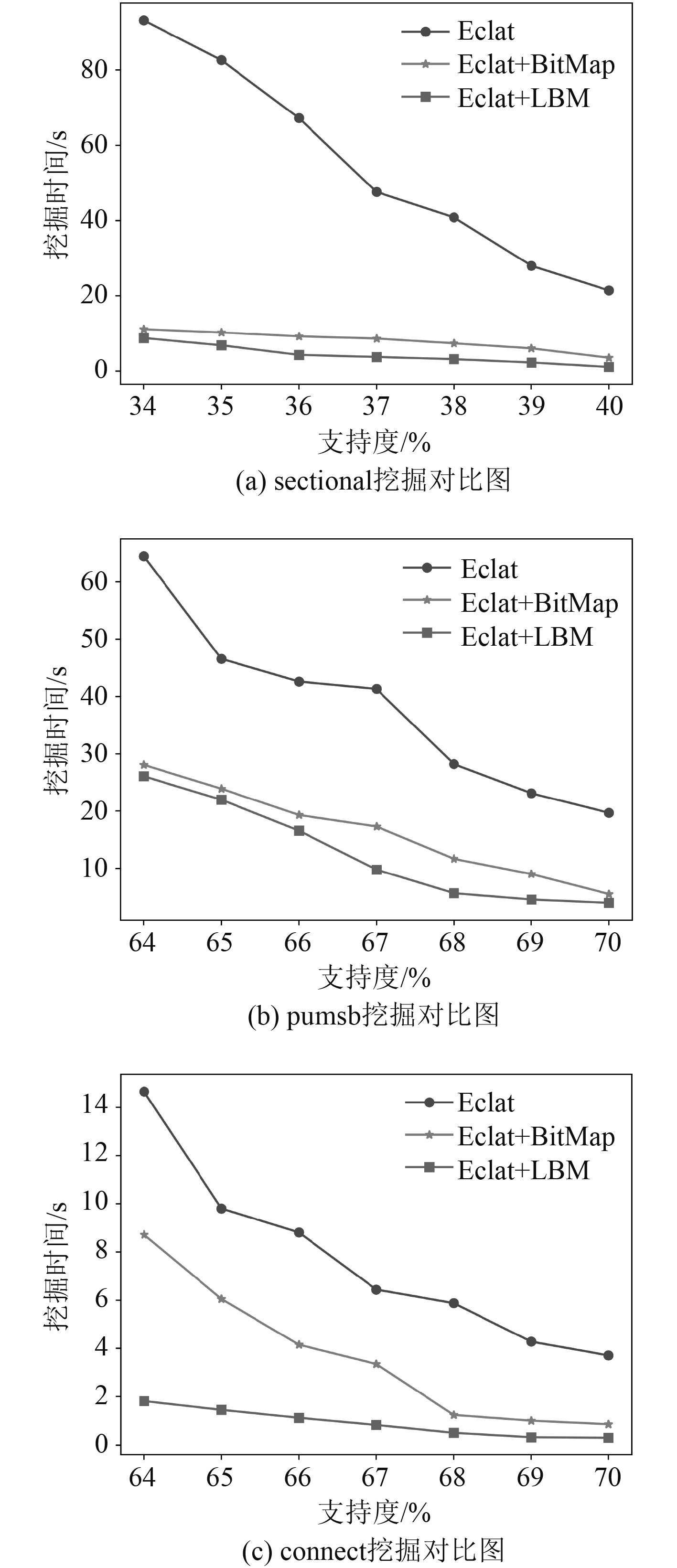
实验2采用密集型数据集sectional,pumsb和connect作为实验对象,采用Eclat算法、基于位图的Eclat算法和LBM-Eclat算法进行对比实验比较消耗的时间和空间,验证使用LBM-Eclat算法在挖掘密集型数据集时,依然有不错的性能。实验结果如图5和图6所示。
|
图 5 密集型数据集挖掘时间消耗对比图 Fig. 5 Comparison of time consumption in dense dataset mining |

|
图 6 密集型数据集挖掘空间消耗对比图 Fig. 6 Comparison of memory consumption in dense dataset mining |
从图5(a)可知,当支持度为34%时,基于位图的Eclat和LBM-Eclat算法的挖掘时间在10s左右,并且随着支持度的提升,挖掘时间逐渐趋近于 平缓。两者都要明显优于Eclat算法。
从图5(b)可知,当支持度为64%时,基于位图的Eclat和LBM-Eclat算法的挖掘时间在27 s左右,并且随着支持度提升到68%,LBM-Eclat算法的挖掘时间逐渐趋近于5 s,而基于位图的Eclat此时的挖掘时间仍高于这一数值,并呈现出趋近的趋势。
从图5(c)可知,当支持度为64%时,LBM-Eclat算法的挖掘时间在2 s左右,明显优于基于位图的Eclat和Eclat算法的挖掘时间。并且随着支持度的提升,LBM-Eclat算法的挖掘时间逐渐趋近于1 s,始终低于基于位图的Eclat和Eclat算法的挖掘时间。
从图6(a)可知,当支持度为34%时,LBM-Eclat算法占用的存储空间为2 100 MB左右,而基于位图的Eclat占用存储空间为5 000 MB左右,Eclat算法占用存储空间为12 000 MB左右。LBM-Eclat算法的空间占比仅为其他2种算法的42%和17%。随着支持度的增加LBM-Eclat算法占用的存储空间逐渐趋近于660 MB,并且在变化的过程中始终低于其他2种算法。
从图6(b)可知,当支持度为64%时,LBM-Eclat算法占用的存储空间为6 000 MB左右,而基于位图的Eclat占用存储空间为7 000 MB左右,Eclat算法占用存储空间为11000 MB左右。在支持度增加的过程中,LBM-Eclat算法占用的存储空间始终在下降,并且当支持度为70%,存储空间仍然有下降的趋势。LBM-Eclat算法的空间占用要优于其他2种算法。
从图6(c)可知,当支持度为64%时,LBM-Eclat算法占用的存储空间为2 500 MB左右,而基于位图的Eclat占用存储空间为6 000 MB左右,Eclat算法占用存储空间为9 000 MB左右。LBM-Eclat算法的空间占比仅为其他2种算法的42%和28%。且当支持度提升到68%时,LBM-Eclat算法占用的存储空间趋近于平稳,达到1 100 MB左右。而基于位图的Eclat在支持度增加到70%时才达到这一数值,Eclat算法则始终高于LBM-Eclat算法的存储空间占用。
通过以上2个实验可以得出结论,对Eclat存储结构的改进,能够有效提高Eclat挖掘过程中的挖掘速度和空间利用率。LBM-Eclat算法能够高效地对事务集数据进行存储,在事务集交集运算中,使用LBM也能够更快得完成计算。因此,LBM-Eclat算法比Eclat算法挖掘效率更高。
4 结 语本文面向多源船舶制造数据从事务集存储结构角度出发,主要研究LBM-Eclat算法中对船舶制造数据存储的改进,以提高事务集的存储效率以及事务集之间逻辑运算速度。研究局部敏感哈希技术以及位图存储技术,利用局部敏感哈希对数据进行分块映射,以实现数据过滤,提高数据比较速度,并在逻辑运算过程中,通过MinHash在保证一定挖掘精确度的情况下,快速估算事务集的支持度,提前实现数据的过滤,提高挖掘的速率。其次针对位图存在存储效率不高的情况,提出了利用编码对位图进行压缩提高存储效率。最后将局部敏感哈希与位图和压缩位图进行结合,提出了LBM数据结构,应用于Eclat的事务集数据存储得到LBM-Eclat算法。通过实验验证,利用LBM存储事务集能够有效提升Eclat算法在数据集挖掘时的效率。
| [1] |
卞德志, 胡昌平, 杨哲, 等. 面向船舶制造的统一数据库集成平台应用研究[J]. 舰船科学技术, 2020, 42(13): 134-138. BIAN De-zhi, HU Chang-ping, YANG Zhe, et al. Research on application of unified database integration platform to shipbuilding enterprises[J]. Ship Science and Technology, 2020, 42(13): 134-138. |
| [2] |
AGRAWAL R. Mining association rules between sets of items in large databases[J]. ACM SIGMOD Record, 1993, 22(2).
|
| [3] |
ZAKI M J. Scalable algorithms for association mining[J]. IEEE Transattions on Knowledge and Data Engineenig, 2000, 12(3): 372-390. DOI:10.1109/69.846291 |
| [4] |
崔馨月, 孙静宇. 改进的Eclat算法研究与应用[J]. 计算机工程与设计, 2018, 39(4): 1059-1063+1147. DOI:10.16208/j.issn1000-7024.2018.04.028 |
| [5] |
KAUR M, GARG U, KAUR S. Advanced eclat algorithm for frequent itemsets generation[J]. International Journal of Applied Engineering Research, 2015, 10(9): 23263-23279. |
| [6] |
BAKAR W A , MAN M, et al. I-Eclat: Performance enhancement of Eclat via incremental approach in frequent itemset mining[J]. Telkomnika, 2020, 18(1): 562-570. DOI:10.12928/telkomnika.v18i1.13497 |
| [7] |
MAN M, JULAILY A J, SAANY S I A, et al. Analysis study on R-Eclat algorithm in infrequent itemsets mining[J]. International Journal of Electrical and Computer Engineering, 2019, 9(6): 5446. |
| [8] |
ABBASI S, MOIENI A. BloomEclat: efficient eclat algorithm based on bloom filter[J]. Journal of Algorithms and Computation, 2021, 53(1): 197-208. |
| [9] |
MURALIDHARAN C, ANITHA R. Risk analysis of cloud service providers by analyzing the frequency of occurrence of problems using E-Eclat algorithm[J]. Wireless Networks, 2021, 27(8): 5587-5595. DOI:10.1007/s11276-019-02191-4 |
| [10] |
高强, 张凤荔, 陈学勤, 等. 基于改进Eclat算法的资源池节点异常模式挖掘[J]. 计算机应用研究, 2018, 35(2): 6. DOI:10.3969/j.issn.1001-3695.2018.02.003 |
| [11] |
YU X, WANG H. Improvement of eclat algorithm based on support in frequent itemset mining[C]// The 6th International Conference on Computer Research and Development, 2014, 9(9): 2116–2123.
|
| [12] |
MA Z, YANG J, ZHANG T, et al. An improved eclat algorithm for mining association rules based on increased search strategy[J]. International Journal of Database Theory and Application, 2016, 9(5): 251-266. DOI:10.14257/ijdta.2016.9.5.26 |
| [13] |
田攀博. 基于等价类变换的快速关联规则挖掘方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [14] |
LV S, HUANG J. An improved eclat algorithm based on pruning optimization and indexing intersection[J]. 2018.
|
| [15] |
李成严, 辛雪, 赵帅, 等. Sp-IEclat: 一种大数据并行关联规则挖掘算法[J]. 哈尔滨理工大学学报, 2021, 26(4): 109-118. |
| [16] |
ONDOV B D, TREANGEN T J, MELSTED P, et al. Mash: fast genome and metagenome distance estimation using MinHash[J]. Genome biology, 2016, 17(1): 1-14. DOI:10.1186/s13059-015-0866-z |
| [17] |
WU K, OTOO E J, SHOSHANI A. Optimizing bitmap indices with efficient compression[J]. ACM Transactions on Database Systems (TODS), 2006, 31(1): 1-38. DOI:10.1145/1132863.1132864 |
 2022, Vol. 44
2022, Vol. 44
