0 引　言

目前，随着互联网科技的不断发展，我国通信技术已经达到海陆空领域无障碍交流的程度。水域环境中一旦出现天气或意外因素影响，舰船导航容易受到噪声干扰，导致出现目标距离判定失败、信息传输时延以及定位失误等问题，严重影响舰船运行的稳定性和安全性。针对上述舰船通信问题，在接收到传播信号时，对导航信号进行滤波是非常有必要^[1]。由于信号中存在过多杂质及多种因素影响，非线性滤波方式要比普通的线性滤波更适用于舰船导航应用。

综合上述问题，提出一种基于船岸通信技术的舰船导航信号非线性滤波方法。船岸通信技术属于全程E-mail通信技术中的一种，其以岸上信号塔作为传输载体，将舰船信息看做普通电子邮件客户对待，只需根据目标地址即可传输相应“邮件”，进而实现船岸通信。这种通信技术下信号传输方式较为简单，在实际应用中容易实现且传输精准度高，耗用较小。基于此特点建立舰船状态方程，得到噪声数据与正常数据的变化参数，将其组成观测序列用做下一步非线性滤波的参照序列。非线性滤波结合航岸通信技术，根据误差谐波方式检测出信道中的非正常信号，采用去噪因子实现替换滤波。

1 舰船噪声信号去噪

舰船导航时容易受到多种因素影响，例如：风向、风速、降水量、磁场以及各种不可抗力，要想提高导航的精准性和稳定性，非线性滤波方法需要综合考虑航行位置、运行速度、方向等变量，确保算法滤波的精准性和实用性。

由于舰船运动时的加速度^[2]一般较小，导航循环计算的周期较短，因此在导航信号非线性滤波处理过程中可以忽略舰船的航线机动与速度机动只考虑与信号噪声相关的问题。设舰船运动状态矢量^[3]值为 ${x_1} = \phi$ （纬度值）、 ${x_2} = \lambda$ （经度值）、 ${x_3} = {v_{CE}}$ （风向东方向值）、 ${x_4} = {v_{CN}}$ （风向北方向值）、 ${x_5} = v$ （舰船航速值）、 ${x_6} = H$ （舰船航向数值）、 ${x_7} = \Omega$ （舰船运行角度变化值）。

假设舰船所在位置的经纬度误差较小，达到接近标准动态近似值的程度，此时，舰船正常运行的状态轨迹参数为：

$\begin{gathered} \phi = {v_{CN}} + v\cos H + {w_1}，\\ \lambda = {v_{CE}} + v\sin H + {w_2}，\\ v = {w_5}，\\ H = \Omega + {w_6}，\\ \Omega = {w_7}。\\ \end{gathered}$

(1)

式中： $v\cos H$ 和 $v\sin H$ 分别表示舰船正切和余切方向的航向； ${w_1}$ ~ ${w_7}$ 表示与 ${x_1}$ ~ ${x_7}$ 对应且与其他因素不相关的零均值高斯白噪声。

由于舰船在海面行驶时，受到的外界干扰信号过多，逐一排查所需要的运算量较大，因此采用一阶马尔可夫归一方程^[4]，将所有干扰信号进行统一化处理并计算其分量值。使全部分量值组成一组序列，并设定一组噪声界定值^[5]，后续滤波算法对比序列界定值后，再采取有效滤波，这样可以大大提升运算效率，且计算误差较小，提高滤波精准度。

一阶马尔可夫归一方程为：

$\begin{gathered} {\xi_{CE}} = - \beta v_{CE} + {w_3}，\\ {\xi_{CN}} = - \beta v_{CN} + {w_4} 。\\ \end{gathered}$

(2)

式中： $\beta v_{CE}$ 和 $\beta v_{CN}$ 分别表示舰船在正东方向和正北方向的信号接收偏差。

联立式（1）与式（2），进行噪声信号离散化^[6]处理，可得：

$\begin{split} \phi \left( k \right) = &\phi \left( {k - 1} \right) + \left( {1 - {e^{ - \beta }}} \right)/{\beta _c}{v_{CN}}\left( {k - 1} \right) - v\left( {k - 1} \right) \times \\ &\cos \left( {H\left( {k - 1} \right) + T/2\Omega \left( {k - 1} \right)} \right)T + {w_1}\left( {k - 1} \right) ，\end{split}$

(3)

$\begin{split} \lambda \left( k \right) =& \lambda \left( {k - 1} \right) + \left( {1 - {e^{ - \beta }}} \right)/{\beta _c}{v_{CE}}\left( {k - 1} \right) - v\left( {k - 1} \right) \times \\ & \sin \left( {H\left( {k - 1} \right) + T/2\Omega \left( {k - 1} \right)} \right)T + {w_2}\left( {k - 1} \right) 。\end{split}$

(4)

式中： ${e^{ - \beta }}$ 表示离散化后得到的高斯噪声标准； $k$ 表示序列样本数量； ${\beta _c}$ 表示在序列中第 $c$ 点的马尔可夫修正系数^[7]； $T$ 表示采样时间间隔。

式中：

$\begin{gathered} {v_{CE}}\left( k \right) = {e^{ - \beta }}{v_{CE}}\left( {k - 1} \right) + {w_3}\left( {k - 1} \right) ，\\ {v_{CN}}\left( k \right) = {e^{ - \beta }}{v_{CN}}\left( {k - 1} \right) + {w_4}\left( {k - 1} \right)，\\ v\left( k \right) = v\left( {k - 1} \right) + {w_5}\left( {k - 1} \right)，\\ H\left( k \right) = H\left( {k - 1} \right) + \Omega \left( {k - 1} \right)T + {w_6}\left( {k - 1} \right)，\\ \Omega \left( k \right) = \Omega \left( {k - 1} \right) + {w_7}\left( {k - 1} \right)。\\ \end{gathered}$

(5)

将公式（5）整合组成分量序列为：

$X\left( k \right) = f\left( {X\left( {k - 1} \right),k - 1} \right) + \Gamma W\left( {k - 1} \right) 。$

(6)

式中： $W\left( k \right)$ 表示舰船接收的高斯白噪声信号序列，正常均值为0，存在噪声时为1； $f$ 表示序列信号标记。

2 舰船导航系统信号量测模型

通常情况下，舰船导航系统会对接收到信号进行相关分类，不同类型的信号输送给不同的接收信道，根据这一特点，建立舰船导航信号量测模型，将量测值分为2组：一组是水平方向的信号量测值，另一组是垂直方向的信号量测值。将2组量测值组成方程组，通过信号接收标准值对比得到导航信号接收偏差^[8]，表达公式为：

$z\left( t \right) = h\left( t \right)x\left( t \right) + v\left( t \right)，$

(7)

其中：

$\begin{gathered} z = \left[ \begin{gathered} \left( {{L_I} - {L_M}} \right){R_M} \\ \left( {{\gamma _I} - {\gamma _M}} \right){R_N}\cos L \\ {h_I} - {h_M} \\ \end{gathered} \right] = \left[ \begin{gathered} {R_M}\varsigma L \\ {R_N}\cos L\varsigma \gamma \\ \varsigma h \\ \end{gathered} \right] = \left[ \begin{gathered} {v_1} \\ {v_2} \\ {v_3} \\ \end{gathered} \right]，\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {}&{{R_M}}&{\begin{array}{*{20}{c}} 0&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{} \end{array}} \\ {{0_3} \times 7}&0&{\begin{array}{*{20}{c}} {{R_N}\cos L}&0&{{0_3} \times 9} \end{array}} \\ {}&0&{\begin{array}{*{20}{c}} 0&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{} \end{array}} \end{array}} \right]。\\ \end{gathered}$

(8)

式中： ${L_I}$ ， ${L_M}$ 分别表示舰船导航接收信号的水平、垂直距离误差； ${\gamma _I}$ ， ${\gamma _M}$ 分别表示导航接收信号的水平、垂直夹角误差； ${h_I}$ ， ${h_M}$ 分别表示导航接收信号的水平、垂直高度误差； ${R_M}$ ， ${R_N}$ 均表示误差集合； $\varsigma$ 表示信号接收偏差标准； ${v_1}$ ， ${v_2}$ ， ${v_3}$ 均表示舰船运行速度。

上述过程建立的导航信号观测模型，不仅可以有效捕捉到信号状态，还可根据状态值计算滤波因子^[9]帮助实现精准滤波。

3 导航信号非线性滤波

以上述建立的量测模型为基础，初步得到舰船导航信号判定结果，根据判定结果对噪声信号进行非线性滤波。采用航岸通信技术结合误差协方差矩阵^[10]进行滤波，运用协方差矩阵计算正常信号和噪声信号的传输时延^[11]，设定转换因子，对噪声信号进行转换替代，完成非线性滤波。舰船导航初始接收信号的状态方程为：

$\begin{gathered} {x_{l + 1}} = {f_l}\left( {{x_l},{u_l},{w_l}} \right)，\\ {y_l} = {g_l}\left( {{x_l},{\upsilon _l}} \right) 。\\ \end{gathered}$

(9)

式中： ${x_l}$ ， ${y_l}$ 分别表示舰船导航系统在 $l$ 时刻接收信号的实时和延时状态向量； ${u_l}$ 表示初始控制输入向量； ${w_l}$ 表示观测噪声^[12]； ${\upsilon _l}$ 表示随机分布的状态噪声。假设， ${w_l}$ 和 ${\upsilon _l}$ 二者相互独立，得到均值方差值为：

$\begin{gathered} E\left( {{w_l}} \right) = {{w''}_l},E\left[ {\left( {{w_l} - {{w''}_l}} \right){{\left( {{w_l} - {{w''}_l}} \right)}^{\rm{T}}}} \right] = {Q_l}，\\ E\left( {{\upsilon _l}} \right) = {{\upsilon ''}_l},E\left[ {\left( {{\upsilon _l} - {\upsilon _l}} \right){{\left( {{\upsilon _l} - {\upsilon _l}} \right)}^{\rm{T}}}} \right] = {F_l} 。\\ \end{gathered}$

(10)

式中： ${w''_l}$ ， ${\upsilon ''_l}$ 分别表示观测噪声、随机分布状态噪声的方差均值^[13]； ${Q_l}$ ， ${F_l}$ 分别表示 ${w''_l}$ 和 ${\upsilon ''_l}$ 误差集合。引入误差协方差矩阵，通过矩阵求解观测噪声和随机分布噪声的实时状态值，引入矩阵因子^[14]进行分解，可得：

$\begin{gathered} {Q_l} = {G_w}G_w^{\rm{T}},{F_l} = {G_\upsilon }G_\upsilon ^{\rm{T}} ，\\ {{\bar P}_l} = {{\bar G}_w}\bar G_w^{\rm{T}},{{\bar P}_l} = {{\bar G}_\upsilon }\bar G_\upsilon ^{\rm{T }}。\\ \end{gathered}$

(11)

由此得到在量测、预测、实时以及延时状态下的非线性滤波方程组为：

$\left\{ \begin{aligned} &{{\bar y}_{l + 1}} = g\left( {{{\bar x}_{l + 1}},{{\bar \upsilon }_{l + 1}}} \right)，\\ &K{{\bar x}_{l + 1}} = {Q_x}Q_{xy}^{\rm{T}}\left[ {{Q_{yx}}Q_{yx}^{\rm{T}} + {F_{yx}}F_{yx}^{\rm{T}}} \right]，\\ &{{\hat x}_{l + 1}} = {{\bar x}_{l + 1}} + K{{\bar x}_{l + 1}}\left[ {{y_{l + 1}} - {{\bar y}_{l + 1}}} \right]，\\ &{{\hat P}_{l + 1}} = \left[ {{Q_x} - K{{\bar x}_{l + 1}}{Q_{yx}}{Q_{y\upsilon }}} \right] \times {\left[ {{Q_x} - K{{\bar x}_{l + 1}}{Q_{yx}}{K_{l + 1}}{Q_{y\upsilon }}} \right]^{\rm{T}}} 。\\ \end{aligned} \right.$

(12)

式中， $K$ 表示噪声滤波个数。

此次研究的滤波方法逻辑表达较为连贯，不是单一的滤波过程，而是将其分为初步噪声观测、状态判定以及最终的因子滤波3个步骤，通过每个步骤的参数关联使得算法的适应度更高、误差率更小。

4 滤波性能测试 4.1 实验背景

为了能有效验证所提出非线性滤波方法的可行性和有效性，实验利用GPS、计程仪、监测器等多种设备进行实时数据采集，保证导航信号覆盖的全面性和准确性。为保证实验数据的精准对比能力，多次测量舰船的速度、位置以及方向等信息，确保导航接收到的信号不受以上因素影响，只考虑噪声问题。

由于舰船在水面上行驶时，实际水声信号与陆地接收信号之间存在时间偏差，为验证由噪声影响，衍生的非线性滤波算法质量和应用效果，在数据集中选取2种不同类型（信号强度）的舰船导航噪声信号作为本次样本数据。

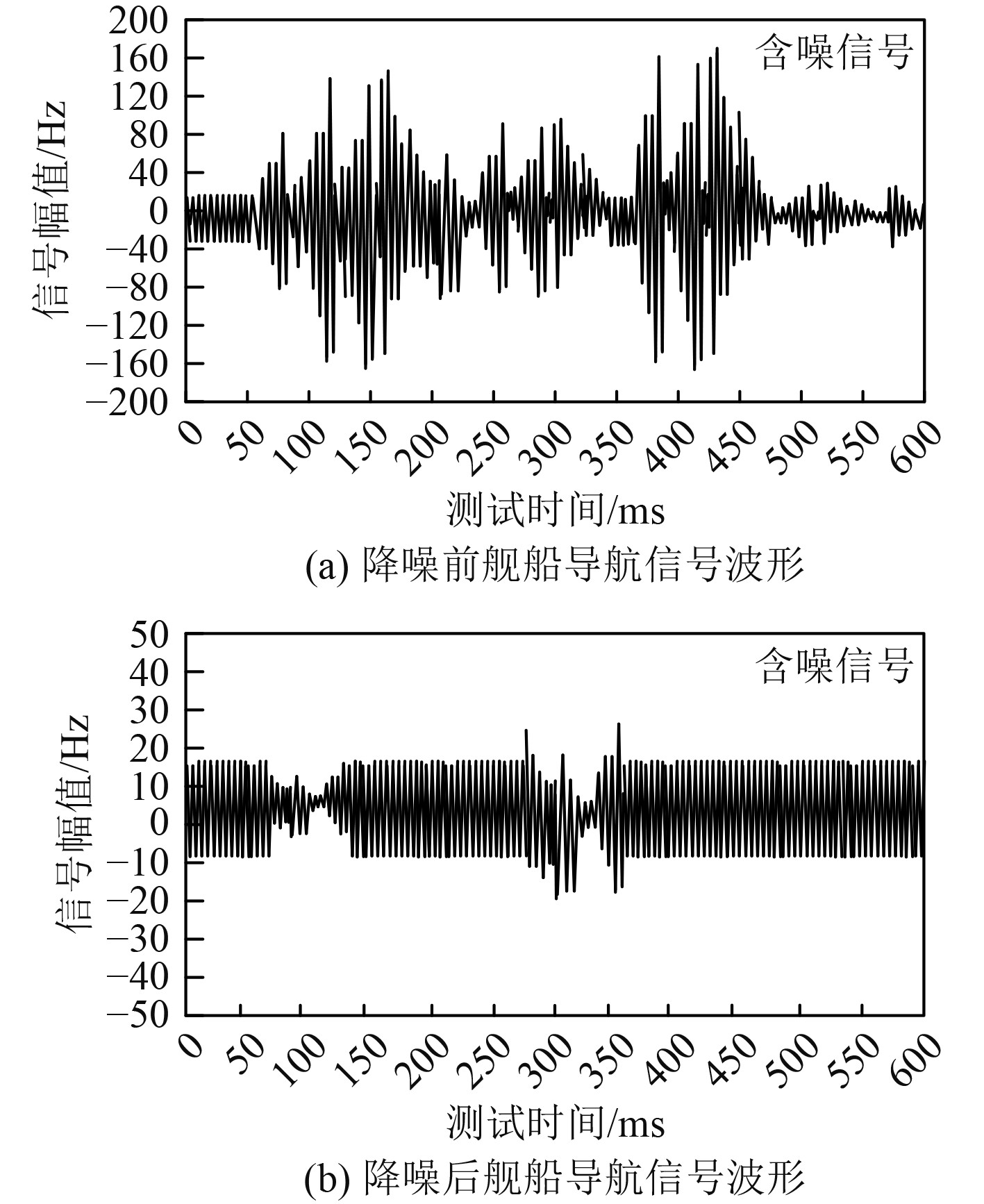
4.2 非线性滤波前后导航信号噪声变化

给定-10 dB和10 dB两种噪声强度信号，分别测试在2种强度条件下算法滤波效果，并与原始无噪信号作为对比。一方面可验证本文方法对噪声信号的滤波效果，另一方面可验证对原始信号的保留效果，是否存在破坏现象。实验结果如图1和图2所示。

从图1（b）可以看出，在-10 dB的噪声强度条件下，未进行降噪的舰船导航接收到信号波形变化较为混乱，整体呈现大幅度波动且高低频变化明显，低峰和高峰之间差距过大。说明，此时已经受到了噪声影响，噪声会耦合进信号中，干扰正常信号的运行使数据传输效率降低。

从图1（c）可以看出，经过本文方法滤波后，含噪信号得到了明显改善，整体波动趋势与无噪信号大致相同，不存在敏感高低峰值，信号波动存在一定规律。由此说明，此时舰船导航信号已经恢复正常接收状态，平稳行驶时，接收到目标信号变化存在规律，信噪比较高。从结果来看，本文方法对噪声信号的滤波效果较好，能够将含噪信号很好地恢复出来，与正常信号表达无异。

可以看出，在更强的噪声环境下，舰船导航信号的含噪量也越大，受噪声影响程度也就越高，此时，降噪前导航信号已经呈现无规律的随机波动现象，整体表现更为混乱。但运用本文方法降噪后，含噪信号依旧得到了有效解决，趋势走向相对平稳，说明本文滤波算法起到了一定作用，制约了噪声的持续影响。

本文提出的非线性滤波方法之所以在高强度的噪声环境下均能实现有效滤波，一是因为算法对量测、预测、实时以及延时4种状态的噪声均进行了测试，使得算法的容错率更高，更不容易出现误差影响；二是本文算法的噪声类型覆盖面较广，对多种噪声就能实现有效处理，算法适应能力更强。

5 结　语

通信信号降噪问题是舰船导航信号滤波处理的基础，根据这一特点提出基于船岸通信技术的舰船导航信号非线性滤波方法。考虑到舰船行驶时容易受到风向、风速、降水量、磁场以及各种不可抗力等多种因素影响，在滤波前先对此类别噪声进行归一化处理。船岸通信技术具备接收时延小、传输方式简单的特点，运用非线性滤波方法，能够快速捕捉噪声特征，帮助高效识别异常信号。此次研究的非线性滤波结合了协方差矩阵，并引入噪声修正因子实现精准滤波。实验数据证明，本文方法在多种噪声强度下均能实现有效滤波。