随着海洋在经济和军事应用中重要性的不断凸显,水声通信作为开发和利用海洋科学勘探、海洋环境监测和水下机器人通信等相关领域的有效工具,受到高度重视[1-3]。在水声通信网络中,一般均采用正交多址接入(orthogonal multiple access, OMA)技术提供数据服务[4],虽然OMA技术通过用户独占时域/频域资源块的方式,极大地避免了数据冲突和用户间干扰,但这种资源接入方式也极大地限制了用户接入数量和资源利用率的提升。而随着水声通信用户不断增加,水声通信网络需要在有限的系统带宽和功率范围内,为越来越多的用户提供服务[5]。因此,探索新的多址接入方式对进一步提高水声通信网络的通信质量和资源利用率至关重要。
与OMA技术相比,非正交多址接入技术(non-orthogonal multiple access,NOMA)通过复用功率域,增加非正交的资源控制,同时发送多个用户信号,达到了大规模提高频谱利用率和用户接入数量的目的[6-7]。近年来,国内外学者从不同的角度,对NOMA技术在水声通信网络中的应用做了初步的探索研究。Goutham V等[8]在非精确串行干扰消除(successive interference cancellation,SIC)技术假设下,研究了基于NOMA技术的水声协作通信网络的可达容量和中断概率,揭示了NOMA技术在水声协作系统资源利用率上的优势。Cheon J等[9]在基于NOMA技术的下行水声通信网络中,提出一种等传输时间的功率分配方案,以避免NOMA节点之间的信息传输时间不等而造成资源浪费。Goutham V等[10]将全双工技术和NOMA技术引入水声协作传感器网络中,分析推导自干扰和非精确SIC假设下系统的遍历容量和能量效率,揭示了中继节点位置、风速和航运程度对系统性能的影响。
虽然NOMA技术应用于水声通信网络可以明显提高系统资源利用率和可达性能,但这些性能改善是在NOMA节点使用相同频段的前提下取得的。实际中,通信距离越远,水声节点适用的最优频率越小,3 dB带宽越窄[11]。值得注意的是,虽然通信距离不同的节点适用的频段不会完全重叠,但分布在同一目的节点周围的节点通信距离不会相差特别大。因此,水声通信场景中,节点的适用通信频段虽然不会完全重叠,但会部分重叠。
Kim B等[12]通过调整NOMA用户间的频段重叠率,提出的部分NOMA (partial NOMA, P-NOMA)技术以达到减少NOMA用户间干扰和进一步提升NOMA系统可达性能的目的。考虑到水声通信场景的独特特点,在文献[11]和文献[12]基础上,本文在上行水声通信中引入P-NOMA技术,并在功率均匀分布和非精确SIC假设下,分析推导各P-NOMA节点在通信频段内的可达容量和能量效率表达式,以期通过P-NOMA技术的引入,进一步有效利用有限的水声频段资源,提高系统资源利用率,为水声通信网络在下一代移动通信网络中服务更多的水声节点/用户奠定基础。
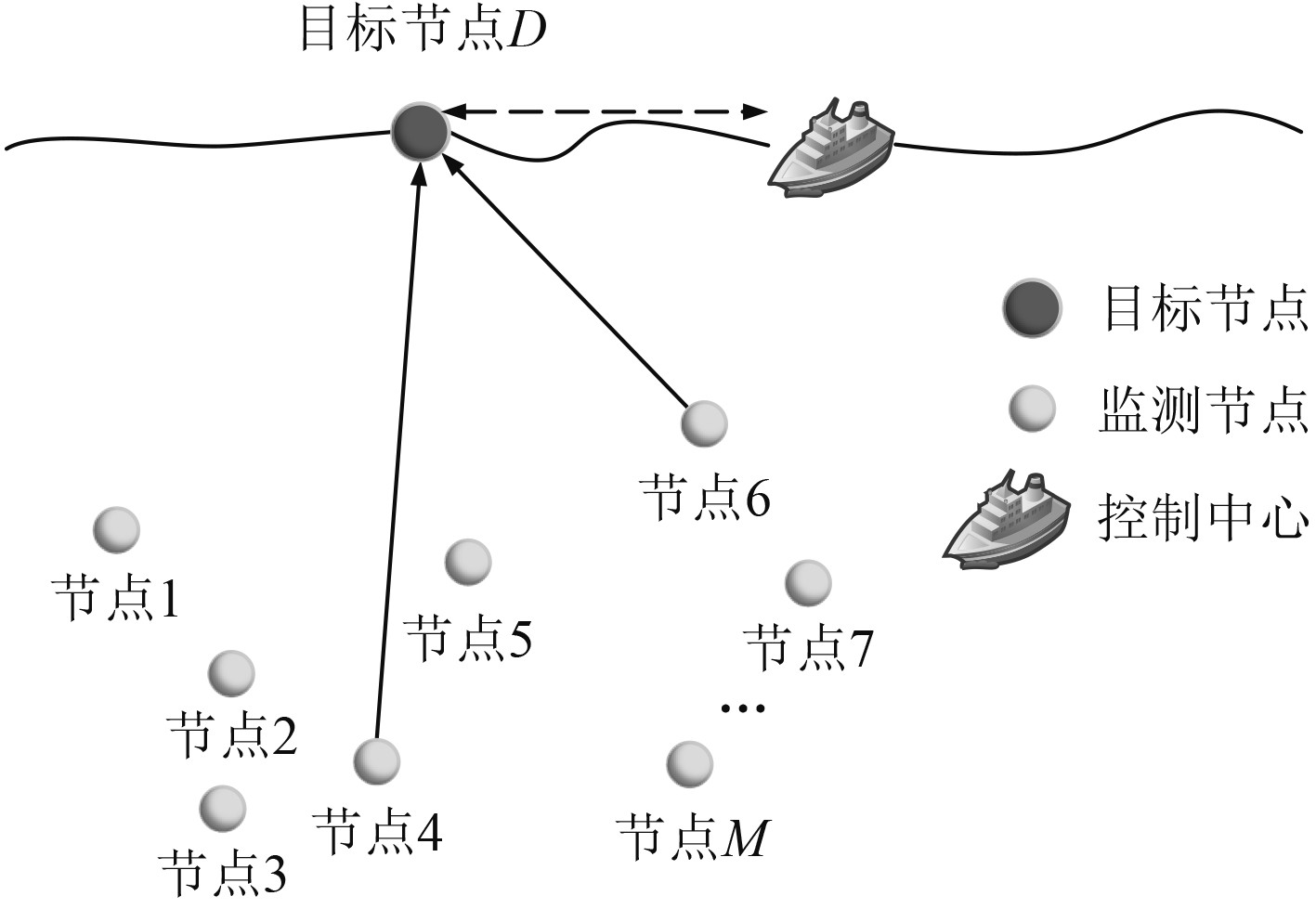
1 系统模型如图1所示,本文所提的面向非精确SIC的P-NOMA水声上行通信网络由一个目的节点和M
|
图 1 系统模型 Fig. 1 Illustration of the considered system model |
|
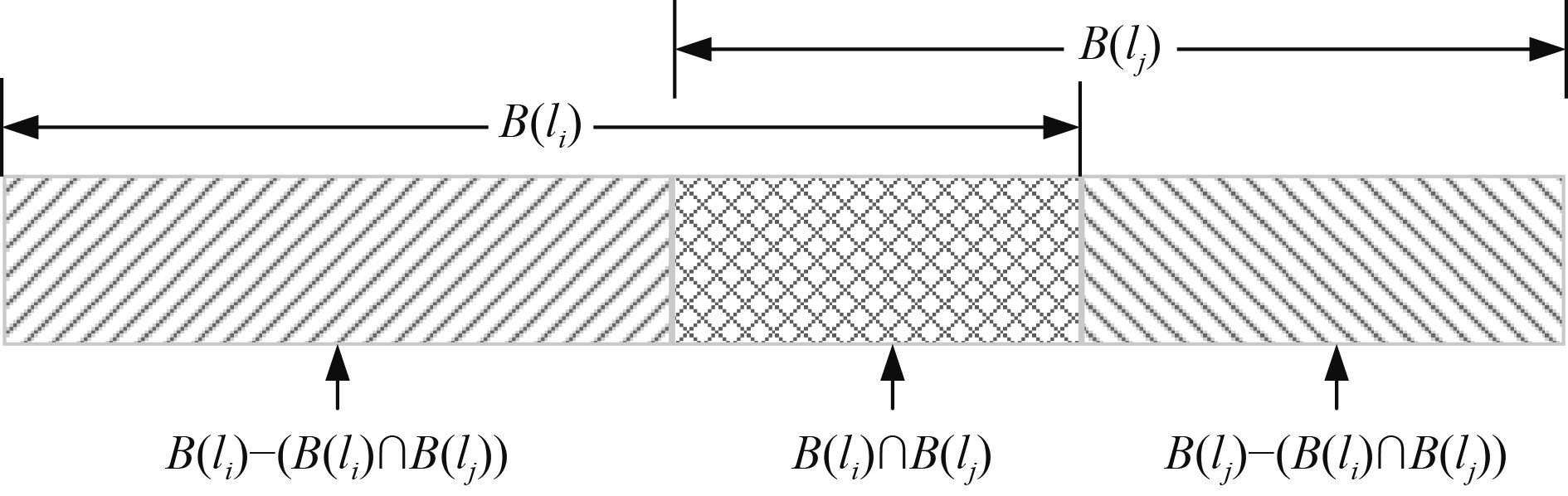
图 2 两节点的P-NOMA Fig. 2 P-NOMA with two nodes |
利用P-NOMA技术,目标节点处接收到的信号为:
| $ y\left( {{f_m}} \right) = \sum\limits_{m = i,j}^{} {\frac{{\sqrt {{P_m}} }}{{\sqrt {A\left( {{l_m},{f_m}} \right)} }}} {X_m}\left( {{f_m}} \right) + N\left( {{f_m}} \right)。$ | (1) |
式中:
| $ 10\lg \left( {A\left( {{l_m},{f_m}} \right)} \right) = {k_m} \times 10\lg {l_m} + \left( {{{{l_m}} \mathord{\left/ {\vphantom {{{l_m}} {{{10}^3}}}} \right. } {{{10}^3}}}} \right) \times 10\lg a\left( {{f_m}} \right)。$ | (2) |
其中:
| $ 10\lg a\left( {{f_m}} \right) = \frac{{0.11f_m^2}}{{1 + f_m^2}} + \frac{{44f_m^2}}{{4100 + f_m^2}} + 2.75 \times {10^{ - 4}}f_m^2 + 0.003 。$ | (3) |
由式(2)~式(3)可知,无论是通信距离还是频率的增加,都会增大水声通信的路径损耗,这就限制了不同通信距离下,水声节点适用的3 dB带宽和最优频率。
| $ N\left( {{f_m}} \right) = {N_{tb}}\left( {{f_m}} \right) + {N_s}\left( {{f_m}} \right) + {N_w}\left( {{f_m}} \right) + {N_{th}}\left( {{f_m}} \right) 。$ | (4) |
式中:
假设
| $ {\gamma _i} = \left\{ {\begin{aligned} &{\dfrac{{\displaystyle\int_{{B_{ionly}}} {{A^{ - 1}}\left( {{l_i},{f_i}} \right){S_i}\left( {{f_i}} \right){\rm{d}}{f_i}} }}{{\displaystyle\int_{{B_{ionly}}} {N\left( {{f_i}} \right){{{\rm{d}}}}{f_i}} }},{f_i} \in {B_{ionly}}} ,\\ &{\dfrac{{\displaystyle\int_{{B_{mix}}} {{A^{ - 1}}\left( {{l_i},{f_{mix}}} \right){S_i}\left( {{f_{mix}}} \right){\rm{d}}{f_{mix}}} }}{{\displaystyle\int_{{B_{mix}}} {\left[ {{A^{ - 1}}\left( {{l_j},{f_{mix}}} \right){S_j}\left( {{f_{mix}}} \right) + N\left( {{f_{mix}}} \right)} \right]{\rm{d}}{f_{mix}}} }},{f_{mix}} \in {B_{mix}}}。\end{aligned}} \right .$ | (5) |
式中:
监测节点j由于距离较远,信号较弱,在频段
| $ \gamma _j = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\displaystyle\int_{{B_{mix}}} {{A^{ - 1}}\left( {{l_j},{f_{mix}}} \right){S_j}\left( {{f_{mix}}} \right){\rm{{\rm{d}}}}{f_{mix}}} }}{{\displaystyle\int_{{B_{mix}}} {\left[ {N\left( {{f_{mix}}} \right) + \xi {A^{ - 1}}\left( {{l_i},{f_{mix}}} \right){S_i}\left( {{f_{mix}}} \right)} \right]{\rm{{\rm{d}}}}{f_{mix}}} }},{f_{mix}} \in {B_{mix}}} ,\\ {\dfrac{{\displaystyle\int_{{B_{jonly}}} {{A^{ - 1}}\left( {{l_j},{f_{jonly}}} \right){S_j}\left( {{f_{jonly}}} \right){\rm{d}}{f_{jonly}}} }}{{\displaystyle\int_{{B_{jonly}}} {N\left( {{f_{jonly}}} \right){\rm{d}}{f_{jonly}}} }},{f_{jonly}} \in {B_{jonly}}} 。\end{array}} \right. $ | (6) |
式中:
如式(1)、式(5)和式(6)所示,在非重合频段内,目标节点接收的信号没有来自其他监测节点信号的干扰;在重合频段内,通信距离较远节点的信号虽然受到通信距离较近节点信号的干扰,但利用SIC技术可大大降低其干扰程度。
因此,在功率均匀分布假设下,各P-NOMA节点的可达容量为:
| $ \begin{split}& R_i^{P - NOMA} = \int_{{B_{ionly}}} {{{\log }_2}} \left( {1 + \frac{{{{{P_i}} \mathord{\left/ {\vphantom {{{P_i}} {B\left( {{l_i}} \right)}}} \right. } {B\left( {{l_i}} \right)}}}}{{A\left( {{l_i},{f_i}} \right)N\left( {{f_i}} \right)}}} \right){\rm{d}}{f_i} +\\ &\int_{{B_{mix}}} {{{\log }_2}} \left( {1 + \frac{{{{{A^{ - 1}}\left( {{l_i},{f_{mix}}} \right){P_i}} \mathord{\left/ {\vphantom {{{A^{ - 1}}\left( {{l_i},{f_{mix}}} \right){P_i}} {B\left( {{l_i}} \right)}}} \right. } {B\left( {{l_i}} \right)}}}}{{{A^{ - 1}}\left( {{l_j},{f_{mix}}} \right){{{P_j}} \mathord{\left/ {\vphantom {{{P_j}} {B\left( {{l_j}} \right)}}} \right. } {B\left( {{l_j}} \right)}} + N\left( {{f_{mix}}} \right)}}} \right){\rm{d}}{f_{mix}} ,\\[-20pt]\end{split}$ | (7) |
| $ \begin{split} & R_j^{P - NOMA} = \int_{{B_{jonly}}} {{{\log }_2}} \left( {1 + \frac{{{{{P_j}} \mathord{\left/ {\vphantom {{{P_j}} {B\left( {{l_j}} \right)}}} \right. } {B\left( {{l_j}} \right)}}}}{{A\left( {{l_j},{f_j}} \right)N\left( {{f_j}} \right)}}} \right){\rm{d}}{f_j} + \\ &\int_{{B_{mix}}} {{{\log }_2}} \left( {1 + \frac{{{{{A^{ - 1}}\left( {{l_j},{f_{mix}}} \right){P_j}} \mathord{\left/ {\vphantom {{{A^{ - 1}}\left( {{l_j},{f_{mix}}} \right){P_j}} {B\left( {{l_j}} \right)}}} \right. } {B\left( {{l_j}} \right)}}}}{{\xi {A^{ - 1}}\left( {{l_i},{f_{mix}}} \right){{{P_i}} \mathord{\left/ {\vphantom {{{P_i}} {B\left( {{l_i}} \right)}}} \right. } {B\left( {{l_i}} \right)}} + N\left( {{f_{mix}}} \right)}}} \right){\rm{d}}{f_{mix}}.\\[-20pt]\end{split}\;\;$ | (8) |
水声通信网络中,水声节点一般依靠海洋热能或电池提供能量,尽管海洋热能能量无穷,但电池充放电次数有限。因此,分析水声通信系统的能量效率比单纯分析系统的可达容量更有意义。基于此,对基于P-NOMA技术的水声上行通信系统的能量效率进行分析。在式(7)和式(8)的可达容量条件下,各P-NOMA节点的能量效率可以写为:
| $ \eta _m^{P - NOMA} = \dfrac{{R_m^{P - NOMA}}}{{\varsigma {P_m} + {P_c}}} 。$ | (9) |
式中:
在采用OMA技术的水声系统模型中,例如采用水声通信系统中常用的时分多址接入技术(time division multiple access,TDMA),假定节点利用功率在不同的时隙内发送信号给目标节点,目标节点处的接收信号为:
| $ y\left( {{f_m}} \right) = \frac{{\sqrt {{P_m}} }}{{\sqrt {A\left( {{l_m},{f_m}} \right)} }}{X_m}\left( {{f_m}} \right) + N\left( {{f_m}} \right) ,$ | (10) |
因此,基于TDMA技术的水声节点m的SINR为:
| $ \gamma _m^{OMA} = \frac{{\int_{{B_m}} {{A^{ - 1}}\left( {{l_m},{f_m}} \right){S_m}\left( {{f_m}} \right)d{f_m}} }}{{\int_{{B_m}} {N\left( {{f_m}} \right)d{f_m}} }}{\text{ }}{f_m} \in {B_m} ,$ | (11) |
可达容量为:
| $ R_m^{OMA} = 0.5\int_{{B_m}} {{{\log }_2}} \left( {1 + \frac{{{{{P_m}} \mathord{\left/ {\vphantom {{{P_m}} {B\left( {{l_m}} \right)}}} \right. } {B\left( {{l_m}} \right)}}}}{{A\left( {{l_m},{f_m}} \right)N\left( {{f_m}} \right)}}} \right){\rm{d}}{f_m}。$ | (12) |
式中:系数0.5表示水声节点i和j各占用半个时隙资源。另外,根据式(9),节点m的能量效率为:
在无风
1)在非精确SIC
|
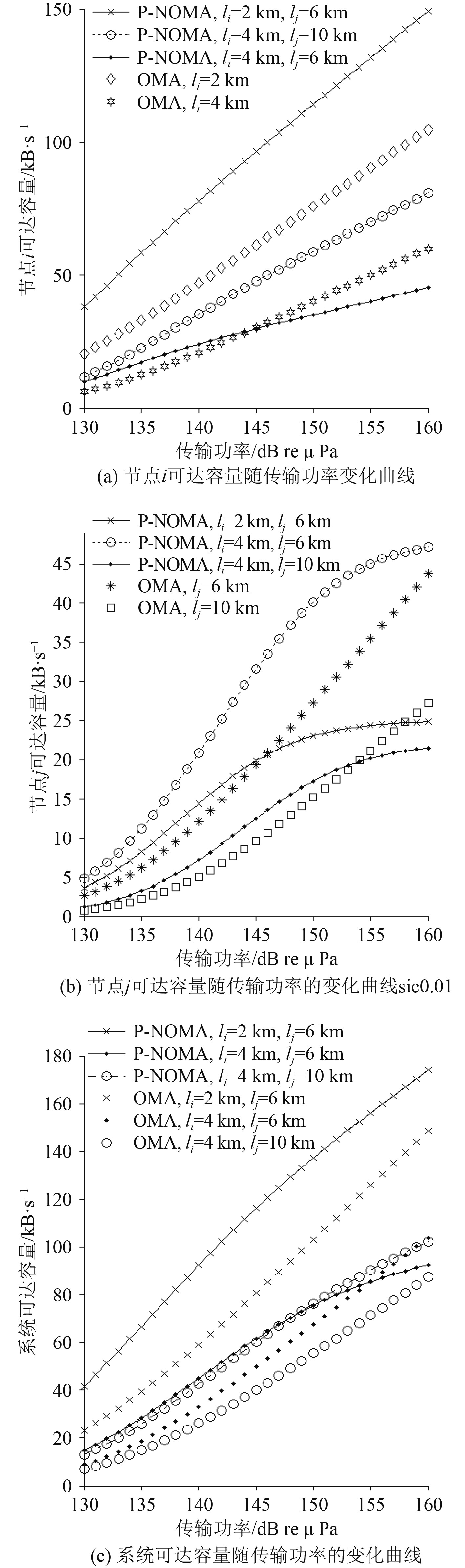
图 3
不同传输距离和多址接入方式下,节点j、节点i 和系统可达容量随传输功率的变化曲线,其中
|
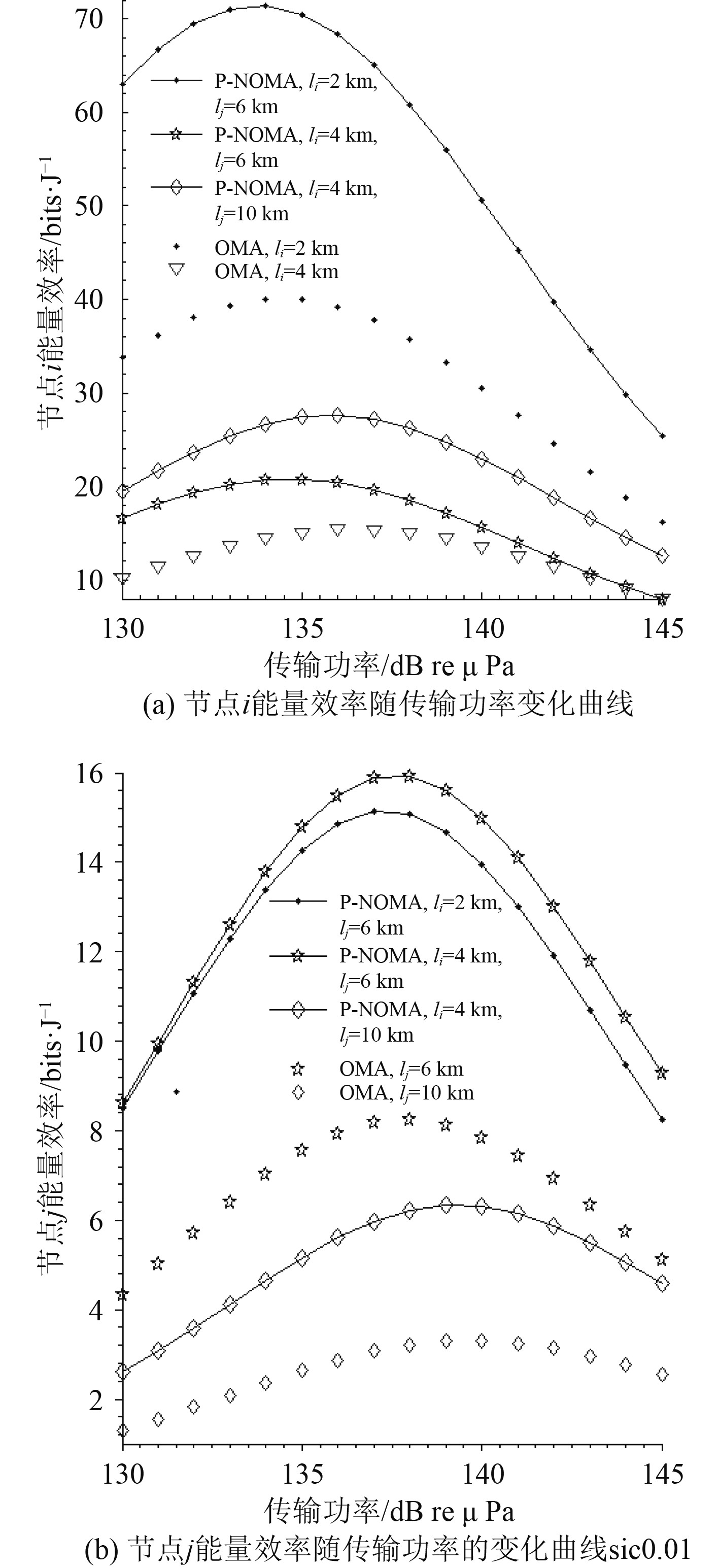
2)根据P-NOMA和OMA下节点i和节点j的可达容量,图4给出了对应节点的能量效率。可以看到,在不同的距离组合中,2种多址接入技术对应的能量效率曲线均先上升后在某个传输功率值处开始下降。可以注意到,增加节点i或节点j的通信距离,会加大能量效率对应的传输功率转折值。同时,与图3相对应,节点i的能量效率随着节点i/j通信距离的增加/减小而减小,节点j的能量
|
图 4 不同传输距离和多址接入方式下,节点i和节点j的能量效率随传输功率的变化曲线 Fig. 4 Energy efficiency of the nodes i andj versus transmission power with different transmission distances and multiple access schemes. |
效率随着节点i/节点j通信距离的减小/增加而减小。此外,可以清楚看到节点i和节点j在P-NOMA技术下的能量效率均明显优于其在OMA技术下的能量效率。根据图4的结论,与OMA技术相比,同等条件下,引入P-NOMA技术的水声通信网络可以获得更高的电池使用效率、更长的电池使用时间和更小的电池容量。
3)为了揭示非精确SIC对可达容量的影响,图5给出了不同通信距离组合下,P-NOMA技术下节点j和系统可达容量随SIC解码非精确程度的变化情况,其中
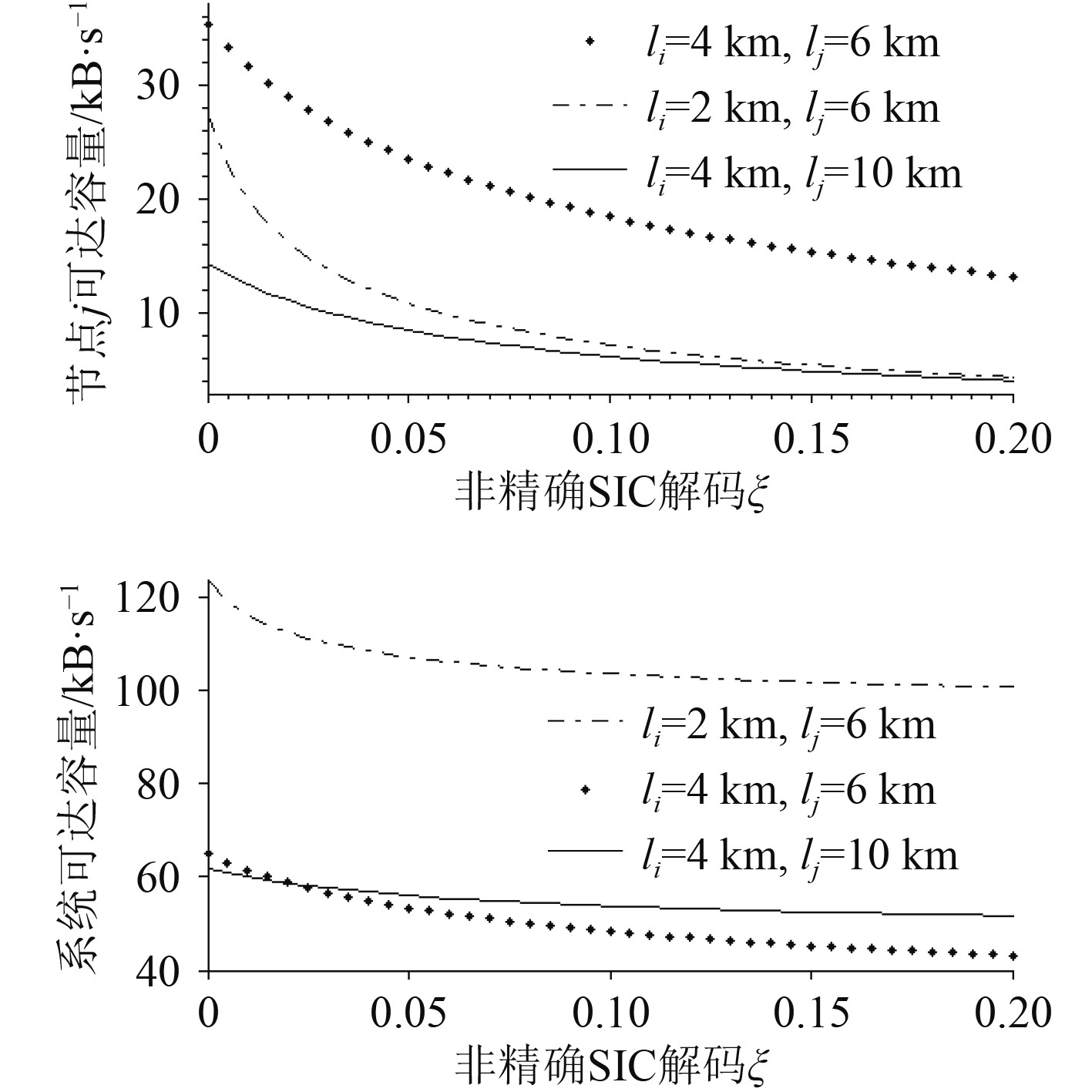
|
图 5 不同SIC解码非精确程度下,节点j和系统可达容量随着传输功率的变化曲线 Fig. 5 The achievable capacities of node j and the considered system versus SIC imperfect severity with different transmission distances. |
为了满足日益增长的水声节点接入需求,以及提高水声通信网络的资源利用率,本文在功率均匀分布假设下,研究了面向非精确SIC的P-NOMA上行水声通信网络的容量分析和能量效率分析。仿真结果表明,与OMA相比,选择合适的P-NOMA节点组,所提方案可以大幅提升水声通信网络的可达容量和能量效率。此外,本文研究了SIC解码非精确程度和位置分布对系统可达容量的影响。
| [1] |
郭子源, 温晓光. 直接序列扩频技术在水声通信中的应用[J]. 舰船科学技术, 2020, 42(18): 139-141. GUO Z Y, WEN X G. Application of direct sequence spread spectrum technology in acoustic communication[J]. Ship Science and Technology, 2020, 42(18): 139-141. |
| [2] |
WANG M, CHEN Y, SUN X, et al. Node energy consumption balanced multi-hop transmission for underwater acoustic sensor networks based on clustering algorithm[J]. IEEE Access, 2020, 8: 191231-191241. DOI:10.1109/ACCESS.2020.3032019 |
| [3] |
YU W, CHEN Y, WAN L, et al.. An energy optimization clustering scheme for multi-hop underwater acoustic cooperative sensor networks[J]. IEEE Access, 2020, 8: 89171-89184. DOI:10.1109/ACCESS.2020.2993544 |
| [4] |
曾睿. 基于节点发送时间和功率联合优化的水声网络MAC协议研究[D]. 广州: 华南理工大学, 2017.
|
| [5] |
ALL M F, JAYAKODY D N L, CHURSLN Y, et al. Recent advances and future directions on underwater wireless communications[M]. Archives of Computational Methods in Engineering, Cham, Switzerland: Springer, 2020: 1379–1412.
|
| [6] |
MARAQA O, RAJASEKARAN A S, AL-AHMADI S, et al. A survey of rate-optimal power domain NOMA with enabling technologies of future wireless networks[J]. IEEE Communications Surveys & Tutorials, 2020, 22(4): 2192-2235. |
| [7] |
YAN X, XIAO H, AN K, et al. Ergodic capacity of NOMA-based uplink satellite networks with randomly deployed users[J]. IEEE System Journal, 2020, 14(3): 3343-3350. DOI:10.1109/JSYST.2019.2934358 |
| [8] |
GOUTHAM V , HARIGOVINDAN V P. NOMA based cooperative relaying strategy for underwater acoustic sensor networks under imperfect SIC and imperfect CSI: a comprehensive analysis[J]. IEEE Access, 2021, 9: 32857-32872. DOI:10.1109/ACCESS.2021.3060784 |
| [9] |
CHEON J , CHO H. Power allocation scheme for non-orthogonal multiple access in underwater acoustic communications[J]. Sensors (Basel, Switzerland), 2017, 17(11): 1-13. |
| [10] |
GOUTHAM V, HARIGOVINDAN V. Full-duplex cooperative relaying with NOMA for the performance enhancement of underwater acoustic sensor networks[J]. ELSEVIER Engineering Science and Technology, 2021, 24(6): 1369-1407. |
| [11] |
STOJANOVIC M. On the relationship between capacity and distance in an underwater acoustic communication channel[J], Computer Science Mobile Computing and Communications Review, 2007, 11(4): 34-43.
|
| [12] |
KIM B, PARK Y, HONG D. Partial non-orthogonal multiple access (P-NOMA)[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1377-1380. DOI:10.1109/LWC.2019.2918780 |
| [13] |
张育芝, 张效民, 王安义, 等. 水声通信网络信道建模与仿真研究进展[J]. 科学技术与工程, 2021, 21(4): 1249-1261. ZHANG Y Z, ZHANG X M, WANG A Y, et al. Research progresses on channel modeling and simulation for underwater acoustic communication and networks[J]. Science Technology and Engineering, 2021, 21(4): 1249-1261. DOI:10.3969/j.issn.1671-1815.2021.04.002 |
| [14] |
JORNET J M, STOJANOVIC M , ZORZI M. On joint frequency and power allocation in a cross-layer protocol for underwater acoustic networks[J]. IEEE Journal of Oceanic Engineering, 2010, 35(4): 936-947. DOI:10.1109/JOE.2010.2080410 |
 2022, Vol. 44
2022, Vol. 44
