0 引　言

航空声呐浮标（简称浮标）是一种主要的航空搜潜装备，空投入水后，漂浮装置保持直立姿态漂浮于水面。水听器接收到的噪声信号经预处理后传给漂浮装置内的天线模块，调制后向空中发射，由飞机上的设备进行接收处理。复杂海况下，漂浮装置的起伏和传输电缆的抖动都会产生各种不必要的噪声和振动信号，传递给水听器，引起水听器内部压电元件的振动并输出电压，从而导致出现虚假信号或者放大电路限幅等不利影响^[1]。浮标一般在五级海况下能够正常工作，为了使浮标能够适应恶劣的环境，有必要设计一套机械减振系统，阻隔漂浮装置的垂直运动向下传递，降低波浪带来的干扰，尽量使水听器保持静止。

1 力学原理

浮标的减振系统一般包括质量元件、弹性元件及阻尼元件等，可以类比成弹簧-质量系统进行分析^[2-3]。

1.1 无阻尼条件下的自由振动

根据牛顿第二定律，自由振动的运动方程为：

$m\ddot{x}+kx=0 。$

(1)

式中： $m$ 为系统质量； $k$ 为弹性元件的弹性系数； $x$ 为系统质点位移； $\ddot{x}$ 为质点加速度。

令 ${\omega }_{0}=\sqrt{k/m}$ ，则 ${f}_{1}={\omega }_{0}/2\text{π}$ 为单自由度无阻尼振动系统的固有频率。

1.2 有阻尼条件下的自由振动

在运动过程中，若考虑系统所受阻力，该阻力与运动大小成正比，方向相反。根据牛顿第二定律，阻尼振动系统的运动方程为：

$m\ddot{x}+R\dot{x}+kx=0。$

(2)

式中： $R$ 为系统阻力系数； $\dot{x}$ 为质点速度；令 $\mathrm{\delta }=R/2m$ ，为系统阻尼系数。

解微分方程（2），得到 $x\left({t}\right)={c}_{1}{e}^{{\mu }_{1}t}+{c}_{2}{e}^{{\mu }_{2}t}$ ，其中 ${\mu }_{1}$ 和 ${\mu }_{2}$ 由特征方程 ${\mu }^{2}+2\mathrm{\delta }\mathrm{\mu }+{\mathrm{\omega }}_{0}^{2}=0$ 决定， ${\mu }_{1},{\mu }_{2}= -\mathrm{\delta }\pm \sqrt{{\delta }^{2}-{\omega }_{0}^{2}}$ 。

若 ${\delta }^{2} > {\omega }_{0}^{2}（{R}^{2} > 4mk）$ ，系统为大阻尼系统，不会发生自由振动。

若 ${\delta }^{2} < {\omega }_{0}^{2}（{R}^{2} < 4mk）$ ，系统为小阻尼系统， ${\mu }_{1}, {\mu }_{2}= -\mathrm{\delta }\pm \mathrm{j}\sqrt{{\omega }_{0}^{2}{-\delta }^{2}}$ ，令 $\mathrm{\Omega }=\sqrt{{\omega }_{0}^{2}{-\delta }^{2}}$ ，则 $x\left(t\right)={c}_{1}{e}^{(-\delta +j\Omega )t}+ {c}_{2}{e}^{(-\delta -j\Omega )t}=\sqrt{{c}_{1}^{2}+{c}_{2}^{2}}{e}^{-\delta t}\rm{cos}(\Omega t+\varphi )$ 。式中： ${c}_{1}$ ， ${c}_{2}$ 和 $\varphi$ 由初始条件决定，系统振幅 $\sqrt{{c}_{1}^{2}+{c}_{2}^{2}}{e}^{-\mathrm{\delta }\mathrm{t}}$ 随时间衰减。系统的固有频率 ${f}_{2}=\mathrm{\Omega }/2\text{π} =\sqrt{{\omega }_{0}^{2}{-\delta }^{2}}/2\text{π}$ ，比无s阻尼时的固有频率降低。在极小阻尼条件下，即 ${\omega }_{0}^{2}{\gg \delta }^{2}$ 时，近似有 ${f}_{2}={f}_{1}$ 。

1.3 有阻尼条件下的受迫振动

系统受到简谐激励，激励的角频率为 $\mathrm{\omega }$ ，激励振幅为 ${{A}}_{0}$ ，有阻尼条件下的受迫运动微分方程为：

$m\ddot{x}+R\dot{x}+kx=k{{A}}_{0}\mathrm{cos}\mathrm{\omega }{t}。$

(3)

解微分方程（3），其解为 $x\left({t}\right)={x}_{1}\left({t}\right)+{x}_{2}\left({t}\right)$ ，其中 ${x}_{1}\left(t\right)=\sqrt{{c}_{1}^{2}+{c}_{2}^{2}}{e}^{-\delta t}\rm{cos}(\Omega t+\varphi )$ ，此解为暂态解，随着时间 ${x}_{1}\left({t}\right)$ 趋近于0，对系统影响忽略； ${x}_{2}\left({t}\right)= k{A}_{0}{e}^{j\omega t}/ (j\omega R+k-m{\omega }^{2})$ 是稳态解，是描述系统稳定运动的函数。

系统受到 ${{A}}_{0}\mathrm{cos}\mathrm{\omega }{t}$ 激励，该激励位移产生简谐力 $k{{A}}_{0}\mathrm{cos}\mathrm{\omega }{t}$ ，系统会受迫振动，其振动幅值记作 $A$ ，将系统内部振动幅值与激励幅值的比值定义为传递函数 $T\left(\mathrm{\omega }\right)$ ，用传递函数来描述激励对静态系统的影响程度。传递函数 $T\left(\mathrm{\omega }\right)$ 满足等式：

$T\left(\omega \right)=\frac{A}{{A}_{0}}=\frac{k}{\sqrt{{\left(\omega R\right)}^{2}+{(k-m{\omega }^{2})}^{2}}}。$

(4)

2 模型建立 2.1 浮标漂浮状态

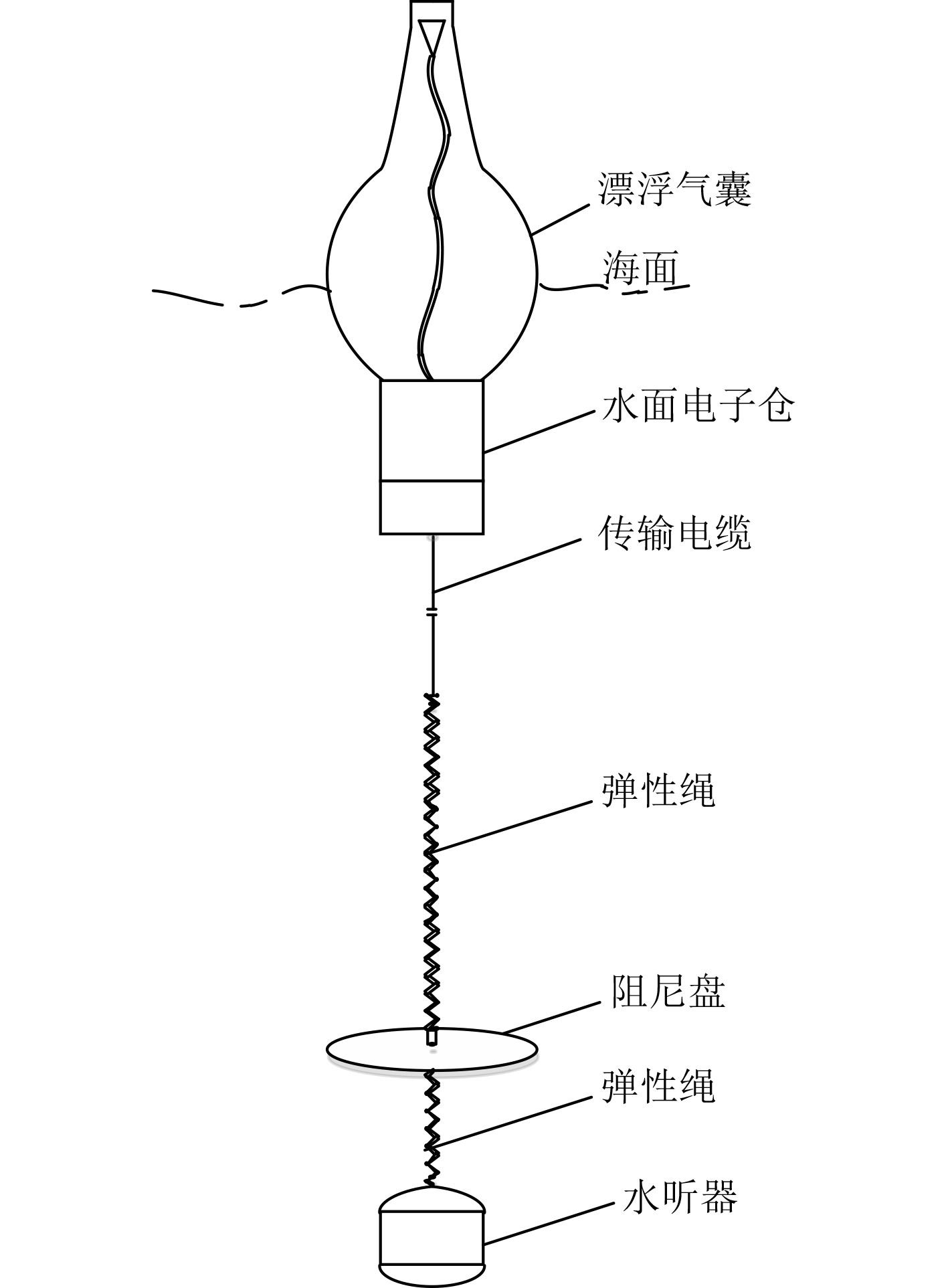
浮标处于漂浮状态时^[4]，漂浮气囊与水面电子仓组成漂浮装置漂浮在海面，漂浮装置随海浪起伏时，产生垂直方向的运动，通过传输电缆传递给水听器，从而引起水听器与周围海水的相对运动，产生各种不必要的噪声和振动信号，影响有用信号的采集。如图1所示，在漂浮装置和水听器之间设计一套减振系统，通过传输电缆与水面电子仓相连。水听器单点悬挂在减振系统上，减振系统主要由柔性元件组成，包括弹性绳和阻尼盘。

2.2 减振系统模型

浮标漂浮状态时，将水听器的水中质量记作 ${m}_{2}$ ；弹性绳的变形量与所受拉伸力成正比，简化为弹簧，其2段弹性绳的弹力系数分别记作 ${k}_{1}$ 和 ${k}_{2}$ ；阻尼盘的质量记作 ${m}_{1}$ ，在水中振动时受到流体阻力，方向与速度方向相反，阻力系数记作 ${R}_{1}$ ；漂浮装置随海浪起伏时，传递位移激励，产生的激励力记作 ${{k}_{1}A}_{0}\rm{cos}\left(\omega t\right)$ 。因此，浮标的水下减振系统构成了一个有阻尼的强迫振动系统。

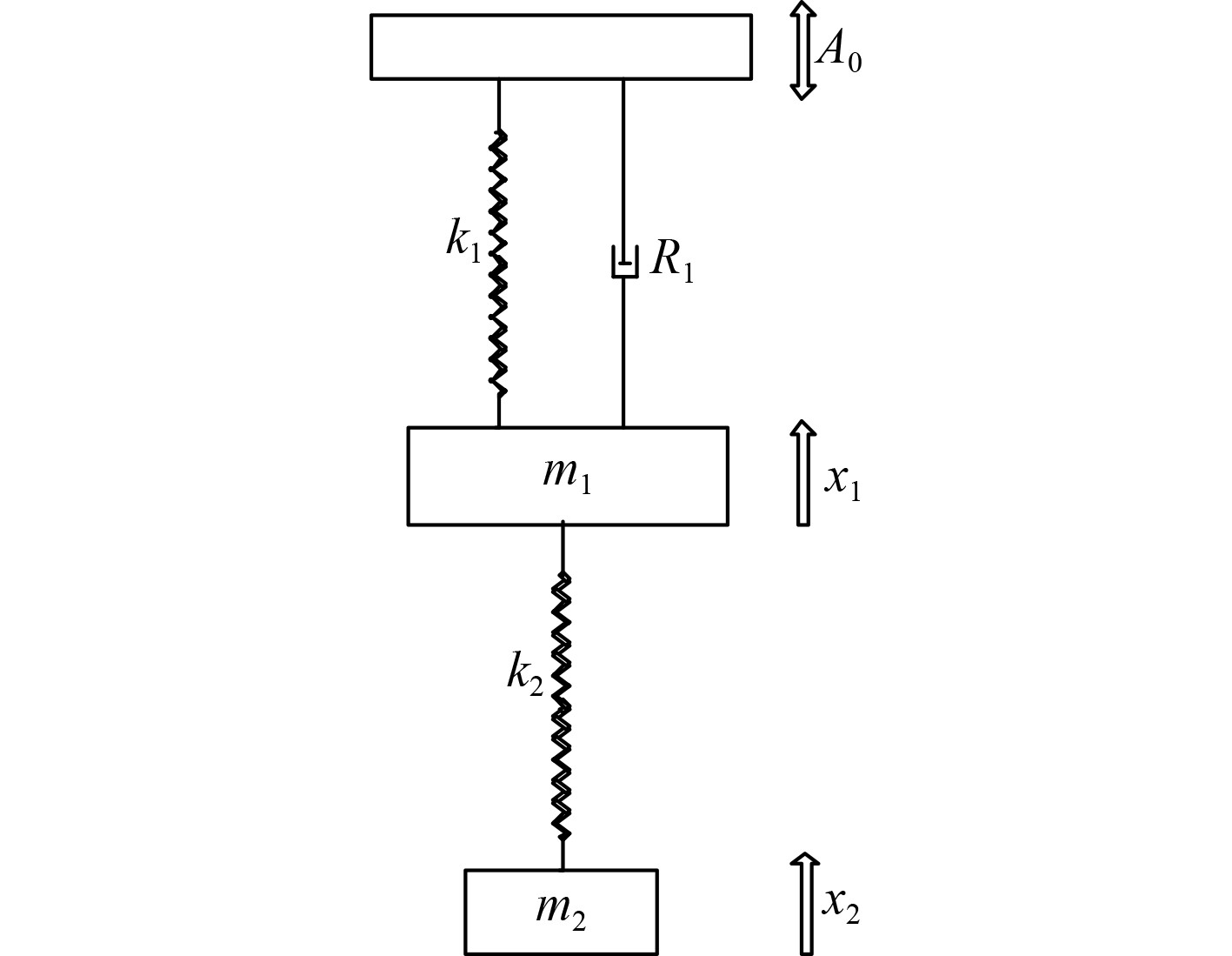
如图2所示， ${A}_{0}$ 为激励位移振幅， ${x}_{1}$ 为阻尼盘的受迫振动位移， ${x}_{2}$ 为水听器的受迫振动位移，该系统为2个自由度的振动系统^[5-6]，运动方程为：

$\begin{aligned}\begin{cases}{m}_{1}\ddot{{x}_{1}}+R\dot{{x}_{1}}+{k}_{1}{x}_{1}+{k}_{2}\left({x}_{1}-{x}_{2}\right)={k}_{1}{{A}}_{0}\mathrm{cos}\mathrm{\omega }{t}，\\ {m}_{2}\ddot{{x}_{2}}+{{k}_{2}x}_{2}-{k}_{2}{x}_{1}=0。\end{cases}\end{aligned}$

(5)

解方程组（5），得到振动系统的稳态位移，其形式为：

$\left\{\begin{array}{c}{{x}_{1}=B}_{1}\mathrm{cos}\left(\omega t+{\varnothing }_{1}\right)={A}_{1}\mathrm{sin}\omega t+{A}_{2}\mathrm{cos}\omega t，\\ {{x}_{2}=B}_{2}\mathrm{cos}\left(\omega t+{\varnothing }_{2}\right)={A}_{3}\mathrm{sin}\omega t+{A}_{4}\mathrm{cos}\omega t。\end{array}\right.$

(6)

式中： ${B}_{1}=\sqrt{{A}_{1}^{2}+{A}_{2}^{2}}$ ， ${B}_{2}=\sqrt{{A}_{3}^{2}+{A}_{4}^{2}}$ ， ${\varnothing }_{1}=-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n} \left({A}_{1}/{A}_{2}\right)$ ， ${\varnothing }_{2}=-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({A}_{3}/{A}_{4}\right)$ 。将式（6）代入方程组（5），对初始条件赋值，得到含 ${A}_{1}$ ， ${A}_{2}$ ， ${A}_{3}$ ， ${A}_{4}$ 的线性方程联立的方程如下：

$\begin{aligned}\begin{cases}\left({k}_{1}+{k}_{2}-{m}_{1}{\omega }^{2}\right){A}_{1}-\omega {c}_{1}{A}_{2}-{k}_{2}{A}_{3}={k}_{1}{A}_{0}，\\ \left({k}_{1}+{k}_{2}-{m}_{1}{\omega }^{2}\right){A}_{2}+\omega {c}_{1}{A}_{1}-{k}_{2}{A}_{4}=0，\\ \left({k}_{2}-{m}_{2}{\omega }^{2}\right){A}_{3}-{k}_{2}{A}_{1}=0，\\ \left({k}_{2}-{m}_{2}{\omega }^{2}\right){A}_{4}-{k}_{2}{A}_{2}=0。\end{cases}\end{aligned}$

(7)

解方程组（7），令 $h=\omega {c}_{1}\left({k}_{2}-{m}_{2}{\omega }^{2}\right)$ ， $e= \Big({k}_{1}+{k}_{2}- {m}_{1}{\omega }^{2} \Big)\left({k}_{2}-{m}_{2}{\omega }^{2}\right)$ ，得到 ${A}_{3}={k}_{1}{k}_{2}h{A}_{0}/[{h}^{2}+{(e-{k}_{2}^{2})}^{2}]$ ， ${A}_{4}={k}_{1}{k}_{2}{A}_{0}(e-{k}_{2}^{2})/[{h}^{2}+{(e-{k}_{2}^{2})}^{2}]$ 。

水听器的振幅 ${B}_{2} = \sqrt{{A}_{3}^{2} + {A}_{4}^{2}} = {k}_{1}{k}_{2}{A}_{0}\bigg/ \sqrt{{h}^{2} + {(e - {k}_{2}^{2})}^{2}}$ ，得到系统的位移振幅传递函数 $T\left(\mathrm{\omega }\right)$ 如下式：

$\begin{aligned} &{T\left(\mathrm{\omega }\right)=\frac{{B}_{2}}{{A}_{0}}=\frac{{k}_{1}{k}_{2}}{\sqrt{{h}^{2}+{(e-{k}_{2}^{2})}^{2}}}=}\\ &{\frac{{k}_{1}{k}_{2}}{\sqrt{{({k}_{2}{R}_{1}\mathrm{\omega }-{m}_{2}{R}_{1}{\omega }^{3})}^{2}+{({k}_{1}{k}_{2}-{m}_{1}{{k}_{2}\omega }^{2}-{m}_{2}{{k}_{1}\omega }^{2}-{m}_{2}{{k}_{2}\omega }^{2}+{m}_{1}{{m}_{2}\omega }^{2})}^{2}}}。}\end{aligned}$

(8)

3 模型分析

减振系统的隔振效果，可以通过传递函数的大小来评价，从传递函数公式（8）来看，位移振幅传递的大小与弹性绳的弹力系数、阻尼盘的阻力系数、阻尼盘质量、水听器质量和激励频率有关。通过对相关参数赋值，可以分析各参数对减振效果的影响。

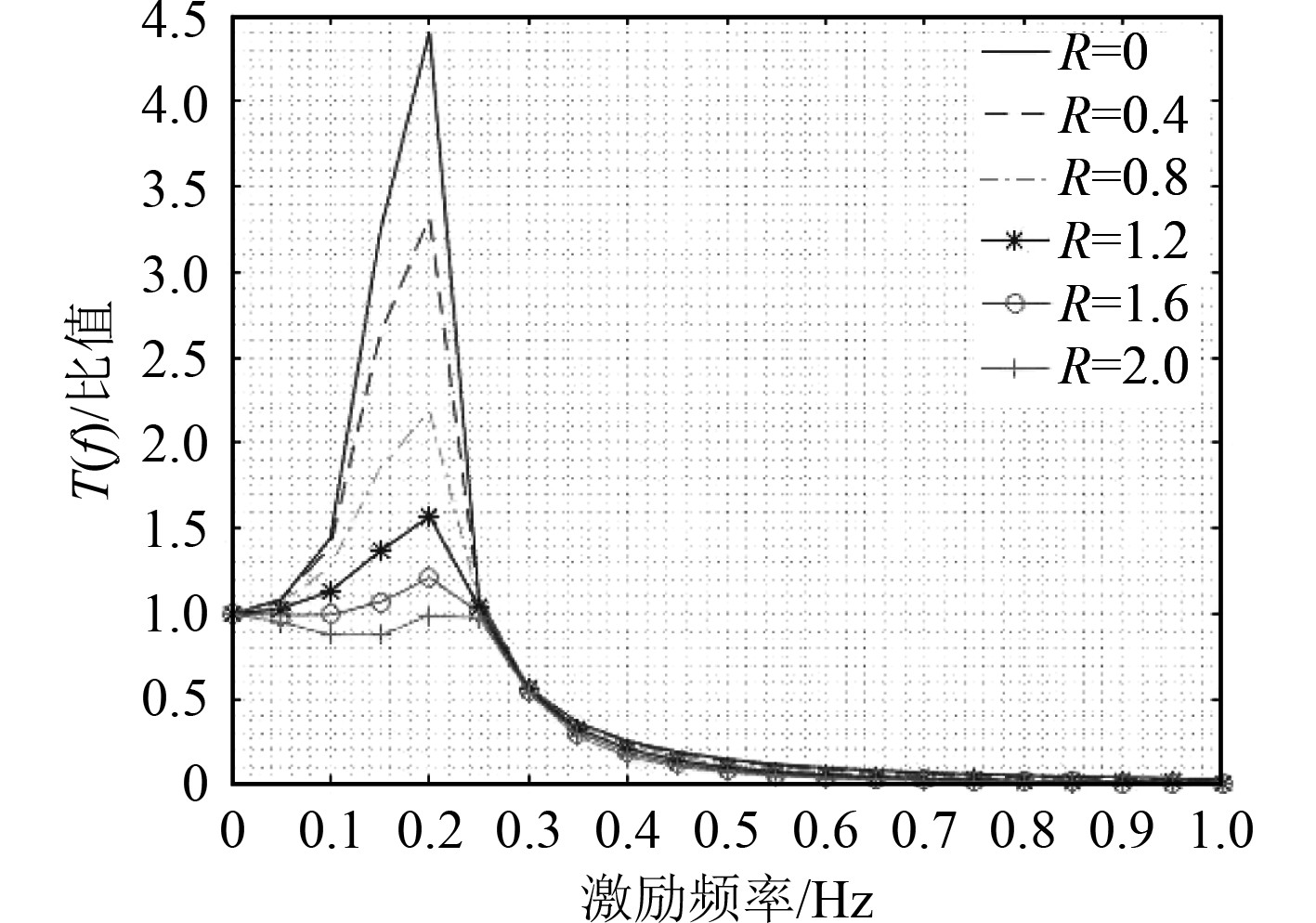
阻尼盘在水下运动时产生的阻力比较复杂，若按照力学运动微分方程认为流体阻力与速度成线性关系。假设水听器的质量为0.4 ${\rm{ kg}}$ ，两段弹性绳的弹力系数都是1.2 ${\rm{N}}/{\rm{m}}$ ，阻尼盘用轻质材料制造，其静态质量较小且变化不大，假设为0.2 ${\rm{kg}}$ 。阻尼盘的阻力系数分别取0，0.4，0.8，1.2，1.6，2等值，并将传递函数转化成激励频率 $f$ 的函数，绘制传递函数 $T\left(f\right)$ 与 $f$ 的关系曲线。从图3可以看出，当阻力系数增大时，传递函数值会减小，说明阻尼盘的阻力系数增大可以显著降低波浪引起的振动幅值。当激励频率远高于固有频率时，传递函数值会快速减小，此时阻尼盘的阻力系数对受迫振动幅值的影响较小。

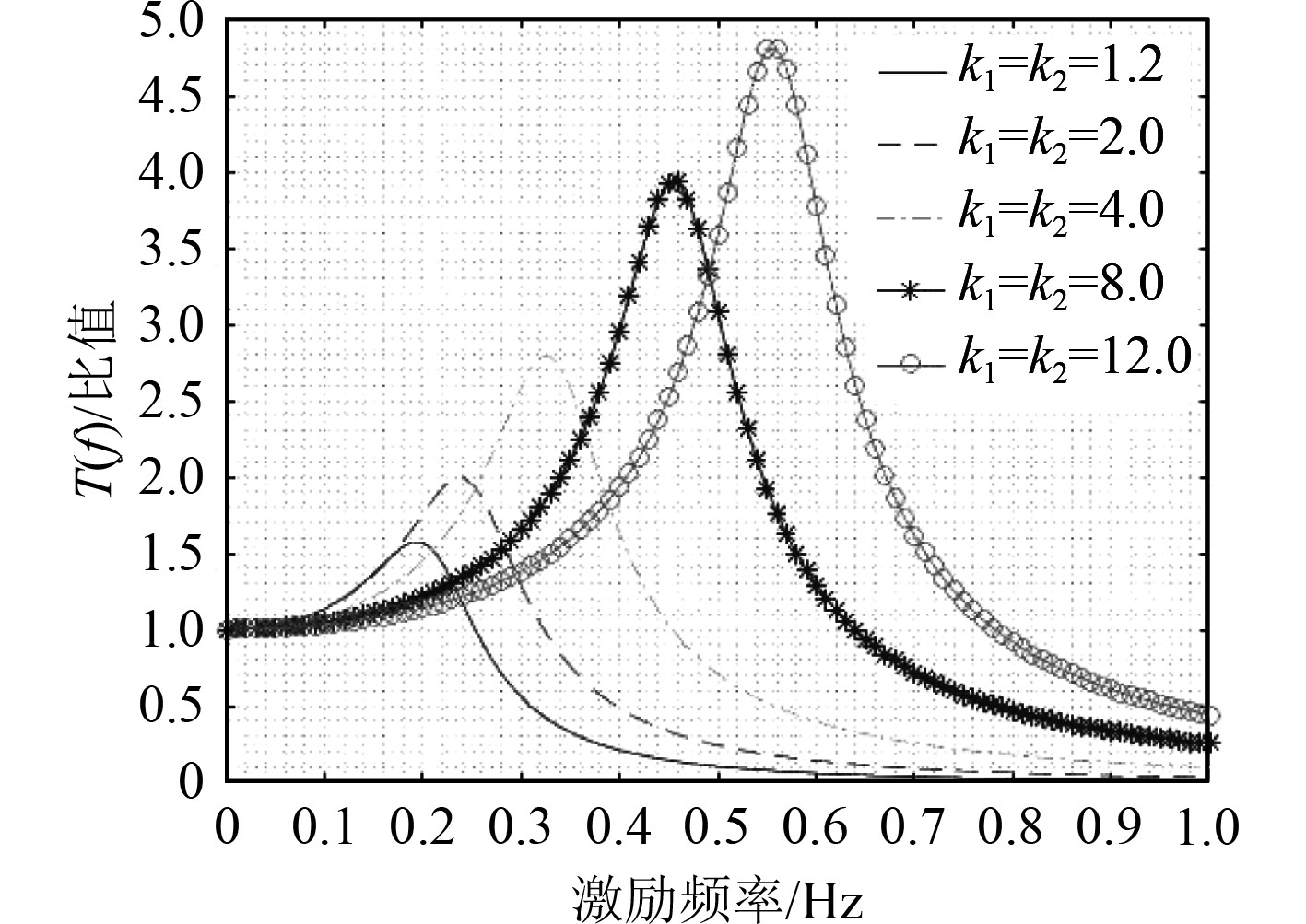
阻尼盘选定后，假设阻尼盘的质量和阻力系数不变，改变弹性绳的弹力系数，设定2段弹性绳的弹力系数相等，依次为1.2 $\mathrm{N}/\mathrm{m}$ ，2 $\mathrm{N}/\mathrm{m}$ ，4 $\mathrm{N}/\mathrm{m}$ ，8 $\mathrm{N}/\mathrm{m}$ ，12 $\mathrm{N}/\mathrm{m}$ ，绘制传递函数 $T\left(f\right)$ 与 $f$ 的关系曲线。从图4可以看出，弹力系数对系统的固有频率改变比较明显，当弹力系数增大时，系统的固有频率增大，同时，传递函数值也增大。说明系统的减振效果随着弹力系数增加而降低。

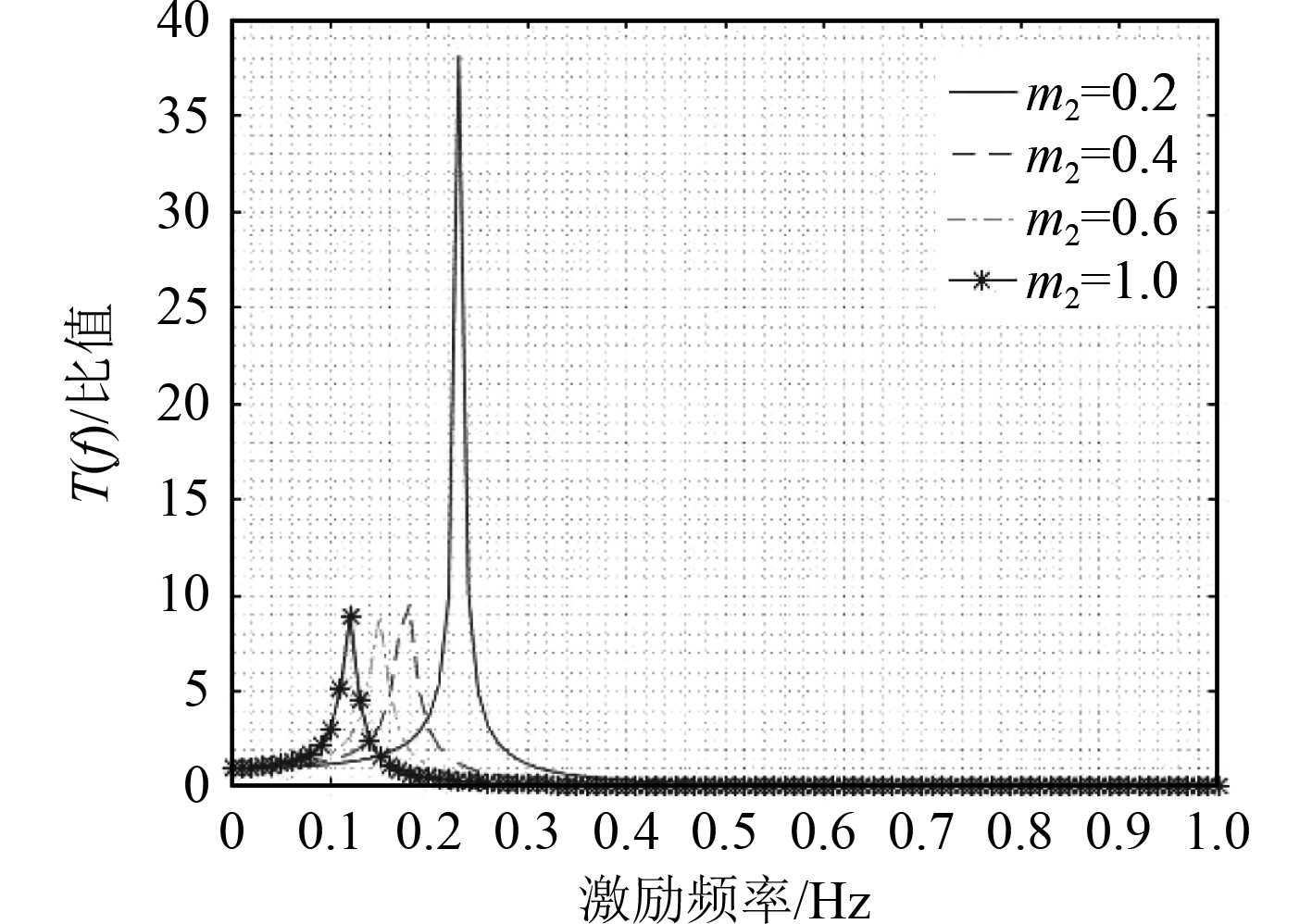
阻尼盘和弹性绳保持不变，选用不同的水听器时，水听器的水下质量依次有0.2 kg，0.4 kg，0.6 kg和1.0 kg，绘制传递函数 $T\left(f\right)$ 与 $f$ 的关系曲线。如图5所示，随着水听器的质量增加，系统固有频率减小。

4 模型拓展

阻尼盘的减振原理主要是由于水下阻力，这种阻力比较复杂。若是按照复杂模型进行分析^[7]，阻尼盘运动时会产生附加质量，将阻尼盘看成直径为 $d$ 的薄圆盘在密度为 $\mathrm{\rho }$ 的流体中运动，阻尼盘的运动阻力与速度并不成线性关系，而是与速度平方成正比。对于近似简谐运动，非线性阻力可以用等效线性阻力来近似表示。忽略阻尼盘静态质量，阻尼盘的附加质量用等效质量表示，等效质量与阻尼盘的振幅 $A$ 有关；等效线性阻力系数与振幅 $A$ 和激励频率 $\omega$ 有关^[8]。简谐运动时的等效质量 ${m}_{e}$ 和等效阻力系数 ${R}_{e}$ 为：

${m}_{e}=\frac{6}{5}\mathrm{\rho }{d}^{5/2}{A}^{1/2}，$

(9)

${R}_{e}=\frac{11}{15}\rho \omega {d}^{5/2}{A}^{1/2}。$

(10)

水听器在水中质量较小，与阻尼盘的附加质量相比可以忽略，将水听器工作点移到阻尼盘的位置，减振系统模型简化成单自由度有阻尼受迫振动，着重研究阻尼盘的振动状态。

将系统的位移振幅传递函数公式（8）进行简化，消掉 ${k}_{2}$ 和 ${m}_{2}$ ，得到简化表达式：

$T\left(\mathrm{\omega }\right)=\frac{{k}_{1}}{\sqrt{{（\mathrm{\omega }{R}_{e}）}^{2}+{({k}_{1}-{m}_{e}{\omega }^{2})}^{2}}} 。$

(11)

化简后的式（11）与力学原理中的式（4）等同，令 $M=1.2\rho {d}^{5/2}{A}_{0}^{1/2}$ ，称为参考质量，则 ${m}_{e}= M {\left|T\left(\mathrm{\omega }\right)\right|}^{1/2}$ 。另外 ${\omega }_{e}=\sqrt{{k}_{1}/{m}_{e}}$ ， ${\varOmega }_{0}=\sqrt{{k}_{1}/M}$ ，进一步化简得到：

$T\left(\mathrm{\omega }\right)=\frac{1}{\sqrt{{0.3734\left(\mathrm{\omega }/{\omega }_{e}\right)}^{4}+{[1-{\left(\omega /{\omega }_{e}\right)}^{2}]}^{2}}}，$

(12)

当系统共振时，传递函数值最大，可以推导出系统的共振频率为：

${f}_{r}=\frac{\omega }{2\text{π} }=\frac{0.88{\varOmega }_{0}}{2\text{π} }=\frac{11}{25\text{π} }\sqrt{\frac{{k}_{1}}{1.2\rho {d}^{5/2}{A}_{0}^{1/2}}}。$

(13)

若是按照复杂模型分析减振系统，考虑阻尼盘的附加质量和非线性阻力。从式（13）可以看出系统的共振频率随弹力系数增大而增大，随阻尼盘的直径增大而减小。

5 弹性绳的弹力系数分析

弹性绳采用橡胶材料制成，当拉伸力变化较大时，变形量与拉伸力并不完全成线性关系。在材质均匀的条件下，选取不同长度的测量试样，在相同的拉伸力作用下，试样的伸长率几乎相同。设弹性绳的自然长度为 ${L}_{0}$ ，伸长率为 $\mathrm{\epsilon }$ ，受到拉伸力为 $F$ ，弹力系数为 $\tau$ ，在单个受力点伸长量与拉伸力成正比，满足下式：

$\tau =\frac{F}{\epsilon {L}_{0}}。$

(14)

选取直径为3.5 mm和2.5 mm两种规格的弹性绳，分别裁取0.5 m，1 m，2 m和4 m的试样进行拉伸试验，试验数据代入式（14）进行处理，求出各组的弹力系数，再绘制曲线。

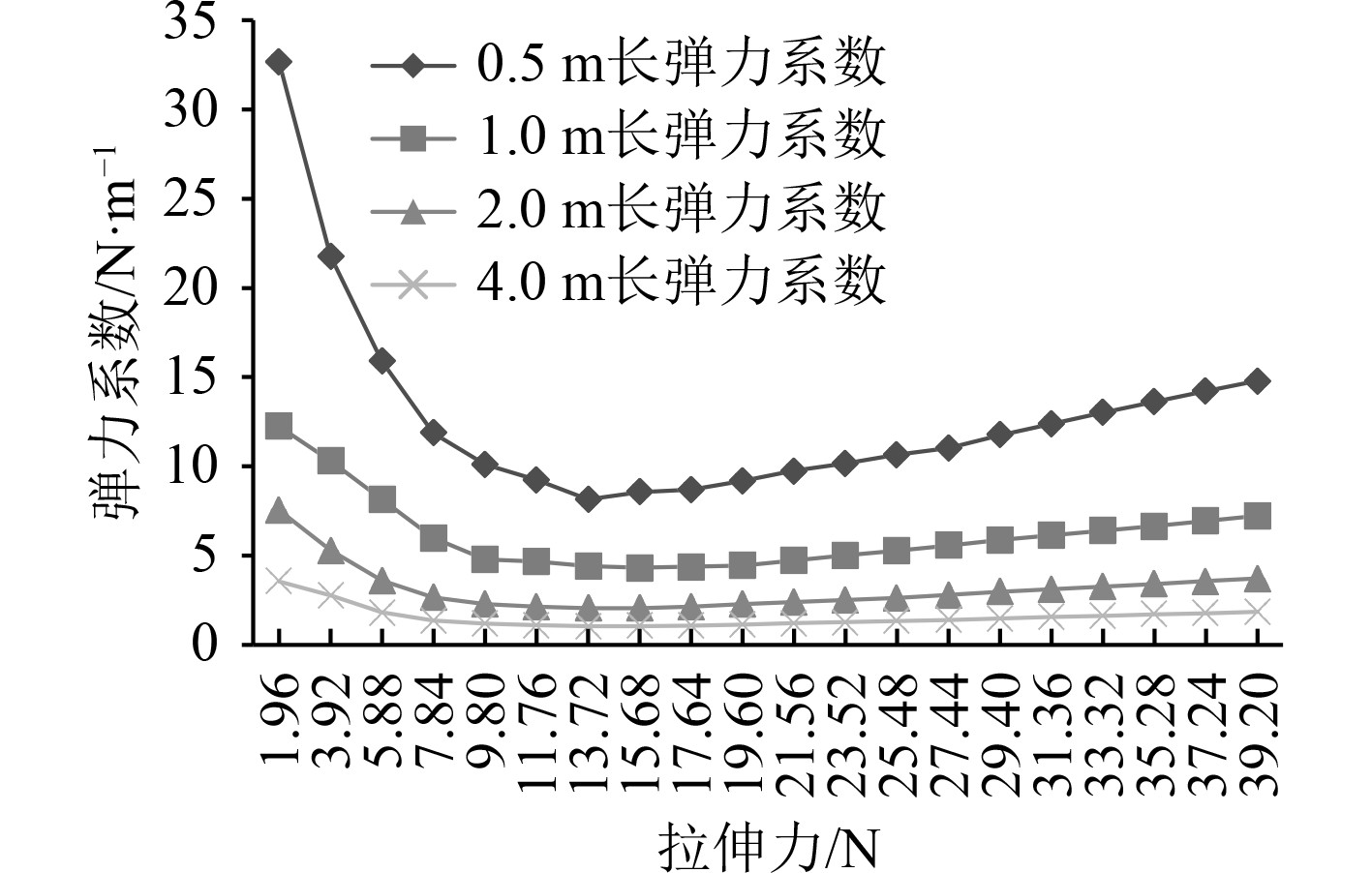
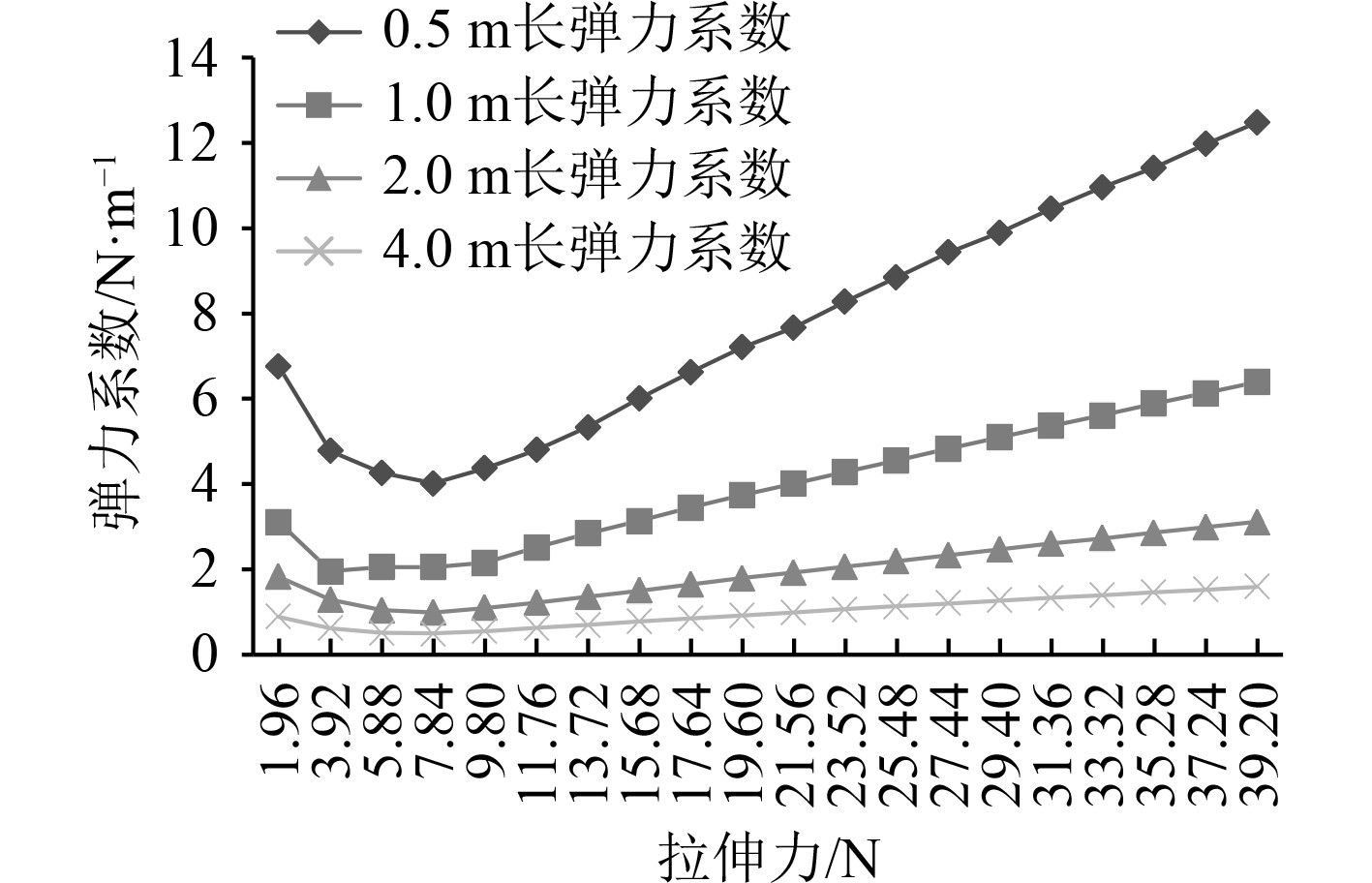
如图6和图7所示，同一规格的弹性绳，弹力系数随自然长度和拉伸力变化，自然长度越大，相同拉伸力作用下弹力系数越小；同一根弹性绳不同拉伸力作用下，弹力系数并不恒定，当拉伸力从零逐渐增大时，弹力系数先减小再逐渐增大；同一规格的弹性绳，自然长度越长，弹力系数随拉伸力减小或增大的幅度越平缓。不同规格的弹性绳，相同的自然长度，相同的拉伸力作用下，直径越大的弹性绳，弹力系数越大。

6 结　语

根据浮标的漂浮状态，设计水下减振系统，该系统主要由弹性绳和阻尼盘组成。本文建立水下减振系统的受迫振动模型，衡量减振效果的标准是位移传递函数，该传递函数等于受迫振动位移振幅与激励位移振幅的比值。为了便于工程化研究，忽略阻尼盘的附加质量，假设阻尼盘的阻力与振速成线性关系，建立2个自由度受迫振动模型。通过求解微分方程推导出了传递函数公式，分析影响传递函数大小的因素有弹性绳的弹力系数、阻尼盘的阻力系数、阻尼盘质量、水听器质量和激励频率等参数。假设阻尼盘的阻力系数变化，其他参数恒定，可以看出阻力系数增加会显著降低振动幅值；假设阻尼盘不变，只改变弹性绳的弹力系数，弹力系数对系统的固有频率改变比较明显，当弹力系数增大时，系统的固有频率和振动幅值都增大；假设阻尼盘和弹性绳保持不变，只增加水听器的质量，发现系统固有频率随着水听器质量增加而减小。为了更全面地分析减振系统，对模型进行拓展，介绍了考虑阻尼盘附加质量和非线性阻力时系统的共振频率。针对显著影响减振效果的弹性绳，重点分析了弹力系数变化情况，弹性绳的弹力与其伸长量并非严格地呈线性关系，弹性绳在拉伸过程中内部结构受到破坏，不能保持原有的弹力系数；通过对不同规格和不同长度的弹性绳测试试验，发现同一规格弹性绳，自然长度越长，弹力系数越小，不同规格弹性绳，直径越大，弹力系数越大。根据航空声呐浮标水下减振系统的研究结论，可以对一套水下减振系统进行定性评价。该研究方法，对设计新的水下减振系统具有借鉴意义。