为了提高现代船舶的综合性能以及在船舶市场上的竞争力,需要在船舶设计制造过程中以先进的技术、较低的经济成本为目标,不断地引进先进的船舶设计制造技术并消化吸收再创新。作为船舶的重要系统之一,船舶主机冷却水系统的任务是确保船舶动力系统能够正常工作,为了提升船舶主机冷却水系统的工作效率,减少船舶在航行过程中的维护成本,需要优化船舶上主机的水冷系统。船舶主机水冷系统中水的温度对船舶主机及其相关机械系统的运行效率有很大影响,为了更好地控制船舶缸套冷却水的出水温度,需要对船舶主机水冷系统的温度控制算法进行研究。现代仿真技术可以通过计算机进行大量的仿真实验,以替代需要消耗大量资金的实物实验,甚至可以完成现实当中由于各种条件限制而无法进行的实验,因此基于计算机的仿真实验测试具有低风险、成本低、效益高、周期短以及可多次实验等显著的特点,被广泛地应用于船舶设计制造的各个方面,推动了船舶技术的快速发展。本文基于计算机仿真技术,对船舶主机温度控制方法进行研究,有助于推动船舶主机技术的发展。
1 船舶主机数学模型的构建 1.1 船舶主机燃烧放热率数学模型船舶主机的燃烧模型是船舶主机建模仿真的重要内容之一,船舶主机燃烧模型的精确程度对船舶主机整体仿真的精度有着重要影响。基于半经验公式韦伯函数构建出的船舶主机燃烧放热率的数学模型,其相关参数可以通过实测示功图获得。船舶主机在燃烧的时候释放出来的热量Qf大部分用于增加船舶主机缸内气体的内能∆U以及对外部做功W,同时会有少量的热量Qw通过缸壁散热出去,船舶主机燃烧的瞬时方程为:
| $ {Q_f} = \Delta U + W + {Q_W}\text{。} $ | (1) |
基于式(1)对曲轴转角φ进行微分运算,则可以获得船舶主机在单位角度内产生的热量,如下式:
| $ \frac{{{\rm{d}}{Q_f}}}{{{\rm{d}}\varphi }} = \frac{{{\rm{d}}U}}{{{\rm{d}}\varphi }} + {p_z}\frac{{{\rm{d}}{V_z}}}{{{\rm{d}}\varphi }} + \frac{{{\rm{d}}{Q_W}}}{{{\rm{d}}\varphi }} = {H_u} \cdot {g_f} \cdot \frac{{{\rm{d}}X}}{{{\rm{d}}\varphi }}\text{。} $ | (2) |
通过式(2),则可以获得船舶主机缸内气体对外做的瞬时功率,如下式:
| $ \frac{{{\rm{d}}W}}{{{\rm{d}}\varphi }} = {p_z}\frac{{{\rm{d}}{V_z}}}{{{\rm{d}}\varphi }}\text{。} $ | (3) |
当采用计算机进行数值解算的时候,则可以将dU/dφ替换成∆U/∆φ,并且当∆φ设置成1o的时候,dU/dφ则约等于∆U,则可以获得下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta U = {m_{z\left( {i + 1} \right)}}{c_{m\left( {i + 1} \right)}}{T_{z\left( {i + 1} \right)}} - {m_{z\left( i \right)}}{c_{m\left( i \right)}}{T_{z\left( i \right)}}},\\ {{m_z} = {m_a} + {g_f}X} 。\end{array}} \right. $ | (4) |
本文基于三韦伯函数来模拟船舶主机的燃烧放热率。第一段曲线为预混合燃烧;第二段曲线为扩散燃烧;第三段曲线为后燃烧,如公式(5)所示,仿真结果如图1所示。
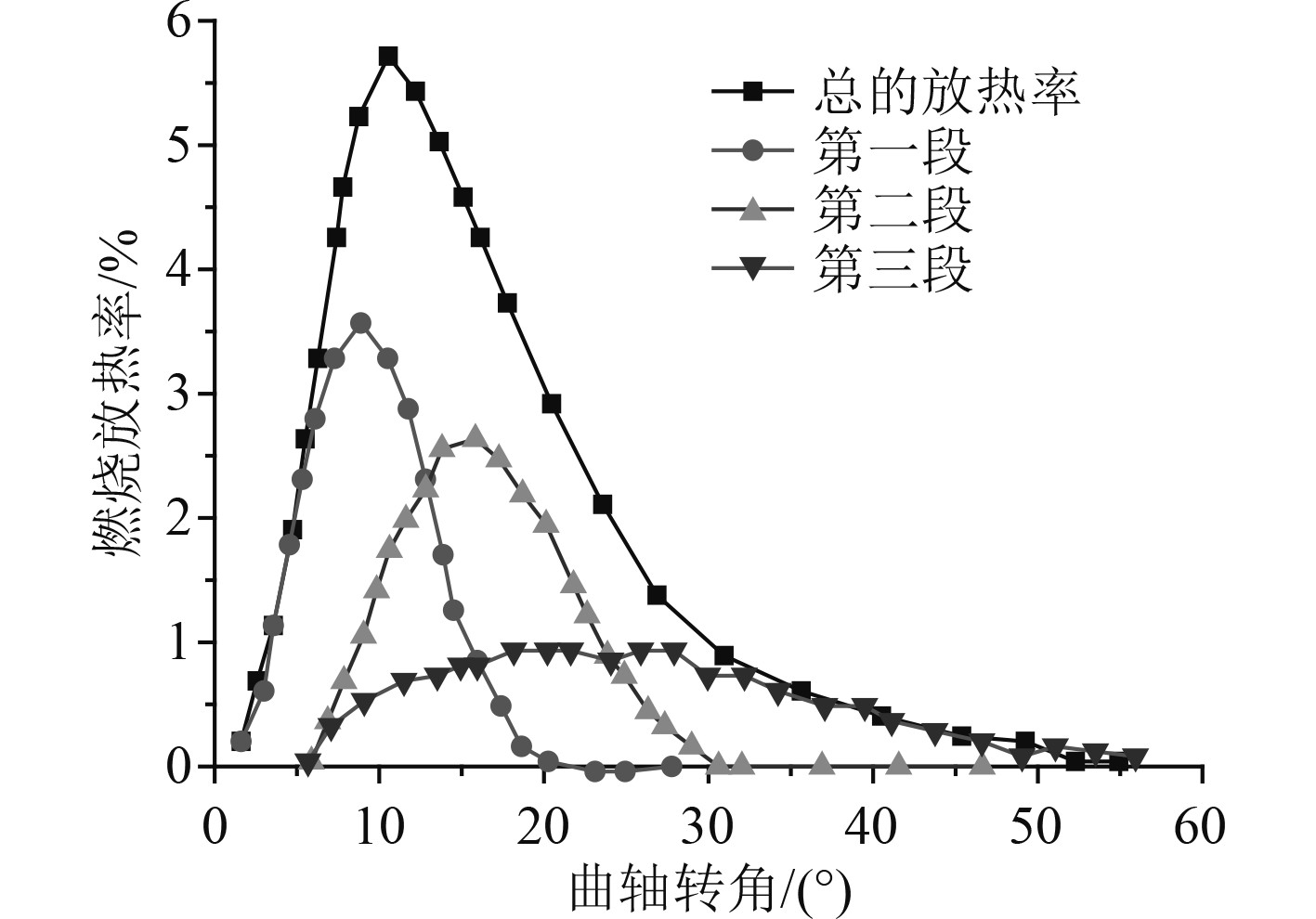
|
图 1 船舶主机燃烧率随曲轴转角的变化曲线 Fig. 1 Curve of combustion rate of marine main engine changing with crankshaft angle |
| $ \frac{{{\rm{d}}X}}{{{\rm{d}}\varphi }} = \frac{{{\rm{d}}{X_1}}}{{{\rm{d}}\varphi }} + \frac{{{\rm{d}}{X_2}}}{{{\rm{d}}\varphi }} + \frac{{{\rm{d}}{X_3}}}{{{\rm{d}}\varphi }}\text{。} $ | (5) |
船舶上装载的燃油也会占用船舶一定的排水量,并且船舶上的燃料油决定了船舶在海面上的续航能力,计算式为:
| $ L = vt\text{,} $ | (6) |
式中:L为船舶的续航能力;v为船舶的航行速度;t为船舶在水面上的航行时间。假设船舶上的总的燃油量为∑m,并且船舶在航行过程中主机的耗油率为B,则船舶主机在航行过程中持续工作时间的计算公式为:
| $ t = \frac{{\sum {m \times {{10}^3}} }}{B}\text{。} $ | (7) |
船舶主机单位时间内的耗油量可以用式(8)表示,船舶在海面上的续航能力可以用式(9)计算。
| $ B = g \cdot p\text{,} $ | (8) |
| $ L = \frac{{v\sum {m \times {{10}^3}} }}{{g \cdot p}}\text{。} $ | (9) |
假设船舶上的总的燃油量∑m以及船舶主机燃油消耗率g恒定,则在船舶航行速度分别为v0以及v1两种航行速度下,船舶的航行速度和船舶的续航能力之间的关系可以表示为
| $ {L_1} = \frac{{{P_0}}}{{{P_1}}} \cdot \frac{{{v_1}}}{{{v_0}}} \cdot {L_0}\text{。} $ | (10) |
式中:L0,L1以及P0,P1分别为船舶在2种速度下的续航能力以及主机功率。通过式(11)可以将式(10)表示成式(12)。
| $ p = c{v^3}\text{,} $ | (11) |
| $ {L_1} = {\left( {\frac{{{v_0}}}{{{v_1}}}} \right)^2} \cdot {L_0}\text{。} $ | (12) |
可以看出,船舶在海面上航行过程中,船舶的续航能力和船舶航行速度的平方成反比例关系。假设需要保证船舶的续航能力L维持不变,则可以计算出在速度v1>v2情况下的船舶所需燃油储备量,即
| $ \sum {{m_1} = {{\left( {\frac{{{v_1}}}{{{v_0}}}} \right)}^2} \cdot \sum {{m_0}} } \text{。} $ | (13) |
可以看出,船舶携带的燃料油和船舶在海面上的速度的平方成正比,因此假如需要将船舶的速度提升20%,则需要将船舶的燃油储备量提升44%。船舶燃油消耗率的变化量和船舶主机有效功率之间的关系如图2所示。
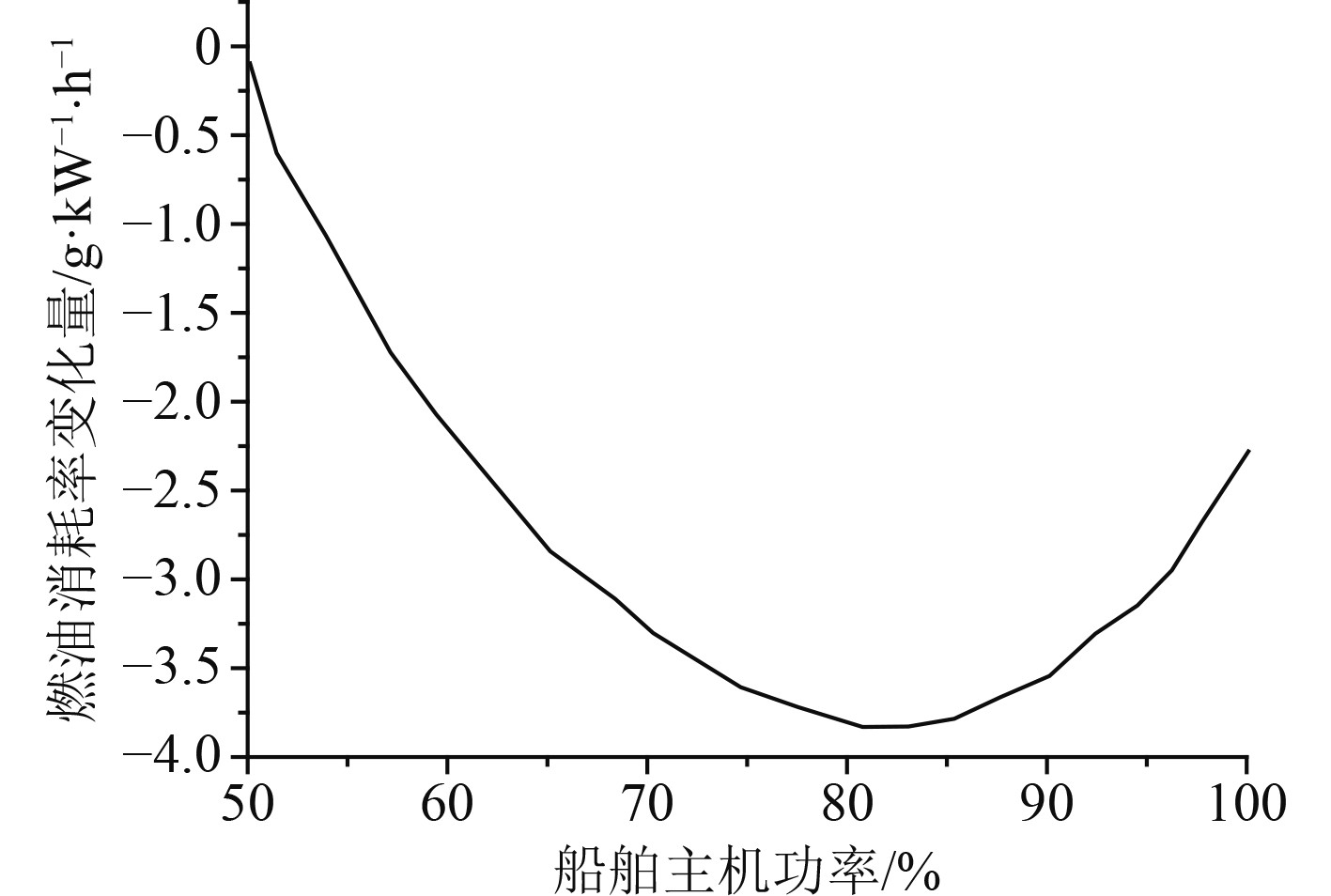
|
图 2 船舶主机燃油消耗率的变化量和主机功率之间的关系 Fig. 2 Relationship between variation of fuel consumption rate of marine main engine and power of marine main engine |
船舶主机水冷系统结构如图3所示,由于船舶主机水冷系统是闭式循环系统,在工作过程中水冷系统中的冷却水总量基本保持不变,船舶主机水冷系统中的高温热水均利用高温水泵实现循环利用。为了降低构建船舶水冷系统热力学模型的难度,需要对冷却系统进行部分优化,假定船舶主机水冷系统中的总水量不变,同时忽略水管的膨胀以及散热,并且只将主要的换热设备纳入考虑范围。

|
图 3 船舶主机水冷系统结构 Fig. 3 Structure of marine main engine water cooling system |
从热量平衡理论可以得到,单位时间内船舶主机燃烧提供给缸套的热能减去单位时间内冷却水吸收掉的热能,则等于单位时间内缸套中的冷却水的蓄热量,如下式:
| $ {W_D}\frac{{{\rm{d}}{t_{hi}}}}{{{\rm{d}}\tau }} = {Q_{{\rm{in}}}} - {Q_{{\rm{out}}}} = Q\left( t \right) - {m_h}{C_w}\left( {{t_{hi}} - {t_{di}}} \right)\text{。} $ | (14) |
式中,WD为缸套中总的蓄热量,计算公式为:
| $ {W_D} = {M_w}{C_w} + {M_c}{C_c}\text{。} $ | (15) |
船舶主机在工作过程中,缸套内部的温度在不断地波动,很难找到一个精确的数学表达式来描述这种情况下的热量变化,因此可以假定船舶上的冷却水恒定带走固定比例的热量,则冷却水吸收的热量为:
| $ Q\left( t \right) = \frac{{f \cdot P \cdot {b_e} \cdot \xi }}{{3600}}\text{。} $ | (16) |
结合式(14)和式(16),则船舶主机缸套的热力学模型为:
| $ \frac{{{\rm{d}}{t_{hi}}}}{{{\rm{d}}\tau }} = - \frac{{{m_h}{C_w}}}{{{W_D}}}{t_{hi}} + \frac{{{m_h}{C_w}}}{{{W_D}}}{t_{di}} + \frac{{f \cdot P \cdot {b_e} \cdot \xi }}{{3600{W_D}}}\text{。} $ | (17) |
船舶主机水冷系统中造水机中高温水的流量解算公式为:
| $ {m_z} = \frac{{K \cdot M}}{{\Delta T}}\text{。} $ | (18) |
式中:单级造水机的K值等于25.6;M为单日的造水量;∆T为进出口水温差。假定船舶水冷系统中的造水机的造水量为每天16 t,则通过式(18)可以得到造水机的热力学模型,具体为:
| $ {t_{zo}} = {t_{hi}} - 25.6 \times \frac{{16}}{{{m_z}}}\text{,} $ | (19) |
| $ {m_z} = \left( {1 - {x_z}} \right){m_h}\text{,} $ | (20) |
| $ {t_{hoi}} = {x_z}{t_{hi}} + \left( {1 - {x_z}} \right){t_{zo}}\text{。} $ | (21) |
船舶主机主要依靠船舶上的缸套冷却水回路进行降温控制。当船舶上的缸套冷却水的出水温度比较高时,则会加剧缸壁的磨损、降低相关零件的强度以及产生输出功率降低等问题;当船舶上的缸套冷却水的出水温度太低的时候,则会导致机械磨损并且增加热损失,使得船舶主机热应力变大,缸壁上会凝结出水珠。因此为了确保船舶主机在高温以及摩擦作用下依旧能够正常工作,则需要对船舶缸套中的冷却水的出水温度进行优化控制。
PID算法在实现过程中不需要构造精确的数学模型,因此简单易懂,是最早在工业控制中得到大规模应用的控制器。PID控制器的输入和输出之间的数学关系为:
| $ u\left( t \right) = {K_p}\left[ {e\left( t \right) + \frac{1}{{{T_i}}}\int {e\left( t \right){\rm{d}}t + {T_d}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}}} } \right]\text{。} $ | (22) |
式中:e(t)为PID算法的输入量,其计算式为:
| $ e\left( t \right) = {y_{set}}\left( t \right) - y\left( t \right)\text{。} $ | (23) |
在整个控制过程中,PID控制器中的比例单元作为最基本的分量一直起作用,积分单元在一开始的时候作用不明显,但是随着时间的积累,其作用不断增强,微分单元在PID控制器中的作用和积分单元相反,一开始作用比较强,随着时间的推移,其作用不断减弱。
为了确保船舶主机能够正常工作,则需要将船舶上缸套冷却水的出水温度tco控制在85℃。假设三通温控阀的开度用x0表示,一旦温度传感器测出缸套冷却水的出水温度tco超过85℃,则需要将三通温控阀的开度进行扩大,以便能够提高流过冷却器的高温水的流量,最终可以降低船舶上缸套冷却水的流入温度tci,从而实现调节出水温度tco的目的。一旦出水温度tco低于预设的数值85℃的时候,则需要降低三通控温阀的开度,以提升缸套水冷却器的旁通流量。使用PID控制器的时候,三通温控阀的开度调节算法可以表示为:
| $ d{x_s}\left( t \right) = {K_p}e\left( t \right) + {K_I}\int {e\left( t \right){\rm{d}}t + {K_D}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}}} \text{。} $ | (24) |
式中:KI为P控制算法的积分参数,计算公式如式(25)所示;KD为控制算法的微分参数,计算公式如式(26)所示。调节之后的阀门开度可以用式(27)表示。
| $ {K_I} = \frac{{{K_p}}}{{{T_i}}}\text{,} $ | (25) |
| $ {K_D} = {K_p} \times {T_d}\text{,} $ | (26) |
| $ {x_s} = {x_0} + d{x_s}\left( t \right)\text{。} $ | (27) |
获得PID控制器的数学模型之后,则可以在simulink中构建出PID算法,并进行仿真。在对缸套冷却系统进行PID控制仿真之前,通过临界比例度法确定控制算法的微分、比例以及积分3个参数的数据值,并且最终Kp,Ki,Kd这3个参数的数值分别采用0.2024、0.002141以及2.2512。在仿真过程中,配置采样时间为1 s,系统的仿真时间为1000 s,船舶上缸套水冷却系统的出水温度初始数值为80℃,目标值为85℃,最后运行仿真系统模块并获得缸套出水温度随时间的变化曲线,如图4所示。可以看出,PID控制器最终可以将缸套水冷却器的出水温度控制在85℃。
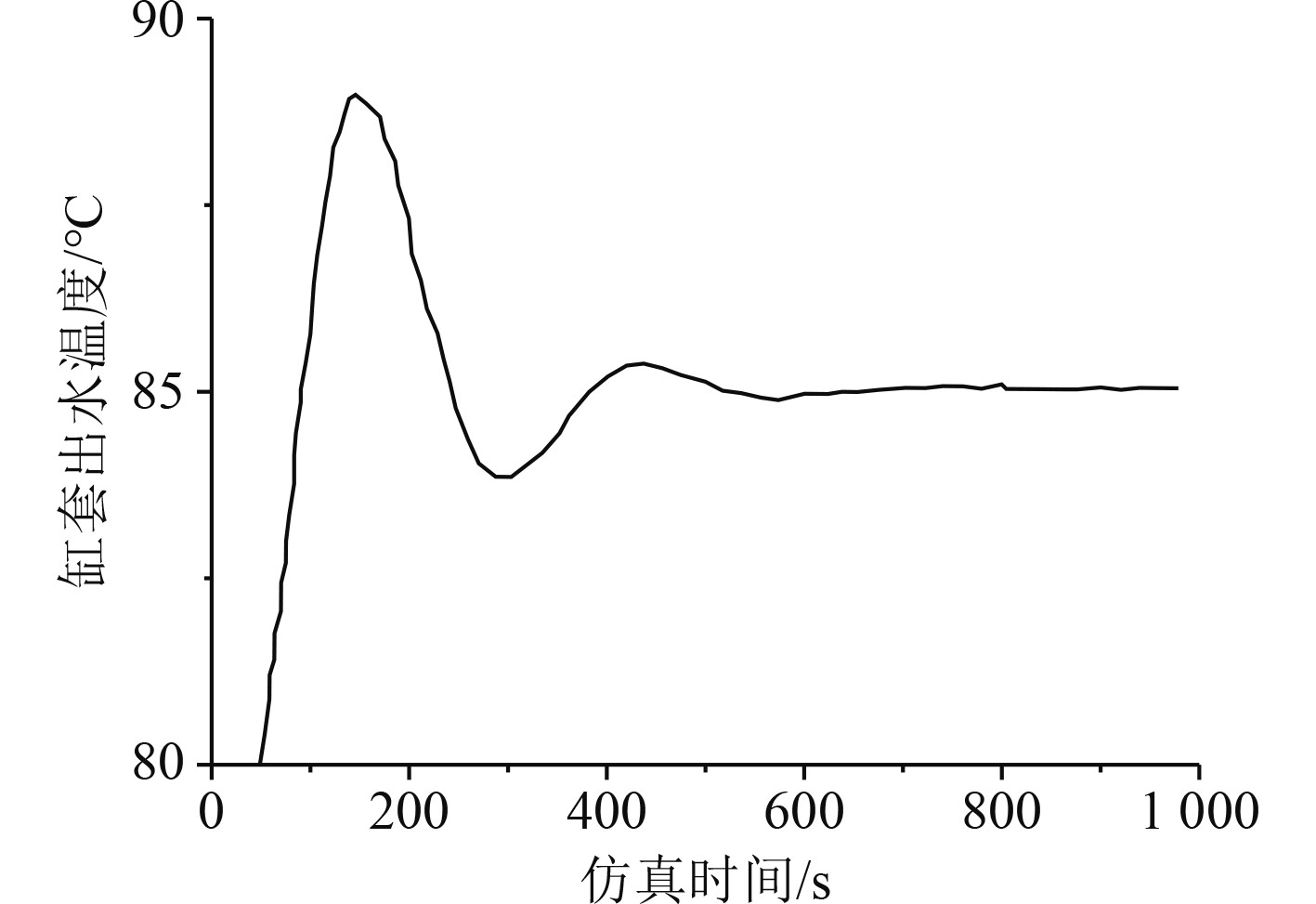
|
图 4 缸套出水温度控制曲线 Fig. 4 Cylinder liner outlet water temperature control curve |
船舶主机冷却水系统利用冷却水的不断循环将船舶主机在工作过程中产生的热能带走,通过这种方法防止船舶主机由于集聚了大量的热量而出现金属疲劳失效现象,因此船舶主机冷却水系统的工作情况对船舶主机的性能有着直接影响,这就需要对船舶主机冷却水系统的控制进行优化,以实现对船舶主机温度更好的控制,最终提升船舶主机的工作性能。本文基于计算机仿真技术,对船舶主机的温度控制方法进行研究,提升了船舶主机的温度控制技术。
| [1] |
何一文, 李珍. 船舶主机温度控制方法优化[J]. 舰船科学技术, 2018, 40(14): 85-87. |
| [2] |
夏洪永. 船舶主机冷却水出口温度控制系统[J]. 舰船科学技术, 2018, 40(12): 121-123. |
| [3] |
屈宽生, 李明哲. 基于计算机模糊神经网络的船舶主机温度控制与仿真[J]. 舰船科学技术, 2020, 40(20): 82-84. |
| [4] |
王永祥, 徐东华, 李春香, 等. 船舶中央冷却水系统变频水泵流量特征[J]. 船舶工程, 2020, 42(3): 74-79+92. |
| [5] |
徐红明, 陈逸宁. 船舶柴油机缸套冷却水系统动态特性建模与仿真[J]. 船海工程, 2010, 39(2): 82-85. DOI:10.3963/j.issn.1671-7953.2010.02.0023 |
| [6] |
马量, 韩雪峰, 张均东, 等. 船舶主机缸套冷却水温度前馈-反馈控制的研究[J]. 船舶工程, 2009, 31(4): 20-23. DOI:10.3969/j.issn.1000-6982.2009.04.006 |
| [7] |
吴桂涛, 尹自斌, 孙培廷. 主机套缸冷却水出口温度控制方法[J]. 交通运输工程学报, 2003(4): 35-38. |
| [8] |
李海峰, 赵殿礼, 张春来. 船舶主柴油机缸套冷却水温度智能控制[J]. 大连海事大学学报, 2007(S1): 77-80. DOI:10.3969/j.issn.1006-7736.2007.z1.023 |
 2022, Vol. 44
2022, Vol. 44
