2. 龙岩学院,福建 龙岩 364012
2. Longyan University, Longyan 364012, China
电力和机械能源的转化,电动机在电力使用方面效果显著。因而,高效节能、环保的永磁同步电动机正日益成为工业界的研究热点。高性能的固态转子高压永磁同步电机是一种新型的高效率能源转化设备,在国家中长期科学发展计划的框架中。近年来,由于永磁材料的工艺水平不断提高,其性能不断改善,其核心技术也在不断发展。尤其是其中的高性能固体转子式高压永磁同步电机的研制,将会极大地推动社会变革,为企业的高能耗发展提供一个关键性变革[1-3]。
从现有资料分析可知,永磁材料的性能直接关系到高性能自启动永磁同步电机的性能。由于温度对永磁材料的特性有较大的影响,所以对其温度场进行细致的分析有一定意义。由于大中型电动机通风系统的结构比较复杂,转子系统的转动对其内部的流场产生了不可忽略的影响,从而使发动机气隙、各通风沟及末端的气流状况变得更为复杂。内燃机的温度场分布不仅取决于各个部件的热源损耗,而且还与其散热性能有很大关系[4-5]。
1 永磁同步电动机的基本结构永磁电动机有2种类型:第一种是无刷直流电动机(BLDC),该电动机由方波电流供电,主要缺点是转矩高。因此,这种类型的发动机主要用于性能要求相对较低时。第二类是永磁同步电动机,与非相机直流电动机相比,不同之处在于它是由正弦波驱动而且可以克服基于非接触式直流电动机。管理系统故障提供了永磁同步电动机的全部优势,因此永磁同步电动机被广泛使用并逐渐成为各个领域中使用的主要发动机功率。
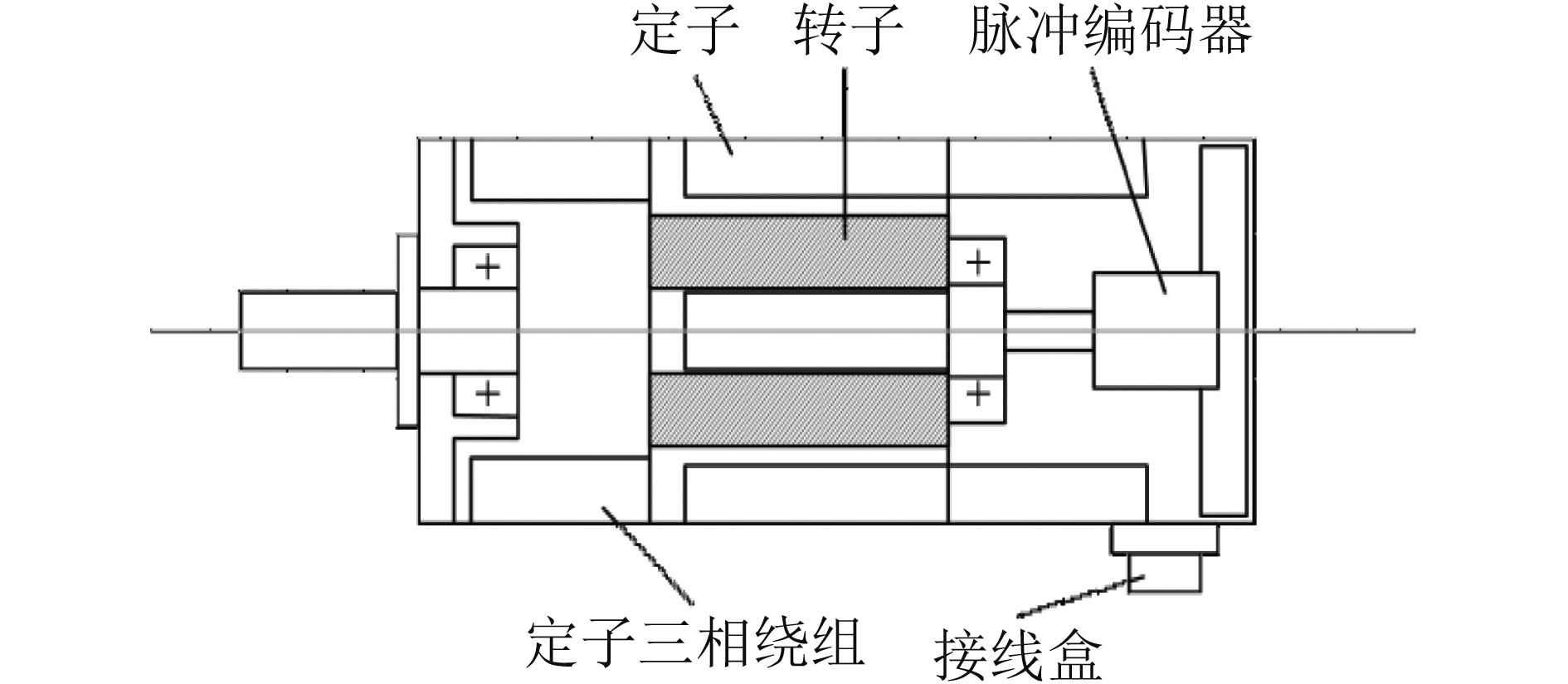
永磁交流同步电动机结构图如图1所示,永磁体位于电动机的转子部分。在电动机的尾部通常是编码器,其与转子相连接,与转子进行同步转动。
|
图 1 永磁交流同步电动机结构图 Fig. 1 Permanent magnet AC synchronous motor structure diagram |
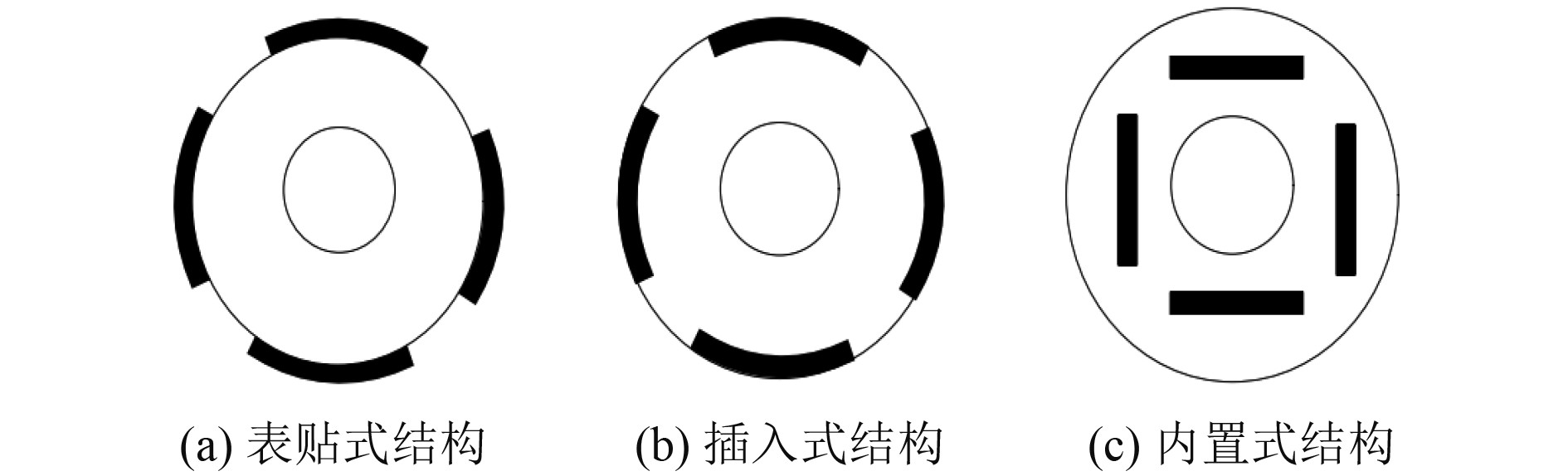
由图1可知,电动机的永磁体位于转子部分中,因此流量连接可视为恒定值。编码器通常安装在发动机的尾部,与转子连接,并与转子一起旋转,永磁同步电动机根据转子结构分类,可分为表贴式、插入式和内置式3种类型,安装在表面上的永磁同步电动机转子结构如图2所示。可知,黑色部分为永磁体部分。图2为当黑色部分是永磁体的一部分时3种不同发动机配置的横截面。
|
图 2 永磁同步电动机转子结构图 Fig. 2 Permanent magnet synchronous motor rotor structure diagram |
图2(a)为该结构的永磁同步电动机制造工艺相对简单,总输入成本低于其他发动机结构,该结构可以促进系统设计,通常用于具有宽范围旋转速度的正弦永磁同步电动机和BLDC。图2(b)中的结构在运行过程中可以增强转子磁路的不对称性,从而提升永磁同步电动机的功率密度以及动态响应。由此可见,安装在表面上的永磁同步电动机适用于正弦的速度控制。图2(c)内置的永磁同步电动机则与前2种结构不同,其工作原理是安装在转子中的永磁体,通过借助电动机极片起到保护永磁体的作用,因此这一结构的永磁同步电动机可以广泛用于对于机体要求严格的场景中。
2 动力系统永磁同步电动机流体计算分析 2.1 流体传热耦合场数学模型分析基于对永磁同步电动机工作原理及基本结构的探讨,对电动机的流体展开计算。考虑到静止矩形坐标转化成以角速度转动的相对基准坐标系,其转动坐标系统的边界理论上相对固定。因此在此基础上选用标准k-ε模型来模拟电动机中的紊流,并分别给出质量、动量守恒等式,如下式:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathop v \nolimits_r } \right) = 0 \text{,} $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho v} \right) + \nabla \cdot \left( {\rho \mathop {vv}\nolimits_r } \right) + \rho \left( {\omega \times v} \right) = - \nabla \rho + \nabla \tau + F \text{。}$ | (2) |
式中:vr为相对速度;p为作用于空气微元体的静压力;r为位置矢量;w为相对参考坐标系旋转角速度;v为绝对速度;r为作用于微元体表面粘性应力;
发动机的入口和出口的温度可以被测量,但是不能被测量到内循环的入口温度。根据电磁场的计算,利用所获得的损失,将其用于电动机的液体换热耦合场,求解电动机和冷却器的流体传热耦合磁场,或者反复计算发动机内部循环的入口温度。在内循环的输出温度接近内循环电动机的输入温度时,将其终止,并将其作为最后的结果。该方法的初始化对计算的结果没有任何影响。为了加速收敛,可以根据实际条件选取初始温度。在本文中,发动机进气温度的初值为50℃。通过6次迭代,得到了69℃的入口温度,迭代误差0.47%。
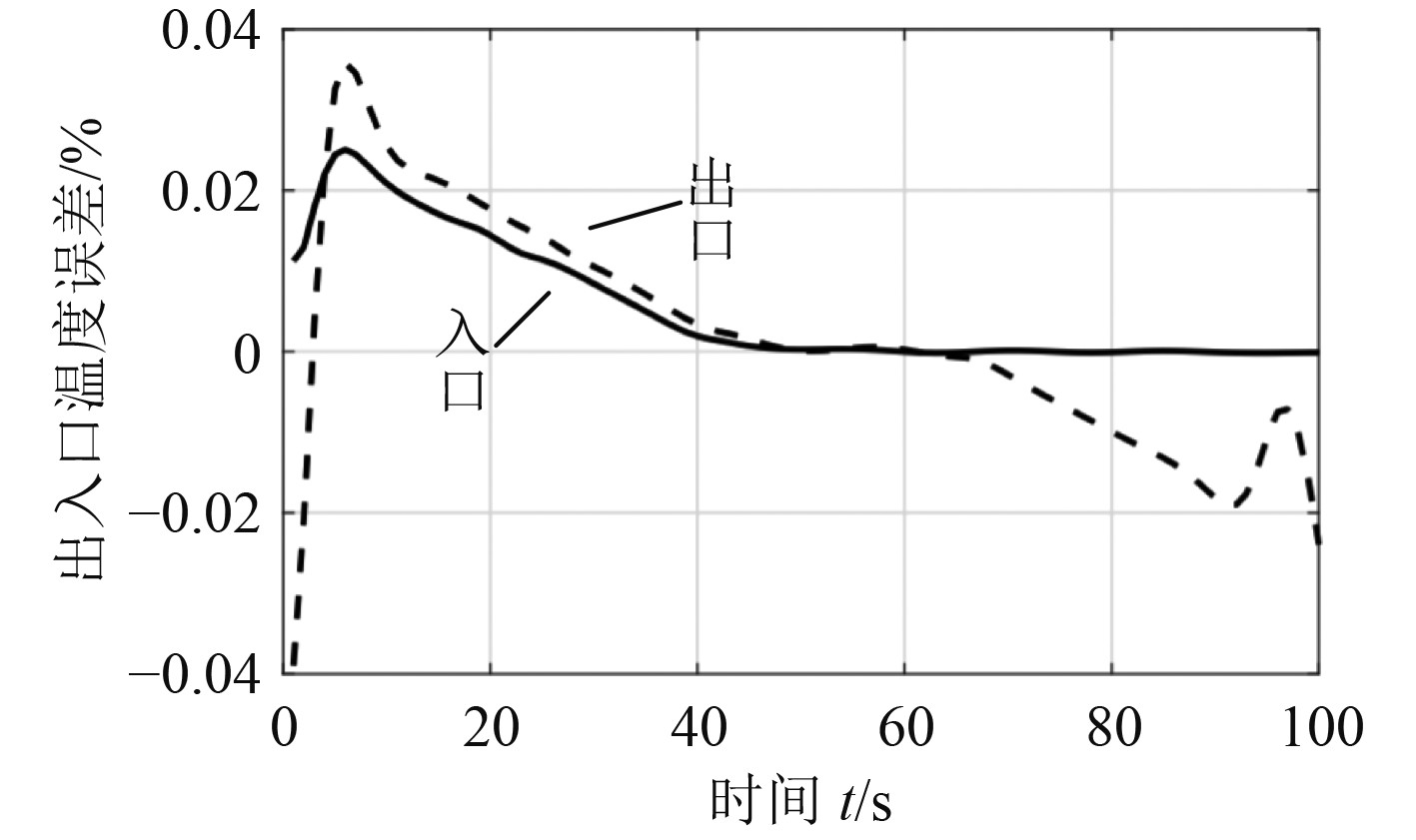
通过对热数学模型进行求解,确定动力系统永磁同步电机内流体流速的分布。电动机冷却器出入口温度误差曲线如图3所示。电机转子为无通风沟的实心结构,因而在研究时只研究定子的通风沟,以及气隙内的流体场。
|
图 3 电动机冷却器出入口温度误差曲线 Fig. 3 Temperature error curve of motor cooler inlet and outlet |
为精确地分析通风沟中气体在径向上的流动,通过对流体场的数值模拟,得到流体场的流速曲线。为了方便研究,假定一个从定子齿轮到定子轭后面的流体出口,是一个以正速表示的空气出口区域;从定子轭后侧的液体流到定子齿上的气流通路是以负流速为代表的进风区。
在气流从气隙进入通风沟时,由于齿部通气面积很小,气流变化很大,所以在靠近槽楔处的上绕组风速最大;当气流持续向齿根处流动时,其速度一般为直线降低,因为通气面积的增大;在关隘山脊附近,通气面积增加,风速明显下降。风沟内的最大流量是1.65 m/s,而在轭背部的最小速度是0.7 m/s。1、2两种风沟的流速分布规律基本一致,1号、2号风沟的风速比3大,说明它们的散热性能较好。3号风沟最大流速为0.8 m/s,而轭背部为0.25 m/s。3号风管的径向风速很低,最大流量只有0.25 m/s,这表明在这一区域中,散热效率很低。定子1号~定子3号径向通风沟速度分布图如图4所示。

|
图 4 定子1-3号径向通风沟速度分布图 Fig. 4 The velocity distribution diagram of stator No. 1-3 radial ventilation channels |
在气流由定子磁轭后方进入通风槽时,其速度几乎没有明显的改变。当气流从齿根处向齿槽区深入时,由于通气面积减小,气流速度逐渐增加,并在上绕组与槽楔的接触部位处出现了最大风速。定子4号和定子5号径向通风沟速度分布图如图5所示。在5号通风口的轭背部进口处,风速最小,1 m/s,在齿根部处,速度提高到2.1 m/s。在齿区,速度在径向上迅速增大,最大速度达到3.35 m/s;4号通风沟的流速与5号通风沟的流速大致相同,在轭背部最小流速为0.5 m/s,在轮轴下的齿数为0.78 m/s,楔与楔形块的接触位置最大流速为1.27 m/s。

|
图 5 定子4号和5号径向通风沟速度分布图 Fig. 5 The velocity distribution diagram of the stator No. 4 and No. 5 radial ventilation ditch |
5个通风沟中,5号风沟的流速最大,散热的效果也好,但是,因为接近风机的前端,在经过前面的排气管后,空气的温度会迅速升高,所以不会最低。排行第2的1号通风沟,其靠近风扇的末端,电动机的有效长度存在温度最低的区域。4号风沟的流动速度最小,它位于电动机的中央,并且在非风扇的顶端有一定的倾角,所以最热的地方就是这个位置。
3 动力系统永磁同步电动机热场分析 3.1 热载荷计算在对于热载荷的计算时,主要采用二维热分析模型对电动机的热流密度进行分析,公式如下:
| $ q = \frac{{{P_{loss}}}}{{sl}} \text{。} $ | (3) |
式中:l为机电长度,s为生热面积,q为热流密度,Ploss为电动机各部分的损耗。
3.2 边界条件与电动机定子表面靠近的空气表面温度,和其热交换系数已知,即
| $ - \lambda \frac{{\partial T}}{{\partial n}}|\Gamma = \alpha (T - {T_\Gamma })\cdot \Gamma \text{。} $ | (4) |
式中,
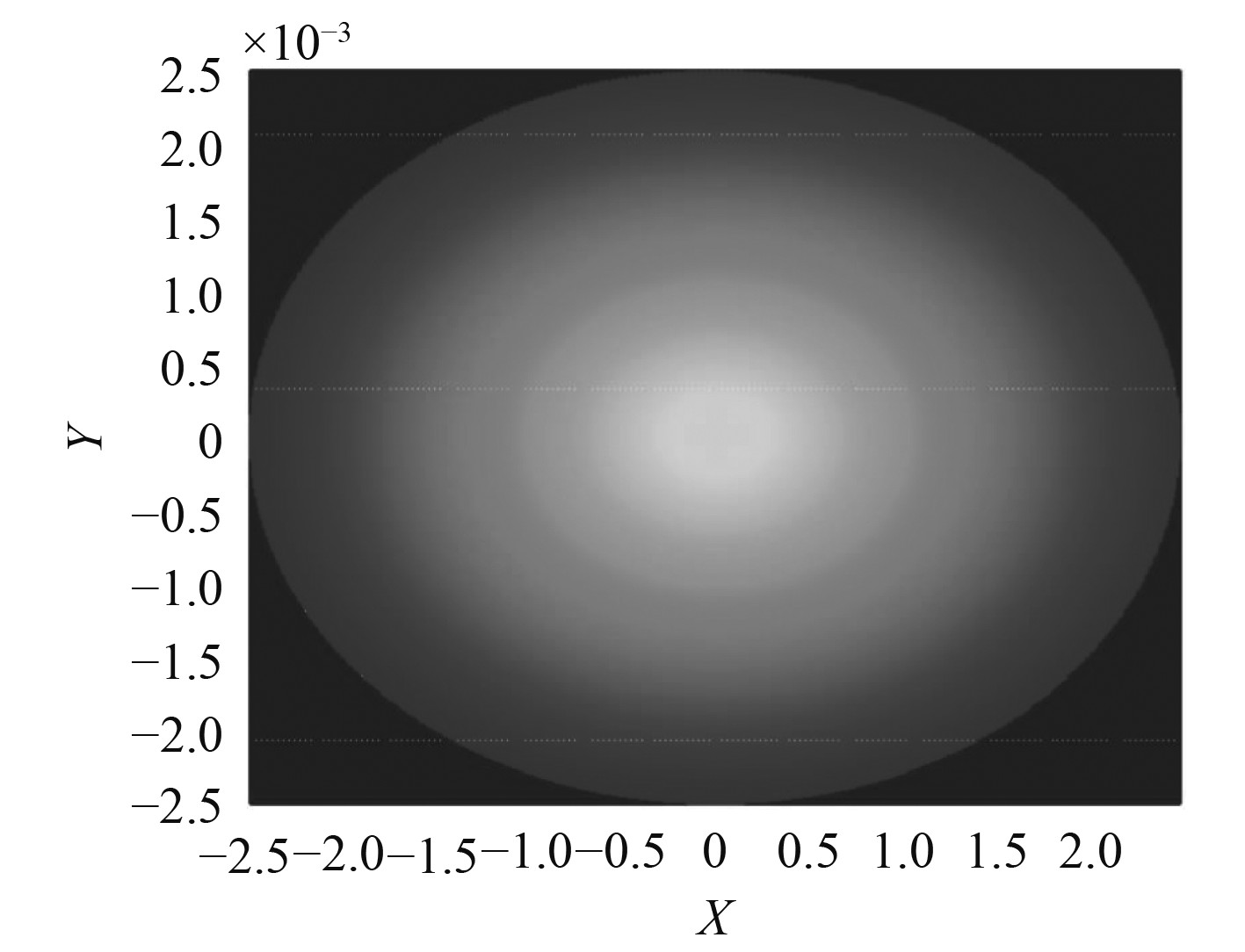
电动机转子热分布图如图6所示。电动机定子、转子之间气隙中的气流由于相互作用的影响,其相关系数表示为:
|
图 6 电动机转子热分布图 Fig. 6 Heat distribution map of motor rotor |
| $ {R_e} = \frac{{2{\delta _E}{\upsilon _e}}}{\upsilon } \text{,} $ | (5) |
| $ {\upsilon _e} = {[\upsilon _\alpha ^2 + {(\upsilon R)^2}]^2} \text{。} $ | (6) |
式中:δE为等效直径;υR为转子的旋转速度;υ为空气粘度,υα为轴向气流速度。
计算出雷诺系数后,可以得出导热系数为:
| $ \alpha = \frac{{\lambda {N_u}}}{{2\delta }} \text{。} $ | (7) |
式中:λ为空气导热系数;Nu为努赛尔数。
3.4 计算结果电动机外壳为循环式油冷却,会产生4.3 m/s的流速和0.18 MPa的压力。由于该发动机为机油泵,其部分燃料功率通过机油泵输送到引擎外壳进行冷却,在不需要附加压力泵的情况下,就可以回到油箱。通过计算,电动机的热场温度如表1所示。
|
|
表 1 计算值与试验值对比 Tab.1 Comparison between calculated value and test value |
动力系统永磁同步电动机广泛应用于多个领域,发挥着强大的功效和作用,它的发展与进步具有重大意义。本文主要分析其流体与热场,更好了解永磁同步电动机,从而不断促进其发展。
| [1] |
汪远林, 窦满峰. 高功率密度永磁同步电动机散热设计及热场分析[J]. 微特电动机, 2013, 41(5): 23-24+31. WANG Yuan-lin, DOU Man-feng. Heat dissipation design and thermal field analysis of high power density permanent magnet synchronous motor[J]. Micro Motor, 2013, 41(5): 23-24+31. |
| [2] |
庄旭, 曾德俊, 曾令全. 基于FEM永磁同步电动机的分析与计算[J]. 东北电力大学学报, 2005, 25(6): 116-119,122. ZHUANG Xu, ZENG De-jun, ZENG Ling-quan. Analysis and calculation of permanent magnet synchronous motor based on FEM[J]. Journal of Northeast Electric Power University, 2005, 25(6): 116-119,122. DOI:10.3969/j.issn.1005-2992.2005.06.027 |
| [3] |
郭昱君, 王爱元, 姚晓东. 基于特征权值小波包能量分析的异步电动机电气故障特征提取[J]. 上海电机学院学报, 2022, 25(3): 142-148. GUO Yu-jun, WANG Ai-yuan, YAO Xiao-dong. Extraction of electrical fault features of asynchronous motors based on eigenweight wavelet packet energy analysis[J]. Journal of Shanghai Institute of Electrical Engineering, 2022, 25(3): 142-148. DOI:10.3969/j.issn.2095-0020.2022.03.004 |
| [4] |
丁杰, 张平, 李益丰, 等. 永磁同步电动机的三维流场温度场耦合计算[J]. 大功率变流技术, 2014(6): 6. DING Jie, ZHANG Ping, LI Yi-feng, et al. Coupling calculation of three-dimensional flow field and temperature field of permanent magnet synchronous motor[J]. High Power Converter Technology, 2014(6): 6. |
| [5] |
庞聪, 胡彬. 永磁同步牵引电动机的温升计算研究[J]. 防爆电动机, 2019, 54(2): 15-17. PANG Cong, HU Bin. Research on temperature rise calculation of permanent magnet synchronous traction motor[J]. Explosion-proof Motor, 2019, 54(2): 15-17. |
 2022, Vol. 44
2022, Vol. 44
