船舶动力系统在运行过程中,需要主机、传动设备、轴系、推进器等设备共同配合完成。其中任何一环出现问题,都会对船舶的正常工作带来影响。因此在掌握船舶推进系统的基本工作原理后,据此设计一个较为科学,带有针对性的风险管理计划,将极大地提升船舶推进系统工作效率。
船舶推进系统的常见主要故障包括磨损、柴油机功率不足、磨合不充分、堵塞、烧损,甚至会发生断裂、腐蚀、咬死、漏泄、松脱等。因此为了可以更为全面地提升船舶推进系统工作效率,降低风险故障发生的频率,本文基于组合预测算法对其科学检修展开研究。
1 组合预测算法体系构建原则本文基于TOPSIS原理对检测指标体系展开分析。在本次关于船舶推进系统故障检测的算法研究上,首先对相关安全指标进行一个规范,然后再从多视角对其展开探讨,从而更为全面地对船舶推进系统出现的故障加以防范。
1.1 整体性和系统性不同维度的不同单项指标,对于船舶推进系统出现安全故障,以及因故障而导致的风险问题都不容忽视,因此,本文在组合预测算法的构建上,从不同角度对船舶推进系统加以评估,更为系统地将各项指标加以涵盖,最终达到整体优化船舶推进系统的目的。
1.2 科学性和合理性船舶推进系统安全故障指标体系的构建以科学理论作为指导,结合专家多年实践经验的总结,提出的指标体系要确保能够准确地反映船舶推进系统安全故障的实质,符合船舶推进系统运营的客观实际,且具有广泛的代表性。
1.3 重要性和代表性选取其中影响影响船舶推进系统故障发生频率较高的几点关键因素展开细化分析,并选取其中代表性问题提出针对性的完善建议,从而达到避免指标庞杂,信息冗余,影响因素过多而缺乏独立性,真正做到追求总体最优的目的[1-3]。
1.4 有效性和敏感性在本次的组合预测算法体系设计过程中,针对不同故障即将发生的信号、故障发生到运维的时间间隔、故障信号强度均存在的差异,以及故障敏感性较强的指标进行分类,从而确保相关运维人员以及操作人员在检修及使用船舶的过程中,能够较早指出船舶推进系统的故障信号,从而给相关操作人员留出足够的时间消除隐患。
2 基于组合预测的船舶推进系统影响因素分析 2.1 影响因素的选择本次研究采取的组合预测法,是基于分析范式而展开的多因素探讨。经整理当下现有研究成果可知,目前影响船舶推进系统导致故障的因素,主要包括驾驶室操纵台、机旁电控箱、集控室操纵台、气控逻辑箱、尾轴和主机测速装置、安保和遥控控制柜。因此,本文从船舶产业结构、船舶推进系统操作行为,以及船舶推进系统发生故障时采取的运维措施展开,而对其进行深入的探讨与研究。
2.2 各因素的影响作用分析1)驾驶室操纵台的影响
回顾船舶推进系统的相关研究可知,船舶推进系统其在研发及运维的过程中,一直呈现出一种螺旋上升的扬弃式发展。在这个过程中,包括波驾驶室操纵台的手柄、辅车钟等操纵设备,都会随着时代的发展,市场监督的规范,以及相关技术的革新而进行着不断的完善。伴随着当前大型中速柴油机推进动力装置的使用范围比较广,驾驶室操纵台也开始向着重量轻、体积小的方向发展,并且可以借助机器辅助,人机结合的方式,对减速比进行合理选配,从而较为科学的降低了船舶推进系统的使用磨损,提前其使用寿命。
2)集控室操纵台
一般情况下,船舶推进系统主要由柴油机、蒸汽轮机以及燃气轮机3部分借助交流器产生电能。而集控室操纵台包含了报警板和主机转速表,当相关技术人员进行操作的过程中,可以通过分析螺旋桨的转速来判断船舶推进系统的使用情况。因此加强集控室操纵台的风险管理预测,能促进船舶推进系统的有效提高[4-6]。
3 故障预测实证分析 3.1 TOPSIS原理本次选取优劣解距离法,在具体的数列设计上,思路如下:
设有比较数列Xi=(xi1,xi2,…,xim),i=1,2,…,m,选择理想数列,设正理想数列为X+=(x1+,x2+,…,xm+),反向数列为X−=(x1−,x2−,…,xm−),而其中的比较数列则为Xi=(xi1,xi2,…,xim),i=1,2,…,m,其与正理想数列X+=(x1+,x2+,…,xm+)的距离如下式:
| $ S_i^ + = \sqrt {\sum\limits_{j = 1}^n {{{({x_{ij}} - x_j^ + )}^2}} } \text{。} $ | (3-1) |
而比较数列Xi=(xi1,xi2,…,xim),i=1,2,…,m与负理想数列X−=(x1−,x2−,…,xm−)的距离如下式:
| $ S_i^ - = \sqrt {\sum\limits_{j = 1}^n {{{({x_{ij}} - x_j^ - )}^2}} } \text{。} $ | (3-2) |
则比较数列Xi=(xi1,xi2,…,xim),i=1,2,…,m到理想数列的相对贴近度如下式:
| $ C_i^{} = \frac{{S_i^ - }}{{S_i^ + + S_i^ - }} \text{。} $ | (3-3) |
基于数列推导原理,罗列出船舶推进系统故障排查组合预测模型。选取其中的对单一预测模型加以验算,从而得出预测结果。本次采集样本内,选取前n个月的船舶推进系统操作历史数据,设为Y=(Y1,Y2,…,Yn)。在基于该系统操作历史数据之上,再采用m种单一的预测模型构建数列,以此模拟船舶推进系统故障发生频率的间隔,假设当第m种单一预测模型对船舶推进系统发生故障的间隔时间n为Xi=(xi1,xi2,…,xim),i=1,2,…,m,则第j(j=1,2,…,n)个月的故障排查组合预测模拟数值如下式:
| $ {\tilde X_j} = {w_1}{x_{1j}} + {w_2}{x_{2j}} + \cdots + {w_m}{x_{mj}} = \sum\limits_{i = 1}^m {{w_i}{x_{ij}}} \text{。} $ | (3-4) |
通过以上构建的模型可知,当m种单一的预测模型进行加权组合后,则可以由此阐明船舶推进系统的故障间隔是一个较为接近现实均值的结果。然而,考虑到本次研究所选取的预测模型会因涉及的内容不同,导入的数据存在一定的误差,因此会产生百十种研究方法。而为了能够更好地模拟出船舶推进系统故障发生的频率,基于之前录入的相关历史数据展开模型建立。
3.3 基于TOPSIS原理的故障预测组合权重确定方法一般而言,预测权重的方法,尽量是让单一预测模型得出的结果对比实际的历史数据,以此来判断其距离的大小。当距离较大时,说明本次构建的模拟方法精密度偏低,当距离接近时,则可以视为本次构建的数据模型最为接近于真实的现实情况。据此,在基于以上确定预测组合权重方法的确定思路上,本文继续采取优劣解距离法对船舶推进系统的故障排查展开研究。设船舶推进系统最初的历史故障序列为Y=(Y1,Y2,…,Yn),由于不考虑负理想序列,因此将正理想序列表示为X+=(x1+,x2+,…,xm+),并针对船舶推进系统或在某一间隔期存在故障的模拟序列进行单一预测,将Xi=(xi1,xi2,…,xim)设为优劣解距离法中的比较序列,让Xi=(xi1,xi2,…,xim)与最终得出的距离结果如下式:
| $ S({X^ + },{X_i}) = \sqrt {\sum\limits_{j = 1}^n {{{({x_{ij}} - x_j^ + )}^2}} } \;\;\; i = 1,2, \cdots ,m \text{。} $ | (3-5) |
需要着重说明的是,当最终得出的结果越低,则说明选取的单一预测方法更接近于现实情况,因此在得出距离结果后,将其中的倒数设为权重的衡量标准,即
| $ {\lambda _i} = {\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 {S({X^ + },{X_i})}}}\right.} \lower0.7ex\hbox{${S({X^ + },{X_i})}$}}\;\;\; {i = 1,2, \cdots ,m} \text{。} $ | (3-6) |
基于对此次获得的数据进行无量纲的表达,进而得到船舶推进系统存在故障的组合权重向量w=(w1,w2,…,wm),可得出:
| $ {w_i} = {{{\lambda _i}} \mathord{\left/ {\vphantom {{{\lambda _i}} {\sum\limits_{k = 1}^m {{\lambda _k}} }}} \right. } {\sum\limits_{k = 1}^m {{\lambda _k}} }}\;\;\; {i = 1,2, \cdots ,m} \text{。} $ | (3-7) |
通过以上数列结果展开,可以得出此次选取的船舶推进系统故障排查组合预测与之前搜集的现实情况相符,由此说明此次基于TOPSIS原理而展开的优劣解距离法研究具有可操作性。
3.4 模型精度检验方法本次探讨故障出现间隔的目的,是为了在今后的作业中能够准确地对船舶推进系统可能存在的故障隐患制定出一个较为科学的运维间隙,从而按照一定时间的维护节奏进行针对性排查。而要想提高故障预测的准确度,就需要对现有的模型进行更为精准的探讨。精度检验作为提升预测可信度的重要研究方法,在原理上是只有满足预测精度的数据结果,才能将其最终应用于本次的船舶推进系统故障排查预测中。据此,针对相对误差精度的检验,采取的计算公式为:
| $ {\bar \Delta _i} = \frac{1}{n}\sum\limits_{k = 1}^n {||\frac{{{Y_k} - {X_{ik}}}}{{{Y_k}}}||} \text{。} $ | (3-8) |
当平均相对误差低于a(其中a<5%)时,则可以认为本次建立的预测模型在针对船舶系统故障预测时具有可行的现实意义。
3.5 故障预测结果分析在技术更新的过程中,传统的设备是否因系统的升级而后劲不足,或是引入的新设备因操作不当而使其使用寿命缩短,甚至是相关操作人员的不重视,都会导致船舶推进系统故障的发生。而本次研究在排除了操作人员个人技术水平不足的大前提下,搜集了近7个月的船舶推进系统故障出现的相关数据,具体为:
| $ Y = ({\text{63}}{\text{.1 ,65}}{\text{.2, 72}}{\text{.8 ,81}}{\text{.2 ,88}}{\text{.7 , 93}}{\text{.5 ,99}}{\text{.1}}) 。$ |
据此,基于选择回归预测对搜集到的数据建立模型,以此分析船舶推进系统未来或将发生故障的趋势。具体如图1所示。
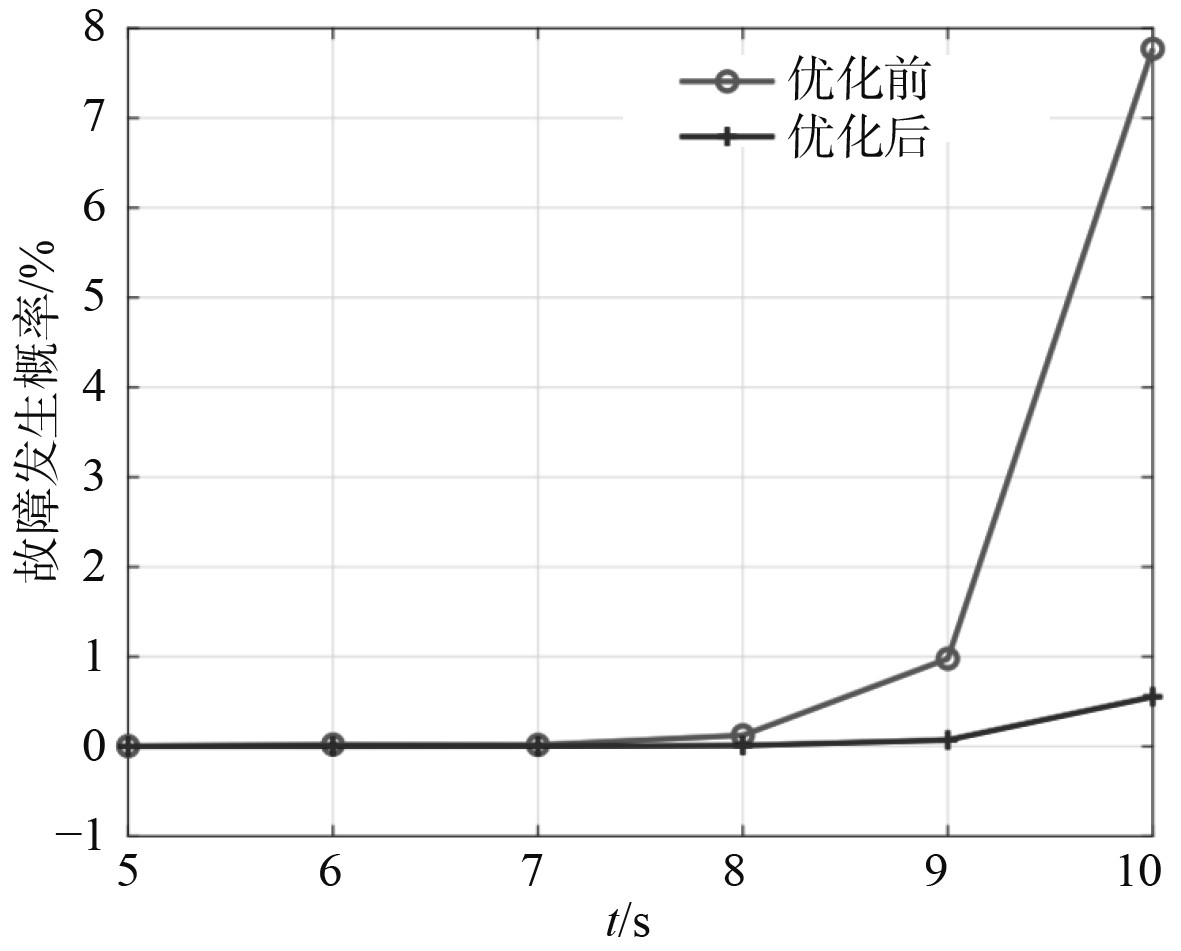
|
图 1 船舶推进系统发生故障变化趋势 Fig. 1 Trend of ship propulsion system failure |
可以看出,船舶推进系统发生故障的变化趋势呈直线性,因此采取一元线性回归对未来发生故障展开预测:
| $ {\tilde y_1} = {\text{54}}{\text{.7286}} + {\text{6}}{\text{.4464}} t ,\;\;\; t = 1,2,3, \cdots \text{。} $ | (3-9) |
基于以上模型,对近9个月的相关故障发生数值进行模拟,并由此得到模拟序列为:X1=(61.6750,67.6214,74.0678,80.5412,86.9606,93.4070,99.8534,106.2998,112.7462),并得出了本次的平均相对误差:
| $ {\bar \Delta _1} = \frac{1}{7}\sum\limits_{k = 1}^7 {|\frac{{{Y_k} - {X_{1k}}}}{{{Y_k}}}|} = {\text{0}}{\text{.0174}} \text{。} $ | (3-10) |
按照相同思路,再利用灰色预测模型进行历史数据构建,其响应式为:
| $ {\tilde y_2}(t) = {\text{ (803}}{\text{.3578)}}{\text{e}}^{\text{0}{\text{.0807}}(t - 1))}{\text{ - 740}}{\text{.2578}} \text{。} $ | (3-11) |
借助GM(1,1)模型再对以上结果进行累减,进而得到船舶推进系统故障出现概率的最终预测序列:X2=(63.1000,67.5174,73.1919,79.3432,86.0115,93.2043,101.0766,109.5714,118.7803),以及前7个样本的平均相对误差,见下式:
| $ {\bar \Delta _2} = \frac{1}{7}\sum\limits_{k = 1}^7 {|\frac{{{Y_k} - {X_{2k}}}}{{{Y_k}}}|} = {\text{0}}{\text{.0167}} \text{。} $ | (3-12) |
为了可以进行一个全面的验证,继续采用指数平滑预测模型(其中平滑参数a=0.2)得出了序列式:X3=(63.1000,64.3558,69.6549,77.8279,87.0518,95.0932,102.6960,109.2724,118.0843)。其平均相对误差为:
| $ {\bar \Delta _3} = \frac{1}{7}\sum\limits_{k = 1}^7 {|\frac{{{Y_k} - {X_{3k}}}}{{{Y_k}}}|} = {\text{0}}{\text{.0242}} \text{。} $ | (3-13) |
经过以上3轮不同的模型单一预测精度检验,再结合优劣解距离法的组合权重确定方法,分别得出了:S(X+,X1)=3.9049,S(X+,X2)=4.4916,S(X+,X3)=6.3373,从而由公式计算得到λ1=0.2561,λ2=0.2226,λ3=0.1578,并由此导入权重计算公式,得到的权重为:
| $ w = ({\text{0}}{\text{.4023 0}}{\text{.3498 0}}{\text{.2479)}} \text{。} $ | (3-14) |
基于以上的预测结构进行加权计算,导出组合预测模拟序列X4=(62.3265,66.7755,72.6675,79.4387,86.6512,93.7667,100.9860,108.1811,116.1802),其平均相对误差为:
| $ {\bar \Delta _4} = \frac{1}{7}\sum\limits_{k = 1}^7 {|\frac{{{Y_k} - {X_{4k}}}}{{{Y_k}}}|} = {\text{0}}{\text{.0150}} \text{。} $ | (3-15) |
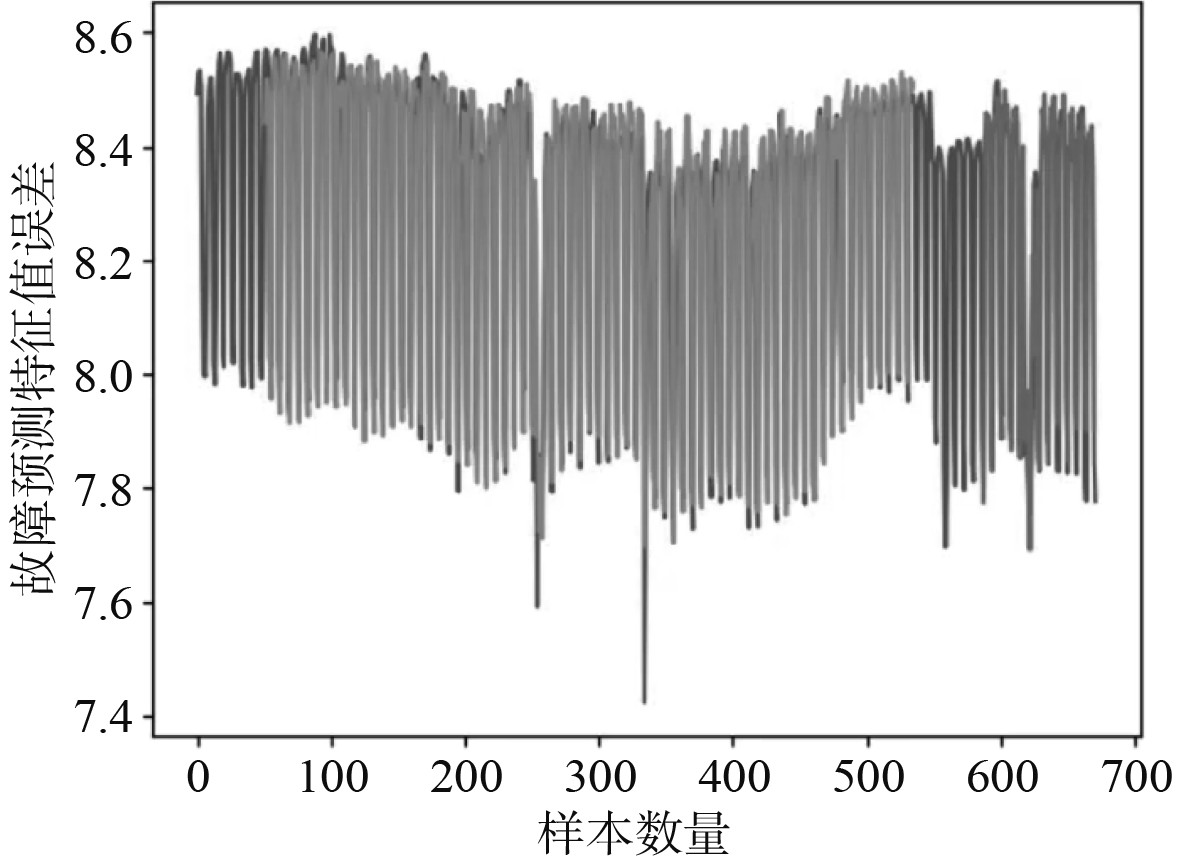
|
图 2 故障预测特征值误差分布图 Fig. 2 Error distribution of fault prediction eigenvalue |
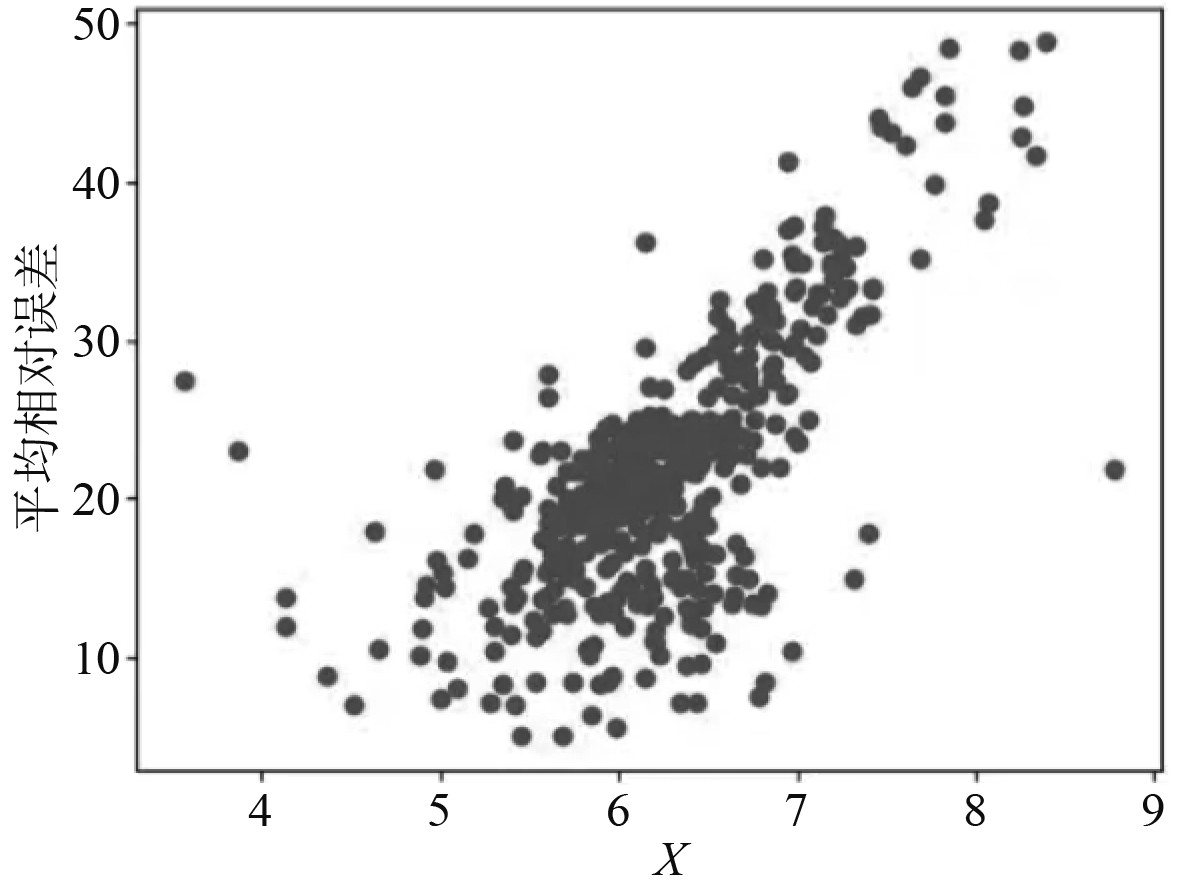
|
图 3 平均相对误差分布图 Fig. 3 Average relative error distribution diagram |
可以看出,此次研究得出的采集模拟数值,其在平均相对误差上普遍偏低,进而再次验证了此次船舶推进系统故障预测的模型构建可行。
依据本次最终通过计算可知,样本内未来1年的故障出现次数预测值为81次,1个月出现故障的次数为6.75次,因此作为船舶推进系统操作人员,需要每隔5天对船舶推进系统的机旁电控箱、气控逻辑箱、尾轴和主机测速装置展开针对性故障排查,并每天加强驾驶室操纵台、集控室操纵台以及遥控控制柜的操作规范宣导。
4 船舶推进系统的维护与修理建议 4.1 船舶推进控制系统运行维护一般而言,自动电站的船舶推进控制系统在实际应用作业过程中,出现故障的几率较小,并主要表现为操作人员的使用不当而致使故障的发生。因此在加强船舶推进控制系统的过程中,需要为相关操作人员进行岗前培训,通过提升其对故障排查、识别、维修及保养的专业能力,从而降低故障发生时及发生后对推进船舶控制系统造成的影响。
4.2 推进船舶核心设备运行维护通过本次分析可知,导致船舶推进系统出现故障的因素众多,而核心设备作为其中尤为重要的一环。以其中的变频器为例,由于该设备在使用的过程中,会因为内部构造的复杂程度而对设备周围的环境条件有一个高要求。在一项研究中指出,变频器附近空气的污染情况以及温度,在理论及实践过程中都会对船舶推进系统的正常工作带来一定的影响。比如操作人员未能让该类设备在运行的过程中进行合理科学的温度控制,都会造成变频器因高于允许极限值或者低于允许极限值,而导致船舶推进系统工作失灵,进而引发相关故障的发生。因此今后在使用船舶推进核心设备时,可以考虑引入人工智能系统,通过计算机辅助来提升运维效率,合理控制环境温度,从而最大程度降低诸如变压器、变频器等设备故障造成的危害。
5 结 语为了可以更为科学地对船舶推进系统的故障加以检测及维护,本文首先针对船舶推进系统的基本工作原理进行分析,并提出指标体系的构建原则。然后借助组合预测算法对其存在的安全隐患进行研究,最后从维护和修理2个方面出发,提出了该系统维修过程中需要注意的重点。
| [1] |
刘翔. 船舶电力推进系统故障诊断与预测技术综述[J]. 船电技术, 2020, 40(6): 30-33+38. DOI:10.3969/j.issn.1003-4862.2020.06.002 |
| [2] |
余国虎. 船舶综合电力推进系统的特征分析[J]. 电子技术, 2021, 50(4): 172-173.
|
| [3] |
王俊龙, 袁伟. 船舶推进系统可靠性分析研究[J]. 四川兵工学报, 2020, 41(7): 208-212. |
| [4] |
冯明, 刘艳年. 船舶推进系统故障诊断和预测关键技术研究[J]. 舰船科学技术, 2022, 44(3): 107-110.
|
| [5] |
张刚. 船舶推进系统安装技术工法研究与质量控制[J]. 船舶物资与市场, 2021(3): 91-92. DOI:10.19727/j.cnki.cbwzysc.2021.03.042 |
| [6] |
张玉龙, 吴炜, 周建辉. 基于灰色系统理论的推进轴系负荷预测分析[J/OL]. 中国舰船研究: 1−7[2022-10-18].
|
 2022, Vol. 44
2022, Vol. 44
