齿轮传动系统广泛应用于汽车、航空、航天以及船舶等领域,其运行状态对所在系统有重要的影响[1]。Kahraman[2-3]对齿轮系统动力学模型的建立和求解进行了大量的研究,为齿轮系统动力学特性分析提供了重要参考。现有研究表明,在大型船舶高速重载的航行工况下,滑动轴承支撑的齿轮系统相较于滚动轴承支撑的齿轮系统具有更高的稳定性[4],且由于滑动轴承具有较大的刚度和阻尼,有利于减小振动和噪声等级,因此随着对系统性能要求的不断提高,齿轮-滑动轴承系统的动态特性研究也受到越来越多的重视。WANG等[5]研究了啮合刚度和间隙非线性对齿轮系统动力学特性的影响。李同杰等[6]考虑了齿轮系统的弯曲和扭转变形的耦合,对滑动轴承支撑下的系统振动特性开展研究。蒋庆晶[7]和周建星[8]分别研究了多级齿轮耦合和内激励作用下的齿轮系统振动特性。张将等[9]考虑了支撑间隙的影响,通过分析相图、Poincare截面和功率谱密度图,对齿轮系统的动力学性能进行研究。
以上研究多针对齿轮系统的理论分析展开,相关实验研究较少,所得结论不能得到有效验证。本文为了研究轴承间隙对齿轮系统的影响,在已有研究基础上,分析轴承间隙、负载转矩对系统动力学的影响规律并进行了实验验证,为实际中分析齿轮-滑动轴承系统提供参考。
1 齿轮啮合动力学模型利用集中参数法,同时考虑齿轮系统的扭转振动、横向振动以及轴承支撑参数,构建齿轮系统动力学建模,如图1所示。

|
图 1 齿轮系统动力学模型 Fig. 1 Coupled model of gear-bearing system |
设图1中齿轮的齿数分别为
根据图1中齿轮系统的集中参数模型,对其应用拉格朗日方程,得到考虑轴承动态特性参数的单级圆柱直齿轮系统运动微分方程:
| $ \left\{ \begin{gathered} {m_1}{{\ddot y}_1} + {c_{by1}}{{\dot y}_1} + {k_{by1}}{y_1} = - {m_1}g - {F_m}(t){\rm{cos}}\alpha,\\ {m_1}{{\ddot x}_1} + {c_{bx1}}{{\dot x}_1} + {k_{bx1}}{x_1} = - {F_m}(t)\sin \alpha,\\ {I_1}{{\ddot \theta }_1} = {T_{in}} - {F_m}(t){r_{b1}},\\ \end{gathered} \right. $ | (1) |
| $ \left\{ \begin{gathered} {m_2}{{\ddot y}_2} + {c_{by2}}{{\dot y}_2} + {k_{by2}}{y_2} = - {m_2}g + {F_m}(t){\rm{cos}}\alpha ,\\ {m_2}{{\ddot x}_2} + {c_{bx2}}{{\dot x}_2} + {k_{bx2}}{x_2} = {F_m}(t)\sin \alpha,\\ {I_2}{{\ddot \theta }_2} = - {T_{load}} + {F_m}(t){r_{b2}}。\\ \end{gathered} \right. $ | (2) |
式中:
齿轮-滑动轴承系统在船舶动力传动中有着重要的应用,其性能的好坏直接决定了船舶动力系统的工作性能。在齿轮-滑动轴承数学模型的基础上对其进行数值仿真,以研究轴承间隙、负载转矩对系统振动特性的影响规律。根据文献[10]中的给出的方法对齿轮-滑动轴承耦合系统模型进行求解。齿轮结构参数以及轴承结构参数如表1和表2所示。
|
|
表 1 齿轮结构参数 Tab.1 Parameters of gears |
|
|
表 2 滑动轴承结构参数 Tab.2 Parameters of lubrication bearing |
由文献[11]可知,轴承间隙会对轴承的支撑力、轴承刚度及阻尼产生直接影响,因此轴承间隙大小的选择尤为关键。为了定义轴承间隙的大小,将直径间隙与轴承公称直径之比称为相对间隙,其计算公式为:
| $ \psi = C/d。$ | (3) |
式中:
| $ \psi = \frac{{{{(n/60)}^{4/9}}}}{{{{10}^{31/9}}}} 。$ | (4) |
式中,n为轴颈转速。
设齿轮输入转速
|
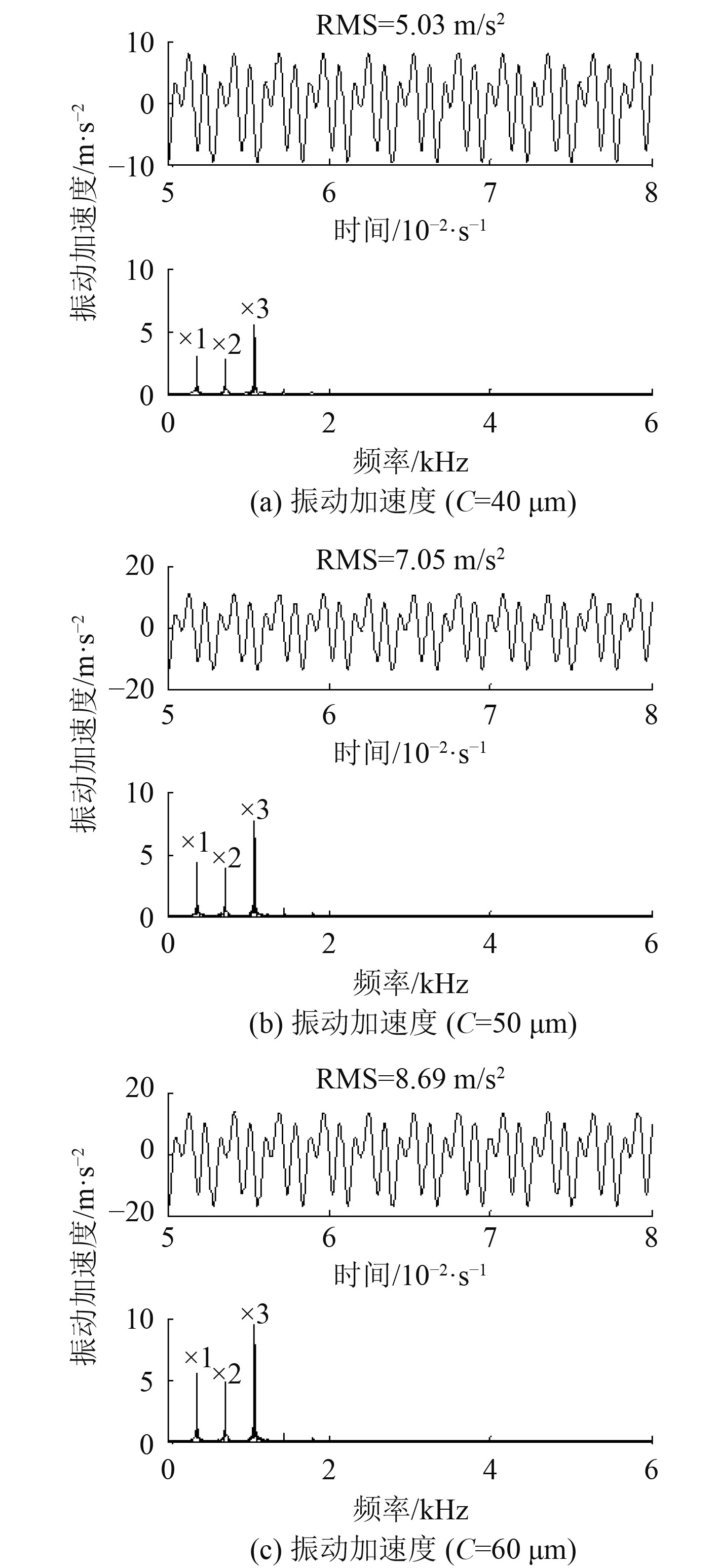
图 2 不同轴承间隙时系统的振动响应 Fig. 2 Vibration response of system with different bearing clearancs |
由图2振动加速度与啮合力的时域曲线可以看出,随着轴承间隙的增加,振动加速度以及啮合力的均方根值均有所增加。增加轴承间隙会使得轴承的支撑刚度和支撑阻尼减小,而轴承支撑刚度的减小则会导致系统振动响应的增加。从影响的结果来看,轴承间隙的变化对振动有较大影响。从振动加速度的频域曲线可以看出,频谱中的主要成分为啮合频率及其2倍频和3倍频。
为了直观地反映齿轮系统在不同负载下,轴承间隙对振动加速度以及啮合力的影响规律,将不同参数下系统加速度的RMS(root mean square)值列于表3。
|
|
表 3 不同负载下系统随轴承间隙变化的振动响应(RMS) Tab.3 Vibration response of system with different bearing clearancs(RMS) |
对表3数据进行分析可知,在负载转矩一定时,轴承间隙的增加会导致系统振动加速度的增加;增加负载转矩,系统的振动也会随之加剧。
3 试验验证试验平台主要组成部分有交流变频电机及其底座、试验齿轮箱及其底座、磁粉制动器以及试验台基座。滑动轴承通过螺栓与箱体侧平台相连,通过销孔实现精确定位。其中陪试滑动轴承与齿轮箱体的位置固定不变,通过螺栓与箱体相连,通过销孔实现定位;试验滑动轴承也通过螺栓与箱体侧板上的平台相连,通过腰形销孔实现定位,轴承可在定位孔的间隙范围内实现移动。通过改变轴承位置使得齿轮实现平行移动,改变齿轮啮合的中心距进而改变齿侧间隙。
为了研究轴承间隙对齿轮系统的影响,同时保持间隙参数与理论模型的一致,在齿轮轴轴颈不变的情况下,加工3组孔径分别为
试验平台所用到的设备型号以及相关参数如表4所示。
|
|
表 4 试验设备型号及参数 Tab.4 Parameters and types of experiment instruments |
由表4中设备参数可知电机可提供的最高转速为6 000 r/min,磁粉制动器能够最高产生50 N·m的负载力矩。加速度传感器121A500的测量范围为
对试验用的一对轴承进行更换,分别更换成间隙为
|
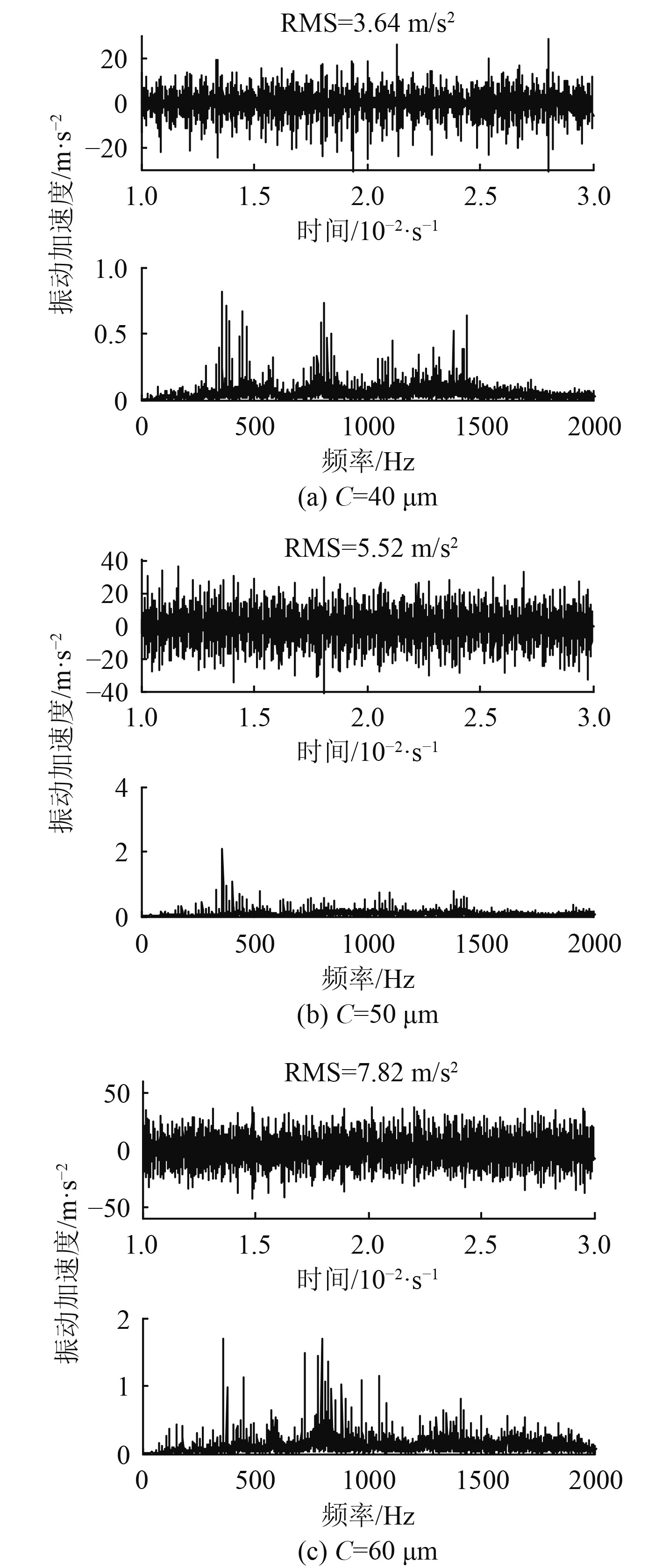
图 3
不同轴承间隙下系统的振动响应(
|
|
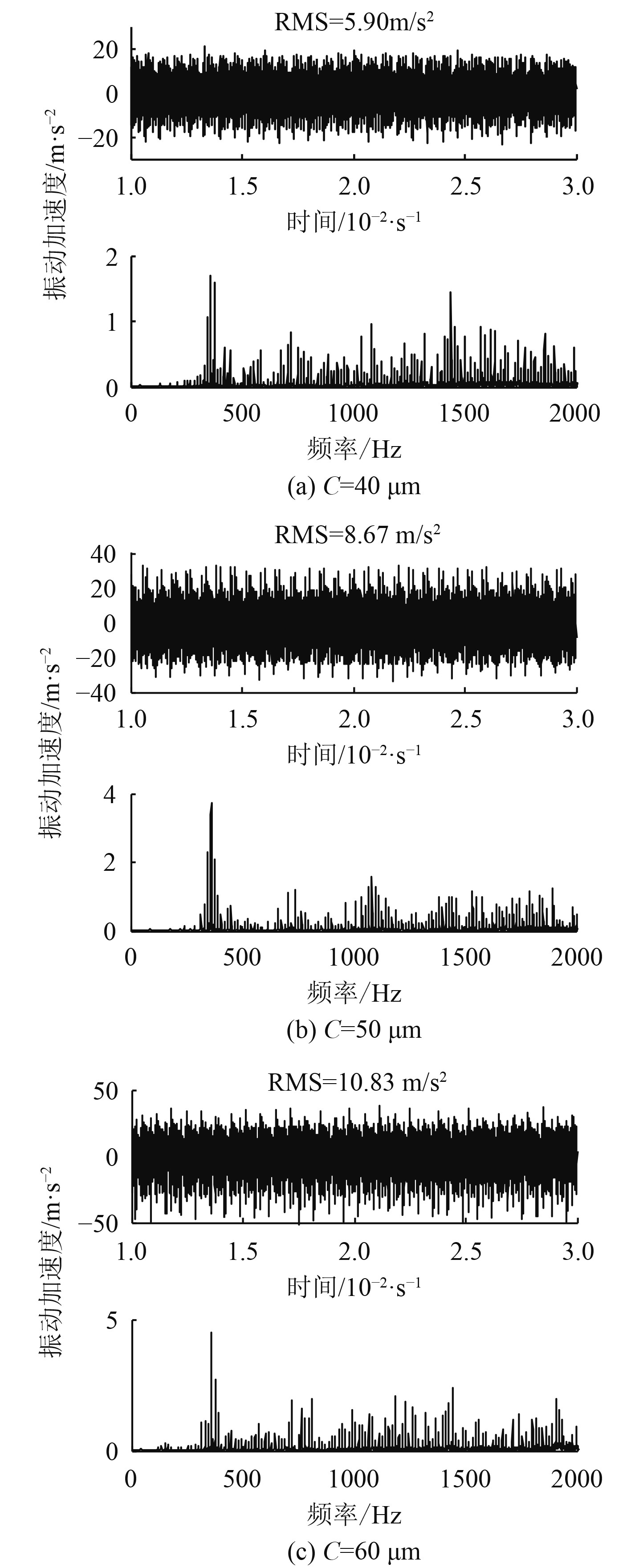
图 4
不同轴承间隙下系统的振动响应(
|
图3为齿轮系统在负载转矩为1 N·m时系统随轴承间隙变化的响应曲线。由时域信号的RMS值可以看出,随着轴承间隙的增加振动加速度的变化较为明显,RMS值由3.64 m/s2增加到了7.82 m/s2,说明轴承间隙的增加会导致系统振动响应幅值的增加,这与理论分析的趋势相一致。
图4为齿轮系统在负载转矩为10 N·m时系统随轴承间隙变化的响应曲线。可知,其振动响应随轴承间隙变化而变化的趋势更加明显。说明齿轮系统所受负载越大,轴承间隙对系统振动响应的影响也就越大。
为了直观对比系统振动响应理论与试验的结果,将各工况下时域信号的RMS值列于表5。可以看出,试验测试结果与理论计算结果具有相同的变化趋势。在负载较小时,试验与理论结果的误差小于15%,当负载增加至10 N·m时两者的误差最大达到了24.63%。
|
|
表 5 轴承间隙实验振动响应结果理论与试验的比较 Tab.5 Comparison of the results between experiment and theoretical analysis |
本文针对滑动轴承间隙对齿轮系统的影响展开研究,建立了滑动轴承支撑的齿轮系统动力学模型并进行了理论分析,搭建了齿轮-滑动轴承系统试验平台,开展了相关试验研究并对测试数据进行了分析,可以得到如下结论:
1)试验测试与理论计算的对比验证了本文建立的齿轮-滑动轴承系统模型的正确性,该模型可用于对系统振动特性的分析;
2)滑动轴承间隙对齿轮系统的振动有显著影响,轴承间隙的增加会导致支撑刚度的减小,进而使得系统振动加剧,因此为了保证齿轮系统可靠、安全的运行,轴承间隙大小应严格监测和控制;
3)负载对系统振动也有重要影响,相同参数下齿轮系统所受负载越大,系统振动幅度也越大。
| [1] |
李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1997.
|
| [2] |
KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linear ties in a geared system[J]. Journal of Sound and Vibration, 1991, 146(1): 135-156. DOI:10.1016/0022-460X(91)90527-Q |
| [3] |
KAHRAMAN A, OZGUVEN H N, HOUSER D R, et al. Dynamic analysis of geared rotors by finite elements[J]. Journal of Mechanical Design, 1990, 114(3): 507-514. |
| [4] |
崔亚辉. 齿轮-转子-滑动轴承系统非线性动力学特性的理论和试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 2-6.
|
| [5] |
WANG J, LIM T C, Li M F. Dynamics of a hypoid gear pair considering the effects of time-varying mesh parameters and backlash nonlinearity[J]. Journal of Sound and Vibration, 2007, 308(1-2): 302-329. DOI:10.1016/j.jsv.2007.07.042 |
| [6] |
李同杰, 靳广虎, 朱如鹏, 等. 滑动轴承支撑下齿轮耦合转子系统弯扭耦合振动特性分析[J]. 中南大学学报(自然科学版), 2018, 49(3): 566-573. LI Tongjie, JIN Guanghu, ZHU Rupeng, et al. Analysis of the vibration characteristics of the bend coupling vibration of the gear coupling rotor system under the support of sliding bearings[J]. Journal of Central South University(Science and Technology), 2018, 49(3): 566-573. DOI:10.11817/j.issn.1672-7207.2018.03.008 |
| [7] |
蒋庆晶, 吴大转, 潭善光, 等. 齿轮传动多转子耦合系统振动特性研究[J]. 振动工程学报, 2010, 23(3): 254-259. JIANG Qing-jing, WU Da-zhuan, TAN Shan-guang, et al. Study on the vibration characteristics of gear drive multi-rotor coupling system[J]. Journal of Vibration Engineering, 2010, 23(3): 254-259. DOI:10.3969/j.issn.1004-4523.2010.03.004 |
| [8] |
周建星, 刘更, 马尚君. 内激励作用下齿轮箱动态响应与振动噪声分析[J]. 振动与冲击, 2011, 30(6): 234-238. ZHOU Jian-xing, LIU Geng, MA shang-jun. Vibration and noise analysis of gear transmission system[J]. Journal of Vibration and Shock, 2011, 30(6): 234-238. DOI:10.3969/j.issn.1000-3835.2011.06.047 |
| [9] |
张将, 秦训鹏, 陈浩冉. 考虑支撑间隙的齿轮系统动力学响应分析[J]. 噪声与振动控制, 2017, 37(5): 50-54+159. ZHANG Jiang, QIN Xun-peng, CHEN Hao-ran. Dynamic response analysis of gear systems with support clearance considered[J]. Noise and Vibration Control, 2017, 37(5): 50-54+159. DOI:10.3969/j.issn.1006-1355.2017.05.011 |
| [10] |
魏维, 郭文勇, 吴新跃, 等. 考虑时变轴承动力学参数的齿轮系统建模与分析[J]. 振动与冲击, 2019, 38(23): 260-266. WEI Wei, GUO Wen-yong, WU Xin-yue, et al. Gear system modeling and analysis considering time-varying bearing dynamics parameters[J]. Vibration and Shock, 2019, 38(23): 260-266. |
| [11] |
杨金福, 刘占生, 于达仁, 等. 滑动轴承非线性动态油膜力及稳定性的研究[J]. 动力工程, 2004, 24(4): 501-505. YANG Jin-fu, LIU Zhan-sheng, YU Da-ren, et al. Research on nonlinear oil film force and its stability of journal bearing[J]. Power engineering, 2004, 24(4): 501-505. |
 2022, Vol. 44
2022, Vol. 44
