作为舰船的主动力装置,燃气轮机具有起动快、机动性能好等优点,而采用间冷循环是提升燃气轮机功率及效率的有效途径[1]。结合船舶动力装置的工作环境和运行特点,船用燃机采用间冷循环具有得天独厚的优势[2]。间冷循环燃气轮机在低压压气机和高压压气机之间加入了间冷器,通过降低高压压气机进口温度来减少高压压气机的耗功,以提升整机的输出功率[3]。船用间冷循环燃气轮机的间冷系统通常采用一台机上气-液换热器和一台机外液-液换热器(海水换热器)组成的“液体耦合式换热器”[4],即通过内回路中的淡水冷却来自低压压气机的高温空气,再通过海水冷却内回路的淡水[5]。然而,现有的海水换热器的冷却能力随海水量和海水温度波动的变化而变化,进而导致内回路淡水温度及高压压气机的进口温度不断变化,从而无法准确地测试及掌握间冷循环船用燃气轮机的真实性能。因此,需要设计一个海水定温掺混系统,保证流入冷却器的海水流量、温度、以及掺混水箱的液位保持恒定。
海水换热器的定温掺混系统的控制目标变量包括流入海水换热器的温度和掺混水箱的液位,通过调节掺混水箱进口调节阀和回水三通调节阀来实现。定温掺混系统是典型的多变量耦合系统,由于各个回路之间的耦合,单回路控制器的设计方法已经不能满足要求,因此需要实现各个回路之间的解耦。随着各种智能算法研究的快速进展,神经网络[6]、模糊控制[7]等方法被广泛应用在非线性系统复杂系统的建模和解耦控制中。虽然这些解耦控制理论发展得比较快,然而,由于神经网络存在局部极小值、过拟合以及网络结构难以确定等缺点[8-9],这使得神经网络难以在实际工程应用中有效实现复杂系统的解耦控制。而PID控制器结构简单,易于接受,在实际控制系统中被广泛应用。但在强耦合的多输入多输出系统中,传统的PID控制器往往达不到满意的效果。若能够将多变量解耦控制与传统PID控制器相结合,对于工业控制具有重要意义。Zhai等[10]将自校正PID控制器与前馈解耦控制策略相结合,提出了闭环自适应PID解耦控制器。李雷等[11]提出了基于多模型的多变量自适应PID解耦控制策略,取消了系统平衡点参数已知的条件。但这些PID解耦控制算法,均未考虑闭环系统零极点的问题,在对闭环系统动态性能要求较高时,难以满足要求。
本文针对船用间冷循环燃气轮机海水换热器定温掺混系统,建立了定温掺混系统的多输入多输出的数学模型。基于该系统的数学模型及实际物理状态,巧妙地通过引入虚拟控制量对整个控制回路进行解耦。结合增量式PID控制算法设计了海水换热器进口水温以及掺混水箱液位的控制器。将该算法真实应用在某型船用间冷循环燃气轮机整机综合试验台上,试验证明,采用本文所提出的多变量PID解耦控制器取得了比较好的解耦控制效果,能够满足海水换热器的工作要求。
1 海水换热器定温掺混系统介绍某型船用间冷循环燃气轮机海水换热器定温掺混系统的结构示意如图1所示。定温掺混系统主要由掺混水箱、定频率离心泵、冷水进水电动调节阀、回水电动三通调节阀、进水路质量流量计、供水路质量流量计、回水路质量流量计、测温热电阻,以及掺混水箱液位传感器构成。定温掺混系统工作时,海水(冷水)通过电动调节阀进入掺混水箱,与通过海水换热器后且经过电动三通调节阀调节的海水(热水)进行掺混,以达到海水换热器所需的恒定供水温度并同时保证水箱液位恒定。定频离心泵将掺混水箱内的恒温掺混水抽出,流经海水换热器,将间冷撬内循环的淡水冷却;循环淡水再流经机上的气液换热器,冷却来自低压压气机的空气。
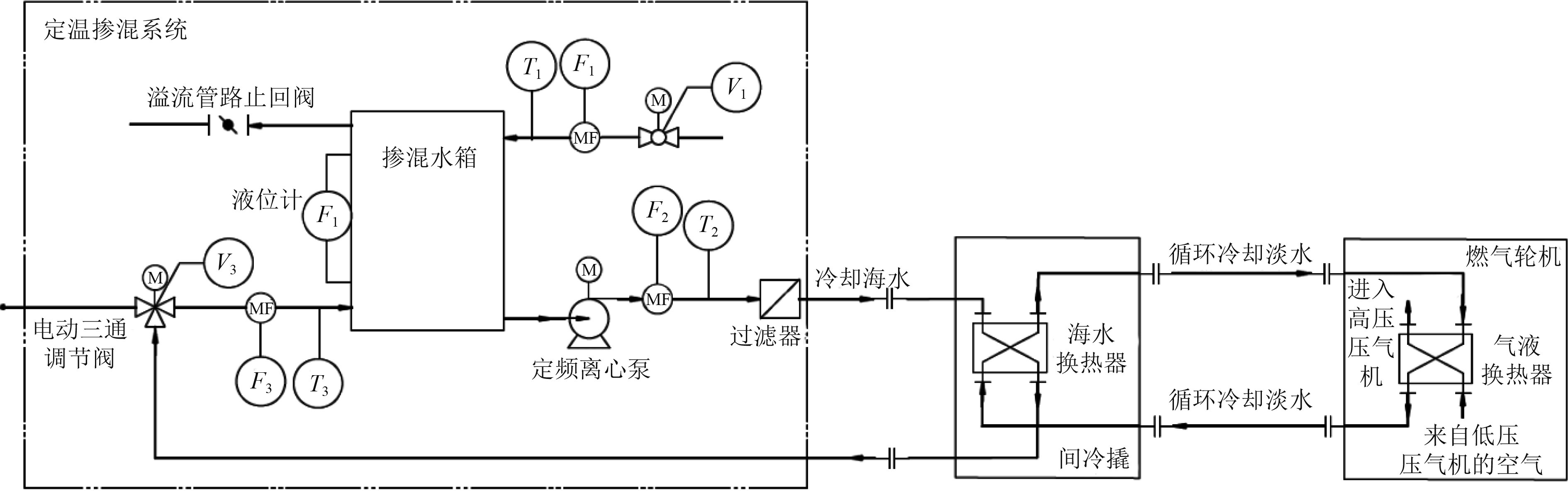
|
图 1 海水换热器定温掺混系统示意图 Fig. 1 Schematic diagram of constant temperature mixing system of seawater heat exchanger |
流入海水换热器的海水流量可以通过定频离心泵调节,海水换热器的定温掺混系统的被控变量包括流入海水换热器的海水温度和掺混水箱的液位,通过调节掺混水箱进口调节阀和回水三通调节阀来实现。
对图1中定温掺混控制系统设计需要用到的一些测量、控制装置及变量进行简要描述:
假设海水的密度为定值,则控制掺混水箱内的液位恒定等同于控制水箱内水的质量保持恒定。定温掺混系统闭环控制目标为设计海水冷水进水的控制阀
不考虑水箱与环境的热交换,根据图1所描述的掺混水箱的冷热水物理热量交换原理,可得:
| $ \frac{{{\rm{d}}M}}{{{\rm{d}}t}} = {F_1} - {F_2} + {F_3},$ | (1) |
| $ \frac{{{\rm{d}}MT}}{{{\rm{d}}t}} = {F_1}{T_1} - {F_2}{T_2} + {F_3}{T_3}。$ | (2) |
由于出水温度与水箱内混合水的温度相同即
| $ \frac{{{\rm{d}}M}}{{{\rm{d}}t}}{T_2} + M\frac{{{\rm{d}}{T_2}}}{{{\rm{d}}t}} = {F_1}{T_1} - {F_2}{T_2} + {F_3}{T_3} ,$ | (3) |
将式(1)代入到式(3)中可得:
| $ M\frac{{{\rm{d}}{T_2}}}{{{\rm{d}}t}} = {F_1}({T_1} - {T_2}) + {F_3}({T_3} - {T_2}),$ | (4) |
当定温掺混系统运行时,存在:
| $ {T_1} < {T_2} < {T_3}。$ | (5) |
根据式(1)、式(4)和式(5)可知,在系统运行过程中,流入水箱中的冷水流量
为了实现解耦控制,首先定义虚拟流量
| $ {F_V} = {F_1} + {F_3},$ | (6) |
| $ {T_V} = \frac{{{F_1}{T_1} + {F_3}{T_3}}}{{{F_V}}} 。$ | (7) |
将式(6)~式(7)代入到式(1)和式(4)中,可以得到:
| $ \frac{{{\rm{d}}M}}{{{\rm{d}}t}} = {F_V} - {F_2},$ | (8) |
| $ \frac{{{\rm{d}}{T_2}}}{{{\rm{d}}t}} = \frac{{{F_V}}}{M}({T_V} - {T_2})。$ | (9) |
定义
| $ M(s) = \frac{1}{s}({F_V}(s) - {F_2}(s)),$ | (10) |
| $ {T_2}(s) = \frac{1}{{{T_m}s + 1}}{T_V}(s)。$ | (11) |
根据式(10)~式(11),以
本文设计的定温掺混系统解耦控制结构如图2所示。图中解耦算法公式如下:
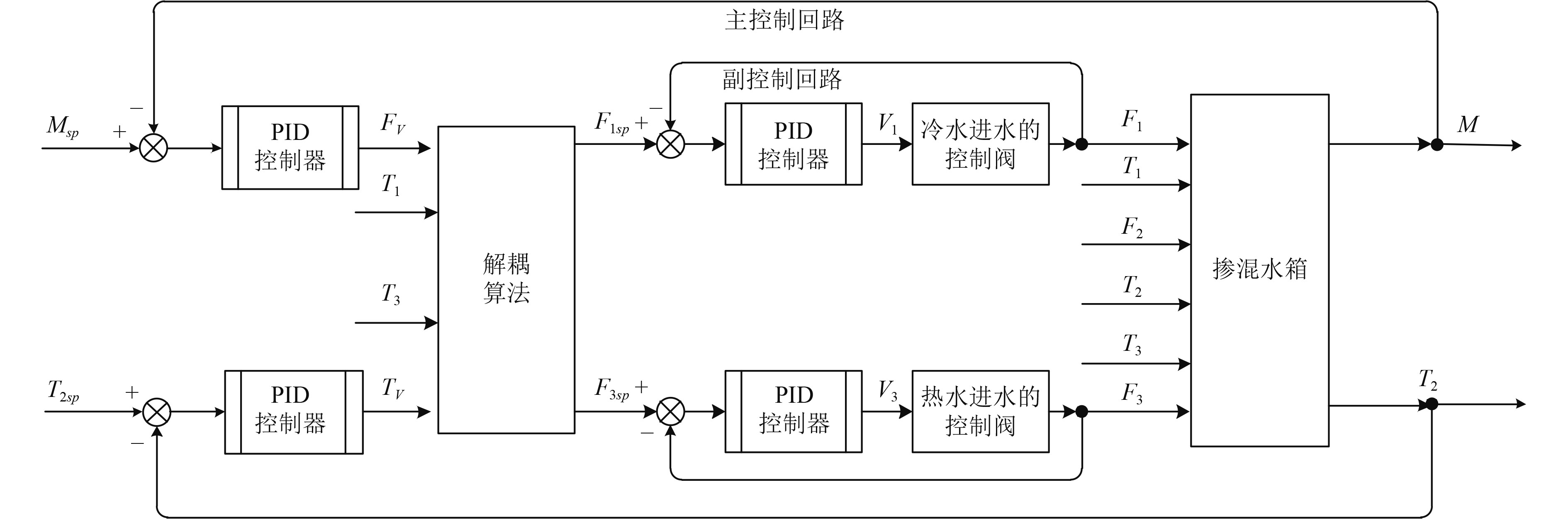
|
图 2 定温掺混系统控制结构图 Fig. 2 Control structure diagram of constant temperature mixing system |
| $ {F_{1sp}} = {F_V}\frac{{{T_3} - {T_V}}}{{{T_3} - {T_1}}},$ | (12) |
| $ {F_{3sp}} = {F_V}\frac{{{T_V} - {T_1}}}{{{T_3} - {T_1}}}。$ | (13) |
以
将本文所设计定温掺混系统应用在某型间冷循环燃气轮机综合性能验证试验台上,在高工况时,海水换热器定温掺混系统控制的目标设定值为:
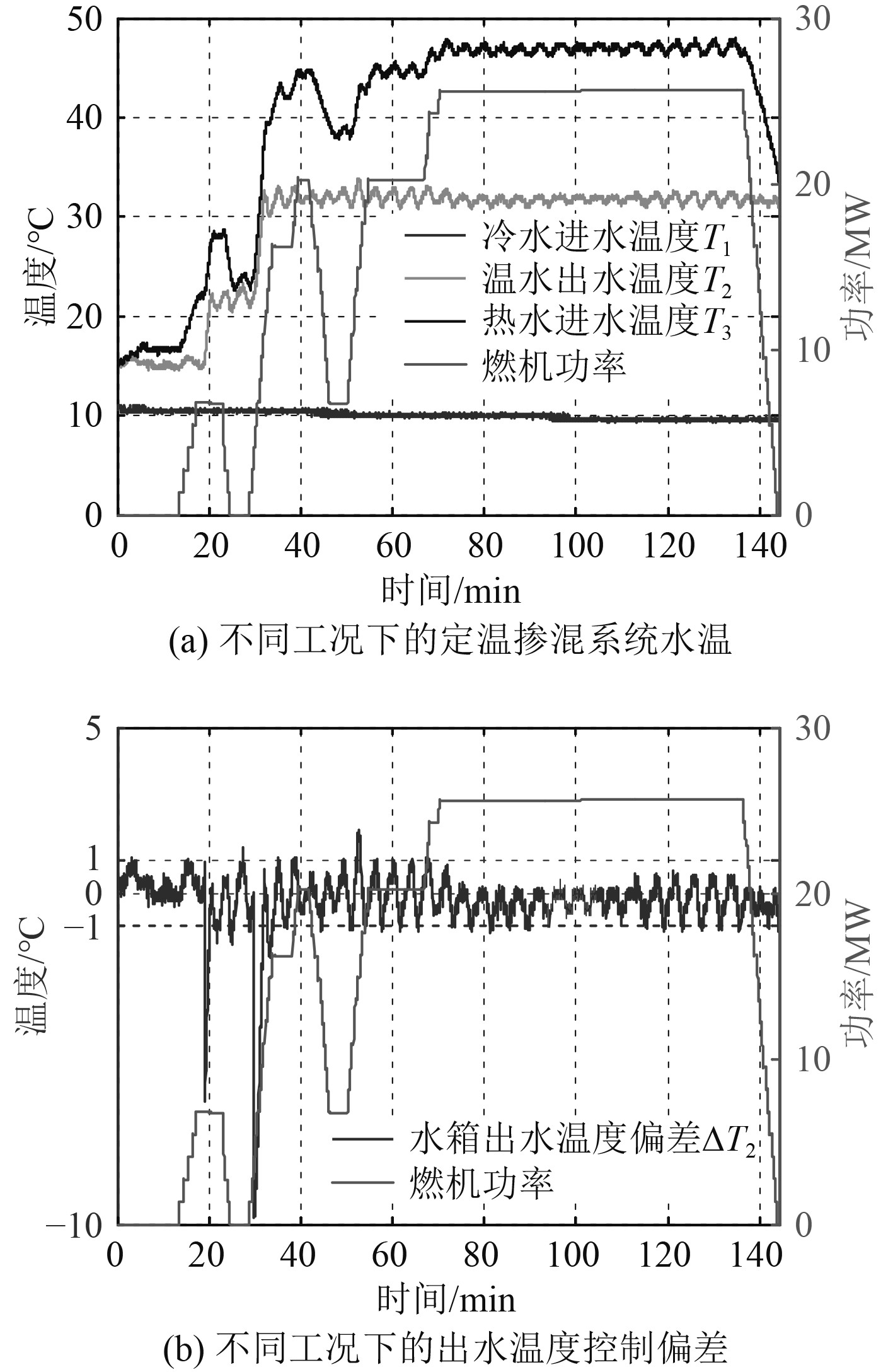
|
图 3 不同工况下的定温掺混系统水温及控制偏差 Fig. 3 Water temperature of constant temperature mixing system under different working conditions |
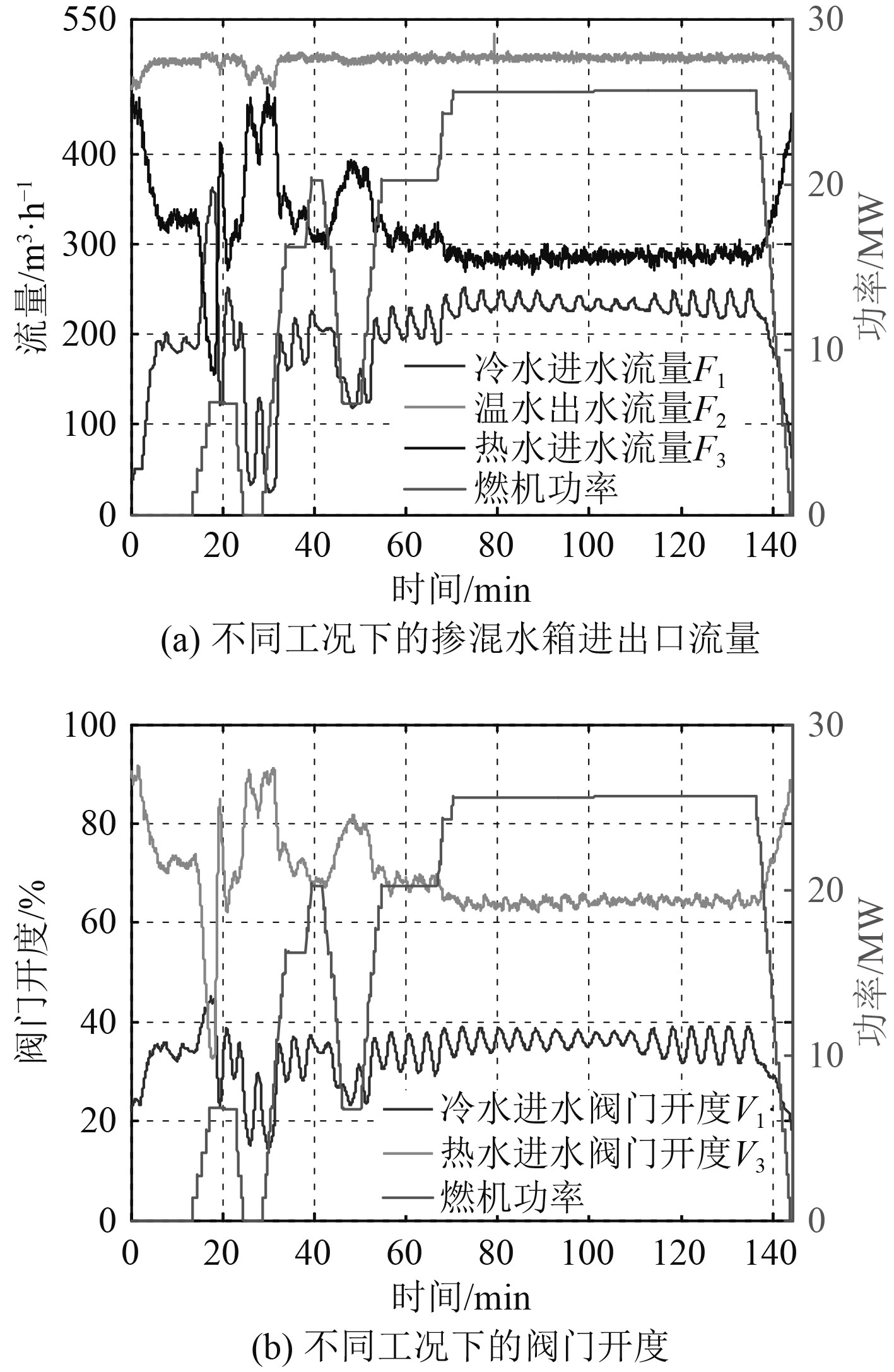
|
图 5 不同工况下的掺混水箱进出水流量及阀门开度 Fig. 5 Inlet and outlet flow of mixing tank and opening of the valve under different working conditions |
图3(a)为燃机不同功率下掺混水箱进水及出水温度的曲线。可以看出,随着燃机工况的不断升高,经过海水换热器热交换后的热水温度逐渐升高,但经过冷、热水掺混后的供水温度始终能稳定保持在设定值附近。图3(b)为不同工况下掺混水箱出水温度控制偏差曲线。可以看出,在稳态情况下,温度偏差可以控制在±1℃以内。图中的2个偏差较大的尖峰区域是由设定值突变引起的,在20 min左右,操作员将设定值由15℃改为22℃,在30 min左右,操作员将设定值由22℃改为32℃。而实际的水温控制是缓慢渐变的,所以产生了较大的控制偏差。
图4为不同工况下掺混水箱的液位变化及控制偏差曲线。从2个图片可以看出,无论燃机处于何种工况,所设计的控制器均能保证掺混水箱液位保持稳定,液位的控制偏差在
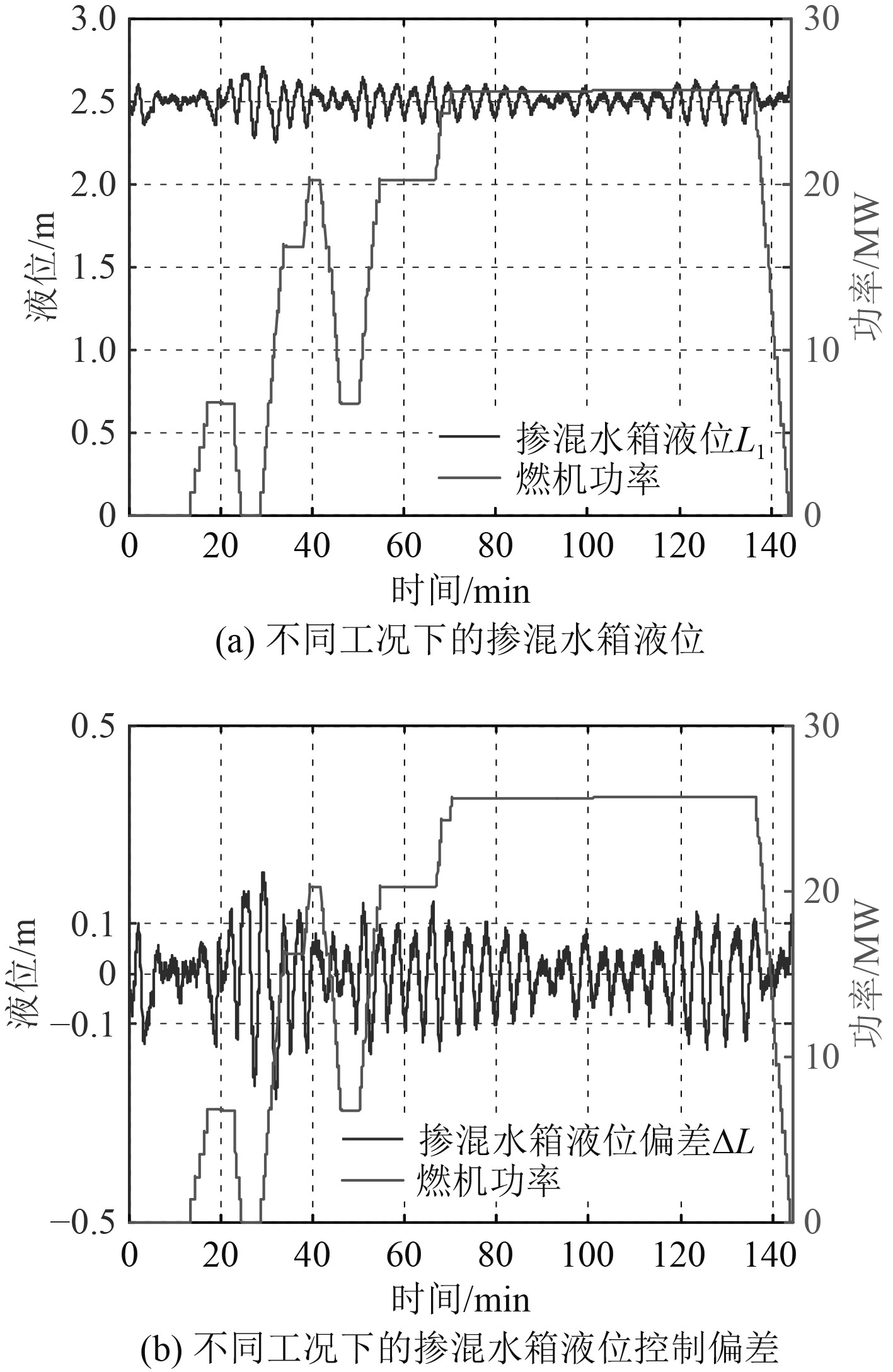
|
图 4 不同工况下的掺混水箱液位及控制偏差 Fig. 4 Mixing tank level under different working conditions |
图5(a)为不同工况下掺混水箱进水及出水流量的变化。图5(b)为不同工况下掺混水箱冷、热水进水控制阀门的调节开度。温水出水流量在定频离心泵的作用下基本保持不变,而冷、热水的进水流量的曲线形式与2个控制阀门的曲线形式类似,在温度设定值发生突变的2个时间点,为了保证供水温度尽快跟踪设定值,2个控制阀门均发生了较大幅度的变化。当温度逐步趋近于稳态值后,控制阀门的变化幅度也随之减小。
4 结 语1)针对船用间冷循环燃气轮机海水换热器的多输入多输出定温掺混系统,基于该系统的数学模型及实际物理状态,通过引入虚拟控制量完成了对整个控制回路的解耦。解耦后的模型便于采用经典的控制算法进行设计。
2)通过在某型船用间冷循环燃气轮机整机综合试验台的试验验证,所设计的海水换热器进口水温以及掺混水箱液位调节的解耦PID控制器,在不同的燃机工况下均能取得比较好的解耦控制效果,满足海水换热器的工作要求。
| [1] |
闻雪友, 肖东明. IC循环船用燃气轮机的可行性研究[J]. 热能动力工程, 2009, 24(1): 60-64+142-143. |
| [2] |
闫大海, 张晗. 船用燃气轮机发展趋势分析[J]. 舰船科学技术, 2021, 43(10): 84-88. YAN D H, ZHANG H. Development trend analysis of marine gas turbine[J]. Ship Science and Technology, 2021, 43(10): 84-88. |
| [3] |
刘瑞. 基于集成仿真的间冷循环燃气轮机性能优化及控制策略研究 [D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [4] |
李铁磊, 刘瑞, 王志涛, 等. 间冷循环燃气轮机集成仿真及优化匹配方法[J]. 哈尔滨工程大学学报, 2021, 42(8): 1195-1202. LI T L, LIU R, WANG Z T, et al. Integrated simulation and optimization matching methods of intercooled gas turbines[J]. Journal of Harbin Engineering University, 2021, 42(8): 1195-1202. DOI:10.11990/jheu.202005028 |
| [5] |
李贝贝, 李飞, 张晓云. 燃气轮机间冷器设计及试验研究[J]. 热能动力工程, 2019, 34(1): 23-26+50. LI B B, LI F, ZHANG X Y. Design and experimental study for gas turbine intercooler[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(1): 23-26+50. |
| [6] |
周爱国, 曾智杰, 乌建中, 等. 风电叶片多点静力测试神经网络PID解耦控制[J]. 测控技术, 2021, 40(3): 123-129. ZHOU A G, ZENG Z J, WU J Z, et al. Neural network pid decoupling control for multi-point static test of wind turbine blades[J]. Measurement & Control Technology, 2021, 40(3): 123-129. |
| [7] |
张玉雪, 周军, 皇攀凌, 等. 改进粒子群的中药提取模糊PID解耦控制研究[J]. 控制工程, 2021, 1-8. ZHANG Y X, ZHOU J, HUANG P L, et al. Research on improved particle swarm optimization fuzzy pid decoupling control for extraction of traditional chinese medicine[J]. Control Engineering of China, 2021, 1-8. |
| [8] |
代冀阳, 应进, 李华英, 等. 基于PID网络的航空发动机多变量系统解耦控制[J]. 计算机仿真, 2011, 28(12): 27-31. DAI J Y, YING J, LI H Y, et al. Multivariable system of aeroengines decoupling controller based on PIDNN[J]. Computer Integrated Manufacturing Systems, 2011, 28(12): 27-31. DOI:10.3969/j.issn.1006-9348.2011.12.008 |
| [9] |
LIU H J, HAN P, YAO W Y, et al. The research of PID neural network decoupling controller and its application in unit load system[C]//Proceedings of 2004 International Conference on Machine Learning and Cybernetics, 2004.
|
| [10] |
ZHAI L, CHAI T. Nonlinear decoupling pid control using neural networks and multiple models[J]. Journal of Control Theory and Applications, 2006, 4(1): 62-69. DOI:10.1007/s11768-006-5260-7 |
| [11] |
李磊, 毛志忠, 刘芳. 多模型自适应PID解耦控制器[J]. 东北大学学报(自然科学版), 2010, 31(11): 1546-1549. LI L, MAO Z Z, LIU F. Nonlinear adaptive pid decoupling controller based on multiple models[J]. Journal of Northeastern University( Natural Science), 2010, 31(11): 1546-1549. DOI:10.12068/j.issn.1005-3026.2010.11.007 |
 2022, Vol. 44
2022, Vol. 44
