2. 中国人民解放军92330部队,山东 青岛 266102
2. No. 92330 Unit of PLA, Qingdao 266102, China
UUV水下航行时,由于受到水流等海洋环境相关不确定因素的影响,应用准确的非线性动力学模型对其航行状态进行描述非常困难。建立UUV动力学模型,是对其航行过程实施有效控制的前提和基础。现有解决方法大多是对其模型进行简化处理,主要是忽略模型中的非线性项。但由此带来的问题是在实际应用中易出现袋深过大、跳水等不稳定现象[1]。滑模控制方法由于具备对干扰和摄动具有自适应性和鲁棒性的特点,成为解决非线性系统控制问题的一种有效方法。设计易于工程实现的滑膜控制器时,由于大多采用不连续切换控制律,从而导致系统产生高频颤动,甚至会引起系统失稳[2-3]。而采用模糊控制方法可以很好地解决这个问题,无需建立准确的系统模型,并且对于系统的颤振具有很好的抑制作用[4-5]。
20世纪90年代以来,滑模模糊控制得到了广泛研究和应用,它结合了滑模控制的鲁棒性好、动态过程可预见与模糊控制的不依靠对象模型、一致逼近等优点,有效提高了非线性系统的控制品质[6-8]。但滑模模糊控制器一般都设计比较复杂,难以在实际工程中得以实现。在综合考量控制精度和工程实现的基础上,设计一种UUV水平运动滑模模糊控制器,并进行计算机仿真,验证其控制性能。
1 UUV水平运动模型UUV水平运动方程如下:
| $ \left\{ \begin{split} m{V_0}\dot \varPsi =& (A_z^\beta V_0^2 + T)\beta + A_z^\delta V_0^2{\delta _r} + A_z^\omega {V_0}{\omega _{yB}} +\\ &{\lambda _{33}}{V_0}\dot \beta + {\lambda _{35}}{{\dot \omega }_{yB}},\\ {J_y}{{\dot \omega }_{yB}} = &A_{my}^\beta V_0^2\beta - A_z^\delta V_0^2{\delta _r} - A_{myB}^\omega {V_0}{\omega _{yB}} -\\ &{\lambda _{55}}{{\dot \omega }_{yB}} - {\lambda _{35}}{V_0}\dot \beta + T{z_b},\\ \dot \psi = &{\omega _{yB}},\\ {{\dot z}_e} = & - {V_0}\sin \varPsi ,\\ \varPsi =& \psi - \beta 。\end{split} \right. $ | (1) |
改写成标准形式:
| $ \left[ \begin{gathered} {\dot \beta } \\ {{\dot \omega }_{yB}} \\ {\dot \psi } \\ {{\dot z}_e} \\ \end{gathered} \right] = \left[ \begin{gathered} {k_{41}}\beta + {k_{42}}{\omega _{yB}} + {k_{43}}{\delta _r} + {k_{44}} \\ {k_{51}}\beta + {k_{52}}{\omega _{yB}} + {k_{53}}{\delta _r} + {k_{54}} \\ {\omega _{yB}} \\ - {V_0}\sin (\psi - \beta ) \\ \end{gathered} \right] 。$ | (2) |
式中各参量含义详见文献[9]。令
| $ X = {[{X_1},{X_2},{X_3}]^{\rm{T}}} = {[\beta ,{\omega _{yB}},\psi ]^{\rm{T}}},$ | (3) |
设其平衡状态为
| $ e = {[{e_1},{e_2},{e_3}]^{\rm{T}}} = {[\beta - {\beta _0},{\omega _{yB}} - {\omega _{yB0}},\psi - {\psi _0}]^{\rm{T}}}。$ | (4) |
针对式(2)所示的二阶非线性水平运动方程,构建如下控制规律[10]:
| $ u = k{\rm{sat}}\left(\frac{s}{\varphi }\right) + {u_{eq}}。$ | (5) |
式中:
| $ s = \dot e + \lambda e,$ | (6) |
式中,
构造李雅普诺夫函数:
| $ V = \frac{1}{2}{s^2}。$ | (7) |
若使系统能够趋近并稳定于滑模面
此滑模控制器具备对外部扰动和系统不确定性具有良好的鲁棒性等优点,但也存在可能产生较为明显的抖振现象等缺点[11]。
2.2 滑模模糊控制器设计非线性控制器,需要解决2个关键问题:1)系统切换曲线的获取,可以利用仿真或开环试验获取此曲线;2)控制器参数的设计,为兼顾控制器的精度和实现难度,可以采用模糊控制器,如Takagi−Sugeno(TS)型模糊控制器[12]。
为提高模糊控制器对水流等外部扰动因素的鲁棒性,将模糊控制和滑模控制结合起来,根据系统滑动模态设计控制器的规则,系统的控制量由模糊控制器的输出确定。综合考虑控制精度与工程实现难度,设计如下模糊规则:
| $ \begin{split}{R_i} :&{\rm{if}}\;e\;{\rm{is}}\;{A_i} \; {\rm{then}}\\ & \begin{split} {u_i} = k{\rm{sat}}\left(\frac{{{s_i} + {c_i}}}{{{\varphi _i}}}\right) =& k{\rm{sat}}\left(\frac{{\dot e + {\lambda _i}e + {c_i}}}{{{\varphi _i}}}\right),\\ & i = - 2, - 1,0,1,2。\end{split}\end{split} $ | (8) |
式中:ci为偏移量,其他参数含义同前,各参数由系统仿真试验确定。
2.3 水平运动滑模模糊控制器设计对于UUV水平运动,
| $ \begin{split}{R_i} :& {\rm{if}}\; {e_3}\; {\rm{is}}\; {A_i} \; {\rm{then}}\\ & \begin{split} {\delta _{ri}} = k{\rm{sat}}\left(\frac{{{s_i} + {c_i}}}{{{\varphi _i}}}\right) = & k{\rm{sat}}\left(\frac{{{\lambda _{3i}}{e_3} + {e_2} + {c_i}}}{{{\varphi _i}}}\right),\\ & i = - 2, - 1,0,1,2。\end{split}\end{split} $ | (9) |
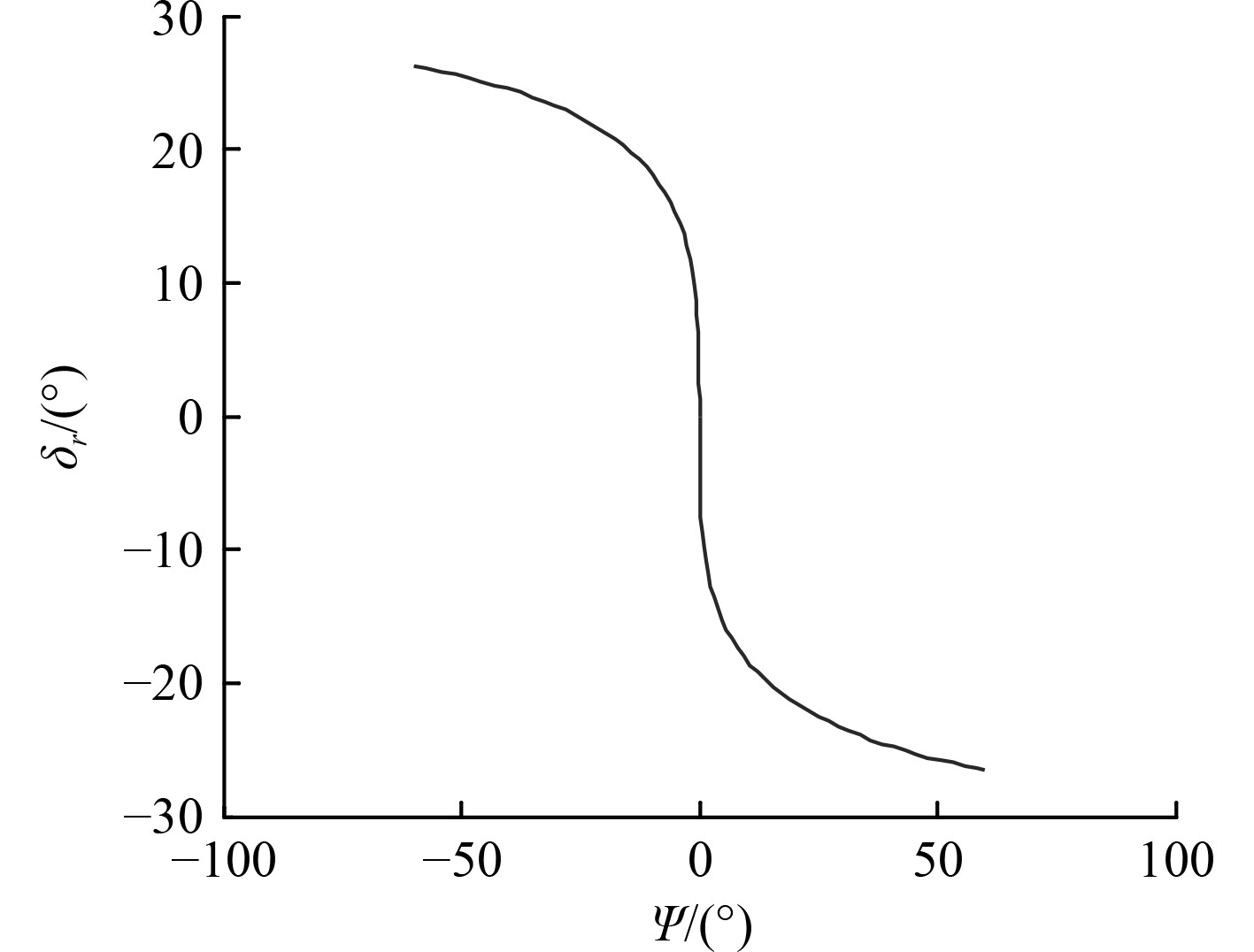
设UUV直舵角最大限值为30°,根据水平运动方程,经计算机仿真,可得直舵角与偏航角的响应曲线如图1所示。
|
图 1
直舵角与偏航角响应曲线
Fig. 1
The relationship between
|
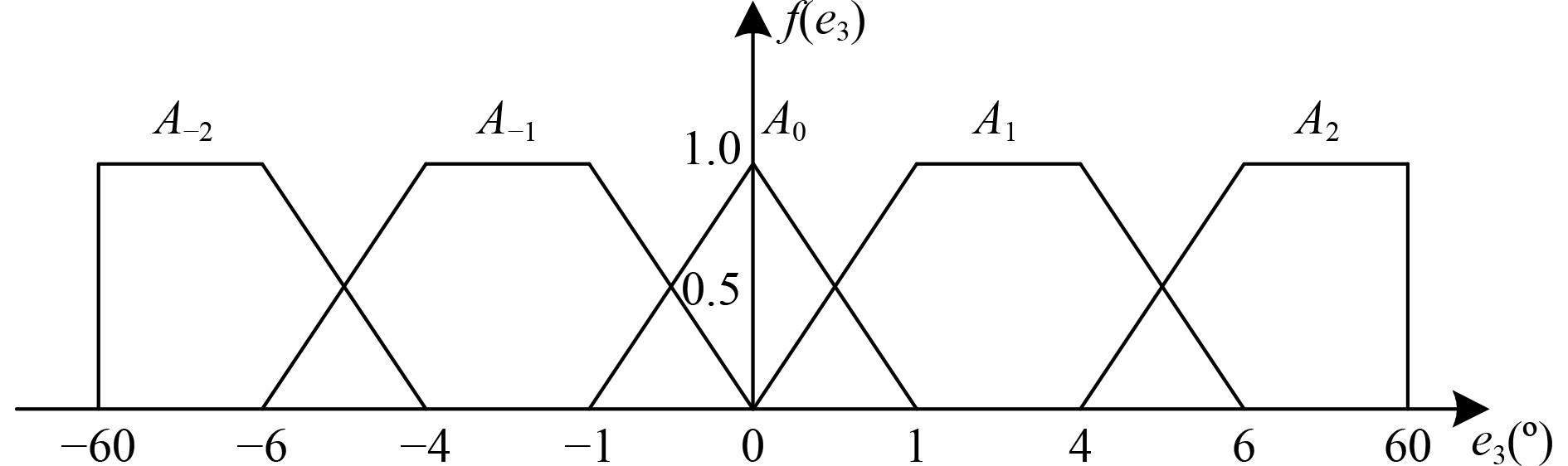
设定输入量
|
图 2
偏航角误差
|
按如下原则确定滑模模糊控制器参数:由图1中曲线斜率确定
|
|
表 1 |
表中,
UUV水平运动包括水平定角航行和水平旋回航行。以国外某UUV为例,其参数详见文献[9],分别对以上2种航行模式下,在前面设计的滑模模糊控制器作用下的航行情况进行仿真。此外,为探讨UUV在无干扰和有干扰情况下的控制品质,分别对流体动力系数无扰动和有扰动条件下的航行情况进行仿真,并与比例控制下的仿真结果进行比较。
3.1 水平定角航行仿真分析设UUV航速为
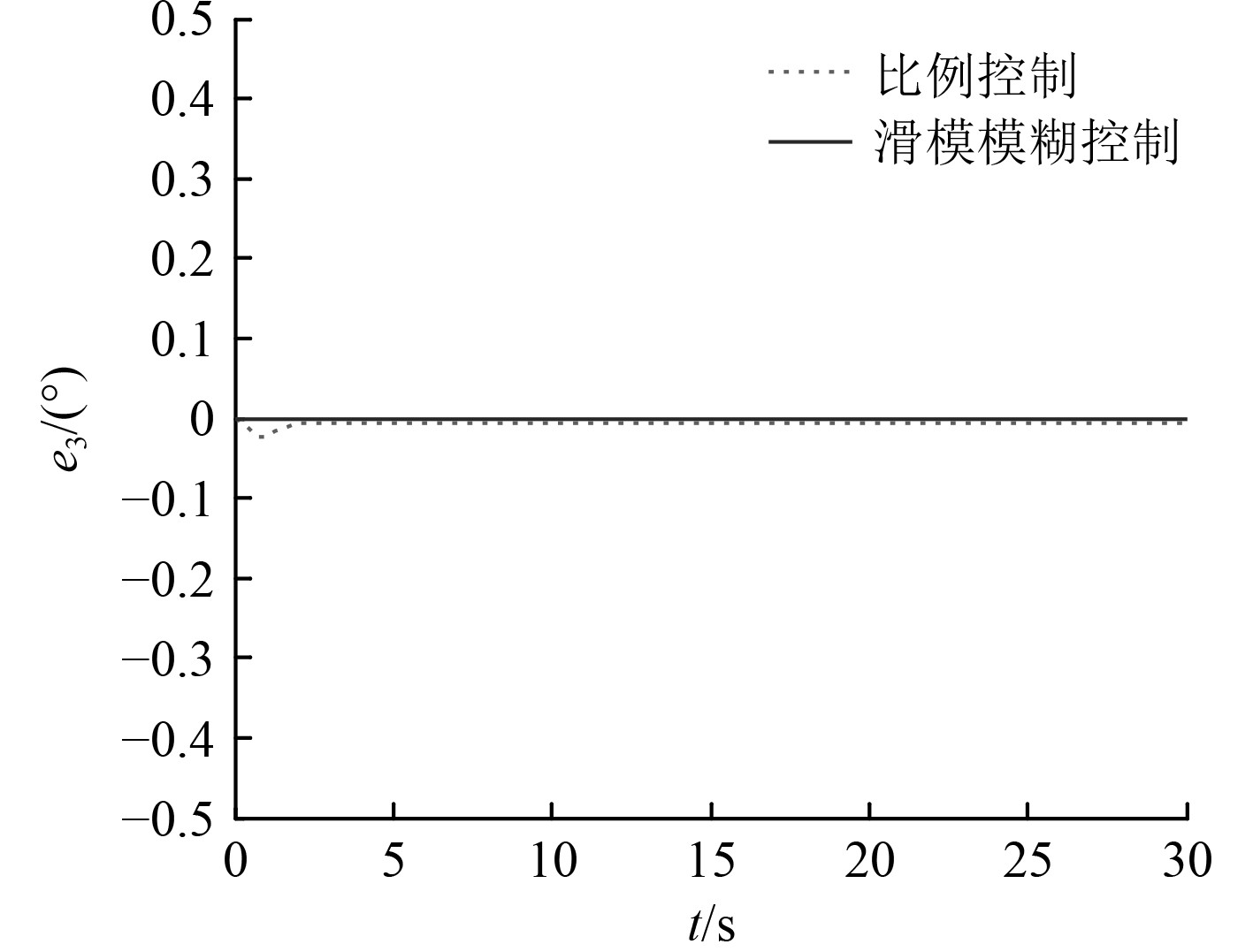
|
图 3 无干扰时UUV航向角误差对比图 Fig. 3 Compare of heading error without disturbance |
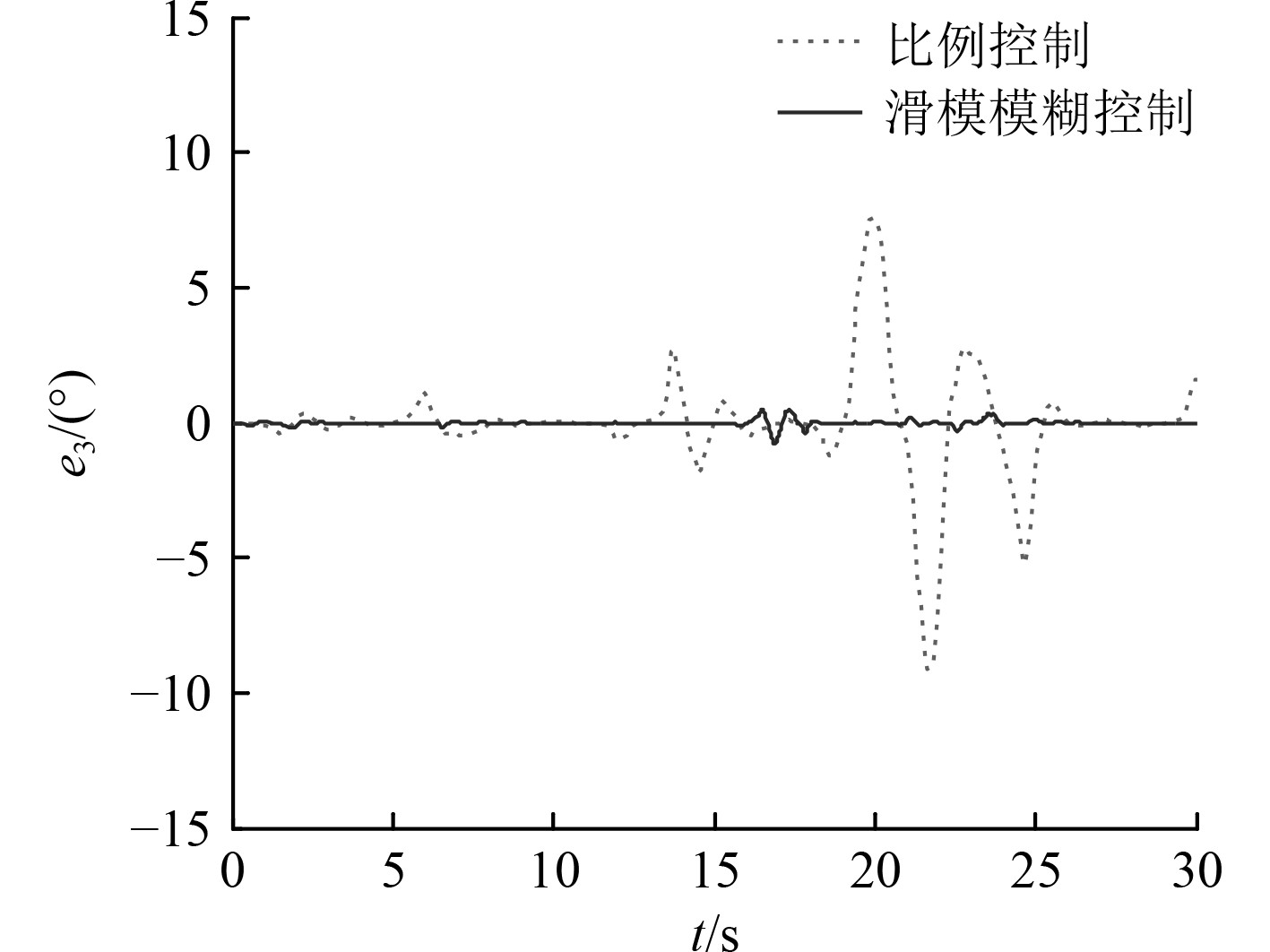
|
图 4 有干扰时UUV航向角误差对比图 Fig. 4 Compare of heading error with disturbance |
可知,无干扰时,2种控制方法都能很好地控制UUV以设定偏航角平稳航行。当存在流体动力扰动时,比例控制下,UUV偏航角产生较大振荡,最大误差达到9.16°。而滑模模糊控制下,UUV基本保持以设定偏航角航行,偏航角振荡很小,最大误差仅为0.77°。
3.2 水平旋回航行仿真分析UUV进行水平旋回运动时,偏航角误差
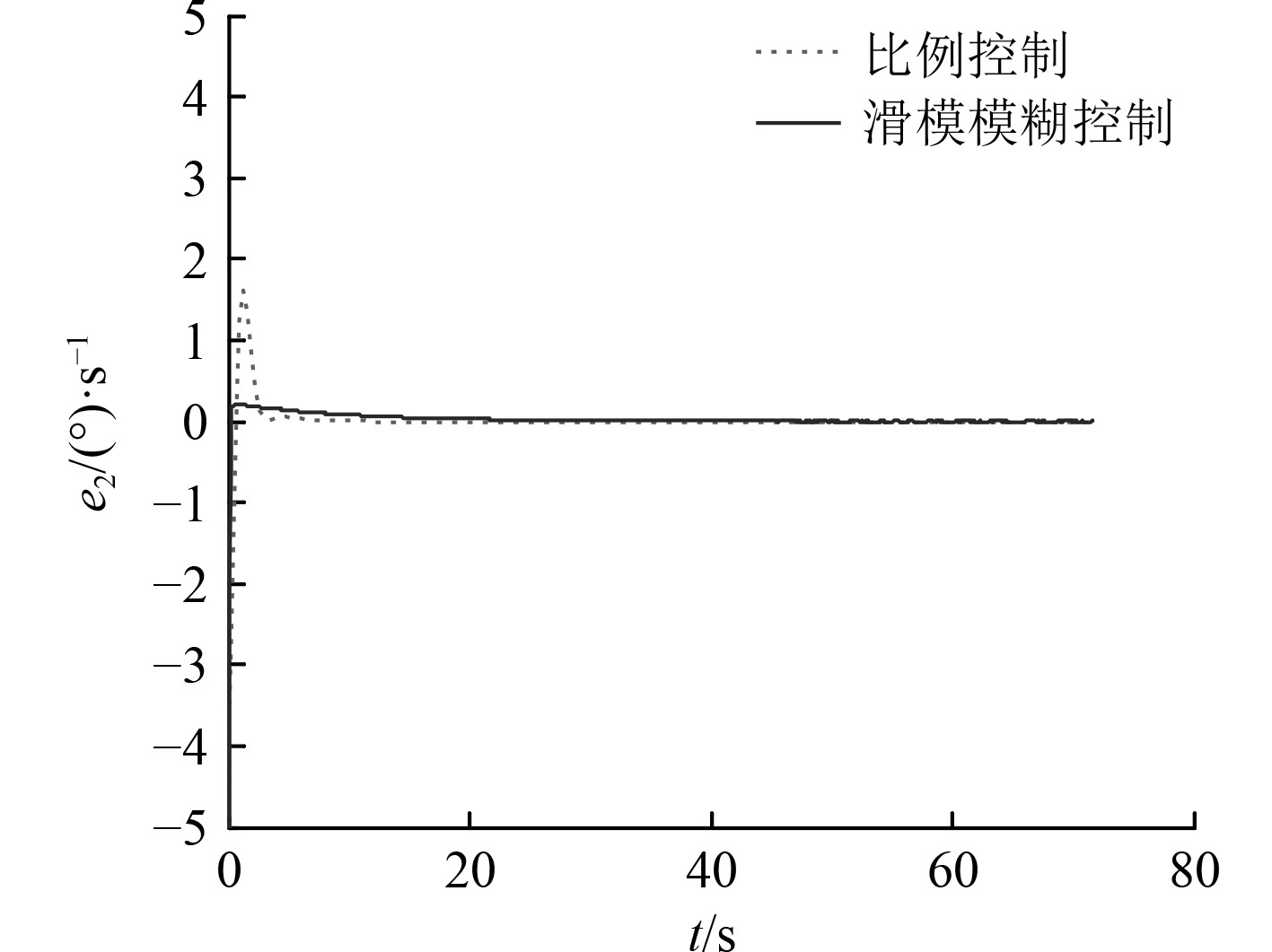
|
图 5 无干扰时UUV旋回角速度误差对比图 Fig. 5 Compare of turnning angular velocity error without disturbance |
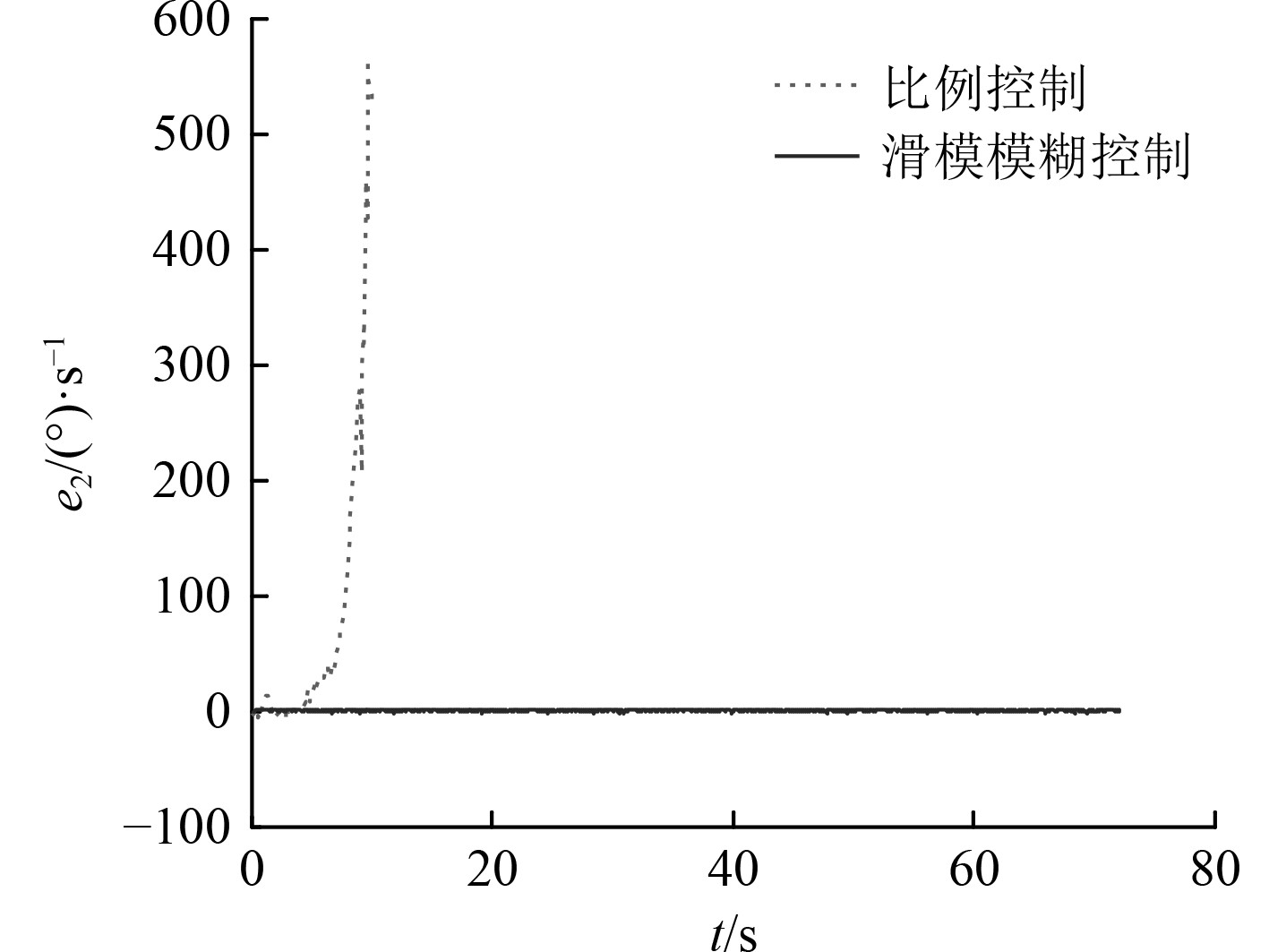
|
图 6 有干扰时UUV旋回角速度误差对比图 Fig. 6 Compare of turnning angular velocity error with disturbance |
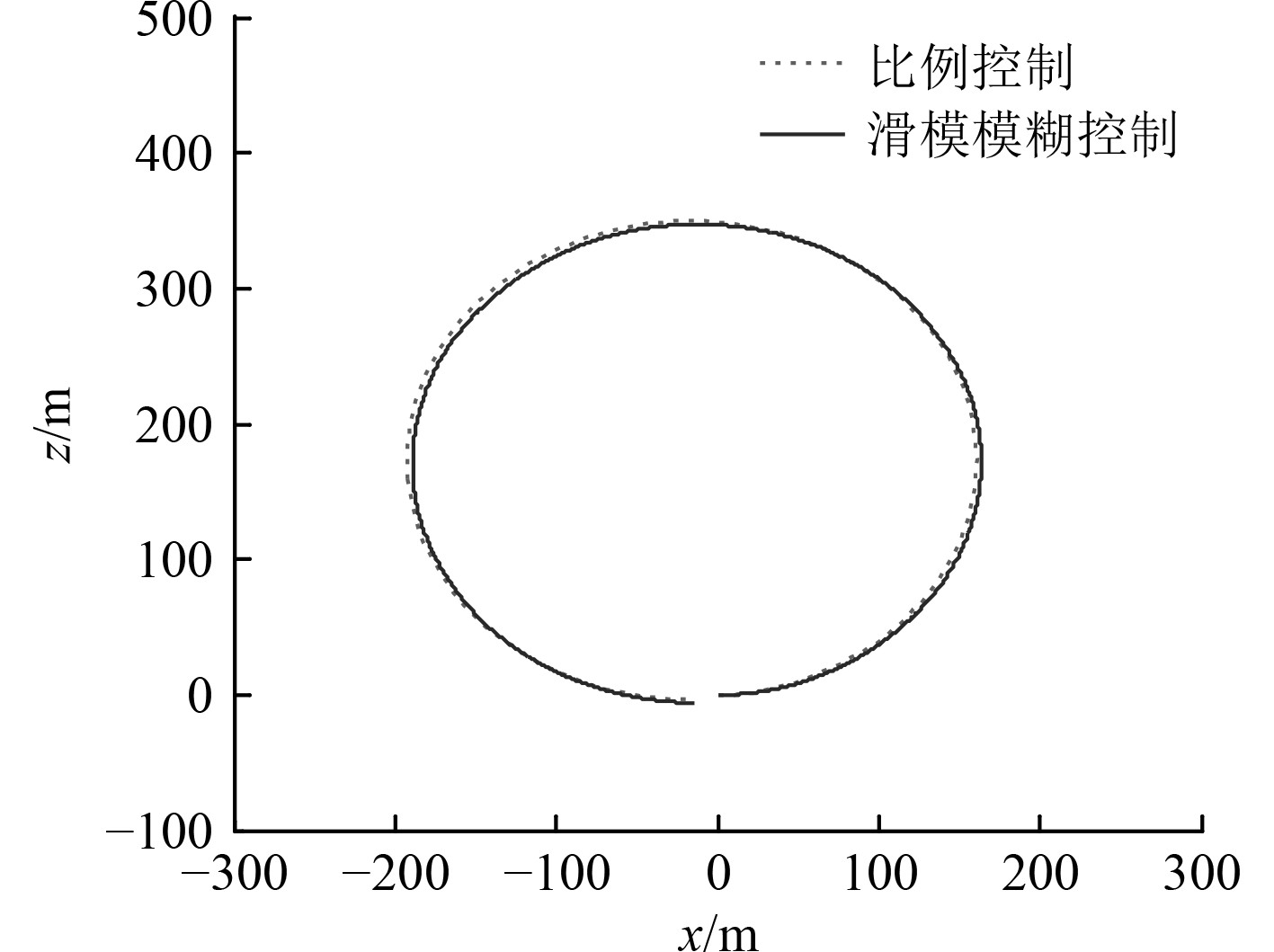
|
图 7 无干扰时UUV水平旋回航行轨迹对比图 Fig. 7 Circle Trajectory Compare without Disturbance |
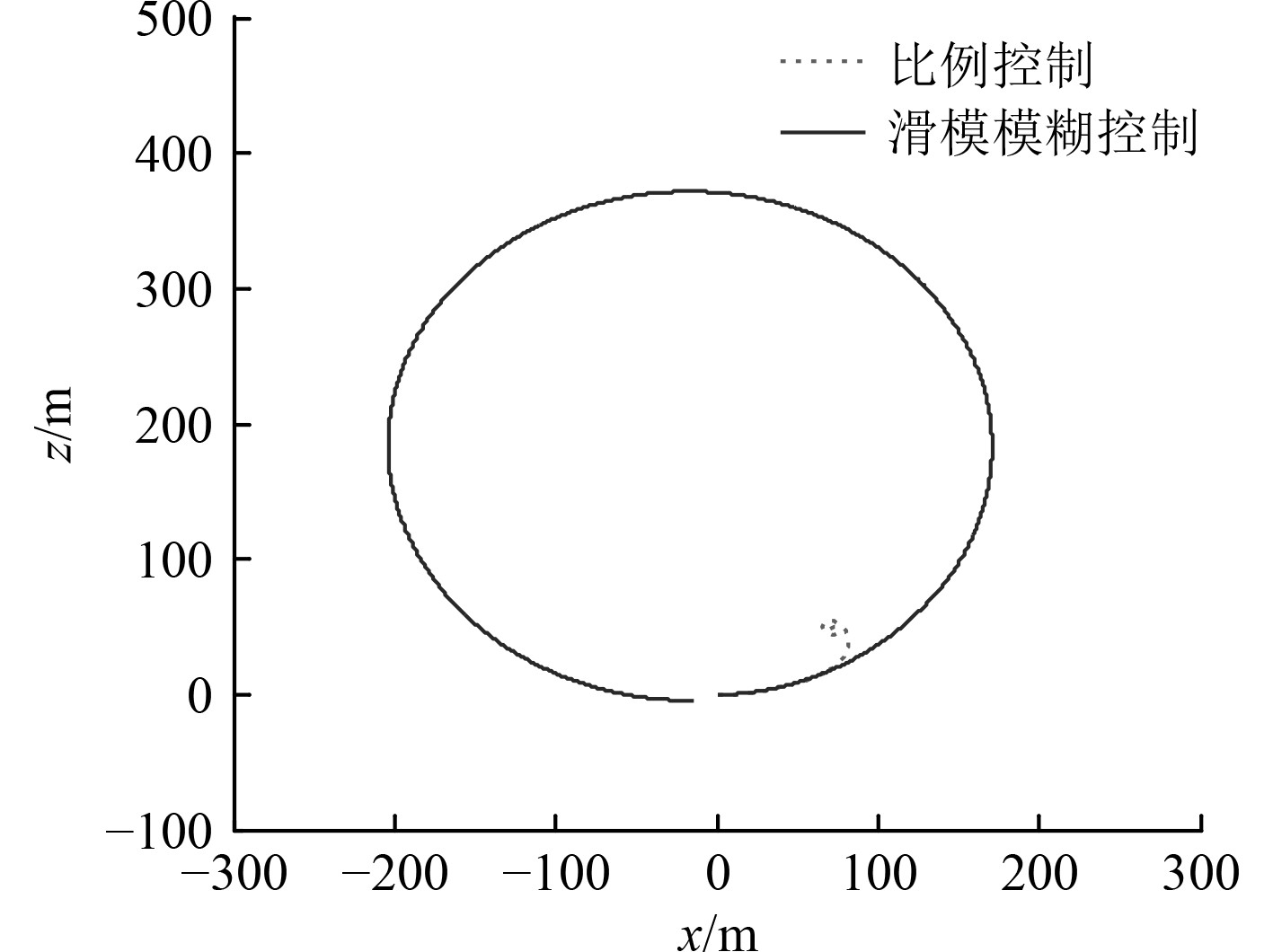
|
图 8 有干扰时UUV水平旋回航行轨迹对比图 Fig. 8 Circle Trajectory Compare with Disturbance |
可知,无干扰时,2种控制方法都能控制UUV完成旋回航行,其旋回角速度和旋回半径基本相同,都与设定值基本吻合。当存在流体动力扰动时,比例控制下,UUV旋回角速度发散,致使其无法完成旋回运动;而模糊滑模控制下,UUV依然能够以设定角速度完成旋回运动。
4 结 语本文利用滑模模糊方法设计UUV水平运动控制器,不需要建立精确的系统动力学模型,通过仿真实验确定模糊规则表,控制器设计简单,易于工程实现。经仿真实验并与比例控制进行对比,结果表明,在无干扰情况下,UUV在2种控制器作用下,航行姿态相似,都能按预定航路稳态航行。加入流体随机扰动后,比例控制下,UUV水平定角运动会产生较大幅度振荡,水平旋回运动甚至出现失稳现象。滑模模糊控制下,UUV依然能够保持按预定航路稳定航行,震颤很小,证明该控制器具有良好的鲁棒性。
| [1] |
丰少伟, 杨云生, 刘佳. 航深对水下航行体动力性能的影响及改善方法[J]. 四川兵工学报, 2015, 36(6): 7-10. |
| [2] |
杨晓骞, 李健, 董毅. 非线性不确定系统的非奇异快速终端滑模控制[J]. 控制理论与应用, 2016, 33(6): 772-778. DOI:10.7641/CTA.2016.15102 |
| [3] |
王建敏, 董小萌, 吴云洁. 高超声速飞行器RBF神经网络滑模变结构控制[J]. 电机与控制学报, 2016, 20(5): 103-110. |
| [4] |
李兴格, 李刚, 熊思宇. 不确定参数摄动的高超声速飞行器滑模控制[J]. 导弹与航天运载技术, 2019, 36(12): 70-78. DOI:10.7654/j.issn.1004-7182.20190614 |
| [5] |
葛红豆, 赫雷, 曹雏清, 等. 基于模糊PID 控制的AGV控制[J]. 兵工自动化, 2017, 36(12): 76-79. |
| [6] |
孙巧梅, 陈金国, 余万. 基于模糊自适应滑模方法的AUV 轨迹跟踪控制[J]. 舰船科学技术, 2017, 39(12): 53-58. DOI:10.3404/j.issn.1672-7649.2017.12.012 |
| [7] |
魏延辉, 周卫祥, 贾献强, 等. AUV 模型解耦水平运动多控制器联合控制[J]. 华中科技大学学报(自然科学版), 2016, 44(4): 37-42. |
| [8] |
邢晓波, 胡剑波, 王应洋, 等. 一类非线性系统的模糊自适应反推滑模控制[J]. 空军工程大学学报(自然科学版), 2018, 19(1): 104-110. |
| [9] |
严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2002: 3−47.
|
| [10] |
TIAN Q Y, WEI J H, FANG J H. Adaptive fuzzy integral sliding mode velocity control for the cutting system of atrench cutter[J]. Frontiers of Information Technology & Electronic Engineering, 2016(6): 55-66. |
| [11] |
LI Q C, ZHANG W S, HAN G F. Fuzzy sliding mode control guidance law with terminal impact angle and acceleration constraints[J]. Journal of Systems Engineering and Electronics, 2016, 27(3): 664-679. DOI:10.1109/JSEE.2016.00070 |
| [12] |
丁浩, 黄波, 崔沁青. 一种水下航行体纵向运动控制方法研究[J]. 兵器装备工程学报, 2021, 42(4): 179-182. DOI:10.11809/bqzbgcxb2021.04.033 |
 2022, Vol. 44
2022, Vol. 44

