2. 北京石油化工学院 安全工程学院,北京 102617;
3. 风帆有限责任公司,河北 保定 071051
2. School of Safety Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China;
3. FENGFAN Co., Ltd., Baoding 071051, China
近年来,随着国家“海洋强国”战略的提出,以及海洋资源与经济的不断发展,我国海洋领域的研究内容也从近海区域逐渐迈向深远海[1]。由于深远海环境复杂,各类救助作业面临着史无前例的挑战[2]。深远海溢油事故一旦发生,会给海洋环境造成相比近海更严重的污染[3]和恶劣的社会影响,同时还会对海洋生态系统产生无法挽回的破坏。因此,为确保深远海溢油回收作业平稳顺利完成,对可能导致作业失败过程的发展路径进行研究具有重要意义。
海洋环境污染的风险随着海洋作业的发展不断增大,学界对海洋作业风险的评估研究也在不断深入。岳汉秋等[4]运用层次分析法建立了附近海域的评价指标体系,并通过建立自动化数据处理流程对海域溢油事故的风险进行了模糊综合评价。汪守东等[5]提出了一种可以用于分析油品码头空间分部及其海域溢油风险分布规律的溢油风险模拟与评估方法。吴瑞杰[6]通过对溢油事故构建模型推导事故发生的概率,并对溢油风险进行评价。郭兴华等[7]考虑到海上溢油风险的不确定性以及“样本少”、“信息少”等特点,采用模糊灰色综合评价法对海上船舶溢油风险进行评估,并提出了加强船舶溢油风险监控的有效建议。张聪等[8]根据不同类型的海上溢油事故提出了针对性的管控措施,为后续海上油田的溢油风险安全管理提出了技术支持。
目前的学者多注重于研究溢油回收作业的安全风险评估等,缺乏以提高溢油回收作业成功率为主体的研究,且目前针对深远海溢油事故的研究也较少。因此,本文针对影响溢油回收作业的内部风险因素相互作用的特性,基于模糊Petri网提出一种多层模糊变权Petri网模型。该模型不仅能够将复杂的问题进行分层计算,还能够基于变权使风险因素的风险值根据事态变化更新,从而更有条理、更准确进行事故演化分析,推演出最有可能导致事故发生的根本原因和传播路径,为救援人员能够安全高效地进行溢油回收作业提供理论依据。本文研究流程如图1所示。
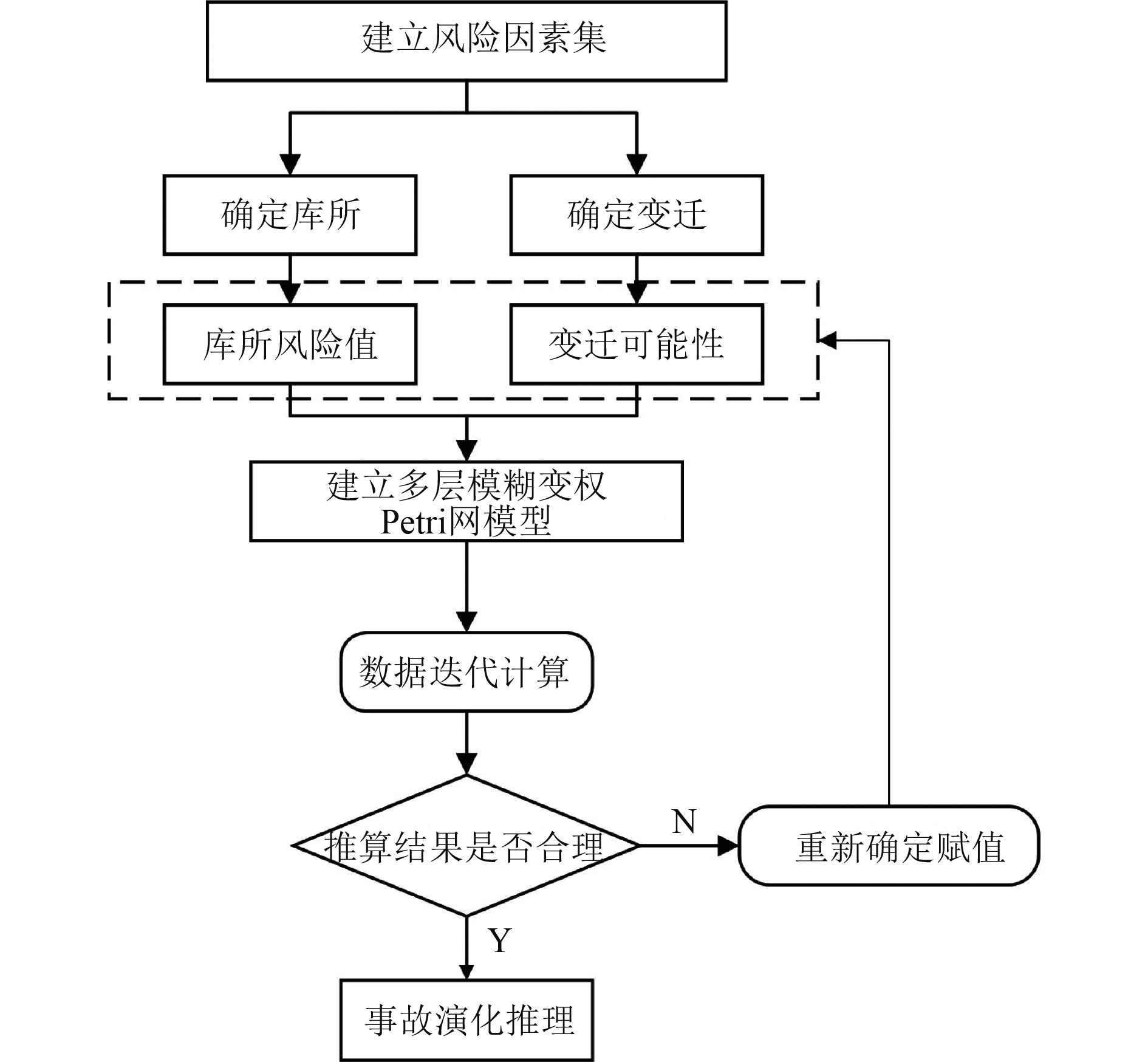
|
图 1 使用方法流程图 Fig. 1 Flow chart of the proposed method |
Petri 网(petri nets, PN)是一种用于分析、描述和模拟系统流程的模型工具。一个基本的Petri网模型主要有3个元素,分别为库所、变迁和有向弧。
模糊 Petri 网(fuzzy petri nets, FPN)是在Petri网的基础上补充了模糊理论和模糊推理判断,可以更容易地处理研究对象的模糊性[9]。模糊Petri网的传播规则是模糊变迁触发规则,利用模糊变迁规则将风险因素之间的逻辑关系转换为FPN模型的有向线。
1.2 网络模型图介绍任何一种FPN模型都会严格遵守PN的规范化图形表示方法,图2为PN规范图形示意图[10]。
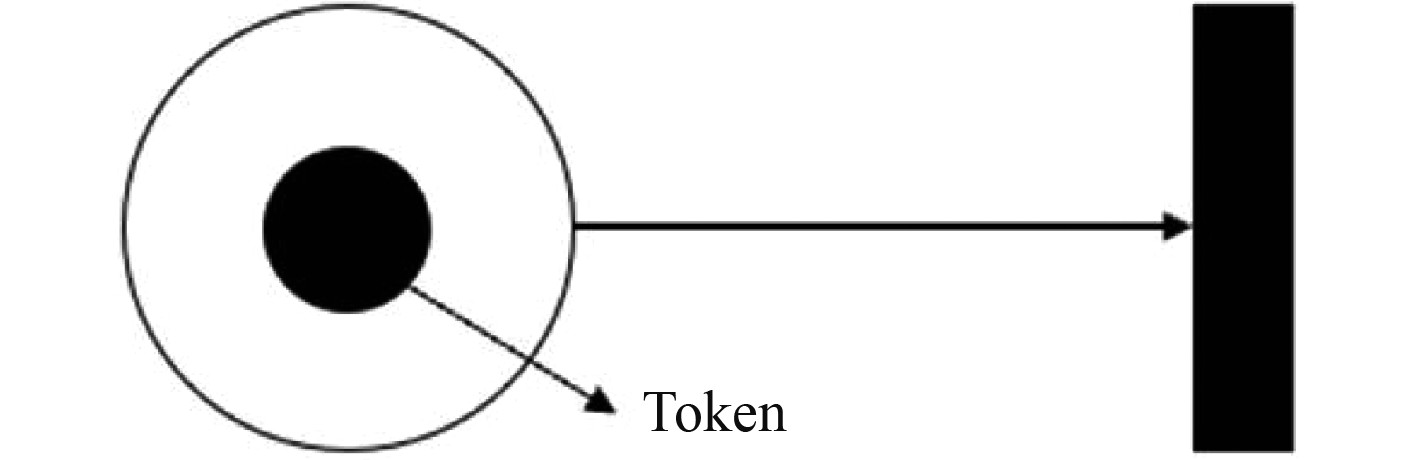
|
图 2 PN模型的规范示意图 Fig. 2 A specification diagram of PN model |
图中,空心圆表示库所集;具有黑色实心的圆表示库所内包含的一种资源或状态,称为Token;带有箭头的线段表示有向弧;实心矩形表示变迁集。
2 多层模糊变权Petri网模型 2.1 多层模糊变权Petri网的定义多层模糊变权Petri网(multi-layer variable weight fuzzy petri nets,MVWFPN)是在模糊Petri网的基础上进行分层化和变权的动态量化模型。多层模糊变权Petri网可以被定义为一个九元组:MVWFPN = (P, T, I, O, W, M, R, m),其中:
P = {p1,p2,…,pm}为库所的集合。每一个pi表示事故风险因素,m为风险因素的个数。
T = {t1,t2,…,tn}为变迁的集合。每一个tj表示风险因素发生的过程,n为过程事件的个数。
I = {
O = {
W
= {wij}为变权输入矩阵,反映前库所对后库所的支持程度,本文权重wij的计算公式见式(1)。其中,
| $ \left\{\begin{array}{l}W_{ij}=\dfrac{\theta_{ij}\cdot\alpha {({p}_{i})}^{\rho }}{{\displaystyle\sum _{i=1}^{n}\theta_{ij}\cdot\alpha {({p}_{i})}^{\rho }}}\text{,}{\displaystyle \sum _{i=1}^{n}\theta_{ij}\cdot\alpha {({p}_{i})}^{\rho }\ne 0},\\ W_{ij}=0\text{,}{\displaystyle \sum _{i=1}^{n}\theta_{ij}\cdot\alpha {({p}_{i})}^{\rho }\text=0}。\end{array}\right. $ | (1) |
M为标识向量,M = ((p1),(p2),(p3),…,(pn))T,初始标识用M0表示;
R= {
m为多层模糊变权Petri网的层数,按照从初始库所到目标库所的方向,将从初始库所到目标库所之间所有的变迁数目相同的输入库所、变迁及输出库所划分为同一层。
2.2 多层模糊变权Petri网(MVWFPN)的推理步骤步骤1 分析事故原因并建立MVWFPN模型
建立事故风险因素集,构建MVWFPN模型。
步骤2 确定MVWFPN模型的层级
按照推理深度划分MVWFPN的层级数目m,不同层级采用不同线框进行分类,构建MVWFPN网络结构。
步骤3 确定初始库所及变迁的置信度
库所pi对应的置信度表示所有风险因素风险等级值,表1为库所风险等级的数值对应表[12]。
|
|
表 1 风险等级对应数值表 Tab.1 Corresponding table of risk level values |
变迁tn代表事故的发展,变迁的可能性用模糊因子来表示,模糊因子的大小决定了前库所对后库所的影响程度,越大,则前库所越有可能导致后库所事件的发生。
步骤4 数据处理及计算
1)令第1层迭代系数k=1,确定第1层输入矩阵、输出矩阵以及初始标识向量M0(除初始库所外,目标库所统一设定为0),计算得到第一层变权矩阵。
2)计算M1,公式如下:
| $ \begin{split}{\boldsymbol{M}}_k & = {\boldsymbol{M}}_{k - 1} \oplus \Big[ \left( {{\boldsymbol{W}}_{k - 1}^{\rm{T}} \cdot {{\boldsymbol{O}}_{k - 1}} \cdot {{\boldsymbol{R}}_{k - 1}}} \right) \otimes \\ &\left( {\overline {{\boldsymbol{I}}_{k - 1}^{\rm{T}} \otimes \overline {{{\boldsymbol{M}}_{k - 1}}} } } \right) \Big],{1 \leqslant k \leqslant {{m}}} 。\end{split} $ | (2) |
引入2个矩阵算子
加法算子
乘法算子
3)令k=k+1,更新变权输入矩阵W,分别计算其他层级Mk。
4)当Mk=Mk−1时,迭代结束,此时获得最终Mk。
步骤5 事故演化推理
根据所计算出的最终标识向量Mk,即各个风险因素的风险数值,结合MVWFPN模型图,推理出最有可能造成事故的传播路径和初始原因。
3 基于多层模糊变权Petri网的深远海溢油事故演化分析为了验证模型的有效性,本文选择的深远海海域界定如下:渤海、黄海及东海距岸200 nmile以远,南海距岸120 nmile以远(台湾岛东海岸、海南岛东海岸及南海岸距岸50 nmile以远)的海域。通过案例分析、资料调研和咨询交通部救助打捞系统专家获取研究所需数据。
3.1 深远海溢油回收风险因素集通过对我国典型深远海救助作业案例进行分析,构建了深远海恶劣海洋环境下溢油回收作业的因素集,如图3所示。

|
图 3 深远海溢油回收作业风险因素集 Fig. 3 Risk factor set of deep-sea oil spill recovery |
步骤1 分析事故原因并建立MVWPFN模型
基于深远海溢油回收作业风险因素集,本文利用MVWFPN进行抽象建模来模拟作业失败的发展过程,MVWFPN模型如图4所示。
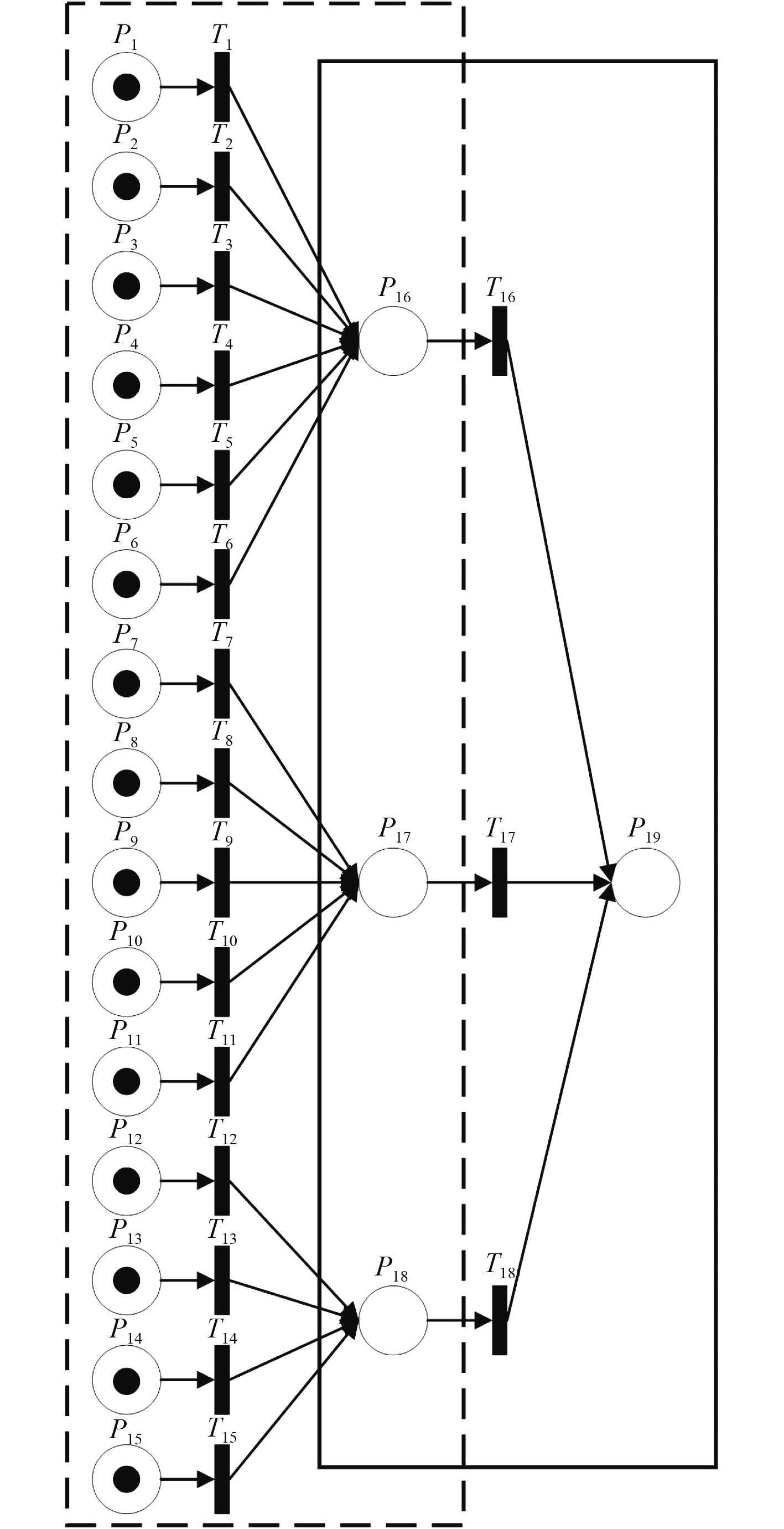
|
图 4 深远海溢油回收作业失败MVWFPN模型图 Fig. 4 MVWFPN model diagram of deep sea oil spill recovery operation failure |
步骤2 确定MVWFPN模型的层级
由图4可知,本文按照推理深度的划分,将深远海溢油回收作业失败MVWFPN模型划分为2层,即m=2,其中虚线框代表第一层级,实线框代表第二层级。
步骤3 确定初始库所及变迁的置信度
本文通过专家打分以及数据标准化处理,得到模型中的初始库所置信度和所有变迁可能性的评估值。评估值如表2和表3所示。
|
|
表 2 初始库所置信度评估值 Tab.2 Confidence values set by the initial place |
|
|
表 3 变迁可能性评估值 Tab.3 Transition possibility value |
步骤4 数据处理及计算
通过以上数据,结合式(2)可对深远海溢油回收作业失败事件进行计算和演化推理。
令k=1,第一层模糊变权Petri网计算如下:
初始标识向量为
M0=[P1,P2,P3,P4,P5,P6,P7,P8,P9,P10,P11,P12,P13,P14,P15,P16,P17,P18,P19]T=[0.57, 0.83, 0.90, 0.97, 0.89, 0.83, 0.58, 0.75, 0.68, 0.68, 0.83, 0.83, 0.91, 0.58, 0.66, 0, 0, 0, 0]T。
第一层输入库所为P1,P2,P3,P4,P5,P6,P7,P8,P9,P10,P11,P12,P13,P14,P15,输出库所为P16,P17,P18。
第一层输入矩阵为
| $ {I_0} = \left[ {\begin{array}{*{20}{c}} 1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \end{array}} \right], $ |
第一层输出矩阵为
| $ {O_0} = v {\left[ {\begin{array}{*{20}{c}} 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 1 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 \end{array}} \right]_{18 \times 15}} 。$ |
通过式(1)计算第一层变权矩阵W0,并构建变迁置信度矩阵R0。根据式(2),可得:
M1=[0.57, 0.83, 0.90, 0.97, 0.89, 0.83, 0.58, 0.75, 0.68, 0.68, 0.83, 0.83, 0.91, 0.58, 0.66, 0.81, 0.47, 0.76, 0]T。
根据第一层的计算方法,以此类推,可获得第二层标识向量。
M2= [0.57, 0.83, 0.90, 0.97, 0.89, 0.83, 0.58, 0.75, 0.68, 0.68, 0.83, 0.83, 0.91, 0.58, 0.66, 0.81, 0.47, 0.76, 0.59]T。
由于继续迭代计算M2的数据不会发生变化。因此M2为最终的标识向量。
步骤5 事故演化推理
将最终的标识向量M2结合图4,可推理出导致溢油回收作业失败的发生概率和演化路径。
如图5所示,在第二层级中,最左边用粗箭头显示的路径表示为最有可能导致溢油回收作业失败的路径,即人员管理失效(α(P16) =0.81)是最有可能导致溢油回收作业失败的因素。在该路径的第一层级中,作业现场出现明火(α(P4) =0.97)具有非常高的危险性。为了有效提高溢油回收作业的成功率,需要针对该风险因素提出以下管控措施:增强溢油回收作业操作和管理人员的相关作业意识、作业现场严禁使用手机以及出现明火、对作业人员上岗机制进行监管等。

|
图 5 溢油回收作业失败演化推理图 Fig. 5 Inference diagram of the failure evolution of the oil spill recovery operation |
在第二层级中,最右边中等箭头显示的路径表示为具有较大几率导致溢油回收作业失败的路径,即环境影响(α(P18) =0.76)是有较大几率导致溢油回收作业失败的因素。在该路径的第一层级中,能见度低(α(P13) =0.91)具有非常高的危险性。针对该风险,作业人员需通过提高侦查气象条件的技术,及早防范气象条件诸如大雾带来的影响,避免造成作业人员的行为判断偏差。
在第二层级中,中间的细箭头显示的路径表示为具有较低几率导致溢油回收作业失败的路径,即设备失效(α(P17) =0.47)相较于其他2个因素发生的可能性最低,有较低的可能性导致溢油回收作业失败。但是在该路径的第一层级中,救助船、平台设备疲劳老化(α(P8) =0.75)具有较高的危险性,需要针对性提出风险预防措施。如做好溢油回收作业过程中设备设施的保护和平时的保养工作,及时发现并维修故障设备,同时也要注重陈旧设备以及故障设备的更新换代率。
4 结 语通过以上研究,总结出以下结论:
1)本文基于传统模糊Petri网模型,提出一种多层模糊变权Petri网模型。该模型首先解决了传统模糊Petri网缺少层次性的问题,分层计算使模糊Petri网更具有结构性。此外,该方法添加了变权的概念,变权可以使风险因素的状态根据事故变化而进行动态的变化,能够更准确地对事故进行演化分析。
2)基于多层模糊变权Petri网建立的深远海溢油回收作业失败模型,通过定量计算推理得到最有可能导致溢油回收作业失败的传播路径和初始原因,并针对危险性大的初始原因提出了相应的建议,为决策者提供决策支持。同时,该研究也为深远海其他作业类型的危险性分析提供了思路。
| [1] |
张钦岳, 殷志明, 李滨. 海洋深远海油气开发应急救援装备发展趋势[J]. 石化技术, 2021, 28(3): 5. DOI:10.3969/j.issn.1006-0235.2021.03.002 |
| [2] |
金浩, 张英香, 王吉武, 等. 水上多元救助力量协同调度系统总体研究[J]. 舰船科学技术, 2021, 43(15): 88-92+109. JIN H, ZHANG Y X, WANG J W, et al. A general study on collaborative dispatching system of multiple rescue forces overwater[J]. Ship Science and Technology, 2021, 43(15): 88-92+109. DOI:10.3404/j.issn.1672-7649.2021.08.017 |
| [3] |
申瑞婷, 胡宗敏, 梁刚. 港口船舶溢油环境风险评价方法研究[J]. 水运工程, 2011, 460(11): 137-141. DOI:10.3969/j.issn.1002-4972.2011.11.026 |
| [4] |
岳汉秋, 甘鑫平, 牟乃夏. 海上船舶溢油事故模糊评估与决策分析[J]. 环境工程学报, 2015, 9(8): 3780-3784. DOI:10.12030/j.cjee.20150831 |
| [5] |
汪守东, 徐洪磊, 程金香. 舟山海域油品码头布局与溢油风险评估[J]. 水运工程, 2016, 518(8): 26-33. DOI:10.3969/j.issn.1002-4972.2016.08.006 |
| [6] |
吴瑞杰. 船舶溢油风险评估方法研究[J]. 舰船科学技术, 2017, 39(16): 166-168. WU R J. Study on risk assessment method of ship oil spill[J]. Ship Science and Technology, 2017, 39(16): 166-168. |
| [7] |
郭兴华, 周旭东, 陶季芳. 基于模糊灰色综合评价法的船舶溢油风险评价[J]. 绿色科技, 2020(4): 2. |
| [8] |
张聪, 袁晓娟. 海上油田溢油风险防控及处理措施研究[J]. 节能, 2021, 40(06): 74-77. DOI:10.3969/j.issn.1004-7948.2021.06.025 |
| [9] |
闫炳强, 黄伟青. 基于模糊Petri网的船用齿轮箱可靠性分析系统[J]. 舰船科学技术, 2018, 40(2): 107-109. YAN B Q, HUANG W Q. Marine gearbox reliability analysis system based on fuzzy Petri net[J]. Ship Science and Technology, 2018, 40(2): 107-109. |
| [10] |
宋皓晨, 杨聚芬, 刘志钢. 基于Petri网的地铁驾驶员应急任务分析方法研究[J]. 物流工程与管理, 2020, 42(9): 161-165. DOI:10.3969/j.issn.1674-4993.2020.09.051 |
| [11] |
褚鹏宇, 刘澜, 尹俊淞. 基于动态变权模糊Petri网的地铁火灾风险评估[J]. 安全与环境学报, 2016, 16(6): 39-44. |
| [12] |
王融涵. 液化天然气(LNG)罐区事故情景构建与反演方法研究[D]. 北京: 中国石油大学(北京), 2019.
|
 2022, Vol. 44
2022, Vol. 44
