舰载导弹垂直发射装置兼具发射和贮运的功能,对发射箱内部燃气流场的研究一直是该领域的重点。某型发射装置发射时要求发射箱的前后盖能够自动打开,以便导弹出箱过程中不受干扰。其主要采用碎裂开盖技术[1-3],工作原理为:导弹点火发射过程中,尾部助推发动机产生的燃气流直接作用在后盖上,达到后盖压力阀值时使后盖破裂打开,为燃气的后续排导提供通道。同时,该过程中产生的压力波经后盖反射,沿着导弹和发射箱的间隙向前传播,最终将发射箱前盖破碎。因此,开展导弹发射箱前后盖开启时内部燃气流场的数值仿真研究具有重要意义。
国内关于发射箱内部燃气流场进行了大量的仿真和试验研究[4-8]。段苏宸等[4]对易碎后盖开启过程时的燃气流场进行了仿真研究和试验验证,得到燃气射流流动受后盖打开过程的影响,冲击作用逐渐减小的结论,牛钰森等[5]基于动网格技术,建立了后盖裂片的运动方程和燃气射流耦合的模型,并分析了燃气射流对后盖运动过程的影响,其结果相对于非耦合工况,更贴近于试验真实情况。夏胜禹[6]研究了不同堵盖开启方式和破膜压力对发射箱后盖开启过程的影响,得出使用热解碳化式堵盖有利于后盖开启的结论。金建锋等[7]通过计算流体力学方法对发射箱内压力波传播过程进行数值分析和试验验证。邵庆等[8]对贮运发射箱前后盖开盖过程进行了二维数值仿真,并进行了试验研究,结果表明后盖经发动机燃气射流作用被冲破,前盖在冲击扰动下能够正常开盖。刘琦等[9]对贮运发射箱内部燃气射流产生的冲击波流场进行了非定常数值模拟,通过前端盖压力分析获得利用冲击波的超压峰值完成发射箱开盖动作的结论。
为确保前盖能够被导弹发射时产生的压力波胀破,通常情况下会在发射箱内增加导流结构[10]。而现有文献中关于导流结构对发射箱内流场的影响研究较少,因此本文选用带有导流格栅结构的发射箱为研究对象,通过计算流体力学方法建立发射箱内流场的三维仿真模型,结合试验分析导流格栅结构对内流场环境的影响,并对不同导流格栅结构进行深入的研究。研究结果为该类型发射箱方案优化提供一定的理论依据和数据参考。
1 理论基础 1.1 基本假设发动机喷出的高温高速燃气流不仅含有大量的粒子流,而且本身成分复杂。另外,在燃气喷射过程中常伴随着复杂的化学反应,甚至出现二次燃烧。为简化计算,在分析计算过程中对燃气流场做出如下假设:
1)燃气流是性质单一、均匀混合的气体,视为理想气体,满足理想气体状态方程,各成分间无化学反应;
2)忽略其粒子流自身影响以及粒子流与燃气间的动量和能量交换;
3)导弹简化为旋转体;
4)前盖、后盖未破碎/裂时为密闭状态,且不随燃气流载荷变形,前盖破碎后假设为完全打开,前后盖打开过程中弹体保持静止状态。
1.2 控制方程通过求解非定常Navier-Stokes方程的方法对发射箱内部燃气流场进行数值模拟,其控制方程如下:
1)质量守恒方程
| $ \frac{\partial \rho}{\partial t}+\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho \omega}{\partial \textit{z}}=0。$ | (1) |
式中:u,ν,ω表示在x,y,z等3个方向上的速度分量,m/s;ρ为密度,kg/m3;t表示时间,s。
2)动量守恒方程
| $ \begin{split} &\frac{\partial(\rho u)}{\partial t}+\frac{\partial(\rho u u)}{\partial x}+\frac{\partial(\rho u v)}{\partial y}+\frac{\partial(\rho u \omega)}{\partial \textit{z}}= \\ &\mu_{\text {off }}\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial \textit{z}^{2}}\right)-\frac{\partial p}{\partial x},\end{split} $ | (2) |
| $ \begin{split} &\frac{\partial(\rho v)}{\partial t}+\frac{\partial(\rho v u)}{\partial x}+\frac{\partial(\rho v v)}{\partial y}+\frac{\partial(\rho v \omega)}{\partial \textit{z}}= \\ &\mu_{\mathrm{eff}}\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial^{2} v}{\partial \textit{z}^{2}}\right)-\frac{\partial p}{\partial y},\end{split} $ | (3) |
| $ \begin{split} &\frac{\partial(\rho w)}{\partial t}+\frac{\partial(\rho w u)}{\partial x}+\frac{\partial(\rho w v)}{\partial y}+\frac{\partial(\rho w w)}{\partial \textit{z}}= \\ &\mu_{\mathrm{eff}}\left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial \textit{z}^{2}}\right)-\frac{\partial p}{\partial \textit{z}}-\rho g \beta\left(T-T_{\mathrm{ef}}\right)。\end{split} $ | (4) |
其中:μeff为有效粘度,μeff=μ1+μt;μ1为流体动力粘度;μt为湍动粘度;T为温度;Tref为参考温度;g为重力加速度;β为气体膨胀系数。
3)能量守恒方程
| $ \begin{split} &\frac{\partial\left(\rho T^{\prime}\right)}{\partial t}+\frac{\partial\left(\rho u T^{\prime}\right)}{\partial x}+\frac{\partial\left(\rho v T^{\prime}\right)}{\partial y}+\frac{\partial\left(\rho w T^{\prime}\right)}{\partial \textit{z}}= \\ &\frac{\lambda_{\text {eff }}}{C_{p}}\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial T^{2}}{\partial \textit{z}^{2}}\right)+S_{T}。\end{split} $ | (5) |
式中:Cp为比热容;ST为用户自定义源项;λeff为有效导热系数。
1.3 湍流模型湍流模型采用标准k-ε双方程湍流模型,此模型的模拟精度高、收敛性好。具体方程表示如下[11]:
1)湍流动能方程
| $ \begin{split} &\frac{\partial(\rho k)}{\partial t}+\frac{\partial\left(\rho k u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{{k}}}\right) \frac{\partial k}{\partial x_{j}}\right] +\\ &G_{k}+G_{b}-\rho \varepsilon-Y_{M}+S_{k}。\end{split} $ | (6) |
2)湍流动能耗散率方程
| $ \begin{split} &\frac{\partial(\rho \varepsilon)}{\partial t}+\frac{\partial\left(\rho \varepsilon u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{\textit{z}}}\right) \frac{\partial \varepsilon}{\partial x_{j}}\right]+ \\ &G_{1 \textit{z}} \frac{\varepsilon}{k}\left(G_{k}+G_{3 \textit{z}} G_{i b}\right)-G_{2 \textit{z}} \rho \frac{\varepsilon^{2}}{k}+S_{\textit{z}}。\end{split} $ | (7) |
其中:k为湍动能;ε为湍流耗散率;Gk与Gb为湍动能k的产生项;实验中YM=0,Sk和Sε为用户定义的源项;G1ε,G2ε,G3ε是经验常数,分别取G1ε=1.44,G1ε=1.92,G1ε=0.09;实验中k和ε取经验值,k=0.001783,ε=5.1E-05。
2 计算模型及边界条件 2.1 计算模型及工况计算模型采用三维模型,主要包括发射箱箱体、弹体、后盖、前盖以及导流格栅结构,如图1所示。计算采用Fluent15.0软件。
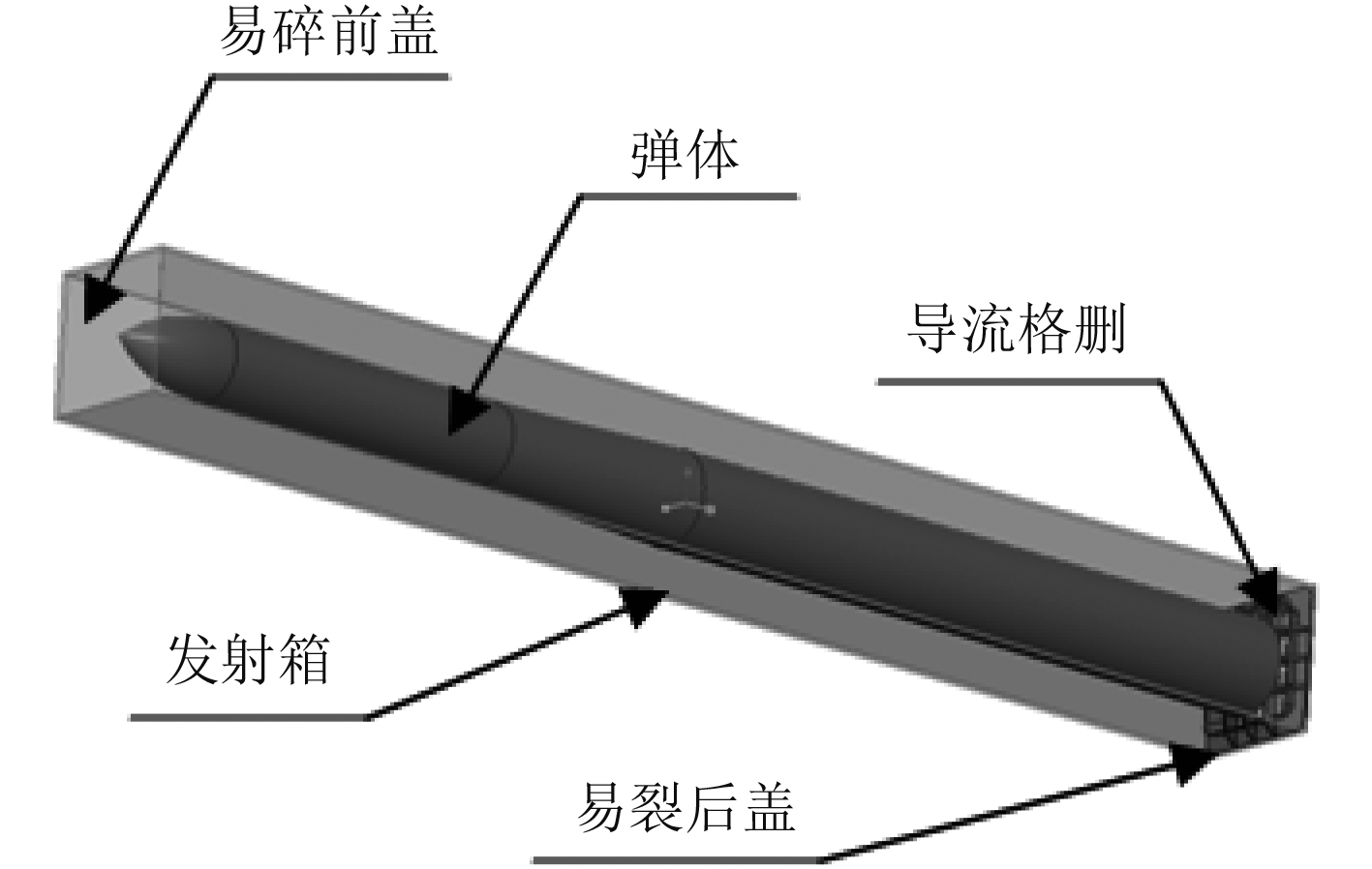
|
图 1 发射箱模型 Fig. 1 The launch canister model |
具体工况设置情况如表1所示。其中,导流格栅分别设置为带导流盘和不带导流盘的2种结构,如图2所示。
|
|
表 1 计算工况 Tab.1 Calculation conditions |
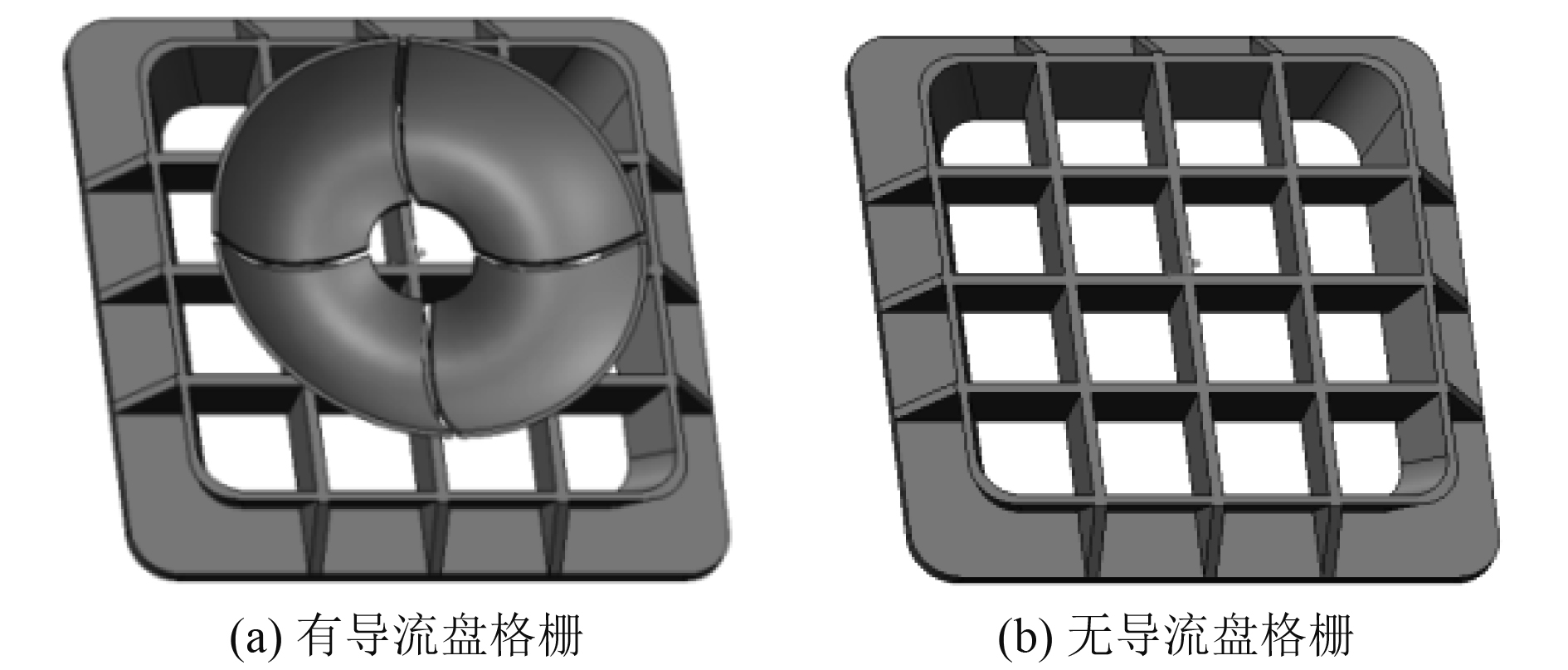
|
图 2 导流格栅模型 Fig. 2 The diversion grille model |
本次计算是在常温(20ºC)状态下进行的,该温度下的发动机燃烧室内压强曲线如图3所示,燃气物理性能参数见表2。

|
图 3 燃烧室压力曲线 Fig. 3 The pressure curve of combustor |
|
|
表 2 燃气物理性能参数 Tab.2 The gas physical performance parameter table |
后盖破裂时,假设裂片之间完全断开,裂片张开过程可简化为裂片绕裙边V型沟槽O点作刚体运动。如图4所示,后盖上支点到转动中心连线距离为l0,该连线与裂片夹角为θ0,裂片转动角度为θ,连杆长度为l,F(θ)与连杆的夹角为a,到转轴距离为L。裂片根部的阻力矩M(θ)为:
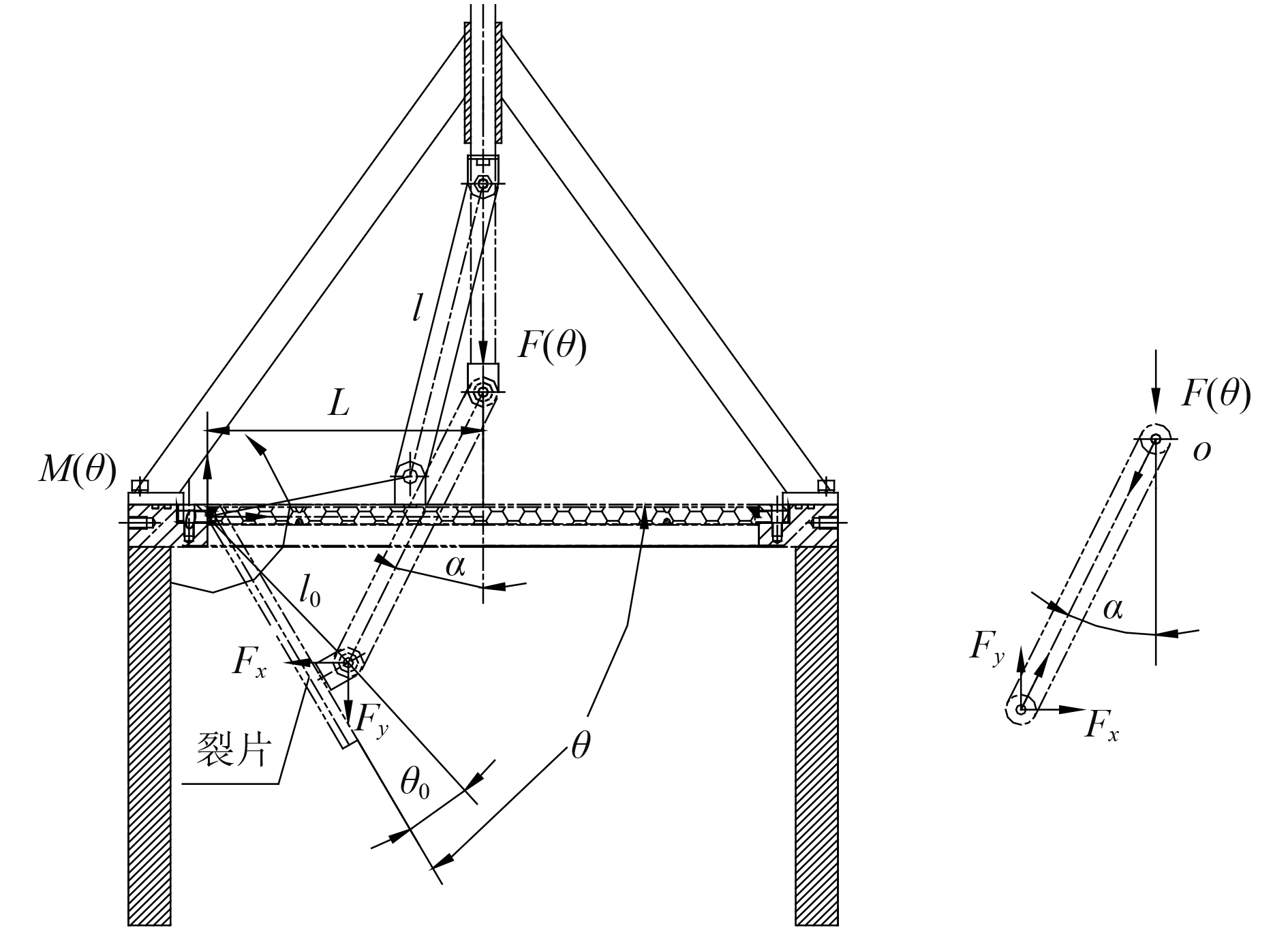
|
图 4 后盖受力分析 Fig. 4 Stress analysis of fragile back cover |
| $ M(\theta)=F_{x} \times L_{0} \sin \left(\theta-\theta_{0}\right)+F_{y} \times l_{0} \cos \left(\theta-\theta_{0}\right)。$ | (8) |
依据连杆受力二力平衡可知:
| $ F_{x}=F(\theta) \operatorname{tg}(a), F_{Y}=F(\theta)。$ | (9) |
因此:
| $ M(\theta)=F(\theta) t_{t}\left(\operatorname{tg}(a) \sin \left(\theta-\theta_{t}\right)+\cos \left(\theta-\theta_{t}\right)\right)。$ | (10) |
其中,连杆与F(θ)夹角为:
| $ \sin a=\left(L-l_{0} \cos \left(\theta-\theta_{0}\right)\right) / l 。$ | (11) |
因此:
| $ f(\theta)=F(\theta) \times \frac{l_{0}\left(\operatorname{tg}(a) \sin \left(\theta-\theta_{0}\right)+\cos \left(\theta-\theta_{0}\right)\right)}{L}。$ | (12) |
如图5所示。对单个裂片,由动量矩定理有:

|
图 5 后盖裂片张开状态受力 Fig. 5 Forced in the open state of back cover lobes |
| $ t \omega=\iint_{t}^{t} r \times P {\rm{d}} r {\rm{d}} y+M_{3}-M(\phi)。$ | (13) |
式中:θ为裂片张开角度;I为转动的后盖裂片转动惯量,理论值为0.0082 kg·m2;ω为后盖裂片打开状态下的转动角速度;r为后盖裂片上一点到转轴O点的距离;P为燃气流作用在r点的压强;S为裂片转动部分的面积;Mg为重力产生的力矩;M(θ)为裂片张开阻力矩,为裂开张开角度θ的函数。
裂片转动部分为三角块,如图6所示,其绕O点转动时重力产生力矩为:
|
图 6 裂片转动部分形状 Fig. 6 Partial shape of rotating lobes |
| $ M_{g}=m g \times \frac{1}{3} L \cos \theta。$ | (14) |
因此,后盖裂片运动满足:
| $ I \dot{\omega}=\iint_{x} r \times P {{\rm{d}}x{\rm{d}}y}+m_{\dot{\theta}} \times \frac{1}{3} L \cos \theta-f(\theta) \times L。$ | (15) |
为验证上述后盖运动方程的正确性,对后盖的胀破过程进行试验验证,并采用高速摄影的方式对后盖胀破过程进行记录。
根据后盖胀破过程,建立燃气流场仿真模型见图7。其中,后盖破裂前,内部为密闭状态,气体初始压强设置为后盖胀破时表压,气体流出区域压强为环境大气压,环境温度为常温(20ºC)。

|
图 7 后盖胀破过程流场计算模型 Fig. 7 Calculation model of flow field in the process of bursting and cracking of fragile back cover |
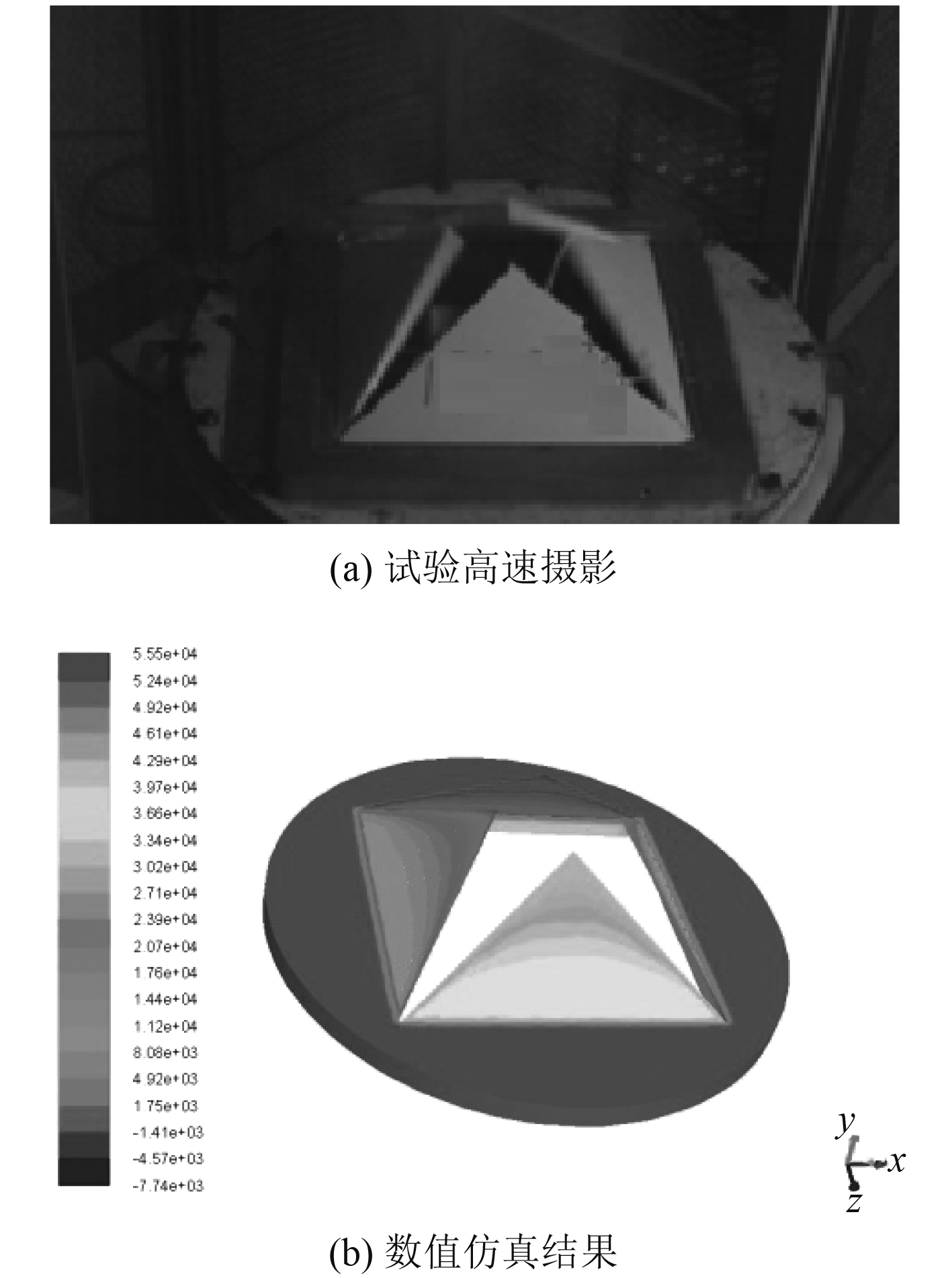
图8给出了后盖裂开时间为8 ms时开盖试验和仿真情况对比。具体试验和数值仿真结果对比如表3所示,二者的后盖从破裂到张开至90°的过程中变化趋势基本相同,说明后盖破裂过程数学模型及计算方法可用于描述后盖的实际开启过程。但由于实际裂片打开过程受裂片根部阻力及相互间影响等因素,导致数值仿真时的裂片开盖时间相较试验时更短。
|
图 8 后盖裂开时间8 ms时试验和仿真对比 Fig. 8 Comparison of test and simulation when the cracking time of fragile back cover is 8 ms |
|
|
表 3 裂片开盖时间对比 Tab.3 Comparison of lobes opening time |
1)入口边界条件
入口边界设在发动机喷管收缩段,采用压力入口边界,总温为燃气的定压燃烧温度,总压为发动机内燃烧室内的压强。
2)出口边界条件
在燃气排导系统流场计算过程中,理论上取无穷远处大气环境状态作为燃气流出口状态,在计算中扩展边界,使计算区域足够大,从而满足出口压强为环境压强,即为1个大气压。
3)壁面边界条件
除入口、出口边界条件外,其他所有区域的边界条件均为壁面边界条件,流体与固体相互作用的边界满足经典边界层函数。其中,壁面热边界条件采用绝热条件。
4)前盖打开条件
前盖破碎压力指标为10000±2500 N,最大值为12500 N。取安全系数1.24,因此前盖破碎压力最大值为15500 N。即在燃气流场计算过程中,假设前盖受到合力为15500 N时打开。
5)后盖破裂条件
后盖设计破裂压力为13500±2500 N。后盖最小破裂压力为11000 N,最大破裂压力为16000 N。取安全系数1.24,则后盖极限最大破裂压力为19840 N,而后盖破裂极限最小值为13640 N。即在燃气流场计算过程中,假设后盖受到合力为13640 N时开始破裂。
另外,计算中设置相对压力为1个大气压,因此云图中显示负压表明该处压力小于环境大气压。
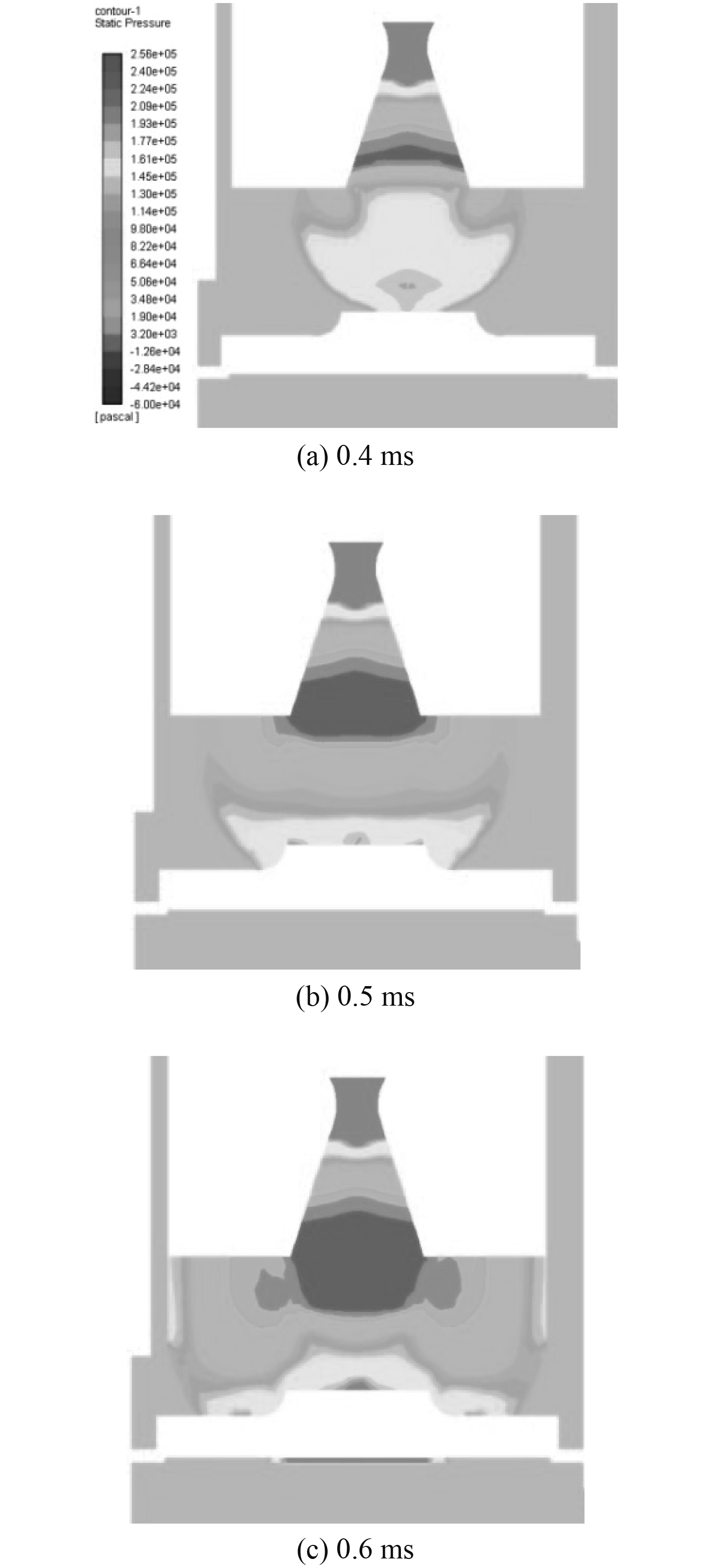
3 计算结果及分析 3.1 燃气运动分析发动机点火后,燃气射流产生的压力波作用在后盖上(见图9),在后盖内表面反射,向前盖方向运动。后盖在发射燃气压力波时,受到燃气压力波冲击。当后盖受压力波强度超过了后盖打开条件设定值时,后盖破裂为4片,在后续燃气流作用下裂片绕根部打开(见图11)。
|
图 9 后盖破裂前压力波在箱内运动情况 Fig. 9 The movement of pressure wave in the box before the crack of fragile back cover |
向前盖方向运动的压力波作用到前盖上时,在前盖内表面反射,在前盖上产生瞬时冲击。前盖受燃气压力波冲击幅值超过了前盖打开条件时,前盖在压力波冲击作用下破碎。
至此,发射箱前后盖均打开,为导弹发射运动和燃气流排导提供通道。
3.2 导流格栅对后盖打开时间影响图9给出了发动机点火后,发射箱后盖附近流场的压力云图。燃气流从发动机喷管喷出后,产生的压力波波阵面呈球形向外运动,直至作用到后盖上。随着压力波在后盖上作用面积增大以及压力波强度增加,后盖上受到合力逐渐增大,直至后盖破裂。
在无导流格栅的燃气流场中,到t=0.60 ms时,后盖上受燃气流作用合力达到13691 N,超过了后盖破裂时受到的合力阀值13640 N,后盖开始破裂。增加无导流盘的格栅结构和带导流盘的格栅结构(Case2和Case3)后,后盖的开启时刻分别为0.58 ms和0.59 ms,基本无变化。这是因为后盖距离发动机喷管距离不变,燃气流压力波可穿过导流格栅作用在后盖上。后盖上压力波作用效果变化不大,导流格栅对后盖开启时刻的影响程度较弱。
后盖破裂后,在燃气流作用下裂片打开角度与时间关系见图10。无导流格栅状态(case1),裂片打开到90°时间为11.07 ms。无导流盘的格栅工况,裂片打开到90°所需时间分别为10.06 ms。有导流盘工况,裂片打开到90°所需时间为9.92 ms。导流格栅及导流盘的存在,导致燃气流分散作用在后盖表面。在裂片未开启时,集中作用在盖体中心的燃气射流更有利于裂片开启。当裂片开启一定角度后,集中在核心区的燃气流大部分从裂片空隙穿过,作用在裂片上开盖力矩迅速降低,裂片打开时间变慢。

|
图 10 后盖裂片打开时间对比 Fig. 10 Comparison of opening time of back cover lobes |
图11给出了后盖破裂过程中,箱内压力波运动到前盖的过程。作用在前盖的冲击波主要是后盖打开过程中,由后盖裂片、导流格栅反射的压力波产生的。前盖受力主要由后盖打开时间和导流格栅结构决定。

|
图 11 后盖打开过程中压力波在箱内运动 Fig. 11 The movement of pressure wave in the canister during the opening of fragile back cover |
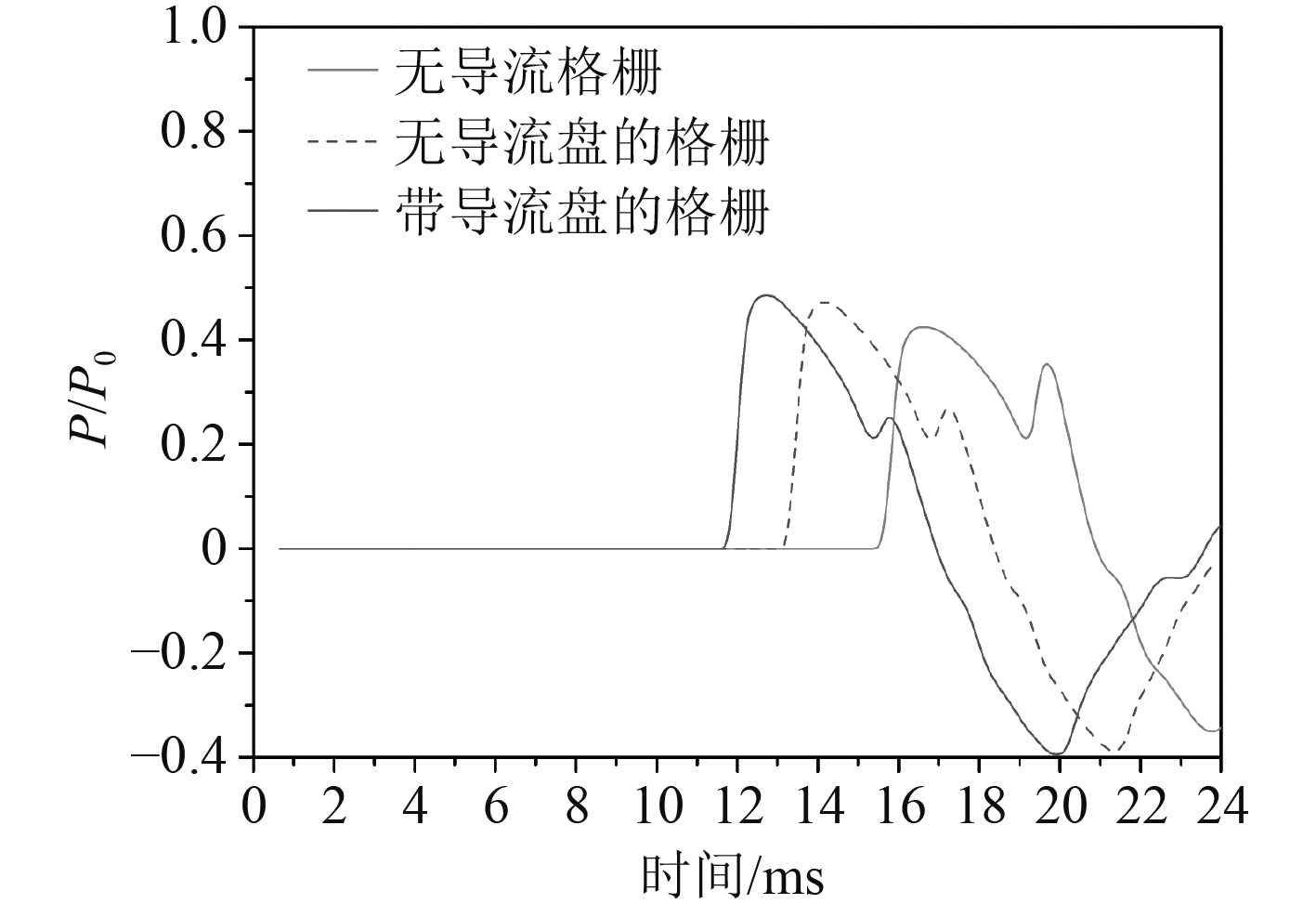
图12给出了不同工况下发射箱前盖附近的压强变化。对于无导流格栅结构的工况,当t=17.6 ms时,压力波在前盖产生的压强载荷合力开始超过前盖破碎极限受力15500 N(前盖打开条件),此时前盖打开。对于无导流盘的格栅工况,当t=14.4 ms时,压力波在前盖产生的压强载荷合力超过15500 N,前盖打开。对于有导流盘的格栅工况,当t=12.1 ms时,压力波在前盖产生的压强载荷合力超过15500 N,前盖打开。导流格栅的加入,增加了反射到前盖的压力波强度,前盖打开时刻由17.6 ms分别缩短至14.4 ms和12.1 ms。
|
图 12 发射箱前盖附近压强曲线变化 Fig. 12 Change of pressure curve near the front cover of launch canister |
表4给出了所有工况的对比结果。可以看出,无导流格栅时,发射箱后盖破裂时刻、裂片完全打开以及前盖打开时刻均最慢;增加导流格栅后,前后盖开启时间都有所缩短,尤其是前盖打开时刻减小至14.4 ms,相对提前了17.7%左右。因此可以推断出导流格栅结构具备显著的改良作用。同时,前盖的峰值压力并没有因额外导流结构的增加而产生较大的变化,这样发射箱内部弹体元器件的受损风险也会降到最低。
|
|
表 4 结果汇总表 Tab.4 Summary of calculation results |
另外,通过增设导流盘改变导流格栅的结构,易裂前盖打开时刻减小至12.1 ms,相对于原导流格栅下的工况提前了15.9%,说明导流盘的增加同样有助于促进导流结构对发射箱内流场的导流作用和压力波的传播。
4 试验验证导流格栅的加入,缩短了前盖打开时间。导弹发射时,采用带导流盘格栅。发射过程中在发射箱对燃气流压强参数进行了测试。发射箱上取3个测点b1~b3,如图13所示。压强编号分别记为Pb1~Pb3,其中测点b1~b3,由试验用发射箱上的测点位置确定。

|
图 13 发射箱内测点布置 Fig. 13 The location of monitoring point in the launcher |
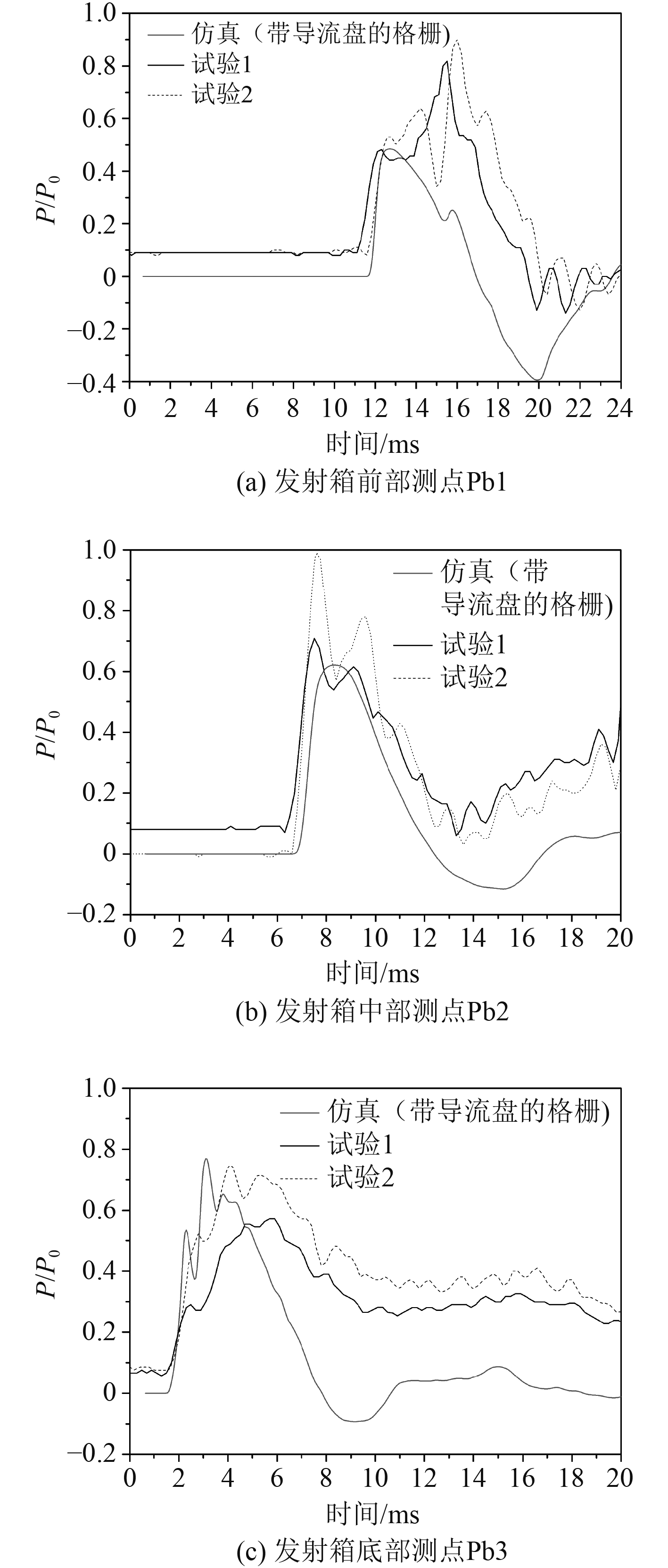
图14给出了仿真工况和试验下的各测点位置压力变化曲线对比情况。可以看出,在前20 ms发射箱底部(Pb3)和中部(Pb2)均只有1个峰值,该峰值为燃气产生的向前盖运动的压力波。数值仿真结果和试验数据基本吻合,变化趋势也大致相同;在前20 ms发射箱上部(Pb1)存在2个峰值,第1个峰值为向前盖方向运动的压力波导致的,第2个峰值为前盖反射回的压力波,该峰值的大小由前盖的破碎过程决定。至于部分区间试验数据和仿真结果差异较大的原因是,仿真中假设前盖达到受压阀值时即瞬时打开,而实际试验中受前盖碎片的干扰影响较大。另外,仿真模型的简化也使得各种实际模型上细小结构引起的微弱扰动被忽略,造成部分测点压力有较大的差异。
|
图 15 发射箱测点压强曲线变化 Fig. 15 Change of pressure curve at monitoring point of launch canister |
本文针对某型发射箱前后盖开启时的内流场为研究对象,对不同导流结构下的工况进行仿真研究,得到导弹发射前易碎易裂盖开启过程中箱内燃气流场的动态变化,并对仿真结果中的最优方案进行了试验验证,结果可行,最终得到如下结论:
1)发射箱内增加导流格栅结构,有助于压力波向前盖传播,缩短前盖开启时间。同时,其对发射箱前部压力峰值影响较小,压力波动范围在0.51%~0.97%左右,避免弹体元件等因压力波动而出现受损的情况。
2)导流格栅结构对后盖开启过程的影响程度不显著,不同仿真工况下的后盖开启时刻基本相近,裂片完全打开时刻的变化范围在1.3 ms以内。
3)通过增设导流盘来改变导流格栅结构,从结果看,会对发射箱的前盖开启时间等性能参数具有一定的影响。带导流盘的格栅结构相对于无导流盘工况,前盖打开时刻缩短的幅度为15.9%。
本文仿真计算相较实际发射过程仍存在误差,其主要原因是:燃气流是多组分、高温高压的超音速混合气流,并且含有大量凝相颗粒,具有严重的冲刷能力。而本文在计算过程中假设燃气流为理想气体,未考虑前盖打开过程对压力波影响,未考虑大量粒子冲击后盖裂片而引起后盖开启过程干扰等因素。后续可以围绕建立更精准的计算仿真模型和导流格栅结构的优化等方面进行深入探索。
| [1] |
陈愚, 孙凤云. 贮运发射箱的结构与设计[J]. 包装工程, 2012, 33(15): 132-135. |
| [2] |
杨雨潼, 吴石, 陈愚, 等. 自然环境对贮运发射箱的影响[J]. 装备环境工程, 2009, 6(6): 82-83,87. DOI:10.3969/j.issn.1672-9242.2009.06.021 |
| [3] |
张艳, 李仙会, 庄辛. 导弹贮运发射箱易碎端盖研究进展[J]. 理化检验(物理分册), 2019, 55(3): 145-150,164. |
| [4] |
段苏宸, 姜毅, 牛钰森, 等. 发射箱易碎后盖开启过程的数值计算[J]. 兵工学报, 2018, 39(6): 1117-1124. DOI:10.3969/j.issn.1000-1093.2018.06.011 |
| [5] |
牛钰森, 姜毅, 史少岩, 等. 与燃气射流耦合的易碎后盖开启过程数值分析[J]. 兵工学报, 2015, 36(1): 87-93. DOI:10.3969/j.issn.1000-1093.2015.01.013 |
| [6] |
夏胜禹. 基于动网格技术燃气开盖研究[D]. 北京: 北京理工大学, 2015.
|
| [7] |
金建峰, 徐刚, 申明辉, 等. 发射箱压力波传播的数值分析及试验验证[J]. 强度与环境, 2014, 41(5): 24-27. DOI:10.3969/j.issn.1006-3919.2014.05.005 |
| [8] |
邵庆, 张保刚, 惠卫华, 等. 贮运发射箱易碎易裂自动开盖研究[J]. 弹箭与制导学报, 2017, 37(1): 27-31. |
| [9] |
刘琦, 傅德彬, 姜毅. 贮运发射箱内燃气射流的非定常冲击波流场数值模拟[J]. 弹箭与制导学报, 2005, 25(2): 382-384. DOI:10.3969/j.issn.1673-9728.2005.02.125 |
| [10] |
吴利民, 陈劲草. 垂直发射装置排导系统内燃气流运动研究[J]. 舰船科学技术, 2007, 29(z1): 69-70,94. |
| [11] |
张兆顺. 湍流[M]. 北京: 国防工业出版社, 2002: 264–266.
|
 2022, Vol. 44
2022, Vol. 44

