2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
随着船舶向大型化快速化的方向发展,大功率主机和螺旋桨的使用愈发普遍,船舶的振动问题也日渐突出。船舶尾部由于截面尺寸收缩,结构刚度较小,同时也是主机、螺旋桨等振源分布较为密集的区域,更易发生振动问题[1]。
为了解决船舶尾部的振动问题,保证结构安全性,提高船员舒适性,学者们开展了许多相关研究[2]。Liu等[3]对一艘全回转推进式海洋工程船进行实船模态和响应测试,分析了船舶尾部振动的原因,总结了尾部结构设计过程中的一些要点和注意事项。刘西安等[4]通过建立不同比例的混合有限元模型和单独尾部模型,讨论了尾部振动计算过程中舱段详细建模比例的选取,并推荐采用虚拟质量法模拟附连水质量的影响。刘晓之等[5]通过有限元计算研究了大型油船阶梯式尾部设计对船体振动特性的影响,验证了该设计的合理性可行性,同时发现局部结构响应增大的现象,需要进行适当改进加强。
然而,此前的研究主要采用实船试验和有限元计算的方法[6-7],相关的模型试验工作开展较少,同时对于船体振动响应特性计算缺乏系统性的研究分析。本文通过模型试验和有限元计算,综合研究船舶尾部响应特性,以验证有限元计算的可靠性和准确性,并针对响应计算中网格划分大小、直接积分法与模态叠加法的差异,以及模态叠加法中截断频率的选取等问题进行探讨。
1 结构振动响应计算理论 1.1 网格划分准则在结构动力学计算中,为了能更准确地反映高频应力波在结构中的传递,需要进行更为密集细致的网格划分。网格划分越细密,求得的结果将更为准确,但也将大幅提高计算量。根据波动理论导出的网格细化标准[8],在一个波长内应至少划分4个单元,即
| $ {c_z} = \sqrt {\frac{E}{{\rho \left( {1 - {\mu ^2}} \right)}}}。$ | (1) |
而板的弯曲波波速和波长为:
| $ {c_w} = \sqrt {2{\text{π}} fr{c_z}},$ | (2) |
| $ {\lambda _w} = \sqrt {\frac{{2{\text{π}} r{c_z}}}{f}}。$ | (3) |
式中:r为板的惯性半径,
| $ \Delta \leqslant \frac{1}{4}{\lambda _{\min }} = \frac{1}{4}\sqrt {\frac{{2{\text{π}} r{c_z}}}{{{f_{\max }}}}} = \frac{1}{4}\sqrt {\frac{{2{\text{π}} r}}{{{f_{\max }}}}\sqrt {\frac{E}{{\rho \left( {1 - {\mu ^2}} \right)}}} } 。$ | (4) |
采用有限元方法进行结构响应计算时,常采用直接积分法和模态叠加法2种方法。对于一般动力系统,其运动方程为:
| $ \left[ M \right]\left\{ {\ddot x} \right\} + \left[ C \right]\left\{ {\dot x} \right\} + \left[ K \right]\left\{ x \right\} = \left\{ {F\left( t \right)} \right\}。$ | (5) |
采用直接积分法求解时,将未知函数在时域内进行离散化,各离散点满足系统运动方程式,离散点之间则采用各种基函数近似插值或采用加权残量法进行离散化,然后基于上一个或数个离散点的位移、速度、加速度进行逐步积分求解,常用的求解算法有中心差分法、Runge-Kutta法、Wilson-θ法等。直接积分法具有精确度较高的优点,但求解大规模复杂结构时计算时间和对硬件的要求大幅提高。
采用模态叠加法求解时,需首先求解结构的模态特性。由于各模态之间的正交独立性,结构的任意变形均可表示为模态的线性叠加形式[9],可将结构的空间坐标转化为模态坐标:
| $ \left\{ x \right\} = \sum\limits_{i = 1}^n {\left\{ {{\phi _i}} \right\}{\eta _i}} = \left[ \phi \right]\left\{ \eta \right\}。$ | (6) |
式中:
| $\begin{split} {\left[ \phi \right]^{\rm{T}}}\left[ M \right]\left[ \phi \right]\left\{ {\ddot \eta } \right\} + {\left[ \phi \right]^{\rm{T}}} \left[ C \right]\left[ \phi \right]\left\{ {\dot \eta } \right\} + {\left[ \phi \right]^{\rm{T}}}\\ \left[ K \right]\left[ \phi \right]\left\{ \eta \right\} = {\left[ \phi \right]^{\rm{T}}}\left\{ {F\left( t \right)} \right\}。\end{split} $ | (7) |
此时系数矩阵转化为对角矩阵,各方程之间相互独立。假定模态阻尼
| $ {\ddot \eta _i} + 2{\omega _i}{\zeta _i}{\dot \eta _i} + {\omega _i}^2{\eta _i} = {f_i}。$ | (8) |
一般而言,模态截断频率越高,计算结果越准确,但所需计算时间也越长。当模态截断频率选取合适时,可保证结果的准确性,同时可大幅度提高计算效率。
2 试验模型及有限元模型 2.1 尾部试验模型本文的试验模型参考某实船尾部结构进行设计。根据文献[4]的分析,选取实船距尾封板约1/5Lpp的横舱壁作为尾部区域的截断位置,截断部分原尺寸为26.00 m × 15.12 m × 9.088 m。考虑到实验室场地限制,试验模型缩尺比设为1∶8,则缩尺后模型主尺度为3.25 m × 1.89 m × 1.136 m。由于加工条件的限制,设计时对结构进行了适当的修改,纵骨间距调整为180 mm,肋距调整为360 mm,同时采用了平直板代替原船舶带曲率的船体外板,但保证了剖面面积和剖面模数与原模型仍满足缩尺关系。试验模型典型剖面图如图1所示[10]。
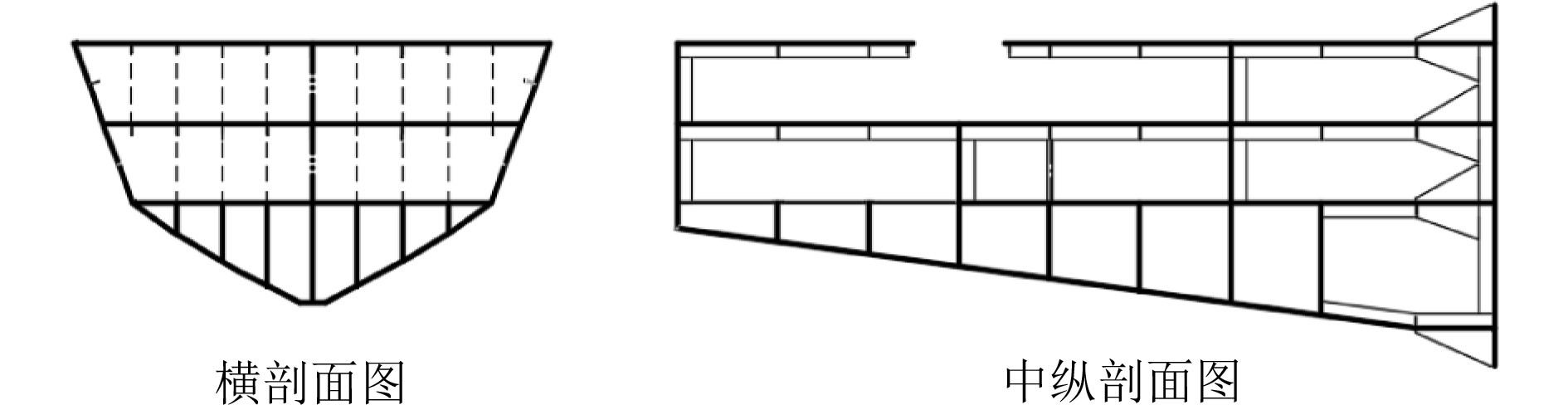
|
图 1 试验模型典型剖面图 Fig. 1 Typical section profiles of test model |
在进行尾部模型振动试验时,试验模型靠近船首的横舱壁一端通过螺栓固定在垂直安装板,尾封板一端为自由端。通过电磁激振器对试验模型施加2~300 Hz动态激励力,并测量响应加速度,得到模型的频响曲线,激励力作用点及加速度测点位置如图2所示。
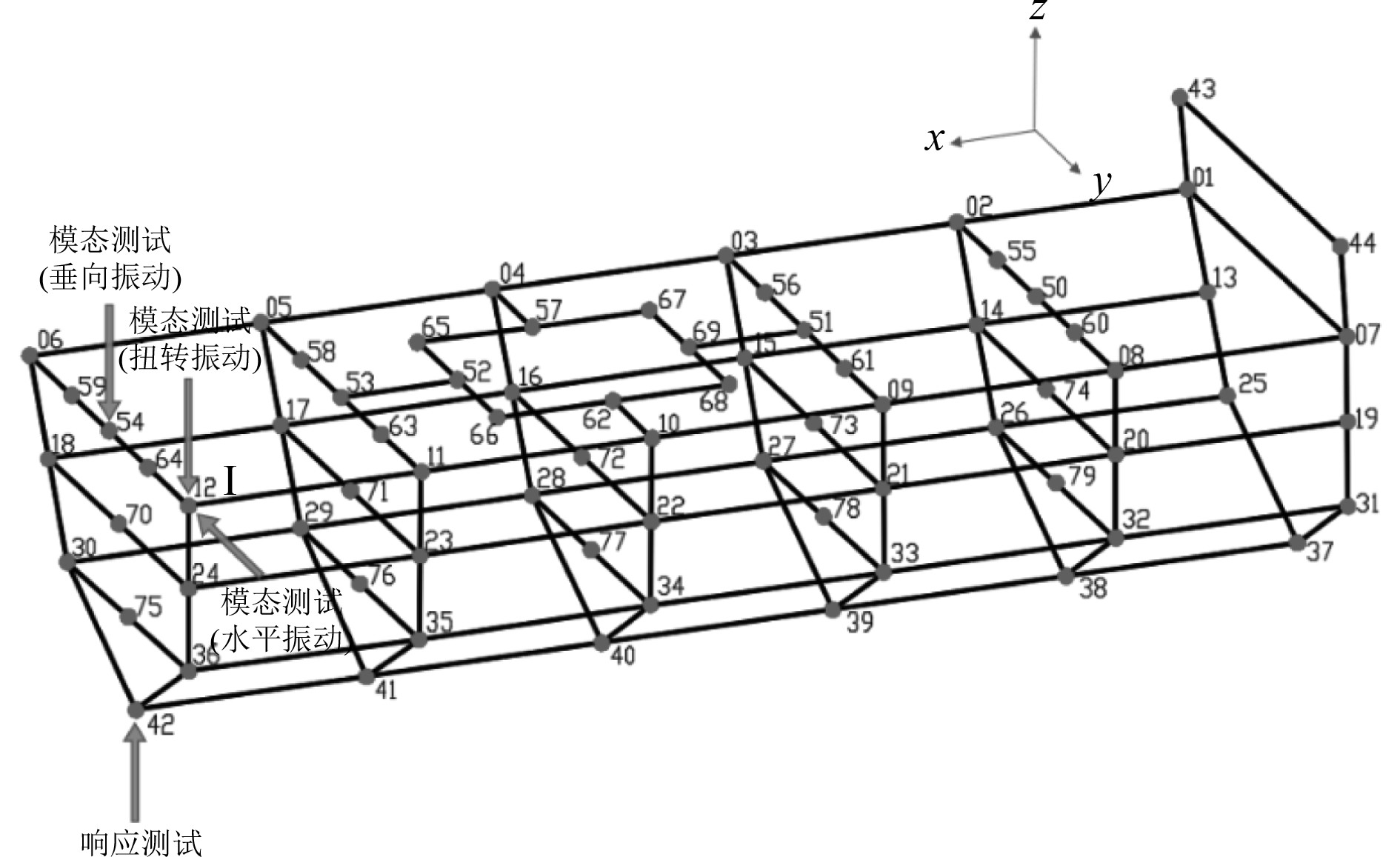
|
图 2 激励点及测点位置 Fig. 2 Locations of excitation and measuring points |
根据尾部试验模型的结构分布特性建立有限元模型,采用板单元模拟舱壁、外壳、T型材腹板等构件,采用梁单元模拟扶强材、加强筋、T型材翼板等构件。由于试验模型固支安装在垂直安装板上,安装板与水箱相互连接,三者之间存在耦合作用,故建立的有限元模型包含试验模型本身、安装板以及水箱。对于该试验模型,板厚

|
图 3 有限元模型(网格尺寸90 mm) Fig. 3 Finite element model (mesh size = 90 mm) |
选取测点53作为分析点,该点位于一甲板中后侧,可反映尾部整体与一甲板局部结构的响应特点,具有典型性。对于3种网格密度的有限元模型,以及试验模型测试,绘出该点在单位激励力作用下的响应结果如图4所示。
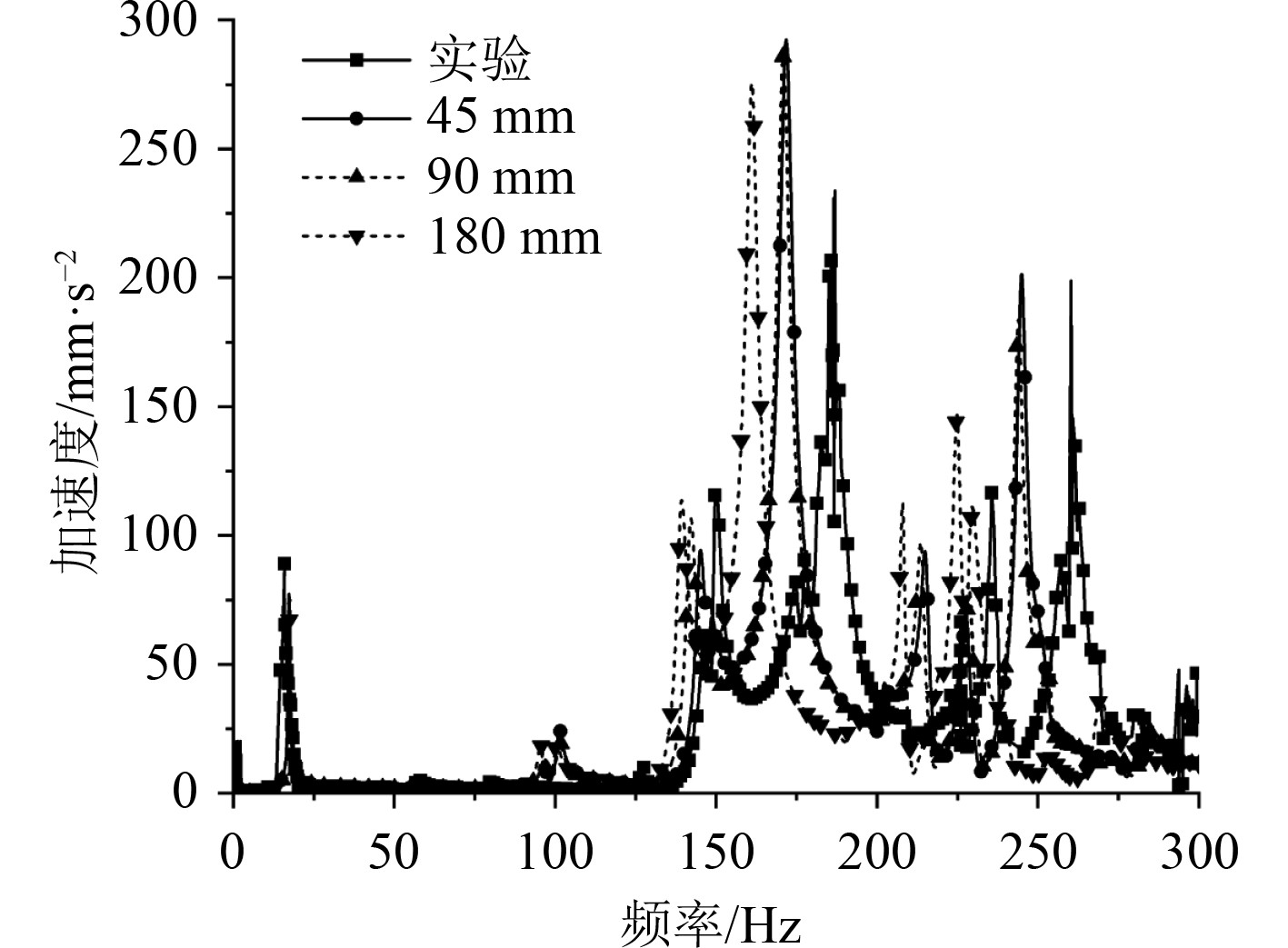
|
图 4 试验结果及3种网格划分下响应计算结果 Fig. 4 Response results of experiment and FE analysis under three mesh schemes |
图中响应最大值对应了一甲板一阶局部振动的固有频率,该响应幅值远超过尾部结构整体发生一阶、二阶垂向振动时的响应,故在设计过程中针对局部板架振动应进行相应的计算,验证在实际激励力作用下其响应是否超差。
另外,对比有限元计算与试验得到的幅频响应曲线,其变化趋势基本一致,有限元计算得到的响应峰值与试验结果基本相同,峰值频率则略低于试验结果。其中,网格密度为180 mm的有限元模型与其余2个有限元模型存在一定误差,且与试验结果差异最大,在150 Hz以上频段出现较为显著的区别,无法准确求取高频段的响应幅值;网格密度为90 mm的模型计算结果与45 mm模型基本一致,与试验结果亦较为接近,可较为准确地得到结构响应特性,同时可有效节约计算时间与资源。后续对模态叠加法及直接积分法进行分析时,均采用90 mm有限元模型计算。
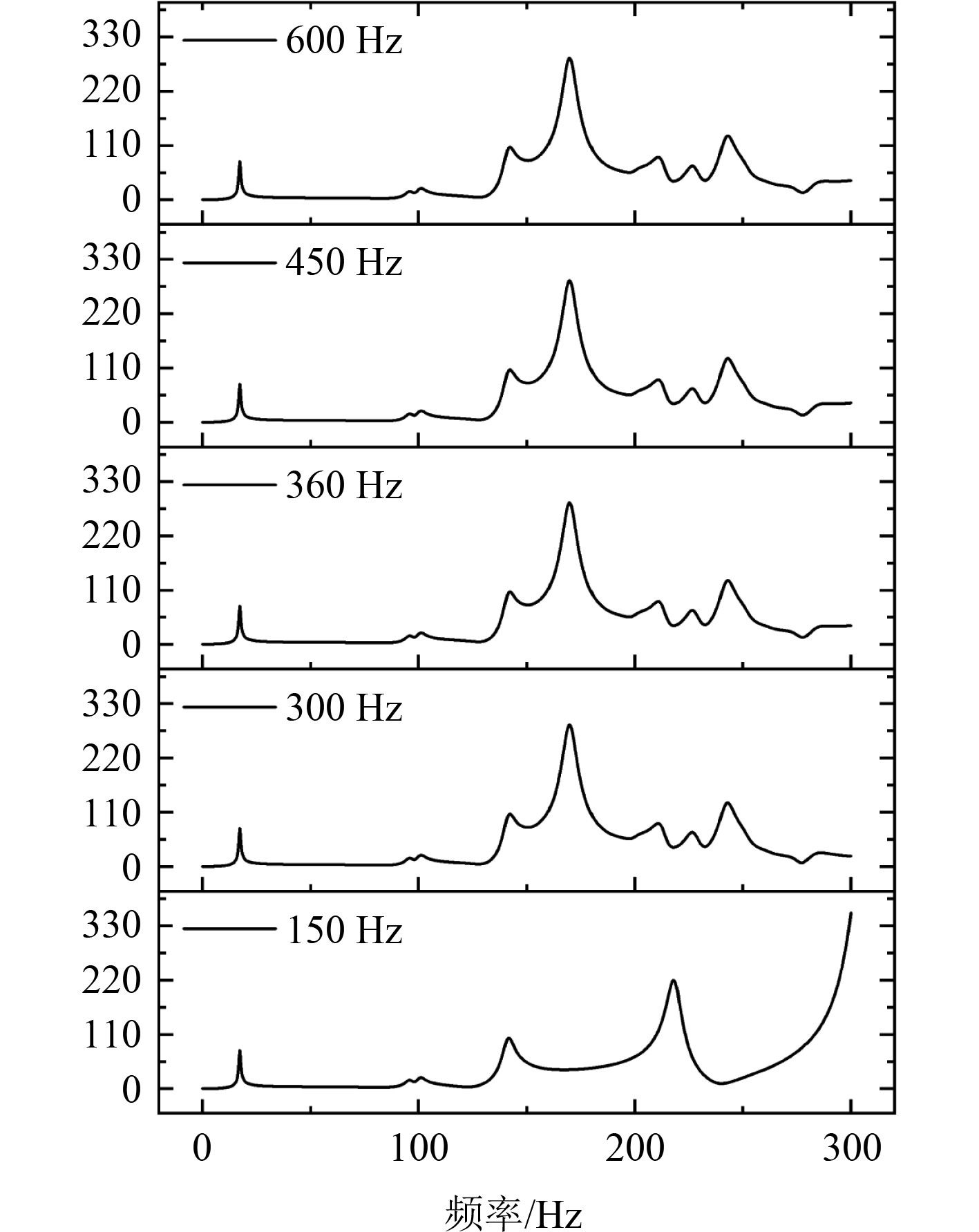
3.2 模态叠加法与直接积分法对比对于90 mm网格的有限元模型,分别采用模态叠加法与直接积分法求解响应幅值。在采用模态叠加法时,模态截断频率分别设置为分析频率上限的0.5倍、1倍、1.2倍、1.5倍、2倍,即截断频率取为150 Hz,300 Hz,360 Hz,450 Hz,600 Hz。各截断频率下得到的幅频响应曲线如图5所示。由于部分曲线相互重叠较难区分,故绘制图6的堆叠图分别展示不同截断频率下的响应曲线。
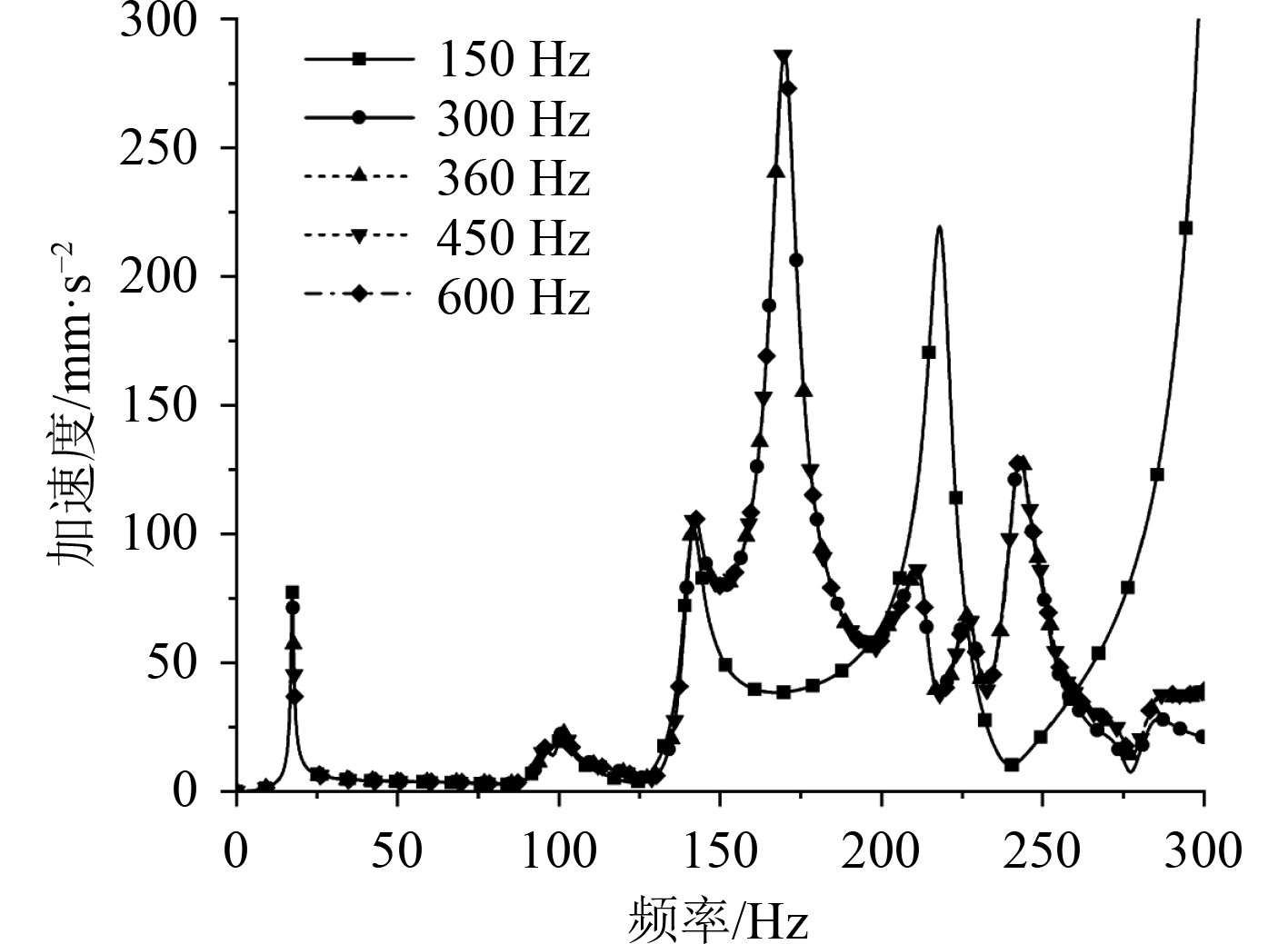
|
图 5 不同截断频率下响应计算结果 Fig. 5 Response calculation results under different truncation frequencies |
|
图 6 不同截断频率下响应计算结果(堆叠图) Fig. 6 Response calculation results under different truncation frequencies (stacked lines) |
由于选取的截断模态越多,响应计算结果越准确,故采用600 Hz的结果作为对比参考。可知,当截断频率为150 Hz时,响应结果在150 Hz以上出现很大误差,无法准确反映结构中高频段的响应;当截断频率为300 Hz时,计算结果基本准确,但在250 Hz以上频段会出现一定的误差;当截断频率为360 Hz及以上时,3组计算结果基本相同,误差很小。
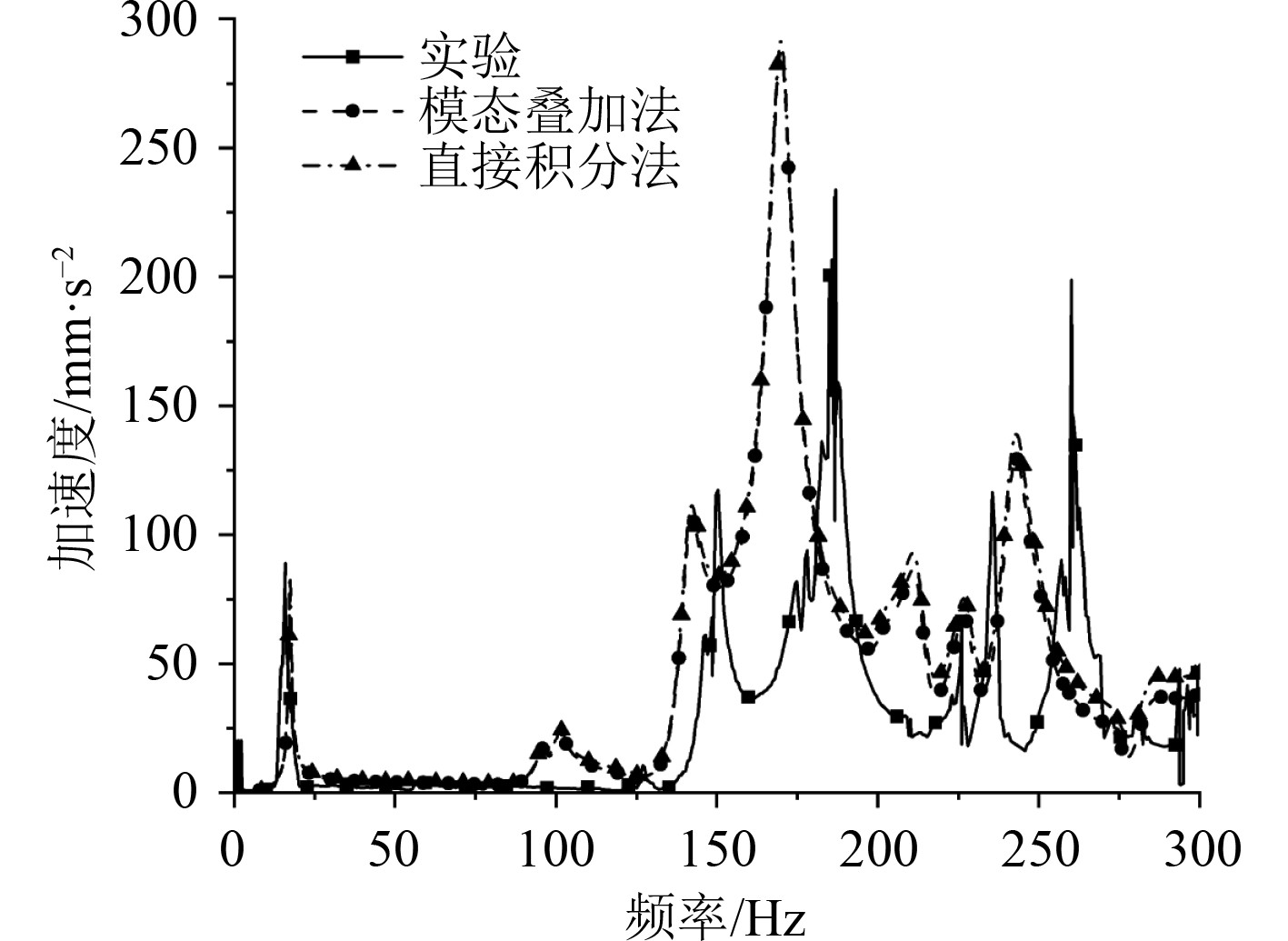
此外,对比模态叠加法(截断频率=360 Hz)、直接积分法以及试验结果,如图7所示。采用1.2倍频率上限进行模态叠加计算时,计算结果与直接积分法基本一致,误差较小,同时计算时间大幅减少。2种有限元方法求解结果均能基本反映试验模型的响应特性,响应峰值及对应的峰值频率等特征基本相符。故综合而言,推荐采用模态叠加法进行振动响应求解,并选取分析频域上限的1.2倍作为模态截断频率,可较为准确地求解分析频域的振动响应,同时有效节省计算时间。
|
图 7 模态叠加法、直接积分法及试验结果对比 Fig. 7 Comparison of mode superposition method, direct integration method and experiment |
船舶尾部局部板架发生共振时容易引起结构响应幅值超差,应进行计算验证。对于求解的有限元模型,其网格大小应遵循单个波长内至少划分4个网格的基本原则;对于求解方法,建议采用模态叠加法,并选取1.2倍分析频率上限作为截断频率。以上结论可在基本保证振动响应求解准确性的基础上,有效缩短计算时间,提高工程设计研究效率。
| [1] |
李志杰. 船舶尾部结构振动特性数值仿真和试验研究[D]. 上海: 上海交通大学, 2016.
|
| [2] |
张玉奎, 詹蓉, 沈玉琦. 某大型公务船的振动性能评估[J]. 船舶, 2017, 28(2): 43-49. DOI:10.19423/j.cnki.31-1561/u.2017.02.043 |
| [3] |
LIU C Q, CHE C D, SHEN X H. Experimental and numerical study on vibration of the full-revolving propulsion ship stern[J]. China Ocean Engineering, 2015, 29(1): 33-48. DOI:10.1007/s13344-015-0003-5 |
| [4] |
刘西安, 吴广明, 李伟杰. 某科考船艉部舱段振动固有频率计算方法[J]. 中国舰船研究, 2017, 12(4): 110-116. DOI:10.3969/j.issn.1673-3185.2017.04.017 |
| [5] |
刘晓之, 夏利娟, 吴嘉蒙. 大型油船阶梯式尾部型式振动特性研究[J]. 舰船科学技术, 2015, 37(10): 26-29+35. DOI:10.3404/j.issn.1672-7649.2015.10.006 |
| [6] |
HAGEMEN R B, DRUMMEN I. Modal analysis for the global flexural response of ships[J]. Marine Structures, 2019, 63(JAN.): 318-332. |
| [7] |
李建彰. 高速型船舶振动响应计算分析[J]. 舰船科学技术, 2018, 40(1): 23-26. DOI:10.3404/j.issn.1672-7649.2018.01.004 |
| [8] |
徐孝诚, 尹立中. 关于结构高频响应分析中有限元网格划分的细化标准[J]. 振动与冲击, 2002(1): 54-55+47+104-105. DOI:10.3969/j.issn.1000-3835.2002.01.014 |
| [9] |
SEPEHRIRAHNAMA S, XU D, ONG E T, et al. Fluid–structure interaction effects on free vibration of containerships[J]. Journal of Offshore Mechanics and Arctic Engineering, 2019, 141(6): 1-27. |
| [10] |
YE X , XIA L. Experimental Investigation and numerical simulation of ship stern structural vibration model[J]. Journal of Shanghai Jiaotong University (Science), 2020(4).
|
 2022, Vol. 44
2022, Vol. 44
