0 引　言

由于船舶在航行过程中，会受到风、浪、流等因素的影响，且船舶是一种典型的欠驱动、非线性控制系统，因此，作为欠驱动船舶的核心技术之一，船舶控制是亟需研究的重点。船舶控制的主要研究内容有航迹跟踪、镇定控制和编队控制，其中航迹跟踪又可分为路径跟踪和轨迹跟踪^[1]。路径跟踪只需完成几何性质的位置跟踪而不依赖于时间信息，轨迹跟踪则指船舶能够在指定的时间到达指定位置。通常情况下，船舶航行时不要求在指定时间到达指定地点，只需沿着路径规划的航线航行，因而路径跟踪具有更重要的研究意义^[2]。

船舶的路径跟踪是指控制船舶在一定的精度范围内沿着最优路径航行，常见的路径跟踪可分为几何跟踪和模型跟踪，几何跟踪是指根据船舶的运动学几何结构，推导出控制量进行跟踪；模型跟踪是指基于算法求解模型，结合船舶运动学和动力学的控制规律，通过最优解等方式计算得到跟踪控制量，适用于不同的模型系统。可以是模型精度高的，也可以是不需要模型的；可以是线性的，也可以是非线性的，因此被广泛应用于路径跟踪领域。近年来，常见的模型跟踪方法有模型预测控制^[3](Model predictive control, MPC)，非线性滑模控制^[4](Nonlinear sliding mode control)，反步法^[5](Backstepping)，神经网络^[6](Neural network)及自适应技术与其他方法的组合^[7]等。但这些方法大都存在计算复杂、稳定性差等缺点。由于视线导航(Line of sight, LOS)算法具有不依赖船舶数学模型、设计简单、计算量小、抗干扰能力强等优点，在国内外路径跟踪的理论基础研究中被广泛应用^[8]。贺宏伟等^[9]将预测的漂角引入LOS以补偿漂角引起的稳态横向偏差。秦梓荷等^[10]提出一种基于视线制导的控制器，克服了参数不确定和波浪扰动对反馈控制带来的困难，实现速度的光滑控制。祝亢等^[11]利用LOS方法将路径跟踪问题转化为马尔科夫决策过程，设计基于强化学习的控制器。Fossen等^[12]采用滑模控制和ILOS设计自适应路径跟踪控制器。Borhaug E等^[13]在传统LOS理论的基础上增加积分项，增强了系统的鲁棒性。Piao Z等^[14]将LOS导航算法应用于船舶自动靠泊的研究中，然而，算法只解决了直线航段的控制问题，在弯道航段的转向点附近没能完成轨迹控制，且最终LOS航向角没有收敛到零。

分析现有研究后，首先建立欠驱动船舶水平面三自由度的动力学模型，接着对传统的LOS方法进行改进应用，通过简单的推导得出航向角，并使其同时适用于直线与曲线航段。最后在PID控制中添加首摇抑制项，设计一种基于视线制导和PID控制的首摇抑制器，提高船舶过弯时的控制性能。

1 船舶动力学模型

船舶在海洋中的运动由于受到环境的影响和本身物理特性的制约，通常比较复杂。相较于一般的机器人模型、车辆模型和飞行器模型等，船舶控制既需要考虑运动学问题，又需要考虑动力学问题。船舶的动力学建模包含三自由度模型、四自由度模型和六自由度模型，6种运动的相互耦合导致海上结构物操纵问题的复杂性，由于研究的是欠驱动船舶的航行和避障问题，只需考虑船舶在水平面上的运动情况，即船舶的横荡、纵荡和首摇。故采用Fossen提出的三自由度模型^[15]。

对Fossen水平面三自由度方程进行简化，因为船舶对称于中纵剖面，大型船舶过弯时速度较慢，可看作弱机动状态，略去二阶以上的项，故可写成如下形式：

$ \left\{ \begin{gathered} (m - {X_{\dot u}})\dot u - mvr - {X_u}u = X ，\\ (m - {Y_{\dot v}})\dot v - {Y_v}v - {Y_{\dot r}}r + (mu - {Y_r}) = Y ，\\ ({I_z} - {N_{\dot r}})\dot r - {N_r}r - {N_v}v - {N_{\dot v}}\dot v = N 。\\ \end{gathered} \right. $

(1)

式中： $ u，v，r $ 分别为船舶沿 $ x $ 轴方向速度、沿 $ y $ 轴方向速度和首摇角速度； $ {X}_{u}，{Y}_{v}，{Y}_{r}，{N}_{v}，{N}_{r} $ 均为速度系数； $ {X}_{\dot{u}}，{Y}_{\dot{v}}，{Y}_{\dot{r}}，{N}_{\dot{v}}，{N}_{\dot{r}} $ 均为加速度系数； $ X，Y，N $ 包含所有外载荷，在狭窄航道中根据航行要求，主要可分为主桨推力、风浪流载荷，以及舵的控制力。由于在一定时间内，固定航道中外载荷不会有剧烈变化，可以近似看作定常。故有如下力分解:

$ \left\{ \begin{gathered} X = {X_T} + {\tau _x} ，\\ Y = {Y_\delta } + {\tau _y} + {Y_b} ，\\ N = {N_\delta }\delta + {\tau _z} + {Y_b}{l_b} 。\\ \end{gathered} \right. $

(2)

式中： $ {X_T} $ 为主推力，在初始速度确定后， $ {X_T} $ 为常数； $ {Y_b} $ 为侧推提供的力； $ {l_b} $ 为侧推到重心的水平距离，正常并不使用，需要使用时可以通过操船人员进行输入； $ \delta $ 为舵角， $ {Y}_{\delta }和{N}_{\delta } $ 为舵角系数；风浪流载荷视为定常，将以上方程转换成矩阵形式，可进行如下表达：

$ {\boldsymbol{M}}\dot {\boldsymbol{V }}+ {\boldsymbol{G}}(V){\boldsymbol{V}} = {\boldsymbol{HF}} + {\boldsymbol{D}} 。$

(3)

$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}&0&0 \\ 0&{m - {Y_{\dot v}}}&{ - {Y_{\dot r}}} \\ 0&{ - {N_{\dot v}}}&{{I_z} - {N_{\dot r}}} \end{array}} \right]，$

(4)

$ {\boldsymbol{G}}({\boldsymbol{V}}) = \left[ {\begin{array}{*{20}{c}} { - {X_u}}&0&{ - mv} \\ 0&{ - {Y_v}}&{mu - {Y_r}} \\ 0&{ - {N_v}}&{ - {N_r}} \end{array}} \right]，$

(5)

$ {\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} u \\ v \\ r \end{array}} \right]，$

(6)

$ {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&{{Y_\delta }}&1 \\ 0&{{N_\delta }}&{{l_\delta }} \end{array}} \right]，$

(7)

$ {\boldsymbol{F }}= {\left[ {\begin{array}{*{20}{c}} 0&\delta &{{Y_b}} \end{array}} \right]^{\rm{T}}}，$

(8)

$ {\boldsymbol{D}} = {\left[ {\begin{array}{*{20}{c}} {{X_T} + {\tau _{xwind}}}&{{\tau _{ywind}}}&{{\tau _{zwind}}} \end{array}} \right]^{\rm{T}}}。$

(9)

式中： $ {\boldsymbol{M}} $ 为质量矩阵； $ {\boldsymbol{G}}({\boldsymbol{V}}) $ 为包含科氏力、向心力和阻尼力的矩阵； $ {\boldsymbol{V}} $ 为速度矩阵； ${\boldsymbol{ HF}} $ 为控制矩阵。

标准状态空间方程为：

$ {\boldsymbol{\dot V}} = - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{GV}} + {{\boldsymbol{M}}^{ - 1}}({\boldsymbol{HF}} + {\boldsymbol{D}}) 。$

(10)

$ {\boldsymbol{V }}= \left[ \begin{gathered} u \\ v \\ r \\ \end{gathered} \right] 。$

(11)

2 计算模型

以某大型集装箱船为研究对象，实船主要参数如表1所示。

取船体重心位置（0,0,0），由于本次航行在狭窄航道内，故需注意在航行过程中，除确保重心按路径航行外，也要通过重心和4个角的相对位置关系，确保整个船体均在航道内。将主船体视为一个长方体，确定四角坐标，具体地，为防止碰撞，四角位置分别设置为：

a₁=（203, –29.5, 6.8），a₂=（203, 29.5, 6.8）, a₃=（–197, 29.5,6.8），a₄=（–197，–29.5,6.8）。

4个角在固定坐标系的位置根据重心位置，a₁，a₂，a₃，a₄和首向角 $ \psi $ 来确定，可以写成如下形式：

$ \dot \eta = {J_\theta }(\eta )v ，$

(12)

$ {J_\theta }(\eta )\mathop = \limits^{3DOF} R(\psi ) = \left[ {\begin{array}{*{20}{c}} {\cos (\psi )}&{ - \sin (\psi )}&0 \\ {\sin (\psi )}&{\cos (\psi )}&0 \\ 0&0&1 \end{array}} \right]。$

(13)

式中： $ \eta = \left[ {x,y,\psi } \right] $ 为船舶的位置信息， $ v = \left[ {u,v,r} \right] $ 为船舶的运动信息。

水动力系数由参考集装箱船 (20600 TEU，满载)给出，如表2所示。

3 基于视线制导和PID控制的首摇抑制器设计 3.1 LOS算法的基本原理和改进应用

在传统的LOS理论中，当船舶到达 $ {P_k} $ 点附近，期望到达 $ {P_{k + 1}} $ 点时，只需对航向角进行控制，不改变船舶速度，船舶就将到达目标位置，如图1所示。假设船舶目前所在位置为 $ P = {\left[ {x,y} \right]^{\rm{T}}} $ ，目标位置 $ {P_{k + 1}} = {\left[ {{x_{k + 1}},{y_{k + 1}}} \right]^{\rm{T}}} $ ，则LOS角可表示为如下形式：

$ {\psi _{LOS}} = ac\tan 2 \Bigg(\frac{{{y_{k + 1}} - y}}{{{x_{k + 1}} - x}}\Bigg) 。$

(14)

需注意 $ {\psi _{LOS}} \in \left[ { - \text{π} ,\text{π}} \right] $ ，以充分满足船舶在各个位置的需求。

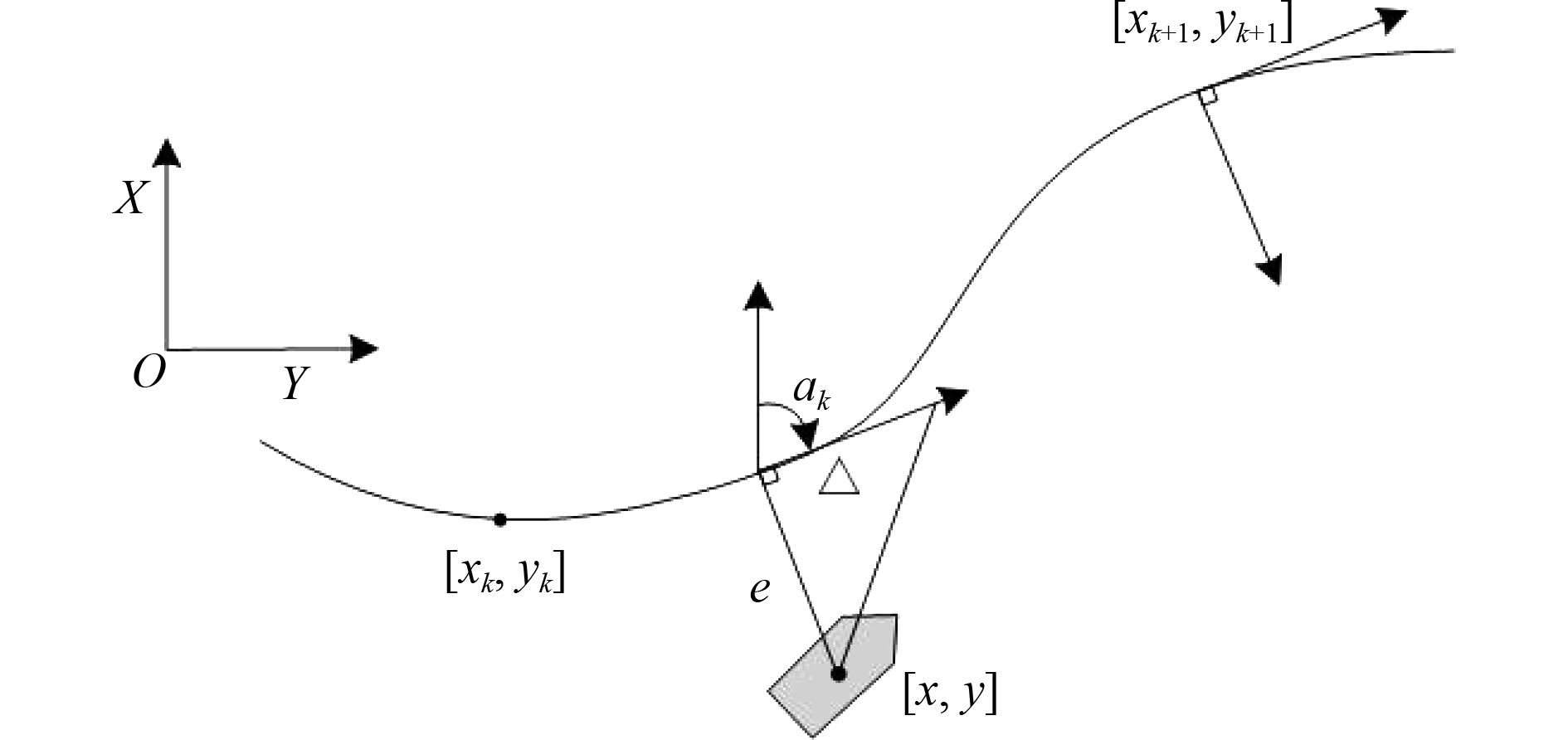
为了让LOS算法能够应用于曲线（见图2），将离船舶最近的航线点切线作为观测指引线，这里与直线航行略有不同，但大体思想一致，即使航向角向LOS角靠近，直至两者相同。

根据图2，可以得到

$ {\alpha _\psi } = {\alpha _k} + {\tan ^{ - 1}}( - e/ \Delta ) 。$

(15)

式中： $ \Delta $ 作为可视距离，根据船长来确定； $ {\alpha _\psi } $ 为船的期望航向角； $ e $ 为船舶到航线的最短距离； $ {\alpha _k} $ 为曲线切线与X方向的夹角。

当航线要求为一个个离散点时，可以将曲线简化为折线，期望航向角仍然使用曲线的公式，而e可以使用点到直线的距离公式来求，如下式：

$ e = \frac{{|A{x_0} + B{y_0} + C|}}{{\sqrt {{A^2} + {B^2}} }}。$

(16)

式中： $ A = {y_{k + 1}} - {y_k},B = {x_k} - {x_{k + 1}},C = {x_{k + 1}}{y_k} - {y_{k + 1}}{x_k} $ 。

此时可得 $ {\psi _e} = {\alpha _\psi } - \psi $ ，其中 $ \psi $ 为实际航向角，作为航向角误差，当 $ {\psi _e} = 0 $ 时，实际航向角与期望航向角一致，即满足导航要求。

导航过程中，期望航向点需要不断变化，只有这样才能确保船舶沿着航线不断向前，因此航向点的转换也需要一个算法，这里将每个期望航向点作为一个圆， $ {R_0} $ 作为圆的半径，当船舶进入这个圆时，就需要进行迭代 $ k = k + 1 $ ，即如下式：

$ \left\{ \begin{gathered} {({x_{k + 1}} - x)^2} + {({y_{k + 1}} - y)^2} \leqslant {R_0}^2，\\ k = k + 1 。\\ \end{gathered} \right. $

(17)

通常这样处理后，已经可以正常使用，但需要注意，当期望点之间的距离太短时，有时会存在还没有进入指定点的圆范围内就已经通过第一个点的情况，因此在每一步计算半径时要确保后一步永远小于前一步，即采用 $ {R_1},{R_2} $ 来不断储存前后两步的半径，并进行比较，当 $ {R_2} \geqslant {R_1} $ 时，也需要进行 $ k = k + 1 $ 的运算。

同时，在运动方程中，实际航向角 $ \psi $ 由积分得到，这就会导致一个问题， $ \psi $ 角会不断变大并远离 $ \left[ { - \text{π} ,\text{π} } \right] $ ，因此需要对 $ \psi $ 进行修正，使得 $ \psi $ 永远位于 $ \left[ { - \text{π} ,\text{π} } \right] $ 区间上，即

$ \psi = \psi - \Biggr(\Biggr[\frac{\psi }{{2\text{π} }} + 0.5\Biggr]\cdot 2 \text{π} \Bigg)。$

(18)

此外对 ${\psi _e} $ 也需要进行同样的处理，以确保当从 $ -\text{π} $ 到 $ \text{π} $ 转向时，是平滑的，即

$ {\psi _e} = {\psi _e} - \Biggr(\Biggr[\frac{{{\psi _e}}}{{2\pi }} + 0.5\Biggr]\cdot 2\text{π} \Biggr)。$

(19)

这是因为从 $ - \text{π} $ 到 $\text{π} $ ，其实方向基本一致，但在输入系统中，却会导致 $ {\psi _e} = - 2\text{π} $ ，控制器认为此时需要一个大的转角，导致船舶在原地打转，经过修正以后 $ {\psi _e} = 0 $ ，不需要转向。

3.2 改进的PID控制

大型船舶过弯时，由于首摇惯性较大，当船舶到达直线航段，惯性将使船舶仍以之前的角速度进行转向，从而偏离航向，为了使船舶保持直线航行，此时需要短时间内打很大的反向舵角，但这样的急速操舵，控制已经滞后，不仅会影响船舶的舒适性、稳定性，同时也会影响船舶的安全性以及舵的寿命。

PID控制由于其鲁棒性好、算法简单、可靠性高，被广泛应用于控制领域。为了能够更加平滑的进行操舵，降低操舵幅度，提高操舵效率，基于PID控制设计了首摇抑制器，通过在 PID 控制器中增加首摇抑制项，抑制有害的首摇。当首摇方向和船舶的期望航向一致时，首摇有益，抑制器并不发生作用，但若首摇方向与期望航向相反，此时首摇有害，抑制器会做出判断，减小首摇对船舶航行的影响。

对系统标准状态空间方程应用能控性和能观性秩判据，经计算，2个判别矩阵均为满秩(r=3)，说明系统既能观又能控。

对于转动惯量较大的船舶，只根据目标角度设计PID控制律存在不足，改进的PID控制规律定义为：

$ u(t) = {K_p}e(t) + {K_I}\int {e(t){\rm{d}}t} + {K_D}\frac{{{\rm{d}}e(t)}}{{{\rm{d}}t}} + {K_\omega }g(e(t),\omega (t))。$

(20)

当 $ e(t)\omega (t) \geqslant 0 $ 时，

$ g(e(t),\omega (t)) = 0 。$

(21)

当 $ e(t)\omega (t) \lt 0 $ 时，

$ g(e(t),\omega (t)) = \omega。$

(22)

式中： $ e(t) $ 为误差， $ u(t) $ 为输出， $ {K_p} $ 为比例系数， $ {K_I} $ 为积分系数， $ {K_D} $ 为微分系数, $ {K_\omega } $ 为首摇抑制项系数， $ \omega $ 为船舶角速度，具体设计控制律时，会将首摇抑制项作为集成项，调参时只调节 $ {K_p} $ ， $ {K_I} $ ， $ {K_D} $ 三个系数。

误差 $ e(t) $ 定义如下：

$ e(t) = {\alpha _\psi }(t) - \psi (t)。$

(23)

4 数值模拟 4.1 参数设置

以2021年苏伊士运河大型集装箱船搁浅事件为数值计算案例，在数值模拟前，先通过卫星地图获取苏伊士运河南部航道两岸的经纬度坐标。出于系统鲁棒性的考虑，将设计基于离散点的控制算法。为实现首摇抑制功能，体现改进后算法的适用性，截取同时包含弯曲航段和近似直线航段的航道。其中，弯曲部分不考虑风载荷的影响，直线航段时，将分为有风和无风2个航段，之所以在直线航段将风载荷考虑在内，是想在过弯后令船舶处于一种更危险的境地，以验证所提策略的抗干扰能力。数值模拟参数见表3。

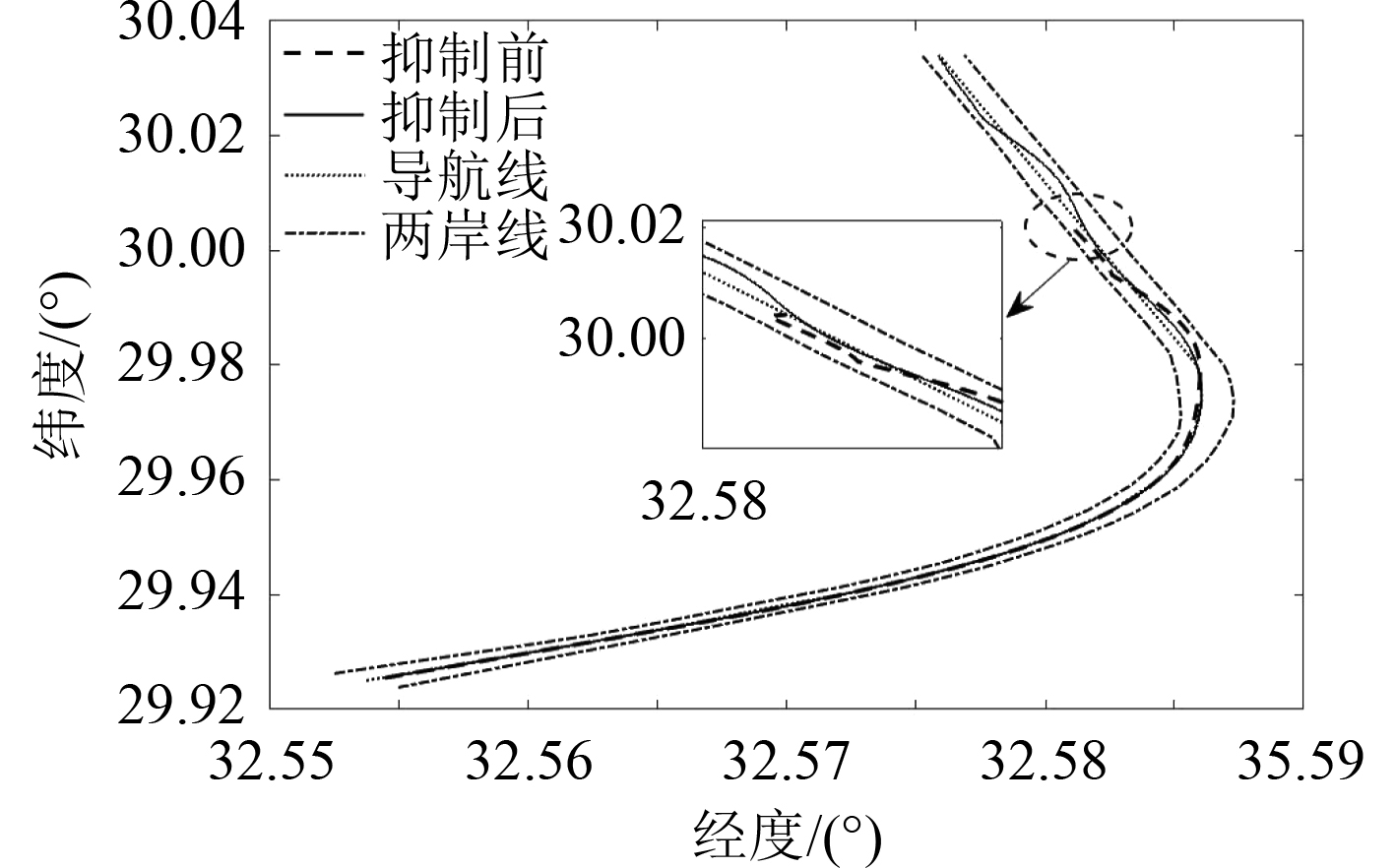
抑制前后船舶航行轨迹对比如图3所示，航行初始阶段，抑制前后轨迹基本重合，进入弯道后，采用首摇抑制器的船舶能有效控制自身航向，回到航线上，过弯后在首摇抑制器和风载荷的共同作用下，航行轨迹偏移量有所增大，航行全程3821 s，其中，船舶距西岸最小船岸距为52.644 m，距东岸最小船岸距为111.891 m,未发生碰撞；而未采用首摇抑制器的船舶过弯后无法控制自身航向，最终几乎完全侧着身子在航道中停了下来，无法继续航行，航行全程仅2680 s。由于航行时间不同，且随着船舶侧身航行，垂向误差等参数虽减小但不具有参考性，为验证首摇抑制策略的有效性，选取从开始过弯到未采用首摇抑制器船舶开始侧身航行的航段为对比航段(航行时间为1084～2663 s,包含部分有风航段)，展开对比分析。

4.2 仿真结果与分析

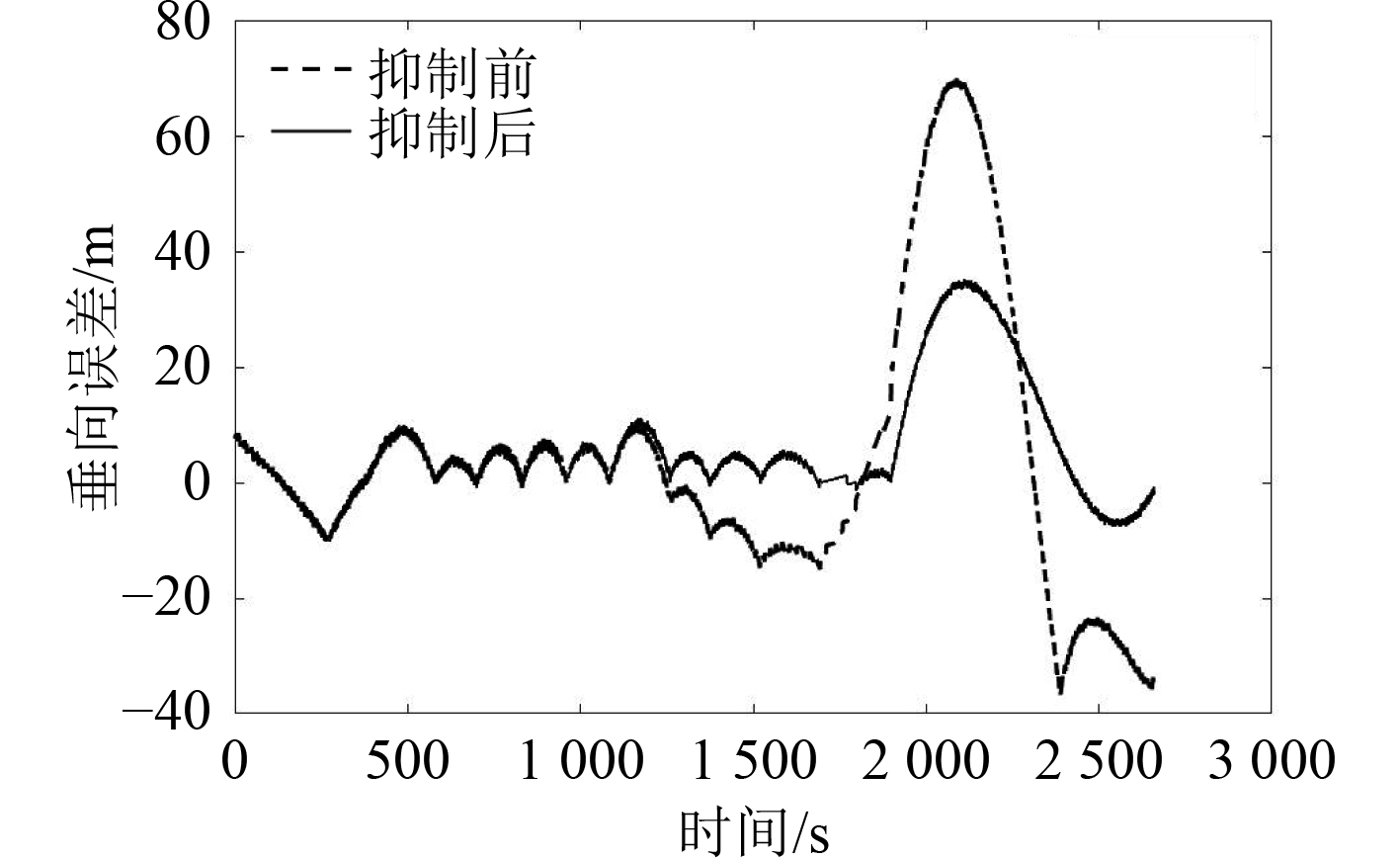
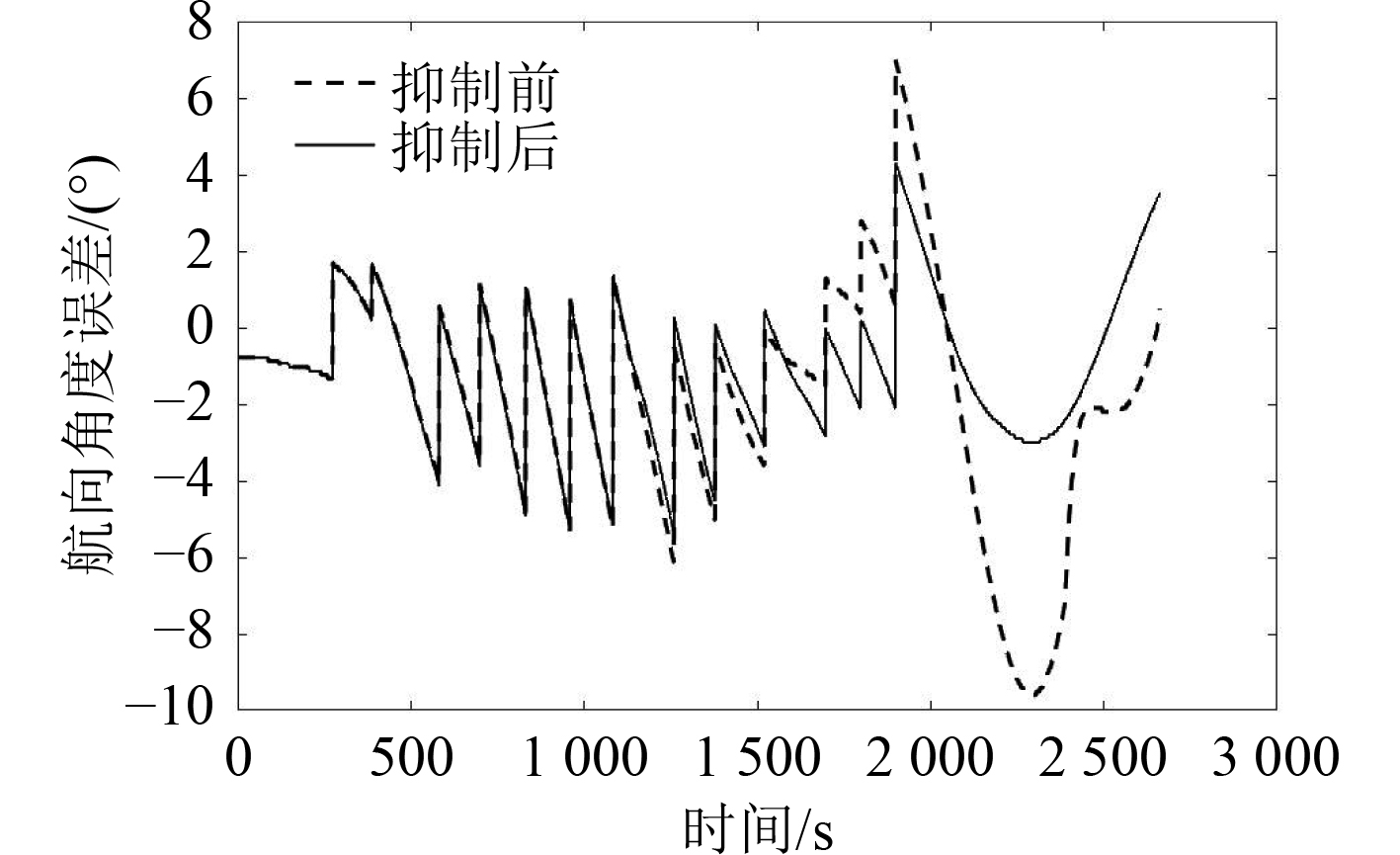
从路径跟踪过程中垂直误差随时间的变化来(见图4)，初始航段首摇抑制前后的垂向误差结果较为接近但不为0。这是因为仿真开始时，并没有令船舶与第一个航向点重合，以此检验船舶以任意初始位置和方向出发时的路径跟踪效果。过弯前的部分航段，没有采取首摇抑制器的跟踪效果甚至略好。对比航段内，首摇抑制器显著降低了船舶的垂向误差，其中，抑制前最大垂向误差为69.903 m，抑制后最大垂向误差为35.105 m，减少49.8%；抑制前平均垂向误差为22.260 m，抑制后平均垂向误差为9.747 m，减少56.2%。同时，可以发现船舶垂直误差的下降伴随着一定程度的震荡。这是由于船舶的操舵产生了左右摇晃。同理，船舶航向角误差也会产生震荡。图5为路径跟踪过程中的航向角误差，变化趋势与垂向误差基本一致，抑制前最大航向角误差为9.600°，抑制后最大航向角误差为5.416°，减少43.6%；抑制前平均航向角误差为3.169°，抑制后平均航向角误差为1.808°，减少42.9%。综上所述，首摇抑制策略具有较好的控制效果，能有效提高路径跟踪精度。

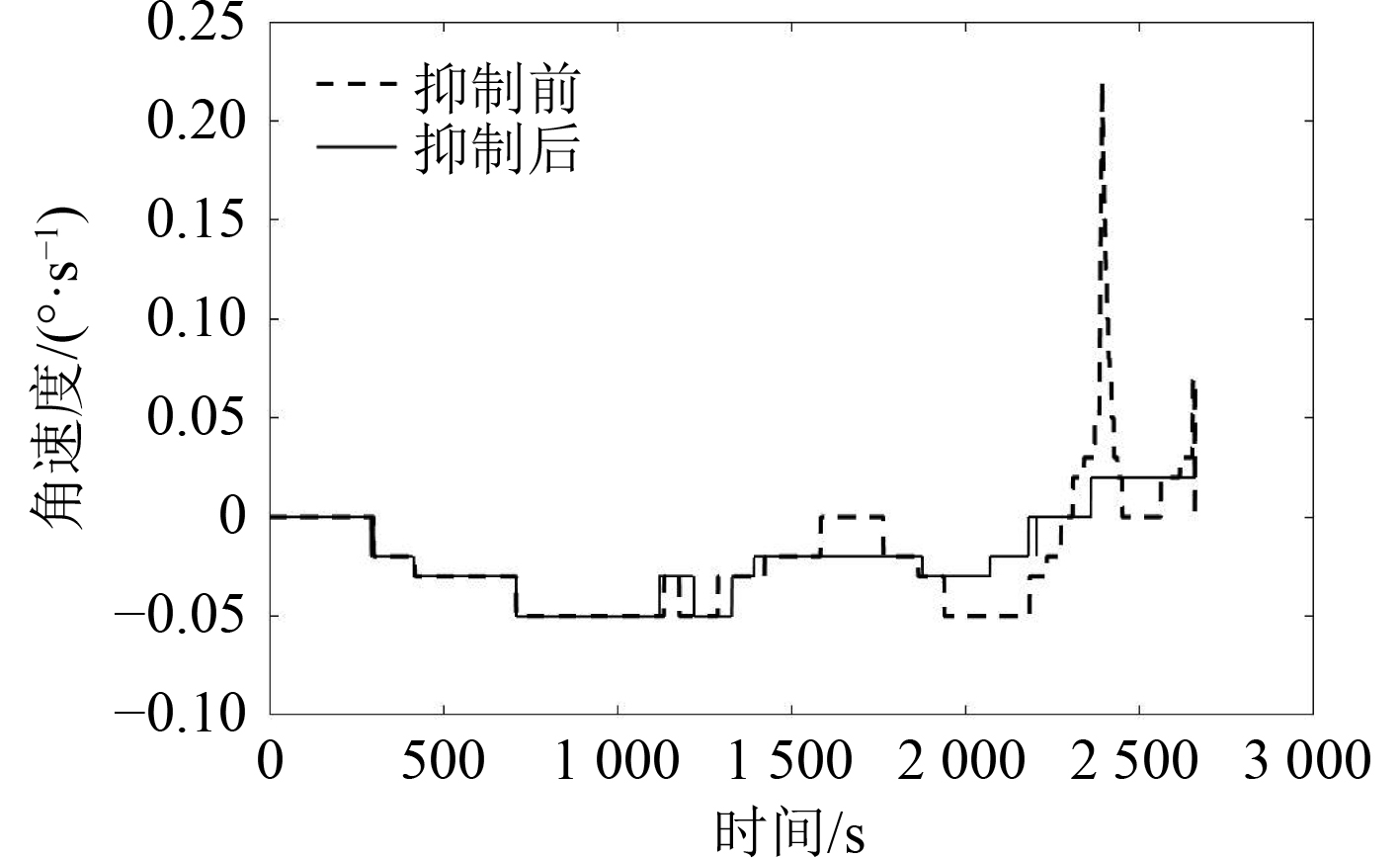
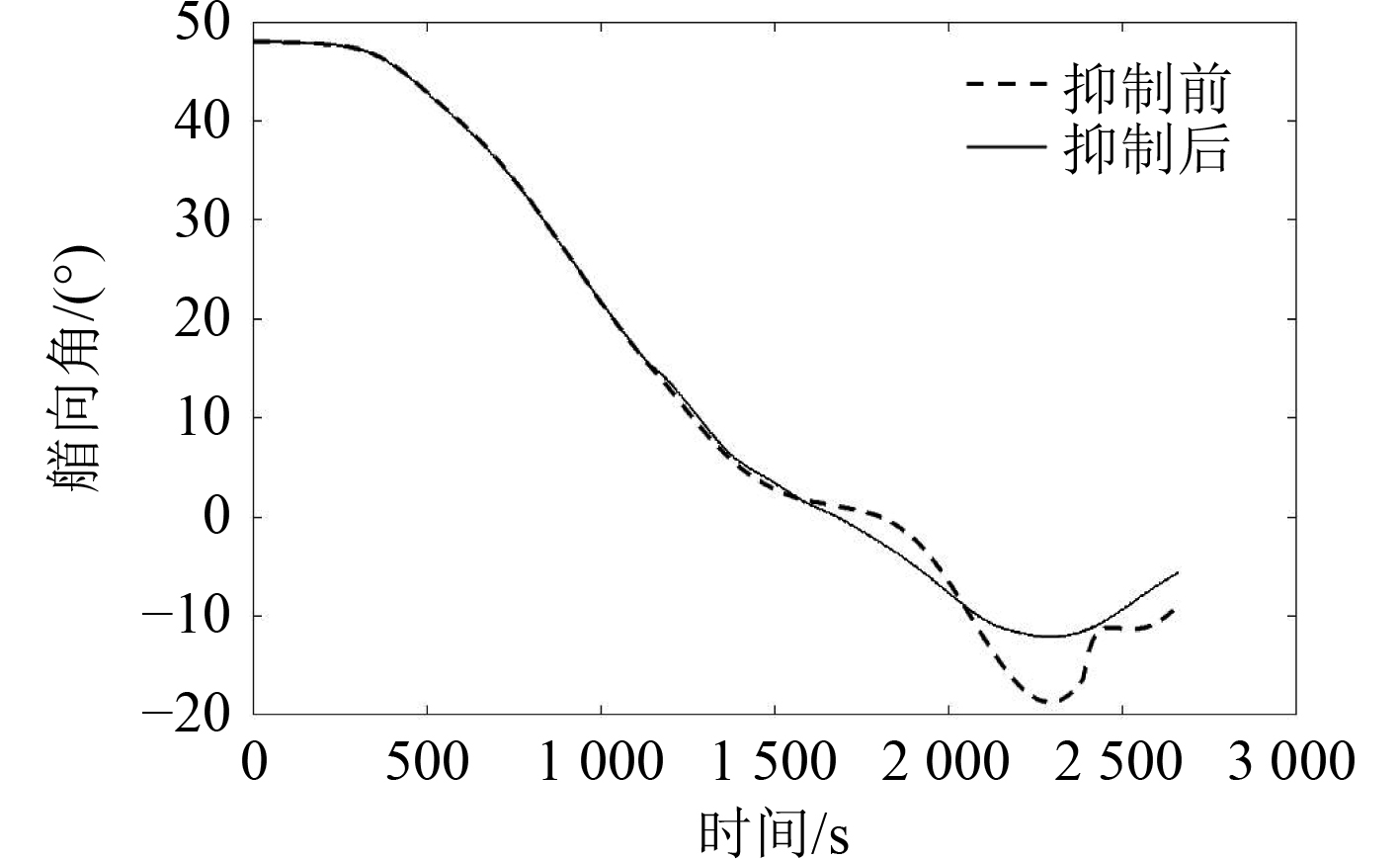
图6和图7分别为船舶的首摇角速度和首向角变化图，可见首摇角速度虽有一定程度的起伏，但变化幅度极小，故抑制前后首向角均未出现震荡较大的情况。对比内(1579 s)，抑制后船舶首摇角速度标准差为0.021，小于抑制前首摇角速度的标准差0.034，导致抑制后首向角的整体变化幅度也小于抑制前。依然验证了首摇抑制器的有效性。

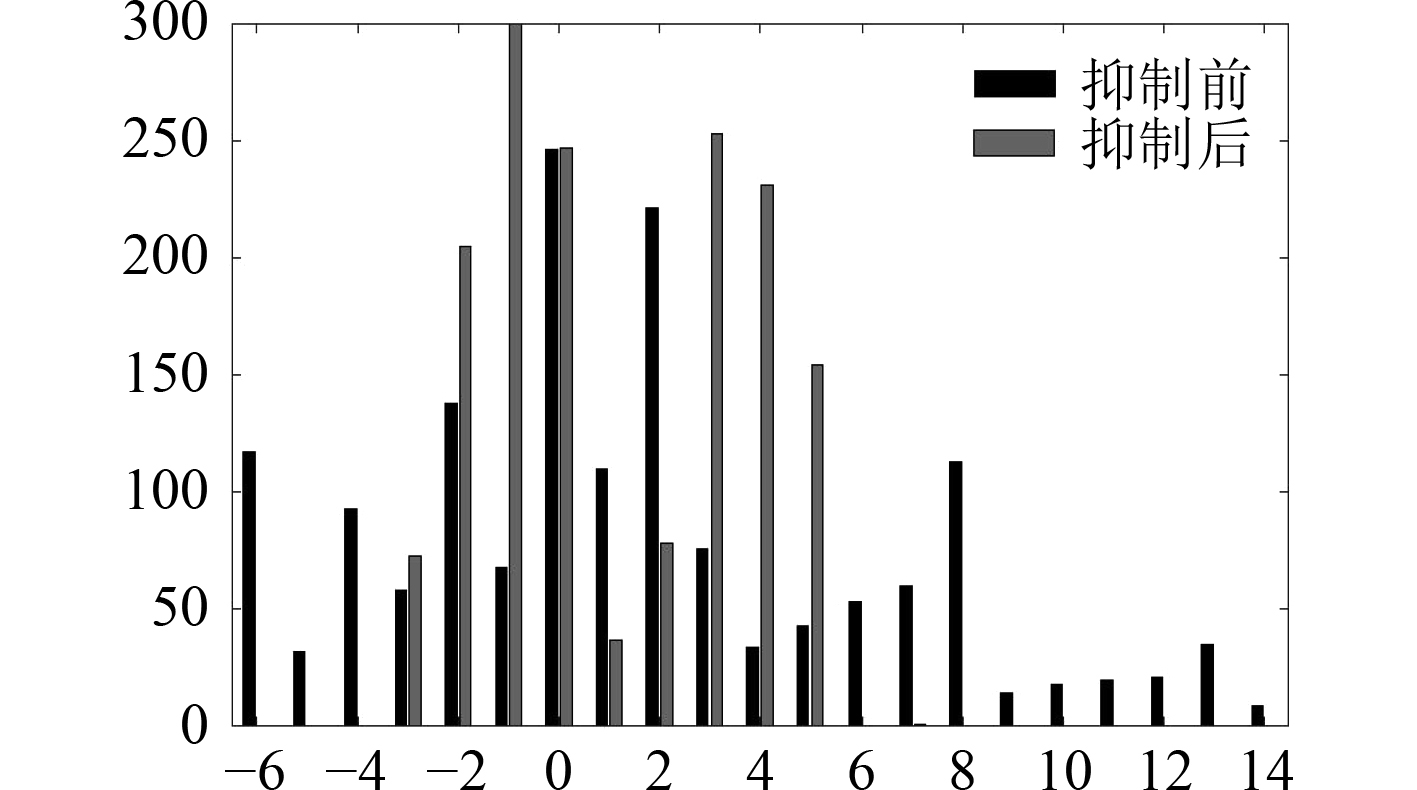
图8为对比航段航行过程中舵角的变化情况。抑制前后均存在震荡现象，这是因为考虑到船舶的动力学特性，PID控制无法对未来一个时间序列内船舶的操作进行优化。可以看出，采用首摇抑制器的船舶控制较为柔和，对比航段内，抑制前最大右舵为14°，最大左舵为–6°，抑制后最大右舵为7°，最大左舵为–3°，均减少至一半；抑制前平均右舵为4.996°，平均左舵为–3.458°，抑制后平均右舵为3.518°，平均左舵为–1.603°，分别减少29.6%和53.6%。舵角分布如图9所示，对比航段内，未采用首摇抑制器的船舶舵角较为分散，出现次数最多的5个舵角占比56.2%，而采用首摇抑制器的船舶舵角集中出现在–2°，–1°，0°，3°和4°，占比78.3%，对船舶动力系统的压力小，可节能提效。因此尽管存在一定程度的震荡，但采用首摇抑制器的船舶航行全程基本为小舵角操船且舵角变化幅度小，可满足生理性、舒适性和稳定性需求。

5 结　语

针对欠驱动船舶的首摇惯性问题，提出一种基于视线制导和PID控制的首摇抑制策略，旨在合理利用首摇方向和目标航向的关系提高过弯时船舶的控制性能。以某大型集装箱船通过苏伊士运河南部航段为数值计算案例，通过对比分析，确定首摇抑制策略的作用，主要结论如下：

1）进入弯道后，首摇抑制策略能有效控制船舶首向，使其回到航线上。

2）对比航段内，首摇抑制策略能有效减小船舶的最大垂向误差(49.8%)、平均垂向误差(56.2%)、最大航向角误差(43.6%)和平均航向角误差(42.9%)，提高路径跟踪精度。

3）对比航段内，首摇抑制策略的控制更为柔和，可降低首摇角速度的变化幅度；可降低操舵幅度，使舵角分布更为集中。