0 引　言

世界范围内经济的快速增长促进了海上物流贸易行业的发展，作为一种安全性高、成本低、综合效益好的商品运输方式，海上航运业在近代以来迎来了爆发式增长。与此同时，海上航线船舶的密度越来越大，导致船舶碰撞、搁浅等事故逐年增加，大量的统计数据表明，海上船舶，尤其是大型油船、集装箱运输船，在船舶海上交通事故中，船舶搁浅和碰撞事故占一半以上。船舶搁浅和碰撞不仅会造成船舶损伤和人员伤亡，还可能造成燃油泄漏等严重的海洋环境问题^[1]，因此必须要对船舶搁浅场景下船体的设计强度进行计算分析。

本文的研究方向是船舶搁浅时对船舷外部结构的损伤数值分析，从弹性力学和有限元分析技术出发，建立船舶搁浅场景的力学模型和有限元仿真模型，有助于指导大型船舶的结构设计，使船舶在搁浅时的损伤降到最低。

1 搁浅状态下船舷外部结构强度的力学基础

船舶搁浅时与暗礁等物体产生碰撞，船舷外部结构件受力过程中会产生弹性应变和塑性应变。

1）应力-应变公式

定义船舷结构搁浅时受到的表面力为：

$ \left[ P \right]{\text{ = }}\left( {{p_x},{p_y},{p_z}} \right) \text{，} $

$ \left[ Q \right]{\text{ = }}\left( {{q_x},{q_y},{q_z}} \right) \text{，} $

产生的位移为：

$ \left[ f \right]{\text{ = }}\left( {u,v,w} \right) \text{，} $

则船舷结构的正应力和切应力为：

$ \left\{ \begin{gathered} \left( {{\sigma _x},{\sigma _y},{\sigma _z}} \right) ，\\ \left( {{\tau _x},{\tau _y},{\tau _z}} \right)。\\ \end{gathered} \right. $

船舷结构的正应变和切应变为：

$ \left\{ \begin{gathered} \left( {{\varepsilon _x},{\varepsilon _y},{\varepsilon _z}} \right)，\\ \left( {{\kappa _x},{\kappa _y},{\kappa _z}} \right)。\\ \end{gathered} \right. $

建立船舷结构弹性力学平衡方程如下式：

$ \begin{gathered} \frac{{\delta {\sigma _x}}}{{\delta x}} + \frac{{\delta {\tau _x}}}{{\delta y}} + \frac{{\delta {\tau _z}}}{{\delta z}} + {q_x} = 0，\\ \frac{{\delta {\tau _x}}}{{\delta x}} + \frac{{\delta {\sigma _y}}}{{\delta y}} + \frac{{\delta {\tau _y}}}{{\delta z}} + {q_y} = 0，\\ \frac{{\delta {\tau _x}}}{{\delta x}} + \frac{{\delta {\tau _y}}}{{\delta y}} + \frac{{\delta {\sigma _z}}}{{\delta z}} + {q_z} = 0 。\\ \end{gathered} $

2）形变公式

船舷结构产生的形变也是导致船体损伤的重要原因，建立船舷结构的形变公式为：

$ {\varepsilon _x} = \frac{{\delta u}}{{\delta x}},{\varepsilon _y} = \frac{{\delta v}}{{\delta y}},{\varepsilon _z} = \frac{{\delta w}}{{\delta z}} \text{，} $

船舷结构的位移公式为：

$ {\kappa _x} = \frac{{\delta u}}{{\delta x}} + \frac{{\delta v}}{{\delta y}},{\kappa _y} = \frac{{\delta w}}{{\delta x}} + \frac{{\delta v}}{{\delta y}},{\kappa _z} = \frac{{\delta u}}{{\delta y}} + \frac{{\delta v}}{{\delta z}} 。$

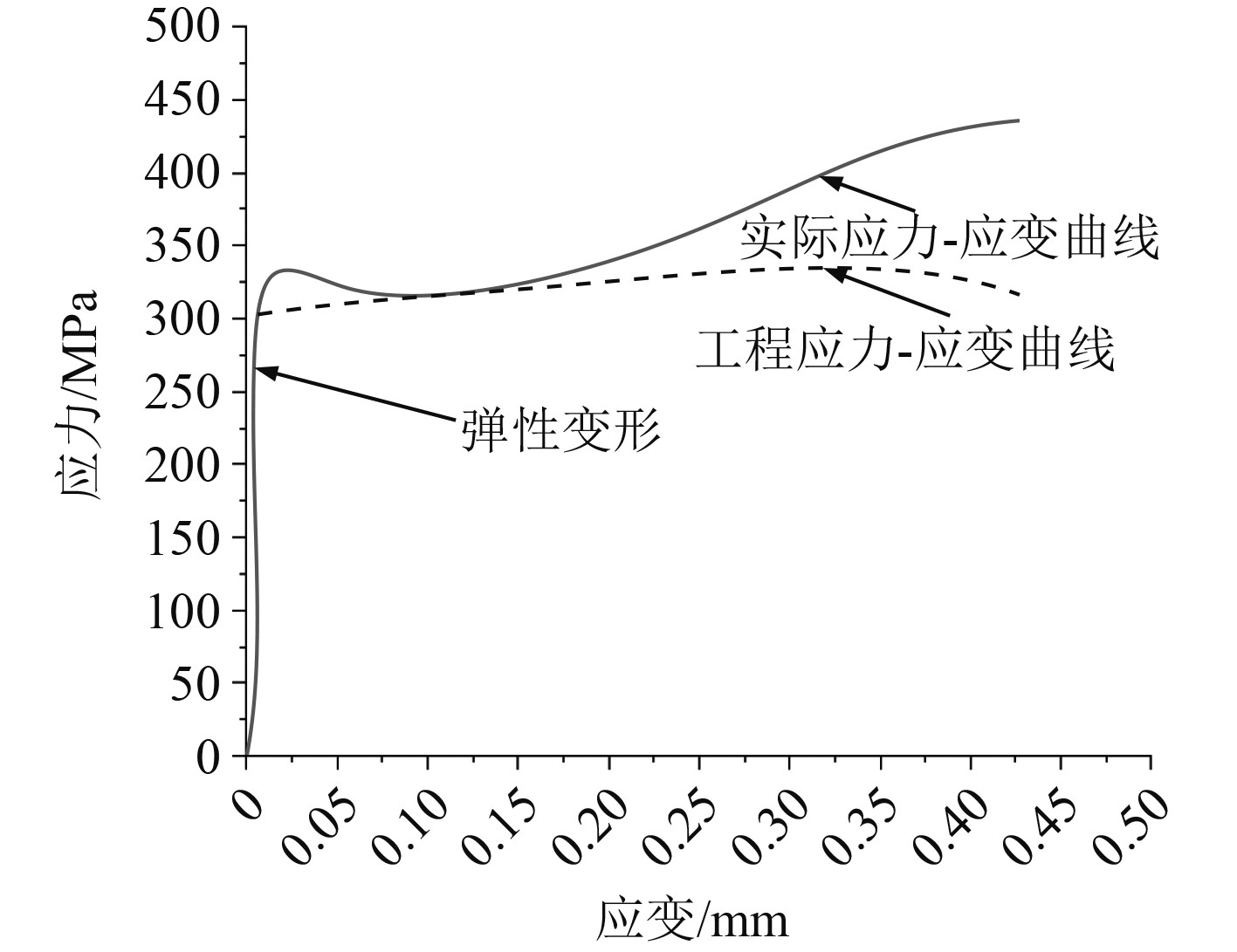
本文研究的船舷外部结构材料为Q345钢，该材料的应力应变曲线由试验得到，如图1所示。

3）材料本构方程

材料的本构方程能够说明材料在弹塑性变形过程的屈服特性，建立船舷结构材料的本构方程如下式：

$ {\sigma _y} = \left[ {1 + {{\left( {\frac{\varepsilon }{c}} \right)}^{\frac{1}{p}}}} \right]\left( {{\sigma _0} + \beta {E_p}\varepsilon _p^{eff}} \right) \text{，} $

式中： $ {\sigma _0} $ 为初始的屈服应力， $ \beta $ 为材料弹性模量， $ {E_p} $ 为材料硬化系数， $ \varepsilon _p^{eff} $ 为材料的塑性应变， $ c $ 取0.56， $ p $ 取0.25。

2 船舶搁浅过程船舷外部结构的载荷分解

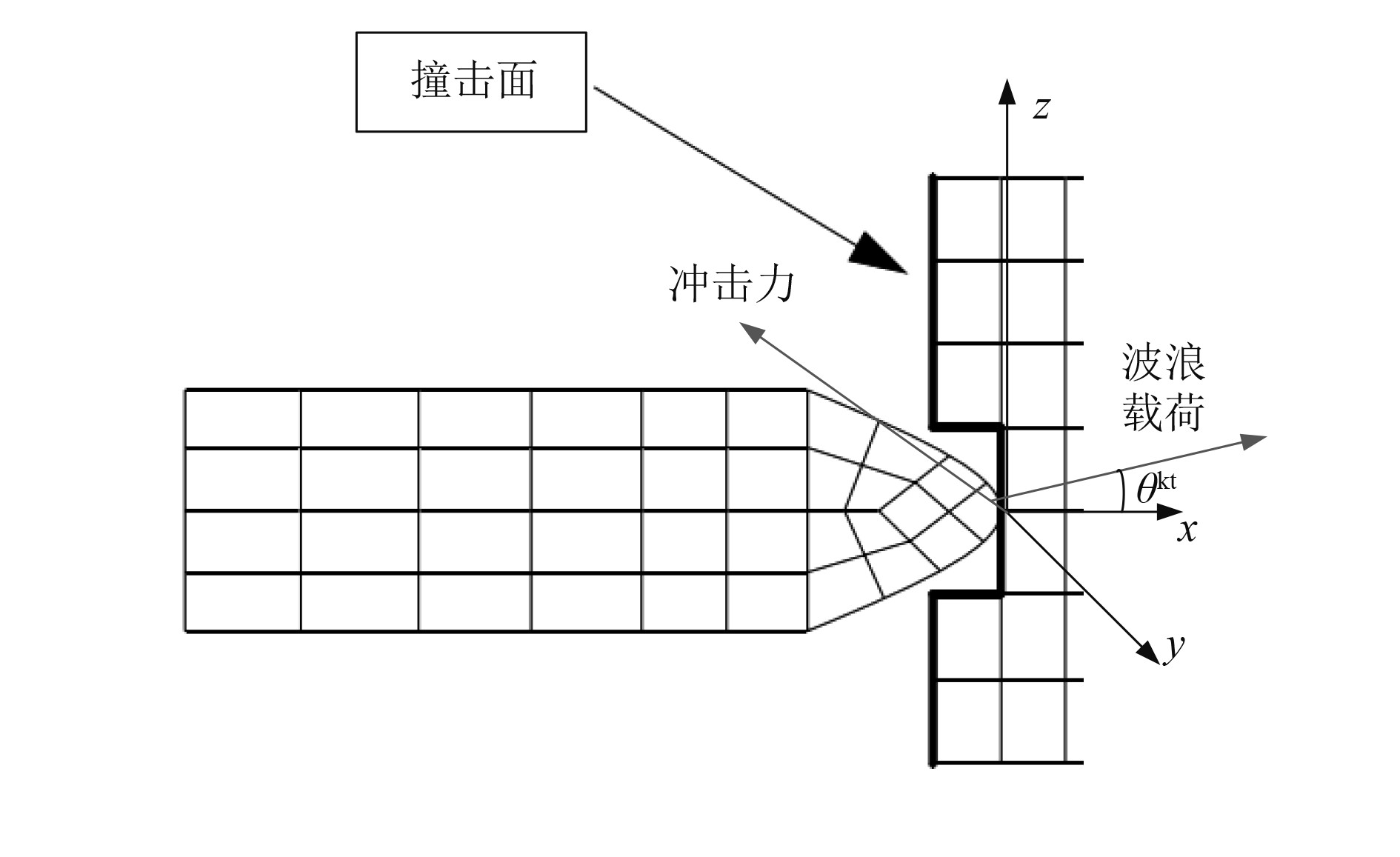
船舶搁浅过程中受到的载荷是暗礁等障碍物冲击载荷与波浪载荷的叠加，因此，为了提高船舶搁浅时船舷结构损伤的计算精度，本文分别对2种载荷的边界条件进行建模，首先建立船舶搁浅时船舷结构的受力分析如图2所示。

1）波浪载荷

本文采用规则波产生的波浪载荷，规则波的波面为：

$ f{\text{ = }}{\varphi _0}\cos \left( {kx - {w_0}t} \right) \text{。} $

式中： $ {\varphi _0} $ 为波浪的振幅； $ {w_0} $ 为频率；k为周期内的波数。

波浪产生的速度场模型为：

$ \begin{gathered} u{\text{ = }}\dfrac{\text{π} }{2}{\varphi _0}{\theta ^{kt}}\cos \left( {kx - {w_0}t} \right) ，\\ w = \dfrac{1}{2}{\varphi _0}{\theta ^{kt}}\sin \left( {kx - {w_0}t} \right)。\\ \end{gathered} $

式中： $ {\theta ^{kt}} $ 为波浪的方位角。

搁浅过程船舷结构受到的波浪载荷如下式：

$ {M_w} = \frac{1}{2}{K_g} \cdot h \cdot B \cdot {A_1} \cdot {A_2} \cdot {L^2} \times {10^{ - 2}} \text{。} $

式中： $ {M_w} $ 为波浪载荷； $ h $ 为吃水深度；L为船长； $ {A_2} $ 为压力系数；B为船宽； $ {K_g} $ 为船体形状影响系数，按下式计算：

$ {K_g} = 1.437\alpha \left[ {0.032 + 0.013\left( {{C_b}/\alpha - 0.60} \right)} \right] $ ， $ \alpha $ 为水线长度系数， $ {C_b} $ 为船舶宽度系数^[2]；

$ {A_1} $ 为速度系数，按下式计算：

$ {A_1} = 1 - \left( {3 + 25{F_{nw}}} \right){M_s}/(D) + 1.5{F_{nw}} \text{。} $

式中： $ {F_{nw}} $ 为波浪附加作用力； $ {M_s} $ 为静水弯矩； $ D $ 为船舶排水量。

2）冲击载荷

船舶搁浅时的冲击载荷基于经验公式表示为：

$ {F_X} = \frac{{3.58{\sigma _0}{t_w}{t^{0.61}}_eb_0^{}}}{{{k_0}}} \text{。} $

式中： $ {\sigma _0} $ 为屈服应力； $ {t_w} $ 为纵向筋板厚度； $ {t_e} $ 为船舷横向筋板厚度； $ b_0^{} $ 为船舷结构宽度； $ {k_0} $ 为修正因子。

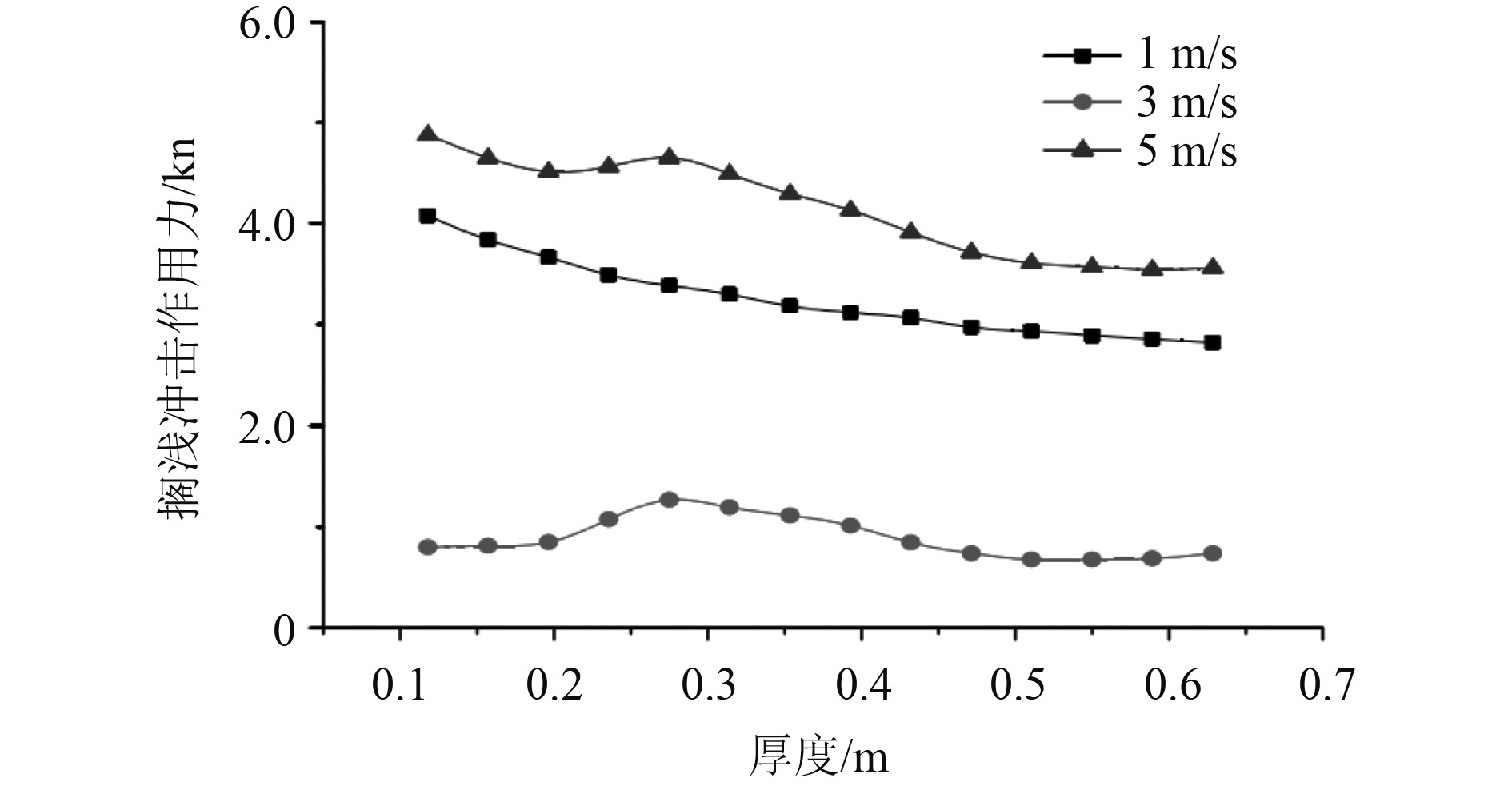
船舷搁浅时的冲击力与横向筋板厚度密切相关，图3为不同风速下冲击作用力与筋板厚度的关系。

3 基于有限元分析技术的船舶搁浅过程船舷外部结构损伤数值计算 3.1 有限元建模

船舶搁浅过程的力学特性非常复杂，如果仅试图通过解析法来求解不科学，因此，结合有限元仿真分析技术，借助计算器强大的数据运算能力来求解船舶搁浅问题。

在有限元建模之前，建立船体搁浅过程的动量和能量守恒边界条件。

1）船体动量和能量守恒方程：

$ \begin{gathered} {F_X}t = m{v_1} - m{v_2}，\\ {F_X}s = \frac{1}{2}m{v_1}^2 - \frac{1}{2}m{v_2}^2。\\ \end{gathered} $

式中： $ {v_1} $ 为碰撞前船舶的速度； $ {v_2} $ 为搁浅瞬间船舶的速度。

2）海水能量守恒方程^[3]：

$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\partial k}}{{\partial t}} + {{\bar u}_i}\dfrac{{\partial k}}{{\partial {x_j}}} = \dfrac{\partial }{{\partial {x_j}}}\left[ {\left( {1 + {\sigma _k}{v_t}} \right)\dfrac{{\partial k}}{{\partial {x_j}}}} \right] + {P_k} - k\omega }，\\ {\dfrac{{\partial \omega }}{{\partial t}} + {{\bar u}_j} = \dfrac{\partial }{{\partial {x_j}}}\left[ {\left( {1 + {\sigma _k}{v_t}} \right)\dfrac{{\partial \omega }}{{\partial {x_j}}}} \right] + 2(1 - {F_i})\delta } 。\end{array}} \right. $

式中： ${v_t}$ 为分散系数； $ {\bar u_i} $ ， $ {\bar u_j} $ 分别为搁浅前后海水的流速分量； $ {P_k} $ 为流体压力； $ \delta $ 为粘度系数； $ {\sigma _k} $ 为单位应力。

有限元建模参数如表1所示。

船舷外部结构有限元模型的材料选用Q345，屈服强度为345 MPa，弹性模量为2.1E10 MPa，泊松比为0.26，建模选用的单元大小100 mm，有限单元类型为solid185单元，船舷局部结构的有限元模型如图4所示。

3.2 船舶搁浅时船舷外部结构的损伤有限元仿真

搁浅过程船舶船舷结构的损伤计算过程包括：

步骤1　有限元模型的导入

步骤2　载荷和边界条件设置

波浪载荷 $ {M_w} $ 和搁浅冲击载荷 $ {F_X} $ 的施加；船舷结构材料本构方程、动量和能量守恒方程的导入。

步骤3　S-N曲线参数的选择

在校核船舷外在结构的疲劳强度时^[4]，首先建立S-N曲线的回归公式为：

$ \log N = 12.16 - 3.0\log S，\;\;\;\;\;t = 45，$

$ \log N = 12.16 - 0.75\log \left( {\frac{t}{{32}}} \right) - 3.0\log S，\;\;\;\;t \ne 45 \text{。} $

式中：t为船舷筋板厚度；N为循环次数。选取船舷材料的S-N曲线为：

$ S_{r} N_{t}^{m^{m}}=1.09 。$

步骤4　求解

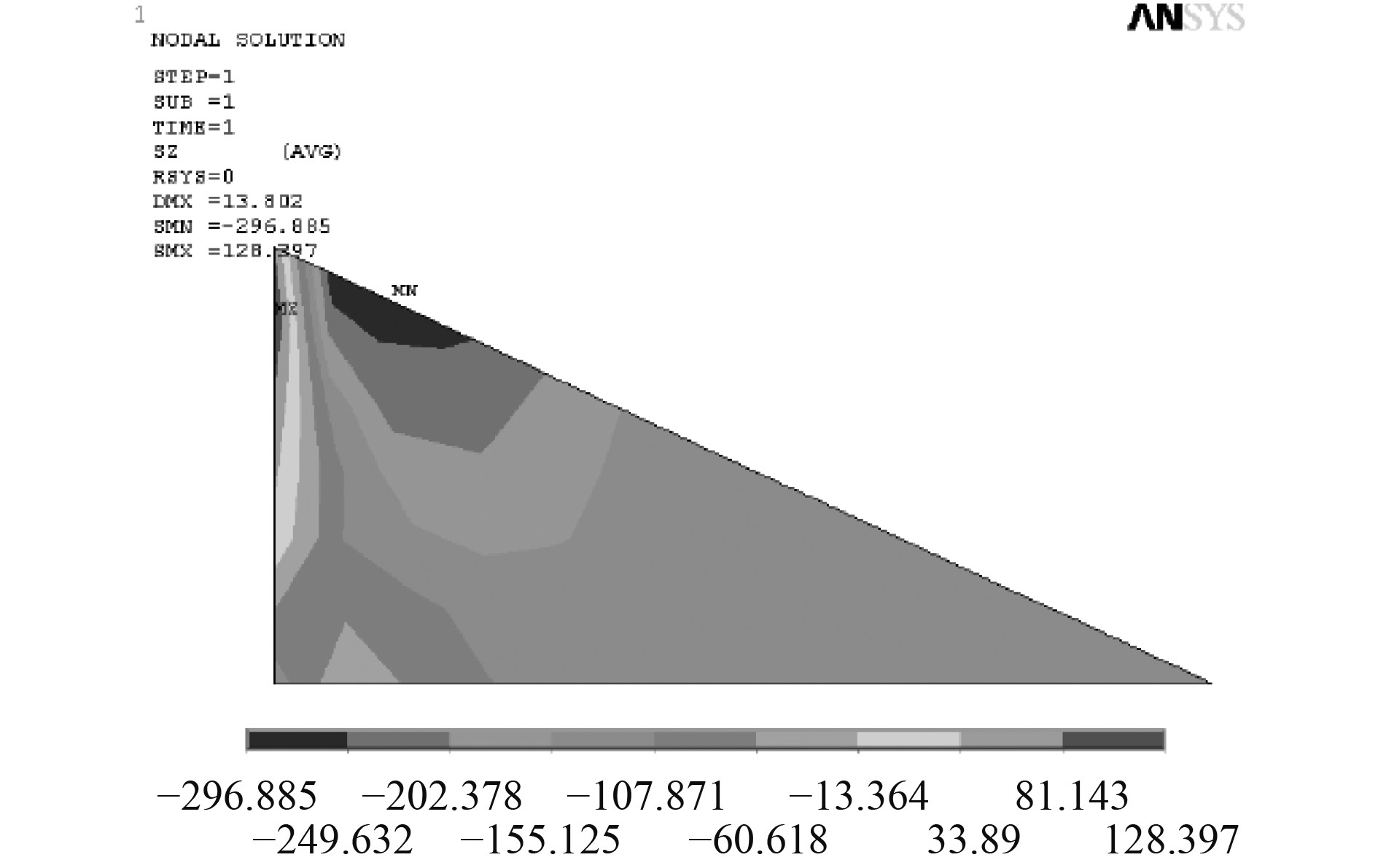
图5为船舷局部结构损伤仿真结果。

4 结　语

船舶搁浅过程的力学特性非常复杂，为了简化运算，本文将搁浅过程的载荷归结为波浪载荷和冲击作用力载荷2种，针对2种载荷进行数学建模，并结合有限元仿真技术对船舷外部结构在搁浅时的损伤特性进行仿真。