2. 上海海事大学 商船学院,上海 200135
2. Merchant Marine College, Shanghai Maritime University, Shanghai 200135, China
船舶航行过程下沉量主要与以下2个因素相关:
1)船底相对海水的流动速度
大型船舶在海水中航行时,船首将海水推开并从船首的两侧向后流向船尾,海水的流动过程中船首位置的液体流速快、压力小,船尾的液体流速慢,压力大。液态在船底的相对流动速度导致船舶首尾压力出现差距,大型船舶整体为了保持平衡就需要一定的下沉量[1]。
2)纵倾运动
船舶受海浪、海风和自身动力系统载荷的影响,船体会发生纵倾运动,纵倾运动导致的下沉量主要是船首和船尾下沉量。
船舶航行下沉量是设计过程中必须要考虑的因素,相对于深水下的船舶航行下沉量,浅水区域的下沉量具有以下不同的特征:
1)海水流动方向不同
在深水区域,船舶底部的液体流动具有在三维空间内流动的特点,船首处液体的方向是向后和向下,船尾处的液体流动方向是向后和向上。而浅水区域中受限于船底与海底的距离影响,船舶首尾部分水的流动只能向两侧,是一种二维平面式的流动,这种液体流动方式又称为浅水效应。
2)下沉量不同
受浅水效应的影响,船舶在浅水中的下沉量会比深水区域的下沉量更大,且船体的纵倾运动幅度更大,运动更明显。
船舶在浅水航行时的下沉量会降低船体的操纵性能,且下沉量叠加船体的吃水,使船舶擦底和搁浅的风险明显提高,因此有必要针对船舶浅水区域的航行下沉量进行深入研究[2]。
本文进行浅水区域船舶航行下的下沉量数值计算,通过建立船体下沉量数学模型和流体动力学方程,结合CFD流体力学分析技术进行了下沉量的准确计算。
因此,船舶航行下沉量的计算精度对估计安全航行所需富余水深有着极其重要的影响。
1 船舶浅水区域航行的下沉量数学模型搭建首先建立船舶下沉量数学模型如图1所示。
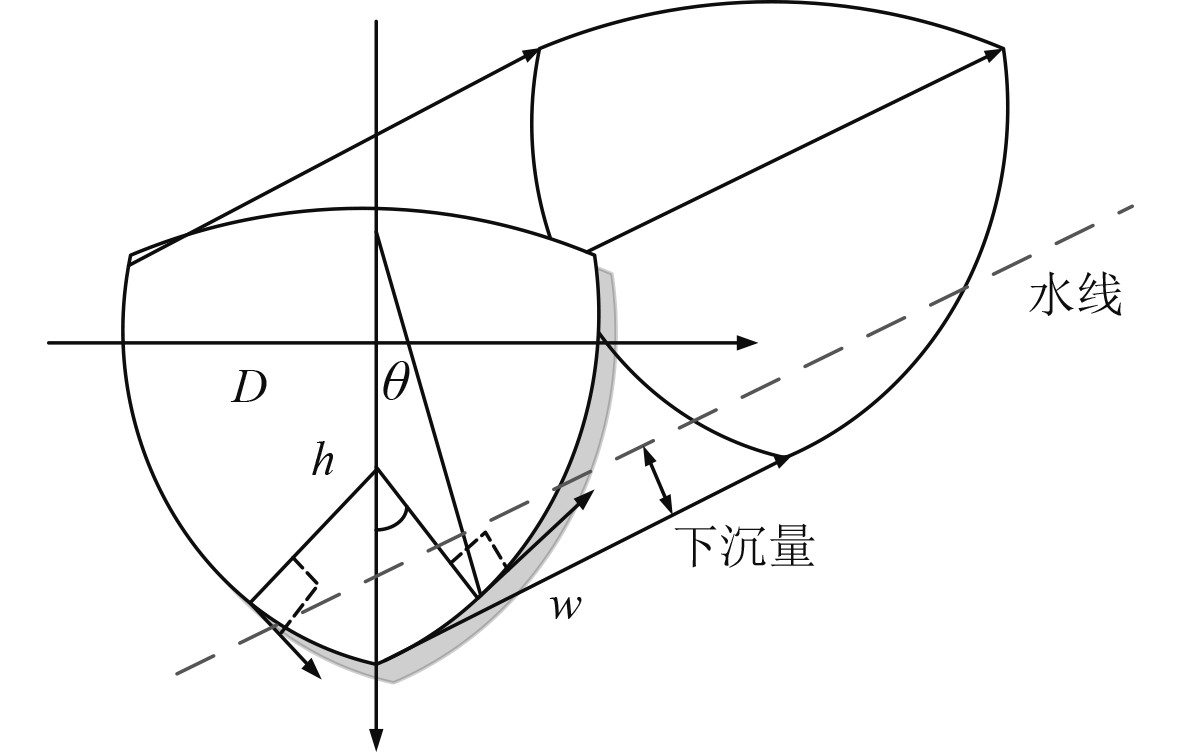
|
图 1 船舶下沉量数学模型 Fig. 1 Mathematical model of ship sinking |
在进行基于CFD计算流体力学的船舶下沉量计算时,采用的控制方程包括流体的连续性方程、动量方程和能量方程[3],忽略船体与液体之间的能量交换,建立CFD控制方程如下式:
| $ \begin{gathered} \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0, \\ \rho \frac{{{\rm{D}}u}}{{{\rm{D}}t}} = \rho {f_x} - \frac{{\partial p}}{{\partial x}} + \mu {\nabla ^2}u, \\ \rho \frac{{{\rm{D}}v}}{{{\rm{D}}t}} = \rho {f_y} - \frac{{\partial p}}{{\partial y}} + \mu {\nabla ^2}v, \\ \rho \frac{{{\rm{D}}w}}{{{\rm{D}}t}} = \rho {f_z} - \frac{{\partial p}}{{\partial z}} + \mu {\nabla ^2}wn 。\\ \end{gathered} $ |
式中:
湍流模型用下式表示:
| $ \begin{gathered} \rho \overline {u_i^\prime u_j^\prime } = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\left( {\rho k + {\mu _t}\frac{{\partial {u_k}}}{{\partial {x_k}}}} \right){\delta _{ij}},\\ k = \frac{1}{2}\overline {u_i^\prime u_j^\prime }。\\ \end{gathered} $ |
式中:
船舶下沉量计算是一种流固耦合计算,流体的雷诺应力方程为:
| $ - \rho \left( {{{u'}_i}} \right) = {\mu _1}\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}} + \frac{{\partial {u_j}}}{{\partial {x_j}}}} \right) - \frac{1}{3}\left( {{\rho _{}}k + {\mu _1}\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right){\sigma _0} 。$ |
式中:
| $ {\mu _1} = {H_0}\frac{k}{\varepsilon }。$ |
式中,
本文使用计算流体力学CFD技术进行船舶航行下沉量的计算,具体计算流程如图2所示。
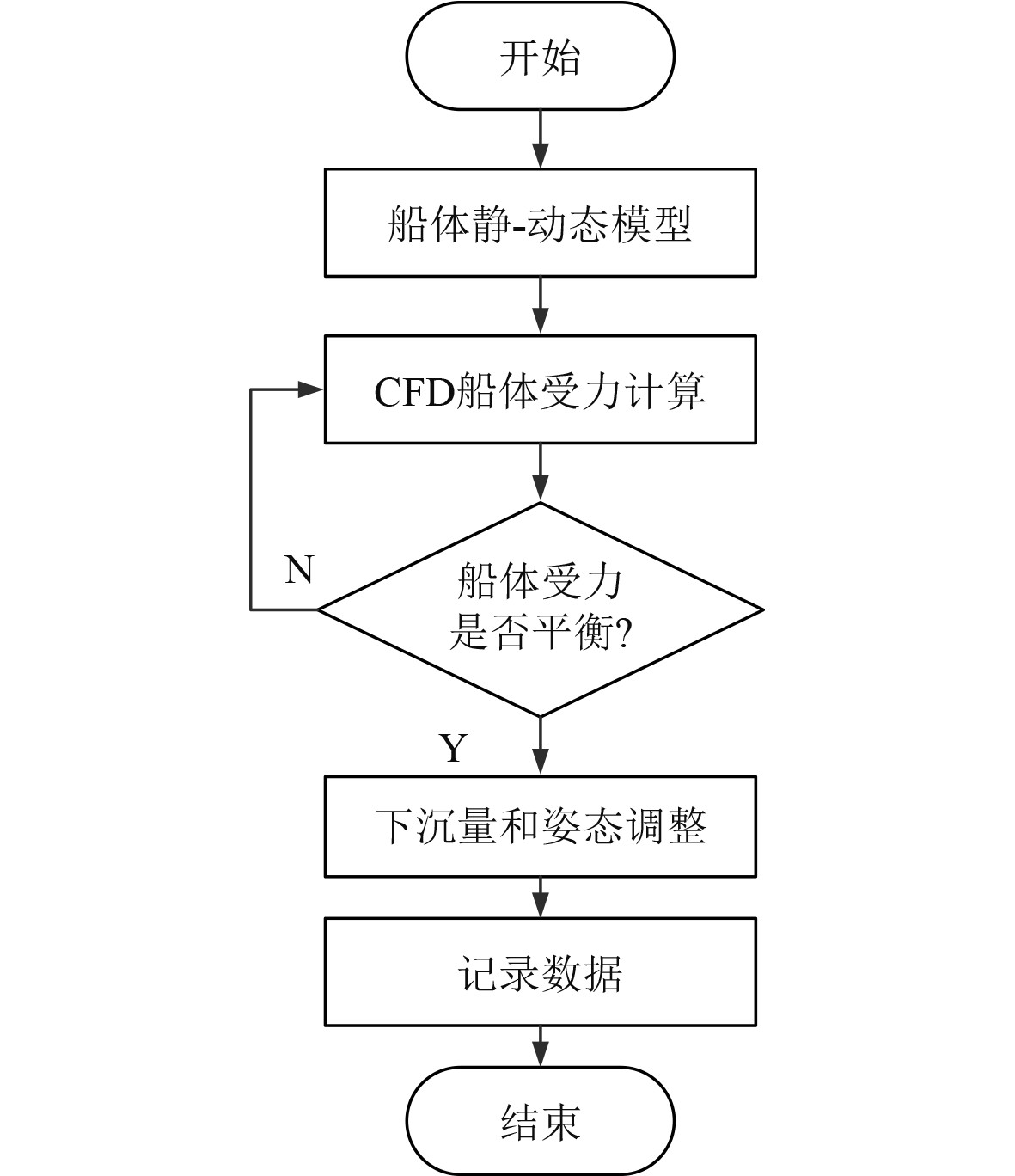
|
图 2 基于CFD的船舶航行下沉量计算流程图 Fig. 2 Flow chart of ship navigation subsidence calculation based on CFD |
首先,建立船舶下沉过程的下沉作用力和纵倾力矩如下式:
| $ \begin{gathered} F = \frac{1}{2}P{V^2}{\left( {\frac{L}{2}} \right)^2}{C_p},\\ M = \frac{1}{2}P{V^2}{\left( {\frac{1}{2}} \right)^3}{{\text{C}}_q}。\\ \end{gathered} $ |
式中:
假定船舶模型相对于重心对称,船舶首尾的下沉量
| $ {S_\varphi } = \frac{d}{{\sin \theta }}\left[ {\sin \left( {{\varphi _0} + \Delta \varphi + \theta } \right) - \sin \left( {{\varphi _0} + \theta } \right)} \right] 。$ |
对于大型船舶,船舶首尾与水平线的夹角
| $ {S_\varphi } = \frac{L}{2}\left[ {\sin \left( {{\varphi _0} + \Delta \varphi } \right) - \sin \left( {{\varphi _0}} \right)} \right] 。$ |
计算船舶浅水区域航行下沉量时选用的船舶模型为Wigley船模,主要原因在于:1)Wigley船模的结构简单,在建有限元模型时能够快速划分网格和单元,提高运算精度;2)Wigley船相关的水池试验数据较多,能够为下沉量计算提供较多的数据参考。
Wigley船模表面的型值点方程如下:
| $ y = \frac{B}{2}\left[ {1 - {{\left( {\frac{{2X}}{L}} \right)}^2}} \right]\left[ {1 - {{\left( {\frac{Z}{T}} \right)}^2}} \right] 。$ |
式中:
基于CFD的船舶航行下沉量计算中,流体与船舶耦合系统的边界条件是流体计算的初始值,将船舶在海水中的流固耦合界面划分如图3所示。
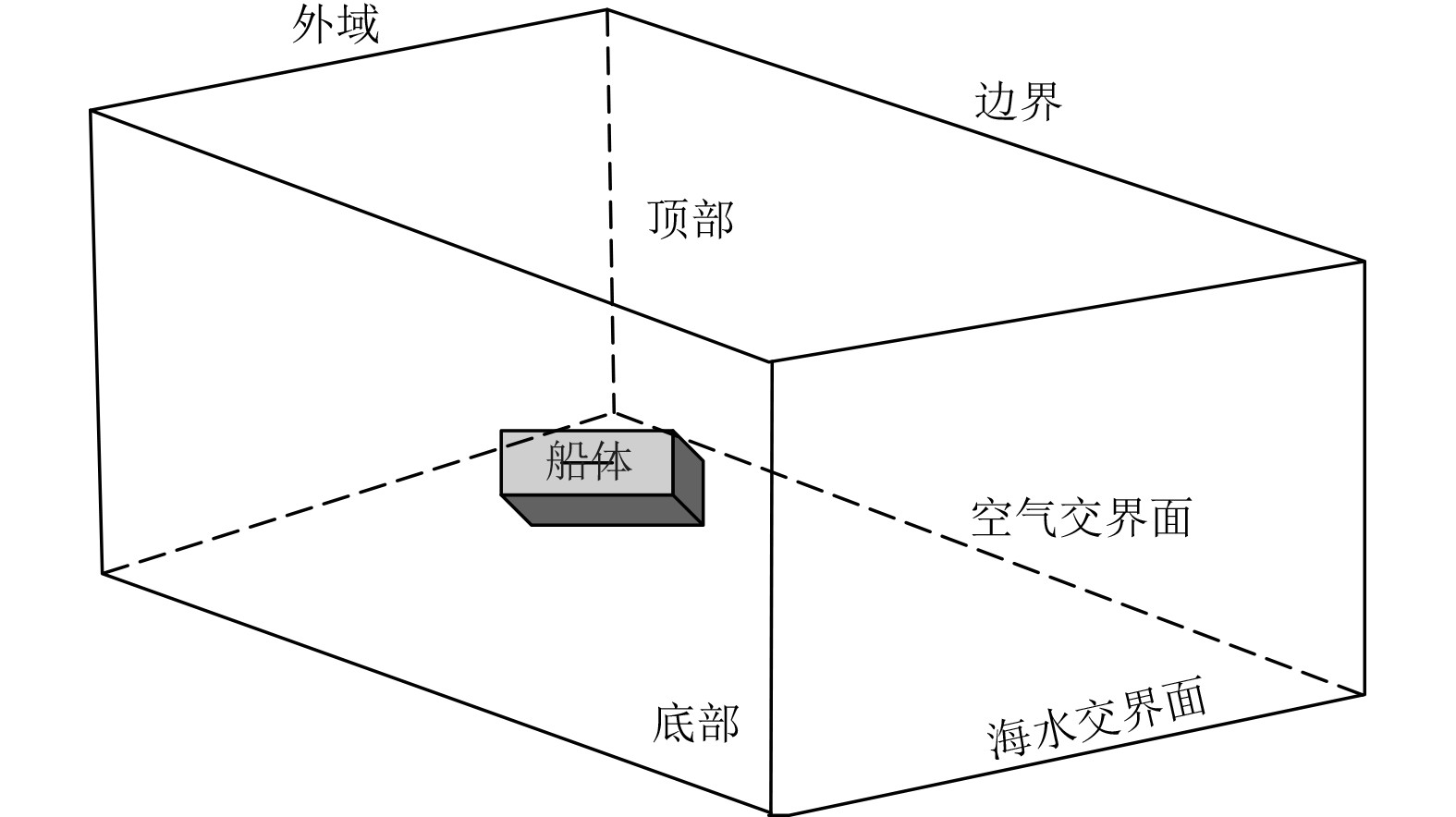
|
图 3 船舶在海水中的流固耦合界面划分 Fig. 3 Division of fluid solid coupling interface of ship in seawater |
将船舶-海水-空气流固耦合空间划分为外域、顶部、底部、空气交界面、海水交界面等[4]。
在求解过程中需要定义的边界条件包括:
1)入口边界条件
给定船舶的航行速度、阻力系数、海水的初始压力等,Wigley船模的阻力系数[4]如下式:
| $ {C_0} = \frac{{{R_0}}}{{0.5\rho {v_m}^2{s_m}}} 。$ |
式中:
2)出口边界条件
定义流固耦合口空间的流体出口速度和压力等参数。
3)壁面边界条件
定义海水为非粘性流体,船舶下沉量计算过程不考虑滑移。
4)对称面边界条件
对称面边界条件是指求解空间的对称性,对于简化计算过程,提高计算效率有重要意义。在求解Wigley船下沉量计算时,对称面的流体运动速度设置为0,整个流体求解空间关于该面对称。
2.3 定义船舶航行下沉量数值计算的计算域在CFD数值计算软件中,计算域的定义为有限元模型的建立过程。在定义船舶下沉量数值计算的有限元模型时,长度方向取2.8倍的船舶长度,宽度方向选取10倍船宽,计算域入口边界距船首位置1倍船长,出口边界距离船尾0.8倍船长。
计算域的有限元网格越靠近船舶固体边界越密,网格尺寸越小。图4为定义的船舶航行下沉量数值模拟计算域。

|
图 4 船舶航行下沉量数值模拟计算域 Fig. 4 Calculation domain of numerical simulation of ship navigation subsidence |
计算域的网格增长因子
| $ {\xi _1} = \frac{{0.07}}{{{{\left( {{{\rm{lg}}Re} - 3} \right)}^2}}} 。$ |
式中,Re为雷诺系数。
2.4 船舶航行下沉量数值计算本文使用的CFD计算软件为Fluent,Wigley船模的基本参数如表1所示。
|
|
表 1 Wigley船模的基本参数 Tab.1 Basic parameters of Wigley ship model |
Wigley船模的吃水平均深度为7.5 m,浅水区域的水深定义为10 m,船底海水的流动速度随船宽方向的分布曲线如图5所示。
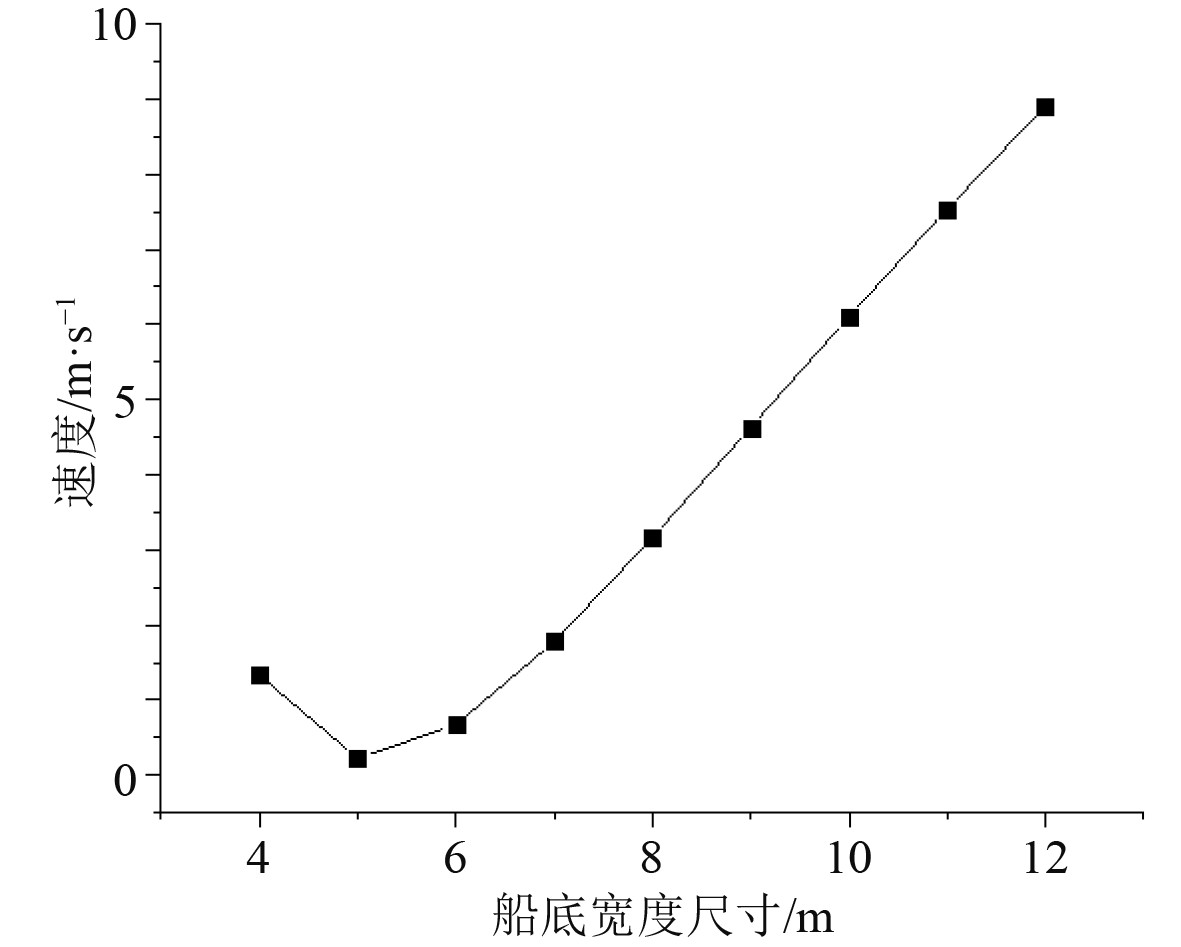
|
图 5 船底海水的流动速度分布曲线 Fig. 5 Flow velocity distribution curve of sea water at ship bottom |
Wigley船模的平均吃水增量如下式:
| $ \Delta d = \frac{{D - {\raise0.7ex\hbox{$F$} \mathord{\left/ {\vphantom {F g}}\right.} \lower0.7ex\hbox{$g$}}}}{{100TPC}} \text{,} $ |
式中:D为排水量;F为浮力;TPC为船舶每厘米的吃水吨数。
在CFD计算软件Fluent中仿真得到浅水区域下沉量与船舶吃水增量的关系如图6所示。

|
图 6 浅水区域下沉量与船舶吃水增量的关系 Fig. 6 The relationship between shallow water subsidence and ship draft increment |
浅水区域船舶下沉量的研究有助于改善船舶的航行安全性,防止船舶在浅水中擦底或搁浅,进而造成严重的事故。本文从CFD的基础理论出发,结合CFD软件进行了船舶浅水区域下沉量的计算与仿真,详述了建模和求解过程。
| [1] |
王澄. 基于计算流体力学的船舶风载荷计算方法分析[J]. 天津理工大学学报, 2021, 37(2): 21-26. WANG Cheng. Analysis of ship wind load calculation method based on computational fluid dynamics[J]. Journal of Tianjin University of Technology, 2021, 37(2): 21-26. DOI:10.3969/j.issn.1673-095X.2021.02.005 |
| [2] |
杨春蕾, 王金宝. 船舶时域破损稳性问题的计算流体力学方法[J]. 中国造船, 2020, 61(S2): 430-438. YANG Chun-lei, Wang Jin-bao. Computational fluid dynamics method for time domain damage stability of ships[J]. China Shipbuilding, 2020, 61(S2): 430-438. DOI:10.3969/j.issn.1000-4882.2020.z2.046 |
| [3] |
杨波, 石爱国, 吴明. 基于计算流体力学理论的船舶横摇阻尼系数计算[J]. 中国航海, 2012, 35(3): 76-80. YANG Bo, SHI Ai-guo, WU Ming. Calculation of ship rolling damping coefficient based on computational fluid dynamics[J]. China Navigation, 2012, 35(3): 76-80. DOI:10.3969/j.issn.1000-4653.2012.03.017 |
| [4] |
陈伟民, 陈霞萍. 计算流体力学在船舶线型优化中的应用[J]. 上海船舶运输科学研究所学报, 2007(1): 30-32. CHEN Wei-min, CHEN Xia-ping. Application of computational fluid dynamics in ship linetype optimization[J]. Journal of Shanghai Institute of Ship Transportation Science, 2007(1): 30-32. DOI:10.3969/j.issn.1674-5949.2007.01.005 |
 2022, Vol. 44
2022, Vol. 44
