水下航行器在水下的纵向滑行需要依靠垂直运动产生的能量完成,而设置在航行器内部的重心调整机构通过调整水下航行器的浮力产生垂直运动的动力。水下航行器[1]具有维护简单、作业范围广、能够多次利用、续航时间长、能耗低等优点,被广泛地应用到航洋环境监测领域中[2]。为了保证水下航行器在海洋中的工作,需要分析水下航行器在滑行过程中受到的阻力。
姜宜辰等[3]在Myring方程的基础上建立水下航行器的数学模型,结合Realizable k-ε湍流模型和CFD方法计算滑行状态下水下航行器的阻力。凌宏杰等[4]结合计算域分区法和黏性流体理论对水下航行器展开数值模拟,在攻角不断变化的情况下分析水下航行器的滑行阻力。
为了减少水下航行器运动过程中的阻力,提出水下航行器变舵角滑行阻力数学建模分析方法。在变舵角工况下通过数学建模对水下航行器在滑行过程中受到的阻力展开分析。
1 数学建模本文通过UG绘制水下航行器的三维图,并在Ansys ICEM中输入parasolid格式的三维图[5-6],在分块思想的基础上划分水下航行器的外围流域,获得六面体网格,并将其输入CFX中展开数学建模分析。
1)建立模型
选取液压伸缩型的机构作为水下航行器的4个支撑机构,通过改变伸缩长度调整水下航行器的姿态。水下航行器模型的主要参数如表1所示。
|
|
表 1 模型参数 Tab.1 Model parameters |
构建水下航行器模型如图1所示。

|
图 1 水下航行器模型 Fig. 1 Underwater vehicle model |
2)工况计算
基于图1的水下航行器模型,分析有小倾角海底和水平海底情况下水下航行器的受力情况。
针对水平海底情况,在航行器轴线距海底距离和海流速度不断变化的情况下分析水下航行器的受力特性,工况模拟结果如表2所示。
|
|
表 2 工况模拟结果 Tab.2 Simulation results of working conditions |
可知,3种工况分别对应的是水平运动、下潜运动、上升运动。结构化六面体网格[7-8]具有边缘层网格易于处理和网格疏密程度方便调整等优点,因此所提方法采用结构化六面体网格对水下滑行器模型展开网格划分,以此提高数学建模的可信度和精度。网格划分结果如图2所示。

|
图 2 网格划分 Fig. 2 Mesh divide |
3)运动模型
设
| $ \chi = \zeta + \varphi。$ | (1) |
式中:
用
| $ \left\{ \begin{gathered} Y_{{x_0}}^e + G_{xw}^e = 0 ,\\ Y_{{y_0}}^e + G_{yw}^e + {M_0} = 0,\\ Y_{{z_0}}^e + G_{zw}^e = 0, \\ {Y_z}T - {Q_x} - H{y_c}\sin \gamma \cos {\vartheta _0} = 0,\\ {Y_y}T' - {Q_y} - H{y_c}\sin \gamma \sin {\vartheta _0} = 0,\\ {Y_x}T - {Q_z} - H{y_c}\sin {\vartheta _0} - H{x_c}\cos {\vartheta _0} = 0,\\ \left[ {\begin{array}{*{20}{c}} {G_{xw}^e} \\ {G_{yw}^e} \\ {G_{zw}^e} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&0&{ - \sin \gamma } \\ 0&1&0 \\ {\sin \gamma }&0&{\cos \gamma } \end{array}} \right], = \left[ {\begin{array}{*{20}{c}} {G_{xw}^1} \\ {G_{yw}^1} \\ {G_{zw}^1} \end{array}} \right], \\ {[{Y_x},{Y_y},{Y_z}]^{\text{T}}} = H_x^{{x_0}}[Y_{{x_0}}^e,Y_{{y_0}}^e,Y_{{z_0}}^e], \\ \beta = {\vartheta _0}, \\ \chi = \zeta + \gamma 。\\ \end{gathered} \right. $ | (2) |
式中:
根据建立的数学模型,分析水下航行器不同工况下的受力情况。
设
| $ \left\{ \begin{gathered} - F\cos \alpha + Z\sin \alpha = \sin \vartheta ,\\ F\sin \alpha + Z\cos \alpha = \cos \vartheta ,\\ G({x_c}\cos \vartheta - {y_c}\sin \vartheta ) = M 。\\ \end{gathered} \right. $ | (3) |
式中:
所提方法用攻角的二次形式表示水下航行器定常滑行状态下的阻力,用攻角的线性形式描述航行器的力矩和升力,如下式:
| $ \left\{ \begin{gathered} F = \frac{{\rho D{X_F}{V^2}}}{2} = {V^2}({L_{F0}} + {L_F}{\alpha ^2}) \\ Z = \frac{{\rho D{X_Z}{V^2}}}{2} = {V^2}({L_{Z0}} + {L_Z}{\alpha ^2}),\\ M = \frac{{\rho ZD{X_M}{V^2}}}{2} = {V^2}({L_{M0}} + {L_M}{\alpha ^2})。\end{gathered} \right. $ | (4) |
式中:
在水下航行器的外形不发生变化的条件下,可通过经验公式和实验数据获取阻力系数、升力系数和功力矩系数。
已知航行器3个部分重心的位置
| $ \left\{ \begin{gathered} {x_c} = \frac{{{m_b}{x_b} + {m_w}{x_w} + {m_f}{x_f}}}{m} ,\\ {y_c} = \frac{{{m_b}{y_b} + {m_w}{y_w} + {m_f}{y_f}}}{m} 。\\ \end{gathered} \right. $ | (5) |
当水下航行器的攻角较小时,存在
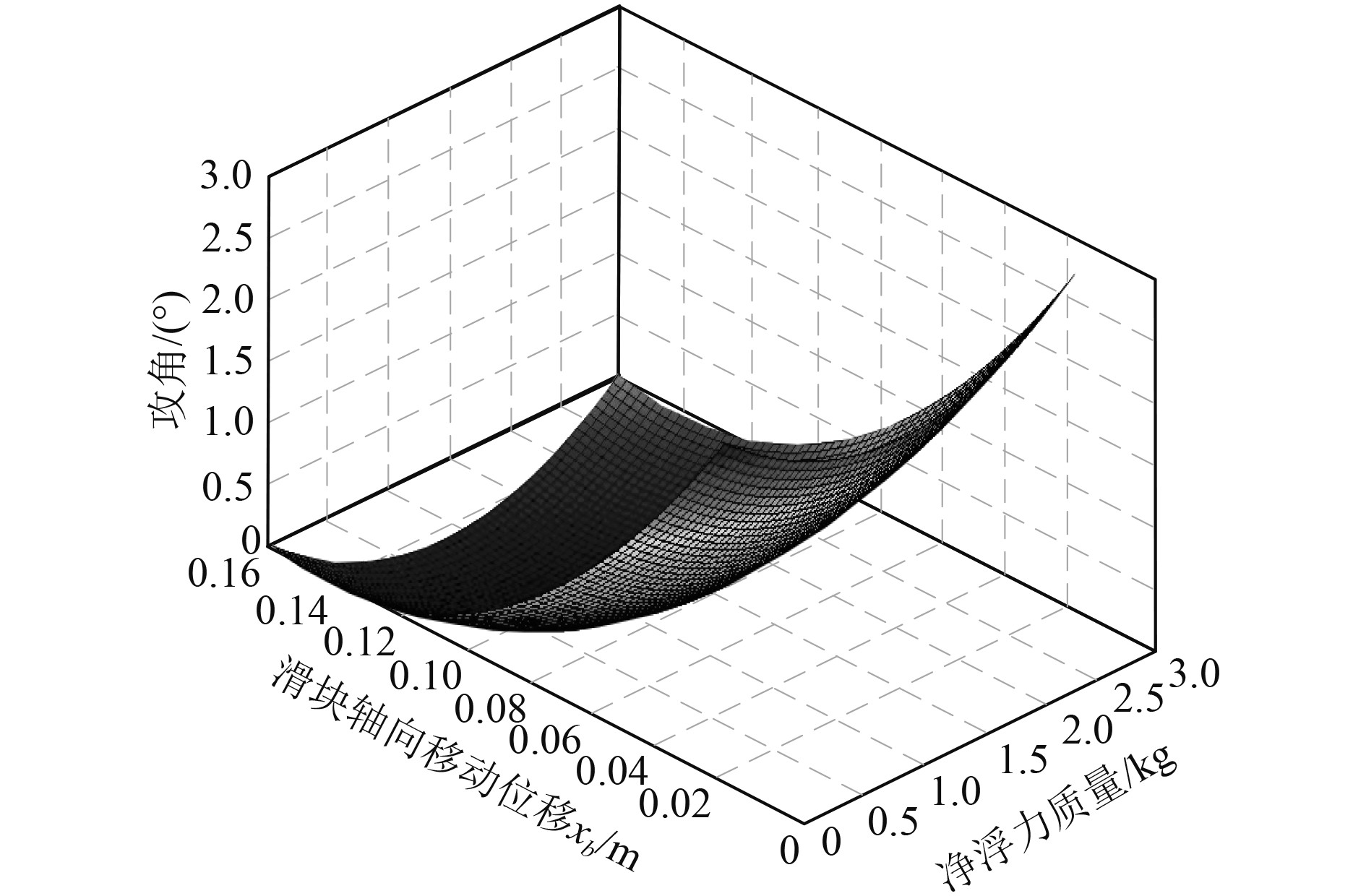
|
图 3 攻角变化情况 Fig. 3 Change of angle of attack |
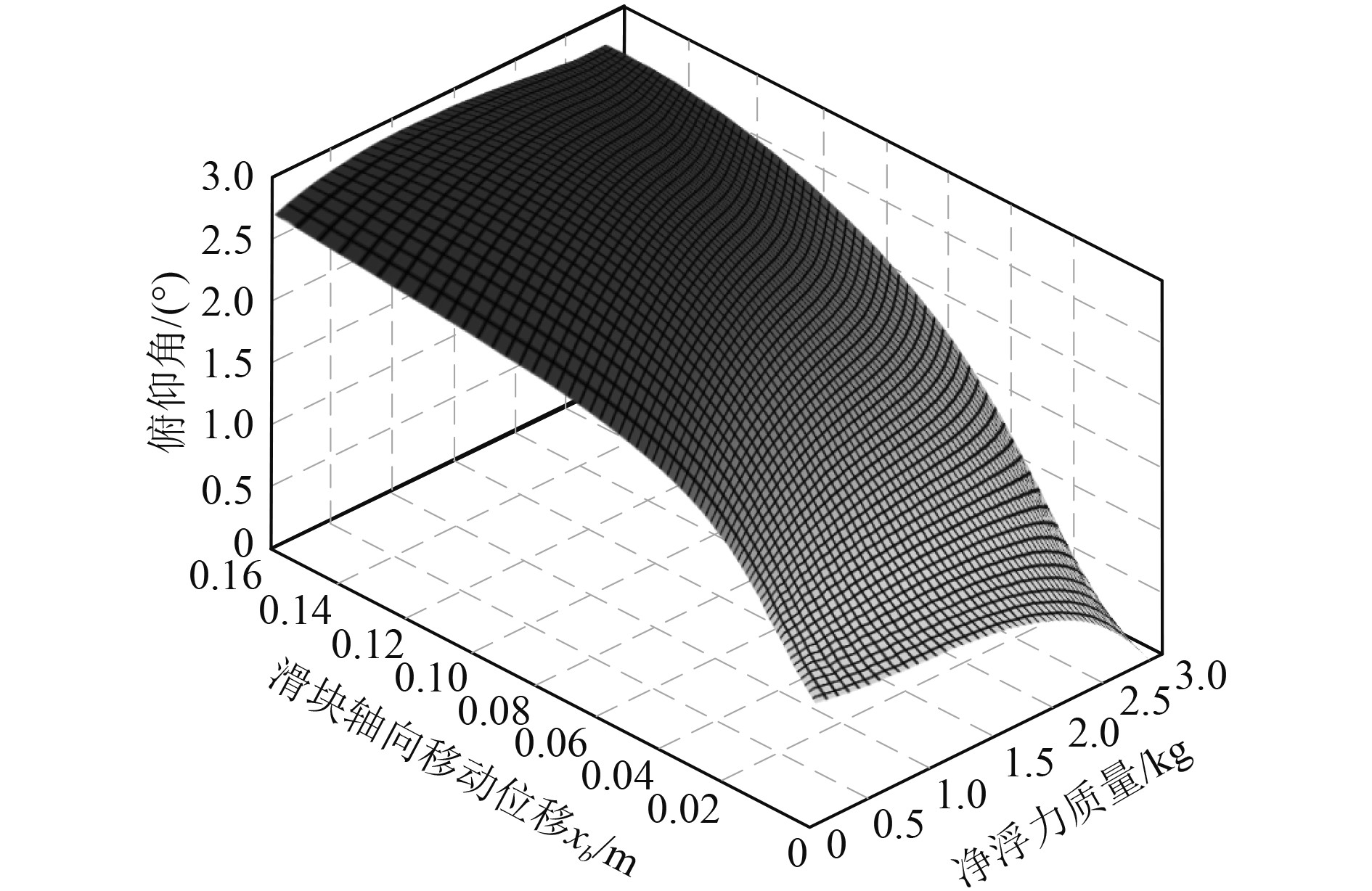
|
图 4 俯仰角变化情况 Fig. 4 Pitch angle change |
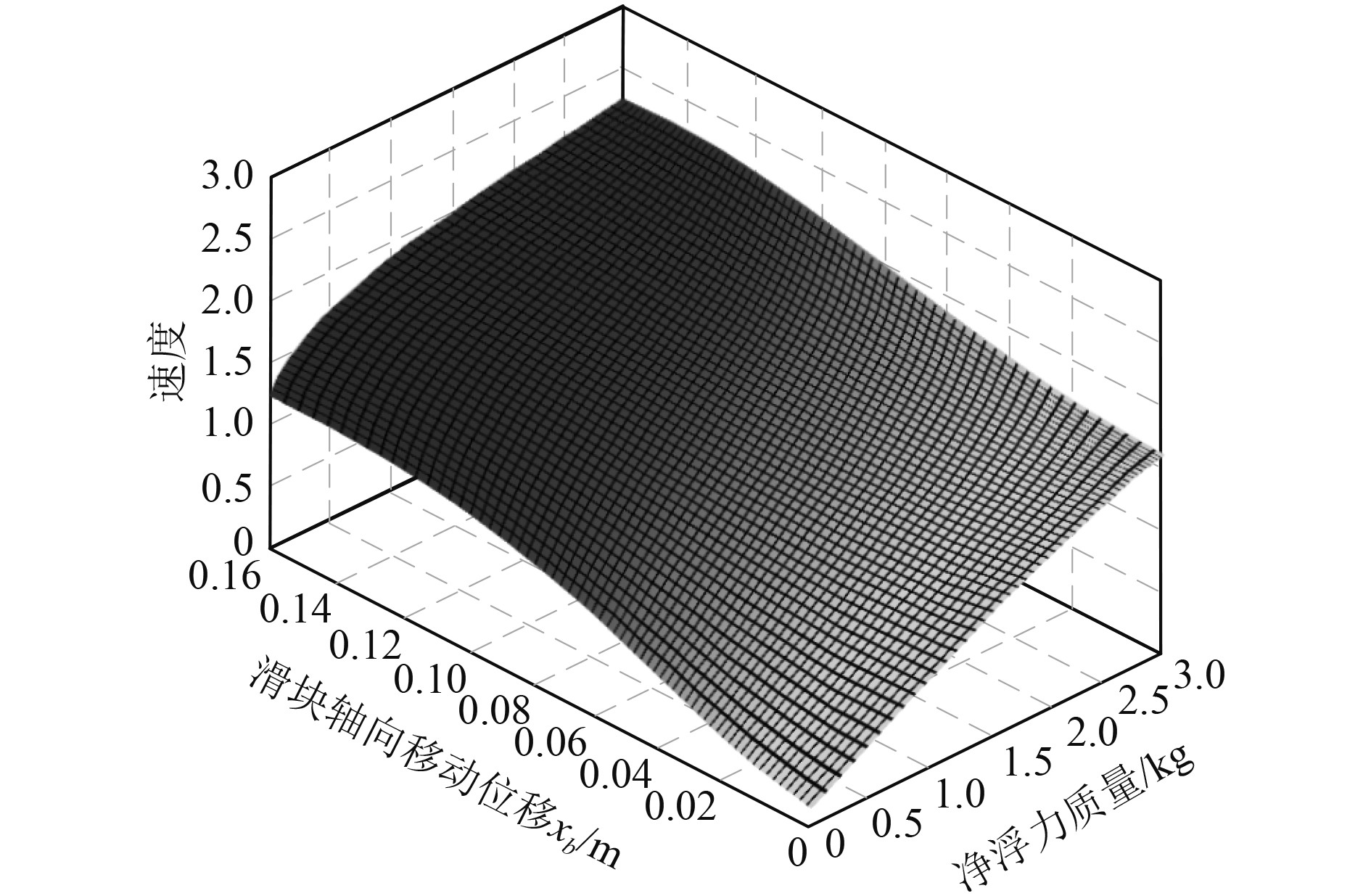
|
图 5 速度变化情况 Fig. 5 Speed change |
水下航行器的舵角是可通过改变两侧水翼转角得以控制,设置不同的航行器水翼转角,以此分析变舵角情况下水下航行器的滑行阻力。
1)水平运动
在水平运动状态下,水下航行器的水翼没有任何角度,此时受力和需要计算的数值较少,在此状态下,将水下航行器的速度变化设置在10~24 km/h范围内,对航行器的受力情况展开分析,结果如表3所示。
|
|
表 3 航行器水平运动状态下的受力情况 Tab.3 Forces of the aircraft in horizontal motion |
水平运动状态下由粘压阻力、附体阻力和摩擦阻力构成水下航行器受到的总阻力,该阻力较小。由表3数据可知,航行器的总阻力与速度成正比,前者的增加会引起后者的增加。
2)下潜运动
当航行器在海中需要执行下潜工作时,通过调整量测水翼的展开角度,为水下航行器提供向下的负升力,以此控制航行器在海中的下潜速度。水面扰动不会对航行器的下潜过程产生影响,此时受力较小。航行器的水翼在下潜过程中发生了转动,因此向下的负升力会对航行器的水翼施加一些阻力,即水翼后方的水流会受到水翼转角的干扰,影响水下航行器原有的总阻力[13-14],所提方法在水翼角度为−10°和−5°情况下分析航行器在下潜运动过程中的总阻力。
针对两侧水翼在下潜过程中受到的升阻力,所提方法采用Finemarine对水下航行器展开受力分析,分析结果如图6所示。
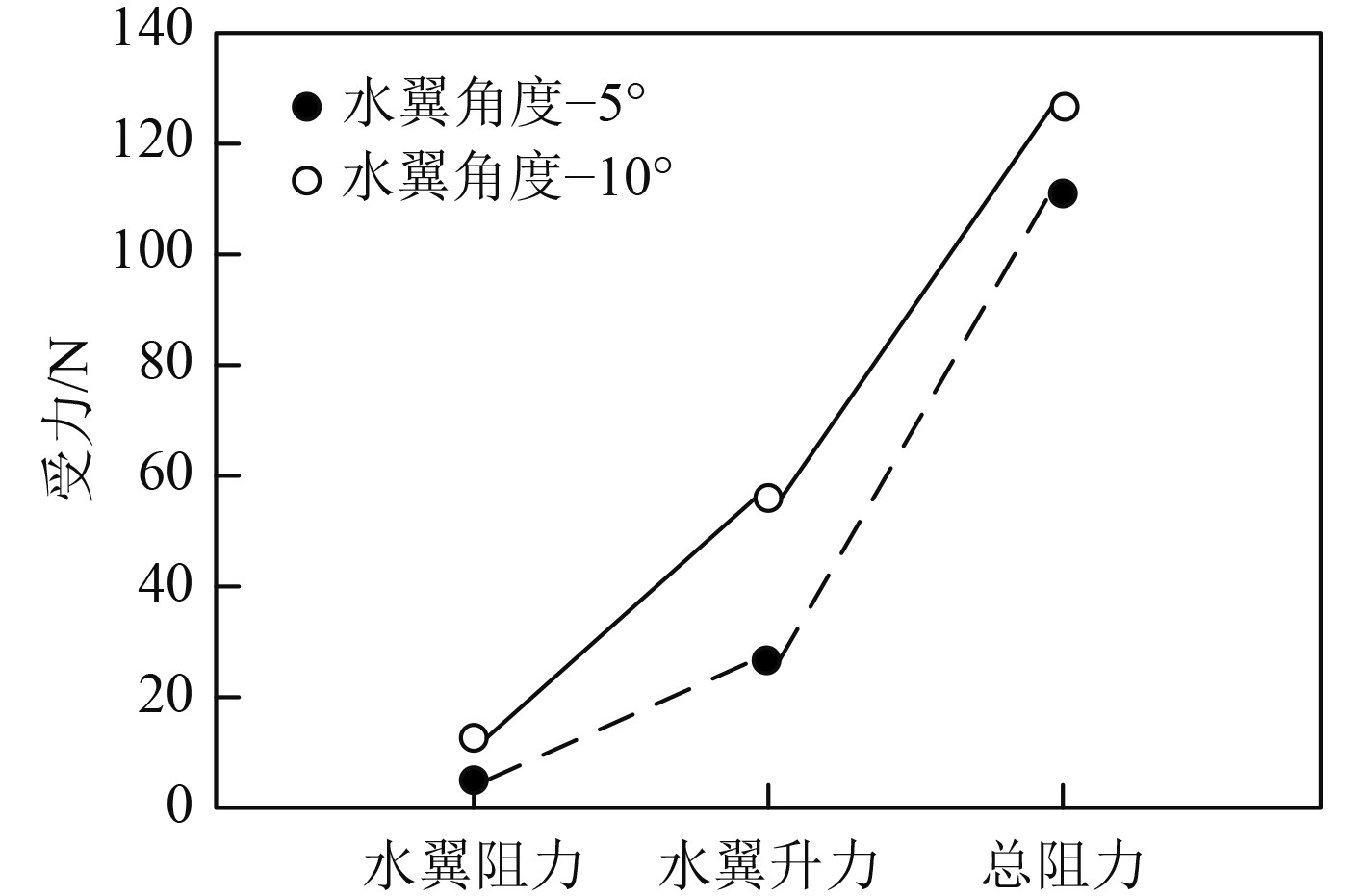
|
图 6 下潜状态下航行器的受力情况 Fig. 6 Forces on the aircraft under submergence |
可知,水下航行器在水翼转角为-5°时,单只水翼阻力、升力和总阻力分别为4.6 N、28 N和110 N;水下航行器在水翼转角为-10°时,单只水翼阻力、升力和总阻力分别为12.5 N、55 N和127 N。经对比发现,水下航行器在以上2种情况下的水翼负升力差异高于水翼阻力和总阻力。
3)上升运动
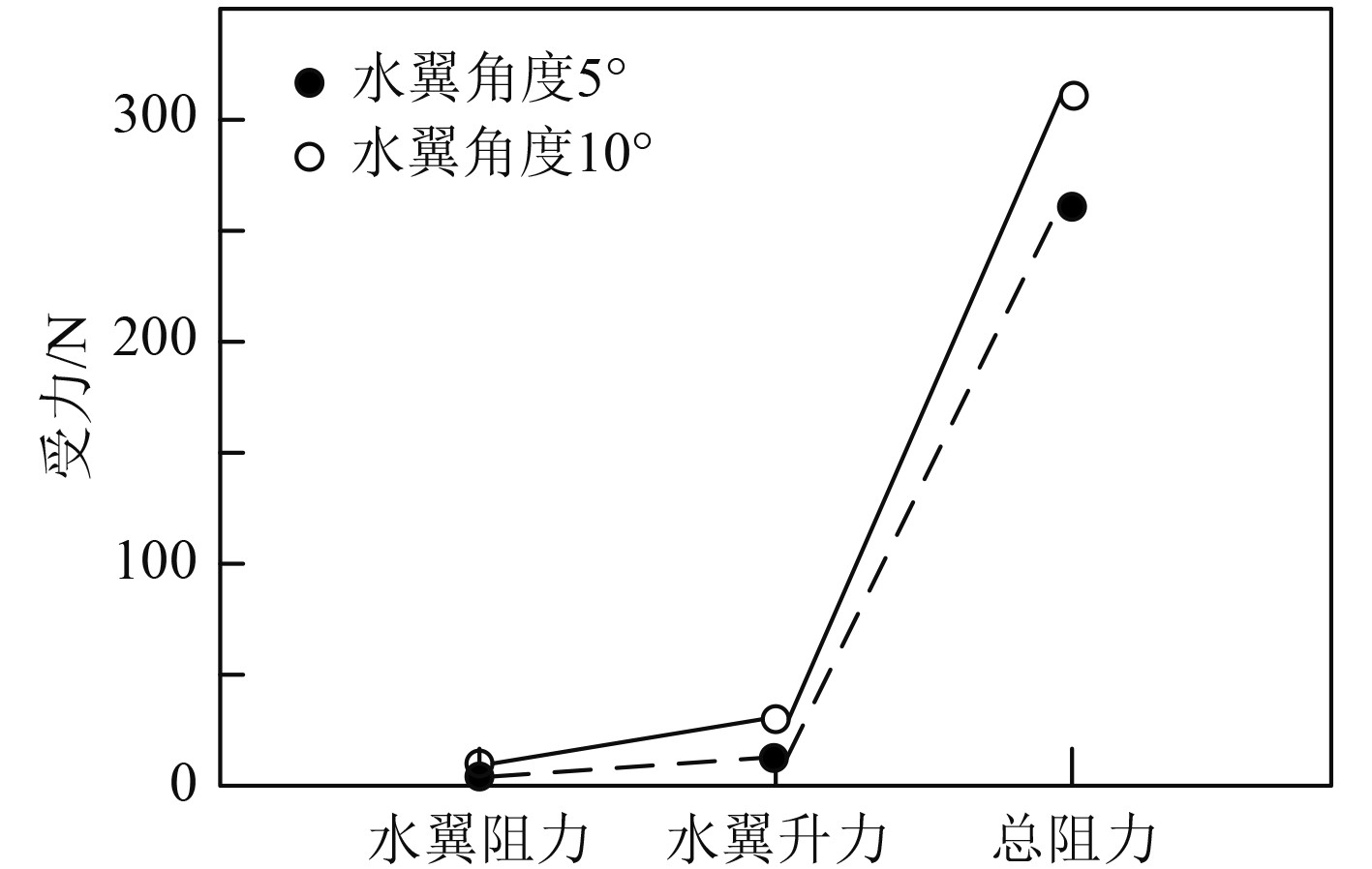
航行器上升过程中的受力与水平运动和下潜运动相比较为复杂,因为在上升过程中航行器会逐渐接近水面,此时水面上的运动会干扰航行器的上升过程,同时在上升过程中会产生兴波阻力,增加了总阻力。将水翼转角设置为10°和5°,对上升过程中水下航行器的受力情况展开分析,并将航行器的速度设置为5 kn,分析结果如图7所示。
|
图 7 上升过程中航行器的受力情况 Fig. 7 Forces on the aircraft during ascent |
可知,航行器在水翼转角为5°时,单只水翼阻力为5 N、水翼升力11 N、航行器的总阻力为262 N;当水翼转角增加至10°时,航行器的单只水翼阻力为9 N、水翼升力为32 N、受到的总阻力为308 N。经对比发现,总阻力在以上2种情况下的变化相对较小。
水翼转角为5°和10°时水下航行器在上升过程中的兴波情况如图8所示。

|
图 8 不同角度下的兴波情况 Fig. 8 Wave making at different angles |
可知,当水翼转角不同时兴波情况存在差异,造成这种现象的主要原因是水下航行器的升力随着水翼转角的变化而变化,进而改变航行器在上升过程中的吃水情况,引起阻力发生变化。
4 结 语水下航行器变舵角滑行阻力数学建模分析方法通过上述分析获得以下结论:
1)在水平运动状态下,航行器主要受到摩擦阻力,在水平运动过程中的阻力随着速度的增大而增大;
2)在航行器下潜过程中改变水翼转角,总阻力的变幅高于水翼阻力;
3)上升运动过程中,受到水上或水面运动的影响,航行器受到了较大的兴波阻力,增加了总阻力。
| [1] |
黄沛烁, 王易因, 关新平, 等. 面向水声传感网的自主水下航行器辅助定位动态路径规划[J]. 电子与信息学报, 2022, 44(6): 1927-1936. DOI:10.11999/JEIT211432 |
| [2] |
滕建平, 梁霄, 陶浩, 等. 无人水下航行器全局路径规划及有限时间跟踪控制[J]. 上海海事大学学报, 2022, 43(1): 1-7. |
| [3] |
姜宜辰, 赵月, 熊济时, 等. 水下航行器艇体形状对阻力及流噪声综合影响[J]. 哈尔滨工程大学学报, 2022, 43(1): 76-82+138. DOI:10.11990/jheu.202008038 |
| [4] |
凌宏杰, 张贝, 王志东, 等. 大翼展混合驱动无人水下航行器水动力特性研究[J]. 船舶工程, 2020, 42(2): 8-12+38. DOI:10.13788/j.cnki.cbgc.2020.02.02 |
| [5] |
魏娟, 窦登科, 侯效东, 等. 基于Ansys-Workbench的谐波减速器柔轮结构优化分析[J]. 机床与液压, 2021, 49(4): 133-139. |
| [6] |
孙健峰, 邢凯峰, 杨洲, 等. 基于Ansys/LS-DYNA的果枝修剪过程仿真与试验研究[J]. 华南农业大学学报, 2022, 43(4): 113-124. |
| [7] |
王瑞, 丁卯, 吴海燕, 等. 六面体网格复杂层插入操作的优化设计方法[J]. 计算机辅助设计与图形学学报, 2020, 32(5): 846-856. |
| [8] |
WANG J , NEUHAUSER C , WESTERMANN R . Interactive focus plus context rendering for hexahedral mesh inspection[J]. Molecular Human Reproduction. 2021, 27(8): 3505-3518.
|
| [9] |
关文信, 陆庆. 楔环连接方式的水下航行器壳体动态特性分析[J]. 机械设计, 2021, 38(S1): 120-125. |
| [10] |
高国章, 张家赫. 基于ADRC参数优化的拖曳式水下航行器定深控制分析[J]. 大连海事大学学报, 2020, 46(2): 17-25. |
| [11] |
王艳, 徐进良, 李文, 等. 超临界Lennard-Jones流体结构特性分子动力学研究[J]. 物理学报, 2020, 69(7): 7-16. DOI:10.7498/aps.69.20191591 |
| [12] |
ARKHIPOV V A, BASALAEV S A, PERFIL'EVA K G, et al. An experimental study of the hydrodynamic drag coefficient of a cooled hard sphere at small reynolds numbers[J]. Technical Physics Letters, 2021, 47(4): 317-320. DOI:10.1134/S1063785021040027 |
| [13] |
常宗瑜, 于振江, 郑中强, 等. 波浪驱动推进机构的最优水翼倾角的确定[J]. 中国海洋大学学报(自然科学版), 2021, 51(1): 111-116. |
| [14] |
李芳, 黄桥高, 潘光, 等. 波状前缘对水翼湍流干涉噪声的影响[J]. 西北工业大学学报, 2021, 39(6): 1266-1273. DOI:10.3969/j.issn.1000-2758.2021.06.012 |
 2022, Vol. 44
2022, Vol. 44
