在工程实际中,由于疲劳、腐蚀、磨损等其他潜在的损伤因素,会经常发生由于断裂产生的破坏事故,尤其是在船舶等结构中,疲劳断裂会对生命和财产造成重大损失。因此,研究裂纹应力强度因子和扩展状态及剩余寿命至关重要。
有限元分析目前已经成熟且有很强的通用性,能够简单有效解决大多数实际问题,其准确的计算结果不受形状和边界条件等限制,逐渐被认可。但在处理疲劳断裂问题上,传统的有限元仍然存在很大的局限性,裂纹必须与单元的边重合,使用1/4节点单元模拟裂纹尖端的奇异应力场,在解决裂纹扩展问题时要重构网格,过程相当复杂和麻烦,工作效率低[1]。
1999年Belytschko等[2]提出扩展有限元法,通过将富集函数引入常规有限元来反映计算区域的不连续性,使裂纹尖端的间断与网格独立,降低了裂纹尖端网格的划分难度,可以有效解决疲劳断裂问题。而且相较于疲劳试验,扩展有限元法应用灵活,周期短,能够模拟多种工况下的疲劳断裂,大大降低了试验成本,已发展成为解决疲劳裂纹扩展问题最主要的方法之一[3-5]。Shi[6]用扩展有限元法模拟岩石变形,使用考虑高阶项的位移外推法计算应力强度因子。Zou[7]分析了等效积分区域法不同积分路径对应力强度因子的影响。马梓聪[8]基于扩展有限元使用等效区域积分法计算了不同裂宽比的应力强度因子。余天堂[9]用相互作用积分法计算应力强度因子,之后,相互作用积分法得到广泛应用[10-12]。还有很多学者基于扩展有限元,对疲劳裂纹的剩余寿命进行预测[13-14],为以后更好地理解和预测疲劳过程及寿命提供依据。
目前,有很多种计算应力强度因子的方法,但未指出哪种方法精度最高,而且对于疲劳裂纹扩展过程的动态应力强度因子计算较少。本文基于Abaqus的扩展有限元法,分别使用位移外推法、等效积分区域法和相互作用积分法计算单边裂纹和中心裂纹的静态应力强度因子,采用相互作用积分法计算裂纹扩展过程的动态应力强度因子。在此基础上,根据Abaqus直接循环法的低周循环分析,结合Paris理论预测试样的剩余寿命,并与文献结果进行比较。
1 裂纹体的扩展有限元方法1999年Moes[15]用阶跃函数加强单元节点,体现了裂纹的不连续特征。近似的广义位移场形式为:
| $ \begin{split}{u^h}(x) =& \sum\limits_{i \in {N_s}} {{u_i}{N_i}(x)} + \sum\limits_{j \in {N_{cut}}}{{a_j}{N_j}(x)H(x)} + \\ &\sum\limits_{k \in {N_{tip}}} {{N_k}(x)\sum\limits_{\alpha = 1}^4 {{b_{k\alpha }}{B_\alpha }(x)} }。\end{split}$ | (1) |
式中:Ni(x)为单元形函数;Ns为常规节点的集合;H(x)为Heaviside阶跃函数。
| $ H(x) = \left\{ \begin{array}{ll} +1 & \psi (x,t) > 0 ,\\ - 1 & \varphi (x,t) < 0 。\end{array} \right. $ | (2) |
Bα(x)计算公式为:
| $\begin{split} [B_{\alpha} (x),\alpha =&1,\cdots \text{,}4]=\\ &\Biggr[\sqrt{r}\text{sin}\frac{\theta }{2}\text{,}\sqrt{r}\text{cos}\frac{\theta }{2}\text{,}\sqrt{r}\text{sin}\frac{\theta }{2}\mathrm{sin}\theta ,\sqrt{r}\text{cos}\frac{\theta }{2}\text{sin}\theta \Biggr]。\end{split}$ | (3) |
其中,(r,θ)为裂纹尖端局部极坐标。
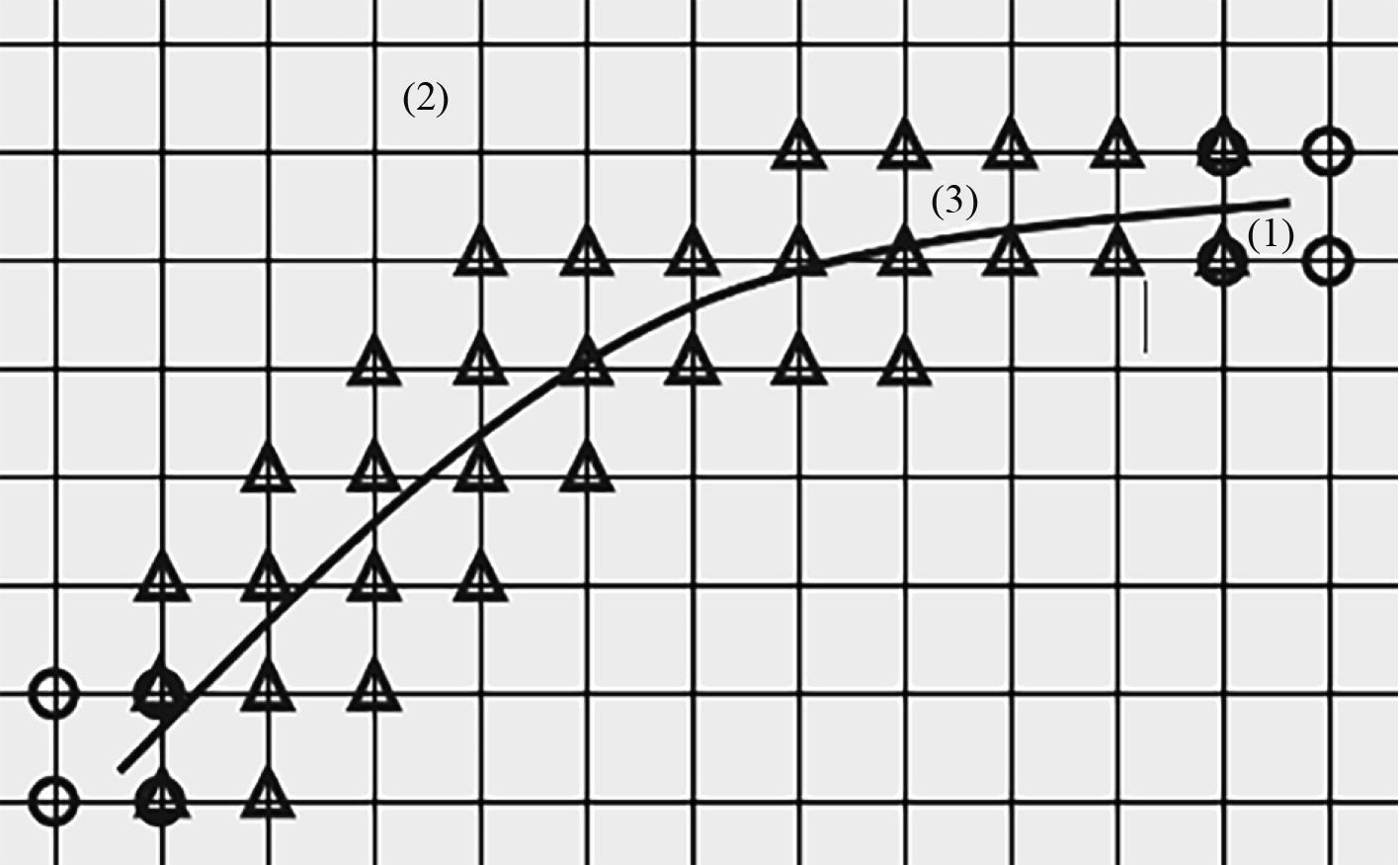
图1为含裂纹结构的加强单元节点,其中有3种单元类型:裂纹尖端单元,常规单元,断裂单元。对于混合节点单元,通过平移加强函数来纠正,如下式:
|
图 1 加强节点分布 Fig. 1 Strengthen node distribution |
| $ \begin{split}{{{u}}^{{h}}}(x) = &\sum\limits_{i \in {N_s}} {{u_i}{N_i}(x)} + \sum\limits_{j \in {N_{cut}}}{N_j}(x)(H(x) - {H_j}(x)){a_j} + \\ &\sum\limits_{k \in {N_{tip}}} {{N_k}(x)\sum\limits_{\alpha = 1}^4 {({B_\alpha }(x) - {B_{k\alpha }}(x)){b_{k\alpha }}} }。\end{split} $ | (4) |
对于I型断裂问题而言,应力强度因子定义为:
| $ {K_{\rm I}} = \mathop {\lim }\limits_{r \to 0} [{\sigma _y}(r,\theta = 0)\sqrt {2\text{π} r} ] 。$ | (5) |
在Abaqus中输出裂纹前端单元节点的纵向位移,每个节点对应一个KIi,构造数据对式如下:
| $ {K_{Ii}} = \frac{{2\mu }}{{\kappa + 1}}{v_i}\sqrt {\frac{{2\text{π} }}{{{r_i}}}},$ | (6) |
式中:μ为剪切模量;vi为节点纵向位移;ri为节点到裂纹尖端距离。
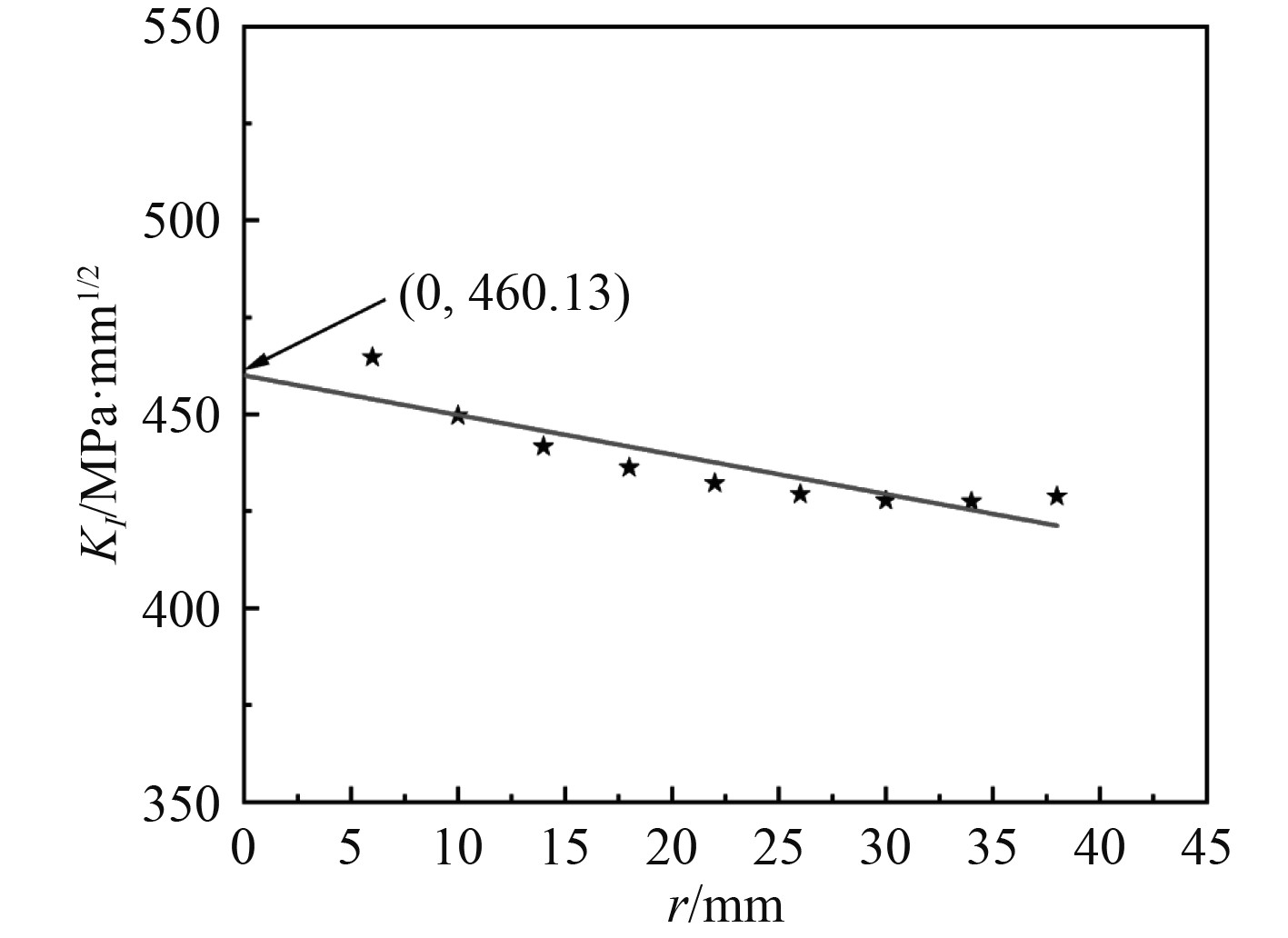
式(7)用最小二乘法拟合数据点,图2为a/B=0.2时拟合得到的应力强度因子。
|
图 2 基于位移的外推法计算应力强度因子 Fig. 2 Displacement based extrapolation to calculate stress intensity factor |
| $ {K_I} \approx \frac{{\displaystyle\sum {{r_i}} \sum {{K_{Ii}}} - N\sum {{r_i}{K_{Ii}}} }}{{{{\left( {\displaystyle\sum {{r_i}} } \right)}^2} - N{{\displaystyle\sum {{r_i}} }^2}}}。$ | (7) |
应力外推法对裂纹尖端的单元尺寸比较敏感,还需要剔除裂纹尖端的节点,而J积分是围路积分,既可以避开裂纹尖端,又不用过分加密网格,其表达式为[16]:
| $ J = \int\limits_\varGamma {W{\rm{d}}y - {p_i}\frac{{\partial {u_i}}}{{\partial x}}} {\rm{d}}s。$ | (8) |
式中:
| $ W = \frac{1}{2}{\sigma _{{{ij}}}}{\varepsilon _{{{ij}}}} 。$ | (9) |
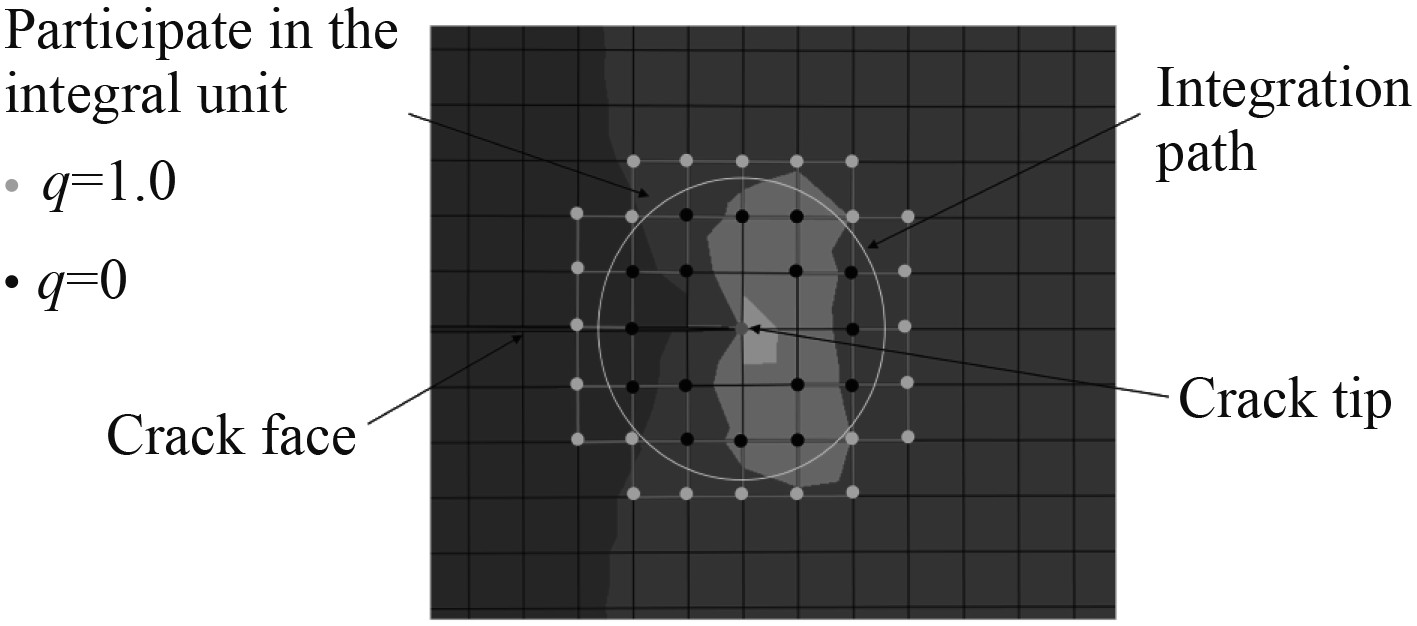
实际上,式(8)不适合数值计算,将其转换为区域积分,用等效积分区域法计算J积分的值,如图3所示。
|
图 3 积分区域 Fig. 3 Integral area |
| $ J = {\smallint _s}\left[\left({\sigma _{xx}}\frac{{\partial u}}{{\partial x}} + {\tau _{xy}}\frac{{\partial v}}{{\partial x}} - W\right)\frac{{\partial q}}{{\partial x}} + \left({\tau _{xy}}\frac{{\partial u}}{{\partial x}} + {\sigma _{yy}}\frac{{\partial v}}{{\partial x}}\right)\frac{{\partial q}}{{\partial y}}\right]{\rm{d}}S 。$ | (10) |
式中:σij为平面应力;q=q(x1,x2)为积分权函数。
2.3 相互作用积分法相互作用积分法如下:
| $ {I^{(1,2)}} = \int_\varGamma {\left[{W^{(1,2)}}{\delta _{1,j}} - {\sigma _{ij}}^{(1)}\frac{{\partial {u_i}^2}}{{\partial {x_1}}} - {\sigma _{ij}}^{(2)}\frac{{\partial {u_i}^1}}{{\partial {x_1}}}\right]} {n_j}{\rm{d}}\varGamma 。$ | (11) |
式中:
| $ {W^{(1,2)}}{\text{ = }}\frac{1}{2}({\sigma _{ij}}^{(1)}{\varepsilon _{ij}}^{(2)} + {\sigma _{ij}}^{(2)}{\varepsilon _{ij}}^{(1)})。$ | (12) |
对于线弹性体,相互作用积分与应力强度因子之间的关系为:
| $ I = \frac{{2({K_I}^{(1)}{K_I}^{(2)} + {K_{{\rm I}{\rm I}}}^{(1)}{K_{{\rm I}{\rm I}}}^{(2)})}}{{E{\text{*}}}}。$ | (13) |
式中:
| $ E^*=\left\{\begin{array}{cc}E& 平面应力,\\ \dfrac{E}{1-{\text{v}}^{\text{2}}}&平面应变。\end{array}\right. $ | (14) |
由上式得:
| $ {K_I} = \frac{{E^*}}{2}{I^{(1,\bmod el{\kern 1pt} I)}},$ | (15) |
| $ {K_{II}} = \frac{{E^*}}{2}{I^{(1,\bmod el{\kern 1pt} II)}} 。$ | (16) |
通过Abaqus有限元分析软件分别建立单边穿透裂纹和中心单裂纹试样模型,如图4所示。裂纹长度分别为a和2a,矩形板B=200 mm,H=200 mm,弹性模量E=2×105 MPa,泊松比v=0.3,单边和中心裂纹试样均采用平面四边形单元,网格尺寸设置为3.5,单元类型为CPS4R,图4(c)为单边裂纹网格划分,图4(d)为单边裂纹试样a/B为0.2时应力云图。由文献[8]可知,单边裂纹和中心裂纹试样受轴向拉伸载荷时,应力强度因子的理论解分别如式(17)和(18)所示

|
图 4 应力强度因子计算模型 Fig. 4 Stress intensity factor calculation models |
| $\begin{split} K =& \sigma \sqrt {\text{π} a} \Biggr[1.12 - 0.23\frac{a}{B} + 10.6{\Biggr(\frac{a}{B}\Biggr)^2} -\\ &21.7{\Biggr(\frac{a}{B}\Biggr)^3} + 30.4{\Biggr(\frac{a}{B}\Biggr)^4}\Biggr](a/B < 0.6),\end{split} $ | (17) |
| $ K=\dfrac{\Biggr(\sigma \sqrt{\text{π} a}\Biggr[1-0.5\Biggr(\dfrac{2a}{B}\Biggr)+0.326{\Biggr(\dfrac{2a}{B}\Biggr)}^{2}\Biggr]\Biggr)}{\sqrt{\Biggr(1-\dfrac{2a}{B}}\Biggr)}(2a/B \leqslant 0.7) 。$ | (18) |
通过编写Python脚本提取单元节点编号、位移等,基于位移外推法、等效积分区域法和相互作用积分法,将节点参数分别代入式(5)~式(16),分别计算单边裂纹和中心裂纹试样的静态应力强度因子,并与理论解进行对比分析,如表1和表2所示。等效积分区域法计算2种裂纹误差在4%以内;位移外推法计算单边裂纹裂宽比小于0.45时,误差在4%以内,在裂宽比为0.5时,相对误差达到了6.06%,计算中心裂纹时,误差基本都在3%以内;相互作用积分法计算中心裂纹误差基本都在2%以内,单边裂纹的误差都在1%以内。可以看出,与等效区域积分法和位移外推法相比,相互作用积分法计算结果比较稳定而且准确度也较高,因此使用相互作用积分法计算裂纹扩展过程中的动态应力强度因子。
|
|
表 1 单边裂纹静态应力强度因子 Tab.1 The static SIF of unilateral crack |
|
|
表 2 中心裂纹静态应力强度因子 Tab.2 The static SIF of center crack |
在Abaqus软件中建立有限元模型,基于扩展有限元方法模拟裂纹扩展,通过编写Python脚本完成,提取增量步的断裂单元、单元节点编号、节点坐标和位移等。通过裂纹尖端节点水平集值和坐标确定裂纹尖端坐标,指定参与积分半径,确定参与积分的单元,对参与积分的单元节点赋予权函数;基于相互作用积分法,将节点的应力应变代入式(11)~式(16),计算得到KI,循环,直至最后一个增量步。
采用单边裂纹模型,施加恒定载荷σ=30 MPa,材料为2024铝合金[17],弹性模量E=68 GPa,泊松比v=0.33,网格设置与单边静态裂纹相同,建立扩展有限元模型,使用相互作用积分法计算相应的应力强度因子,提取a/B分别为0.10,0.15,0.20,0.25,0.30,0.35,0.40的计算结果,如表3所示。
|
|
表 3 单边裂纹动态应力强度因子 Tab.3 The dynamic SIF of center crack |
可以看出,随着裂纹的长度增加,相互作用积分法与理论解之间的误差都在3%以内,证明该方法计算动态应力强度因子可以得到比较准确的结果,为计算疲劳裂纹扩展过程中动态应力强度因子提供依据。
3 疲劳裂纹扩展过程及剩余寿命分析目前,通常使用应力强度因子范围△K和疲劳裂纹扩展速率da/dN来表征材料的抗疲劳性能,也是预测材料疲劳寿命的重要指标。Paris将稳定扩展区的△K与da/dN联系起来,提出著名的Paris公式[18]:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C{(\vartriangle K)^m}。$ | (19) |
式中,C和m为材料常数。
在Abaqus中建立扩展有限元模型,使用低周疲劳分析进行疲劳裂纹扩展模拟,裂纹的启裂和扩展准则为结构在最大值和最小值加载时的相对能量释放率△G,定义[19]为:
| $ f = \frac{N}{{{c_1}\vartriangle {G^{{{\text{c}}_2}}}}} \geqslant 1.0。$ | (20) |
裂纹的开裂与扩展遵循Paris公式,疲劳裂纹扩展速率可以根据相对能量释放率计算,公式如下:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = {c_3}{(\vartriangle G)^{{{\text{c}}_{\text{4}}}}}。$ | (21) |
其中:c1~c4均为材料常数。
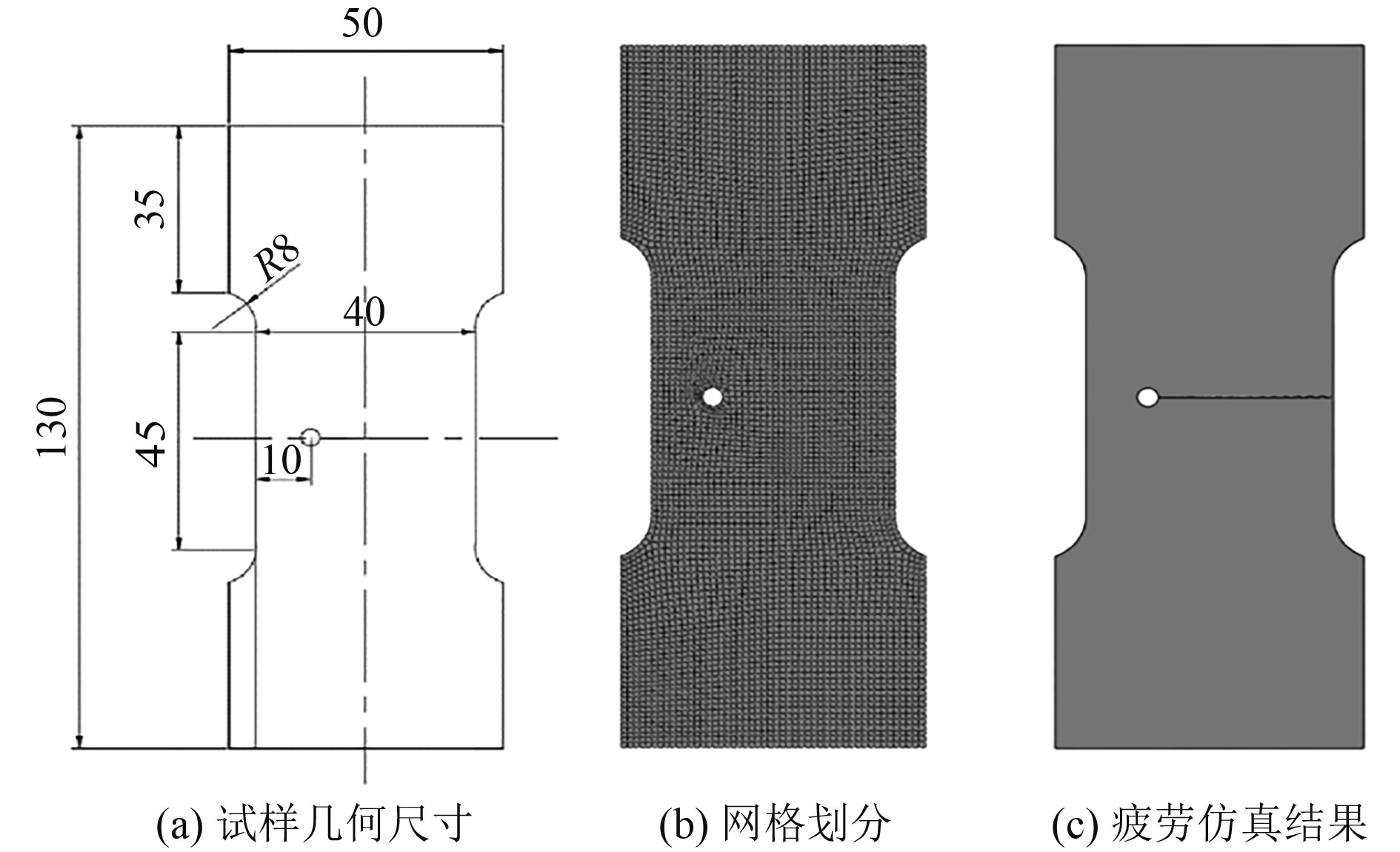
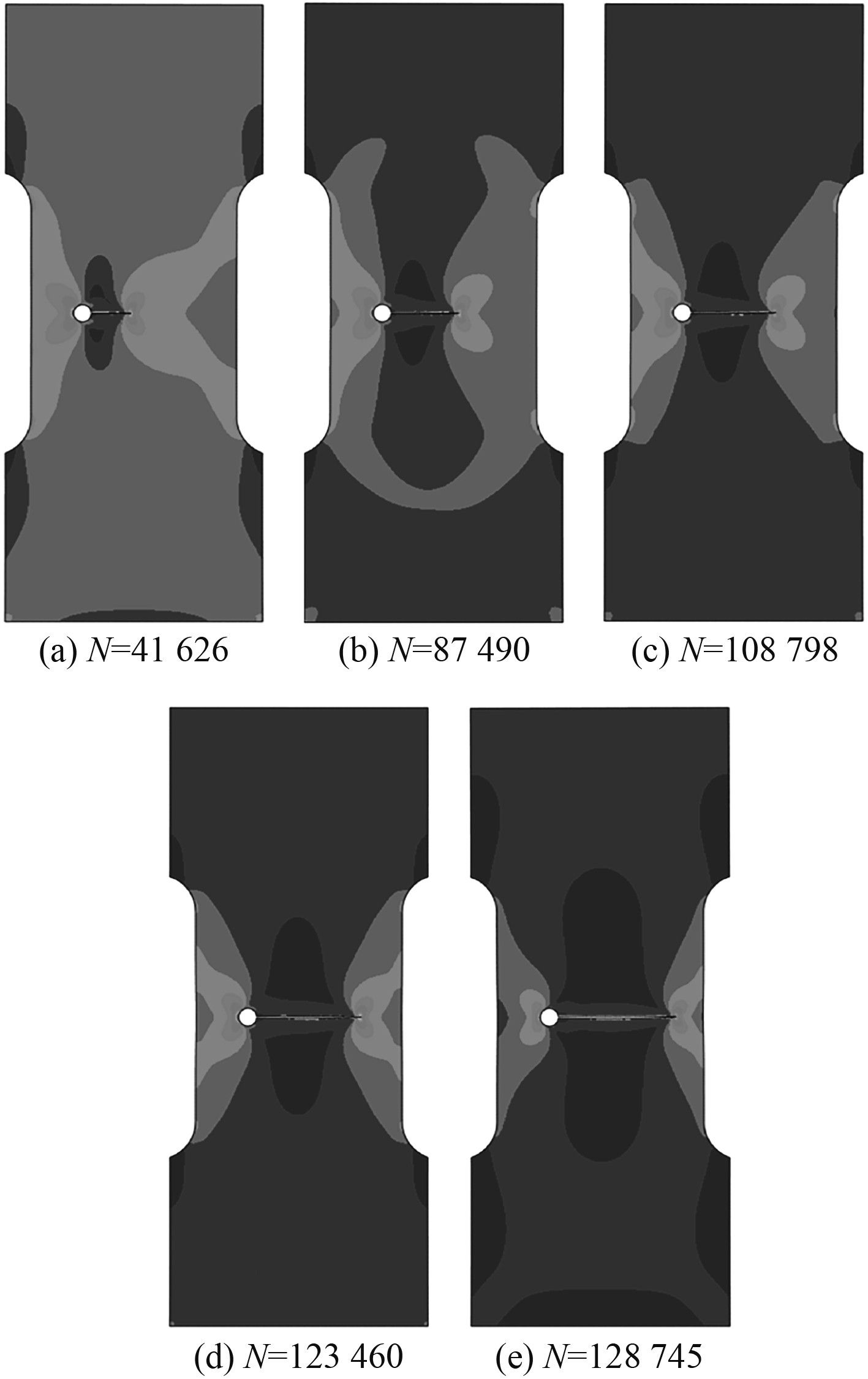
本文研究对象如图5(a)所示。试样长度为130 mm,宽度为50 mm,圆孔直径为3.5 mm,在孔边预制长度为5 mm的裂纹,应力比为0.1,所受轴向最大和最小拉伸载荷分别为87.5 MPa和8.75 MPa。图5(b)为网格划分,网格尺寸为0.5,单元类型为CPS4R,单元数为22605;图5(c)为裂纹扩展路径。材料参数由文献[20]给出,弹性模量E=7.409×104 MPa,泊松比v=0.31,C=2.4×10−7,m=2.86。图6为裂纹扩展过程不同循环周次下的应力云图。
|
图 5 疲劳裂纹扩展试样模型 Fig. 5 Fatigue crack growth specimen model |
|
图 6 疲劳裂纹扩展过程应力云图 Fig. 6 Stress cloud diagram of fatigue crack propagation process |
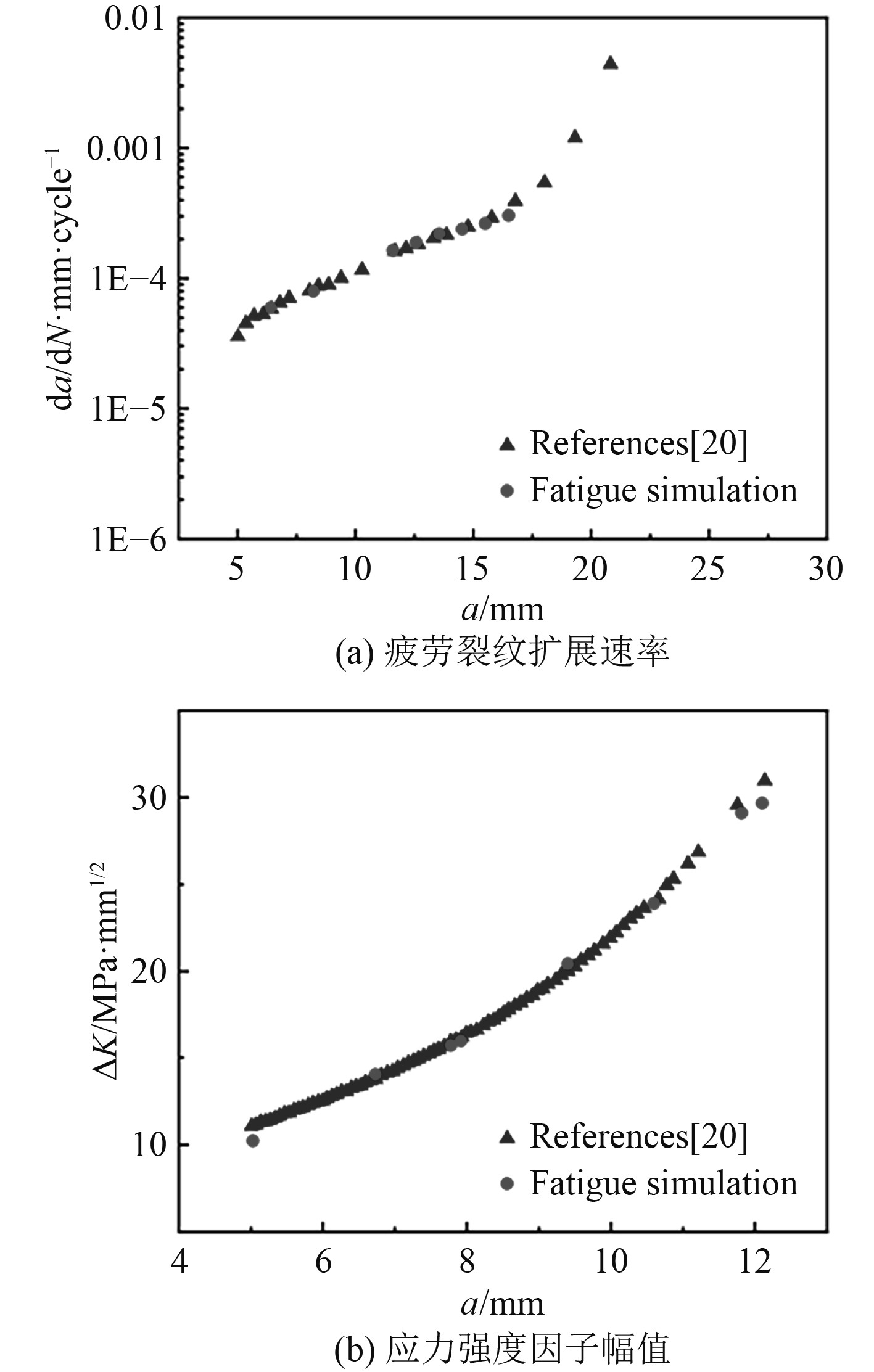
图7(a)为疲劳裂纹扩展速率曲线。可以看出,仿真的疲劳扩展速率与文献[20]中试验数据的疲劳裂纹扩展稳定阶段基本一致。这是因为疲劳仿真的损伤参数由Paris公式确定,而Paris公式由试验稳定扩展区数据拟合得到。图7(b)为应力强度因子幅值与裂纹长度之间的关系。可以看出,随着裂纹长度增加,仿真结果与文献[20]试验结果基本吻合。
|
图 7 疲劳裂纹扩展速率预测 Fig. 7 Prediction of fatigue crack growth rate |
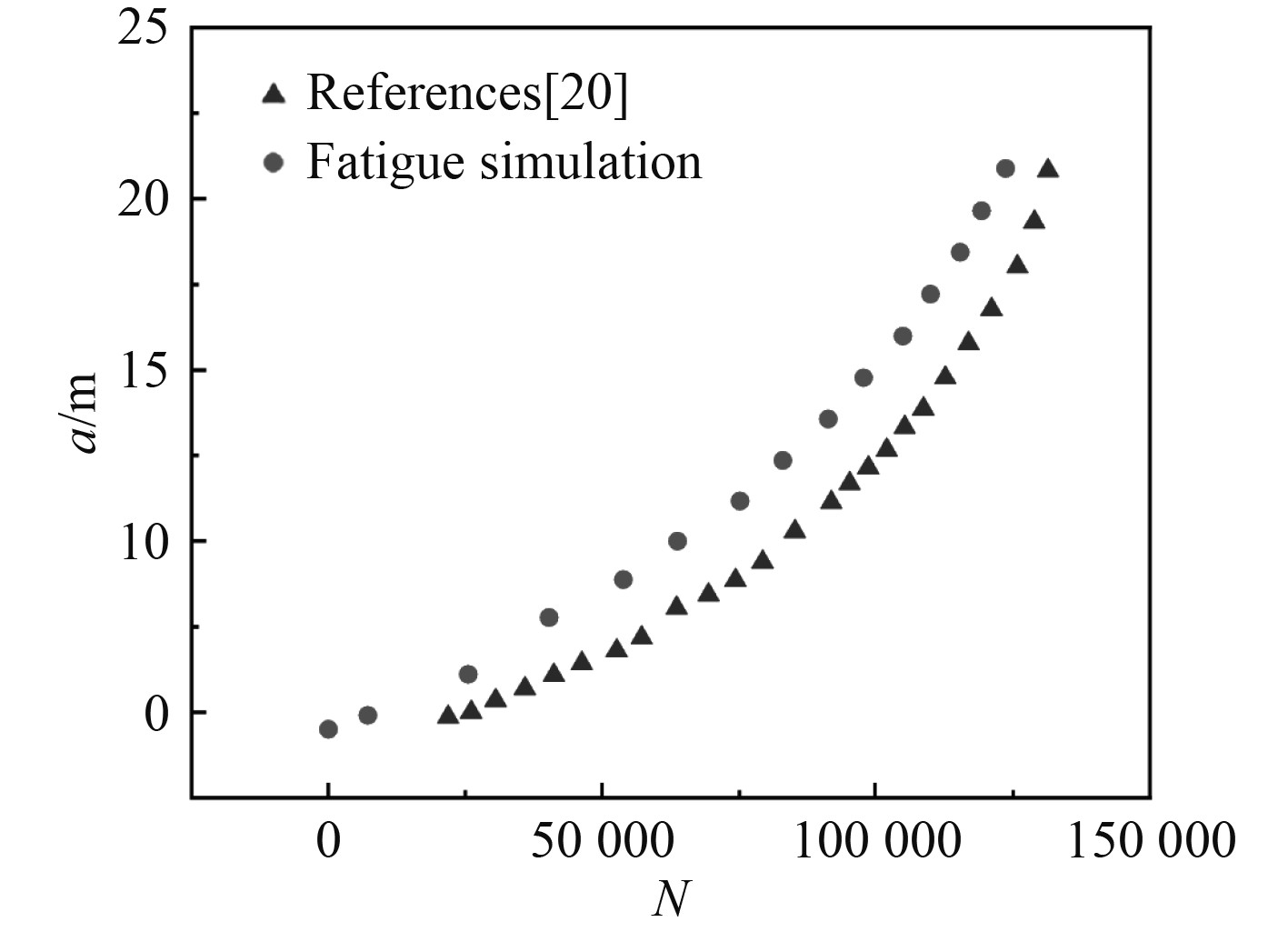
图8为试样剩余寿命的预测结果。可以看出,疲劳仿真的结果与文献[20]的疲劳试验结果比较吻合,循环周次分别为129407和124591,相差3.8%,因此利用低周疲劳分析结合相互作用积分法在解决疲劳问题可以得到可靠的结果。
|
图 8 疲劳裂纹扩展a/N曲线 Fig. 8 Fatigue crack growth a/N curve |
1)在Abaqus中基于扩展有限元法建立了疲劳裂纹扩展模型,通过Python脚本实现了静态裂纹和裂纹扩展的动态应力强度因子计算。
2)分别使用位移外推法、等效积分区域法和相互作用积分法计算单边裂纹和中心裂纹的应力强度因子,发现相互作用积分法计算结果最稳定、相对误差最小,在2%以内。
3)使用相互作用积分法计算了单边裂纹扩展过程的动态应力强度因子,计算误差在3%以内。
4)计算了疲劳裂纹扩展过程的动态应力强度因子,结合Paris公式,使用低周疲劳分析,对孔边裂纹的剩余寿命进行预测,与试验结果相比,误差为3.8%,并且疲劳裂纹扩展稳定阶段的试验结果与扩展有限元分析基本一致。
| [1] |
底月兰, 王海斗, 董丽虹, 等. 扩展有限元法在裂纹扩展问题中的应用[J]. 材料导报, 2017, 31(3): 70-74+85. DI Yuelan, WANG Haidou, DONG Lihong, et al. Application of the extended finite element method in crack propagation[J]. Materials Reports, 2017, 31(3): 70-74+85. DOI:10.11896/j.issn.1005-023X.2017.03.012 |
| [2] |
T, Belytschko, T, Black. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45: 602-620. |
| [3] |
FENG S Z, LI W. An accurate and efficient algorithm for the simulation of fatigue crack growth based on XFEM and combined approximations[J]. Applied Mathematical Modelling, 2017, 55(MAR.): 600-615. |
| [4] |
NAGASHIMA T, WANG C. XFEM analyses using two-dimensional quadrilateral elements enriched with only the heaviside step function[J]. International Journal of Computational Methods, 2022, 19(2): .2150063. DOI:10.1142/S0219876221500638 |
| [5] |
薛河, 王双, 王正, 等. 基于扩展有限元法的三维裂纹前缘应力强度因子计算方法[J]. 舰船科学技术, 2022, 44(3): 1-5. XU He, WANG Shuang, WANG Zheng, et al. XFEM-based calculation mothod for stress intensity factor of three-dimensional crack front[J]. Ship Science And Technology, 2022, 44(3): 1-5. DOI:10.3404/j.issn.1672-7649.2022.03.001 |
| [6] |
SHI F, LIU J. A fully coupled hydromechanical XFEM model for the simulation of 3D non-planar fluid-driven fracture propagation[J]. Computers and Geotechnics, 2021, 132(5): 103971. |
| [7] |
ZOU G, HE C. Path-dependent J-integrals under mixed-mode loads of mode I and mode II[J]. Theoretical and Applied Fracture Mechanics, 2018, 96: 380-386. DOI:10.1016/j.tafmec.2018.05.014 |
| [8] |
马梓聪. 含裂纹海洋平台结构剩余疲劳强度评估方法研究[D]. 大连: 大连理工大学, 2018.
|
| [9] |
余天堂. 含裂纹体的数值模拟[J]. 岩石力学与工程学报, 2005, 24(24): 4434–4439.
|
| [10] |
汪必升, 李毅波, 廖雅诗, 等. 基于扩展有限元模型的动态应力强度因子计算[J]. 中国机械工程, 2019, 30(11): 1294–1301.
|
| [11] |
MH A, BNN A, MTA B, et al. A new numerical approach in the seismic failure analysis of concrete gravity dams using extended finite element method. Engineering Failure Analysis. 2021. 132: 105835.
|
| [12] |
OT A, HO B, YY C. A New approach of the interaction integral method with correction terms for cracks in three-dimensional functionally graded materials using the tetrahedral finite element[J]. Theoretical and Applied Fracture Mechanics, 2021, 103065. |
| [13] |
GRBOVIC A, KASTRATOVIC G, SEDMAK A, et al. Fatigue crack paths in light aircraft wing spars[J]. International Journal of Fatigue, 2019, 123(JUN.): 96-104. |
| [14] |
LI Qiang, CHEN Zhixiang, LUO Shaohui. Reflection crack analysis of asphalt overlay on cement concrete pavement based on XFEM[J]. Advances in Civil Engineering. 2021, 1230447.
|
| [15] |
MOES N. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46: 131-150. DOI:10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J |
| [16] |
夏世林, 磨季云. 基于J积分的含裂纹加筋板在单轴拉伸载荷下的极限强度计算[J]. 舰船科学技术, 2021, 43(7): 34–39, 59. XIA Shi-lin. MO Ji-yun. Ultimate strength calculation of cracked stiffened-panel under loading of uniaxial tension using J-integral theory[J]. Ship Science and Technology. 2021, 43(7): 34–39, 59. |
| [17] |
BENVENUTI E. An effective XFEM with equivalent eigenstrain for stress intensity factors of homogeneous plates[J]. Computer Methods in Applied Mechanics & Engineering, 2017, 321(1): 427-454. |
| [18] |
PARIS P, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4).
|
| [19] |
马颖涵, 张振, 郭孟雨, 等. F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟[J]. 机械工程材料, 2021(4). 65–17, 80.
|
| [20] |
JIN Huijin, WU Sujun. A new driving force parameter for fatigue growth of multiple cracks[J]. International Journal of Fatigue, 2017, 10-16. |
 2022, Vol. 44
2022, Vol. 44
