海洋结构物中的管状结构在工作载荷或环境条件下不可避免会产生初始裂纹或缺陷,裂纹的扩展会造成结构局部或整体破坏失效,因此必须及时对裂纹管进行修复。工程上传统的修复方法是焊接加固,但在有些复杂的工作环境中焊接操作非常困难,并会造成结构组织及性能劣化。复合材料修复技术因具备免焊不动火、操作简单、施工安全、修补强度高等优点,在船舶、航天等建筑结构维护中得到越来越广泛的应用。这种修复方法主要利用环氧树脂胶将碳纤维或玻璃纤维等高模量、高强度、耐疲劳的增强型复合材料加固在圆管裂纹处,从而提高受损圆管的承载能力。
SEICAMV等[1]对修复后的简支钢管进行了四点弯曲准静态试验,证明了复合材料能够较好地增强海底受损钢管的极限强度和抗弯刚度。Houssam等[2]研究了不同复合材料对管壁性能的影响,指出碳纤维复合材料比玻璃纤维和芳纶纤维能更有效地提高管道承压能力。唐洪元等[3]对碳纤维布加固后的方管进行了轴压试验,结果表明结构在碳纤维布后加固后承载力峰值有所提升,且碳纤维布层数达到4层时,试件不再有明显的屈曲现象。Sundarraja[4]对碳纤维布加固空心方钢的轴向性能进行了多项试验,指出增加碳纤维布铺层宽度和厚度能够延迟方管局部屈曲,并有助于承载额外的荷载,试样承载力的最大增幅为44.32%。Gao[5]通过轴压试验研究了碳纤维布加固钢管构件的屈曲行为,结果表明碳纤维层能明显增强钢管的强度和刚度,碳纤维布加固层数与承载力基本呈线性关系。
目前,碳纤维增强聚合物主要用于混凝土等结构的加固,对金属结构尤其是裂纹圆管的加固修复研究相对较少。本文对完整圆管、裂纹圆管以及碳纤维布修复裂纹圆管进行轴压试验,将得到的载荷位移曲线及失效模式与有限元结果进行对比验证,并进一步研究不同长度和方向的裂纹圆管在碳纤维布加固修复下的承载特性以及碳纤维布层数、宽度对修复效果的影响。
1 轴压试验 1.1 试件设计试验选取圆管直径

|
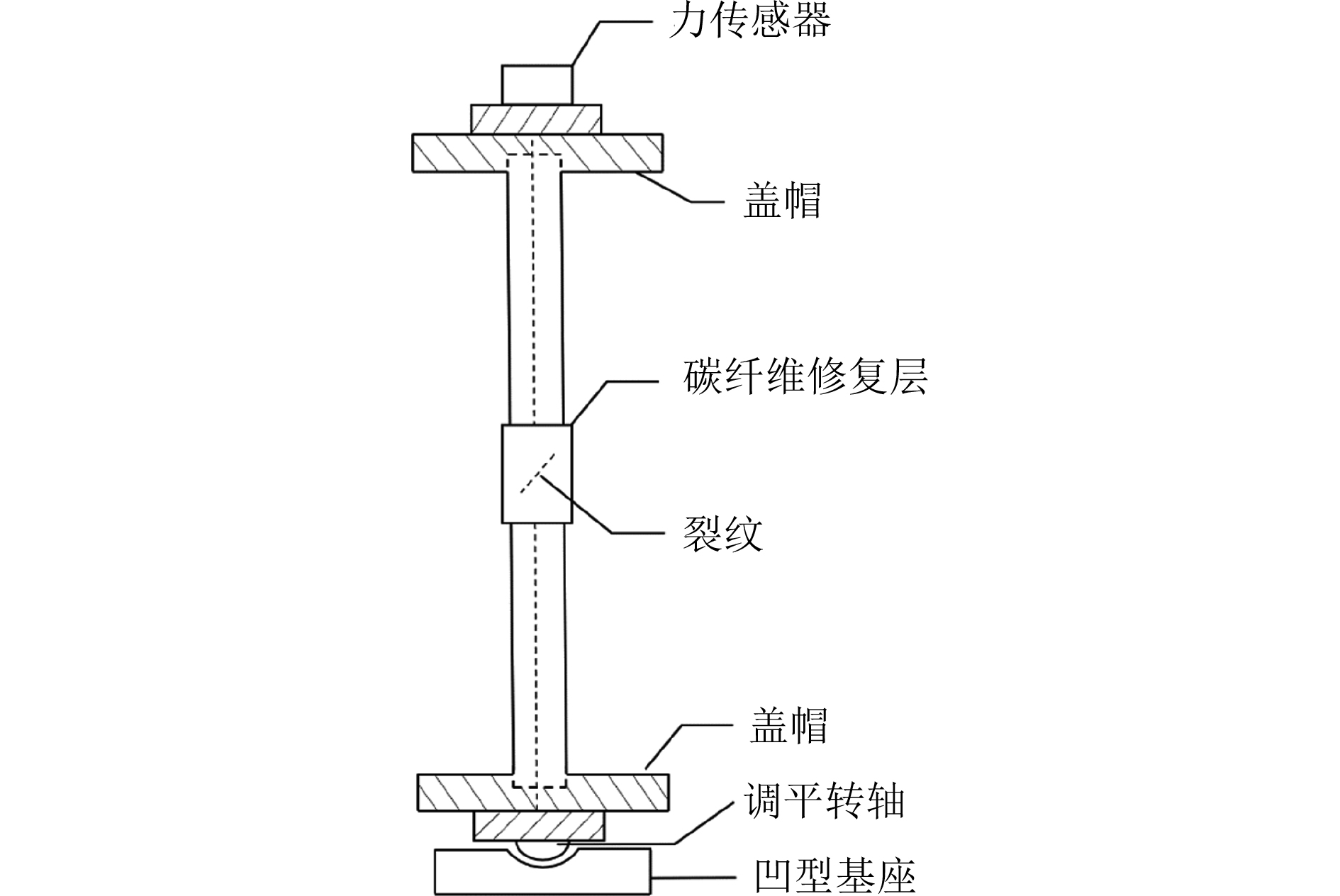
图 1 试件加固示意图 Fig. 1 Diagram of the reinforced specimen |
碳纤维布修复宽度
| $ L=2{L}_{\text{over}}+{L}_{{\rm{defect}}}+2{L}_{{\rm{taper}}},$ | (1) |
| $ {L}_{\text{over}}=2.5\sqrt{Dt/2}。$ | (2) |
式中:D为圆管外径;
|
|
表 1 试件编号及参数 Tab.1 Number and parameters of specimens |
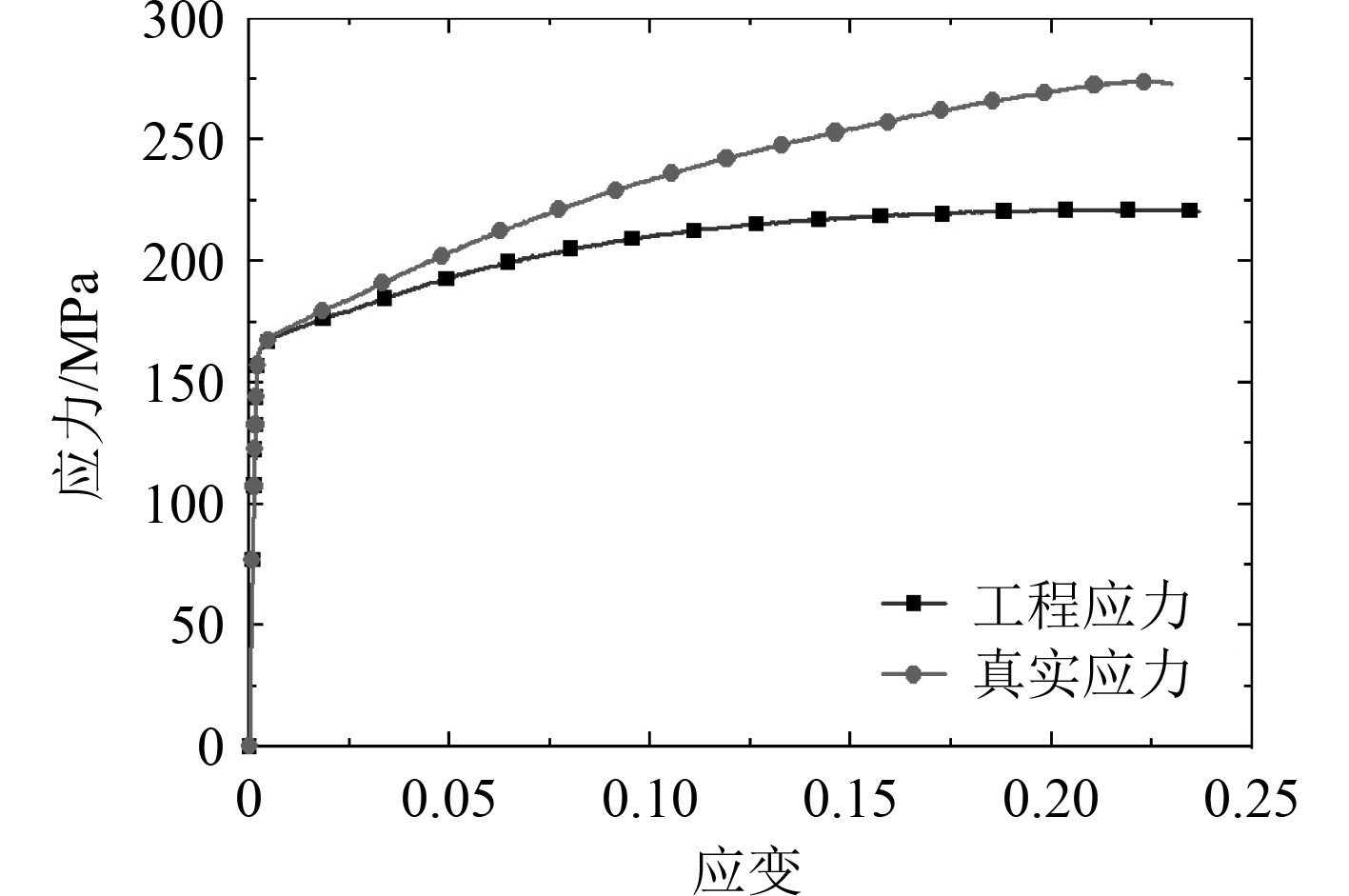
试验用圆管为6063铝合金,采用拉伸试验机根据GB/T228.1-2010[7]标准测定了圆管的力学性能,如图2所示。试件弹性模量
|
图 2 试件应力应变曲线 Fig. 2 Stress-strain curve of specimen |
试验选用厚度为0.167 mm、密度为300 g/cm2的单向高强度12K碳纤维编织布,粘结剂选用包含A组环氧树脂胶以及B组固化剂的浸渍胶。碳纤维布以及环氧树脂的材料性能如表2所示。
|
|
表 2 碳纤维和环氧树脂材料性能 Tab.2 Mechanical properties of CFRP and epoxy |
步骤1 管道裂纹制备。利用线切割在铝合金圆管指定位置切出宽度约0.2 mm的裂纹,为保证更好的粘结性能,用抛光机对裂纹附近区域进行抛光打磨至呈银白色,然后使用酒精对补强区域进行清洁。
步骤2 粘结剂制备。将A组环氧树脂、B组固化剂在恒温箱25 °C保温30 min,分别在桶内搅拌均匀,然后按2:1的比例混合在一起,用电钻搅拌3 min混合均匀。
步骤3 缠绕碳纤维布。首先在补强区域均匀涂刷底胶,然后缠绕裁剪好的碳纤维布,在缠绕过程中需连续均匀的涂胶,同时用刮板沿纤维方向轻轻挤压,排除碳纤维布层间的气泡,使碳纤维布层间浸渍胶分布更加均匀。
步骤4 后处理。在碳纤维布缠绕完成后,用刮板挤压出多余的粘结剂,同时均匀转动圆管避免粘结剂不均匀流动,直至其初步凝胶,置于恒温箱60 °C保温24 h,最后在室温下保存12 h待其完全固化。
试件在WAW-600E型号拉压试验机上进行轴压试验,试验装置如图3所示。设置加载速度为2 mm/min,圆管两端装备有直径大小凹槽的可拆卸方形钢板,方便圆管的轴向加载,通过负荷传感器和位移传感器测量轴压载荷和位移。
|
图 3 试验装置 Fig. 3 Experimental device |
不同碳纤维布层数加固试件轴向压缩试验后破坏模式如图4(a)所示。试件L0-0-45-0.3裂纹上端区域在轴压载荷下沿裂纹方向向下滑移,引起裂纹尖端处进一步撕裂,加固试件L1-150-45-0.3在轴向加载过程初期出现了连续的胶层断裂的噼啪声,圆管受到的载荷通过胶层传递给复合材料层,但由于修复层较薄,碳纤维布在裂纹中部区域出现了明显的向内屈曲变形,且在裂纹尖端处随着裂纹扩展而鼓起膨胀,试验结果表明1层碳纤维布不能很好地阻止裂纹扩展。相比之下,缠绕2层碳纤维布试件L2-150-45-0.3裂纹处局部变形要明显变小,但修复效果仍不理想;3层碳纤维布修复下试件L3-150-45-0.3的变形模式出现了明显不同,碳纤维层并未发生明显变形,较好地抑制了裂纹的扩展,该试件最终在复合材料层上端出现象足式屈曲破坏,这主要是因为高强度、高模量的复合材料层使圆管塑性变形在修复层端部集聚,圆管轴向压应力以及环向拉应力达到了材料屈服极限,并最终屈曲破坏。L4-150-45-0.3和L3-150-45-0.3的损伤模式相似,裂纹在轴向载荷下并未进一步扩展,碳纤维布也未发生明显变形。

|
图 4 失效模式 Fig. 4 Failure modes |
不同碳纤维宽度加固效果如图4(b)所示。试件L3-125-45-0.3与L3-150-45-0.3的变形模式基本一致,说明宽度为125 mm的碳纤维布也能起到非常好的修复效果,但碳纤维布宽度为100 mm的试件L3-100-45-0.3在修复层上端边界出现的明显的凹陷变形并伴有脱胶现象,这是因为修复层宽度过短造成粘结面积不足,且由于铝合金管具有良好的延展性,在受载过程中和修复层在上端粘结界面出现了较大相对剪切变形,同时边界处几何突变产生应力集中进一步加剧了该处基体胶层的断裂失效。
3种不同裂纹长度圆管在宽度为150 mm的3层碳纤维布修复前后破坏模式如图4(c)所示。试件L3-150-45-0.45修复层有轻微的变形,裂纹出现了一定扩展,对于同样尺寸的修复层,裂纹长度达到
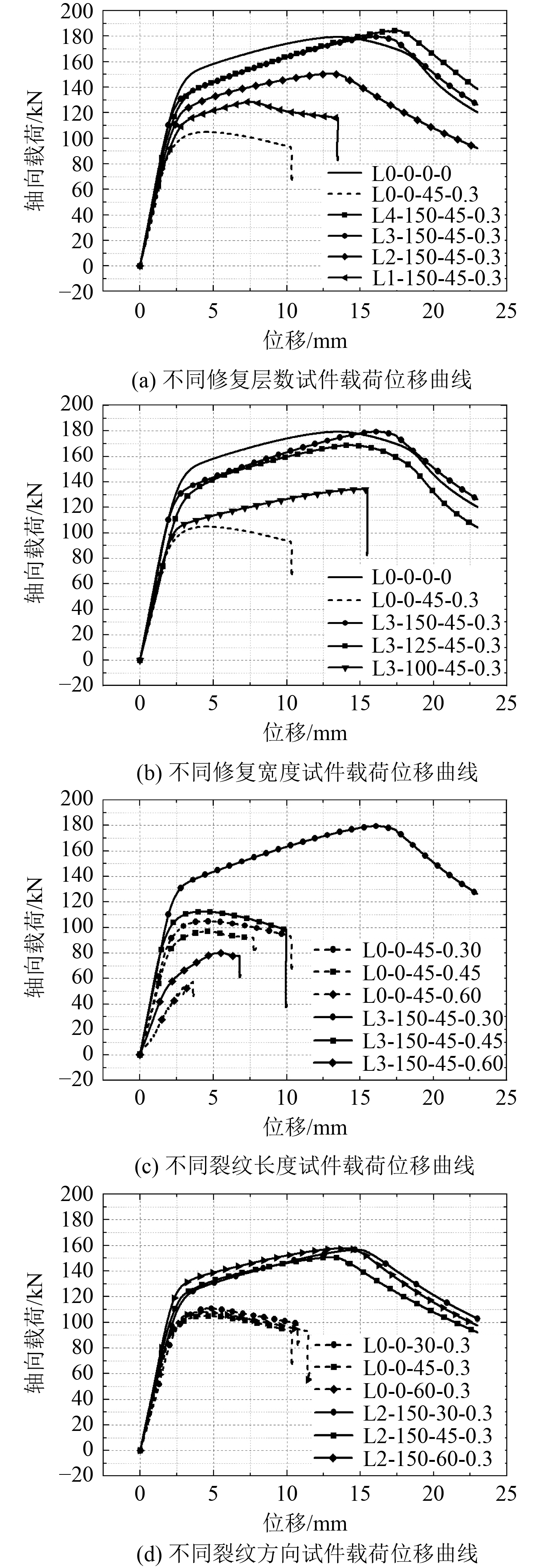
不同碳纤维布加固裂纹圆管的荷载-位移曲线如图5所示。未修复裂纹圆管L0-0-45-0.3荷载-位移曲线如图5(a)虚线所示,近似为抛物线形状,轴向载荷在达到峰值后逐渐降低直到圆管破坏;而无缺陷圆管以及碳纤维修复圆管载荷位移曲线可以分为3个阶段:线弹性阶段、塑性屈服阶段和损伤阶段。在线弹性阶段试件修复后载荷位移曲线的斜率比裂纹圆管稍高,说明在缺陷区域屈服前,碳纤维层能够略微提高圆管的轴向强度,但加固作用比较有限,圆管主要靠自身承担承担轴压载荷;第二阶段试件表现出非弹性行为,轴向载荷增加速度变缓,补强层抑制了裂纹尖端扩展和圆管径向变形,起到加固修复作用;第三阶段主要表现为2种趋势,L1-150-45-0.3和L3-100-45-0.3等修复试件在载荷达到峰值后发生突变急剧降低,主要是因为碳纤维层数和铺层宽度不足试件发生破坏,而试件L3-150-45-0.3在载荷达到峰值后表现出和完整圆管相同的缓慢下降趋势,这表明裂纹圆管经加固后已经达到了完整圆管的承载能力。试件L4-150-45-0.3的极限承载力达到了184 kN,甚至超过了完整圆管的承载力,相比试件L0-0-45-0.3的105 kN提高了约75%。
|
图 5 载荷位移曲线 Fig. 5 Load-displacement curve |
图5(a)表明,随着碳纤维布加固层数增加,修复试件的承载力峰值随之增加,但3层和4层碳纤维布的载荷位移曲线十分接近,这表明在达到一定程度后,再增加碳纤维布层数修复效果提升的非常有限。图5(b)表明碳纤维修复宽度对修复效果也有很大影响,但同样随着修复宽度的增加,修复效果对修复宽度的敏感性逐渐降低。如图5(c)和5(d)所示,宽150 mm的3层碳纤维布对裂纹长度
采用Abaqus对碳纤维修复裂纹管道进行三维显式动力学模拟分析,圆管厚度方向上划分3层网格,裂纹处网格局部细化。环氧树脂采用基于双线性本构的COH3D8内聚力单元模拟,碳纤维根据试验加固尺寸采用实体扫略单元建模,指派网格堆叠方向为厚度方向,碳纤维铺层方向为环向即铺层角为0°。
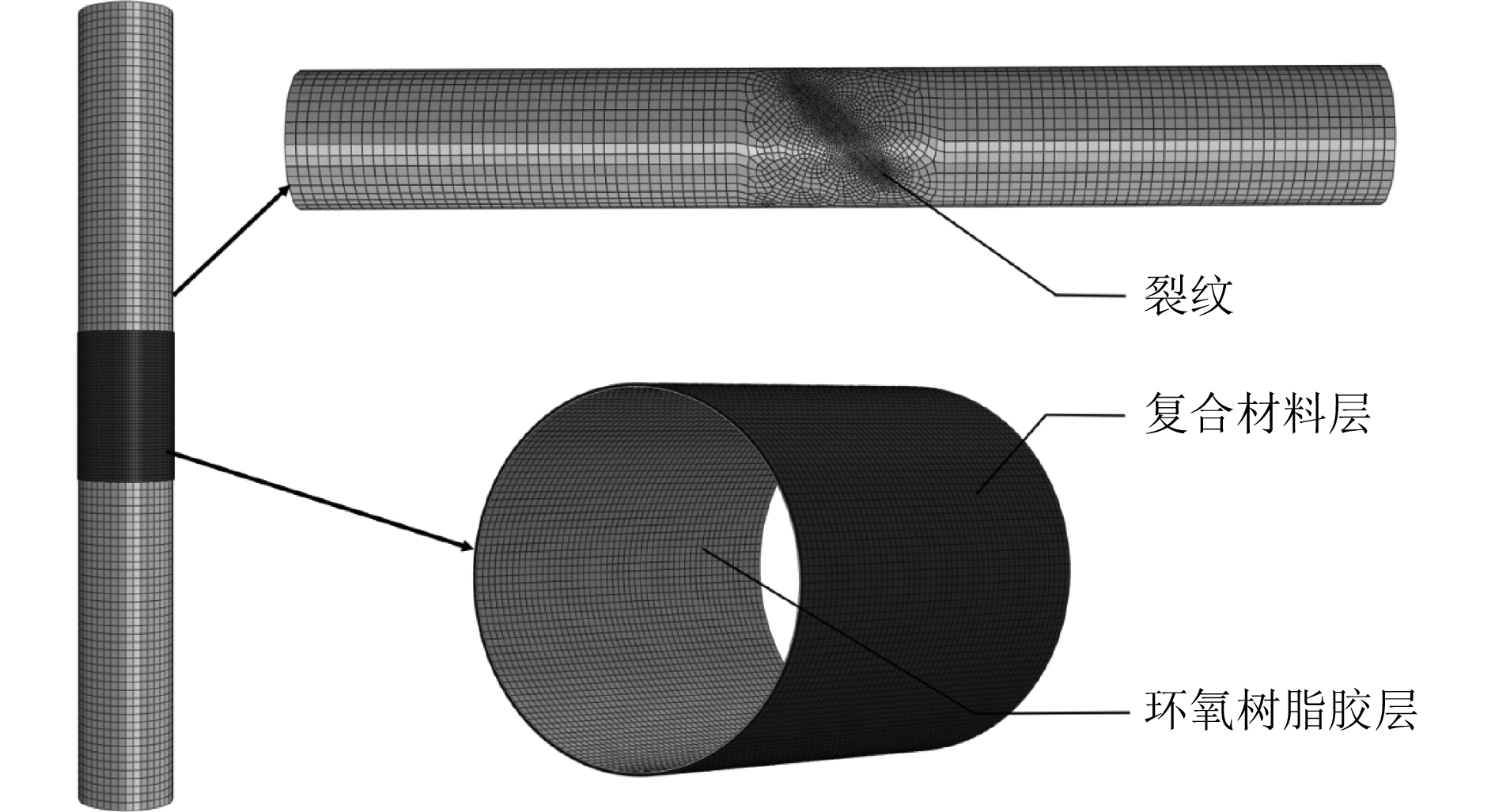
|
图 6 载荷位移曲线 Fig. 6 Load-displacement curve |
铝合金管损伤产生的判断准则选取Ductile损伤准则[8]。Ductile损伤模型假设损伤状态变量与断裂等效塑性应变之间呈线性关系,可以预测延展性金属内部微孔洞、裂纹的产生及演化。圆管应变率取0.1,断裂应变取0.27[9-10]。
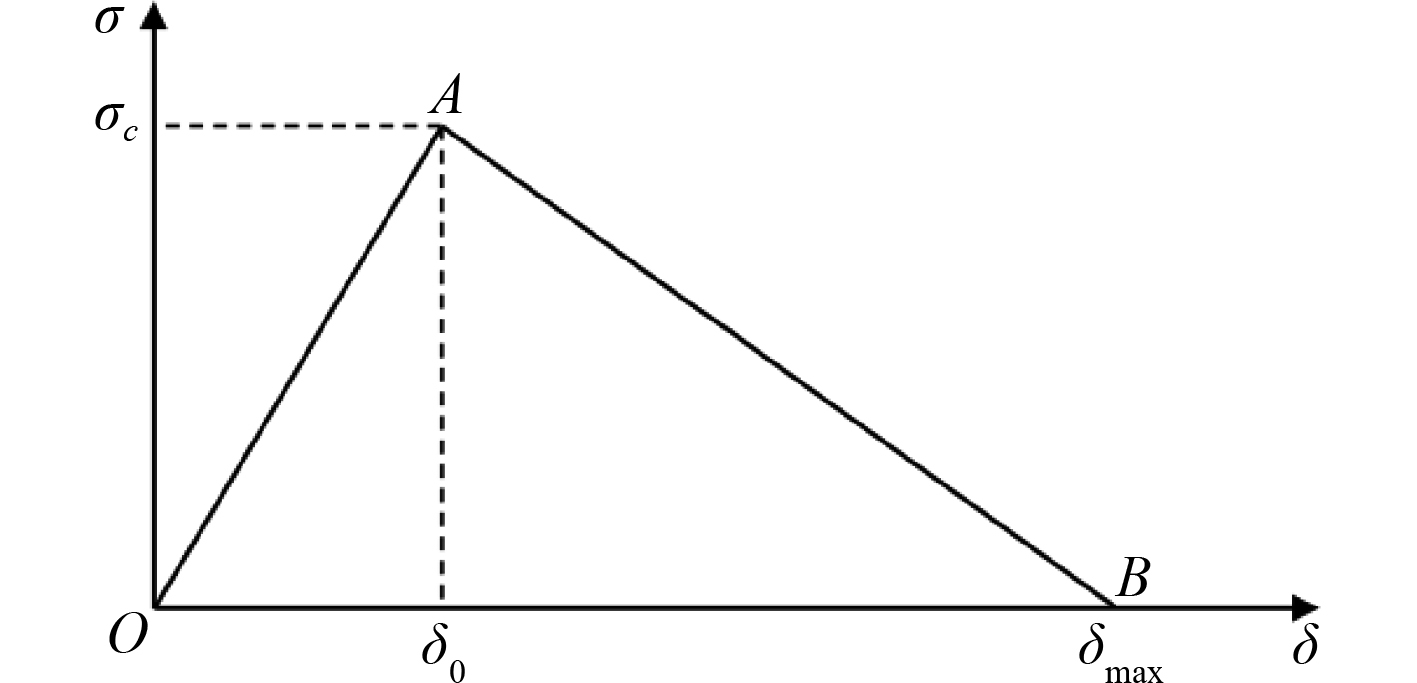
采用基于Traction-seperation Law准则的内聚力单元来模拟胶层,内聚力胶层单元采用双线性的本构模型,如图7所示,该模型能够准确地模拟复合材料的层间及基体损伤。
|
图 7 内聚力单元双线性本构模型 Fig. 7 Bilinear constitutive model of cohesive element |
内聚力单元的损伤过程主要包括2个阶段:损伤起始与损伤演化。当
| $ {\left( {\frac{{\left\langle {{\sigma _n}} \right\rangle }}{{{N_{{\rm{max}}}}}}} \right)^2} + {\left( {\frac{{{\sigma _s}}}{{{S_{{\rm{max}}}}}}} \right)^2} + {\left( {\frac{{{\sigma _t}}}{{{T_{{\rm{max}}}}}}} \right)^2} = 1。$ | (3) |
式中:
图(7)中AB部分表示损伤演化阶段,采用Bengeggagh-Kenane[12]损伤演化准则,定义失效退化参数SDEG为:
| $ SDEG = \frac{{\delta _m^f\left( {{\delta _{\max }} - {\delta _0}} \right)}}{{{\delta _{\max }}\left( {\delta _m^f - {\delta _0}} \right)}},$ | (4) |
| $ \delta _m^f = \frac{{2{G_c}}}{{T_{eff}^0}}。$ | (5) |
式中:
Hashin破坏准则[13]可以非常准确地模拟复合材料的基体断裂、剪切损伤以及纤维断裂等失效模式。本文采用Fortran语言编译了改进的三维Hashin失效准则来模拟三维复合材料的损伤响应,其中复合材料在3个方向上的弹性模量、泊松比、剪切模量以及拉伸强度、压缩强度、剪切强度定义如表3所示。
|
|
表 3 Abaqus子程序定义参数 Tab.3 Parameters defined in Abaqus subroutine |
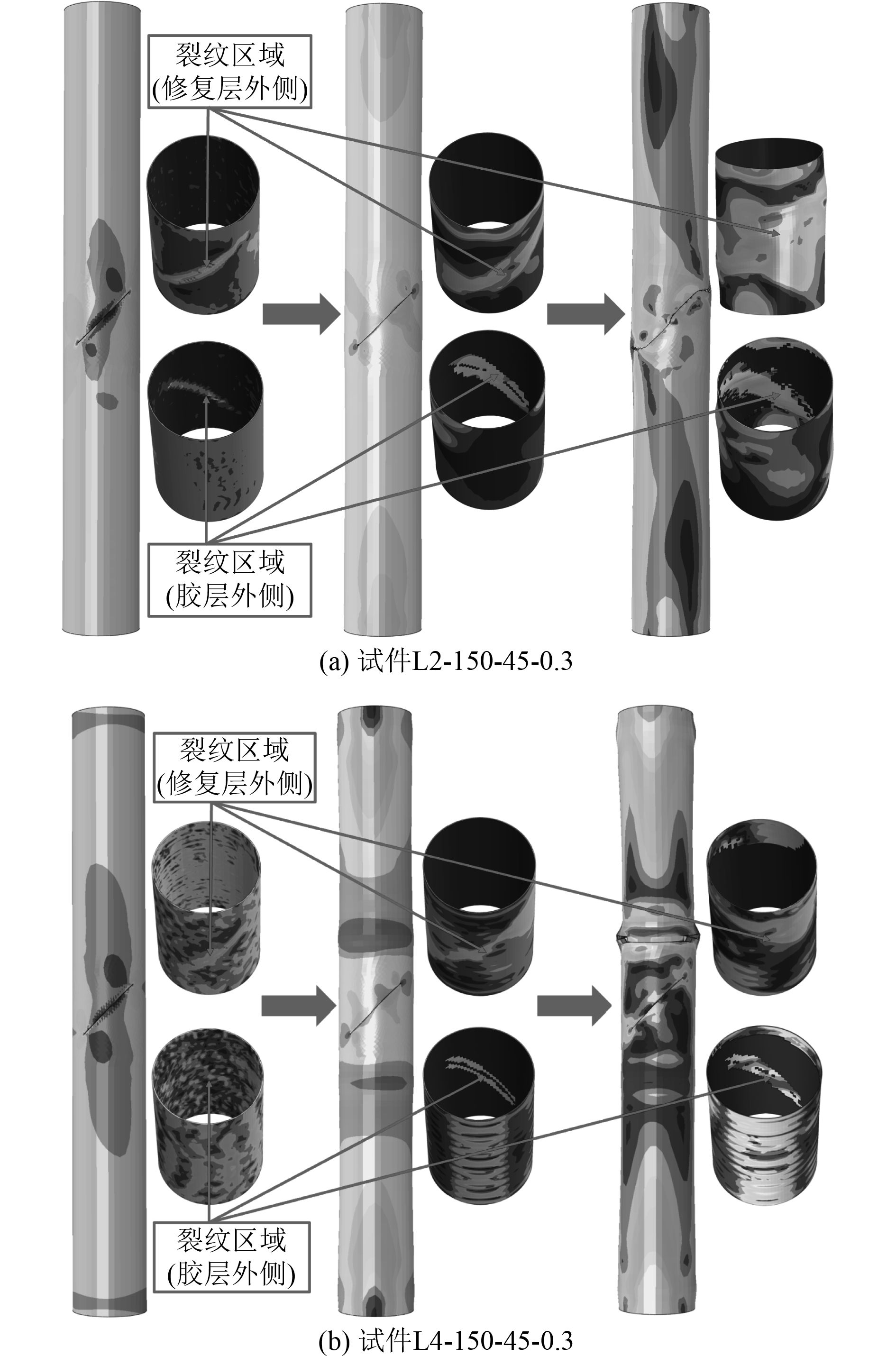
试件L2-150-45-0.3和L4-150-45-0.3数值模拟结果如图8所示,仿真得到的破坏模式与试验结果基本一致。试件L2-150-45-0.3加载初期裂纹尖端和裂纹处修复层出现了一定的应力集中现象,圆管受到的载荷通过胶层传递给了修复层,但是由于裂纹修复层较薄,裂纹变形没有得到有效抑制,裂纹附近胶层达到了极限剪切承载能力而破坏,复合材料层在裂纹尖端处受到裂纹扩展引起的圆管径向鼓胀出现了应力集中。试件L4-150-45-0.3在加载初期粘结性能良好,修复层的应力分布非常均匀,随着进一步加载,裂纹处胶层首先出现了小范围破坏,裂纹背侧修复层出现了多条横向应力集中带,最终圆管在修复层上端边界处屈曲破坏,碳纤维层未发生明显变形,有效地抑制了裂纹的撕裂和圆管变形,起到了很好的修复加固作用。
|
图 8 加固圆管仿真过程图 Fig. 8 Simulation process diagram of reinforcement pipes |
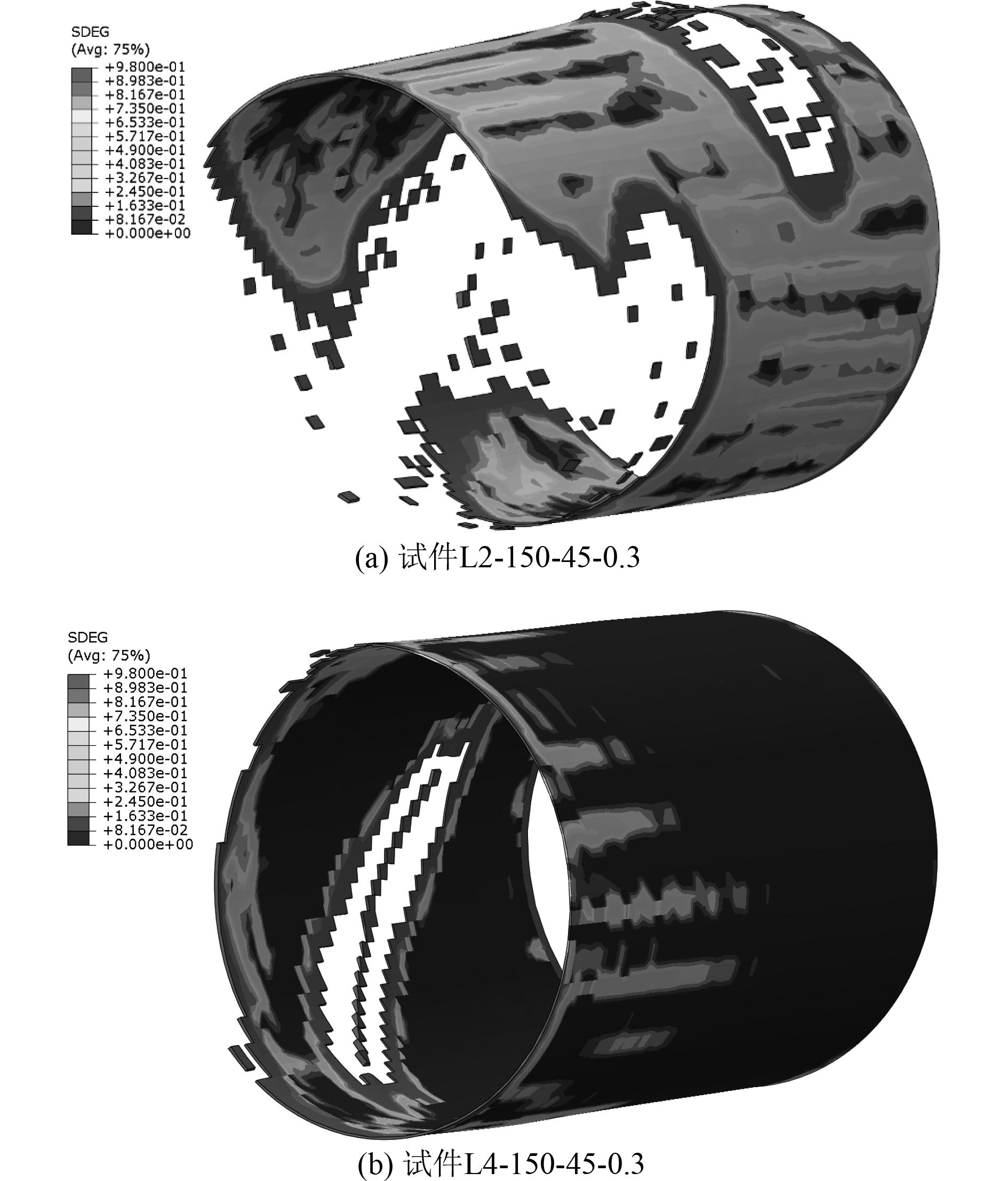
内聚力单元损伤云图如图9所示。图中无量纲参数SDEG表示胶层的损伤状态变量,取值范围为0~1,当SDEG达到1时,内聚力单元完全丧失承载能力从模型中删除,图中观察到试件L2-150-45-0.3裂纹附近以及修复层上端大部分内聚力单元最终失效,修复层与圆管在该区域发生粘结分离现象,以至无法有效抑制裂纹扩展。试件L4-150-45-0.3的胶层单元仅在裂纹附近很小区域以及修复层上端边界处出现了少量完全失效现象,复合材料和裂纹圆管之间粘结界面性能仍然良好,可有效传递载荷。仿真结果表明,胶层的破坏是碳纤维加固裂纹圆管最主要也是最先发生的失效形式。
|
图 9 内聚力单元损伤云图 Fig. 9 Damage of cohesive element |
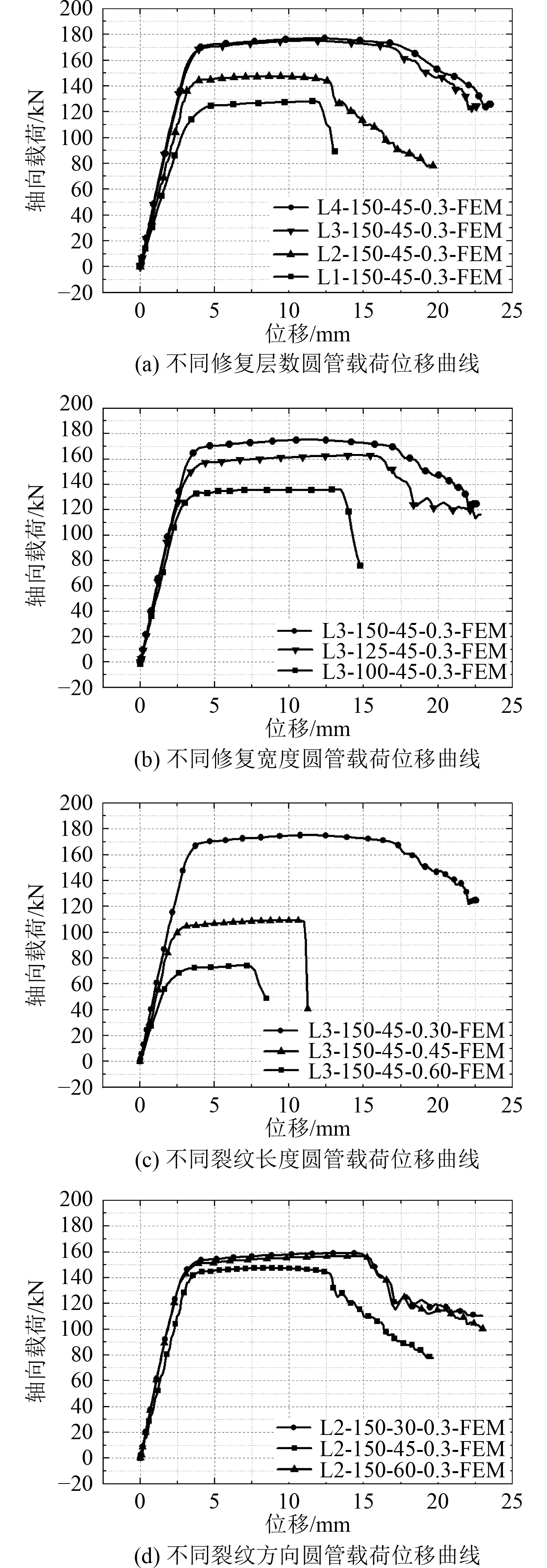
数值分析得到的试件载荷位移曲线分别如图10所示。仿真结果和试验结果基本保持了相同的变化趋势,在线弹性阶段数值模拟得到的曲线和试验非常接近,载荷-位移关系都呈线性,但多组结果表明试验要先于数值模拟进入塑性强化阶段,且塑性强化阶段试验曲线斜率以及峰值载荷要略高于有限元结果,这除了是因为仿真参数定义产生的误差外,试验中环氧树脂胶层涂刷不均匀或胶层并未完全固化会导致修复层强度比理想情况偏弱。仿真与试验在达到峰值载荷时对应的加载位移非常接近,且在试件破坏阶段二者下降斜率差别不大,说明本文采用的数值模拟方法能够较好地模拟环氧树脂和碳纤维布的失效过程。
|
图 10 仿真载荷位移曲线 Fig. 10 Load-displacement curve simulation |
本文对铝合金裂纹圆管以及碳纤维布修复加固后的裂纹圆管进行轴向压缩试验和数值仿真研究,分析裂纹试件修复前后在轴压载荷下的破坏模式及最大承载力,同时讨论了裂纹长度和方向、碳纤维布修复层数和宽度等因素对修复效果的影响,得出以下结论:
1)碳纤维布在试件塑性屈服阶段能够有效抑制裂纹的扩展和圆管的径向变形,大幅度恢复裂纹圆管的极限承载能力。采用Abaqus模拟了碳纤维布修复裂纹圆管的轴压力学行为,仿真结果与试验结果比较接近,说明双线性内聚力单元和改进的三维Hashin准则可以较为准确地模拟和预测环氧树脂胶层和碳纤维层的失效。
2)不同加固试件裂纹附近以及修复层边界区域胶层的损伤是最先发生的失效形式,因此,在轴向载荷下,保证加固试件足够的粘结强度比提高复合材料层的性能更加重要。
3)碳纤维布修复效果对裂纹长度十分敏感,修复试件的承载力峰值随着裂纹长度的增加快速衰减,在同样的修复层尺寸下,裂纹长度因子
4)碳纤维布尺寸对修复效果影响较大,试件承载力峰值随着修复层数和宽度的增加而快速增加,但当碳纤维布尺寸增大到一定水平后,继续增加其层数和宽度,试件的承载能力提升非常有限,裂纹长度因子
| [1] |
SEICAMV. FRP materials for the rehabilitation of tubular steel structures for under water applications[J]. Composite Structures, 2007, 80(3): 440-450. DOI:10.1016/j.compstruct.2006.05.029 |
| [2] |
HOUSSAM T. Stress modeling of pipelines strengthened with advanced composites materials[J]. Thin-Walled Structures, 2001, 39: 153-165. DOI:10.1016/S0263-8231(00)00049-5 |
| [3] |
唐红元, 许龙, 马梦淋, 等. 外贴碳纤维复材加固不锈钢方管短柱轴心受压试验研究[J]. 工业建筑, 2018, 48(7): 188-195. |
| [4] |
SUNDARRAJA P, SRIRAM G, GANESH P Strengthening of hollow square sections under compression using FRP composites[J]. Advances in Materials Science and Engineering, 2014: 1-19.
|
| [5] |
GAO XY, BALENDRA T, KOH CG. Buckling strength of slender circular tubular steel braces strengthened by CFRP[J]. Engineering structures, 2013, 2–4(46): 547–556.
|
| [6] |
The American Society of Mechanical Engineers. Repair of pressure equipment and piping: PCC-2-2015[S]. New York: ASME, 2015: 143-195.
|
| [7] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1-2010[S]. 北京: 中国标准出版社, 2011.
|
| [8] |
GUO Y Q, SAANOUIN K, CHEROUAT A, et al. Two methodologies for the simulation of ductile damage in sheet metal forming processes[J]. Journal of Plasticity Engineering, 2002, 43(373): 3227-3237. |
| [9] |
孟利平, 程远征. 应变率和应力三轴度对Q345B 钢动态力学性能的影响研究[J]. 船舶力学, 2019, 23(10): 1210-1220. DOI:10.3969/j.issn.1007-7294.2019.10.007 |
| [10] |
朱浩, 朱亮, 陈剑虹. 应力三轴度和应变率对6063 铝合金力学性能的影响及材料表征[J]. 材料科学与工程学报, 2007(3): 358-362. DOI:10.3969/j.issn.1673-2812.2007.03.009 |
| [11] |
DENG J, LI J, WANG Y. Numerical study on notched steel beams strengthened by CFRP plates[J]. Construction and Building Materials, 2018, 163(28): 622-633. |
| [12] |
D SIMULIA. ABAQUS 6.11 Analysis User's Manual[J]. Abaqus 611 documentation, 2011, 22.22. |
| [13] |
吴振, 陈健. 基于Hashin 准则的复合材料层合结构低速冲击研究[J]. 沈阳航空航天大学学报, 2017, 34(5): 12-20. DOI:10.3969/j.issn.2095-1248.2017.05.002 |
 2022, Vol. 44
2022, Vol. 44
