2. 江苏科技大学 海洋装备研究院,江苏 镇江 212003;
3. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003
2. Marine Equipment and Technology Institute, Jiangsu University of science and technology, Zhenjiang 212003, China;
3. School of Ship and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
舵是航行船舶进行操纵的重要设备,按照支撑形式分为多支撑舵、双支撑舵、半悬挂舵和悬挂舵[1]。随着船舶吨位和舵面积的不断增大,半悬挂舵的应用越来越广泛[2]。目前进行舵设计时,主要采用规范计算法进行。首先根据船体主尺度、吃水和航速等参数计算舵叶受力,经受力分析后确定舵销、挂舵臂等部位的受力和扭矩,进一步确定舵叶厚度以及舵杆、舵销的直径[3]。目前对舵的研究多集中在舵的性能和结构设计方面,对舵的波浪载荷研究较少。
在舵的性能计算和舵力估算方面,有大量的试验和经验公式可供参考。林友红[1]应用Fluent软件,基于RANS方程,针对某半悬挂舵的敞水水动力性能进行了数值预报,评估了不同舵角下半悬挂舵的挂舵臂升力、挂舵臂阻力以及舵叶对舵杆的扭矩。叶金铭等[4]对扭曲舵的剖面几何攻角进行设计,采用CFD方法分析舵的水动力性能,并经过拖曳水池的舵力测量试验加以验证,其研究结果表明,在不同的航速和舵角条件下,扭曲舵减小了直航时舵上的横向力和舵轴力矩,有利于舵和舵机的受力。王小龙[5]采用CAESES和STAR-CCM+软件分别进行舵的参数化建模和舵周流场的数值计算,基于流场信息完成舵的扭曲设计,计算结果表明,其设计的扭曲舵负压力系数峰值明显减小,并使船舶直航时舵上的横向力和对舵轴的力矩比普通舵的小得多。Cong Sun等[6]采用RANS方法分析了实尺度KCS船在自航状态下的船-桨-舵系统的瞬态载荷,并进一步对瞬态载荷进行频谱变换,分析了舵载荷的频域特征。张维鹏等[7]采用数值计算方法对KCS船和KP505螺旋桨结合下的桨-舵耦合过程进行研究,分析了舵两侧的压力偏移现象,发现压力偏移进而使舵上出现法向力和沿螺旋桨轴向的扭矩。H. Yasukawa等[8]采用模型试验,研究了船体-桨-舵相互作用下舵受到的法向力以及舵的纵向和侧向来流速度,发现在船体慢漂角小于45°时,基于来流速度计算的舵力系数接近常量。
在舵的结构设计和强度直接计算方面,甘水来[9]以某32万吨级超大型油船(VLCC)为目标,针对挂舵臂的弯曲、剪切、扭转和等效强度进行计算,对挂舵臂的设计和强度校核提供了有益的建议。田野等[3]对不同船级社规范中对舵系的相关计算要求进行研究和对比,以“渤船”第五代苏伊士油船舵装置设计为基础,对直舵杆型式的半平衡悬挂舵进行计算。邓先国[10]对50000 t无限航区自航半潜船的舵系开展满足Ice Class B冰区加强要求、水密性要求以及破冰要求的舵叶和舵杆的设计。郝恒[11]提出对于波浪冲击引起舵的水动力载荷,应通过海况资料分析得到动力载荷系数,舵的设计水动力载荷应当为动力载荷系数与正常工作载荷之积,但在实际计算时难以确定动力载荷系数。
通过以上文献回顾发现,在舵力数值计算和基于规范进行设计时,主要针对航行状态的船舶,对船体系泊在位状态下舵受到的波浪载荷研究鲜有报道。本文针对系泊状态FSO(海洋石油121号)遭遇极端波浪时的舵载荷进行研究,分析舵叶在实际海况下的作用力。受2020年第20号台风影响,海洋石油121号在作业时,舵叶与舵杆之间发生20°左右的滑移,影响避台航行。因此系泊在位状态下船舶的舵系波浪载荷应当引起关注。
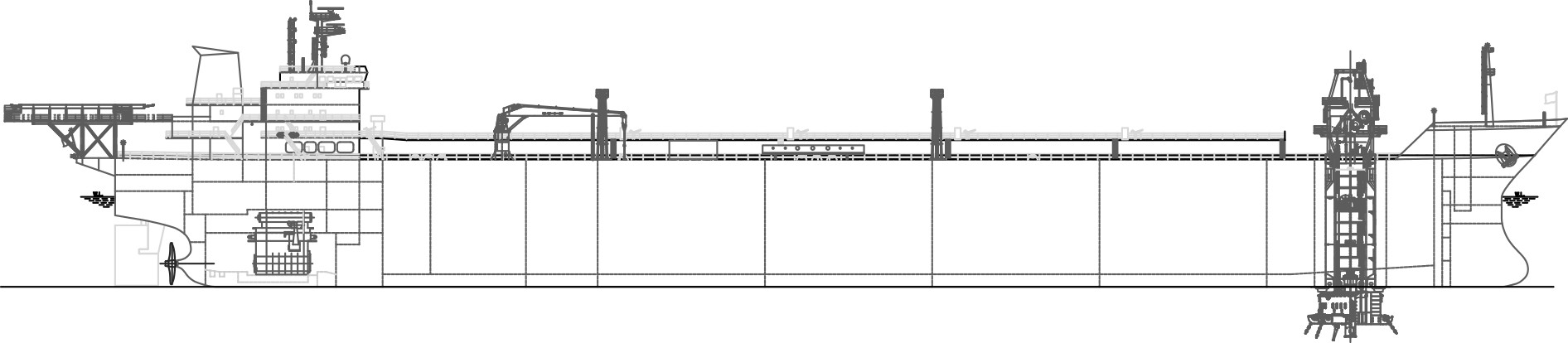
1 船体和舵结构尺度 1.1 船体参数海洋石油121是一艘具有自航能力,采用可解脱单点系泊的FSO,作业水深约106~150 m,具备油气水生产处理、原油储存和外输功能,船体总布置如图1所示,船体主尺度如表1所示。FSO采用内转塔式单点系泊,该FSO服役于陆丰油田,为了满足自航要求,保留了原有舵设备。
|
图 1 海洋石油121总布置 Fig. 1 General layout of “Haiyang shi you 121” |
|
|
表 1 海洋石油121主尺度参数 Tab.1 Main scale parameters of offshore oil 121 |
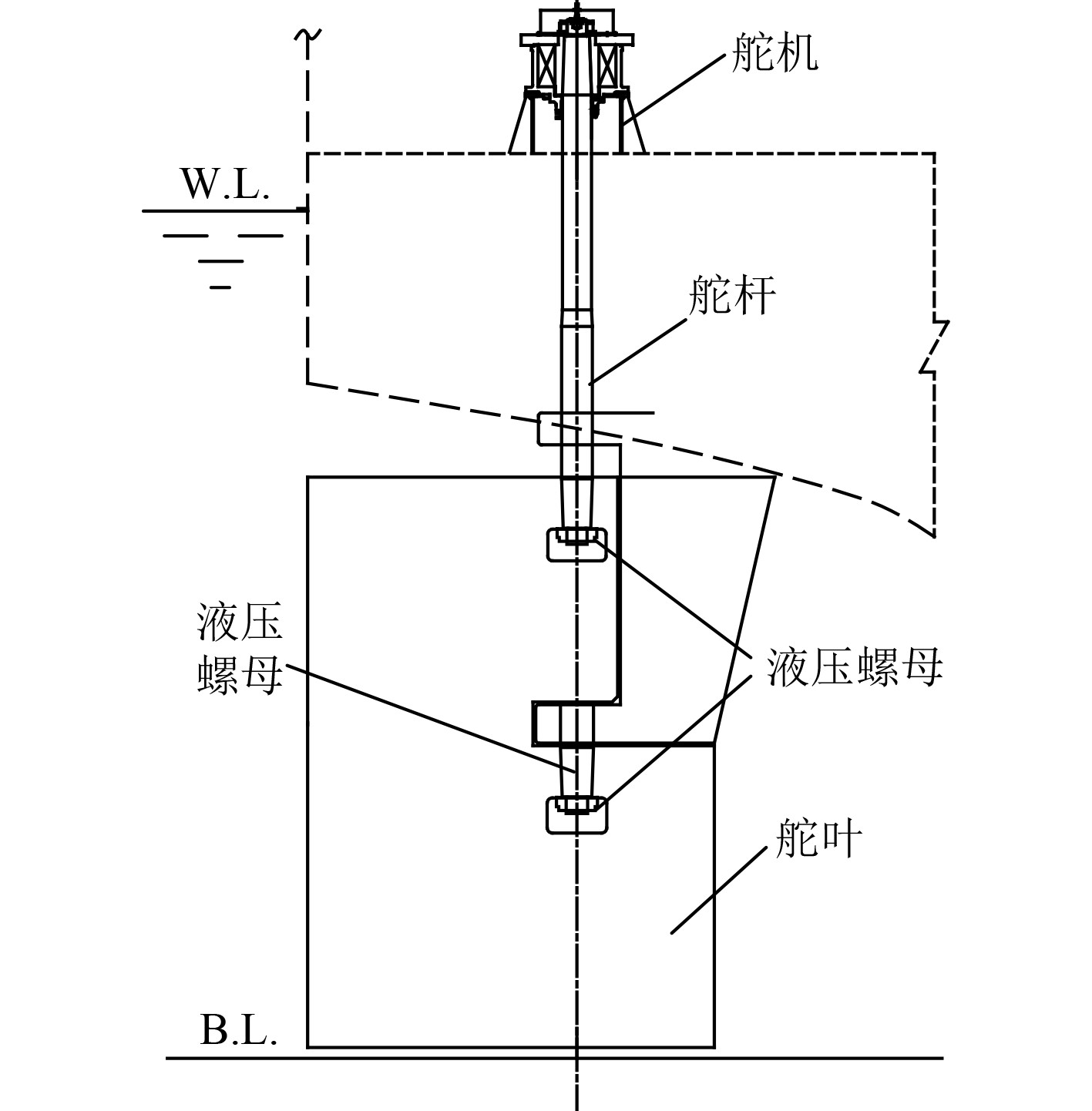
本船舵系采用半悬挂方案,舵叶上部通过舵杆插与挂舵臂连接,舵叶下部通过舵销与挂舵臂连接,舵机与舵杆连接,舵叶下半部分呈悬挂状,舵系布置和三维模型如图2和图3所示。该舵系统主要由舵机、舵叶、舵杆、舵销、舵承和液压螺母等关键构件组成。舵杆与舵机、舵杆与舵叶均采用锥体连接,依靠液压螺母的压紧力使椎体和承座间产生很大的摩擦力,通过摩擦力的作用使三者固定。
|
图 2 舵设备布置图 Fig. 2 Rudder equipment layout |
该舵叶的高度为10.4 m,下端宽度为7.4 m,上端宽度为5.64 m,舵叶下端在基线上0.2 m,舵叶面积为67.1 m2。挂舵臂下端距离基线高度为5.5 m,挂舵臂高度为4.9 m,其上部宽度为2.81 m。舵叶和挂舵臂尺寸见图4,舵系主要参数如表2所示。按照中国船级社规范[12]计算得到的正车和倒车扭矩分别为1757.3 kN·m和1148.9 kN·m。
|
|
表 2 舵设备主要参数 Tab.2 Main parameters of rudder equipment |

|
图 3 舵系结构三维模型 Fig. 3 3D model of rudder system structure |

|
图 4 舵叶及挂舵臂尺寸 Fig. 4 Dimensions of rudder blade and rudder horn |
FSO处于系泊状态时,船体会对舵区域的波浪起到较大的遮蔽效应,按照经验,船体与波浪的遭遇角越小,船体对舵所在位置的波浪遮蔽效应越明显,舵受到的波浪载荷也越小,因此在进行舵载荷计算时应先确定船体在实际海况下可能发生的最大首摇角。本文采用Aqwa软件建立目标FSO水动力模型和系泊模型,计算解脱海况下船体与波浪可能发生的最大首摇角,作为舵载荷直接计算时船体与波浪的遭遇角。
根据FSO船体说明书,船体与系泊系统解脱时的临界海况为7.4 m,谱峰周期为10.4 s,结合作业区环境条件,确定极限风速为24.7 m/s,流速为1.0 m/s。
FSO内转塔下方布置8根悬链式系泊缆,系泊缆呈对称径向布置在内转塔上。系泊缆绳由有档顶链、钢缆、拖地钢缆和锚链等组成,系泊缆总长为1 272 m,系泊半径为1 170.5 m。图5为海洋石油121系泊系统布置图。
|
图 5 FSO系泊布置图 Fig. 5 Mooring layout of FSO |
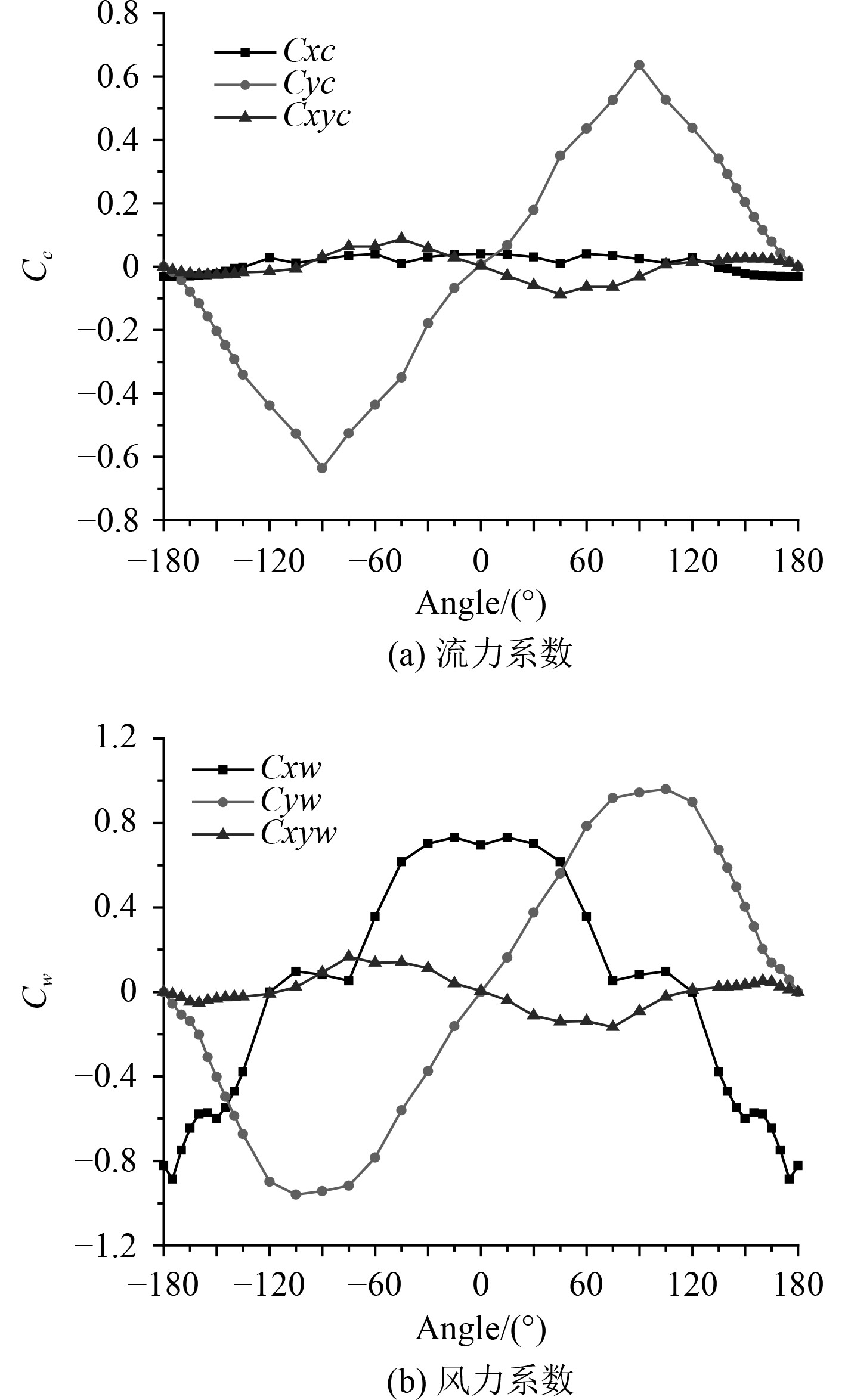
为评估FSO风载荷和流载荷大小,采用Fine/Marine软件计算得到船体的风流载荷系数如图6所示。
|
图 6 风流载荷系数 Fig. 6 Wind and current load coefficient |
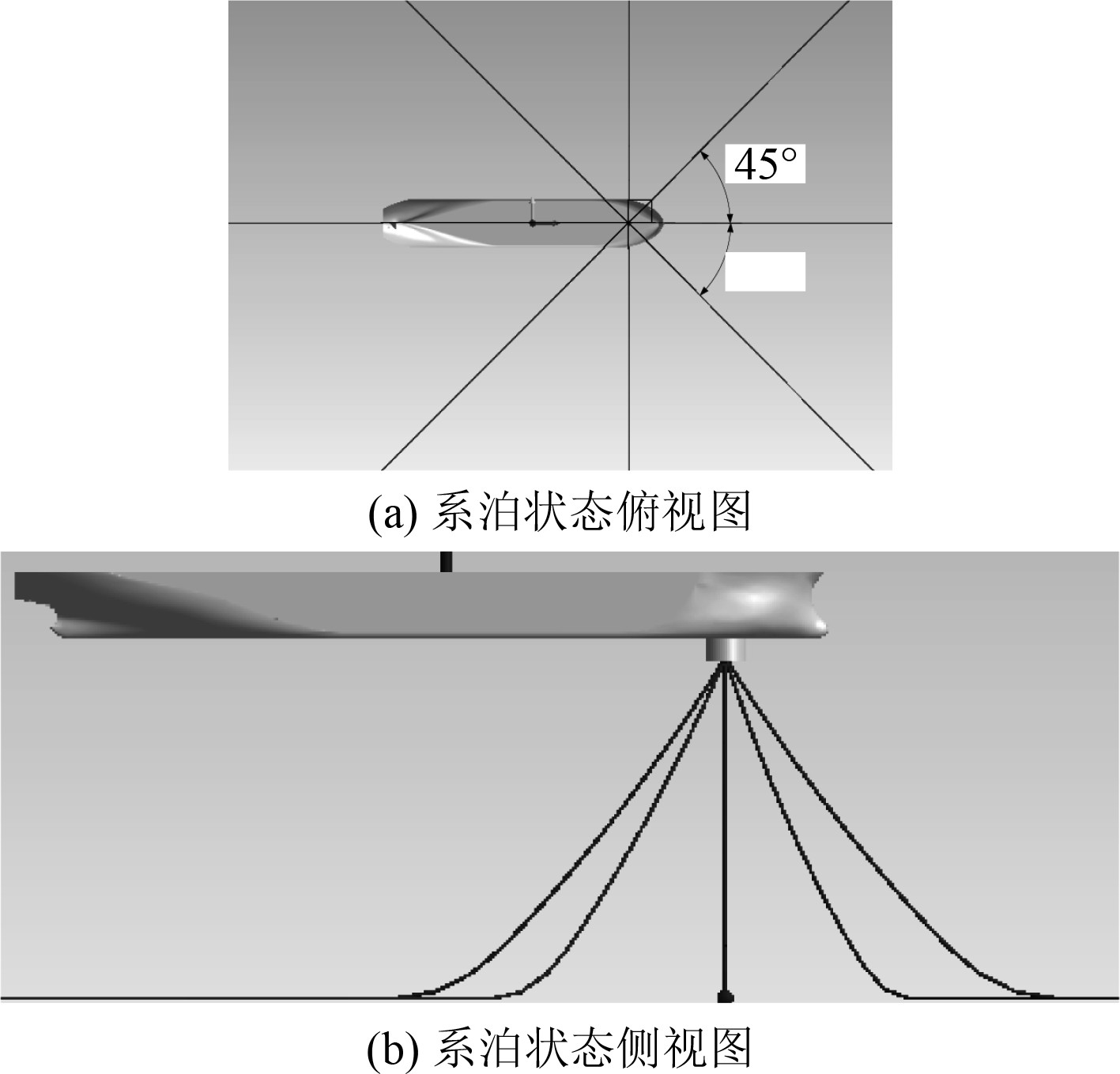
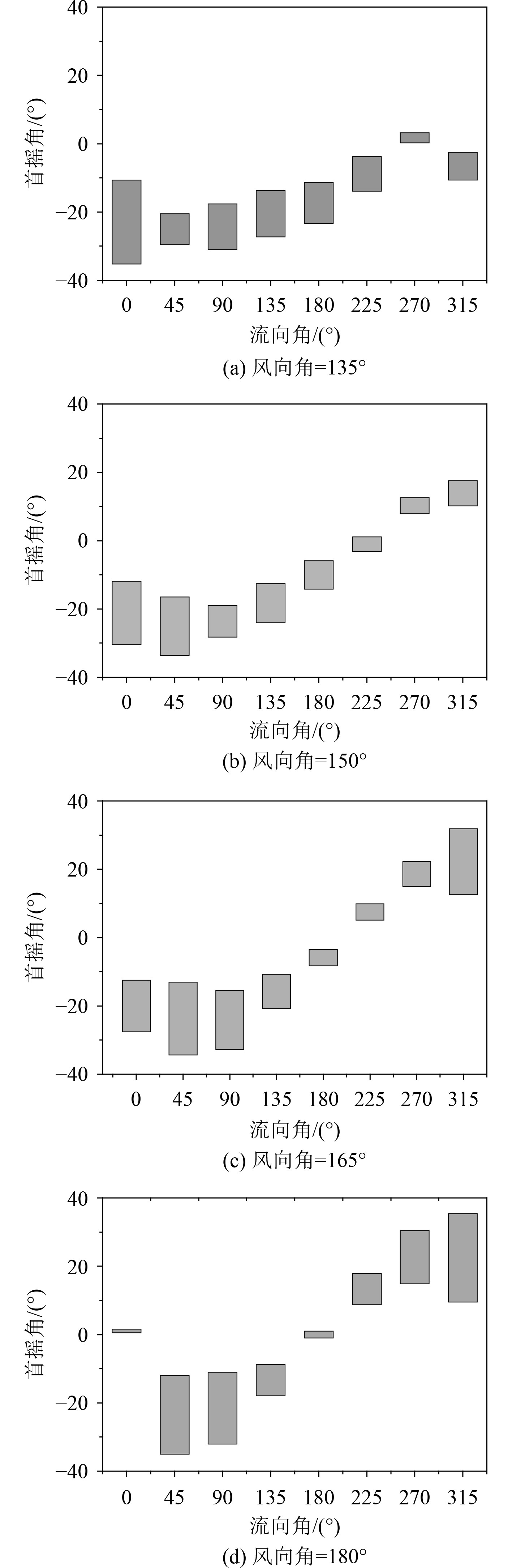
由于船体采用单点系泊,船体在风、浪、流联合作用下,会产生“风标”效应。在计算船体的首摇角时,初始浪向选择首迎浪方向,风向与浪向呈0°~45°,间隔为15°,流向与浪向呈0°~360°,流向间隔为45°,共32个风-流向组合。计算得到不同工况下船体的首摇角如图7所示。由于内转塔系泊的“鱼尾运动”效应[13-14],船体在整体进入准平衡位置后,发生首摇摆尾,首摇角会在一定范围内波动。
|
图 7 不同风-流组合下首摇角范围 Fig. 7 Yaw angle range under different wind current combinations |
从图7可以看出,在风向为180°流向为315°时,首摇最大值为35.4°,在风向为135°流向为0°时,首摇最小值为−35.2°。在该海况下FSO的首摇角达到35°左右,因此在舵载荷数值计算时船体与波浪的遭遇角取为35°。
3 数值计算方法 3.1 数值水池建立数值水池采用的缩尺比为1∶50,数值水池长11.5 m,宽10.25 m,高12 m,静水面以上的高度为3 m。水池长度为2.5倍船长,宽度为2.2倍船长,高度为2.6倍船长,水线面以下2倍船长,水线以上为0.6倍船长。数值水池坐标原点位于舵杆中心处。波浪传播方向与船体中纵剖面成35°夹角。为考虑系泊在位状态船体的运动响应,采用DFBI(dynamic fluid body interaction)[15]模型和重叠网格法对船体运动进行模拟。
为避免长时间数值计算时波浪的能量耗散,数值水池采用2个流体域进行计算,前部分为船体所在的波浪传播域,后部分为消波域,波浪传播域与消波域之间采用内部交界面连接。波浪传播域长8.5 m,船体处于波浪传播域中部,消波域长3 m。
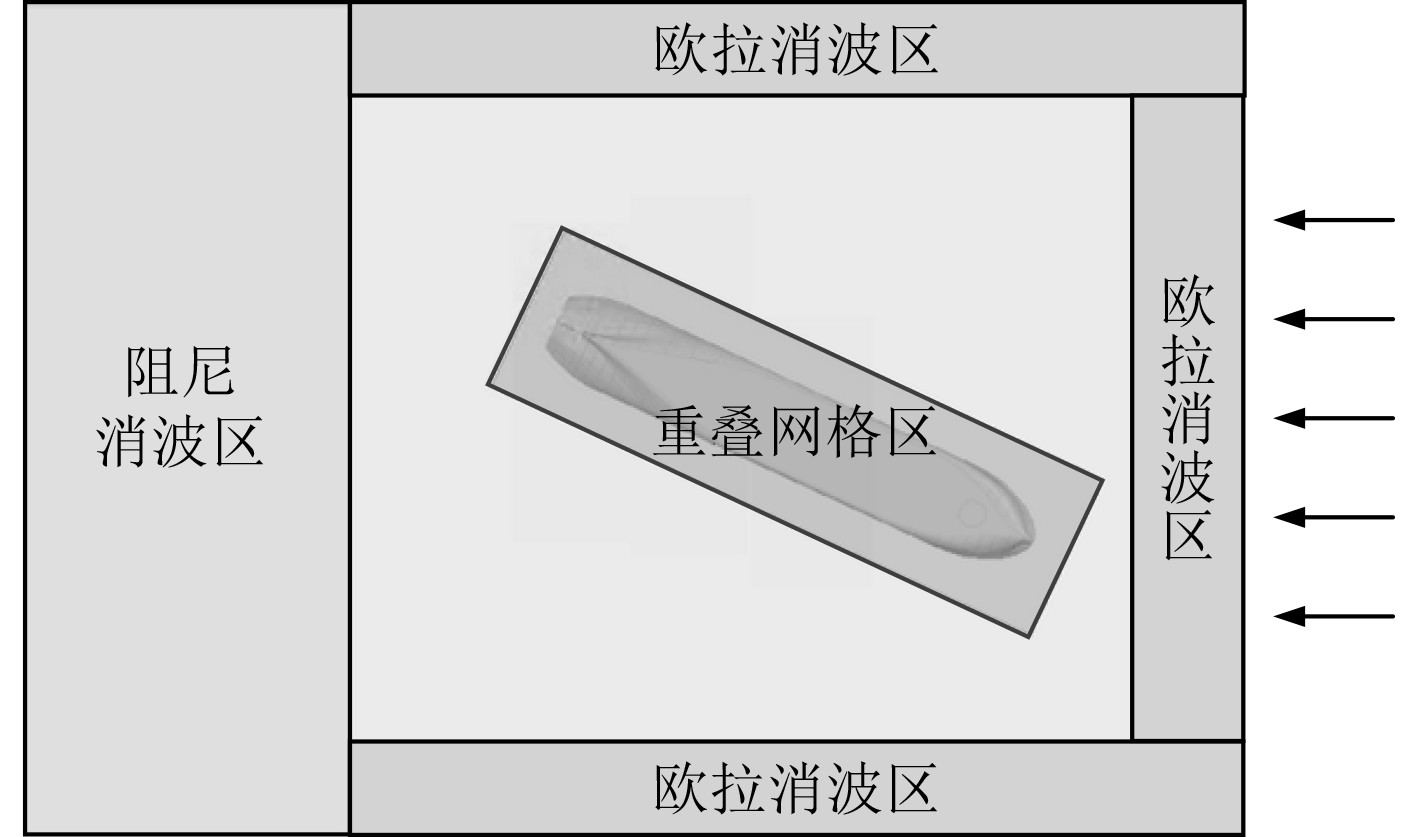
为保证造波质量,在波浪传播域前侧和两侧均设置宽度为2 m的欧拉消波区,以抑制船体两侧和造波入口处的波浪反射。整个消波区域设置为阻尼消波区,可以有效地抑制后部的波浪反射。整个计算域及重叠网格布置如图8所示。
|
图 8 三维数值水池计算域划分图 Fig. 8 Layout of calculation domain of 3D numerical wave tanker |
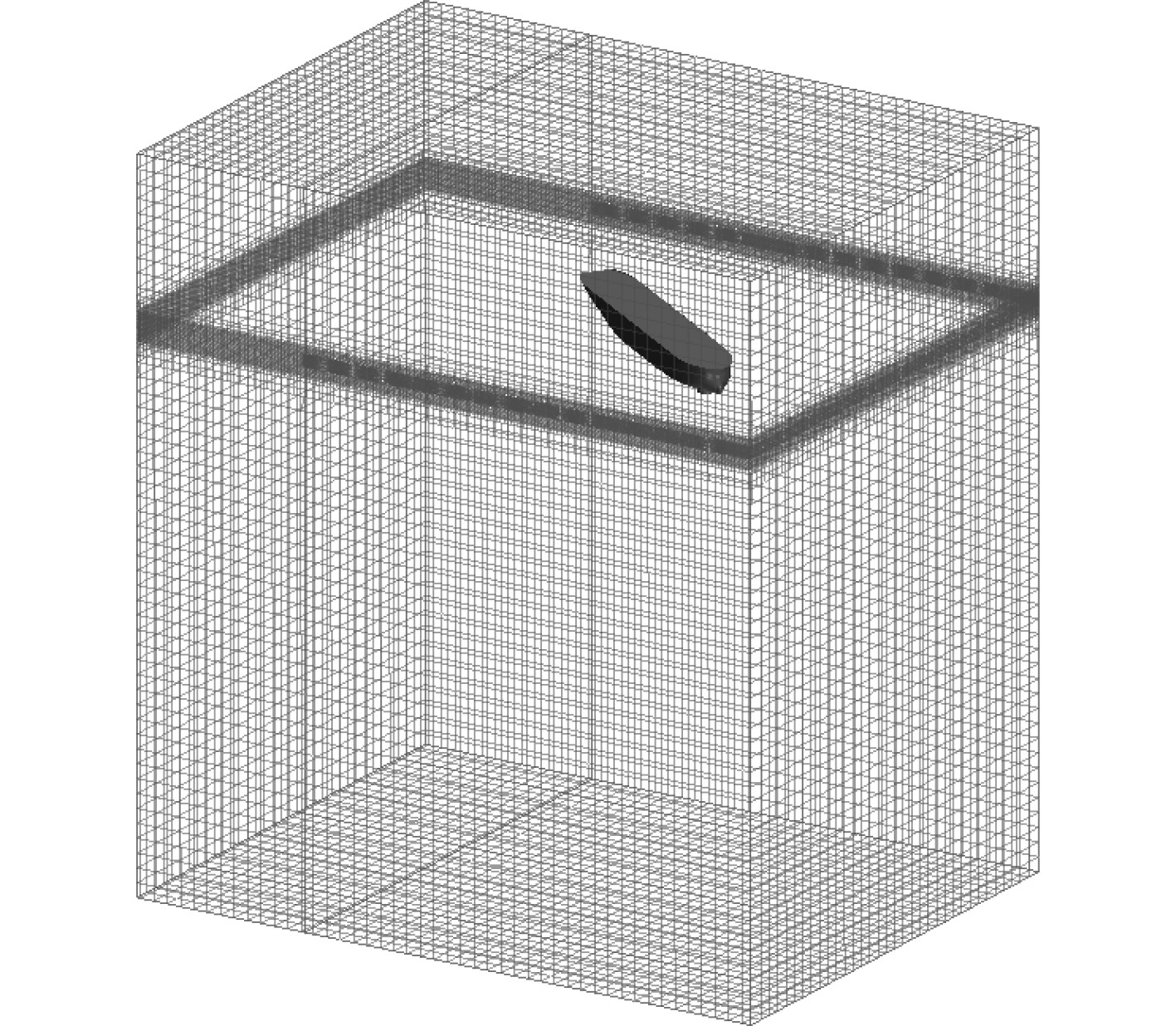
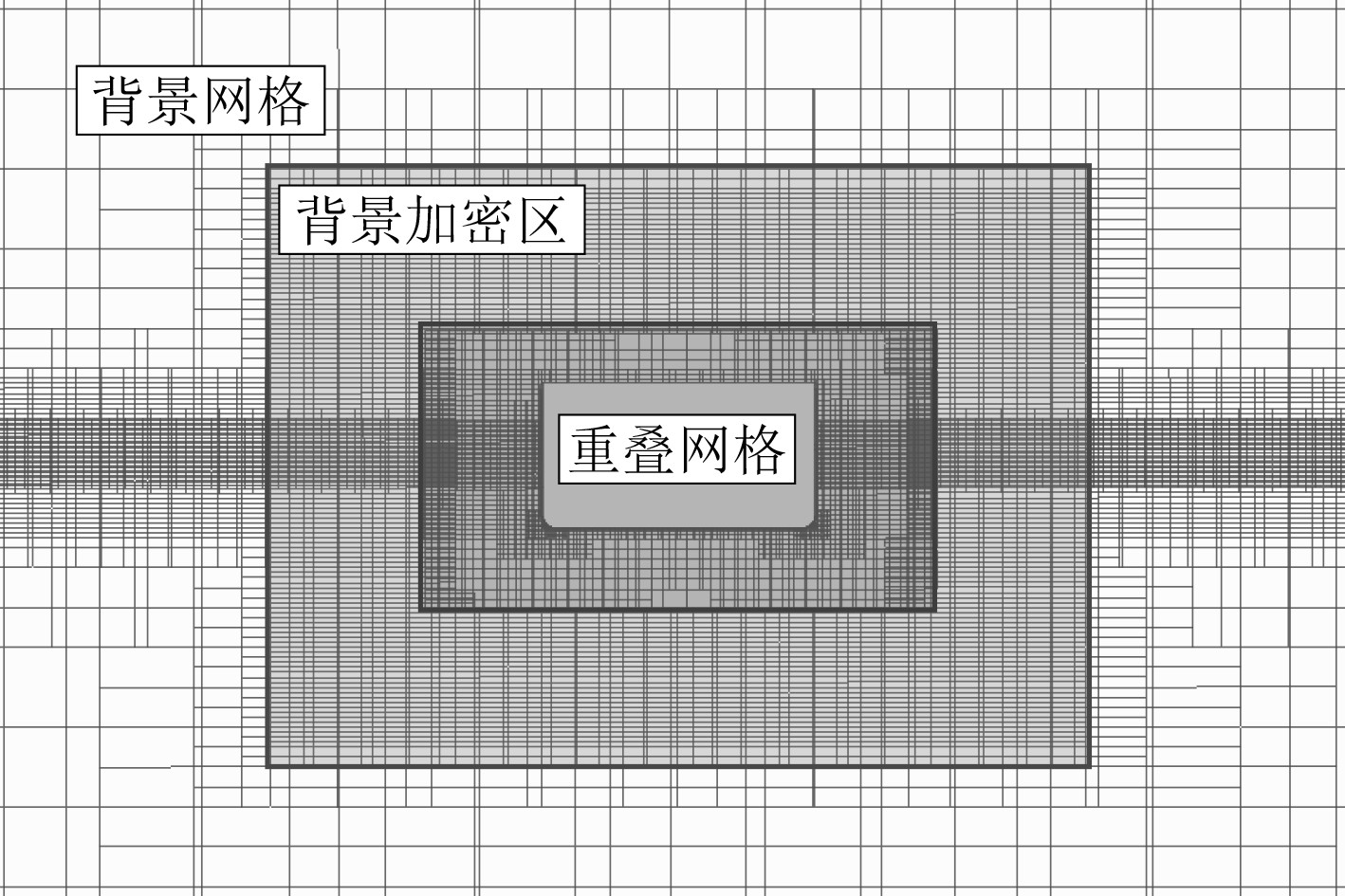
计算域最大网格尺寸为0.24 m,船体表面网格尺寸为0.03 m,在一个船长范围内约划分150个网格。自由液面区域网格最大的长宽比为2,自由液面处高度方向的最小网格尺寸为0.007 5 m(一个波高内16个网格),计算域横向和纵向方向最小网格为0.015 m。整体网格划分如图9所示,计算域横剖面重叠网格如图10所示。
|
图 9 计算域网格 Fig. 9 Mesh generation of computing domain |
|
图 10 重叠网格划分 Fig. 10 Mesh generation of overset mesh |
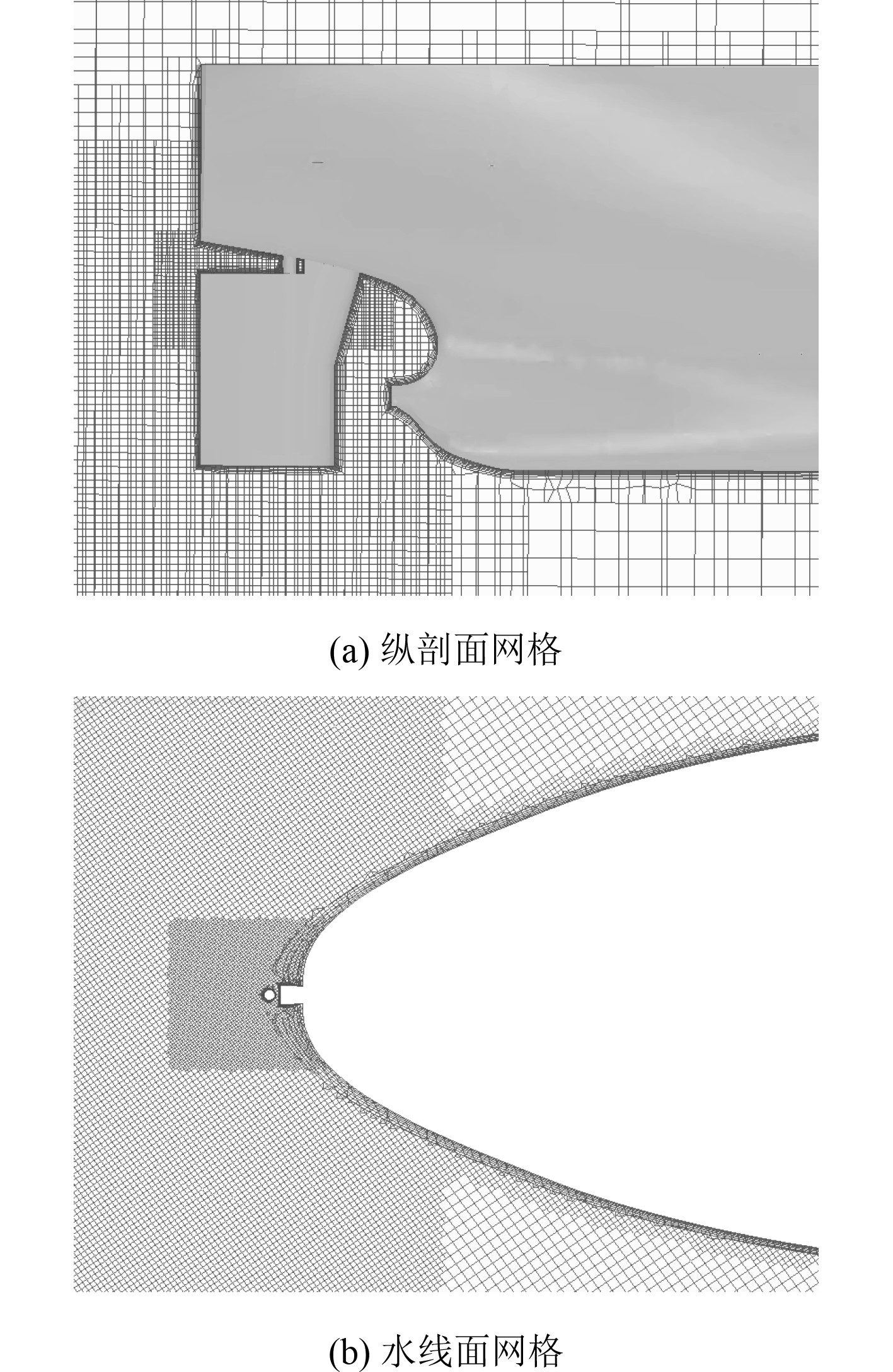
为捕捉波浪在船体尾部的绕射以及船体运动引起的辐射波面,在舵系所在区域进行空间加密,舵系区域网格细化网格如图11所示。计算网格数量为697.3万,其中重叠网格区域网格数为224.7万,背景网格数量为472.6万。
|
图 11 舵系区域网格细化 Fig. 11 Mesh refinement of rudder zone |
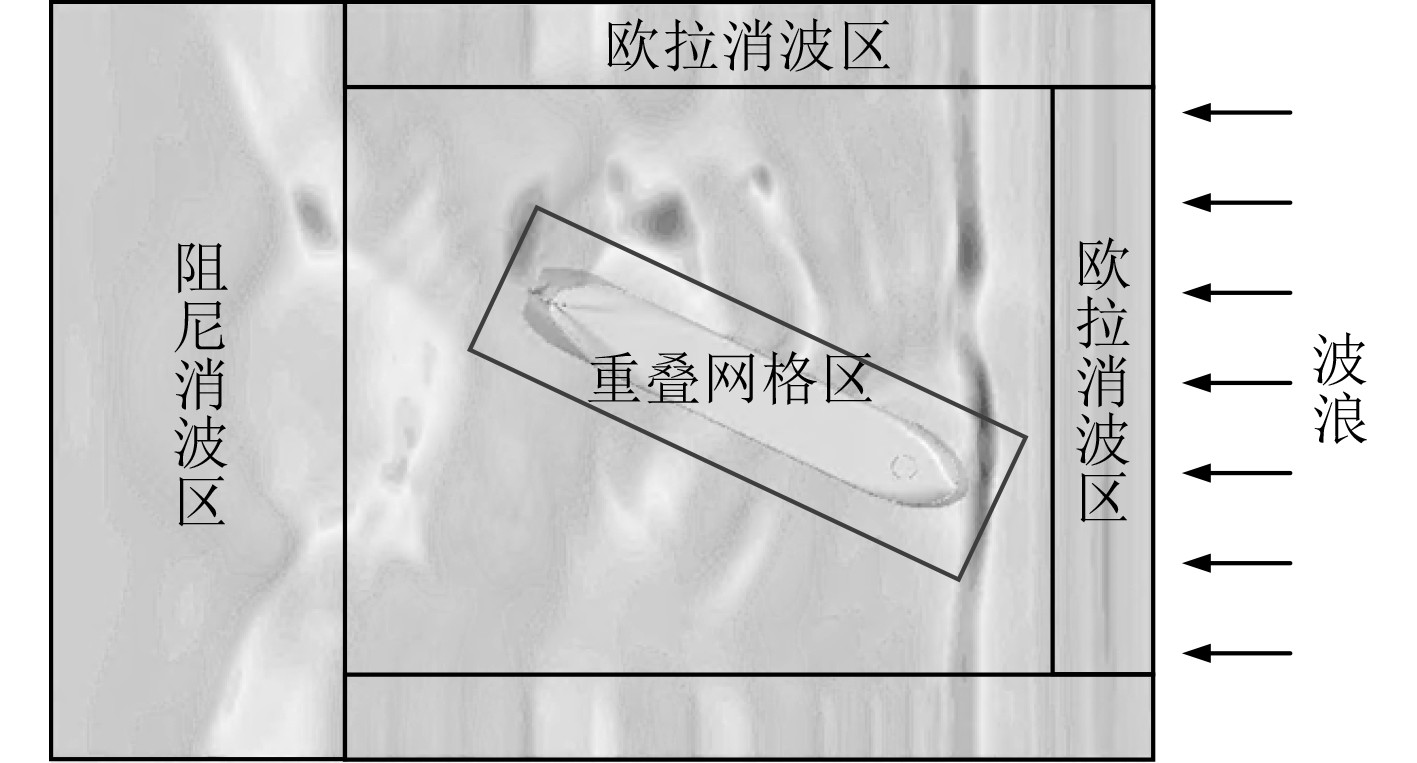
在数值水池入口处定义速度边界产生波浪,在水池入口和出口端采用欧拉重叠法进行消波处理;底部采用对应入射波的速度入口边界条件从而实现模拟无限水深环境,水池两侧采用对称边界,波浪出口设置为速度入口边界条件,顶部为压力出口边界。通过以上边界条件设置,结算得到数值水池内波面传播情况如图12所示。
|
图 12 计算域和波浪分布图 Fig. 12 Simulation domain and wave distribution |
数值计算采用三维非定常分离隐式求解,流域为不可压缩流体,采用层流模型,自由液面采用VOF方法进行追踪。动量方程、湍动能及湍动耗散率均采用二阶迎风格式,近壁处采用壁面函数法处理。采用SIMPLE压力速度耦合方式求解离散行的动量方程和离散方程,迭代得到收敛的压力场和速度场。
计算时间步长经过造波质量测试,最终选取为0.008 s。计算采用128核心,主频2.25 GHz,双路AMD EPYC 7742 CPU工作站,计算时长为424 h。
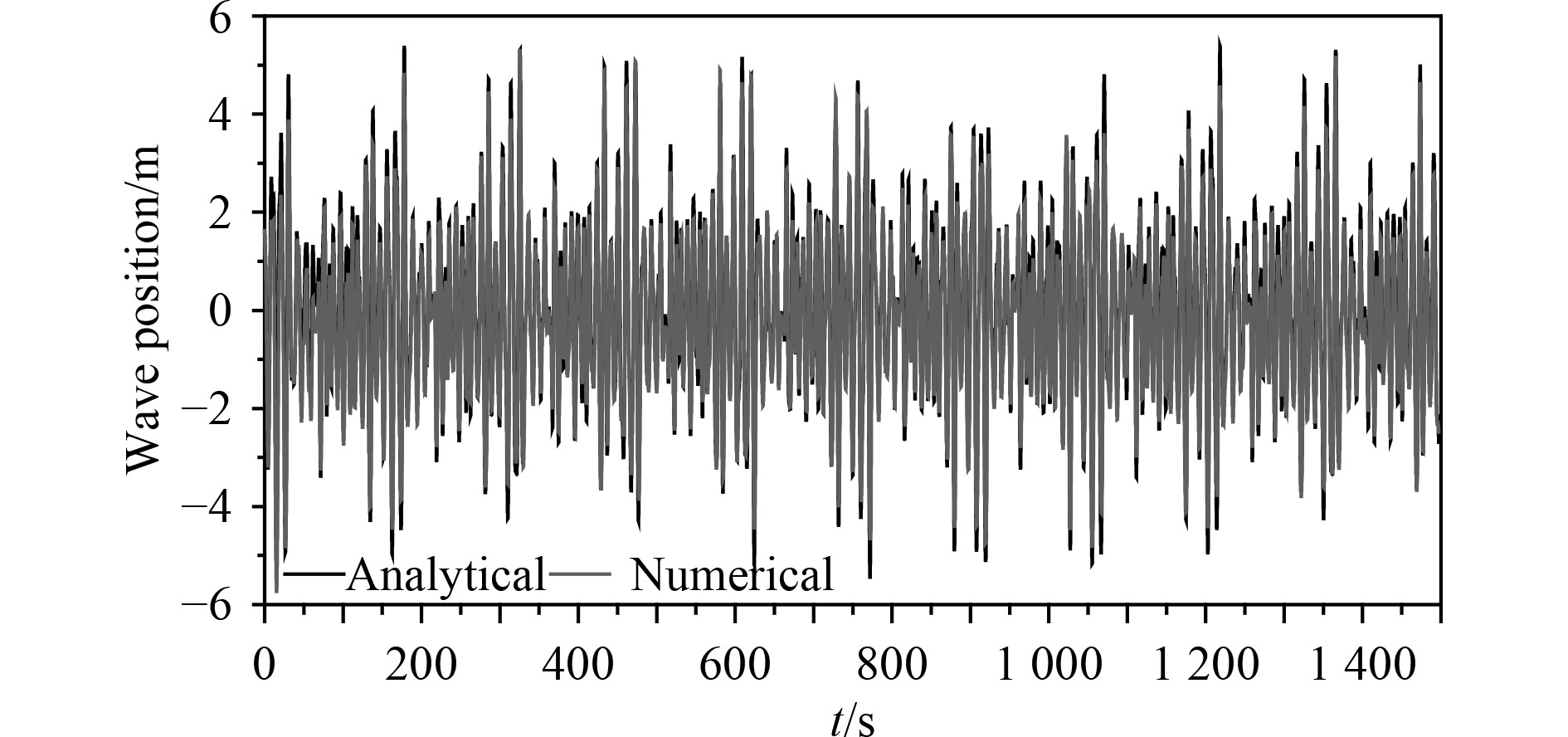
3.5 造波质量验证为验证数值水池网格划分和造波质量,在无船体状态下,监测舵杆所在位置的实际模拟波高(Numerical)与STAR-CCM+理论波高(Analytical)进行对比,有义波高为7.4 m,谱峰周期为10.4 s时波面位置理论值与数值模拟值时历曲线对比如图13所示,可以看出数值计算得到的波浪时历与理论值吻合较好。
|
图 13 波高理论值与数值模拟值对比 Fig. 13 Comparison between analytical value and numerical value of wave height |
舵叶受到的力矩是舵系设计中最重要的载荷,也是本船舵叶与舵杆发生偏移的主要影响因素,因此将舵叶绕舵杆中心的力矩进行分析,作为舵载荷校核依据。
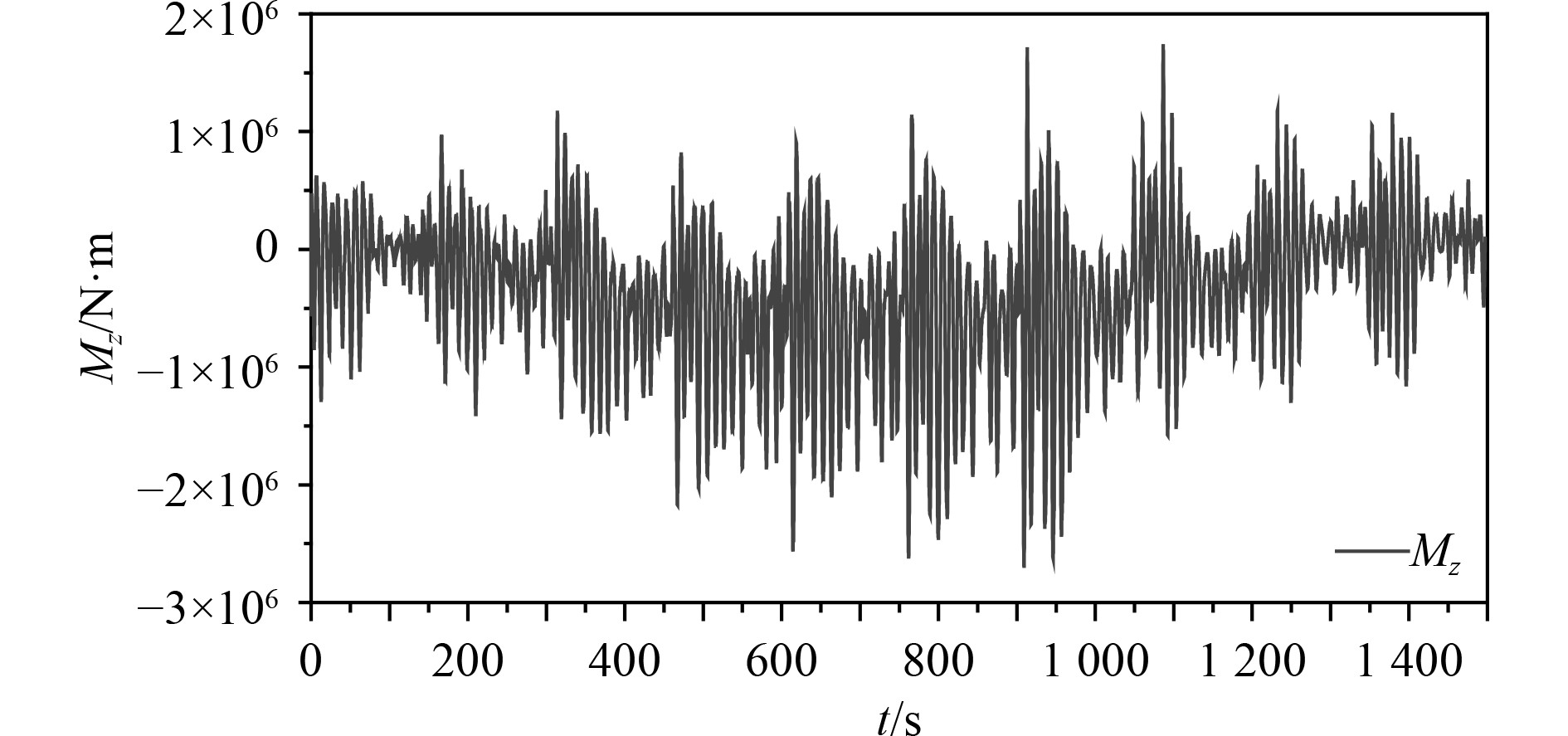
对计算载荷进行实尺度换算后,舵力矩时历曲线如图14所示。数值计算的时间为1500 s,约为25 min。可以看出最大舵力矩约为2706 kN·m,舵力矩幅值多次出现大于设计舵力矩(1757.3 kN·m)的情况。FSO在此状态下的舵力矩超出了由规范公式计算的设计舵杆扭矩。
|
图 14 舵力矩时历曲线 Fig. 14 Time history of rudder torque |
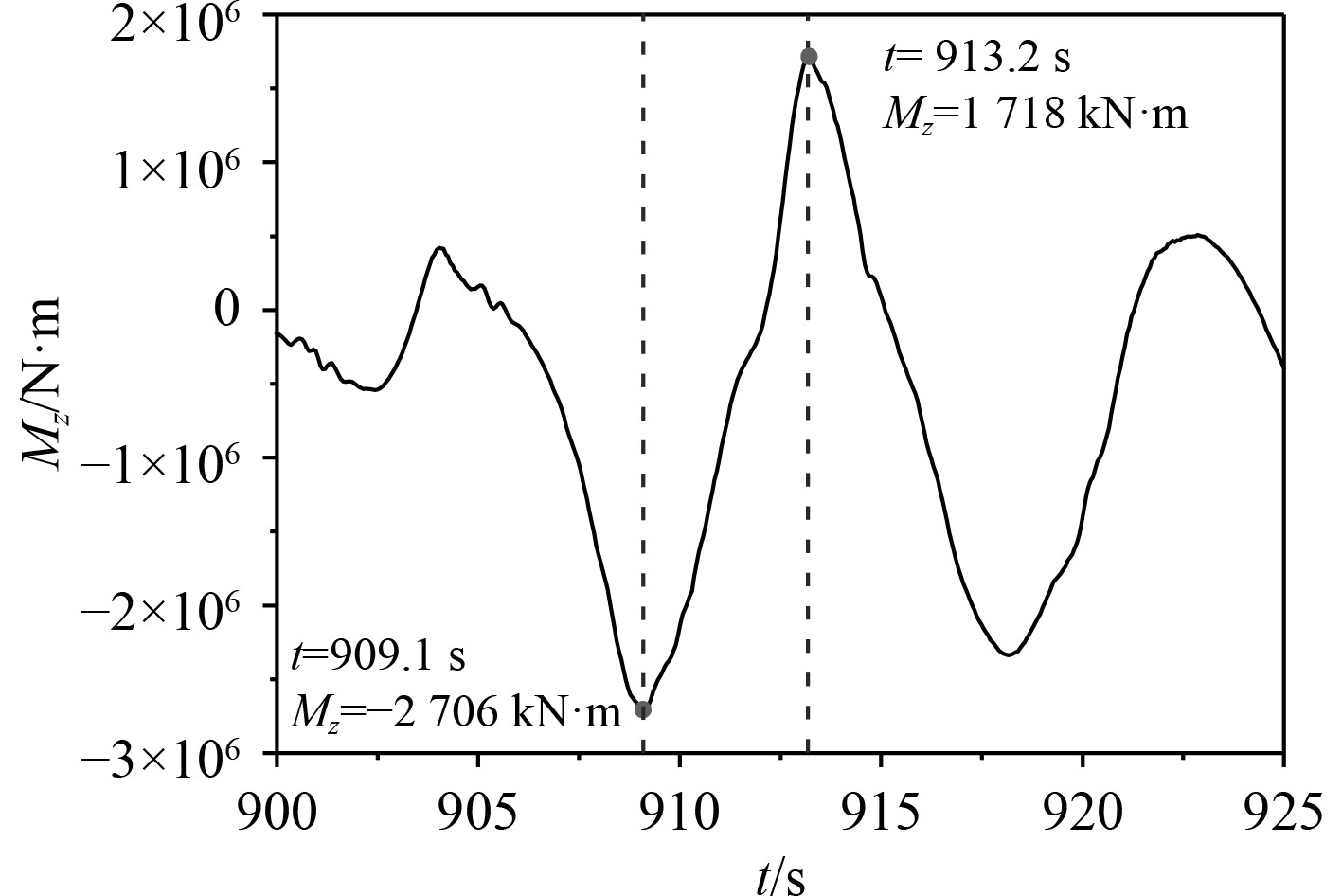
为进一步分析舵力矩的时间特征,截取900~925 s时舵力矩时历,如图15所示。可以看出,舵负向力矩最小值出现在909.1 s,此时舵力矩为2 706 kN·m,在913.2 s时,舵正向力矩出现最大值1 718 kN·m,舵力矩在4.1 s内出现了方向转变,变化幅值达到4424 kN·m。
|
图 15 900~925 s时间段舵力矩曲线 Fig. 15 Rudder torque curve during 900~925 s |
根据波浪和砰击理论,在波面附近的波浪能量较大,从而引起的砰击载荷也相对较大,本船在半载状态下舵叶上部接近平均静水面位置,且舵叶上部靠近水面区域的面积形心远离舵杆中心,造成舵力矩较大,对舵系结构安全造成威胁。为降低波浪载荷对舵系安全的影响,建议系泊作业船舶在遭遇较大波浪时,应通过调整浮态,避免舵叶暴露在水面区域或者提前撤离台风影响海域。
4.2 舵系区域波面变化本文计算状态为船体半载状态,吃水为11.01 m,此时舵叶上端在平均静水面下方0.6 m。图16为计算过程典型的舵区域波面状态,可以看到入射波浪经船体绕射后,与船体的横摇、纵摇和垂荡运动产生的辐射波浪产生进行叠加,导致舵叶附近的水面情况十分复杂,舵叶时而淹没,时而出水,波面与船体严重拍击时会出现波浪破碎。

|
图 16 舵区域典型波面状态 Fig. 16 Typical wave surface scenes of rudder zone |
通过对典型的舵面出水和入水过程分析发现:舵面出水时,上升的波面会与船体尾部发生拍击,造成波浪在挂舵臂区域产生破碎,并产生气室,水面完全淹没舵叶后,气室消失;舵面入水过程中舵叶顶部的水面下降具有一定的滞后性,导致舵叶上部短时积水。
5 结 语本文对海洋石油121FSO在遭遇恶劣海况下的首摇运动响应进行模拟,评估了船体最大首摇角,进一步计算在最大首摇角状态下和设计解脱海况下的舵力矩大小,主要结论和建议如下:
1)通过风-浪-流组合下系泊在位FSO运动响应分析发现,设计解脱工况下船体的最大首摇角达到35°左右。
2)在计算极端海况下,舵实际受到舵力矩远大于船级社经验公式的计算值,可能对舵结构造成损伤;舵叶附近的水面情况复杂,舵叶出现往复出水和入水现象,波面与船体严重拍击时会出现波浪破碎。
3)建议同类型作业船舶的舵设计需考虑在位工况船体运动和吃水变化,尽量让舵叶远离轻载水线,并尽量减少舵面积。操作方面,建议该类浮式装置在台风来临前进行必要的压载以使船体吃水最大或提前撤离台风影响海域。
| [1] |
船舶设计实用手册(舾装分册)[M]. 北京: 国防工业出版社, 2013.
|
| [2] |
林友红. 半悬挂舵的敞水水动力性能与舵力预估方法研究[J]. 舰船电子工程, 2015, 35(10): 142-147. DOI:10.3969/j.issn.1672-9730.2015.10.037 |
| [3] |
田野, 张文斌, 王平, 等. 舵系直接计算法设计[J]. 造船技术, 2020(4): 34-37. |
| [4] |
叶金铭, 王威, 于安斌, 等. 抗空化扭曲舵的设计及其水动力性能分析[J]. 上海交通大学学报, 2017, 51(3): 314-319. DOI:10.16183/j.cnki.jsjtu.2017.03.011 |
| [5] |
王小龙, 樊涛, 王璐玭. 悬挂式扭曲舵的设计和计算[J]. 船舶工程, 2020, 42(6): 49-54. |
| [6] |
SUN C, WANG C, SUN S, et al.. Numerical prediction analysis of the fluctuating pressure and rudder force of full-scale hull-propeller-rudder system[J]. Ocean Engineering, 2018, 147: 580-590. DOI:10.1016/j.oceaneng.2017.11.006 |
| [7] |
张维鹏, 胡健, 陈崇格. 船-桨-舵结合下的舵两侧载荷偏移现象分析[C]//第三十一届全国水动力学研讨会论文集(下册), 2020: 456−461.
|
| [8] |
H YASUKAWA, ISHIKAWA T, YOSHIMURA Y. Investigation on the rudder force of a ship in large drifting conditions with the MMG model[J]. Journal of Marine Science and Technology, 2021, 1-18. |
| [9] |
甘水来, 吴幼奇, 靳盼盼. 大型船舶挂舵臂设计研究[J]. 船舶工程, 2019, 41(4): 17-22+113. DOI:10.13788/j.cnki.cbgc.2019.04.04 |
| [10] |
邓先国, 党长青, 葛兴伟. 50000吨半潜船满足冰区加强舵系设计研究与优化[J]. 广船科技, 2021, 41(3): 12-16. DOI:10.3969/j.issn.2095-4506.2021.03.005 |
| [11] |
郝恒, 杜一凡, 曹海斌. 船舶舵设备可靠性设计[J]. 舰船科学技术, 2019, 41(1): 48-53. DOI:10.3404/j.issn.1672-7649.2019.01.009 |
| [12] |
中国船级社. 钢质海船入级规范[S]. 2001. 北京.
|
| [13] |
KAASEN K E, LUDVIGSEN H , NYGAARD I , et al. Theoretical and experimental study of heading stability and heading control of a turret-moored FPSO[C]//Asme International Conference on Ocean, 2017.
|
| [14] |
Sanchez-Mondragon J, AO Vázquez-Hernández, Cho S K, et al. Yaw motion analysis of a FPSO turret mooring system under wave drift forces - ScienceDirect[J]. Applied Ocean Research, 2018, 74: 170-187. DOI:10.1016/j.apor.2018.02.013 |
| [15] |
Siemens Digital Industries Software, STAR-CCM+ Documentation Version 16.03[M], Texas: 2020.
|
 2022, Vol. 44
2022, Vol. 44
