结构物入水砰击过程是一个复杂的强非线性问题,广泛存在于船舶、航空航天、武器装备等领域[1]。结构物以较高速度入水时会遭受流体强烈的砰击,虽然砰击过程持续的时间较为短暂,但会给结构带来很大的瞬时压力峰值和加速度。
国内外很多学者围绕结构入水砰击过程开展了广泛研究,在公开发表的文献中,Von Karman[2]和Wagner[3]是较早开展入水问题研究并建立理论模型的学者。Watanabe[4],Howison[5]等通过匹配渐进法对Wagner理论模型进行修正,对自由液面与物体表接触处的流场进行局部射流分析,在平板假设的基础上引入部分非线性边界条件,针对Wagner计算模型求解物面压力分布时边缘处的奇异性问题,其通过内域解和外域解匹配的方法给出了一种解决方案。Dobrovol'skaya[6]通过研究二维楔形体零加速度速入水问题,较为完整地给出了对称楔形体匀速入水过程中受力的相似解。Zhao等[7]运用非线性边界元算法求解了该匀速入水问题,求解精度有所提升。卢炽华[8]运用边界元算法求解了U形带外飘船体截面的入水砰击问题,研究了典型船体剖面入水过程中水动力特性,为工程设计提供参考。Wu等[9]进一步用边界元法分析了二维楔形体的自由入水问题,在楔形体尖点触水瞬时取相似解为流域初始解来解决速度、压力等物理量剧烈变化带来的求解发散。Xu等[10-11]求解了对称楔形体以恒等速度斜向入水的水动力问题,后又将该方法成功拓展到楔形体的多自由度自由入水问题。Sun等[10]用非线性边界元算法对三维物体入水过程进行研究,以圆锥体为算例给出了较为准确的计算结果。
仿真研究入水问题的常用有限元软件有Ls-dyna,Dyrtan,Fluent,Abaqus等,主流算法有拉格朗日算法、欧拉算法、ALE算法、SPH算法等。陈震[13]用Dytran仿真求解了平板结构入水砰击问题,研究了入水过程捕捉空气形成的空气垫对平板入水过程的影响。朱显玲[14]使用Ls-dyna求解了夹心平板结构入水载荷并据此对夹心结构参数进行优化。陈光茂[15]使用SPH方法对楔形体入水过程进行仿真,分析了斜升角、入水角等参数对砰击载荷的影响规律。云忠[16]使用STAR-CCM+软件对跨介质飞行器入水过程的动力学性能进行计算,为飞行器结构X设计和入水参数选择提供指导。Wang S和Soares C G用Ls-dyna分别对二维对称楔形体[17]、二维非对称楔形体[18]、三维椭球体结构[19]入水过程进行了仿真求解,对物面压力分布、压力时历、结构整体砰击力、自由液面及压力场进行了有效模拟。曹正林[20]和段芳[21]分别用Ls-dyna和Dytran软件求解了三体船结构入水问题,验证了两软件求解负杂曲线结构入水问题的能力。
结构入水过程中涉及自由液面的排挤、扭曲、飞溅、破碎等复杂物理现象,理论和数值计算时通常需要引入一些假设对实际问题进行诸多简化。为得到砰击过程中更为真实的载荷及结构响应规律,并对理论和数值算法解加以验证,落体试验方法在研究过程中还是不可或缺的手段之一。孙辉[22]针对6个不同角度和厚度组合的楔形体模型开展了一系列落体砰击试验,研究模型入水过程中的加速度和结构响应规律,开展了结构响应对各参数的敏感度分析。Zhao[23]开展了斜升角30°的V型楔形体入水冲击试验,测量了模型加速度及表面砰击压力,验证了其非线性边界元算法的数值计算结果。莫立新[24]通过开展4个不同刚度板架结构的落体砰击试验,研究了结构刚度对砰击载荷及结构动响应的影响规律。张哲[25]在射弹入水试验中初步验证了PVDF压电薄膜测量入水压力的可行性。
本文对求解结构入水问题的基于边界元算法的数值计算方法、基于任意拉格朗日-欧拉耦合算法的数值仿真方法、自由落体入水砰击试验3种常用的研究手段进行了综合对比研究。分别用3种方法对楔形结构自由入水过程进行研究,给出了砰击压力沿物面的分布、典型点处的压力时历、物体运动特性并进行了对比分析。
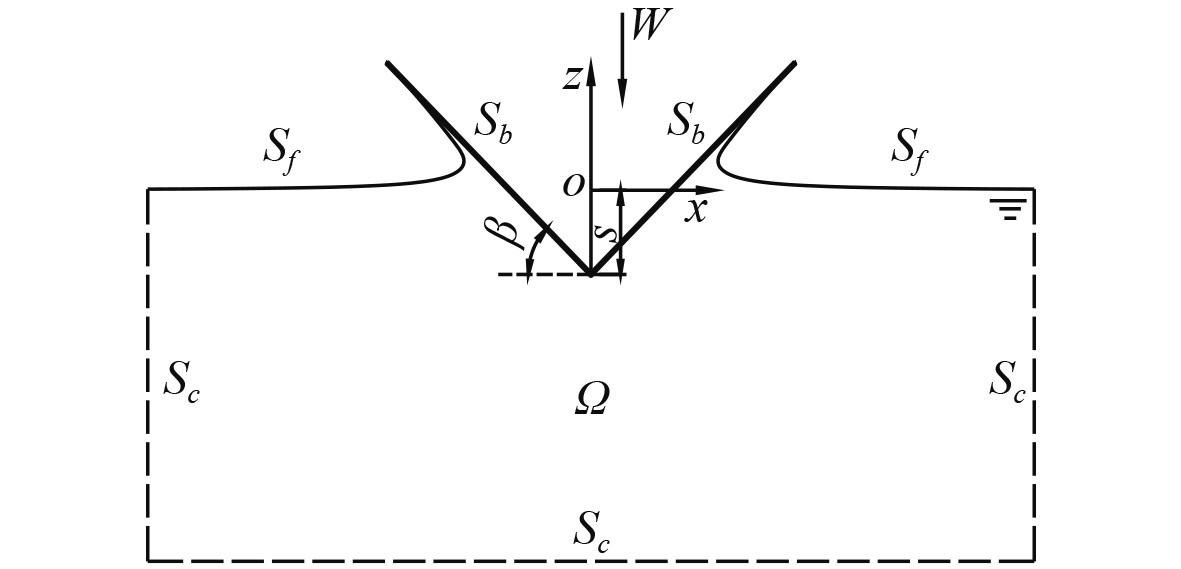
1 基于边界元算法的数值计算方法 1.1 数学模型建立如图1所示的数学模型,其中o-xz为模型坐标系,原点位于结构入水前水平面与楔形体对称线的交点处,坐标轴方向如图1所示。W为楔形体实时入水速度,是关于时间t的函数,方向定义为向下为正;s为楔形体尖点在自由液面以下的深度即入水深度,同样是关于时间t的函数;β为楔形体底升角;Ω为整个流体域;Sb为楔形体物面;SF为自由液面;Sc为远场边界条件。
|
图 1 典型结构入水问题示意图 Fig. 1 Schematic diagram of water entry problem |
流体满足无粘、无旋、不可压缩的假设,则流体速度势
| $ {\nabla ^{\text{2}}}\phi {\text{ = 0}}。$ | (1) |
在楔形物面Sb上满足物面不可穿透边界条件:
| $ \frac{{\partial \phi }}{{\partial n}} = - W{n_z} 。$ | (2) |
式中,n=(nx,nz)为物面的单位外法向量。
瞬时自由液面SF上满足的欧拉形式运动学和动力学自由面边界条件分别表示如下:
| $ \frac{{\partial \zeta }}{{\partial t}} = {\phi _z} - {\phi _x}{\zeta _x} ,$ | (3) |
| $ \frac{{\partial \phi }}{{\partial t}} = - \frac{1}{2}\left( {\phi _x^2 + \phi _z^2} \right) - gz 。$ | (4) |
式中:
假定在无穷远处流场不受扰动,在远场边界SC上满足如下边界条件:
| $ \frac{{\partial \phi }}{{\partial n}} \to 0,\;\;\;\;\;\;\;\sqrt {{x^2} + {z^2}} \to \infty。$ | (5) |
为保证计算精度和计算速度的协调统一,引入如下拓展坐标系o-αβ:
| $ \varphi = \phi /sW \text{,} \alpha = x/s , \beta = z/s , s = \int_{}^{} {W{\rm{d}}t}。$ | (6) |
在拓展坐标系内速度势
| $ \frac{{\partial \varphi }}{{\partial n}} = - W{n_\beta } 。$ | (7) |
式(3)和式(4)中的自由面边界条件变为:
| $ \frac{{\partial s\overline \zeta }}{{\partial s}} = {\varphi _\beta } - {\varphi _\alpha }{\overline \zeta _\alpha } ,$ | (8) |
| $ \frac{{\partial sW\varphi }}{{W\partial s}} = - \frac{1}{2}\left( {\varphi _\alpha ^2 + \varphi _\beta ^2} \right) - \frac{{gs\beta }}{{{W^2}}}。$ | (9) |
其中
远方控制面上依然满足:
| $ \frac{{\partial \varphi }}{{\partial n}} \to 0,\;\;\;\;\;\;\;\sqrt {{\alpha ^2} + {\beta ^2}} \to \infty。$ | (10) |
通过格林公式可以将拓展坐标系下的Laplace 方程转化为积分表达形式:
| $ A(p)\varphi (p) = \int {\left[ {G(p,q)\frac{{\partial \varphi (q)}}{{\partial {n_q}}} - \varphi (q)\frac{{\partial G(p,q)}}{{\partial {n_q}}}} \right]} {\rm{d}}{s_q}。$ | (11) |
式中:
| $ G(p,q) = \frac{1}{2}\ln \left[ {{{\left( {{x_p} - {x_q}} \right)}^2} + {{\left( {{z_p} - {z_q}} \right)}^2}} \right]。$ | (12) |
为了求解式(12),将流体边界离散成一定数量的线性单元,假设离散为n份,认为单元内速度势线性分布,即可用线性插值函数近似表示离散单元内部的速度势φ和速度势在法线方向的方向导数φn。将它们的线性插值函数代入方程(12),整理得到:
| $ \left[ {{{\boldsymbol{H}}}} \right]{}_{n' \times n'} \cdot {[\varphi ]_{n' \times {\text{1}}}}{\text{ = }}\left[ {{{\boldsymbol{G}}}} \right]{}_{n' \times n'} \cdot {[{\varphi _n}]_{n' \times {\text{1}}}} 。$ | (13) |
式中:n为整个边界上划分节点个数,
ALE算法是计算流固耦合问题时比较适用的算法之一,其综合吸收了2种算法的优势又规避了单一算法的劣势[26]。
定义材料移动速度为v,网格移动速度为u,则w=v-u表示相对运动速度。ALE算法满足如下守恒方程[26]:
质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} = - \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} - {w_i}\frac{{\partial \rho }}{{\partial {x_i}}},$ | (14) |
动量守恒方程
| $ \rho \frac{{\partial {v_i}}}{{\partial t}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} + \rho {b_i} - \rho {w_i}\frac{{\partial {v_i}}}{{\partial {x_j}}},$ | (15) |
能量守恒方程
| $ \rho \frac{{\partial E}}{{\partial t}} = {\sigma _{ij}}\frac{{\partial {v_i}}}{{\partial {x_j}}} + \rho {b_i}{v_i} - \rho {w_j}\frac{{\partial E}}{{\partial {x_j}}}。$ | (16) |
式中:ρ为流体密度;b为作用在流体上的单位体积力;E为流体比内能;σij为应力张量。
2.2 软件计算流程Ls-dyna提供了ALE算法平台,本文仿真使用MSC.PATRAN进行建模,使用LS-Prepost进行关键字修改、耦合定义及后处理,提交Ls-dyna求解器进行计算。
Ls-dyna中通过空材料加状态方程来描述水和空气2种流体材料的物理及力学特性[27]。
理想气体用关键字*EOS_LINAR_POLYNOMIAL定义的线性多项式状态方程模拟,表达式如下:
| $ P = [{C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3}] + [{C_4} + {C_5}\mu + {C_6}{\mu ^2}] \cdot {\rho _0}e。$ | (17) |
式中:C0~C6为多项式拟合系数;ρ0为空材料*MAT_NULL关键字里定义的材料参考密度;ρ为实时密度,
水用*EOS_GRUNEISEN关键字中定义的Gruneisen状态方程描述,表达式如下:
| $ \begin{split}\left\{\begin{array}{l}P=\dfrac{{\rho }_{0}{C}^{2}\mu [1+(1-\dfrac{{\gamma }_{0}}{2})\mu -\dfrac{a}{2}{\mu }^{2}]}{[1-({S}_{1}-1)\mu -{S}_{2}\dfrac{{\mu }^{2}}{\mu +1}-{S}_{3}\dfrac{{\mu }^{3}}{{(\mu +1)}^{2}}}+\\ \qquad({\gamma }_{0}+a\mu ){\rho }_{0}e,\quad\quad\quad\quad\quad\,\,\,压缩状态,\\ P={\rho }_{0}{C}^{2}\mu +({\gamma }_{0}+a\mu ){\rho }_{0}e,\quad\quad \,膨胀状态。\end{array} \right. \end{split}$ | (18) |
式中:ρ0为水密度;C为水中声速;S1,S2,S3,γ0为状态方程系数系数;a是对γ0的一阶体积修正。
为与其他2种方法的结果进行对比并节省计算时间,本文计算时将入水结构定义为刚体材料(*MAT_RIGID)。结构物与流体的耦合关系通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID来实现的,通过罚函数法实现流固界面力学参量的传递,建模时需注意单元法向量的统一。这种耦合定义方式建模时不需要固体网格与流体网格间共节点,这极大地降低了建模的复杂程度。
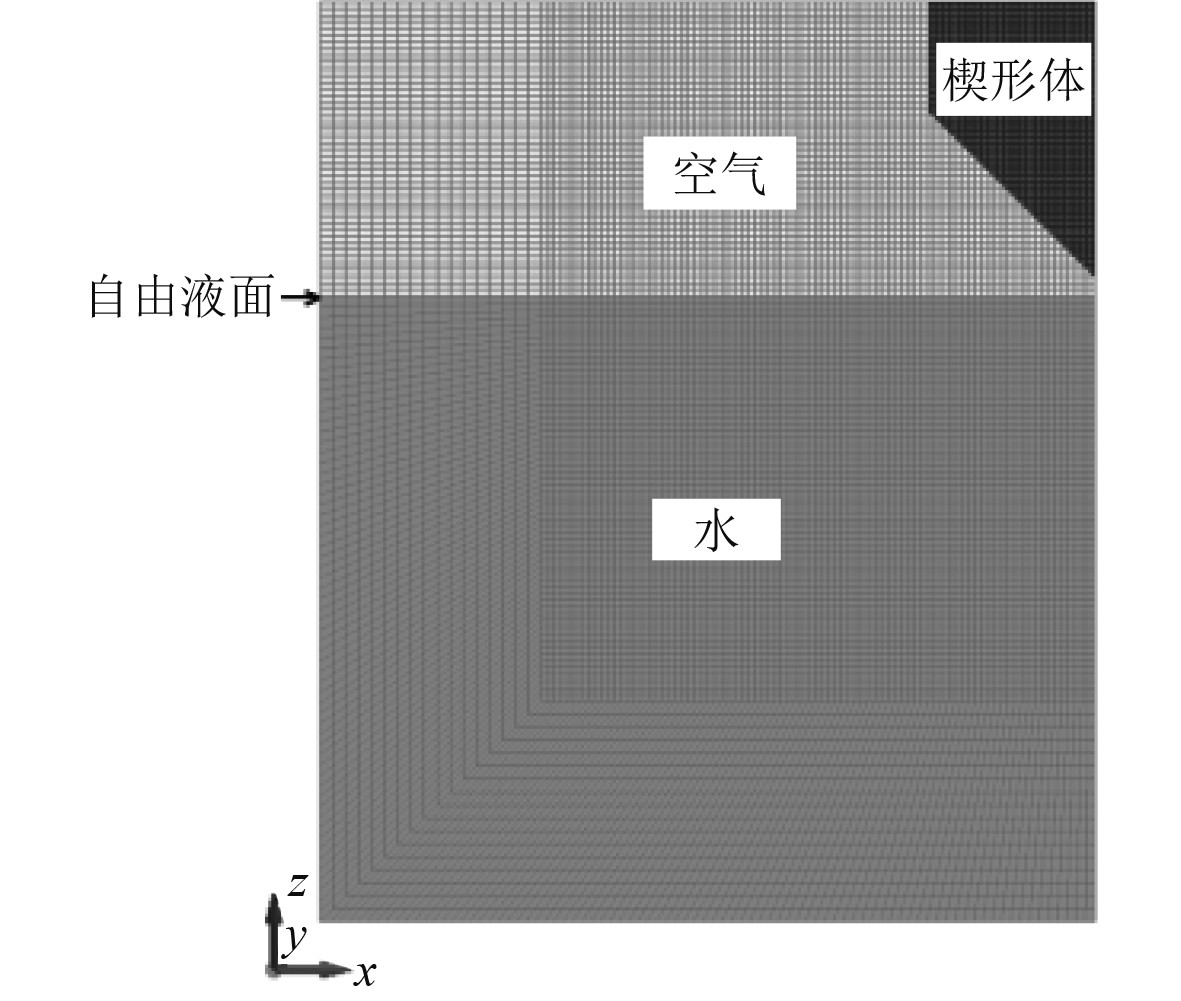
在Ls-dyna中建立楔形体入水问题数值仿真模型如图2所示,采用二维仿真方式,在楔形体长度方向只设置一层单元。入水结构物用Lagrange单元离散,赋予刚体属性;流体域离散为欧拉实体单元并划分为两部分,分别赋予空气、水属性,2种流体交界面上共节点。为在保证计算精度的前提下提升计算速度,水和空气在远离核心区的范围网格划分逐渐变粗,核心区的网格密度最终由求解前开展的网格收敛性分析确定。同时利用本文求解问题的对称性,仅建立一半模型进行仿真计算,在对称面上建立对称面边界条件。初始时刻楔形体位于水面以上较小高度处,根据自由落体计算给其以一定的初速V0便可模拟试验中不同高度工况下的自由落体入水过程。
|
图 2 典型结构物入水问题仿真模型 Fig. 2 Simulation model of water entry problem |
边界条件设置:二维仿真中约束了欧拉单元节点在图2坐标系y轴方向的运动。流体域除对称面外的其余3个面施加无反射边界条件以免反射回波影响计算结果,对称面上设置刚性墙并限制刚体的运动自由度,计算过程中考虑了重力场的影响。
3 落体砰击试验方法落体入水试验是将试验件提升至水平面以上一定高度后释放,在重力作用下试验件获得所需的入水速度,与水发生相互作用来模拟砰击现象。本次试验在长宽深为108 m×7 m×3.5 m的水池上开展,其上设计有一套完整的落体试验装置实现试验件起吊、释放并保证所需入水姿态。本文试验的楔形体模型由某型舰船舷侧板架结构缩比设计而来,试验模型底升角为45°,长宽高为1.5 m×0.9 m×0.75 m,整个模型(含配重)总重553 kg,在模型中横剖面自上而下布置了5个压力测点,模型及测点布置局部放大图见图3。试验中通过压力传感器监测入水过程中结构底部外表面受到的砰击压力,通过拉绳式的位移传感器测量模型入水过程中的位移变化过程,取微分可得到模型入水过程中的速度。试验中每个工况至少重复3次以验证试验开展过程的稳定性。

|
图 3 试验模型 Fig. 3 Test model |
分别使用3种方法对图3所示的楔形结构入水载荷和运动特性进行计算。给出入水结构与水平面接触时刻速度V1=4.427 m/s工况下的结果对比,并将此时刻定为时间零点,P1~P5五个测点的具体位置见图3(b)。
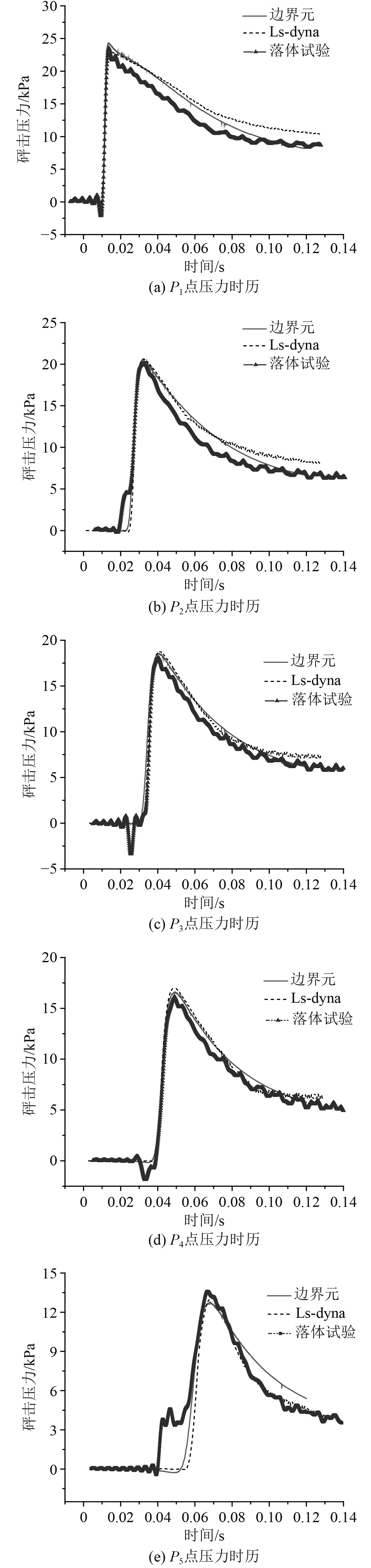
将3种方法得到的各测点砰击压力信号统一时间轴绘制得到图4,可以看出Ls-dyna仿真、BEM算法和落体入水试验3种方法得到的结果一致性良好,砰击压力信号整体趋势、持续时间、压力峰值等关键参数都较为一致,具体的压力峰值差异在6.5%以内。
|
图 4 砰击压力时历对比 Fig. 4 Comparison of slamming pressure history |
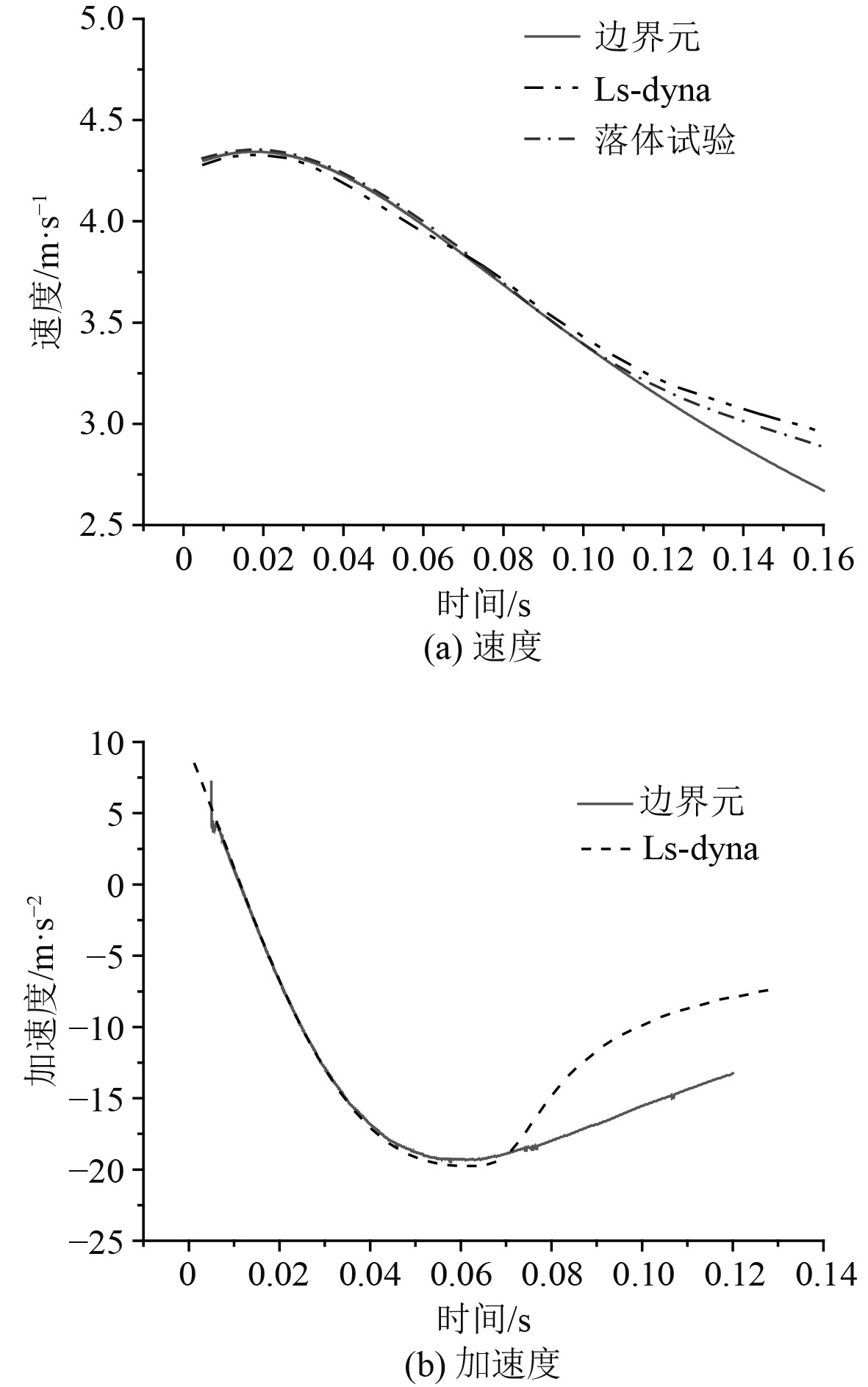
用3种典型方法对入水过程中的结构速度进行求解或测量,结果见图5(a)。可见在0.075 s之前三者吻合很好,0.075 s之后边界元求解结果开始偏离Ls-dyna仿真结果和试验数据。这是由于在边界元算法求解时引入了物面无限大的假设,忽略了射流越过楔形体“肩部”后真实存在的复杂的流动分离现象,图5(b)中的加速度曲线表现出了同样的规律。Ls-dyna软件为复杂结构入水问题提供了方便的建模、求解方式,相比边界元算法对所求解入水结构复杂程度的包容性较强。
|
图 5 入水过程中速度及加速度对比 Fig. 5 Comparison of model velocity and acceleration history during water entry |
图6给出了边界元算法得到的P3点砰击压力达峰时刻的楔形体位置、自由液面形状、砰击压力物面分布情况。可见此时刻入水深度s=0.174 9 m,P3点处于未受扰动的水平面之上,物面压力在楔形结构物尖点和入水激起的射流根部取得极值,其中第1个极值中包含了楔形体尖点的静水压力,第2个极值对应的物面尚处于水面之上,体现的全部是砰击带来的的物面载荷。第2个极值之后物面压力逐渐下降,在楔形体半宽L等于(1.4~1.6)倍入水深度s范围内迅速下降,当L=0.295 4 m(约1.7倍入水深度)时压力下降为0,即砰击载荷作用在半宽L小于1.7倍入水深度的物面范围内。

|
图 6 自由液面及物面压力分布 Fig. 6 Free surface and surface pressure distribution |
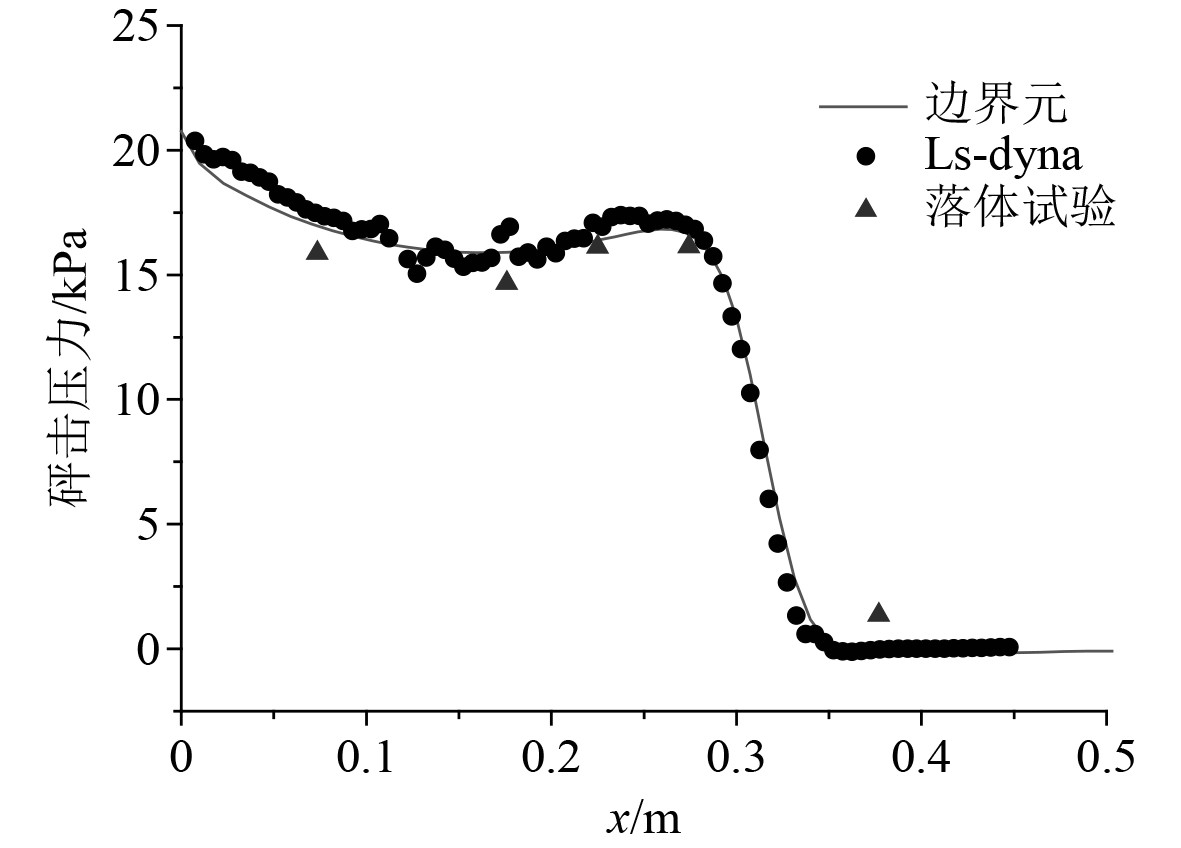
图7给出了3种方法得到的楔形体入水0.05 s(入水深度s=0.214 7 m)时刻的物面压力分布情况,整体来看3种方法求解结果一致性较好。边界元算法中通过拓展坐标变换的方法,网格划分更为灵活,可得到比较光滑的物面压力曲线;Ls-dyna仿真过程中需要在结构网格上分布设置足够多的压力监测点,在各点压力时历数据中提取关注时刻的砰击压力,进而拟合出关注时刻的物面压力分布;落体试验中则是通过在试验件上布设的点式压力传感器测量得到,要想通过试验方法准确拟合出砰击压力沿物面的分布则需要布置大量的点式压力传感器,试验成本会大幅上升。
|
图 7 物面压力分布对比 Fig. 7 Comparison of surface pressure distribution |
图8给出了6个典型时刻Ls-dyna仿真方法和边界元模拟方法得到的自由液面发展情况对比,t1~t5分别是P1~P5监测点压力达到峰值的时刻,t6为入水深度为0.35 m的时刻。从前5个时刻可见对于对砰击载荷影响较大的射流根部及以下区域,2种方法的结果较为一致,从第6个时刻可见当射流根部越过楔形体肩部位置时2种方法的仿真差异变大,原因如前所述是因为边界元算法中未考虑流场越过楔形体肩部时复杂变化,从图9试验高速摄像也可以看出,射流到达肩部之前流动比较规则,越过肩部以后,射流开始出现破碎、飞溅,这给边界元数值方法求解带来困难,相对而言Ls-dyna采用的ALE算法可以更为真实的模拟这种现象。

|
图 8 Ls-dyna仿真与边界元法自由液面对比 Fig. 8 Free surface comparison between Ls-dyna simulation and BEM |
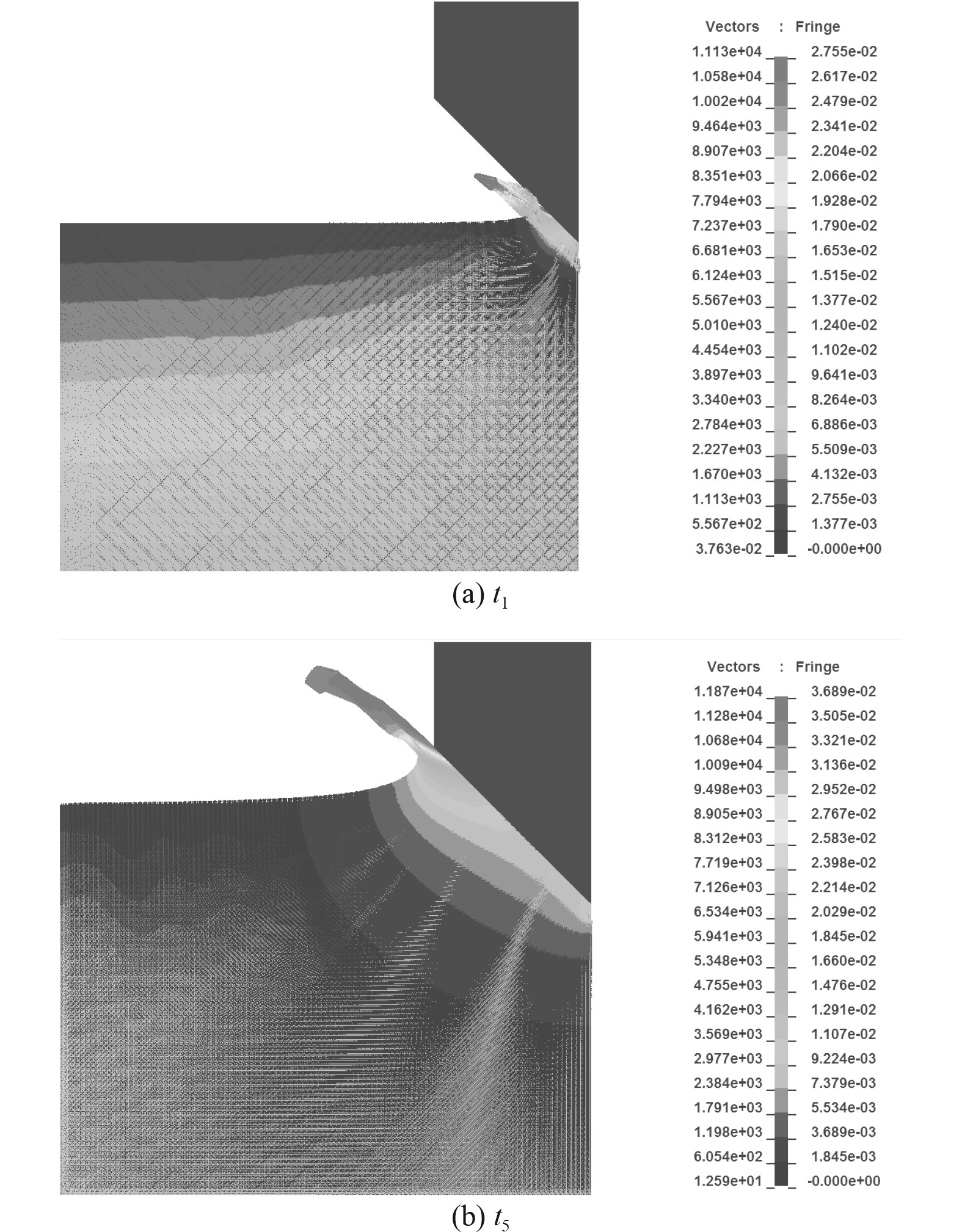
图10为Ls-dyna仿真得到的典型时刻流体域压力场及速度场云图。可以看出入水过程中流体域中压力较大的区域集中在物面上,流体速度较大的位置集中在射流区域。

|
图 9 落体试验过程中射流发展情况 Fig. 9 Development of jet flow during free falling test |
|
图 10 典型时刻压力场及速度场仿真结果 Fig. 10 Simulation results of pressure field and velocity field at typical time |
本文介绍了3种求解结构入水问题的典型技术途径,通过对比分析得出以下结论:
1) Ls-dyna仿真方法和边界元数值模拟方法均可对楔形结构入水砰击问题进行有效求解,通过与试验结果对比,验证了2种方法求解入水载荷及运动特性的精度。
2) Ls-dyna仿真方法和边界元数值方法均可有效模拟出楔形体结构入水后的自由液面变化情况,Ls-dyna可对流动分离、复杂形状结构入水等数值方法较难处理的问题给出满意的求解。
3) 底升角为45°的楔形结构入水过程中砰击载荷作用范围为楔形半宽<1.7倍入水深度的区域。
4) 随着入水深度的增加,射流根部逐渐“健壮”,表现在压力上是从下至上各测点取得峰值时处于静水平面之上的高度逐渐增大,但各测点压力峰值由于结构入水速度的降低会逐渐降低。
| [1] |
孙玉松, 周穗华, 张晓兵. 非周期性入水冲击问题研究进展[J]. 舰船科学技术, 2020, 42(1): 6-10. SUN Yu-song, ZHOU Sui-hua, ZHANG Xiao-bing. Research progress on the nonperiodic water-entry impact problem[J]. Ship Science and Technology, 2020, 42(1): 6-10. DOI:10.3404/j.issn.1672-7649.2020.01.002 |
| [2] |
VON KARMAN T. The impact on seaplane floats during landing [R]. NACA Technical note no. 321, 1929.
|
| [3] |
WARNER H. Uber stoss-und gleitvorgange und deroberflache von flussigkeiten [J]. ZAMM. 1932, 12(4): 193−215.
|
| [4] |
WATANABE I. Analytical expression of hydrodynamic impact pressure by matched asymptotic expansion technique[J]. The Japan Society of Naval Architects and Ocean Engineers, 1986, 77-85. |
| [5] |
HOWISON S D. Incompressible water-entry problems at small deadriseangles[J]. Journal of Fluid Mechanics, 1991, 222(222): 215-230. |
| [6] |
Dobrovol'Skaya ZN. On some problems of similarity flow of fluid with a free surface[J]. Journal of Fluid Mechanics, 1969, 36(4), 805−829.
|
| [7] |
ZHAO R, FALTINSEN O M, AARSNES J V. Water entry of arbitray two-dimensional sections with and without flow separation[C]// Proc. 21st Symposium on Naval Hydrodynamics, 1996: 408−423.
|
| [8] |
卢炽华, 何友声. 二维弹性结构入水冲击过程中的流固耦合效应[J]. 力学学报, 2000, 32(2): 129-140. LU Chi-hua, HE You-sheng. Coupled analysis of nonlinear interaction between fluid and structure during impact[J]. Chinese Journal of Theoretical and Applied Mechanics, 2000, 32(2): 129-140. DOI:10.3321/j.issn:0459-1879.2000.02.001 |
| [9] |
WU G X, SUN H, HE Y S. Numerical simulation and experimental study of water entry of a wedge in free fall motion[J]. Journal of Fluids & Structures, 2004, 19(3): 277-289. |
| [10] |
XU G D, DUAN W Y, WU G X. Numerical simulation of oblique water entry of an asymmetrical wedge[J]. Ocean Engineering, 2008, 35(16): 1597-1603. DOI:10.1016/j.oceaneng.2008.08.002 |
| [11] |
XU G D, DUAN W Y, WU G X. Simulation of water entry of a wedge through free fall in three degrees of freedom[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 2010, 466(466): 2219-2239. |
| [12] |
SUN S L, WU G X. Oblique water entry of a cone by a fully three-dimensional nonlinear method[J]. Journal of Fluids & Structures, 2013, 42(4): 313-332. |
| [13] |
陈震, 肖熙. 空气垫在平底结构入水砰击中作用的仿真分析[J]. 上海交通大学学报, 2005, 39(5): 670-673. CHEN Zhen, XIAO Xi. Simulation analysis on the role of air cushion in the slamming of a flat-bottom structure[J]. Journal of shanghai jiaotong university, 2005, 39(5): 670-673. DOI:10.3321/j.issn:1006-2467.2005.05.002 |
| [14] |
朱显玲, 陈艳霞, 梁双令. I型夹芯夹层板入水砰击数值仿真及结构参数化研究[J]. 舰船科学技术, 2020, 42(11): 40-44. ZHU Xian-ling, CHEN Yan-xia, LIANG Shuang-ling. Numerical simulation and structural parameter study on water entry slamming of I-core sandwich plate[J]. Ship Science and Technology, 2020, 42(11): 40-44. DOI:10.3404/j.issn.1672-7649.2020.11.008 |
| [15] |
陈光茂, 郑小波, 毋晓妮, 等 二维楔形体入水问题的数值和实验研究[J]. 舰船科学技术, 2021, 43(1): 53−60. CHEN Guang-mao, ZHENG Xiao-bo, WU Xiao-ni, et al. Numerical and experimental study of water entry problem of two-dimensional wedge[J]. Ship Science and Technology, 2021, 43(1): 53−60. |
| [16] |
云忠, 温猛, 罗自荣, 等. 仿翠鸟水空跨介质航行器设计与入水分析[J]. 浙江大学学报, 2020, 54(2): 407-415. YUN Zhong, WEN Meng, LUO Zi-rong, et al. Design and plunge-diving analysis of underwater-aerial transmedia vehicle of bionic kingfisher[J]. Journal of Zhejiang University, 2020, 54(2): 407-415. |
| [17] |
WANG S, SUARES C G. Analysis of water impact of symmetric wedges with a multi-material Eurlerian formulation[J]. Int. J. Maritime Eng. , 2012, 154: 191−206, .
|
| [18] |
WANG S, SOARES C G. A symmetrical water impact of two-dimensional wedges with roll angle with multi-material eulerian formulation[J]. International Journal of Maritime Engineering, 2014 156(A2): 115−130.
|
| [19] |
WANG S, SOARES C G. Numerical study on the water impact of 3D bodies by an explicit finite element method[J]. Ocean Engineering, 2014, 78(3): 73-88. |
| [20] |
曹正林. 高速三体船砰击强度研究[D]. 武汉: 武汉理工大学, 2008.
|
| [21] |
段芳. 三体船砰击响应特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [22] |
孙辉, 卢炽华, 何友声. 二维楔形体冲击入水时的流固耦合响应的试验研究[J]. 水动力学研究与进展, 2003, 18(1): 104-109. SUN Hui, LU Zhi-hua, HE You-sheng. Experimental research on the fluid-structure interaction in water entry of 2D elastic wedge[J]. Journal of Hydrodynamics, 2003, 18(1): 104-109. |
| [23] |
ZHAO R, FALTINSEN O. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics, 1992, 246(-1): 593-612. |
| [24] |
莫立新, 王辉, 蒋彩霞, 等. 变刚度楔形体板架落体砰击试验研究[J]. 船舶力学, 2011, 15(4): 394-401. MO Li-xin, WANG Hui, JIANG Cai-xia, et al. Study on dropping test of wedge grillages with various types of stiffeness[J]. Journal of Ship Mechanics, 2011, 15(4): 394-401. DOI:10.3969/j.issn.1007-7294.2011.04.011 |
| [25] |
张哲, 李振旺, 吴文婷, 等. 基于PVDF压电薄膜的入水冲击压力测试技术[J]. 舰船科学技术, 2021, 43(5): 20−23. ZHANG Zhe, LI Zhen-wang, WU Wen-ting, et al. Research on the test technology of water impact pressure based on PVDF. Ship Science and Technology[J]. 2021, 43(5): 20−23. |
| [26] |
尚晓江, 苏建宇. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 北京: 中国水利水电出版社, 2006.
|
| [27] |
LS-DYNA Keyword user's manual[M]. Livermore Software Technology Corporation, 2007.
|
 2022, Vol. 44
2022, Vol. 44
