近年来,极地地区受全球变暖的影响愈加明显,北极地区夏季冰区范围缩小,海冰厚度下降,使北极航道的建设成为可能,加上北极地区优越的资源条件,世界各国正加紧对极地研究。但我国对极地的相关研究起步较晚,基础较为薄弱,所以对极地相关进行研究迫在眉睫,极地的海冰覆盖范围可以分为海冰边缘区和密集冰区,海冰边缘区密集度较低,存在大量碎冰冰块[1]。
碎冰作为一种典型的海冰类型,是研究极地必须要考虑的重要条件,通过理论分析、数值仿真和实验研究的办法对船舶与碎冰相互作用进行研究[2]。其中,数值仿真具有时间短、成本低等优点,所以目前主要利用数值仿真的办法进行研究,通过假设碎冰形状为规则的圆形和四边形形成碎冰区[3]。葛媛[4]利用二维离散元方法,与半经验公式相结合修正船-冰作用力,李紫麟[5]采用三维圆盘单元模拟碎冰区,分析航速与冰况对船体冰载荷的影响,Liu[6]利用扩张多面体单元离散元模拟计算极地冰区浮式结构冰载荷,考虑冰载荷的厚度、密集度等参数的影响。这些方法可以建立有规律的碎冰区域,但所建的仿真碎冰区不能满足真实情况下碎冰的无规则分布以及无规律形状的要求,在研究船-冰碰撞过程中如何建立较为符合实际冰情的碎冰模型显得十分重要。
元胞自动机是一种时间和空间都离散的动力学系统,满足碎冰空间随机分布的特点,Lu[7]提出一种扩展场元胞自动机来描述行人群体的步行行为,Zhao[8]利用元胞自动机随机模型,模拟聚集行为的人员疏散情况,比较人员随机分布和聚集分布的疏散情况,李永行[9]利用元胞自动机模型建立行人仿真模型。以上文献中元胞自动机用来模拟无序的人群结构,考虑其随机特点,将其应用于冰区研究,构建碎冰模型。
本文参照真实碎冰区域中碎冰MCD分布规律,基于元胞自动机理论,利用犀牛软件构建碎冰模型,并建立参数化控制碎冰块的几何形状、密集度等碎冰参数,开发一种接近于真实碎冰区域的碎冰创建方法。
1 元胞自动机理论元胞自动机是一种在时间和空间都离散的演化动力系统,具有局部的相互作用和时间因果关系,可以用来研究从局部简单规则到整体复杂动态的演化过程[10],元胞按照一定规则排列形成一个空间区域,每个元胞都有连续或离散的状态,并按同样的规则继续下一步运行,通过这些规则构建元胞自动机。
1.1 元胞自动机的构成元胞自动机主要由元胞、元胞空间、邻居和演化规则4个部分组成[10]。
1)元胞
元胞是元胞自动机最基本的组成部分之一,被分布在离散的一维、二维、三维及以上的空间晶格点上。元胞形状作为元胞最直观的特征会随元胞空间的不同划分而变化,并且在建立元胞自动机时根据实际情况设置元胞属性。
2)元胞空间
在所有元胞分布的空间称为元胞空间,元胞自动机基于维数一般分为一维、二维和三维及以上,其中常用的是二维元胞自动机,在此维数中,元胞空间有三角形、正方形和六边形3种划分图形。
3)邻居
元胞自动机的运行范围是局部的,某一元胞状态运行时所需要探索的空间范围叫做该元胞的邻居,换句话说,能够对某一元胞下一状态产生影响的元胞就是该元胞的邻居。
4)演化规则
演化规则可以用来表示元胞向某方向运动的可能性,是一种概率函数,元胞自动机构成过程建立在每个元胞按照相同演化规则上运动的基础上 ,演化过程是元胞自动机的核心组成部分。
1.2 元胞自动机的分类元胞自动机模型没有固定的建立方式,其组成方式复杂,分组种类众多,按照不同的角度可以对元胞自动机进行不同的分类。在众多的分类方法中,最具有代表性的是S.Wolfram通过总结计算机实验基础并研究一维元胞自动机演化过程,将元胞机的动力学行为归纳为平稳型、周期型、混沌型和复杂型。这4种类型主要是通过元胞在经历一段时间的运行之后所处的状态进行判断,元胞空间处于平稳状态为平稳型;元胞空间处于简单的固定结构或周期结构为周期型;元胞出现非周期行为,呈现混沌状态为混沌型;元胞出现局部混沌状态的同时,保持有些元胞的继续运行,这一类型为复杂型。
元胞自动机具有同质性、空间离散、时间离散等特征,经过多年的发展和进步,元胞自动机已经发展的相对成熟,在生物、物理、交通等方面有着重要的应用,考虑将元胞自动机与碎冰构建相结合,建立碎冰模型。
2 基于元胞自动机构建碎冰模型的优化设计 2.1 基于元胞自动机理论构建分布点模型Grasshopper是一款利用程序算法生成模型的插件,基于蚂蚁规则可以在此环境中构建元胞自动机。蚂蚁规则是指蚂蚁在黑白两色的方形网格上运动,当网格为白色时,向左转90o并将该元胞变为黑色;当网格为黑色时,向右转90o并将该元胞变为白色。
构建元胞自动机有Hoopsnake法和VB脚本法2种,VB脚本基于蚂蚁规则,利用横纵坐标表示位置,利用0和1表示网格颜色,将问题数值逻辑化,对比Hoopsnake法可以大大减少计算时间。因此利用VB脚本法构建元胞自动机,构建流程如图1所示。

|
图 1 VB脚本法创建元胞自动机流程图 Fig. 1 VB script method to create a flow chart of cellular automata |
VB脚本运算规则是引入字母i和j代表元胞的横纵坐标,引入数字0和1代表元胞的黑白颜色。
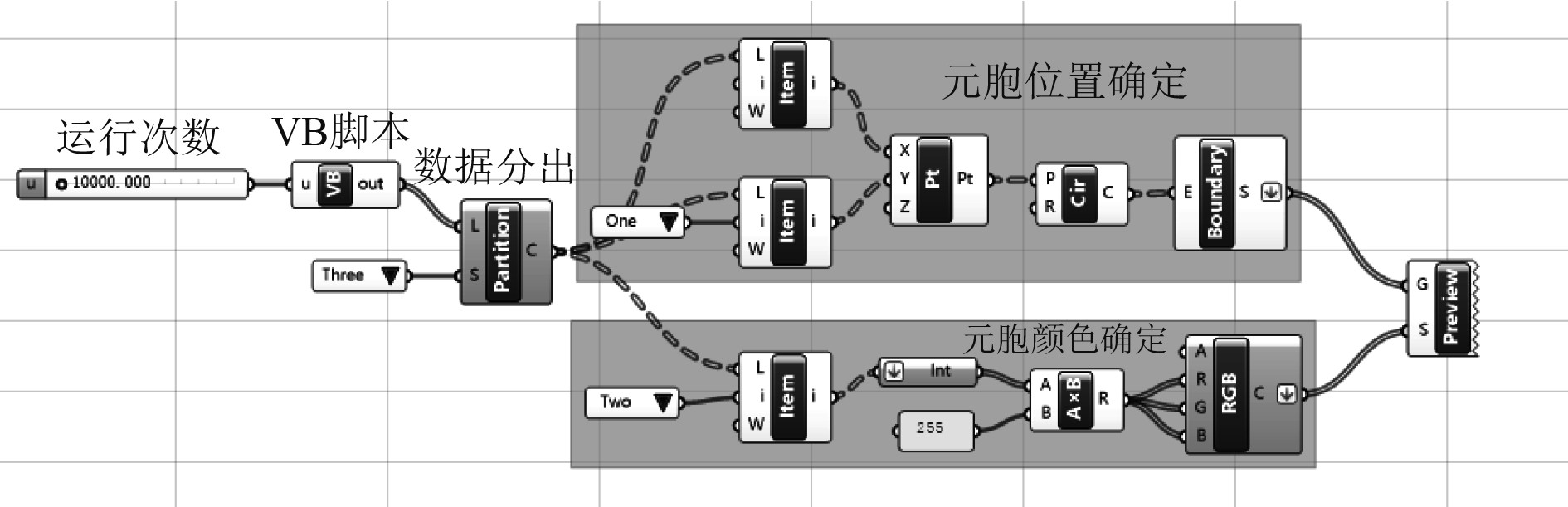
利用Grasshopper插件将上述VB脚本算法转化为电池组流程图,如图2所示。
|
图 2 VB脚本法构建元胞自动机流程图 Fig. 2 Program diagram of a cellular automaton by VB script method |
利用VB脚本法构建元胞自动机的运算过程不会逐步显示,但利用坐标值和颜色数值化的运算,提高了运行时的计算速度,大幅增强了处理大数据时的计算能力。图3为按照上述算法构建元胞自动机分布点示意图。可以看出运行前期正常,当元胞运行至10000步时,元胞虽处于混沌状态,但已出现明显的逃逸现象,形成逃逸公路离开所选区域范围。

|
图 3 VB脚本法生成元胞点模型 Fig. 3 Cellular point model created by VB script method |
为使元胞运行至10000步时处于混沌状态的同时也在所选区域范围内,对VB脚本进行优化,在初始时加入多个已确定的元胞点,在代码“定义初始元胞颜色为白”中,于a(70, 70) = 1后加入:a(42,65)=1; a(85,43)=1,增加了初始元胞点,扰乱逃逸规则,避免出现逃逸现象,得到元胞点分布如图4所示。可知,在运行至10000步时,元胞处于混沌状态且未发生逃逸现象满足要求,此时生成的元胞自动机分布点模型即为所需要建立的碎冰分布点模型。

|
图 4 优化后VB脚本法生成元胞点模型 Fig. 4 Cellular point model created by VB script method after optimized |
泰森多边形是一组由连接两邻点线段的垂直平分线组成的连续多边形,可以对二维多边形和三维多面体进行几何随机划分,本文利用泰森多边形对上述由元胞自动机生成的随机点建立多边形模拟碎冰模型。
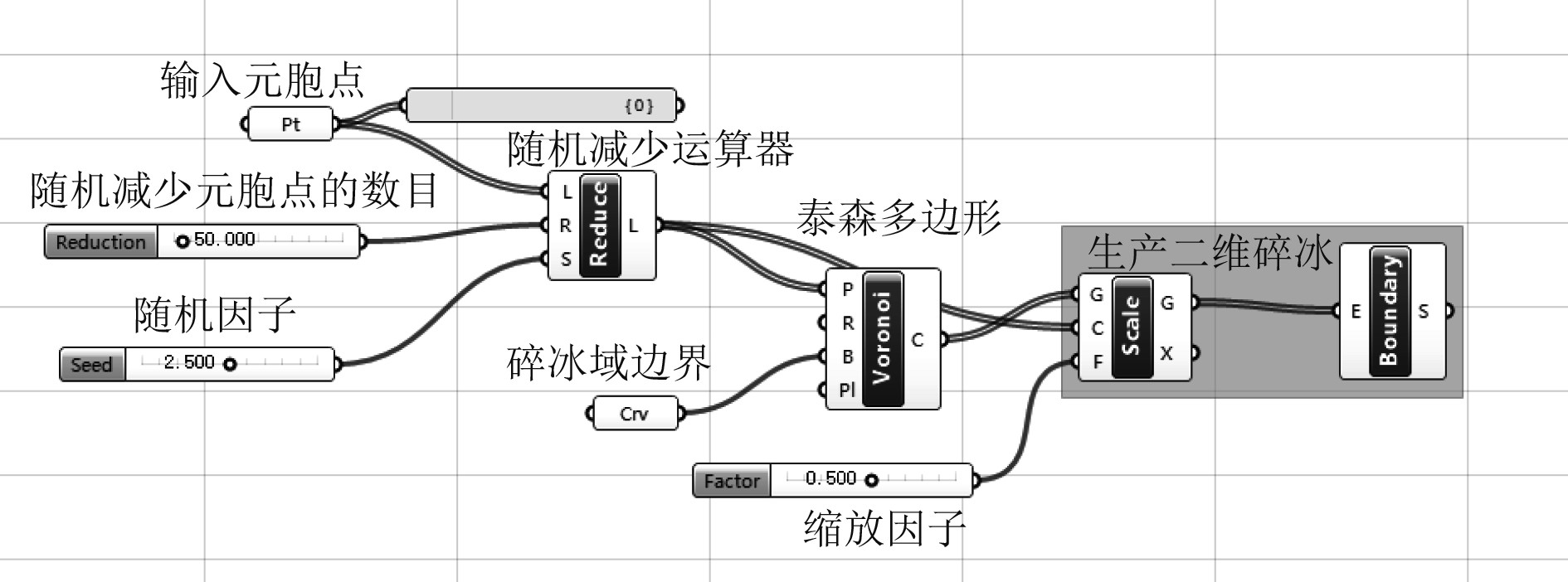
元胞自动机通过VB脚本生成的分布点数量多,分布密集,不利于基于泰森多边形理论的二维碎冰划分,因此可以在生成随机点之后加入随机减少运算器,得到数量合适、离散恰当的分布点,为二维碎冰的划分做准备。图5为构建二维碎冰的电池组程序图,输入由VB脚本法生成的元胞点,并根据实际碎冰尺度和密集度对元胞点进行随机删减优化,对优化后的元胞点利用泰森多边形理论进行划分,同时引入缩放因子对划分的图形进行缩放得到二维碎冰模型,这一构建过程分步结果如图6所示。
|
图 5 二维碎冰构建程序图 Fig. 5 Program chart of 2D crushed ice construction |

|
图 6 构建二维碎冰分步结果图 Fig. 6 Result chart of creating 2D crushed ice step by step |
由于船舶在极地冰区航行时发生碰撞的碎冰都是不规则多边形,所以考虑建立碎冰模型之前需要将碎冰的尺寸进行统一表示,引入MCD理论表征碎冰模型尺寸,MCD又称碎冰等效直径,是由Renat Yulmetov等[11]所定义,具体公式为:
| $ D = l/\text{π}。$ | (1) |
式中:
基于极地碎冰区域的实际测量值,经过总结归纳得到碎冰MCD概率分布近似符合负指数幂函数:
| $ {f_{MCD}} = \frac{{ - \beta }}{{{D_{\max }}^{ - \beta } - {D_{\min }}^{ - \beta }}}{D^{ - \beta - 1}},D \in \left[ {{D_{\min }},{D_{\max }}} \right] 。$ | (2) |
式中:
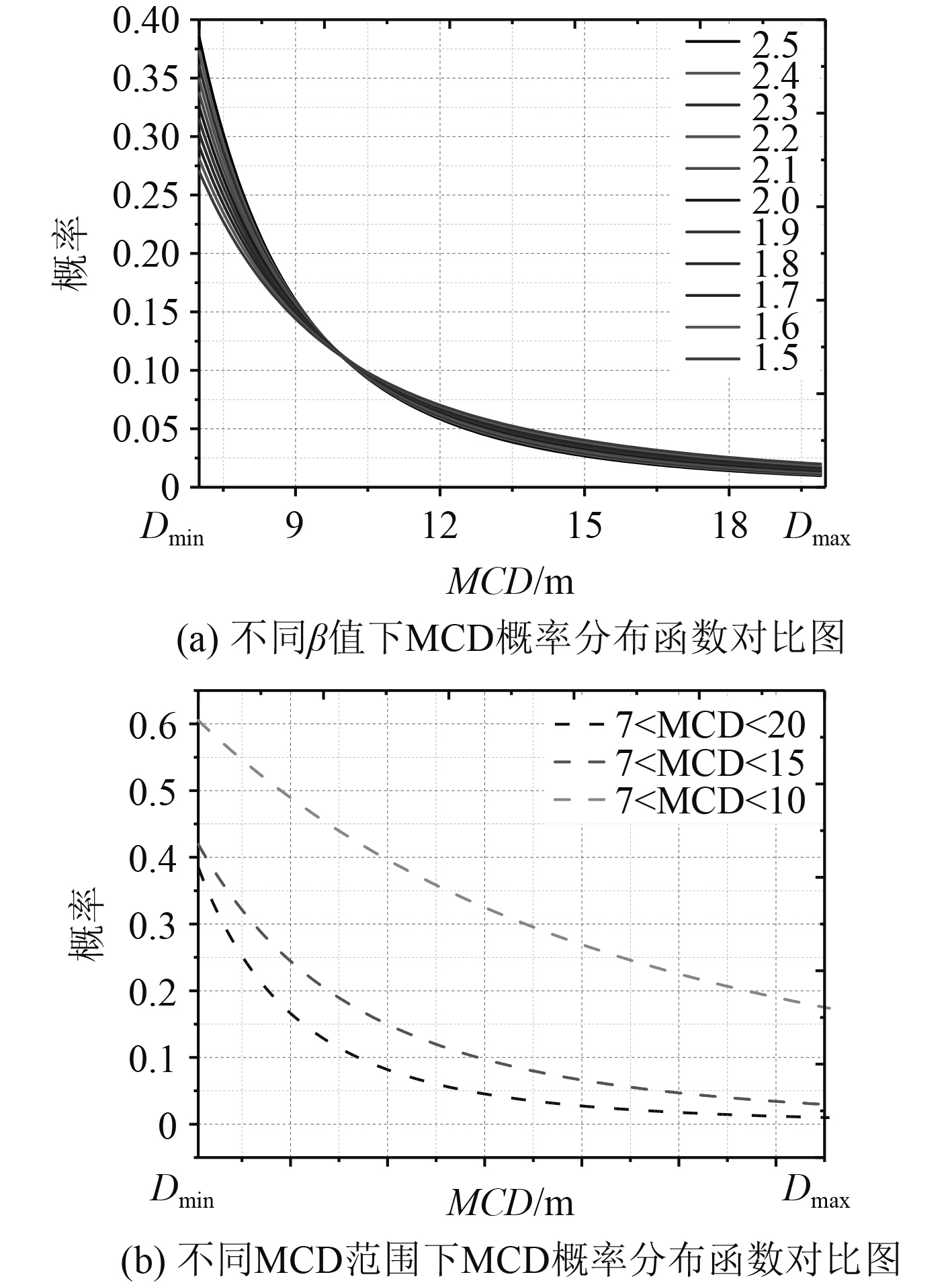
参数
|
图 7 不同情况MCD概率分布函数对比图 Fig. 7 Comparison chart of MCD probability distribution function in different situations |
根据MCD概率分布函数图,取
|
|
表 1 碎冰模型MCD概率分布值 Tab.1 MCD probability distribution value of crushed ice model |
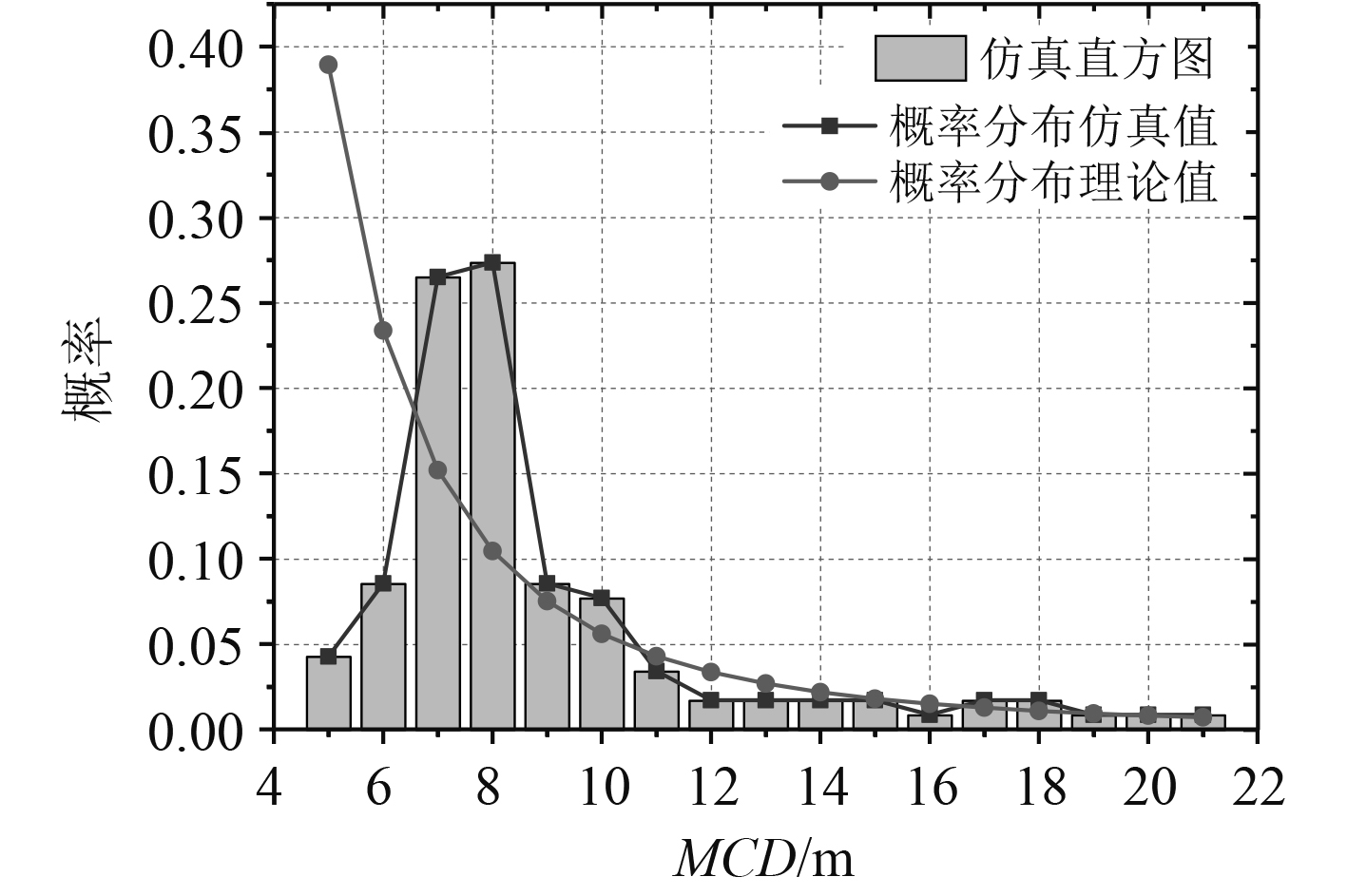
可以看出,构建模型的碎冰等效直径范围为5~21 m,碎冰模型MCD分布概率与数值理论分布概率的误差均值为43.85%,方差为0.143,从方差看出,生成碎冰模型MCD概率分布值较为分散,受到累计差值影响较大。图8为未经优化的碎冰MCD概率分布曲线理论值和仿真值对比图。从图中可以直观地看出当等效直径过小时,仿真概率分布曲线与理论分布曲线相差很大,曲线整体趋势与理论曲线有着明显差距,需要对该碎冰构建过程进行优化。
|
图 8 碎冰模型MCD概率分布函数曲线图 Fig. 8 MCD probability distribution function curve of crushed ice model |
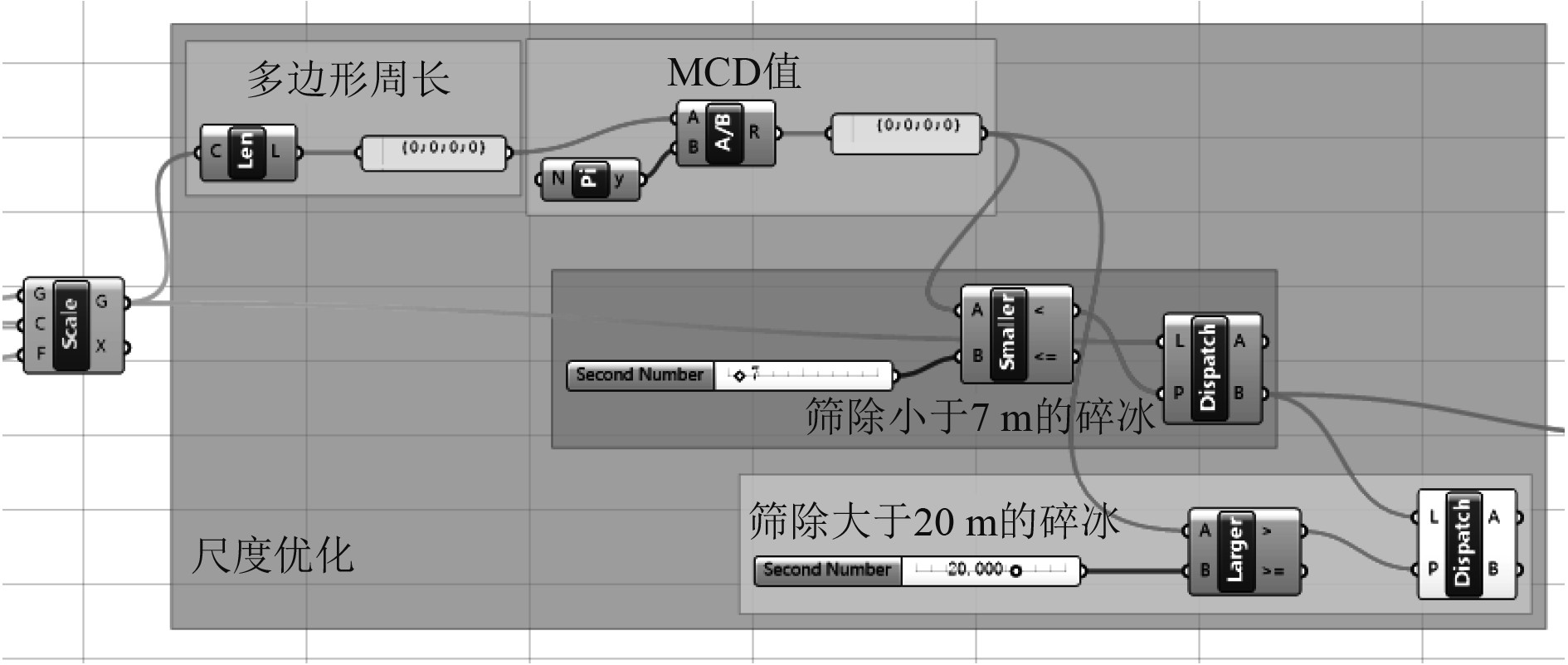
通过图8可以发现MCD值过小或过大都会对碎冰概率分布造成不可忽略的影响,为减少此类影响,对碎冰尺度进行优化,设定MCD范围为7~20 m,对模型中生成的等效直径小于7 m和大于20 m的碎冰进行筛选删除。在程序中生成二维碎冰之前计算出每块碎冰的有效直径,利用大小比较运算器筛除留下等效直径为7~20 m的碎冰,具体尺度优化程序如图9所示。
|
图 9 尺度优化程序图 Fig. 9 Scale optimization procedure diagram |
|
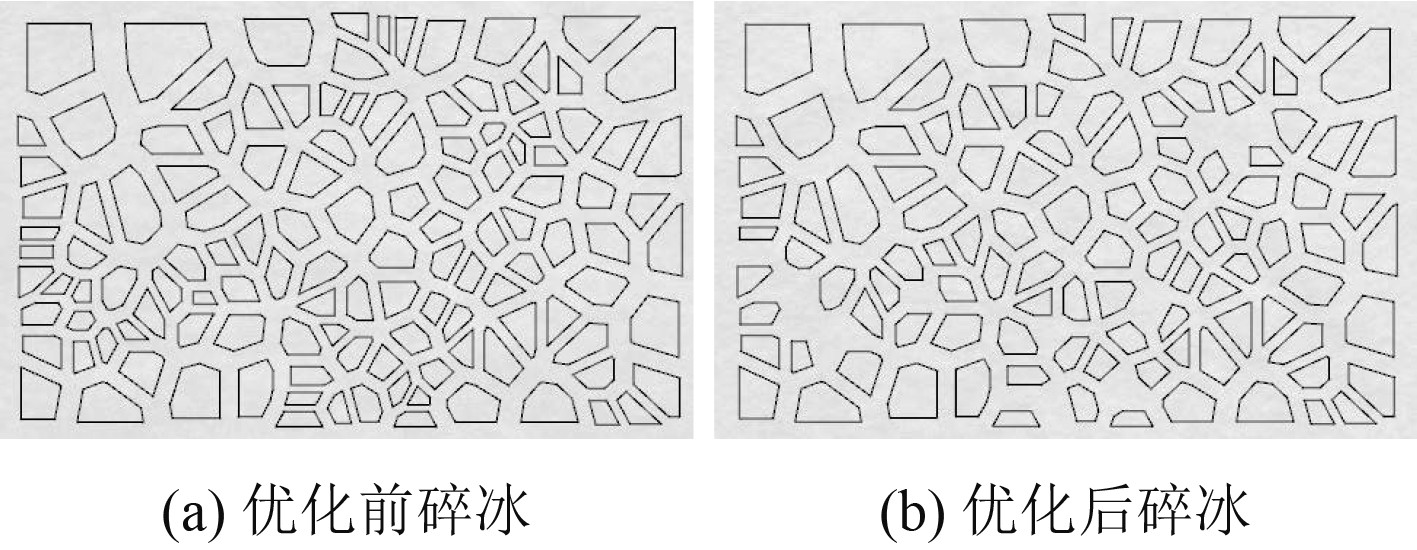
图 10 尺度优化前后的二维碎冰模型 Fig. 10 2D crushed ice model before and after scale optimization |
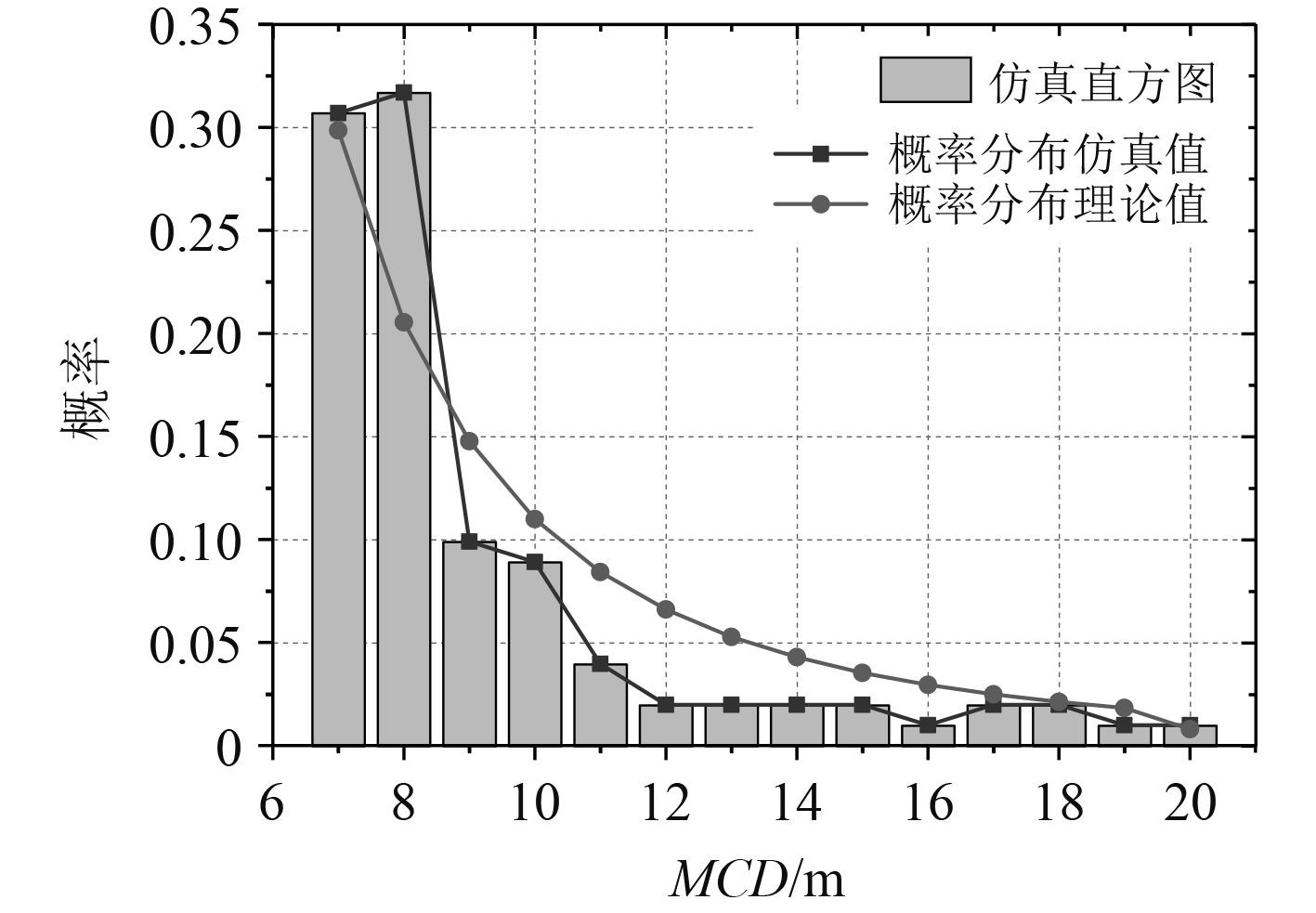
碎冰模型经过尺度优化后,等效直径范围定为7~20 m,并将其概率分布值与理论概率分布值进行误差计算,得到误差均值为39.64%,方差为0.005,误差均值与方差与优化前相比都下降了,碎冰模型的MCD概率值更加接近理论概率值,尤其是方差的大幅降低说明控制了误差数据的分散。同时将两者分布概率曲线进行对比得到图11,可以发现较未优化时,概率曲线出现明显缓和,减少了碎冰面积累计差值的影响,整体趋势更接近理论上的概率分布曲线。
|
图 11 尺度优化后的碎冰模型MCD概率分布函数曲线图 Fig. 11 Curve of MCD probability distribution function of crushed ice model after scale optimization |
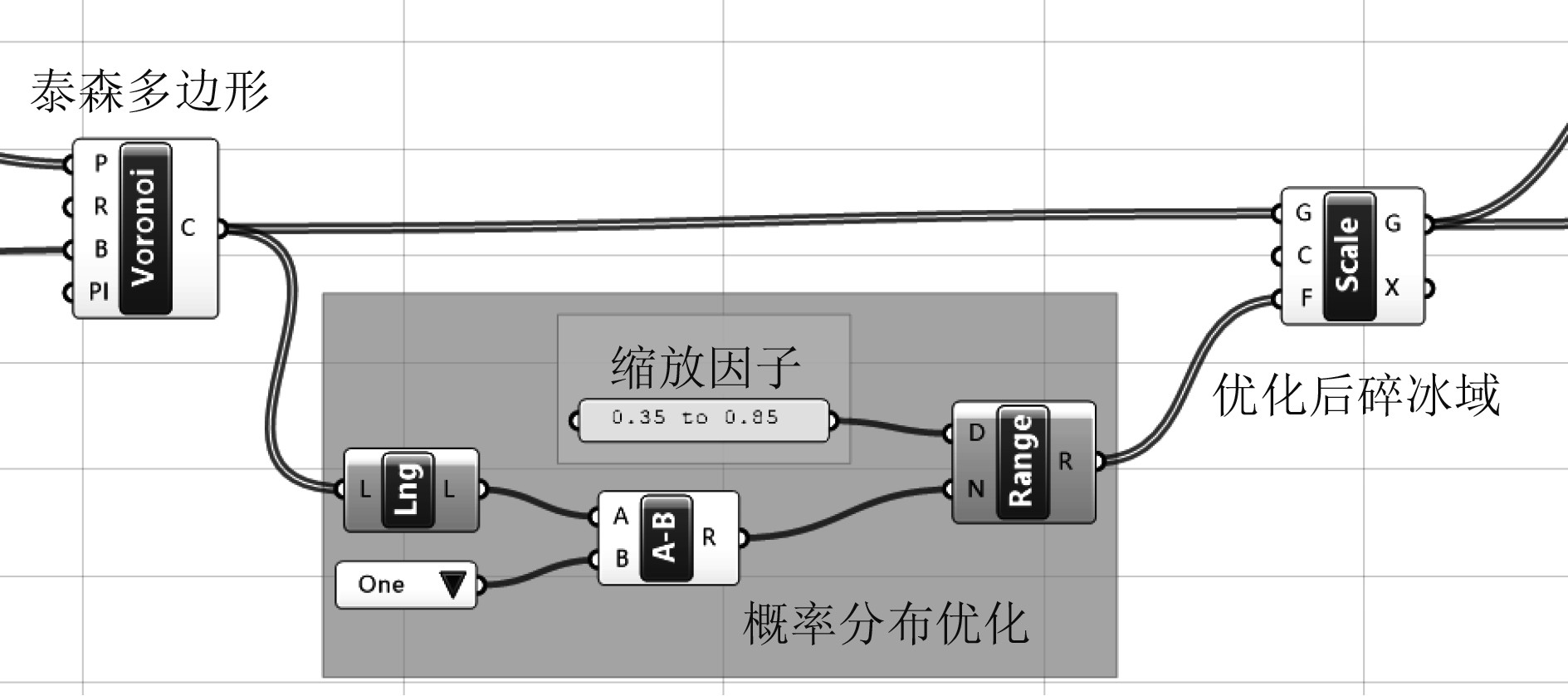
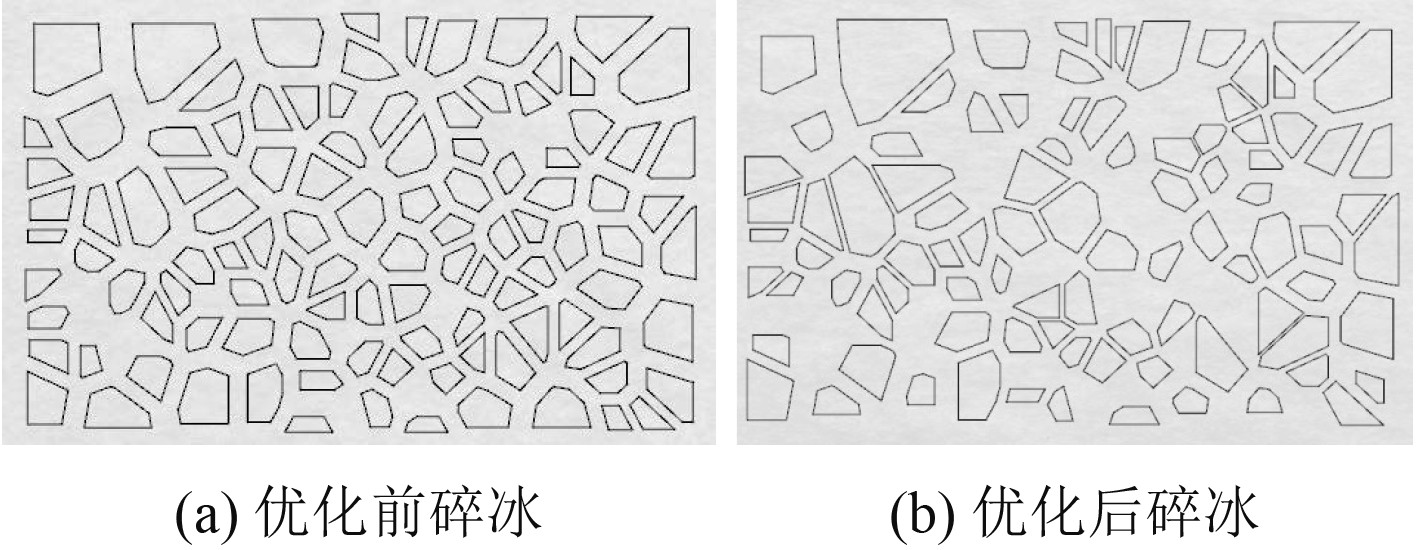
在上述碎冰模型构建过程中,基于泰森多边形理论对碎冰进行统一缩放,使构建的每块碎冰之间距离相似,分布规则过于规律,与实际冰况中碎冰的无规则分布不符。为解决这一情况,对概率范围分布进行优化,主要是将统一缩放因子优化为一定缩放范围,利用泰森多边形原理进行划分碎冰块之后,赋予每块碎冰不同的缩放因子,图12和图13分别为概率优化程序图及结果对比图。从图13可以看出,经过优化后,碎冰尺度和距离都更加无序化,直观上更加接近真实冰况。
|
图 12 范围分布优化程序图 Fig. 12 Range distribution optimization program diagram |
|
图 13 概率范围优化前后的二维碎冰模型 Fig. 13 2D ice model before and after optimization of probability range |
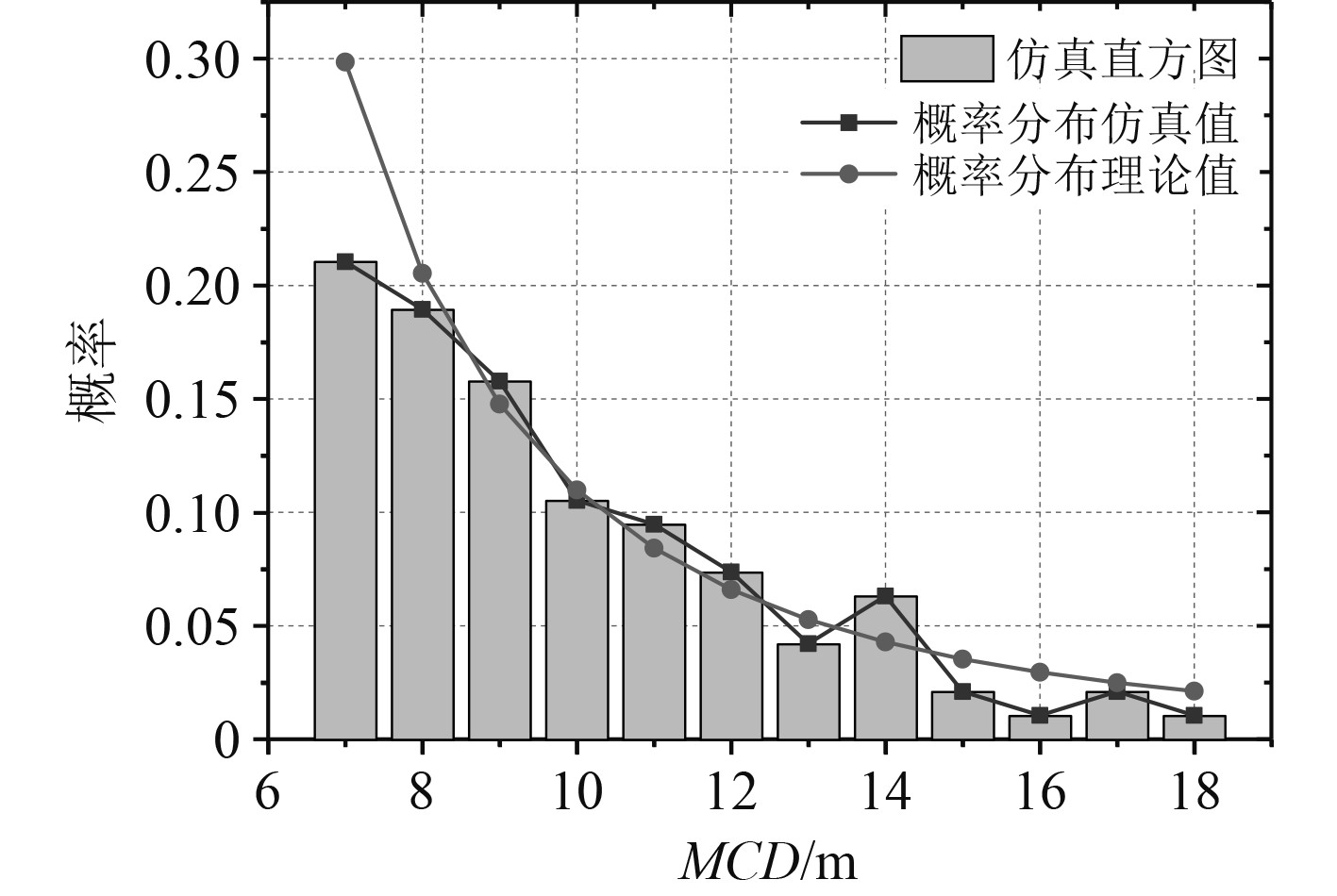
概率范围分布优化也会对碎冰MCD值产生影响,优化后MCD范围为7~18 m,将碎冰模型分布概率值和理论概率值进行误差计算,得到误差均值为25.86%,方差为0.037,误差均值与方差均进一步减少,进一步优化了碎冰模型结构。将优化后的MCD概率分布曲线与理论概率分布曲线进行对比,得到图14。可以发现,图中仿真概率分布曲线相比未优化前趋势与理论概率分布曲线趋势相近,说明优化后的碎冰模型更接近实际冰况,此时已对二维碎冰进行了优化处理。
|
图 14 概率范围优化后MCD概率分布函数曲线对比图 Fig. 14 Comparison diagram of MCD probability distribution function curve after probability range optimization |
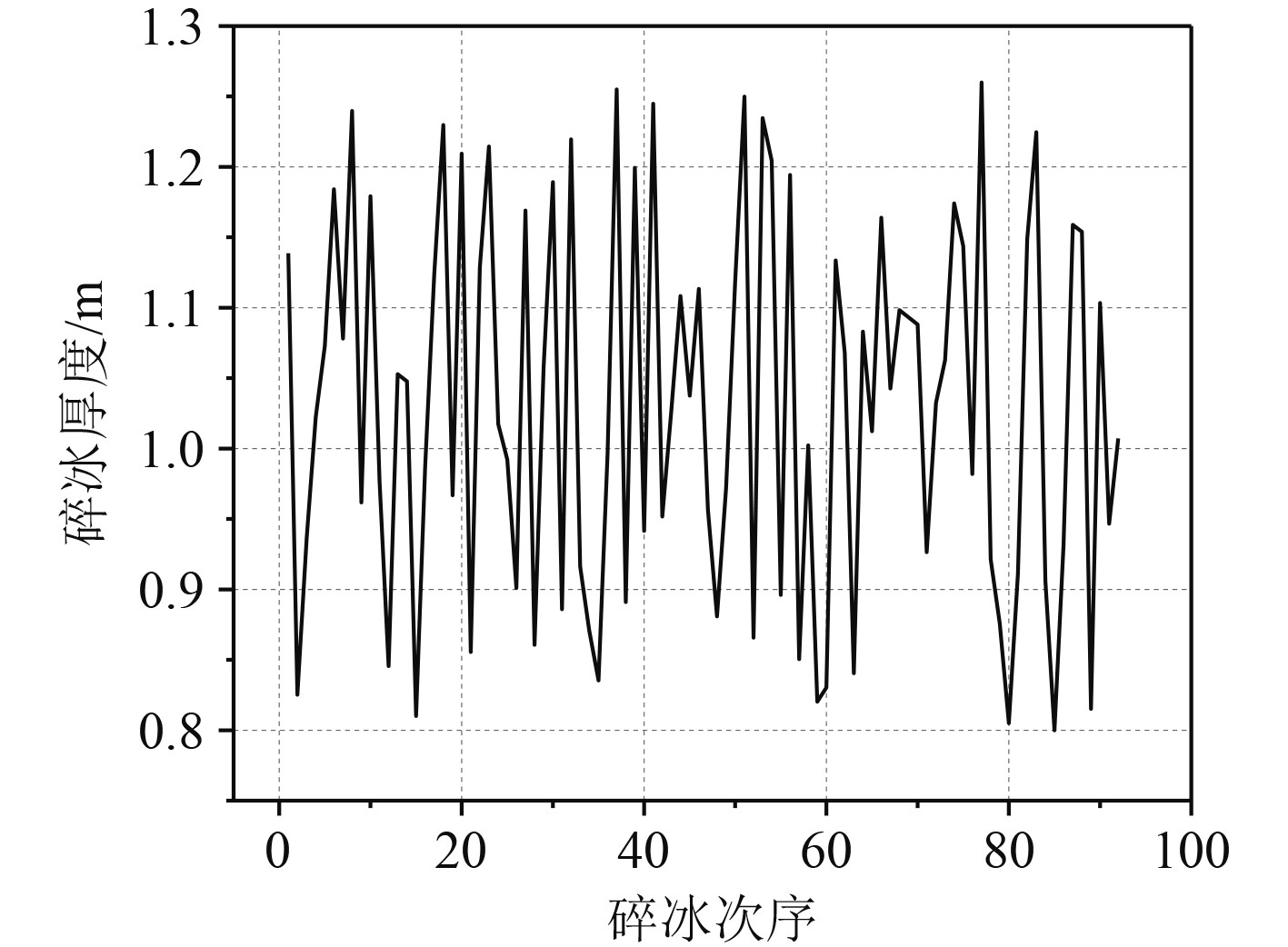
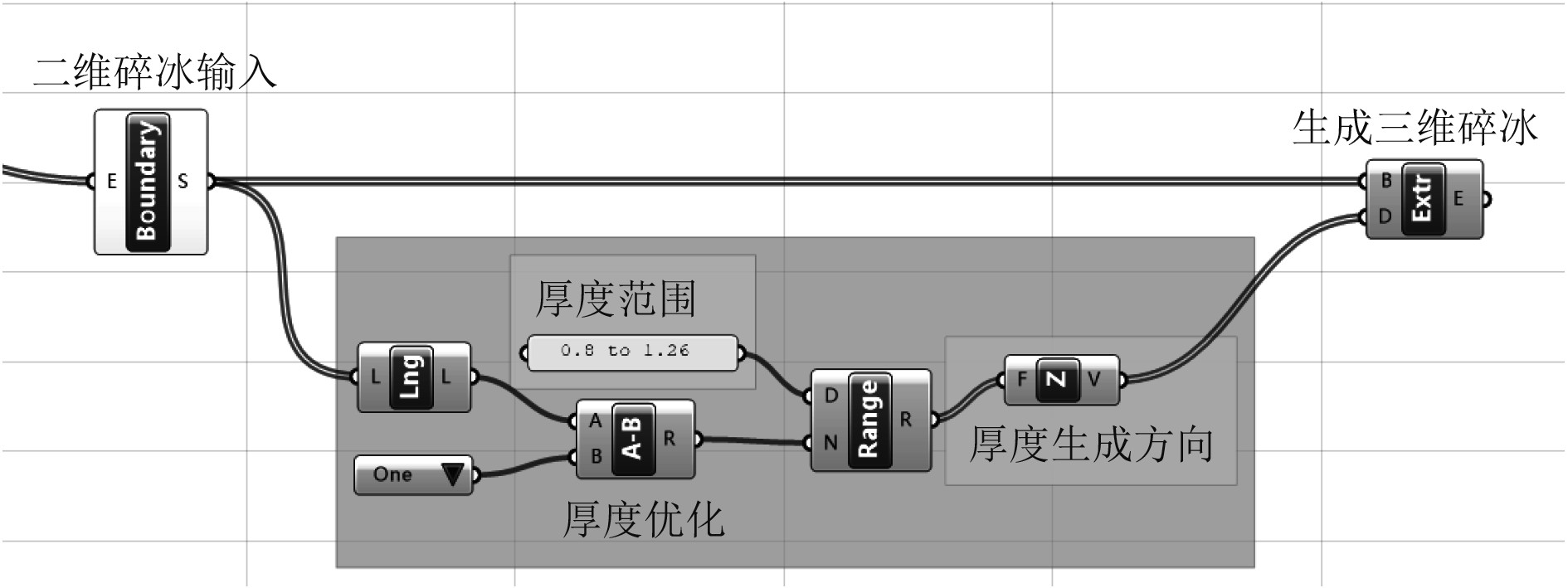
碎冰模型不单单需要考虑二维碎冰的优化处理,碎冰厚度也是建立碎冰模型的重要考虑因素,一般构建的碎冰模型均采用的是单一厚度因子,生成厚度完全相同的碎冰区域,这一特征碎冰与真实水域三维碎冰厚度存在差距,故将单一厚度值优化成厚度范围。拟定碎冰厚度范围为0.8~1.26 m,获得优化后的碎冰厚度分布图,从图16可以看出,厚度在拟定厚度范围中无序分布,更符合实际冰区冰况。
|
图 16 厚度优化后碎冰厚度分布图 Fig. 16 Thickness distribution map of crushed ice after thickness optimization |
|
图 15 厚度范围优化程序图 Fig. 15 Thickness range optimization program diagram |
为了建立接近真实冰情的碎冰模型,本文结合元胞自动机和泰森多边形理论构建碎冰模型,利用犀牛软件及其参数化设计插件Grasshopper,并参照MCD概率分布规律,计算碎冰概率分布理论值,将所构建的碎冰模型概率曲线与理论值概率曲线进行对比,优化碎冰模型构建过程,使优化后的碎冰模型概率曲线接近概率分布理论曲线,得到更加真实的碎冰区。主要针对以下3个方面进行优化:
1)碎冰尺度优化。筛选剔除MCD值小于7 m和大于20 m的碎冰,可以发现碎冰模型筛除了过大和过小的碎冰后,使碎冰MCD仿真值概率曲线更加合理,碎冰数量更为集中,受碎冰面积的累计差值影响减小。
2)碎冰概率范围分布优化。将单一缩放因子优化为随机缩放范围,可以使不同的缩放因子作用在各个碎冰块,得到优化后的碎冰分布更具有随机性,碎冰面积尺寸更接近实际碎冰情况。
3)厚度优化。将单一厚度的碎冰优化为一定厚度范围的碎冰,可以使每块碎冰都具有不一样的厚度。该优化可以从三维角度随机赋予每块碎冰不同的厚度,使优化后的碎冰冰厚更接近真实冰区。
| [1] |
刘成龙, 赵进平. 夏季北极密集冰区范围确定及其时空变化研究[J]. 海洋学报, 2013, 35(4): 36-46. |
| [2] |
HUANG Y. Model test study of the nonsimultaneous failure of ice before wide conical structures[J]. Cold Regions Science and Technology, 2010, 63(3): 87-96. DOI:10.1016/j.coldregions.2010.06.004 |
| [3] |
NI B. Review on the interaction between sea ice and waves/currents[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(03): 641-654. |
| [4] |
葛媛. 二维离散方法的破冰船层冰破冰阻力数值预报[D]. 大连: 大连海事大学, 2020.
|
| [5] |
李紫麟. 船舶在碎冰区航行的离散元模型及冰荷载分析[D]. 大连: 大连理工大学, 2013.
|
| [6] |
LU L, JI S. Ice load on floating structure simulated with dilated polyhedral discrete element method in broken ice field[J]. Applied Ocean Research, 2018, 7(5): 53-65. |
| [7] |
LI-LI L, GANG R, WEI W, et al. Modeling walking behavior of pedestrian groups with floor field cellular automaton approach[J]. Chinese Physics B, 2014, 23(8): 088901. DOI:10.1088/1674-1056/23/8/088901 |
| [8] |
ZHAO D, WANG J, ZHANG X, et al. A Cellular Automata occupant evacuation model considering gathering behavior[J]. International Journal of Modern Physics C, 2015, 26(08): 1550089. DOI:10.1142/S0129183115500898 |
| [9] |
李永行. 城市轨道交通车站行人微观行为建模与仿真[D]. 长春: 吉林大学, 2018.
|
| [10] |
王奕修. Grasshopper入门&晋级必备手册[M]. 北京: 清华大学出版社, 2013.
|
| [11] |
YULMETOV R, LUBBAD R, LØSET S. Planar multi-body model of iceberg free drift and towing in broken ice[J]. Cold Regions Science & Technology, 2016, 121(2): 154-166. |
 2022, Vol. 44
2022, Vol. 44
