0 引　言

弹筒匹配系统是指发射装置中在航行体和发射筒之间设置的设备和装置所组成的系统，具有适配、减震、导向的功能。目前航行体多采用适配器^[1]弹筒匹配方式，而气密环-减震垫^[1]弹筒匹配方式具有可多次使用，兼顾发射导向与贮存减震等优点，在美、俄等在役航行体中广泛应用。

对于航行体尤其是带翼航行体，在发射出筒过程中，由于横向偏移可能会划伤发射气密环，从而对发射压力产生影响，可能导致发射失败。因此需要研究不同航速、减震垫刚度等发射条件下，战术航行体出筒过程的横向偏移，对气密环-减震垫弹筒匹配方案进行指导。

对于垂直发射横向动力的研究，赵世平^[2]采用简化模型，研究了横向流对潜艇垂直发射航行体的影响，分析了发射条件如潜艇艇速、适配器刚度和航行体运动速度等影响因素，对潜载垂直发射航行体的受力和出筒运动参数的影响，提出了减小航行体受到横向对影响的途径。尚书聪^[3]通过对2种横向支撑方式对航行体出筒过程力学特性的仿真分析，说明弹筒匹配采用适配器方式时出筒姿态较好，但是航行体受到的载荷更大。

本文针对气密环-减震垫弹筒匹配方案，通过建立减震垫变形模型并进行数值分析，研究潜艇航速、减震垫刚度等发射条件对带翼航行体垂直发射的受力和出筒姿态的影响，对水下垂直航行体的发射弹筒匹配方案论证与发射载荷预示具有指导意义。

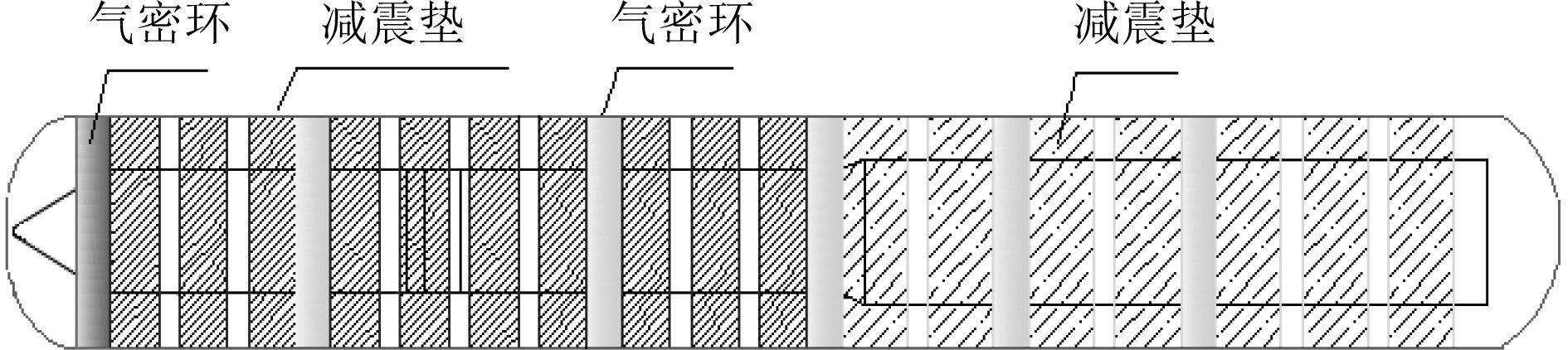
1 模　型

计算模型为某带翼战术航行体，外形示意见图1。气密环减震垫弹筒匹配如图2所示。

从图2可以看出，弹翼在从右至左的第3圈气密环以上，因此，判断弹翼在气密环处的横向偏移，只需要计算弹翼在出筒过程中在第4圈、第5圈和第6圈气密环处的横向偏移量。

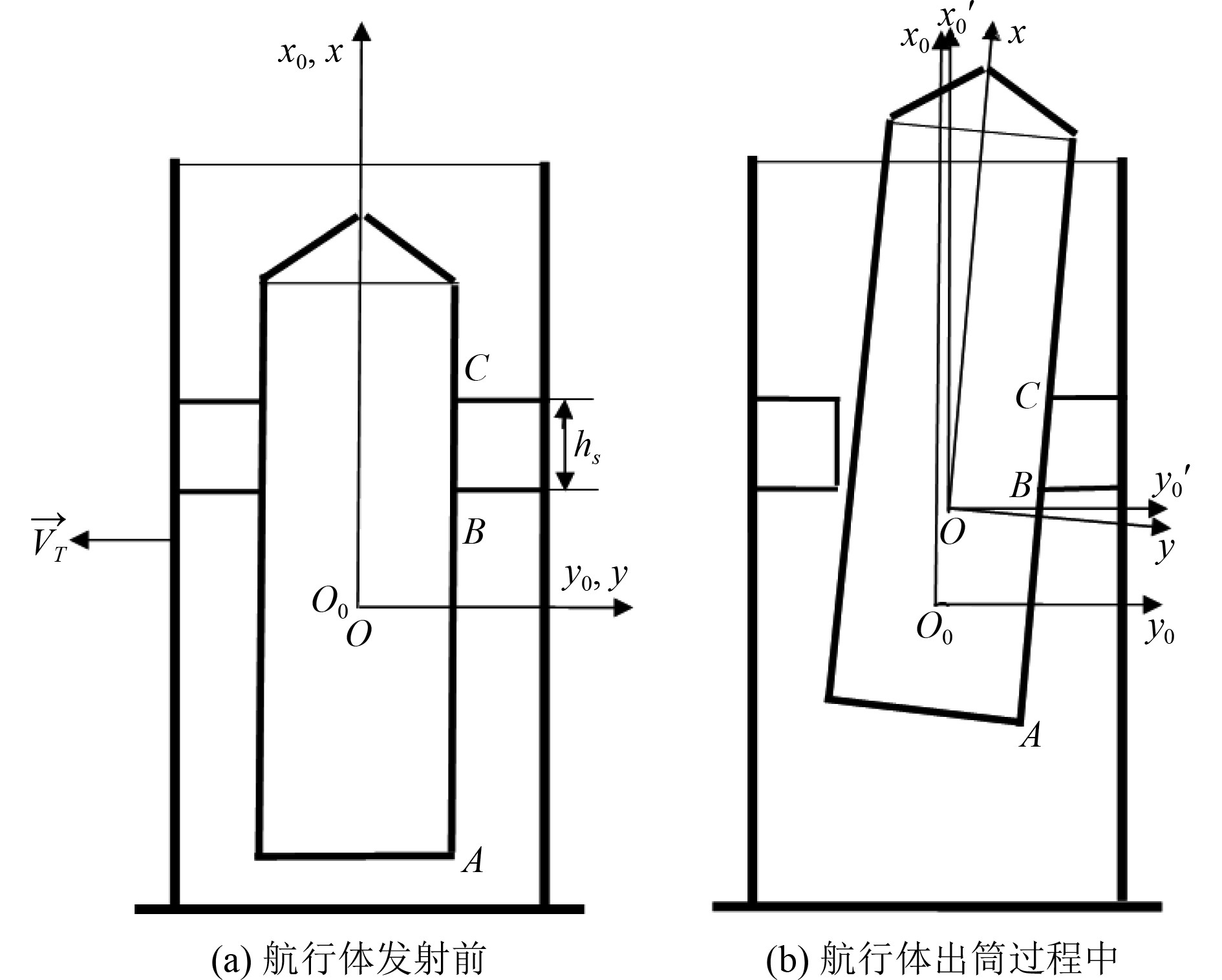
2 减震垫变形模型

减震垫的变形是由于航行体出筒过程中对减震垫的挤压造成的。为了确定减震垫在航行体出筒过程中的变形，以一个减震垫的右侧为例建立减震垫的变形模型，如图3所示。

若减震垫的高度为 $ {h_s} $ ，减震垫厚度为 $ d $ ，发射筒上端右侧点为点A，减震垫上、下端面内侧点为B和C。在航行体发射前，B和C在发射筒坐标系中的坐标分别为 $ (b,R) $ $ (b + {h_s},R) $ ，A在发射筒坐标系和航行体坐标系中的坐标相同，为 $ (a,R) $ 。

在发射筒坐标系中，有以下相对位置关系：

1) 如果 ${x_{0A}} \leqslant {x_{0B}}$ ，减震垫完整作用于航行体；

2) 如果 ${x_{0B}} < {x_{0A}} < {x_{0C}}$ ，减震垫部分作用于航行体；

3) 如果 $ {x_{0A}} > {x_{0C}} $ ，减震垫完全脱离了航行体。

此处只考虑变形与变形量成线性关系的情况。减震垫作用力为：

$ {F_y} = {k_1}\int\nolimits_C^B {\Delta {d_M}{\rm{d}}{h_{SM}}}。$

式中， ${k_1}$ 为线性刚度。

3 数值计算方法

航行体坐标系原点建立在航行体的质心位置，在航行体坐标系中建立航行体平面运动方程组^[4-5]：

$ {v_x} = {v_x}(t) ，$

$ \left( {m + {\lambda _{22}}} \right)\frac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}} + {\lambda _{26}}\frac{{{\rm{d}}{\omega _z}}}{{{\rm{d}}t}} + m{v_x}{\omega _z} = Y + {Y_S}，$

$ \left( {{J_z} + {\lambda _{66}}} \right)\frac{{{\rm{d}}{\omega _z}}}{{{\rm{d}}t}} + {\lambda _{26}}\frac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}} = {M_z} + {M_{zS}} ，$

$ \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = {\omega _z}，$

$ \frac{{{\rm{d}}{x_0}}}{{{\rm{d}}t}} = {v_x}\cos \theta - {v_y}\sin \theta，$

$ \frac{{{\rm{d}}{y_0}}}{{{\rm{d}}t}} = {v_x}\sin \theta + {v_y}\cos \theta。$

式中： $ m $ 为航行体质量； $ {J_z} $ 为绕 $ oz $ 轴的转动惯量； $ Y $ 为流体法向力； $ {M_z} $ 为俯仰力矩； $ {\lambda _{22}} $ 为流体法向附加质量； $ {\lambda _{66}} $ 和 $ {\lambda _{26}} $ 分别为绕 $ oz $ 轴的附加转动惯量和附加静矩； $ {Y_S} $ 为减震垫变形产生的在航行体坐标系中对发射筒的法向作用力。

计算过程如下：

1）初值

发射起始时刻，航行体位于发射筒内，无横向流作用，航行体倾斜角为0，减震垫横向力作用力为0。

2）运动方程组求解

航行体与减震垫/气密环的相互作用是通过减震垫/气密环对航行体的作用力形式体现在运动方程组中，在航行体的出筒运动过程中，航行体与减震垫/气密环之间有相互作用与匹配过程。因此在数值计算中，需要进行迭代耦合计算。具体计算方法如下:

a) $ t = t{}_1 + \Delta t $

① 求解运动方程组，计算航行体运动；

②根据航行体横向位移与倾角，计算各减震垫及气密环形变；

③根据变形计算各减震垫及气密环作用力；

④以新的减震垫及气密环作用力计算航行体运动，进行代计算，直至航行体的横向运动参数与减震垫及气密环的变形量趋于一致，停止迭代，转入下一时间步长计算。

b) $ t = t{}_1 + \Delta t + \Delta t $

……

c) 直至完全出筒

通过以上过程，可以求解航行体出筒过程中每一时刻的运动参数、减震垫作用力、气密环作用力，得到每一圈减震垫每一时刻的变形，以及弹翼处每一时刻的横向偏移量，通过分离体方法，计算任意截面载荷，从而可以得到航行体发射过程中危险截面的力与力矩。

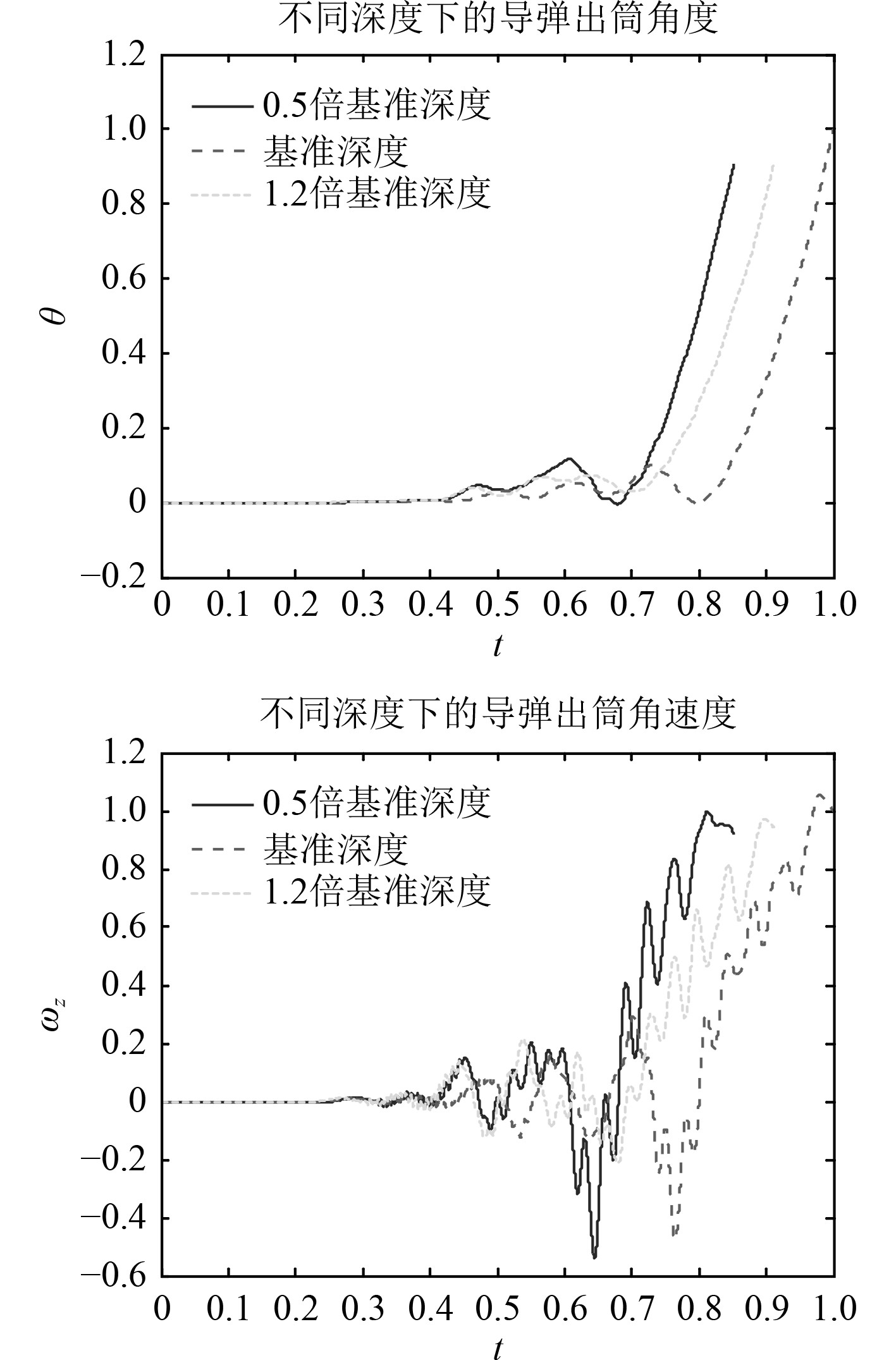
4 仿真结果及分析 4.1 发射深度影响

针对气密环-减震垫弹筒匹配方式的计算对象，进行基准深度、0.5倍基准深度和1.2倍基准深度计算。图4为不同发射深度下航行体的出筒角度和角速度。可以看出，不同发射深度下，出筒角度与出筒角速度趋势一致，发射深度对出筒姿态影响不大。

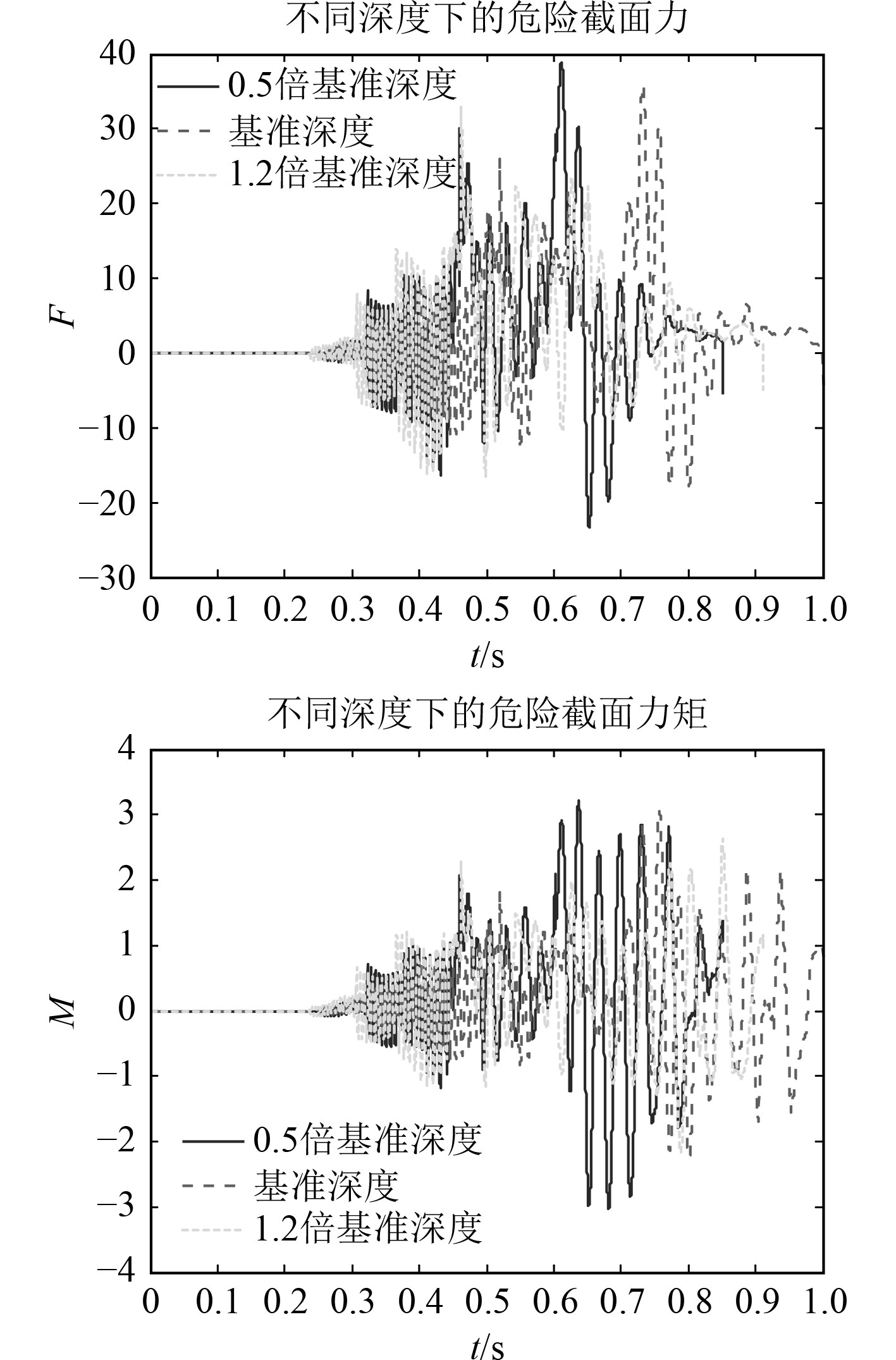
图5为不同发射深度下的航行体的危险截面受到的载荷。可以看出，不同发射深度下，危险截面受到的力和力矩曲线趋势一致，发射深度对危险截面载荷影响不大。

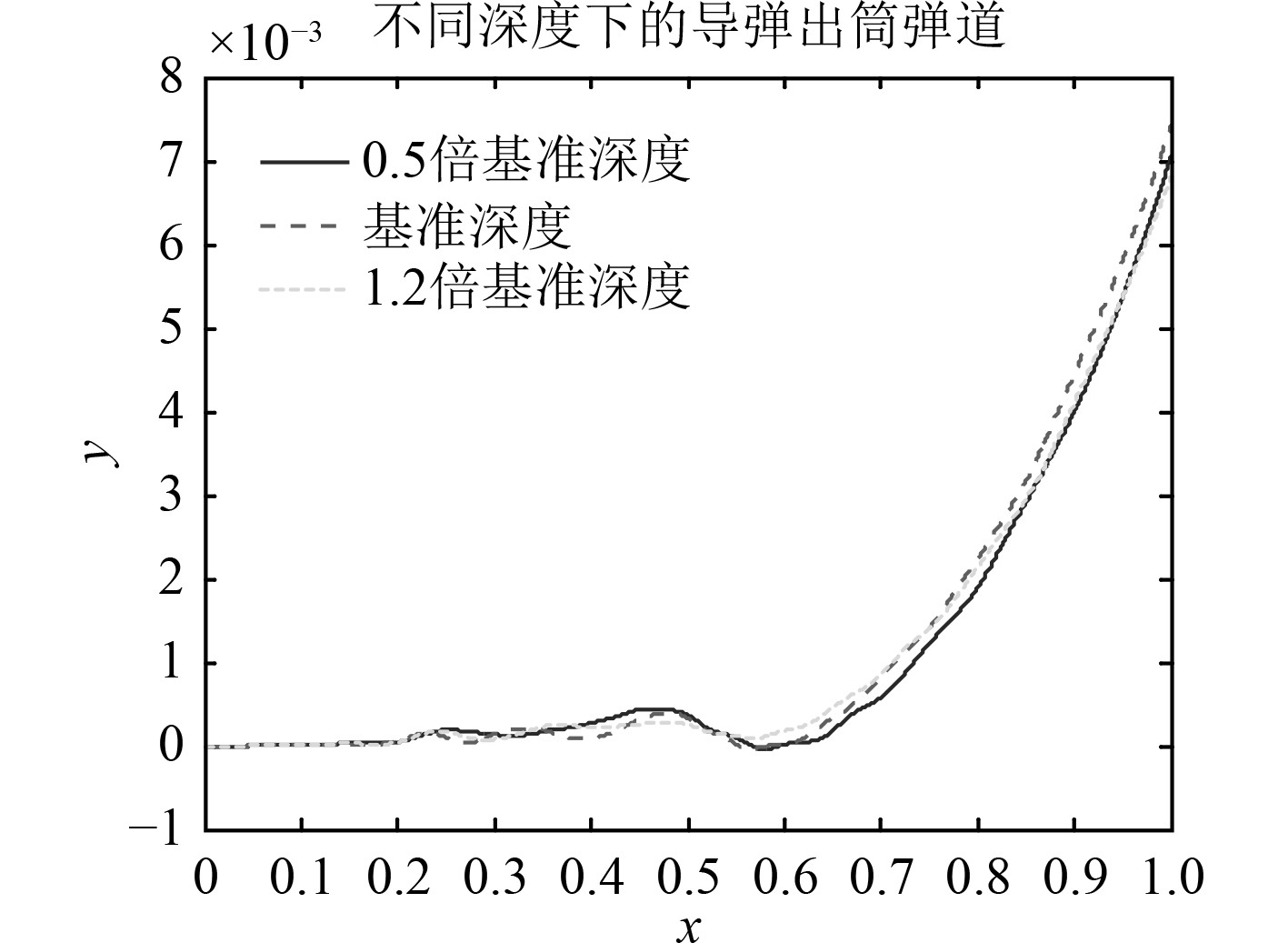
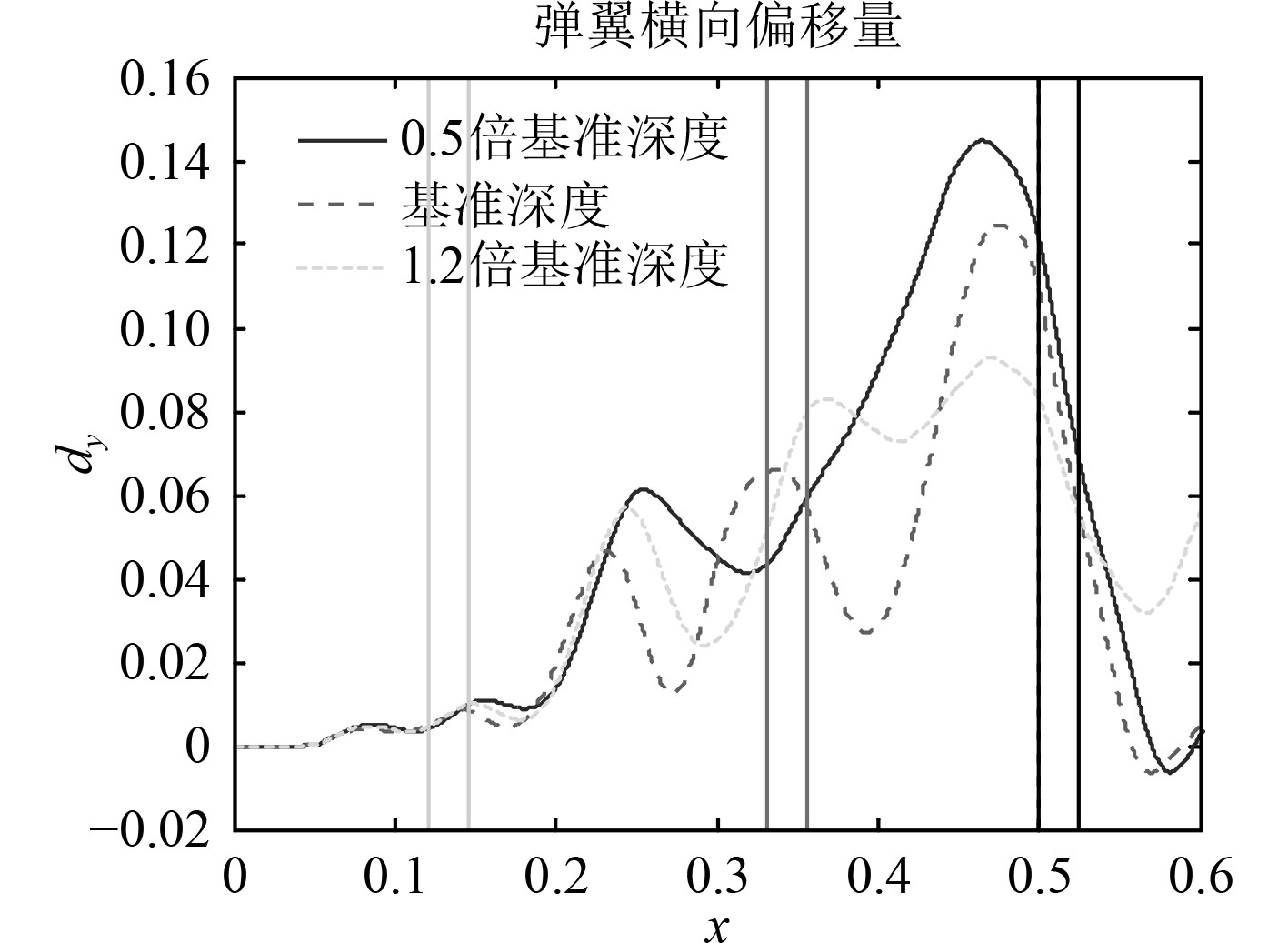
图6和图7为不同深度下出筒弹道和翼横向偏移与气密环相对位置关系。图中，从左到右的3组进竖线分别为第4圈、第5圈和第6圈气密环。

从图7可以看出，不同发射深度条件下，弹翼横向偏移趋势一致，振荡上升。弹翼在气密环处横向偏移量与振荡频率有关，与航速没有明显的关系，各圈气密环的横向偏移量见表1。

4.2 航速影响

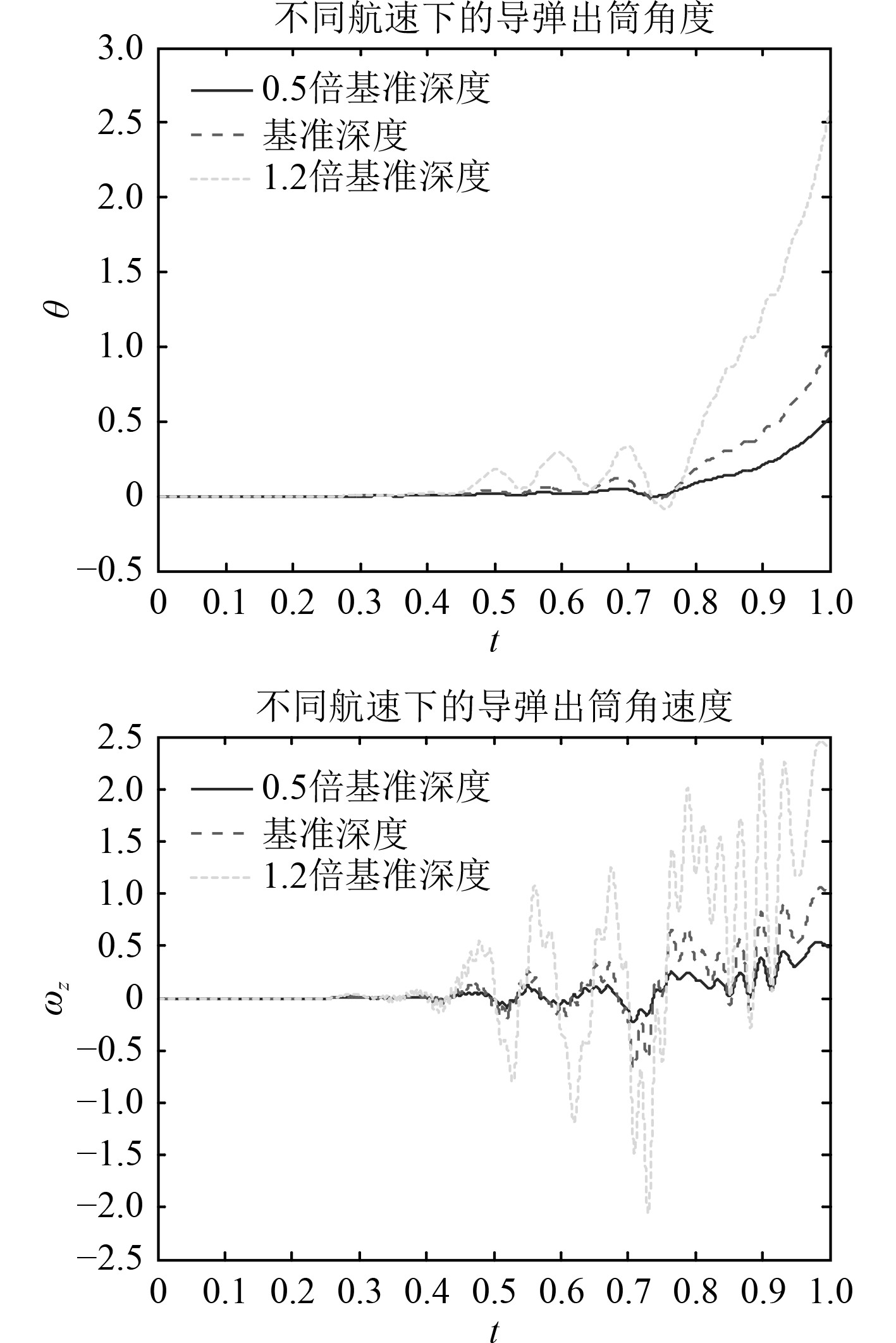
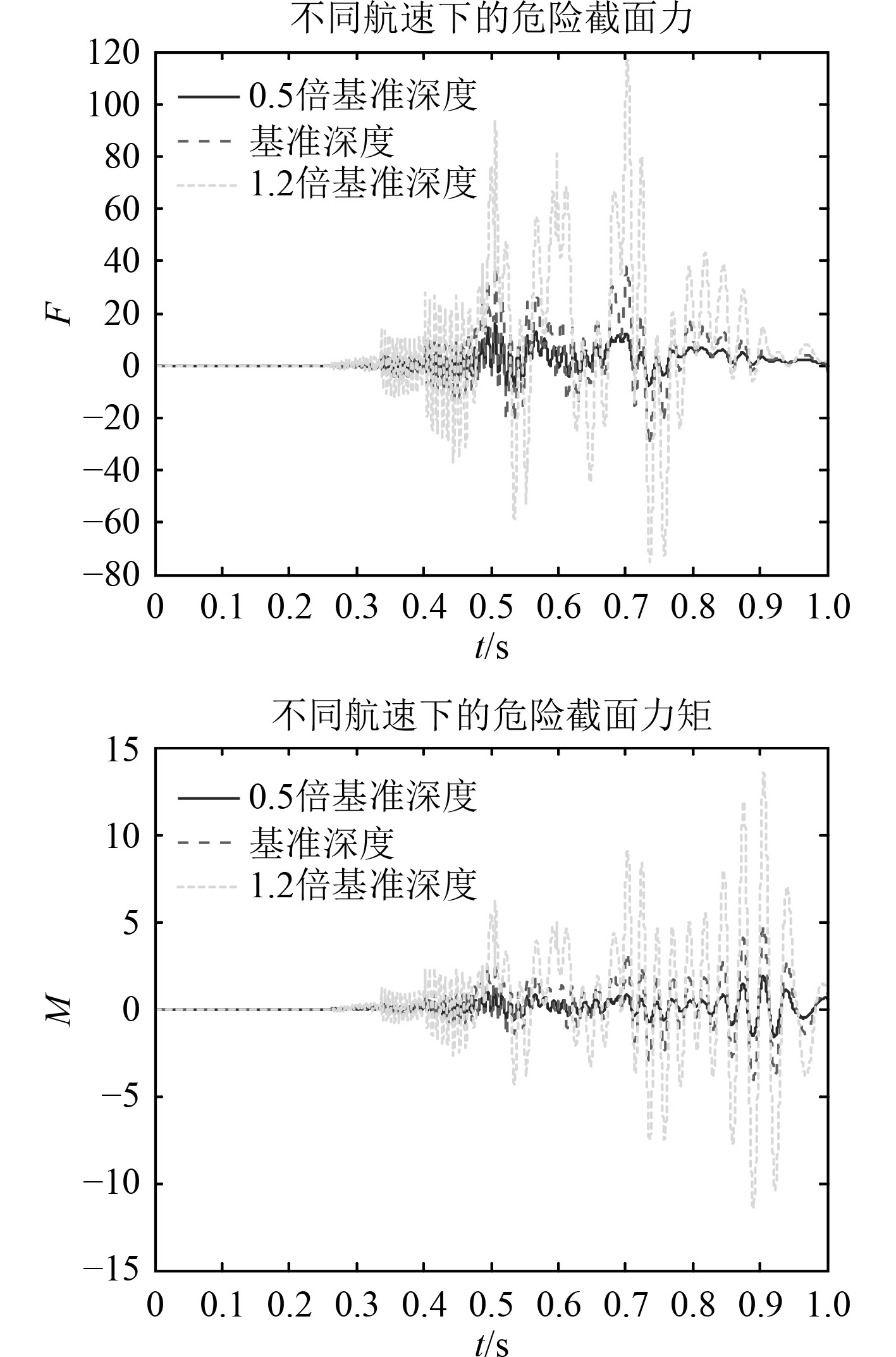
针对气密环-减震垫弹筒匹配方式的计算对象，进行基准航速、0.5倍基准航速和1.2倍基准航速计算。图8为不同平台航速下的航行体的出筒姿态。可以看出，不同发射深度下，出筒角度与出筒角速度趋势一致，航速越高出筒角度与角速度越大，这是由于航速越大，与水流的相对速度越大，从而航行体出筒横向力越大。图9为不同深度下的危险截面载荷。可以看出，不同航速下，危险截面力和力矩曲线趋势一致，航速越大，危险截面受到的力与力矩越大，载荷波动越明显。

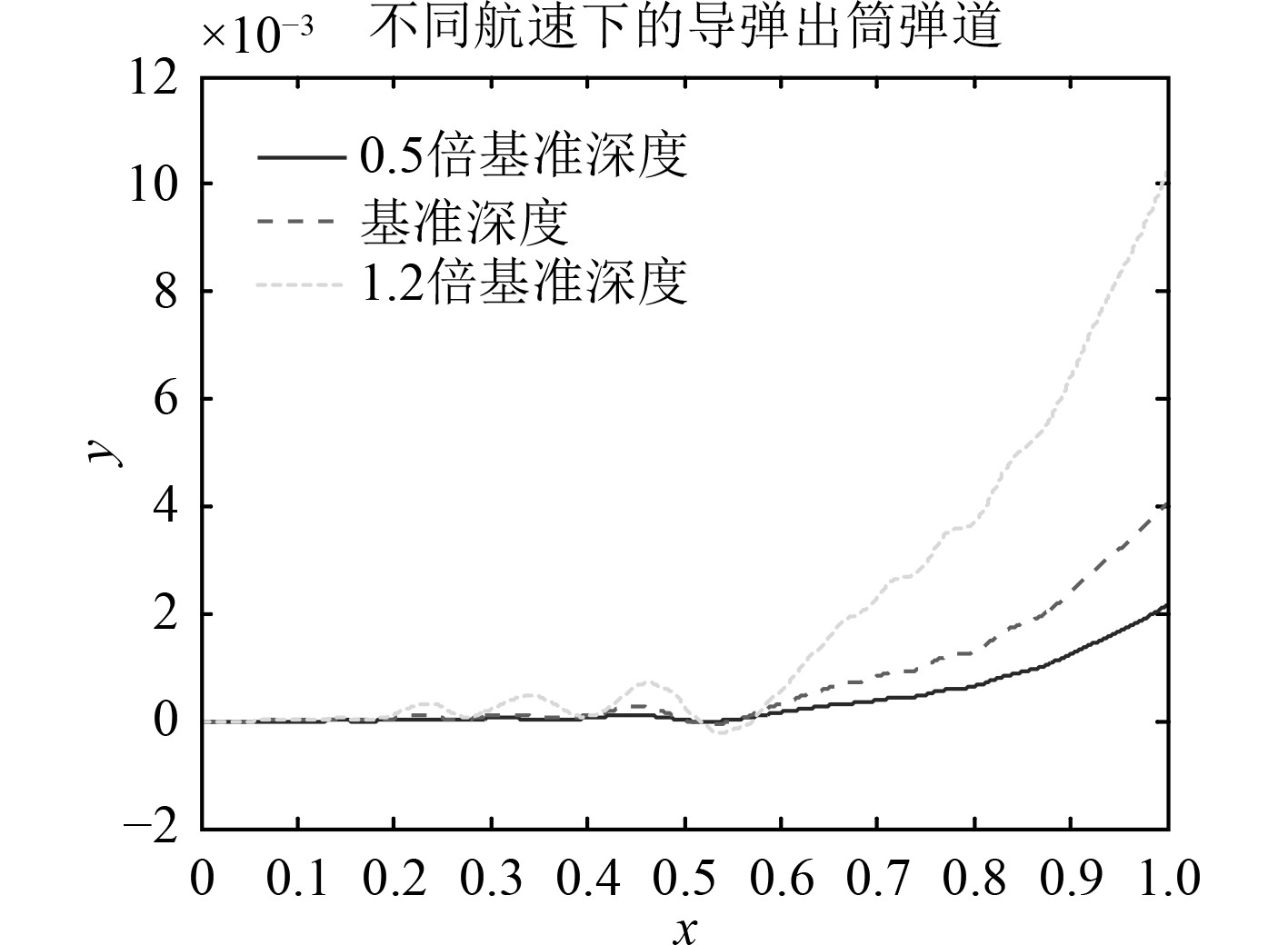
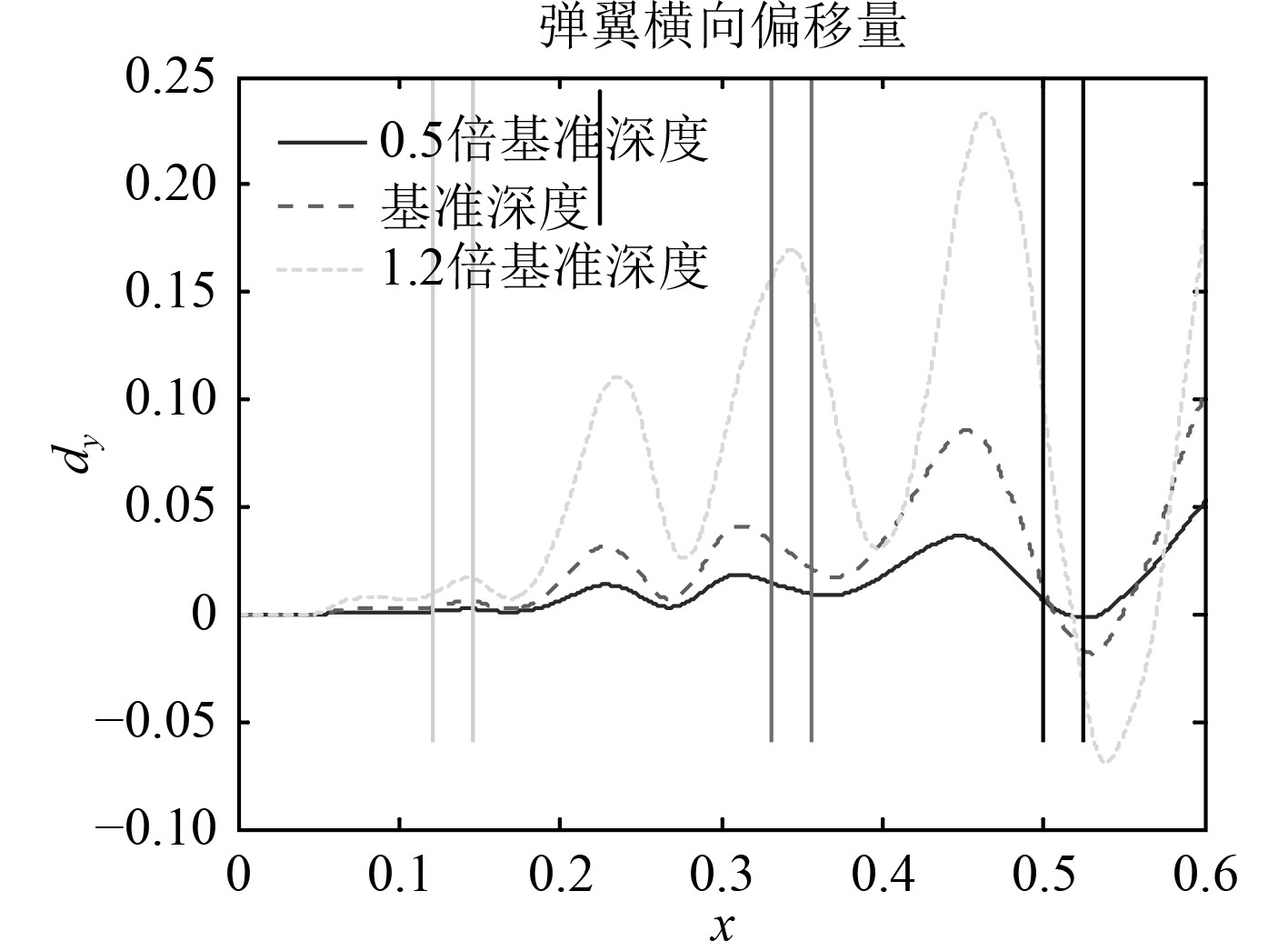
图10和图11为不同航速下出筒弹道和弹翼横向偏移与第3圈、第4圈和第5圈气密环相对位置关系。

从图11可以看出，不同发射航速条件下，弹翼横向偏移趋势一致，振荡上升。航速越低，弹翼偏移的横向偏移量振荡频率越高。弹翼在气密环处横向偏移量不仅与航速有关，还与振荡频率有关。各圈气密环的横向偏移量见表2。

4.3 减震垫刚度影响

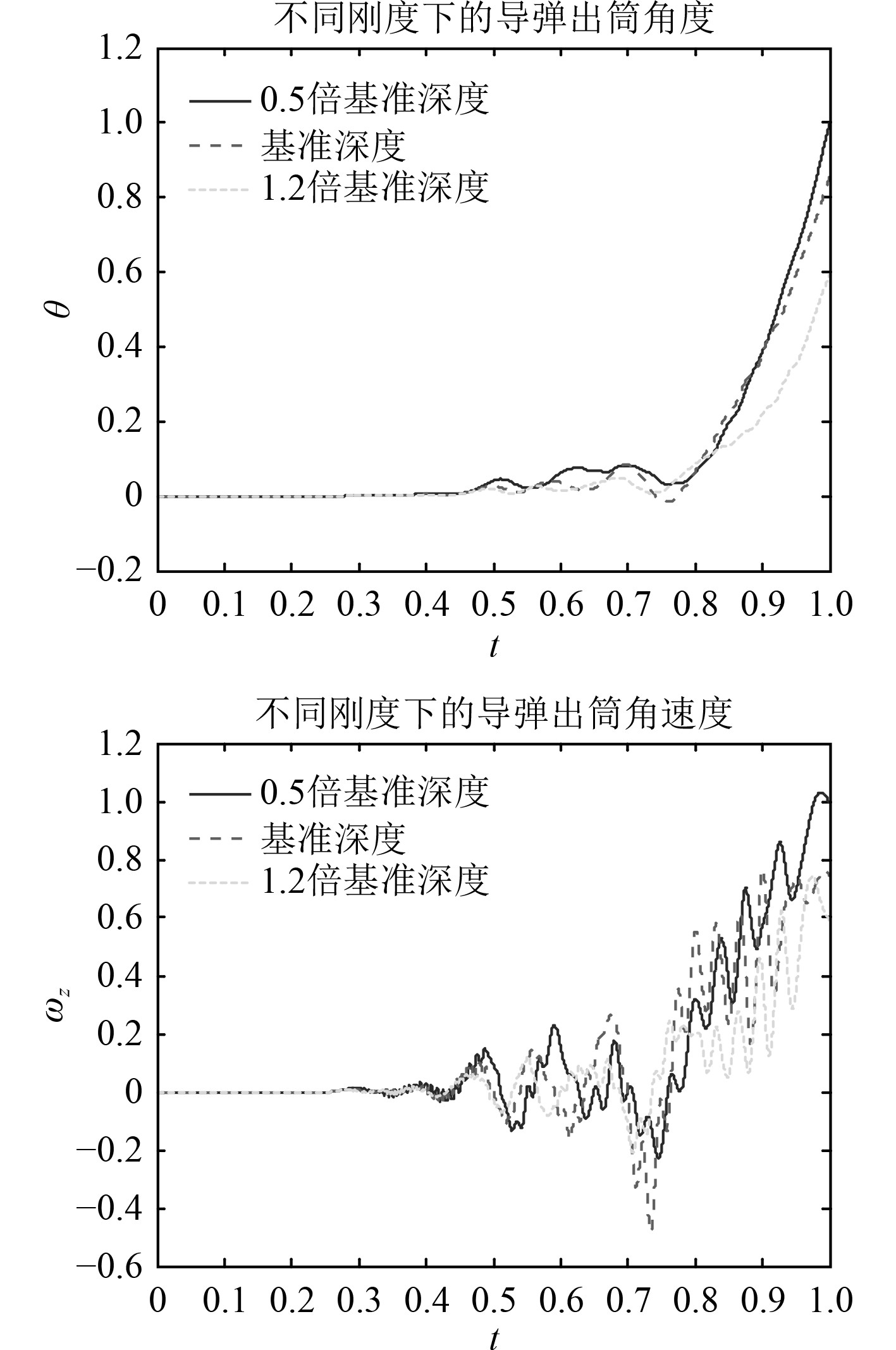
针对气密环-减震垫弹筒匹配方式的计算对象，进行基准刚度、1.5倍基准刚度和2倍基准刚度计算。图12为不同刚度下的航行体的出筒姿态。可以看出，不同减震垫刚度条件下，出筒角度与出筒角速度趋势一致，减震垫刚度越高出筒角度与角速度越小。这是由于减震垫刚度越大，导向性能越好，对航行体在筒内的约束力越大，从而航行体出筒姿态越小。高刚度情况，出筒姿态振荡频率略高。

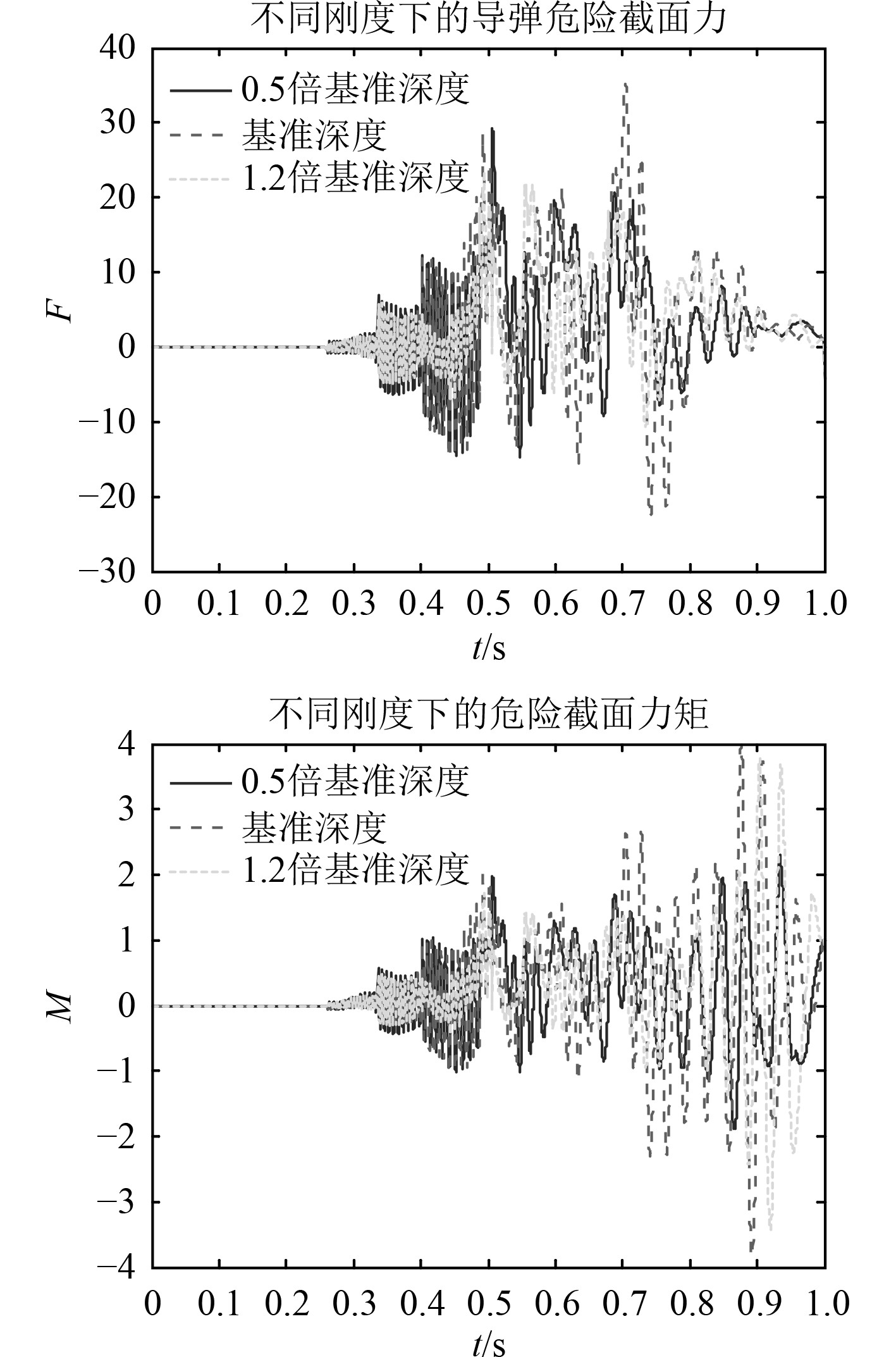
图13为不同深度下的危险截面载荷。可以看出，不同减震垫刚度条件下，危险截面力和力矩曲线趋势一致，减震垫刚度越大，危险截面力与力矩的振荡频率越高。

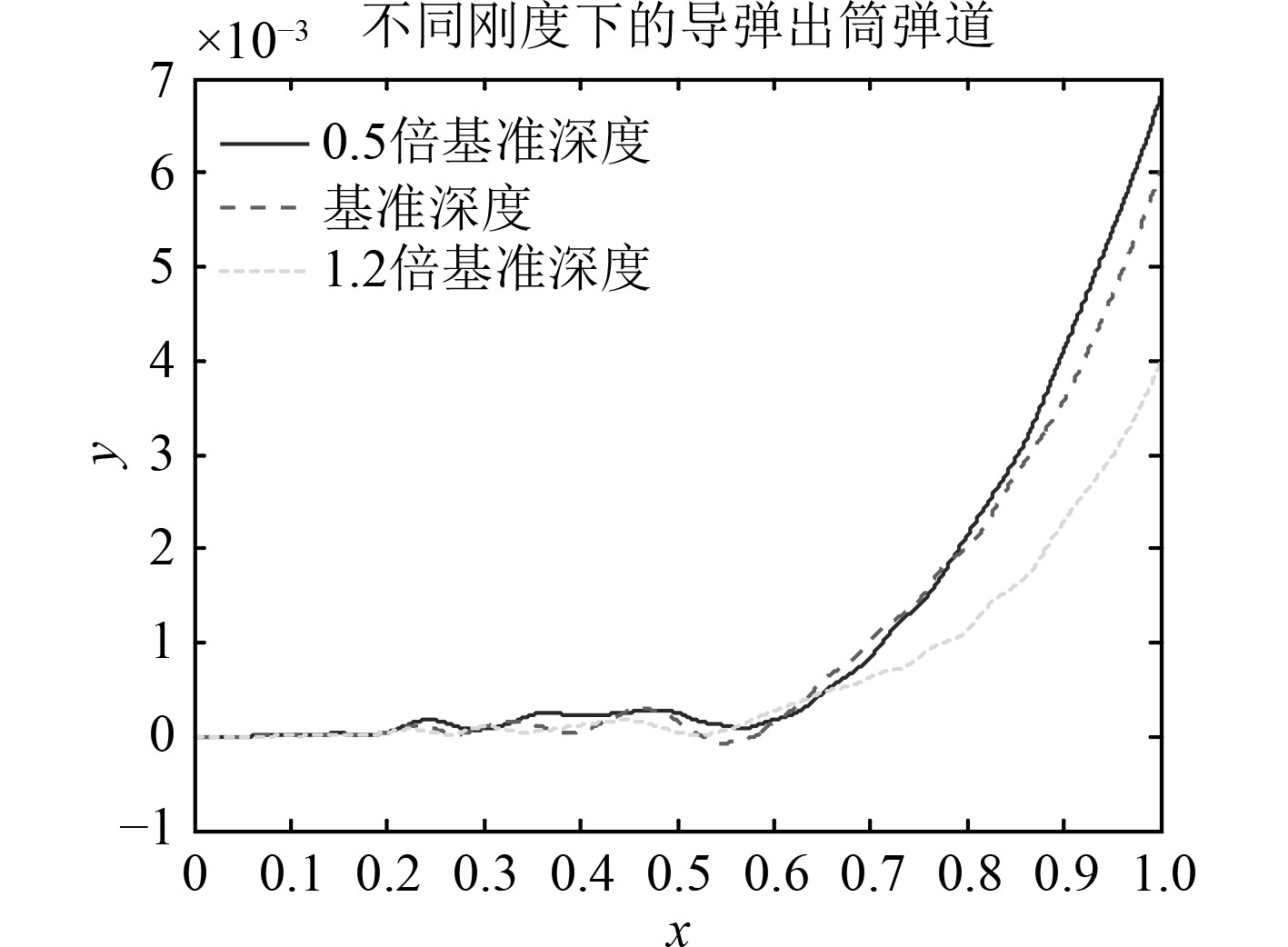
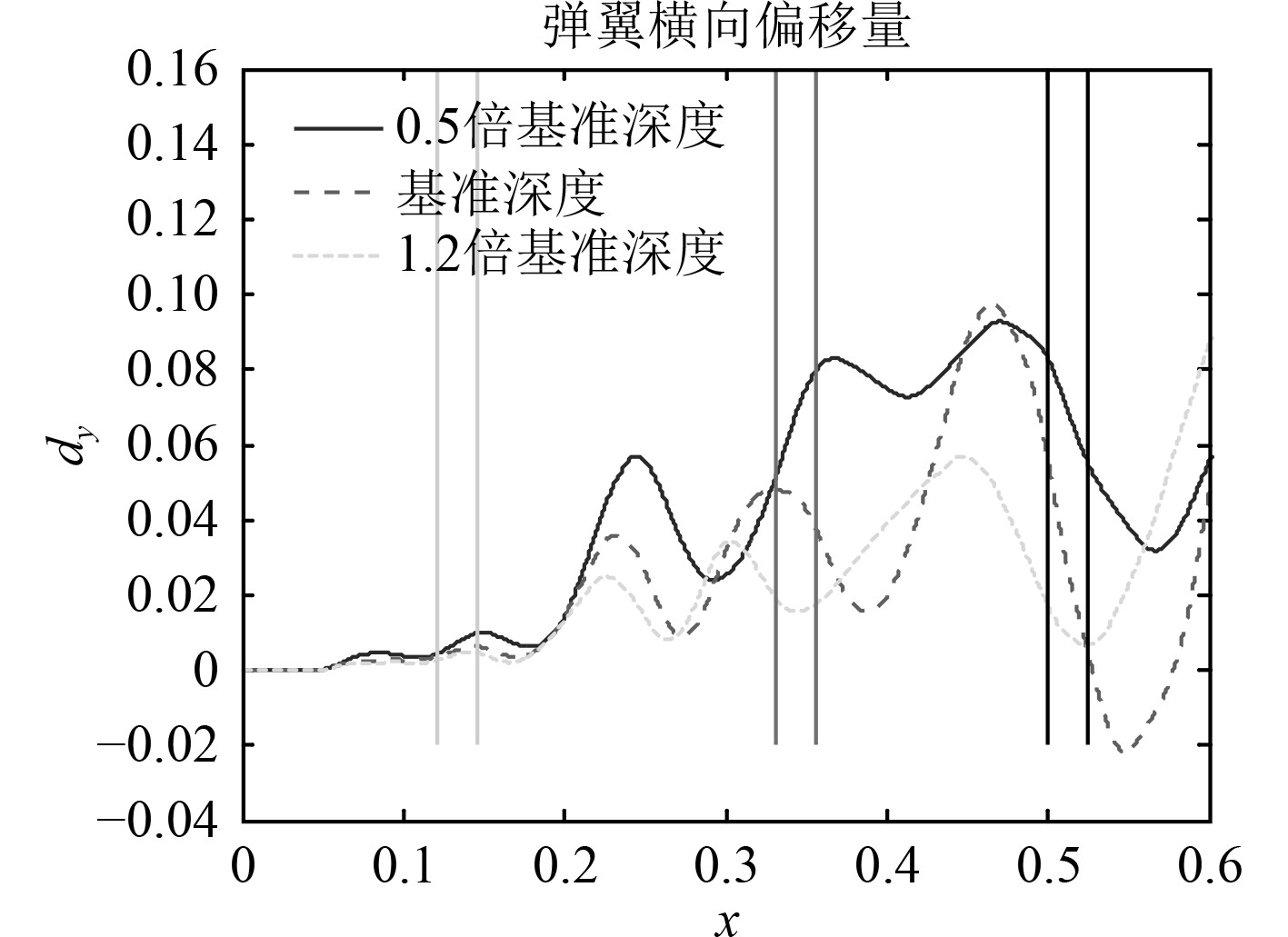
图14和图15为不同航速下出筒弹道和弹翼横向偏移与第3圈、第4圈和第5圈气密环相对位置关系。

从图15可以看出，不同减震垫刚度条件下，弹翼横向偏移趋势一致，振荡上升。刚度越大，弹翼偏移的横向偏移量振荡频率越高。弹翼在气密环处横向偏移量与振荡频率有关。各圈气密环的横向偏移量见表3。

5 结　语

本文根据减震垫变形模型和航行体出筒横向力计算方法，对某带翼战术航行体垂直发射过程的横向动力进行了仿真，获得了不同平台航速、发射深度、减震垫刚度条件下的出筒姿态、危险截面力与力矩，以及弹翼在过各圈气密环时的横向偏移量。仿真结果表明，发射深度对弹翼出筒过程中的横向偏移影响不大，减震垫刚度越大、航速越大时，弹翼出筒过程中的横向偏移越大。但在各圈气密环处，弹翼的偏移不仅与发射条件相关，还与偏移的振荡频率有关，在弹筒匹配方案设计时，要充分考虑与论证，以保证航行体经过时翼不划伤气密环。