在舰船目标识别与路径规划等领域中,需远程传输舰船数字图像。为提升舰船数字图像传输的安全性,确保舰船安全航行,需对舰船数字图像进行水印处理,防止遇到攻击时,出现信息泄露问题[1-3],影响舰船航行安全。
为此需研究图像水印算法,提升图像安全性,确保舰船安全航行。沈艳冰等[4]将舰船RGB图像变更成YCrCb图像,并提取Y分量,得到对角矩阵,通过加性规则将水印嵌入对角矩阵内,完成水印嵌入,该算法在承受噪声攻击时,可有效嵌入水印,具备较优的水印嵌入效果。李淑芝等[5]先分块处理原始图像,通过各分块的灰度共生矩阵,得到图像的纹理特征,并求解纹理特征的复杂度,再降序排列纹理特征,用于确定水印嵌入位置,依据嵌入位置求解各分块的JND值,通过JND值设计水印嵌入规则,完成图像水印嵌入,该算法具备水印嵌入的可行性。但这2种方法均不具备抗旋转与抗剪切攻击能力,当图像存在旋转与剪切情况,这2种算法的水印嵌入效果均较差。
改进压缩感知理论可利用较少的信息,完成原始图像的重构,大幅度减轻信息传输的压力[6],具备较优的稳定性与抗剪切攻击能力等,正交匹配追踪为常见的压缩感知重构算法。为此研究改进压缩感知的舰船数字图像水印算法,提升水印嵌入与提取效果。
1 舰船数字图像水印算法利用改进压缩感知理论,对舰船数字图像进行水印处理,提升舰船数字图像的安全性,具体原理为:先通过离散小波变换(discrete wacelet transform,DWT)稀疏分解舰船数字载体图像,获取舰船数字载体图像的高频与低频系数矩阵;再通过改进压缩感知理论获取测量观测矩阵,依据观测矩阵处理高频与低频系数矩阵,获取相应的舰船数字图像系数矩阵观测值;然后在高频系数矩阵观测值内嵌入水印,并存储嵌入位置的分块索引,构建索引矩阵。最后通过改进压缩感知理论内的改进正交匹配追踪算法,重构高频与低频舰船数字图像系数矩阵的观测值,获取高频与低频系数矩阵,并融合这2个矩阵,同时对其展开离散小波反变换处理,获取嵌入水印的舰船数字图像。
1.1 基于DWT的舰船数字图像稀疏分解利用改进压缩感知理论水印处理舰船数字图像水印时,舰船数字图像信号越稀疏,重构效果越佳[7],因为原始舰船数字图像矩阵不是稀疏矩阵,所以需要通过DWT稀疏分解原始图像。
利用DWT稀疏分解原始舰船数字图像信号后,可获取图像各子频段的信号,且获取的信息非常丰富[8],为舰船数字图像重构提供丰富的信息,提升舰船数字图像重构质量。令舰船数字图像系数处理时,离散小波是
| $ {\psi _{m,n}}\left( t \right) = \dfrac{{\psi \left( {\dfrac{{t - nba_{}^m}}{{a_{}^m}}} \right)}}{{\sqrt {a_{}^m} }}。$ | (1) |
其中:
舰船数字图像的DWT如下:
| $ {W_f}\left( {m,n} \right) = \int_R {f\left( t \right){\psi _{m,n}}\left( t \right){\rm{d}}t}。$ | (2) |
其中:
利用高通滤波器处理的舰船数字图像
| $ {X'_1} = \sum\limits_{z = - \infty }^\infty {{W_f}X\left( z \right)h\left( {m - z} \right)}。$ | (3) |
其中:
通过扩展尺度因子,扩展倍数为2倍,可提升DWT的可逆性,扩展后的舰船数字图像信号高频系数矩阵为:
| $ {\hat X_1} = \sum\limits_{z = - \infty }^\infty {{W_f}X\left( z \right)h\left( {2m - z} \right)},$ | (4) |
利用低通滤波器处理
| $ {\hat X_2} = \sum\limits_{z = - \infty }^\infty {{W_f}X\left( z \right)g\left( {2m - z} \right)}。$ | (5) |
其中,
利用压缩感知理论获取获取舰船数字图像高频与低频系数矩阵的观测值,以获取低频系数矩阵的观测值为例,令舰船数字图像高频系数矩阵的信号长度为
| $ {y_1} = {\boldsymbol{\varphi}} \theta 。$ | (6) |
其中:
令舰船数字图像高频系数矩阵的观测矩阵是
| $ {s_1} = {{\boldsymbol{\varPhi}} _1}{\boldsymbol{\varphi}} \theta = {{\boldsymbol{Q}}_1}\theta,$ | (7) |
其中:
利用Kent混沌序列替换
Kent混沌映射为离散混沌系统,且具备代表性,表达公式如下:
| $ {\hat x_{1,l + 1}} = \left\{ \begin{array}{*{20}{l}} \dfrac{{{{\hat x}_{1,l}}}}{v},& 0 < {{\hat x}_{1,l}} \leqslant v ,\\ \left( {1 - {{\hat x}_{1,l}}} \right)\left( {1 - v} \right),& v< {{\hat x}_{1,l}} < 1 。\\ \end{array} \right. $ | (8) |
其中:
利用
| $ {\hat {\boldsymbol{\varPhi}} _1} = \frac{1}{{\sqrt M \cdot \sigma \cdot \lambda }}\left( \begin{array}{*{20}{c}} {{\hat x}_{1,0}}&{{\hat x}_{1,M}}& \cdots & {{\hat x}_{1,M\left( {L - 1} \right)}} \\ {{\hat x}_{1,1}}&{{\hat x}_{1,M + 1}}&\cdots& {{\hat x}_{1,M\left( {L - 1} \right) + 1}} \\ { \vdots}& \vdots& \cdots& \vdots \\ {{\hat x}_{1,M - 1}}& {{\hat x}_{1,2M - 1}}& \cdots&{{\hat x}_{1,ML - 1}} \end{array} \right)。$ | (9) |
其中:
利用
在舰船数字图像高频系数矩阵的观测值内嵌入水印后,利用改进压缩感知理论内的改进正交匹配追踪算法,重构舰船数字图像高频与低频系数矩阵的观测值。具体步骤如下:
步骤1 输入压缩感知矩阵
步骤2 计算残差
步骤3 如果某原子符合
步骤4 更新
步骤5 通过最小二乘法求解原始舰船数字图像系数矩阵观测值的估计值
步骤6 更新残差
舰船数字图像高频与低频系数矩阵观测值均由上述步骤进行重构,重构后的高频与低频舰船数字图像系数矩阵是
在舰船数字图像系数矩阵观测值嵌入水印的具体步骤如下:
步骤1 分块处理原始舰船数字载体图像
步骤2 通过尺寸是
步骤3 Arnold置乱处理待嵌入的舰船数字图像水印
| $ \left[ \begin{gathered} {p'} \\ {q'} \\ \end{gathered} \right] = \left[ \begin{gathered} 1\mathop {}\nolimits_{} 1 \\ 1\mathop {}\nolimits_{} 2 \\ \end{gathered} \right]\left[ \begin{gathered} p \\ q \\ \end{gathered} \right]\bmod \rho。$ | (10) |
其中:水印置乱前后的像素是
步骤4 在
| $ {s'_{1,2\tau }} = \left\{ \begin{array}{*{20}{l}} {s_{1,2\tau - 1}} + \alpha \varsigma \varpi ,& \left| {{s_{1,2\tau }} - {s_{1,2\tau - 1}}} \right| < \varepsilon ' ,\\ {s_{1,2\tau }},& {\rm{else}} 。\ \end{array} \right. $ | (11) |
其中:
嵌入时,令各分块舰船数字图像系数矩阵观测值最多能够嵌入一次
步骤5
以大小为512×512的舰船数字图像为实验载体图像,以大小为50×50的二值化图像为水印,利用本文算法将水印嵌入舰船数字图像内,分析本文算法的水印嵌入与提取效果。
实验舰船数字图像与水印图像如图1所示。

|
图 1 舰船数字图像与水印图像 Fig. 1 Ship Digital Image and Watermark Image |
利用本文算法在实验舰船数字图像内嵌入水印,嵌入水印后的舰船数字图像如图2所示。

|
图 2 嵌入水印后的舰船数字图像 Fig. 2 Digital image of ship embedded with watermark |
由图2可知,本文算法可有效在实验舰船数字图像内嵌入水印,与原始图像对比可知,嵌入水印后的图像与原始图像基本无差别,说明本文算法具备较优的水印嵌入透明性。
在嵌入水印后的舰船数字图像内加入椒盐噪声,利用本文算法在加入噪声后的舰船数字图像内,提取水印,提取结果如图3所示。

|
图 3 水印提取结果 Fig. 3 Watermark extraction results |
由图3可知,本文算法可有效在加入椒盐噪声后的实验舰船数字图像内,提取水印,与原始水印对比可知,提取的水印内虽然包含大量噪声,但依旧能够提取完整的水印。实验证明:在舰船数字图像内加入椒盐噪声后,本文算法具备水印提取的有效性。
利用峰值信噪比(PSNR)衡量水印嵌入的透明性,利用归一化相关系数(NC)衡量水印提取精度,PSNR与NC值越高,说明水印嵌入与提取的透明性越佳、精度越高,PSNR以及NC分别对应的阈值是30 dB与0.7。分析本文算法在不同图像压缩质量因子时,对实验舰船 水数字图像嵌入与提取效果,分析结果如图4所示,压缩质量因子大小与压缩后舰船数字图像内有效信息量呈正比。
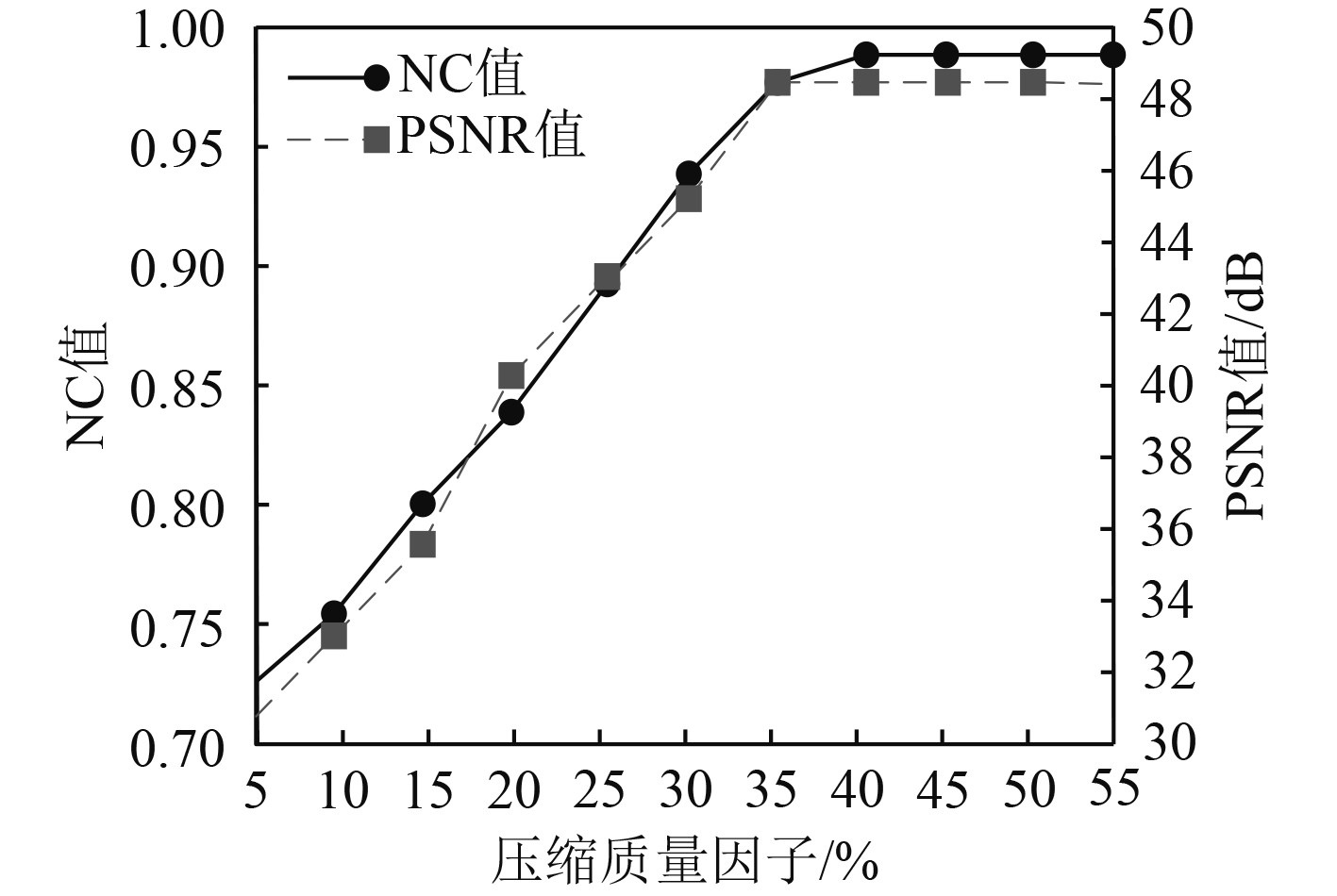
|
图 4 舰船数字图像水印嵌入与提取效果 Fig. 4 Watermark embedding and extraction effect of ship digital image |
由图4可知,随着图像压缩质量因子的提升,本文算法提取舰船数字图像水印时的NC值呈上升趋势,当图像压缩质量因子达到40%时,NC值上升至最高值,并趋于稳定,稳定在0.98左右,最低NC值在0.73左右,并未低于设置阈值,说明在不同图像压缩情况下,本文算法提取的水印与原始水印均非常接近,即水印提取精度较高;图像压缩质量因子与PSNR值具有正相关关系,当图像压缩质量因子达到35%时,PSNR值达到最大值,并趋于稳定,稳定在48 dB左右,最低PSNR值在31 dB左右,并未低于设置阈值,说明在不同图像压缩情况下,本文算法嵌入水印的透明性均较优。
3 结 语在传输舰船数字图像时,需对其进行水印处理,提升舰船数字图像的安全性。为此,本文研究改进压缩感知的舰船数字图像水印算法,提升水印嵌入的透明性与水印提取精度,应用水印算法后,可有效提升图像的安全性,为促进舰船数字图像水印领域的发展提供参考依据。
| [1] |
李伟岸, 熊祥光, 夏道勋. 基于Schur分解和混沌置乱的彩色图像鲁棒水印算法[J]. 计算机工程与科学, 2021, 43(7): 1243-1249. DOI:10.3969/j.issn.1007-130X.2021.07.013 |
| [2] |
牛盼盼, 王向阳, 杨思宇, 等. 基于二元Weibull分布的非下采样Shearlet域图像水印算法[J]. 计算机研究与发展, 2019, 56(7): 1454-1469. DOI:10.7544/issn1000-1239.2019.20180278 |
| [3] |
齐向明, 徐嫚, 李玥, 等. 一种尺度空间特征区域的强鲁棒性水印算法[J]. 计算机应用研究, 2019, 36(6): 1793-1796+1802. DOI:10.19734/j.issn.1001-3695.2018.01.0056 |
| [4] |
沈艳冰, 杨阳, 李竹. 一种适用于QR码的彩色图像数字水印算法[J]. 智能系统学报, 2020, 15(5): 949-955. DOI:10.11992/tis.201903016 |
| [5] |
李淑芝, 龙香玉, 邓小鸿, 等. 结合纹理复杂度和JND模型的图像水印算法[J]. 计算机应用研究, 2019, 36(2): 528-531+542. DOI:10.19734/j.issn.1001-3695.2017.09.0900 |
| [6] |
王楠, 李智, 程欣宇, 等. 基于均值比例与压缩感知的视频双水印算法[J]. 计算机工程, 2019, 45(3): 250-255+261. DOI:10.19678/j.issn.1000-3428.0052206 |
| [7] |
李莹莹, 张毅锋, 程旭, 等. 基于DWT最优多子图和SIFT几何校正的鲁棒水印算法[J]. 计算机应用研究, 2019, 36(6): 1819-1823+1827. DOI:10.19734/j.issn.1001-3695.2018.01.0042 |
| [8] |
刘琰, 周理. 基于小波变换域的数字图像嵌入和提取方法[J]. 沈阳工业大学学报, 2019, 41(1): 68-72. DOI:10.7688/j.issn.1000-1646.2019.01.13 |
 2022, Vol. 44
2022, Vol. 44
