0 引　言

近年来，信息技术与计算机技术得到了大力的发展与普及，数字视频技术也迎来了高速发展期，受到多个领域的关注与应用，尤其是航海领域^[1]。嵌入式网络的出现，使得船舶之间通信更加便利、稳定。嵌入式网络具有较好的适用性与便捷性，能够直接搭载在船舶，为船舶视频监控提供有效的支撑。

船载嵌入式网络视频监控图像由于天气因素、环境因素、设备因素等影响，存在着大量的噪声点、模糊点，使得视频监控图像清晰度较差，细节信息无法得到完整的、准确地显示，影响视频监控图像的应用以及船舶航行状态的判定，是现今导致船舶航行事故发生的关键原因之一^[2]。为了避免上述事件的发生，引入模糊集理论提出船载嵌入式网络视频监控图像模糊细节增强系统设计。

1 视频监控图像模糊细节增强系统 1.1 视频监控图像预处理

由于船舶航行环境较为复杂，致使船载嵌入式网络视频监控图像存在着颜色失真的现象，对细节增强具有不利影响，故通过动态范围拉伸模式预处理视频监控图像。由于图像细节增强过程中，计算机系统对亮度变化较为敏感，因此在视频监控图像预处理过程中只对亮度通道进行处理^[3]。为了方便研究的进行，将拉伸后的图像RGB颜色空间转换为HSI颜色空间，转换公式为：

$ \left[ {\begin{array}{*{20}{c}} H&S&I \end{array}} \right] = \xi _{RGB}^{HSI}\left[ {\begin{array}{*{20}{c}} {R'}&{G'}&{B'} \end{array}} \right]。$

(1)

式中， $ \xi _{RGB}^{HSI} $ 是颜色空间RGB→HSI的转换函数。

上述过程完成了视频监控图像的预处理，消除了视频监控图像颜色失真现象，为后续视频监控图像细节模糊熵的计算奠定基础。

1.2 视频监控图像细节模糊熵计算

以上述预处理后的视频监控图像 $ f'\left( {x,y} \right) $ 为依据，基于模糊集理论计算视频监控图像细节模糊熵，为图像细节增强做好准备^[4]。将视频监控图像看作为一个模糊集合，传统系统采用隶属度函数表示模糊集合的不确定性，其会受到主观影响，无法实现模糊程度的定量描述^[5]。因此，引入模糊熵概念，对视频监控图像细节模糊程度进行定量表示。假设视频监控图像 $ f'\left( {x,y} \right) $ 模糊集合表示为 $ F = \{ {f'_1},{f'_2}, \cdots , {f'_i}, \cdots ,{f'_n}\} $ ， $ {f'_i} $ 代表像素 $ i $ 对应的模糊子集，其模糊熵计算公式为：

$ E\left( {{f'_i}} \right) = 1 - \frac{{{\chi _e}{\delta _\alpha }\left( {{f'_i},{f'_j}} \right)}}{{{n^{1/\alpha }}}}。$

(2)

式中： $ E\left( {{f'_i}} \right) $ 为模糊子集 $ {f'_i} $ 对应的模糊熵； $ {\chi _e} $ 为模糊参数； $ {\delta _\alpha }\left( {{f'_i},{f'_j}} \right) $ 为模糊子集 $ {f'_i} $ 与 $ {f'_j} $ 之间的相似程度，由 $ {\delta _\alpha }\left( {{f'_i},{f'_j}} \right) = {\left[ {\displaystyle\sum\limits_{i = 1}^n {{{\left| {{\beta _{{f'_i}}} - {\beta _{{f'_j}}}} \right|}^\alpha }} } \right]^{1/\alpha }} $ 计算获得， $ {\ \beta _{{f'_i}}} $ 与 $ {\ \beta _{{f'_j}}} $ 为模糊子集 $ {f'_i} $ 与 $ {f'_j} $ 的隶属度数值； $ \alpha $ 为随机常数，主要作用为降低模糊熵计算误差； $ n $ 为模糊子集的总数量。

以计算结果−模糊熵 $ E\left( {{f'_i}} \right) $ 衡量模糊集合 $ F = \left\{ {{f'_1},{f'_2}, \cdots ,{f'_i}, \cdots ,{f'_n}} \right\} $ (视频监控图像)的模糊程度，判定图像细节是否属于一个模糊子集的程度，为后续最佳模糊参数的确定提供便利^[6]。

1.3 最佳模糊参数确定

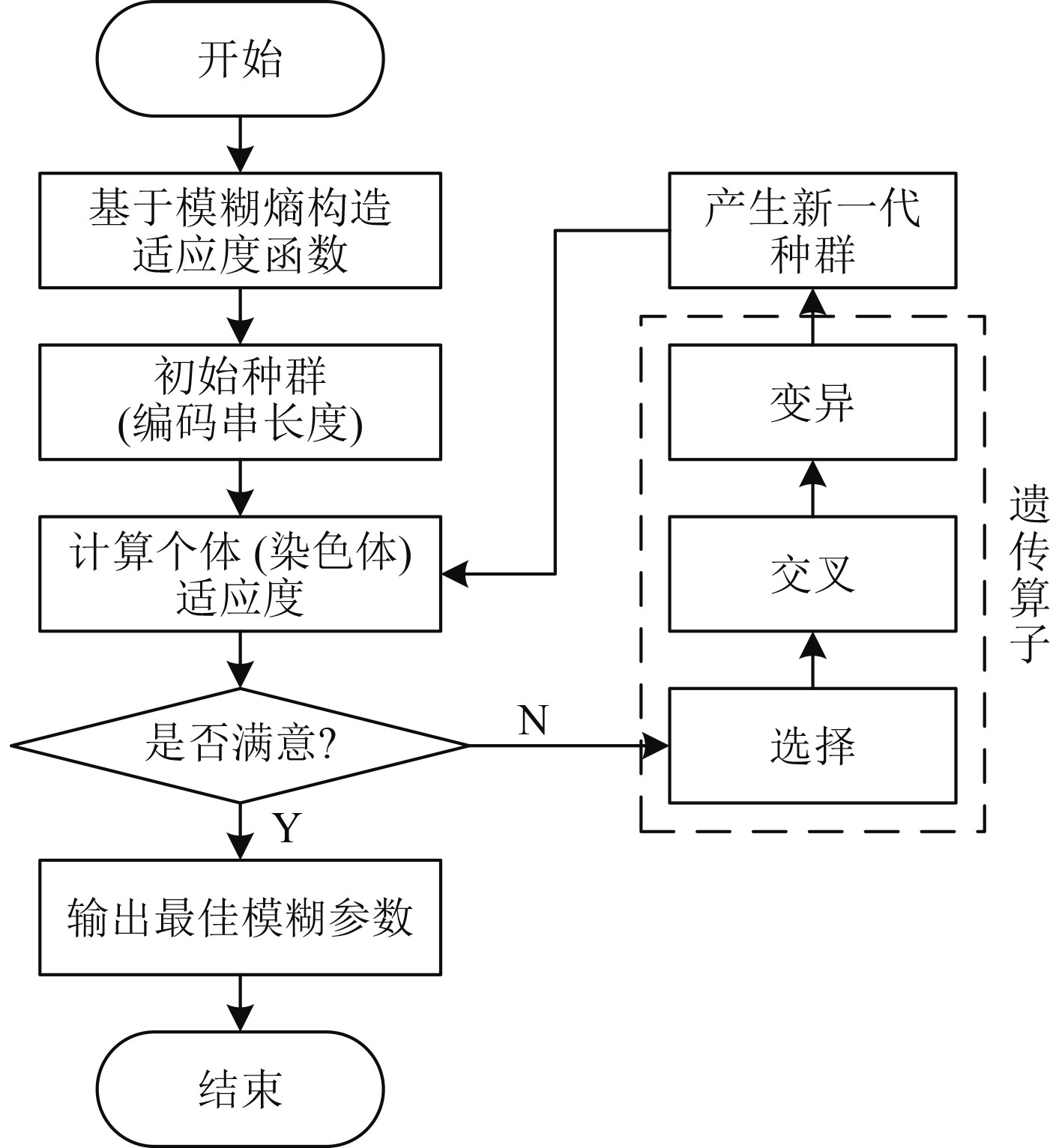
以获得的视频监控图像细节模糊熵为基础，利用遗传算法确定最佳模糊参数，为最终图像细节增强做准备。遗传算法具有较强的并行性自动搜索与全局寻优能力，可以在最短时间内获取最佳模糊参数，以此来降低图像细节增强运算时间，便于设计系统的实际应用^[7]。基于遗传算法的最佳模糊参数确定程序如图1所示。

对视频监控图像 $ f'\left( {x,y} \right) $ 中的每一个细节进行编码处理，编码结果显示为8为二进制串，由数字0与1构成^[8]。另外，由于视频监控图像灰度值范围为[0.255]，则模糊参数 $ {\chi _e} $ 的取值范围为[0.255]，其初始数值采用随机方式产生。适应度函数的构造是遗传算法的关键环节，此研究以模糊熵为基础，构造合理的适应度函数，表达式为：

$ K\left({x}_{i}\right)=\frac{E\left({f}^{\prime }_{i}\right)}{M}+{\varepsilon }_{i}=\frac{1}{M}-\frac{{\chi }_{e}{\delta }_{\alpha }\left({f}^{\prime }_{i},{f}^{\prime }_{j}\right)}{M\times {n}^{1/\alpha }}+{\varepsilon }_{i}。$

(3)

式中：K(x_i)为适应度函数，x_i为第 $ i $ 个染色体； $ M $ 为染色体种群规模；ε_i为误差校正项，主要作用是调节适应度数值的计算精度。

依据式(4)对全部个体适应度数值进行计算，以此为基础，选择前 $ m $ 个染色体作为交叉、变异操作的对象，设置交叉方式为单点交叉，获取新的个体，表示为：

$ {x'_i} = \frac{{{x_i} \times {P_1} \times {P_2}}}{{{\tau ^o}}}。$

(4)

式中： $ {x'_i} $ 为经过交叉、变异操作后的染色体；P₁与P₂为交叉概率与变异概率，其决定着遗传算法全局寻优能力的优劣； $ {\tau ^o} $ 为代沟，其最佳取值为0.9。

计算新染色体的适应度数值，重复进行上述操作，直至适应度数值达到最大值 $ \max \left[ {K\left( {{x_i}} \right)} \right] $ 为止，其对应的模糊参数 $ {\chi _e} $ 即为最佳模糊参数，将其记为 $ {\hat \chi _e} $ 。

应用遗传算法获得了最佳模糊参数 $ {\hat \chi _e} $ ，为后续图像模糊细节增强模型的提供准确参数支撑。

1.4 视频监控图像模糊细节增强

以上述确定的最佳模糊参数为基础，计算扩散系数，融合视频监控图像模糊梯度场情况，应用变分法求解修正隶属度函数，通过逆变换将视频监控图像从模糊域转换到灰度域，即可获得细节增强后的船载嵌入式网络视频监控图像。为了体现视频监控图像细节的模糊信息，基于最佳模糊参数计算扩散系数，表达式为：

$ \eta \left( {{{\hat \chi }_e}} \right) = 1 + \frac{\gamma }{{1 + {{\left( {{{\hat \chi }_e}/\kappa } \right)}^2}}}。$

(5)

式中： $ \eta \left( {{{\hat \chi }_e}} \right) $ 为最佳模糊参数 $ {\hat \chi _e} $ 对应的扩散系数； $ \gamma $ 为视频监控图像细节的放大因子； $ \kappa $ 为随着最佳模糊参数 $ {\hat \chi _e} $ 的增大，扩散系数 $ \eta \left( {{{\hat \chi }_e}} \right) $ 的衰减速度。

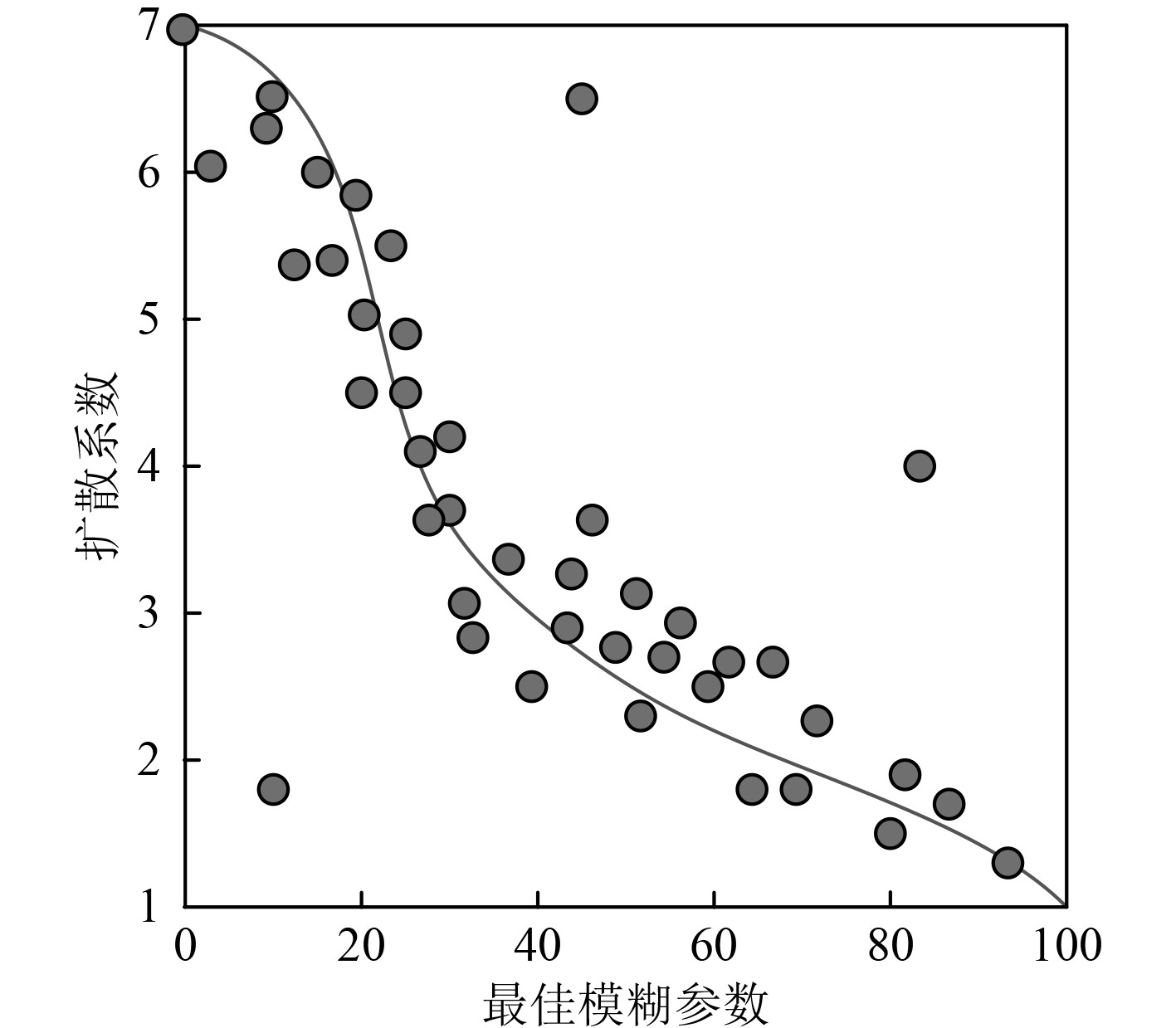
由式(6)可以看出最佳模糊参数与扩散系数之间存在着紧密的联系，关系拟合曲线如图2所示。可知，随着最佳模糊参数的增大，扩散系数呈现逐渐下降的趋势，最终趋向于1。扩散系数的添加，可以避免视频监控图像边缘细节过分增强的现象，使增强后的图像更加柔和。

视频监控图像模糊梯度场情况也是细节增强的关键所在。原始隶属度函数由视频监控图像灰度值决定，表达式为：

$ \beta \left( {x,y} \right) = \frac{{R\left( {x,y} \right) - {R_{\min }}\left( {x,y} \right)}}{{{R_{\max }}\left( {x,y} \right) - {R_{\min }}\left( {x,y} \right)}}。$

(6)

式中：β(x,y)为像素素(x,y)对应的隶属程度；R(x,y)为像素(x,y)的灰度值；R_min(x,y)与R_max(x,y)为灰度值的最小值与最大值。

以式(6)计算结果为基础，获取像素(x,y)的模糊梯度： $\varGamma \left( {x,y} \right)$ 是模糊梯度数值，可获得放大后的视频监控图像模糊梯度场模型，表达式为：

$ T\left( {x,y} \right) = \eta \left( {{{\hat \chi }_e}} \right) * \varGamma \left( {x,y} \right)。$

(7)

式中，T(x,y)为放大处理后的图像模糊梯度场。

以此为基础，构造泛函公式，表达式为：

$ \Upsilon \left[ {\beta '\left( {x,y} \right)} \right] = \int {\int {{{\left| {\nabla \beta \left( {x,y} \right) - T\left( {x,y} \right)} \right|}^2}{\rm{d}}x{\rm{d}}y} }。$

(8)

式中： $ \Upsilon \left[ {\beta '\left( {x,y} \right)} \right] $ 为泛函公式； $\ \beta '\left( {x,y} \right) $ 为修正隶属度函数。

应用变分法对式(8)进行求解，当泛函 $ \Upsilon \left[ {\beta '\left( {x,y} \right)} \right] $ 取值最小时，对式(8)进行变分处理，通过化简得到Euler-Lagrange方程，基于梯度下降法对Euler-Lagrange方程进行循环迭代运算，当局部极小值出现时停止迭代，输出结果即为修正隶属度函数 $\ \beta '\left( {x,y} \right) $ ，通过逆变换将视频监控图像从模糊域转换到灰度域，从而获得细节增强后的视频监控图像g(x,y)，为海上、船舶情况实时监控提供帮助。

2 仿真实验 2.1 实验准备

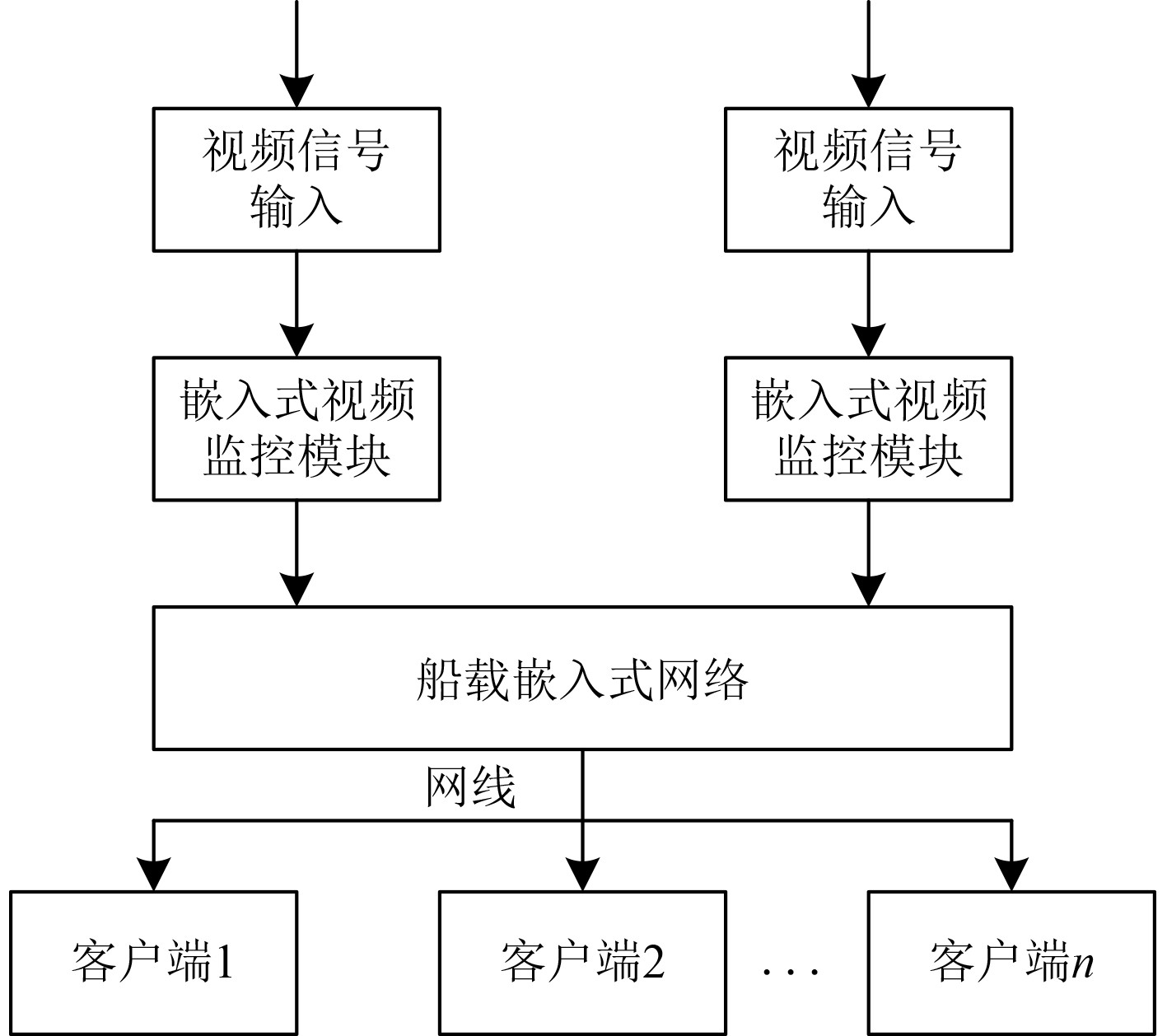
为了验证设计系统的应用性能，选取某船载嵌入式网络为实验对象，内部结构如图3所示。船载嵌入式网络会连接多个客户端——船舶、岸上基站或者监测设备等，会获取限定范围海域的视频监控图像，将其作为实验数据。

在视频监控图像获取过程中，由于各种因素(设备振动、海上环境等)的影响，使得视频监控图像中包含大量的噪声，并且存在着图像轮廓不清晰的现象，若是直接将其作为实验数据，会降低实验结论的精度。因此，在实验进行之前，对实验数据−视频监控图像进行预处理。首先，应用中值滤波去除视频监控图像中的噪声，表达式为：

$ G\left( {i,j} \right) = {\rm{Med}}\left\{ {F\left( {i + s,j + t} \right),\left( {s,t} \right) \in M\left( {i,j} \right)} \right\}。$

(9)

式中： $ F\left( {i,j} \right) $ 与 $ G\left( {i,j} \right) $ 为含噪与无噪视频监控图像； $ {\rm{Med}}\left\{ \cdot \right\} $ 为中值滤波函数； $ M\left( {i,j} \right) $ 为滤波窗口， $ \left( {s,t} \right) $ 为 $ M\left( {i,j} \right) $ 的子集。

其次，应用拉普拉斯算子锐化处理视频监控图像，表达式为：

$ D\left( {i,j} \right) = G\left( {i,j} \right) - {\mu ^o}{\nabla ^2}G\left( {i,j} \right)。$

(10)

式中：D(i,j)是锐化处理后的视频监控图像； $ {\mu ^o} $ 为锐化系数。一般情况下，锐化系数 $ {\ \mu ^o} $ 越大，视频监控图像锐化效果越好；反之，锐化系数 $ {\ \mu ^o} $ 越小，视频监控图像锐化效果越差。

2.2 实验结果分析

以实验准备内容为依据，进行视频监控图像模糊细节增强实验。以某一幅视频监控图像为例，基于设计系统对其进行处理，获得视频监控图像模糊细节增强结果如图4所示。

可知，应用设计系统后，原始视频监控图像中未显示的细节信息得到了增强与恢复，充分证实了设计系统的可行性。

3 结　语

视频监控是船舶航行过程中的关键保障手段，不但能够对船舱内部、外部环境进行监测，也能通过网络获取整个海域情况，实时为船舶航行提供图像数据支撑。但是，由于海上环境多变，监控设备自身缺陷等多种因素的影响，致使视频监控图像存在着细节缺失、模糊等现象，威胁着船舶的航行安全，故提出船载嵌入式网络视频监控图像模糊细节增强系统设计。实验数据显示：设计系统大幅度提升了增强图像的信息熵数值，能获取具备更对细节信息的视频监控图像，为船舶航行决策制定提供精准依据，也为图像增强相关研究提供一定的借鉴作用。